Low-Rank Matrix Recovery from Noise via an MDL Framework-Based Atomic Norm
Abstract
1. Introduction
- (1)
- We present an MDL principle-based atomic norm method for low-rank matrix recovery. Unlike other model selection algorithms, the proposed MDLAN uses the description length as a cost function to select the two smallest sets of atoms that can span the low-rank matrix and sparse matrix, respectively.
- (2)
- We empirically test the MDL framework-based atomic norm and find that it outperforms the state-of-the-art methods when the number of observations is limited or if the observations have gross outliers.
- (3)
- It is difficult to address the original optimization problem for MDLAN due to the combination of description length and the atomic norm. Thus, we devise a new alternating direction method of multipliers (ADMM)-based algorithm that considers an approximation of the original non-convex problem.
2. Related Works
3. An MDL Principle-Based Atomic Norm for Low-Rank Matrix Recovery
3.1. Atomic Norm
3.2. Atomic Norm-Based Low-Rank Matrix Recovery
3.3. Minimum Description Length Principle
3.4. The Proposed Method
3.5. Optimization by ADMM
| Algorithm 1 ADMM [13,47] for the MDLAN method. |
Input: Observation .
|
3.5.1. Recovering the Low-Rank Matrix
3.5.2. Rejecting the Sparse Outliers
3.6. Discussion
4. Experiments
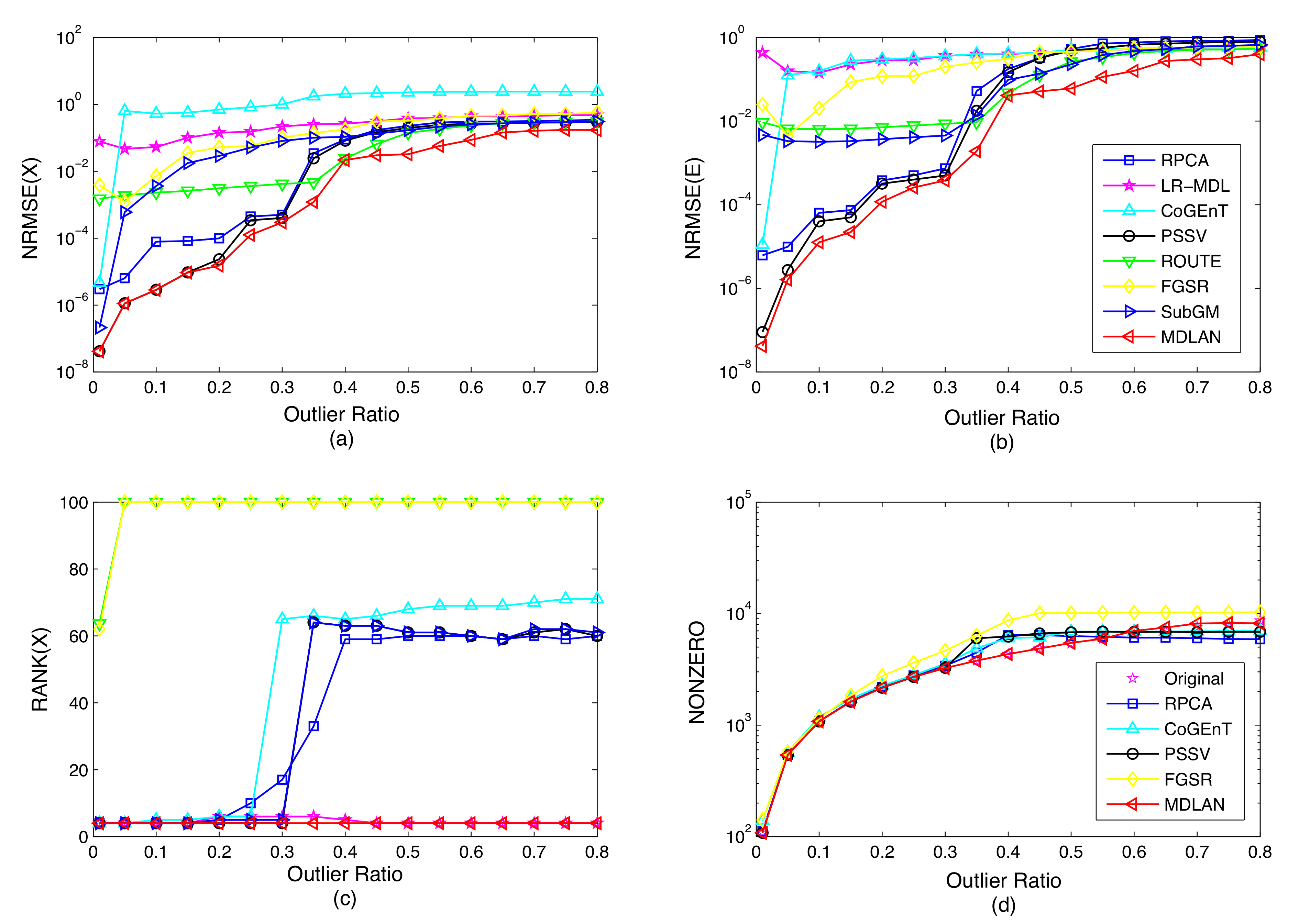
4.1. Experiments with Synthetic Data
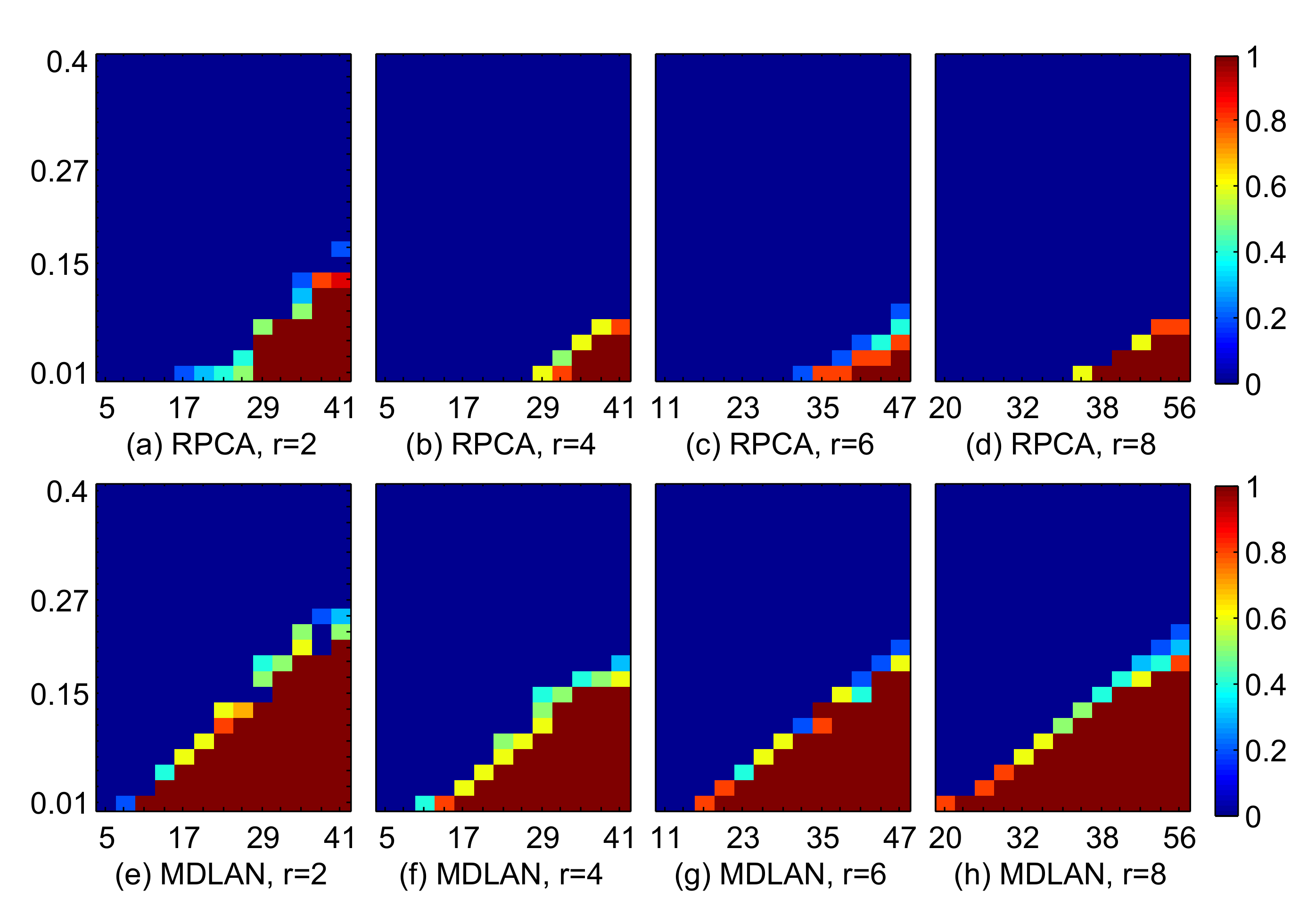
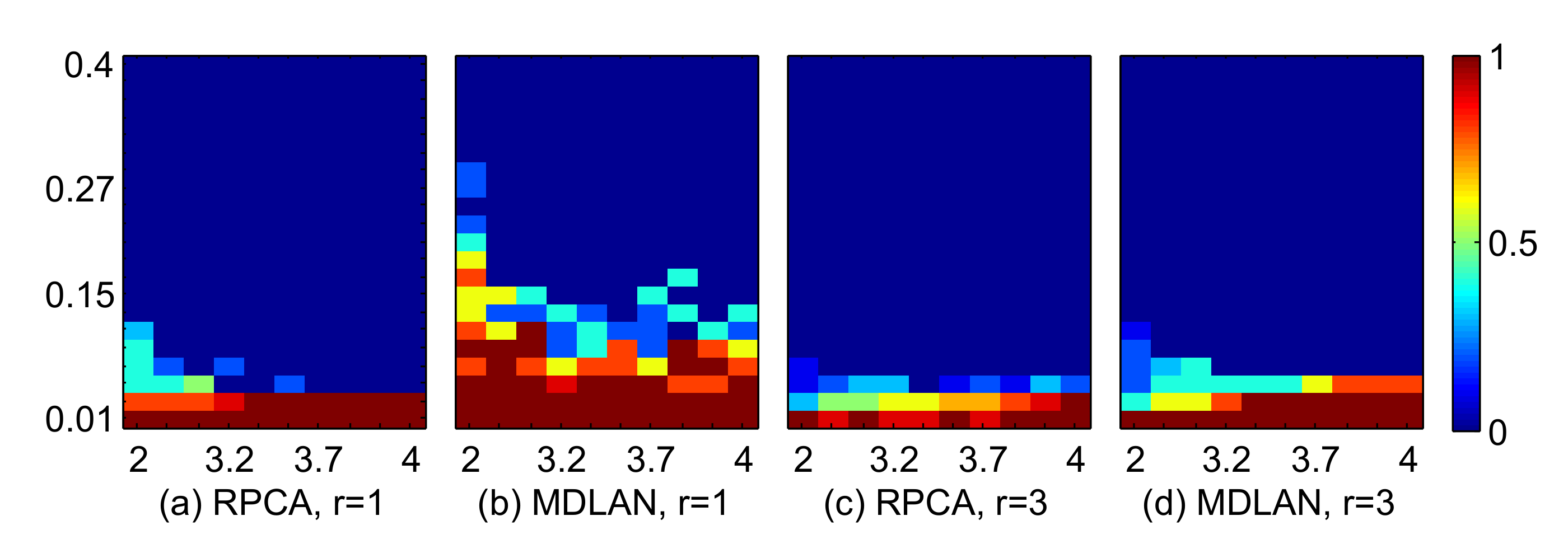
4.1.1. Comparison of the Success Ratio
4.1.2. Comparisons with Other Low-Rank Ratrix Approximations
4.2. Real-World Sensing Applications
4.2.1. High Dynamic Range (HDR) Imaging
4.2.2. Background Modeling Based on Video Sensor
4.2.3. Removing Noise and Shadows From Faces
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
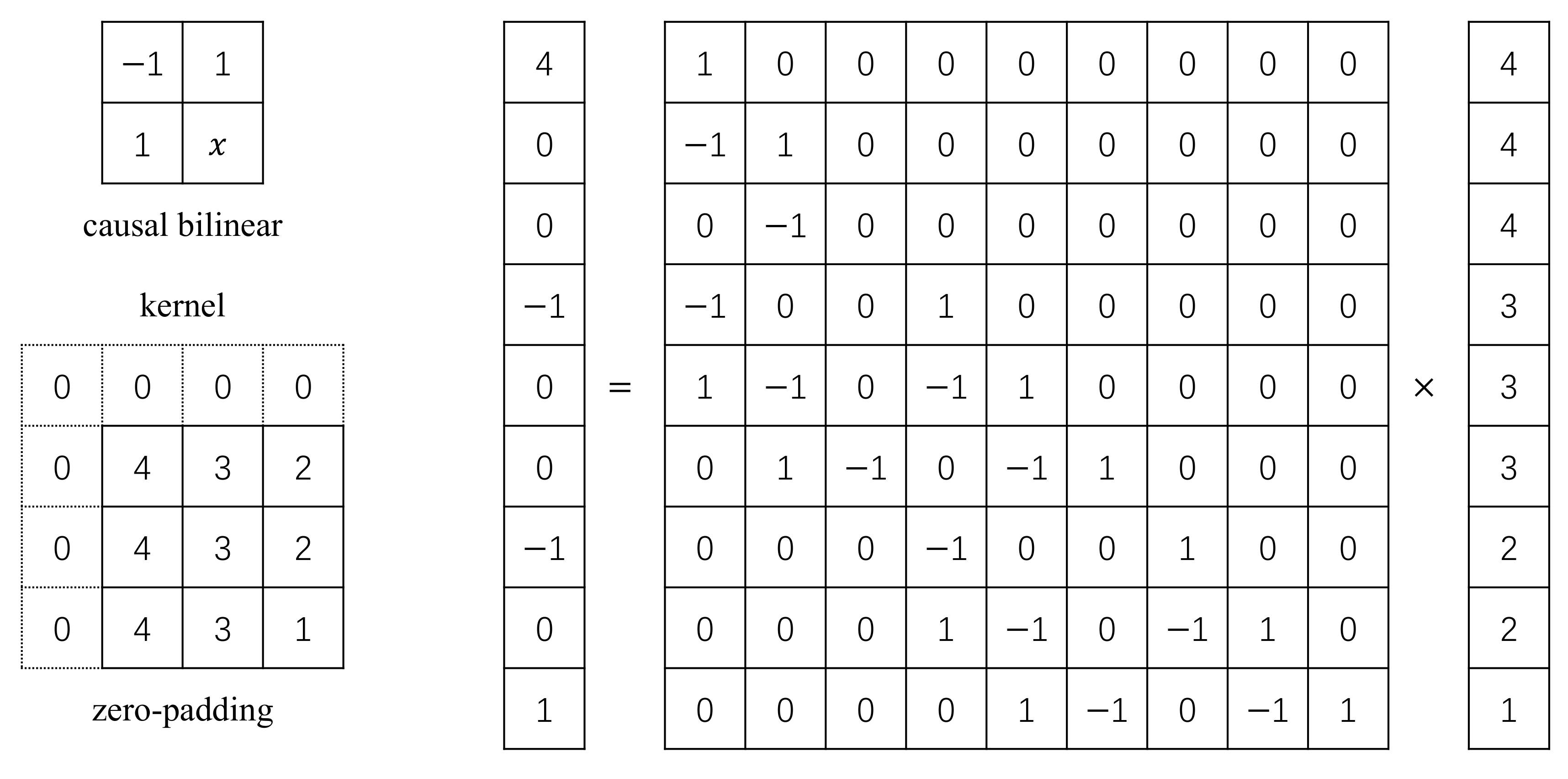
Appendix A. Encoding Scheme
Appendix A.1. Encoding the Sparse Matrix
Appendix A.2. Encoding the Low-Rank Matrix
References
- Zhao, Q.; Meng, D.; Xu, Z.; Zuo, W.; Zhang, L. Robust Principal Component Analysis with Complex Noise. In Proceedings of the 31st International Conference on Machine Learning (ICML 2014), Beijing, China, 21–26 June 2014. [Google Scholar]
- Oh, T.H.; Tai, Y.W.; Bazin, J.C.; Kim, H.; Kweon, I.S. Partial Sum Minimization of Singular Values in Robust PCA: Algorithm and Applications. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 744–758. [Google Scholar] [CrossRef] [PubMed]
- Xia, G.; Sun, H.; Chen, B.; Liu, Q.; Hang, R. Nonlinear Low-Rank Matrix Completion for Human Motion Recovery. IEEE Trans. Image Process. 2018, 27, 3011–3024. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, L.; Gao, S.; Tang, J.; Wang, J.; Lin, Z.; Ma, Y.; Yu, N. Constructing a Nonnegative Low-Rank and Sparse Graph With Data-Adaptive Features. IEEE Trans. Image Process. 2015, 24, 3717–3728. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Gong, C.; Qian, J.; Zhang, B.; Xu, C.; Yang, J. Efficient Recovery of Low-Rank Matrix via Double Nonconvex Nonsmooth Rank Minimization. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2916–2925. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Qian, J.; Zhang, B.; Yang, J.; Gong, C.; Wei, Y. Low-Rank Matrix Recovery via Modified Schatten-p Norm Minimization With Convergence Guarantees. IEEE Trans. Image Process. 2020, 29, 3132–3142. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zhou, J.; Ye, J. Integrating low-rank and group-sparse structures for robust multi-task learning. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD 2011), San Diego, CA, USA, 21–24 August 2011. [Google Scholar]
- Chen, W. Simultaneously Sparse and Low-Rank Matrix Reconstruction via Nonconvex and Nonseparable Regularization. IEEE Trans. Signal Process. 2018, 66, 5313–5323. [Google Scholar] [CrossRef]
- Xie, X.; Wu, J.; Liu, G.; Wang, J. Matrix Recovery with Implicitly Low-Rank Data. Neurocomputing 2019, 334, 219–226. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis; Springer: Berlin/Heidelberg, Germany, 1986; Volume 14, pp. 231–246. [Google Scholar]
- Ganesh, A.; Ma, Y.; Rao, S.; Wright, J. Robust Principal Component Analysis: Exact Recovery of Corrupted Low-Rank Matrices via Convex Optimization. Adv. Neural Inf. Process. Syst. 2009, 87, 2080–2088. [Google Scholar]
- Candes, S.E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis. J. ACM 2011, 58, 1–73. [Google Scholar] [CrossRef]
- Chen, M.; Lin, Z.; Ma, Y.; Wu, L. The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-Rank Matrices. Available online: https://people.eecs.berkeley.edu/~yima/psfile/Lin09-MP.pdf (accessed on 25 October 2020).
- Wright, J. Low-Rank Matrix Recovery and Completion via Convex Optimization. Available online: http://perception.csl.illinois.edu/matrix-rank/home.html (accessed on 25 October 2020).
- Ramirez, I.; Sapiro, G. Low-rank data modeling via the minimum description length principle. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Prague, Czech Republic, 22–27 May 2011. [Google Scholar]
- Bouwmans, T.; Zahzah, E.H. Robust PCA via Principal Component Pursuit: A review for a comparative evaluation in video surveillance. Comput. Vis. Image Underst. 2014, 122, 22–34. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, G.; Yao, J.; Qi, C. Background subtraction based on low-rank and structured sparse decomposition. IEEE Trans. Image Process. 2015, 24, 2502–2514. [Google Scholar] [CrossRef] [PubMed]
- Gallo, O.; Gelfandz, N. Artifact-free High Dynamic Range Imaging. In Proceedings of the 2009 IEEE International Conference on Computational Photography (ICCP), San Francisco, CA, USA, 16–17 April 2009. [Google Scholar]
- Celebi, A.T.; Duvar, R.; Urhan, O. Fuzzy fusion based high dynamic range imaging using adaptive histogram separation. IEEE Trans. Consum. Electron. 2015, 61, 119–127. [Google Scholar] [CrossRef]
- Mariani, A.; Giorgetti, A.; Chiani, M. Model Order Selection Based on Information Theoretic Criteria: Design of the Penalty. IEEE Trans. Signal Process. 2015, 63, 2779–2789. [Google Scholar] [CrossRef]
- Ding, J.; Tarokh, V.; Yang, Y. Model Selection Techniques: An Overview. IEEE Signal Process. Mag. 2018, 35, 16–34. [Google Scholar] [CrossRef]
- Ramirez, I.; Sapiro, G. An MDL Framework for Sparse Coding and Dictionary Learning. IEEE Trans. Signal Process. 2011, 60, 2913–2927. [Google Scholar] [CrossRef]
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–471. [Google Scholar] [CrossRef]
- Chandrasekaran, V.; Recht, B.; Parrilo, P.A.; Willsky, A.S. The Convex Geometry of Linear Inverse Problems. Found. Comput. Math. 2012, 12, 805–849. [Google Scholar] [CrossRef]
- Rao, N.; Shah, P.; Wright, S. Forward-Backward Greedy Algorithms for Atomic Norm Regularization. IEEE Trans. Signal Process. 2014, 63, 5798–5811. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, Y.Y.; Li, L. Minimum Error Entropy Based Sparse Representation for Robust Subspace Clustering. IEEE Trans. Signal Process. 2015, 63, 4010–4021. [Google Scholar] [CrossRef]
- Qin, A.; Shang, Z.; Zhang, T.; Ding, Y.; Tang, Y.Y. Minimum Description Length Principle Based Atomic Norm for Synthetic Low-Rank Matrix Recovery. In Proceedings of the 2016 7th International Conference on Cloud Computing and Big Data (CCBD), Macau, China, 16–18 November 2016. [Google Scholar]
- Zhou, X.; Yang, C.; Yu, W. Moving object detection by detecting contiguous outliers in the low-rank representation. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 597–610. [Google Scholar] [CrossRef]
- Xu, J.; Ithapu, V.K.; Mukherjee, L.; Rehg, J.M.; Singh, V. GOSUS: Grassmannian online subspace updates with structured-sparsity. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013. [Google Scholar]
- Xin, B.; Tian, Y.; Wang, Y.; Gao, W. Background subtraction via generalized fused lasso foreground modeling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Xin, B.; Kawahara, Y.; Wang, Y.; Gao, W. Efficient generalized fused lasso and its application to the diagnosis of Alzheimer’s disease. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, Québec City, QC, Canada, 27–31 July 2014. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Physics D 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Erfanian, S.; Ebadi; Izquierdo, E. Foreground Segmentation with Tree-Structured Sparse RPCA. IEEE TTrans. Pattern Anal. Mach. Intell. 2018, 40, 2273–2280. [Google Scholar]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC superpixels compared to state-of-the-art superpixel methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [PubMed]
- Shah, S.; Goldstein, T.; Studer, C. Estimating sparse signals with smooth support via convex programming and block sparsity. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Zha, Z.; Liu, X.; Huang, X.; Shi, H.; Xu, Y.; Wang, Q.; Tang, L.; Zhang, X. Analyzing the group sparsity based on the rank minimization methods. In Proceedings of the IEEE International Conference on Multimedia and Expo (ICME), Hong Kong, China, 10–14 July 2017. [Google Scholar]
- Cabral, R.; Torre, F.D.L.; Costeira, J.P.; Bernardino, A. Unifying Nuclear Norm and Bilinear Factorization Approaches for Low-Rank Matrix Decomposition. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013. [Google Scholar]
- Guo, X.; Lin, Z.; Center, C.M.I. ROUTE: Robust Outlier Estimation for Low Rank Matrix Recovery. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017. [Google Scholar]
- Guo, X.; Lin, Z. Low-rank matrix recovery via robust outlier estimation. IEEE Trans. Image Process. 2018, 27, 5316–5327. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Zhang, D.; Ye, J.; Li, X.; He, X. Fast and Accurate Matrix Completion via Truncated Nuclear Norm Regularization. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2117–2130. [Google Scholar] [CrossRef]
- Guo, X.; Zhao, R.; An, G.; Cen, Y. An algorithm of face alignment and recognition by sparse and low rank decomposition. In Proceedings of the 2014 12th International Conference on Signal Processing (ICSP), Hangzhou, China, 19–23 October 2014. [Google Scholar]
- Oh, T.H.; Lee, J.Y.; Tai, Y.W.; Kweon, I.S. Robust High Dynamic Range Imaging by Rank Minimization. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1219–1232. [Google Scholar] [CrossRef]
- Peng, Y.; Suo, J.; Dai, Q.; Xu, W. Reweighted low-rank matrix recovery and its application in image restoration. IEEE Trans. Cybern. 2014, 44, 2418–2430. [Google Scholar] [CrossRef]
- Huang, C.; Ding, X.; Fang, C.; Wen, D. Robust Image Restoration Via Adaptive Low-Rank Approximation and Joint Kernel Regression. IEEE Trans. Image Process. 2014, 23, 5284–5297. [Google Scholar] [CrossRef]
- Gao, P.; Wang, R.; Meng, C.; Joe, H. Low-Rank Matrix Recovery From Noisy, Quantized, and Erroneous Measurements. IEEE Trans. Signal Process. 2018, 66, 2918–2932. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley: New York, NY, USA, 2005; Volume 1, pp. 1–748. [Google Scholar]
- Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Available online: https://web.stanford.edu/~boyd/papers/pdf/admm_distr_stats.pdf (accessed on 25 October 2020).
- Candès, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing Sparsity by Reweighted l1 Minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Hale, E.T.; Yin, W.; Zhang, Y. Fixed-Point Continuation for ℓ1-Minimization: Methodology and Convergence. Siam J. Optim. 2008, 19, 1107–1130. [Google Scholar] [CrossRef]
- Fan, J.; Ding, L.; Chen, Y.; Udell, M. Factor group-sparse regularization for efficient low-rank matrix recovery. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Li, X.; Zhu, Z.; Man-Cho So, A.; Vidal, R. Nonconvex robust low-rank matrix recovery. Siam J. Optim. 2020, 30, 660–686. [Google Scholar] [CrossRef]
- Davis, J.; Goadrich, M. The relationship between Precision-Recall and ROC curves. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006. [Google Scholar]
- Li, L.; Huang, W.; Gu, Y.H.; Tian, Q. Statistical Modeling of Complex Backgrounds for Foreground Object Detection. IEEE Trans. Image Process. 2004, 13, 1459–1472. [Google Scholar] [CrossRef] [PubMed]
- Basri, R.; Jacobs, D. Lambertian Reflectance and Linear Subspaces. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 218–233. [Google Scholar] [CrossRef]
- Georghiades, A.S.; Belhumeur, P.N.; Kriegman, D.J. From few to many: Illumination cone models for face recognition under variable lighting and pose. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 23, 643–660. [Google Scholar] [CrossRef]









| 0.05 | 0.5 | |||
|---|---|---|---|---|
| Low-Rank | Sparse | Low-Rank | Sparse | |
| RPCA | 0.000007 ± 0.0 | 0.00001 ± 0.0 | 0.25 ± 0.005 | 0.591 ± 0.014 |
| LR-MDL | 0.061 ± 0.024 | 0.200 ± 0.072 | 0.379 ± 0.034 | 0.490 ± 0.024 |
| CoGEnT | 0.082 ± 0.032 | 1.218 ± 0.082 | 1.604 ± 0.585 | 1.541 ± 0.144 |
| BSGFL | 0.030 ± 0.004 | 0.275 ± 0.063 | 0.351 ± 0.026 | 10.04 ± 1.423 |
| PSSV | 0.000002 ± 0.0 | 0.00002 ± 0.0 | 0.207 ± 0.002 | 0.486 ± 0.005 |
| ROUTE | 0.002 ± 0.0001 | 0.007 ± 0.0001 | 0.141 ± 0.009 | 0.264 ± 0.015 |
| FGSR | 0.001 ± 0.0001 | 0.004 ± 0.0001 | 0.324 ± 0.007 | 0.454 ± 0.008 |
| SubGM | 0.0006 ± 0.0 | 0.003 ± 0.0001 | 0.168 ± 0.039 | 0.227 ± 0.005 |
| MDLAN | 0.000002 ± 0.0 | 0.000003 ± 0.0 | 0.01 ± 0.007 | 0.019 ± 0.013 |
| Shopping Mall | HumanBody2 | MPEG | ||||
|---|---|---|---|---|---|---|
| F-Measure | Times (s) | F-Measure | Times (s) | F-Measure | Times (s) | |
| RPCA | 0.6975 | 585 | 0.6881 | 985 | 0.7437 | 4087 |
| LR-MDL | 0.5021 | 912 | 0.6294 | 106 | 0.7977 | 446 |
| CoGEnT | 0.6846 | 1534 | 0.0676 | 586 | 0.7735 | 6498 |
| BSGFL | 0.6406 | 11628 | 0.6806 | 2219 | 0.7987 | 14942 |
| PSSV | 0.7060 | 20.1 | 0.7377 | 37.1 | 0.7756 | 207 |
| ROUTE | 0.7181 | 62.4 | 0.7801 | 41.5 | 0.8110 | 340 |
| FGSR | 0.7175 | 61.8 | 0.7837 | 50.2 | 0.8141 | 304 |
| MDLAN | 0.7536 | 28.6 | 0.7941 | 40.7 | 0.8264 | 227 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, A.; Xian, L.; Yang, Y.; Zhang, T.; Tang, Y.Y. Low-Rank Matrix Recovery from Noise via an MDL Framework-Based Atomic Norm. Sensors 2020, 20, 6111. https://doi.org/10.3390/s20216111
Qin A, Xian L, Yang Y, Zhang T, Tang YY. Low-Rank Matrix Recovery from Noise via an MDL Framework-Based Atomic Norm. Sensors. 2020; 20(21):6111. https://doi.org/10.3390/s20216111
Chicago/Turabian StyleQin, Anyong, Lina Xian, Yongliang Yang, Taiping Zhang, and Yuan Yan Tang. 2020. "Low-Rank Matrix Recovery from Noise via an MDL Framework-Based Atomic Norm" Sensors 20, no. 21: 6111. https://doi.org/10.3390/s20216111
APA StyleQin, A., Xian, L., Yang, Y., Zhang, T., & Tang, Y. Y. (2020). Low-Rank Matrix Recovery from Noise via an MDL Framework-Based Atomic Norm. Sensors, 20(21), 6111. https://doi.org/10.3390/s20216111





