Electrical Resistance Tomography for Control Applications: Quantitative Study of the Gas-Liquid Distribution inside A Cyclone
Abstract
1. Introduction
2. Materials and Methods
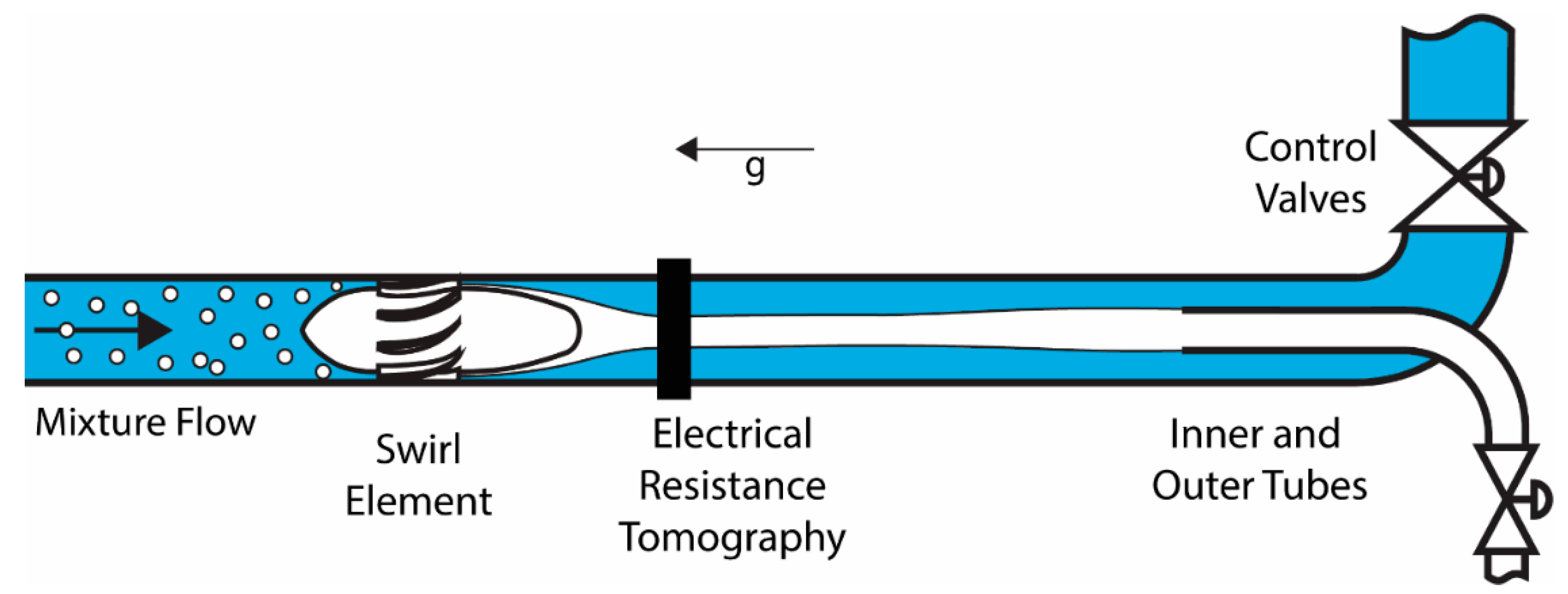
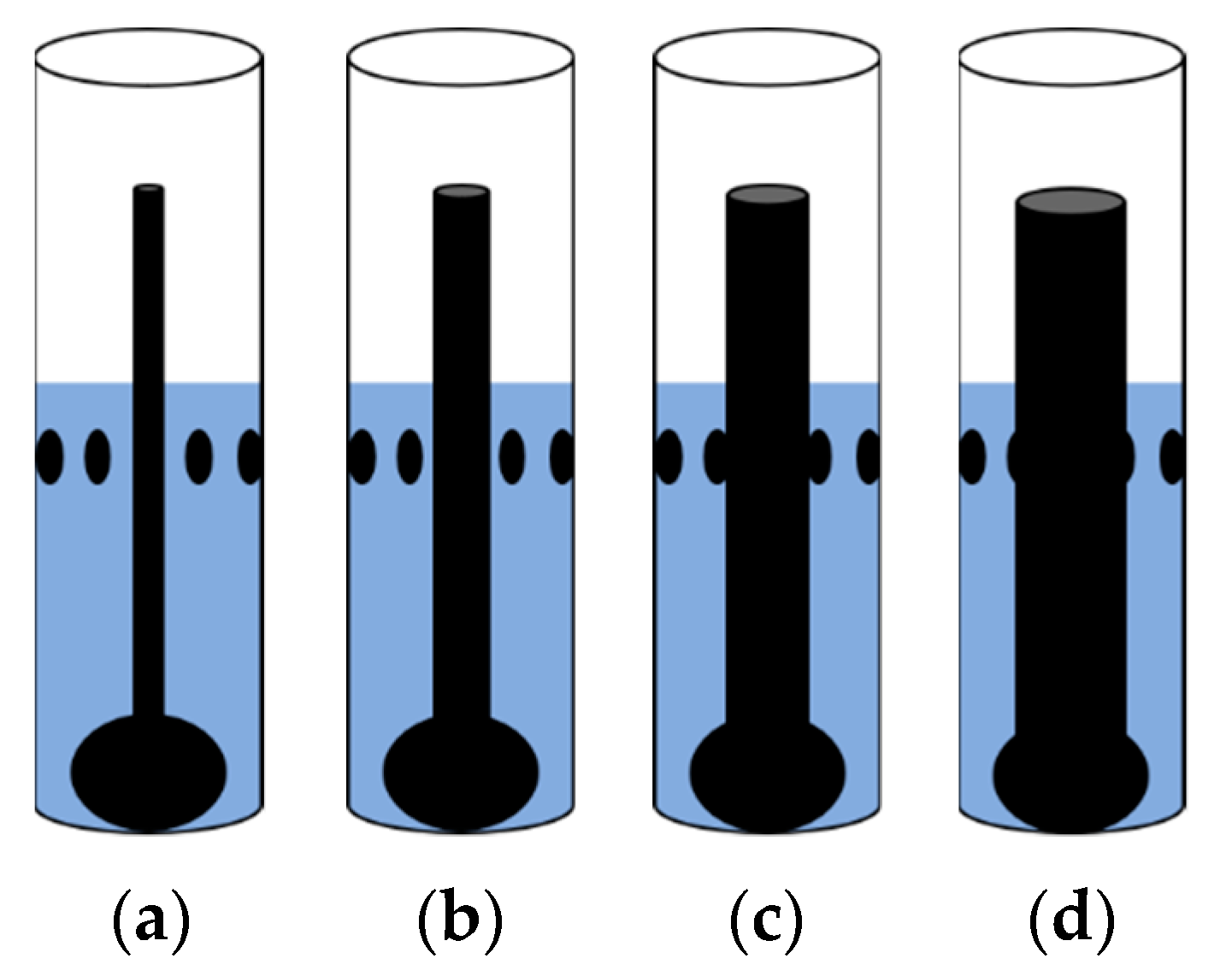
2.1. Flow Test Facility and Phantoms
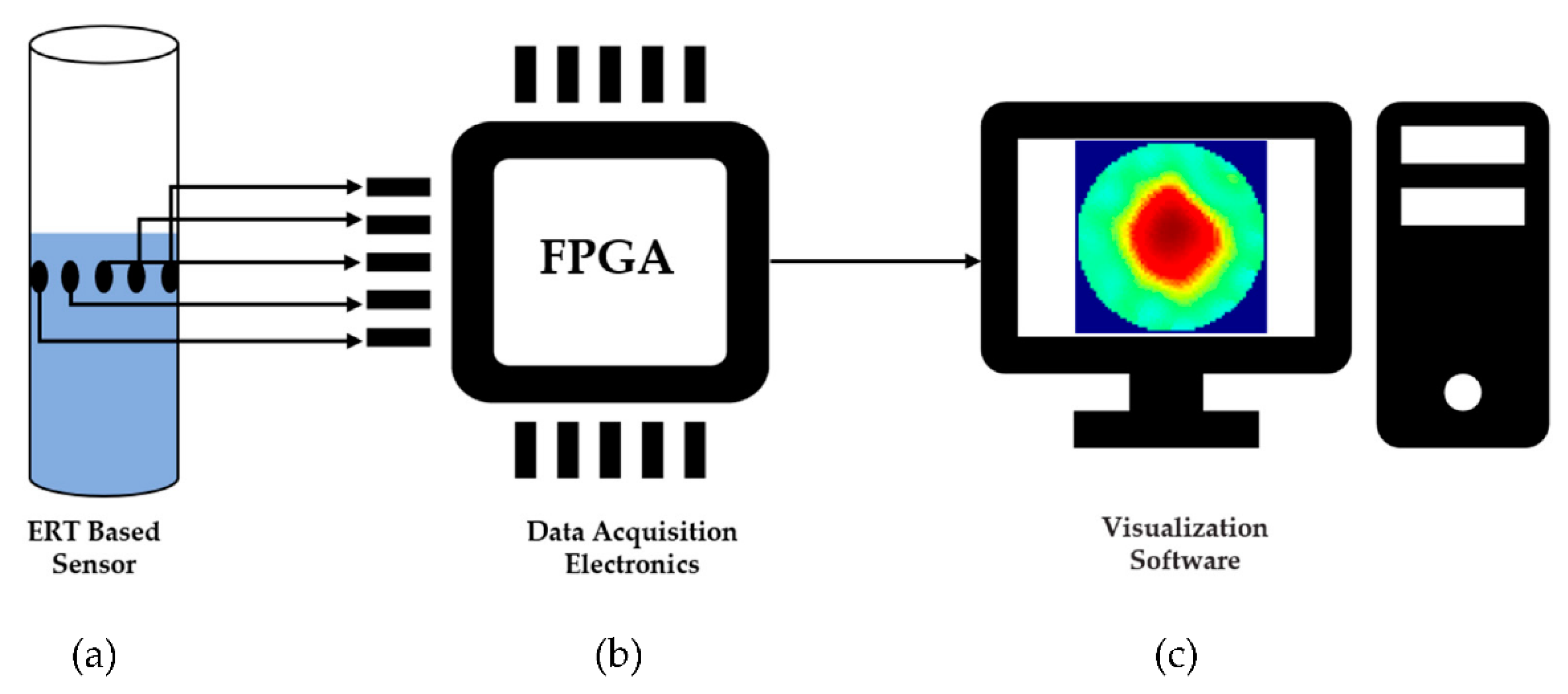
2.2. ERT Sensor snd Measurement Protocol
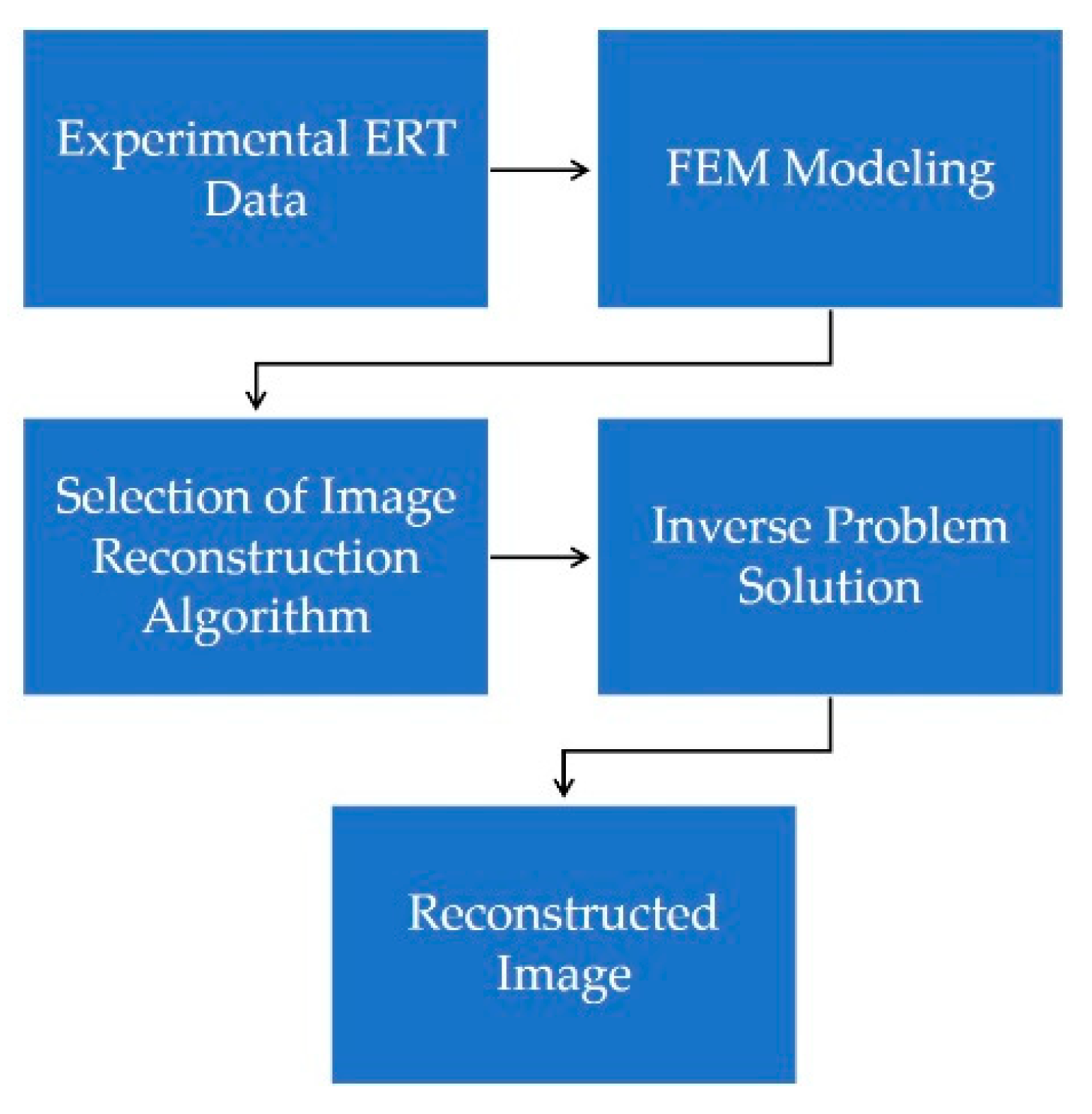
2.3. Image Reconstruction Algorithms
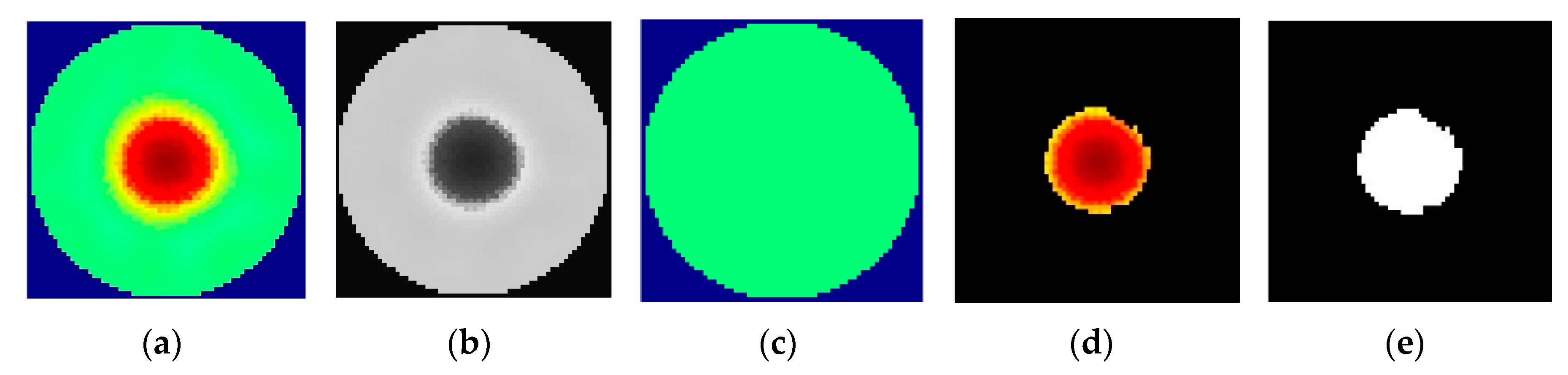
2.4. Image Processing
2.4.1. ERT Image Handling
- Averaging the grayscale images.
- Image segmentation of the images
2.4.2. Fast Camera Image Processing
Pre-Processing Routine
Gas Core Calculations
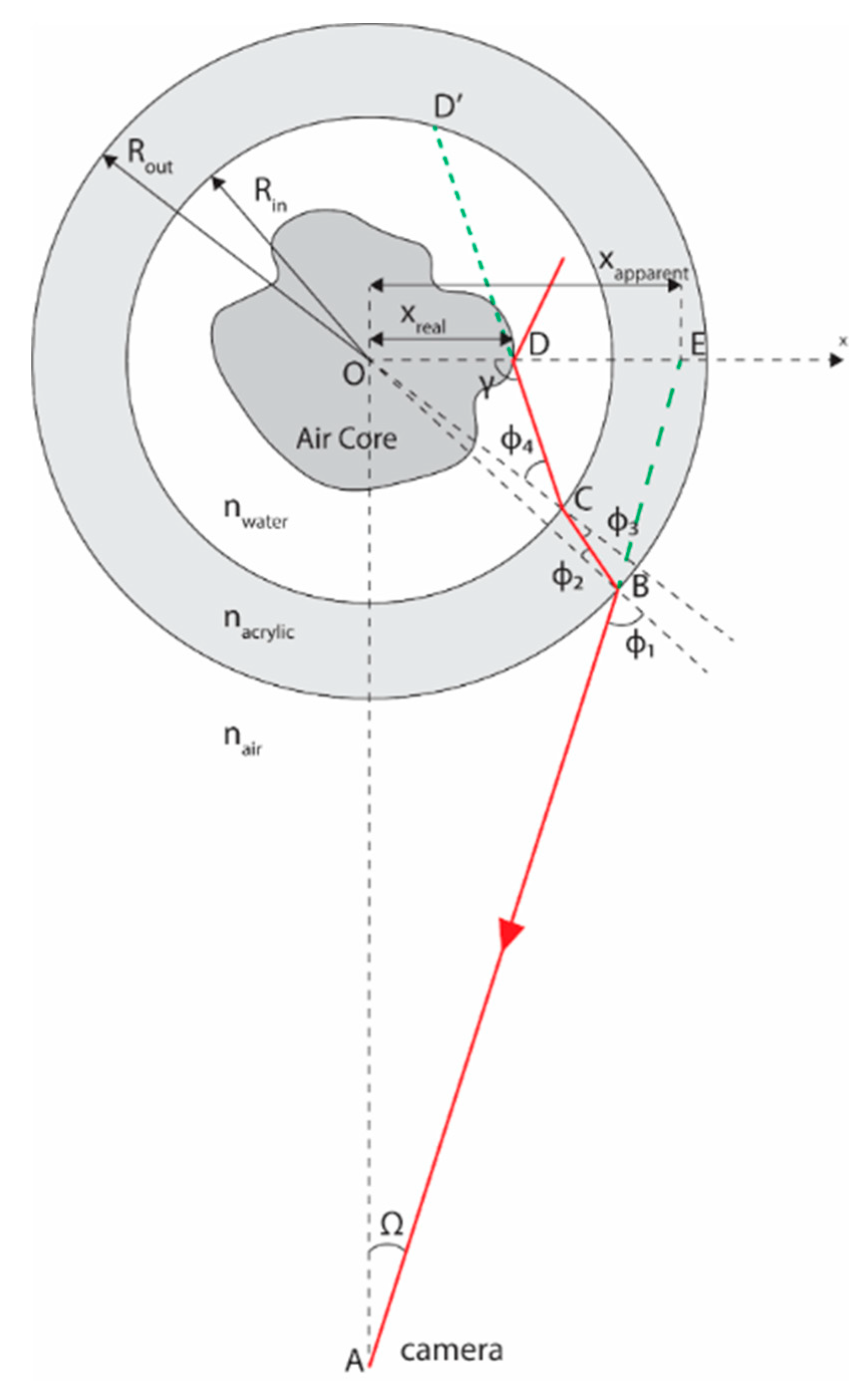
Refraction Correction
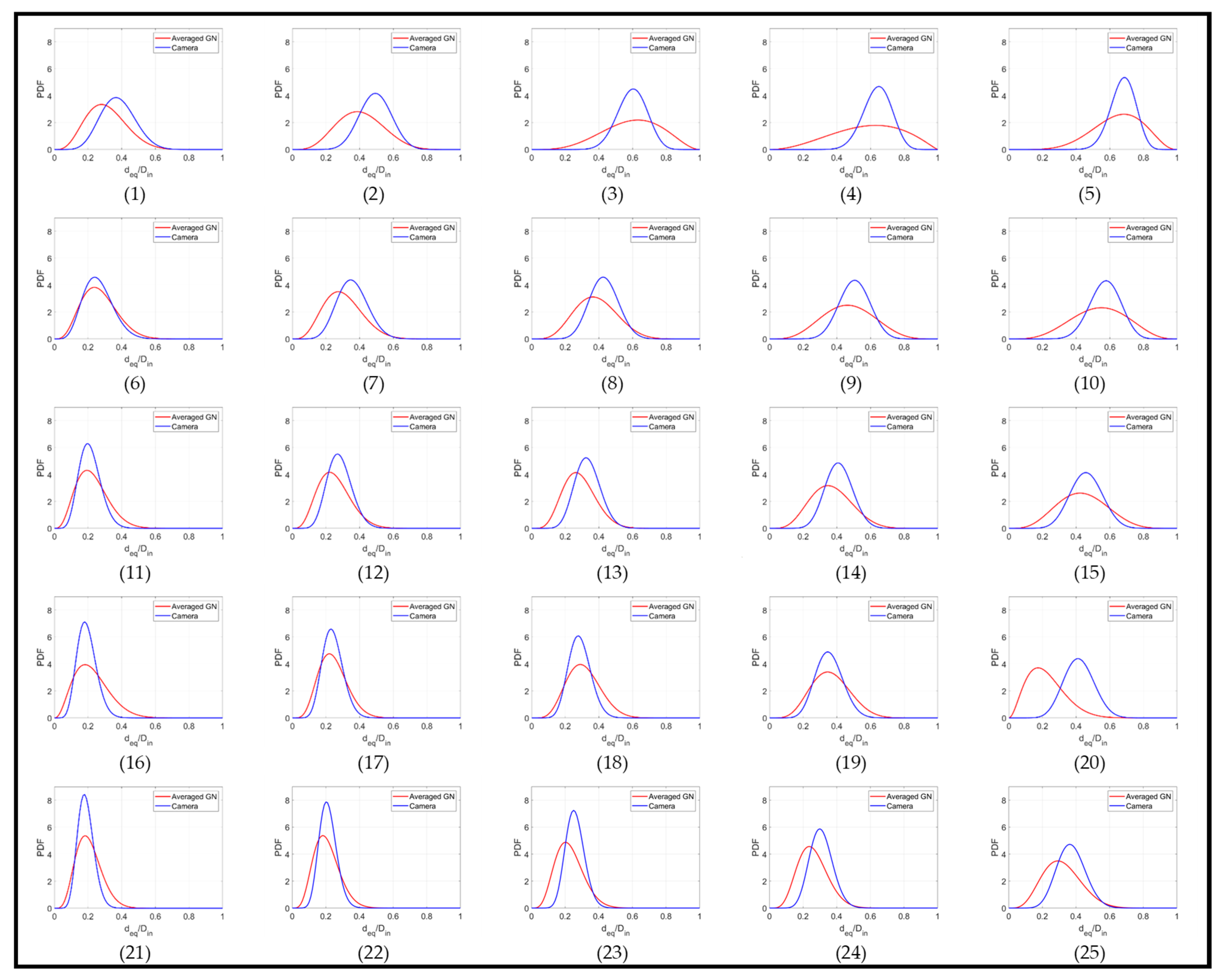
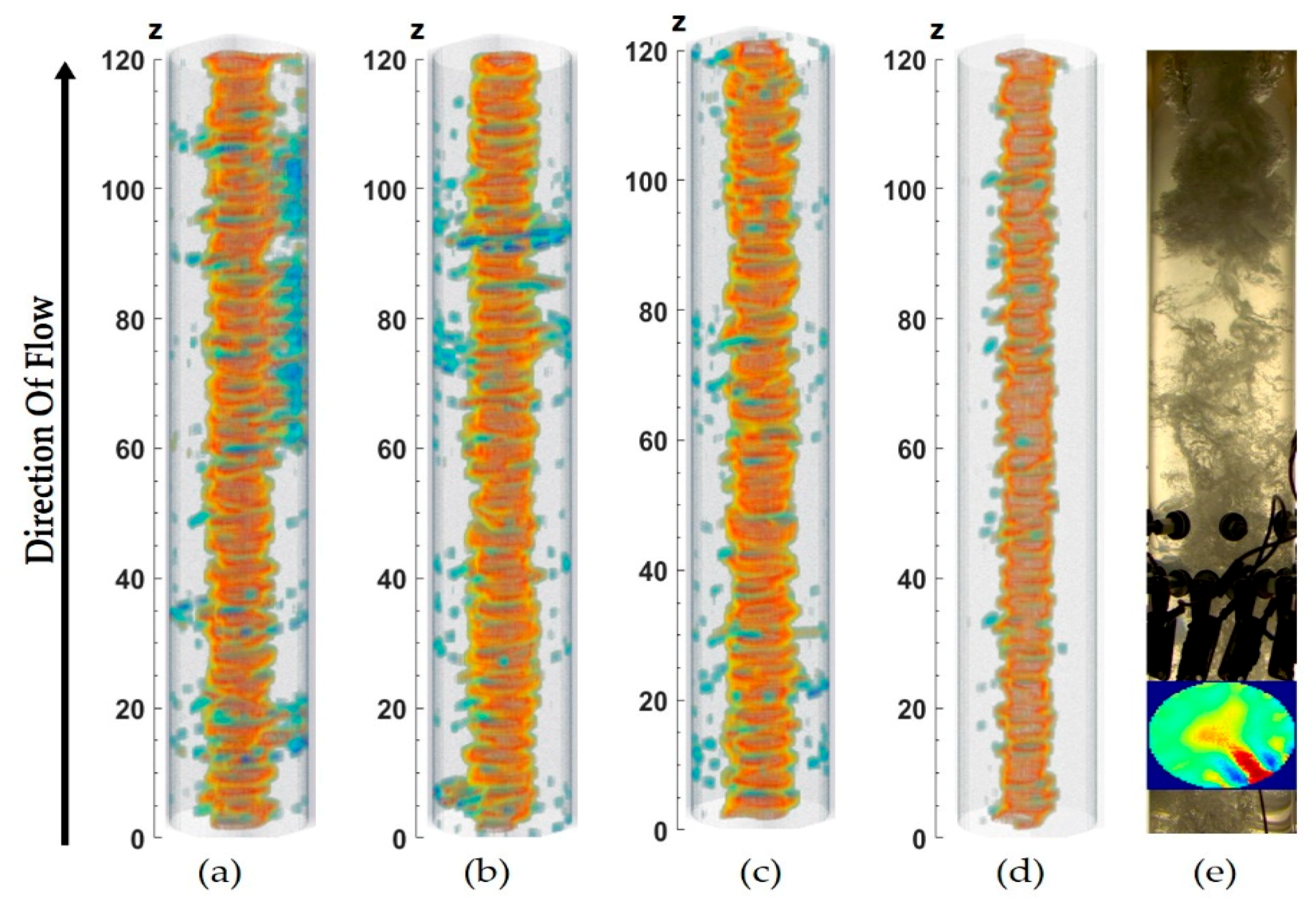
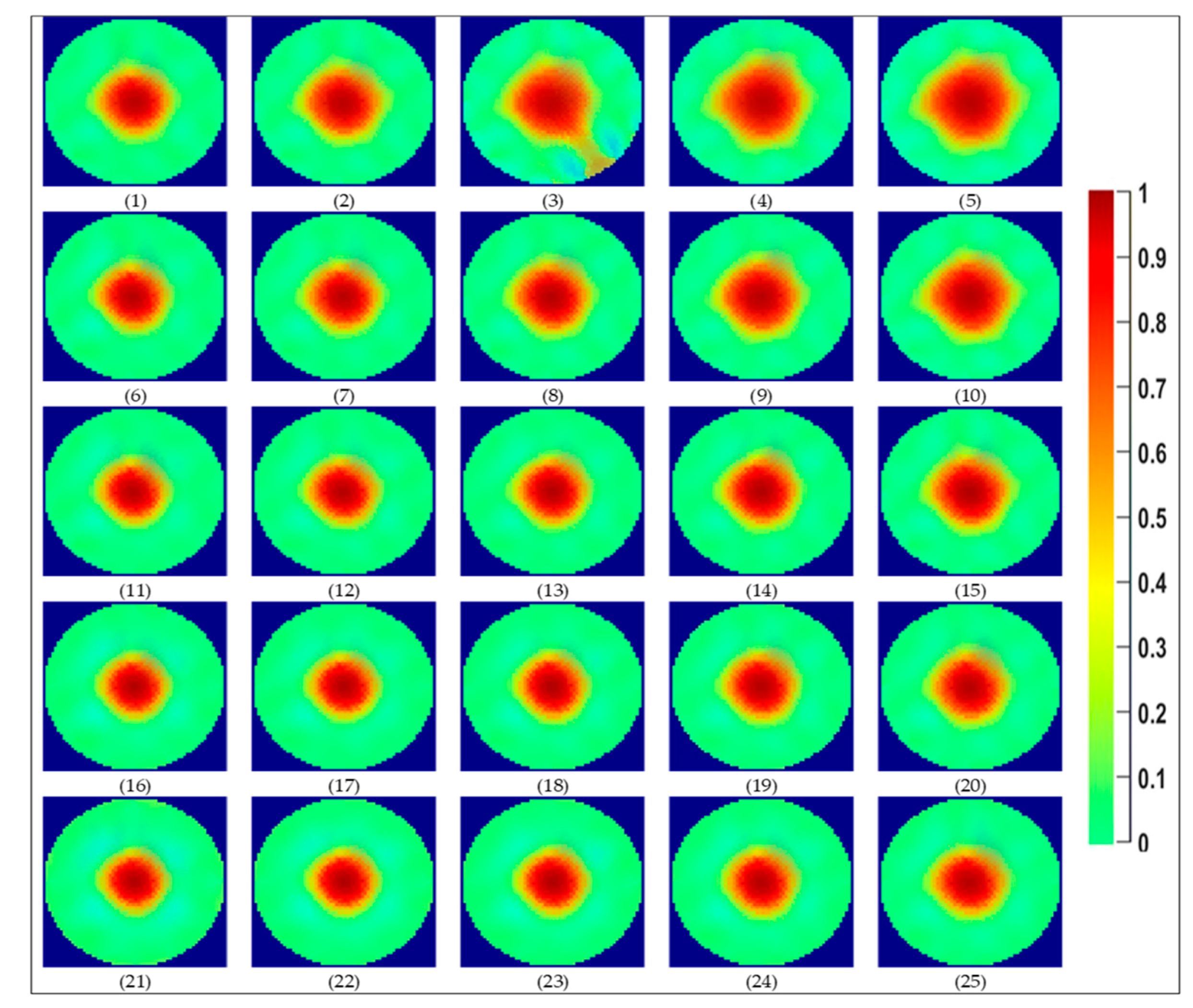
3. Results
3.1. Static Measurements
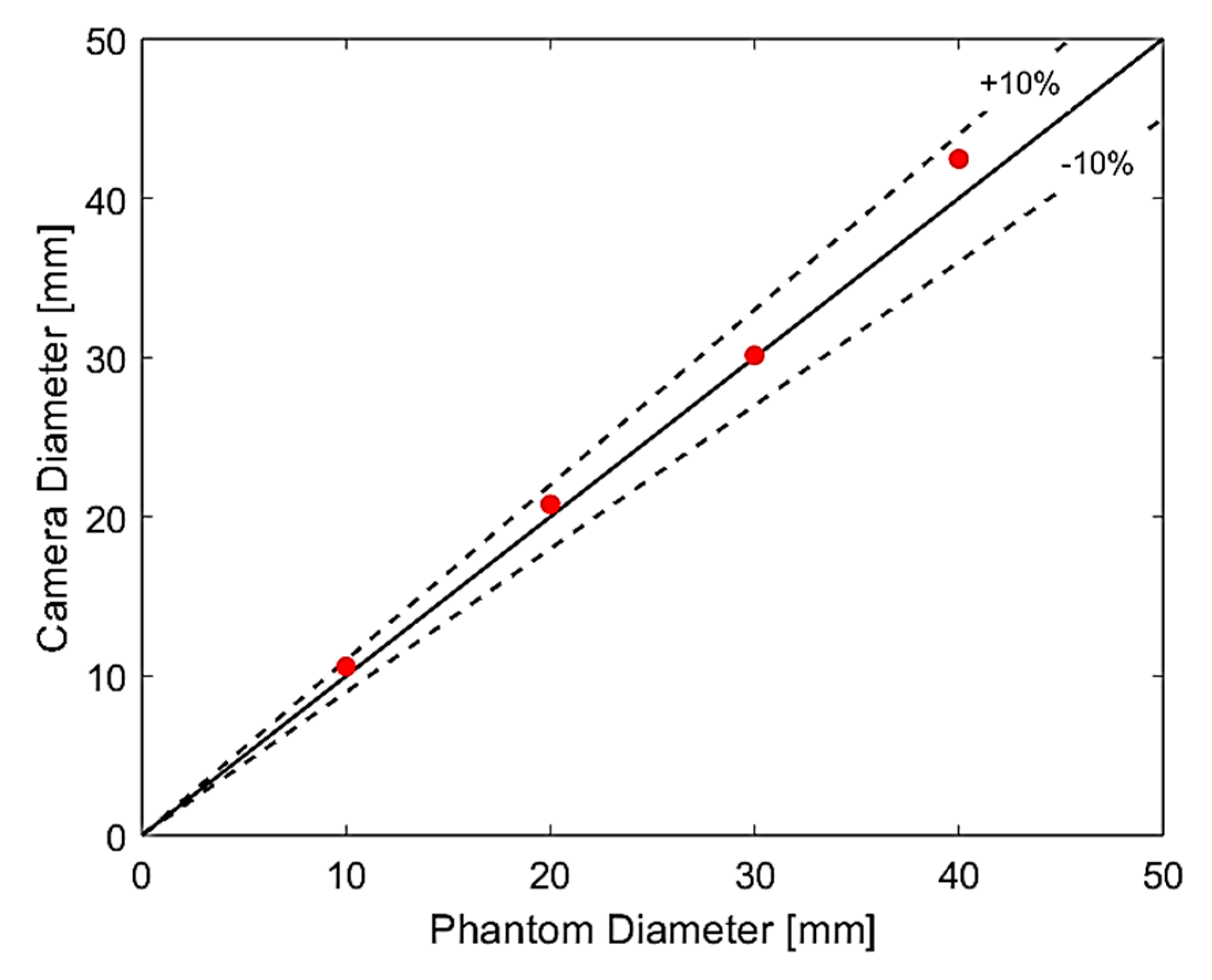
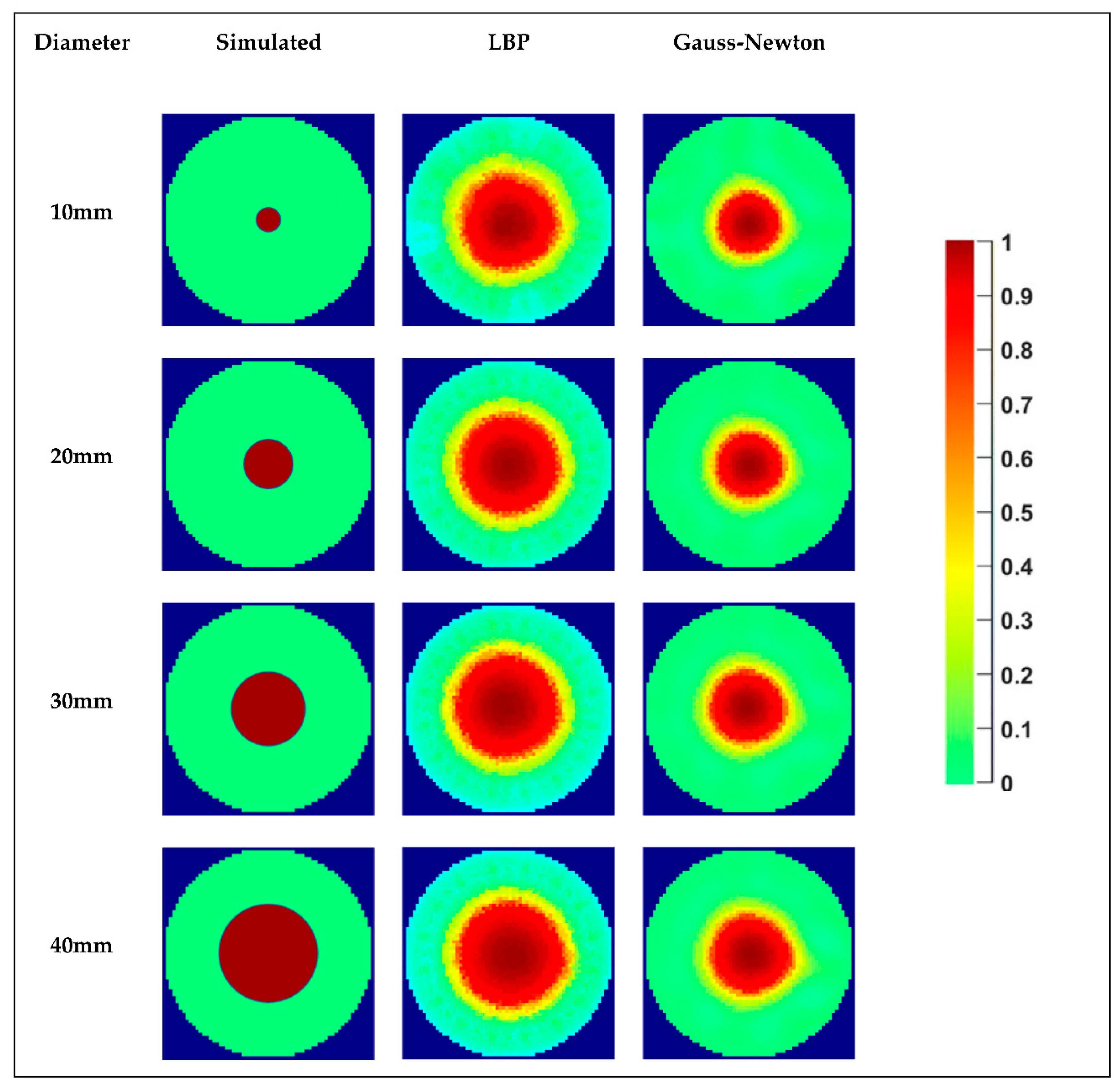
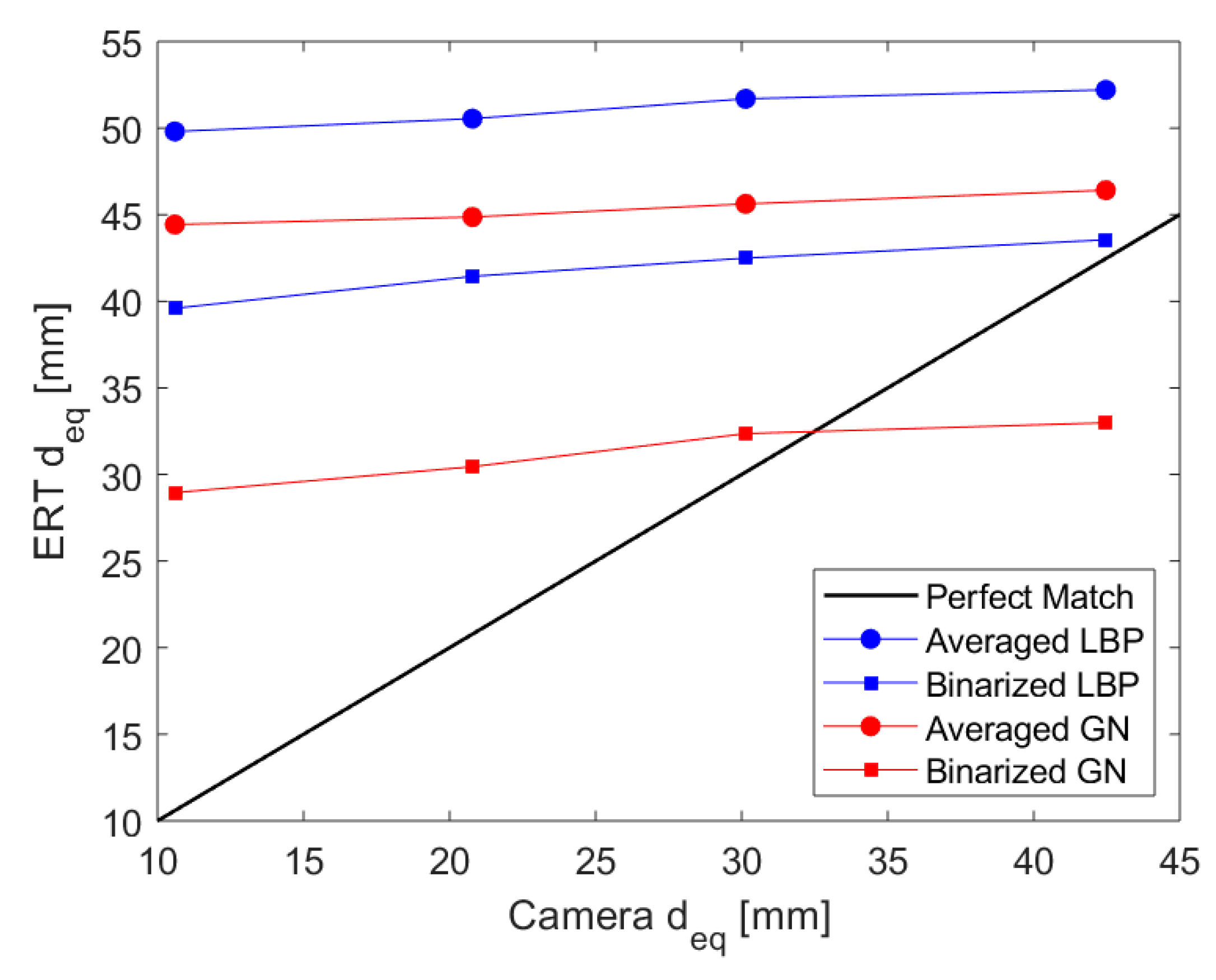
3.1.1. Camera Results
3.1.2. ERT results
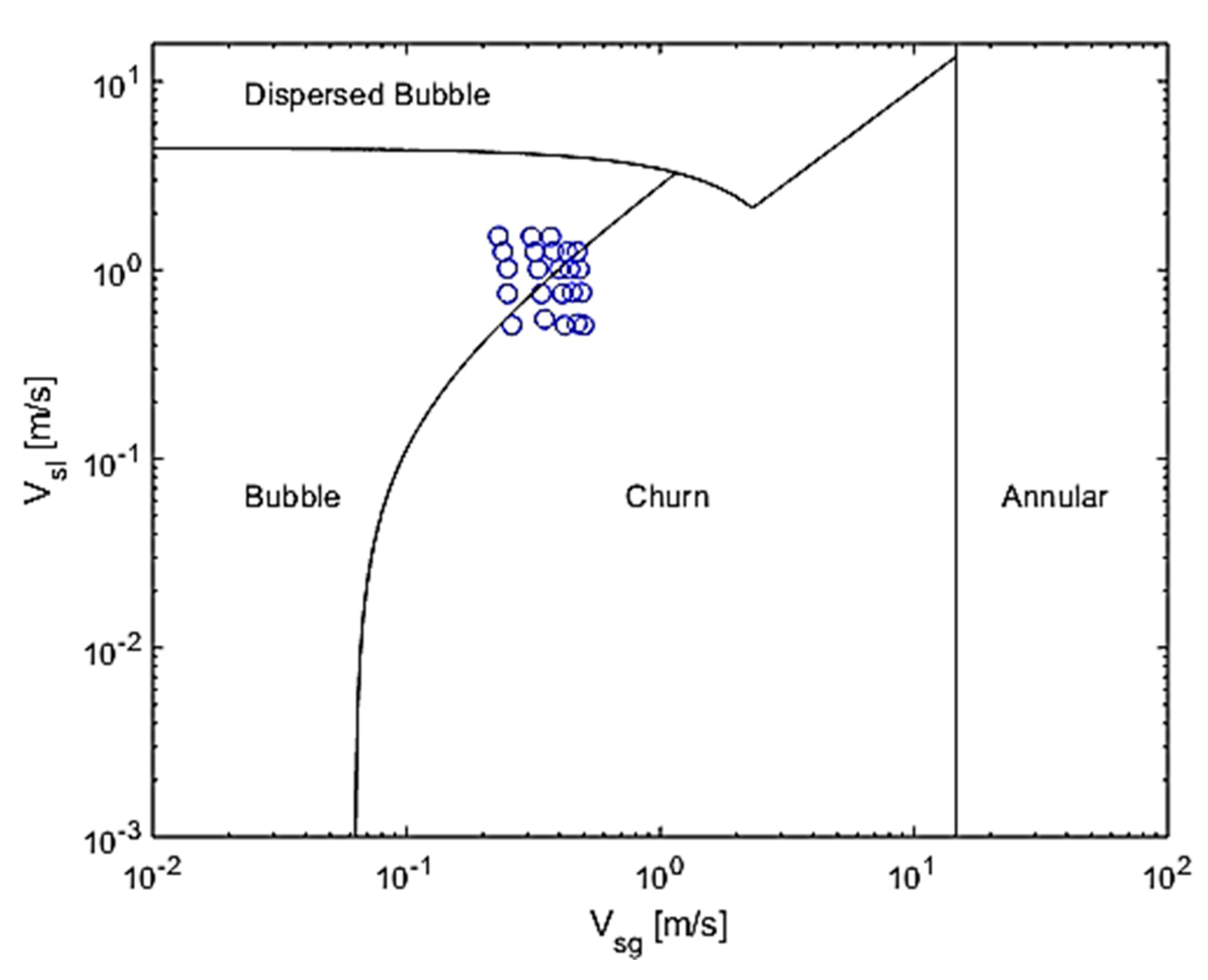
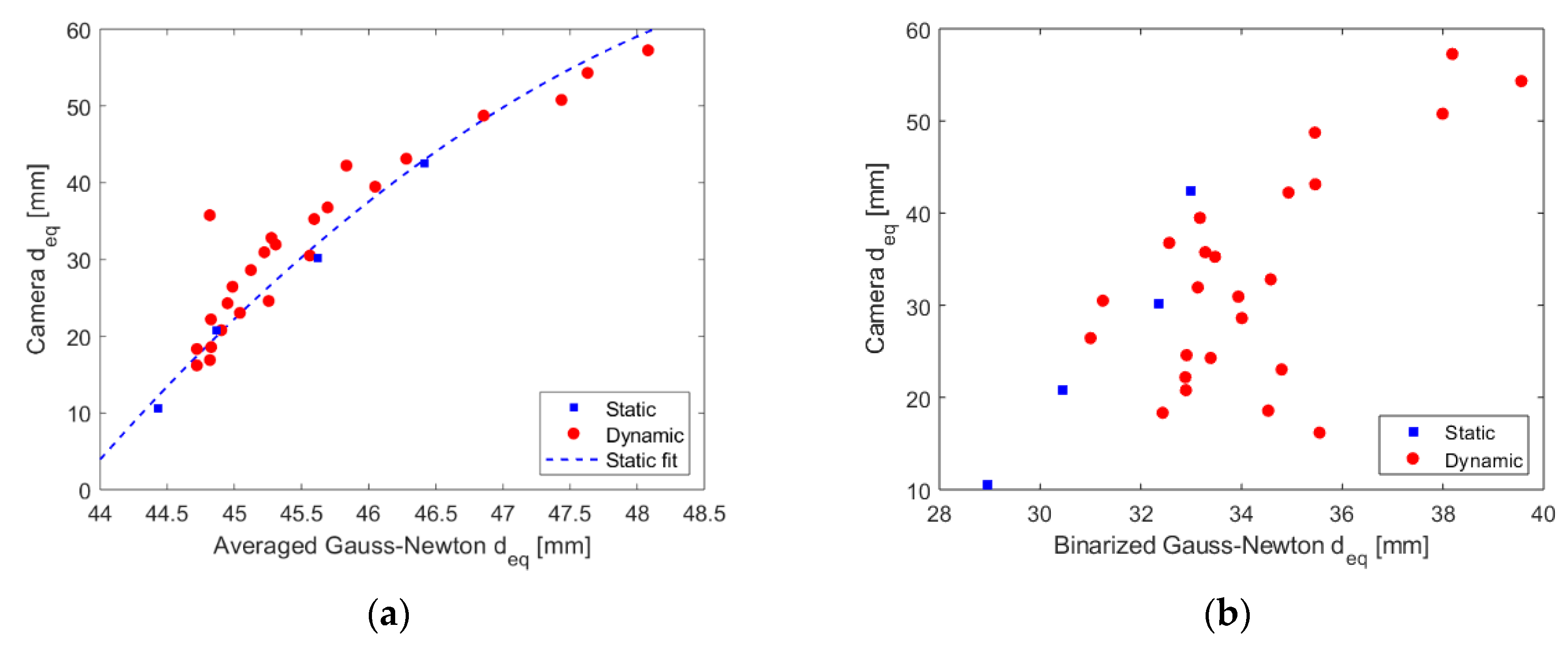
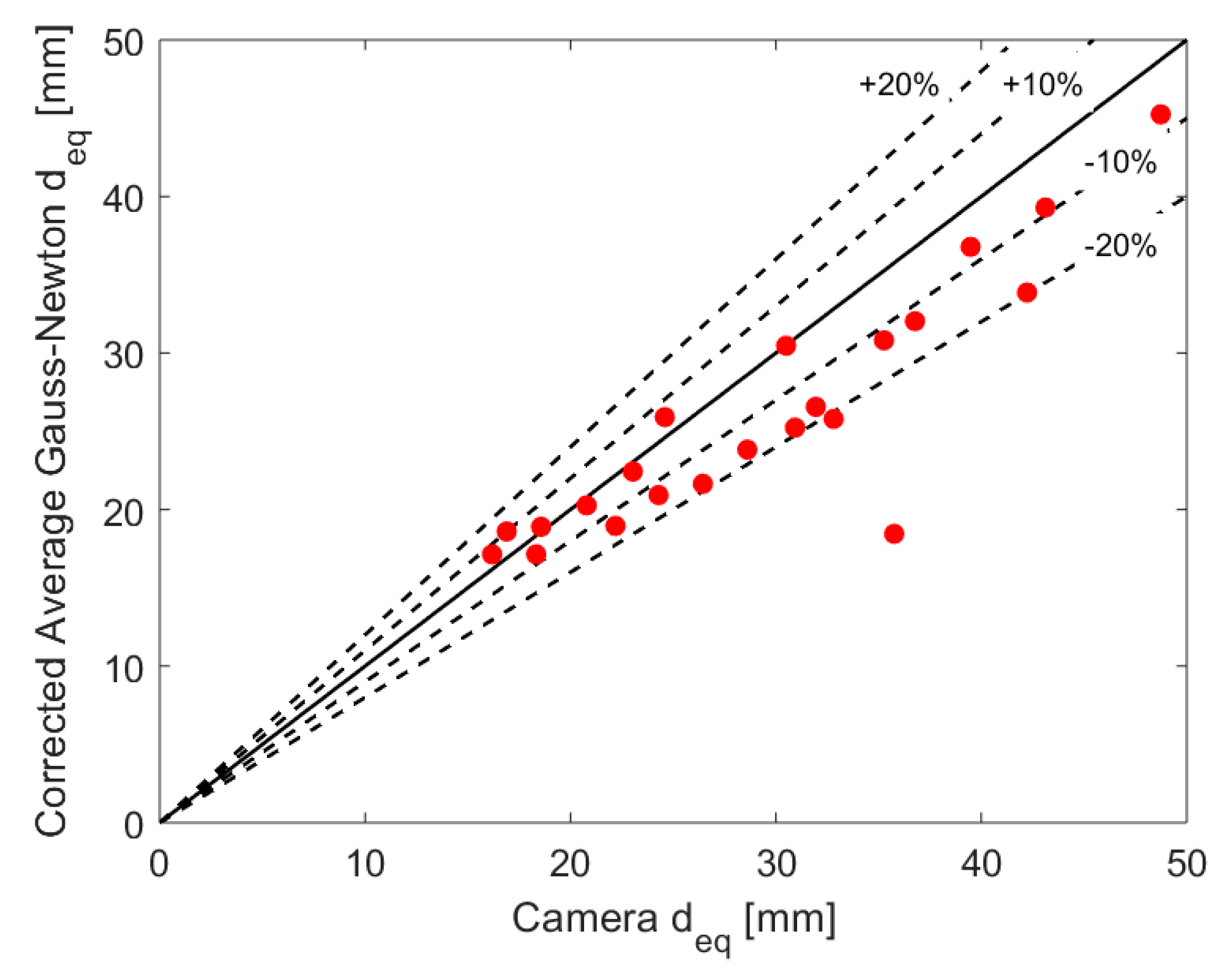
3.2. Dynamic Measurements
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Experiment Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0.51 | 0.55 | 0.51 | 0.52 | 0.51 | 0.75 | 0.75 | 0.75 | 0.76 | 0.76 | |
| 0.26 | 0.35 | 0.42 | 0.47 | 0.50 | 0.25 | 0.34 | 0.41 | 0.45 | 0.49 | |
| Experiment Number | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1.02 | 1.01 | 1.01 | 1.01 | 1.01 | 1.25 | 1.25 | 1.26 | 1.25 | 1.25 | |
| 0.25 | 0.33 | 0.40 | 0.44 | 0.48 | 0.24 | 0.32 | 0.38 | 0.43 | 0.47 | |
| Experiment Number | 21 | 22 | 23 | 24 | 25 | |||||
| 1.51 | 1.50 | 1.50 | 1.50 | 1.50 | ||||||
| 0.23 | 0.31 | 0.37 | 0.42 | 0.46 | ||||||
| Experimental Point | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| CAMERA | Mean | 31.7 | 41.5 | 50.2 | 53.9 | 56.9 | 21.8 | 30.0 | 36.1 | 42.5 | 48.1 |
| Standard Deviation | 8.47 | 7.80 | 7.38 | 7.08 | 6.15 | 7.33 | 7.43 | 7.11 | 7.51 | 7.59 | |
| CORRECTED GN | Mean | 25.79 | 33.86 | 50.71 | 49.77 | 54.67 | 22.43 | 25.23 | 32.03 | 39.29 | 45.24 |
| Standard Deviation | 10.05 | 11.45 | 14.58 | 16.70 | 12.70 | 8.83 | 9.58 | 10.33 | 12.74 | 13.53 | |
| Experimental Point | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| CAMERA | Mean | 17.8 | 23.5 | 27.9 | 34.6 | 38.7 | 16.2 | 20.2 | 24.0 | 29.7 | 35.0 |
| Standard Deviation | 5.36 | 6.00 | 6.25 | 6.71 | 7.83 | 4.83 | 5.09 | 5.42 | 6.71 | 7.40 | |
| CORRECTED GN | Mean | 18.90 | 20.93 | 23.83 | 30.81 | 36.78 | 18.60 | 20.27 | 25.91 | 30.47 | 18.45 |
| Standard Deviation | 7.96 | 8.17 | 8.15 | 10.16 | 11.96 | 9.10 | 7.22 | 8.52 | 9.58 | 9.68 | |
| Experimental Point | 21 | 22 | 23 | 24 | 25 | ||||||
| CAMERA | Mean | 15.7 | 17.8 | 21.7 | 25.8 | 31.2 | |||||
| Standard Deviation | 4.05 | 4.30 | 4.58 | 5.66 | 6.98 | ||||||
| CORRECTED GN | Mean | 17.14 | 17.14 | 18.96 | 21.64 | 26.56 | |||||
| Standard Deviation | 6.70 | 6.70 | 7.04 | 7.46 | 9.64 | ||||||
References
- Sahovic, B.; Atmani, H.; Sattar, M.A.; Garcia, M.M.; Schleicher, E.; Legendre, D.; Climent, E.; Zamansky, R.; Pedrono, A.; Babout, L.; et al. Controlled Inline Fluid Separation Based on Smart Process Tomography Sensors. Chem. Ing. Tech. 2020, 92, 554–563. [Google Scholar] [CrossRef]
- Lim, E.W.C.; Zhang, Y.; Wang, C.H. Effects of an electrostatic field in pneumatic conveying of granular materials through inclined and vertical pipes. Chem. Eng. Sci. 2006, 61, 7889–7908. [Google Scholar] [CrossRef]
- Grudzien, K. Visualization System for Large-Scale Silo Flow Monitoring Based on ECT Technique. IEEE Sens. J. 2017, 17, 8242–8250. [Google Scholar] [CrossRef]
- Grudzien, K.; Romanowski, A.; Chaniecki, Z.; Niedostatkiewicz, M.; Sankowski, D. Description of the silo flow and bulk solid pulsation detection using ECT. Flow Meas. Instrum. 2010, 21, 198–206. [Google Scholar] [CrossRef]
- Grudzień, K.; Chaniecki, Z.; Babout, L. Study of granular flow in silo based on electrical capacitance tomography and optical imaging. Flow Meas. Instrum. 2018, 62, 186–195. [Google Scholar] [CrossRef]
- Romanowski, A. Big Data-Driven Contextual Processing Methods for Electrical Capacitance Tomography. IEEE Trans. Ind. Inf. 2019, 15, 1609–1618. [Google Scholar] [CrossRef]
- Malik, D.; Pakzad, L. Experimental investigation on an aerated mixing vessel through electrical resistance tomography (ERT) and response surface methodology (RSM). Chem. Eng. Res. Des. 2018, 129, 327–343. [Google Scholar] [CrossRef]
- Rimpiläinen, V.; Poutiainen, S.; Heikkinen, L.M.; Savolainen, T.; Vauhkonen, M.; Ketolainen, J. Electrical capacitance tomography as a monitoring tool for high-shear mixing and granulation. Chem. Eng. Sci. 2011, 66, 4090–4100. [Google Scholar] [CrossRef]
- Rao, G.; Sattar, M.A.; Wajman, R.; Jackowska-Strumillo, L. Application of the 2D-ERT to Evaluate Phantom Circumscribed Regions in Various Sucrose Solution Concentrations. In Proceedings of the 2019 International Interdisciplinary Ph.D. Workshop (IIPhDW), Wismar, Germany, 15–17 May 2019; pp. 34–38. [Google Scholar] [CrossRef]
- Rao, G.; Aghajanian, S.; Koiranen, T.; Wajman, R.; Jackowska-Strumiłło, L. Process monitoring of antisolvent based crystallization in low conductivity solutions using electrical impedance spectroscopy and 2-D electrical resistance tomography. Appl. Sci. 2020, 10, 3903. [Google Scholar] [CrossRef]
- Kaczmarek, Ł.; Mieszkowski, R.; Kołpaczyńsk, M.; Pacanowski, G. Application of Electrical Resistivity Tomography (ERT) in the investigation of quaternary landslide zones, based on the selected regions of Płock slope. Stud. Quat. 2014, 31, 101–107. [Google Scholar] [CrossRef]
- Parvareh, A.; Rahimi, M.; Alizadehdakhel, A.; Alsairafi, A.A. CFD and ERT investigations on two-phase flow regimes in vertical and horizontal tubes. Int. Commun. Heat Mass Transf. 2010, 37, 304–311. [Google Scholar] [CrossRef]
- Almutairi, Z.; Al-Alweet, F.M.; Alghamdi, Y.A.; Almisned, O.A.; Alothman, O.Y. Investigating the characteristics of two-phase flow using electrical capacitance tomography (ECT) for three pipe orientations. Processes 2020, 8, 51. [Google Scholar] [CrossRef]
- Ren, Z.; Kowalski, A.; Rodgers, T.L. Measuring inline velocity profile of shampoo by electrical resistance tomography (ERT). Flow Meas. Instrum. 2017, 58, 31–37. [Google Scholar] [CrossRef]
- Stevenson, R.; Harrison, S.T.L.; Miles, N.; Cilliers, J.J. Examination of swirling flow using electrical resistance tomography. Powder Technol. 2006, 162, 157–165. [Google Scholar] [CrossRef]
- Wang, M.; Lucas, G.; Dai, Y.; Panayotopoulos, N.; Williams, R.A. Visualisation of bubbly velocity distribution in a swirling flow using Electrical Resistance Tomography. Part. Part. Syst. Charact. 2006, 23, 321–329. [Google Scholar] [CrossRef]
- Sattar, M.A.; Wrasse, A.D.N.; Morales, R.E.M.; Pipa, D.R.; Banasiak, R.; Da Silva, M.J.; Babout, L. Multichannel Capacitive Imaging of Gas Vortex in Swirling Two-Phase Flows Using Parametric Reconstruction. IEEE Access 2020, 8, 69557–69565. [Google Scholar] [CrossRef]
- Sahovic, B.; Atmani, H.; Wiedemann, P.; Schleicher, E.; Legendre, D.; Climent, E.; Zamanski, R.; Pedrono, A.; Hampel, U. A study on the relationship between upstream and downstream conditions in swirling two-phase flow. Flow Meas. Instrum. 2020, 74, 101767. [Google Scholar] [CrossRef]
- Ren, S.; Zhao, J.; Dong, F. Dimensionality reduced simultaneous iterative reconstruction technique for electrical resistance tomography. Flow Meas. Instrum. 2015, 46, 284–291. [Google Scholar] [CrossRef]
- Faraj, Y.; Wang, M. ERT investigation on horizontal and vertical counter-gravity slurry flow in pipelines. Procedia Eng. 2012, 42, 588–606. [Google Scholar] [CrossRef]
- Putensen, C.; Hentze, B.; Muenster, S.; Muders, T. Electrical Impedance Tomography for Cardio-Pulmonary Monitoring. J. Clin. Med. 2019, 8, 1176. [Google Scholar] [CrossRef]
- Avis, N.J.; Barber, D.C. Image reconstruction using non-adjacent drive configurations (electric impedance tomography). Physiol. Meas. 1994, 15. [Google Scholar] [CrossRef]
- Harikumar, R.; Prabu, R.; Raghavan, S. Electrical Impedance Tomography (EIT) and Its Medical Applications: A Review. Int. J. Soft Comput. Eng. 2013, 3, 193–198. [Google Scholar]
- Henderson, R.P.; Webster, J.G. An Impedance Camera for Spatially Specific Measurements of the Thorax. IEEE Trans. Biomed. Eng. 1978, BME-25, 250–254. [Google Scholar] [CrossRef]
- Nowicki, D. Electrical Impedance Tomography. In Current Generators; Webster, J.G., Ed.; IOP: Bristol, UK, 1990; pp. 29–42. [Google Scholar]
- Isaacson, D. Distinguishability of Conductivities by Electric Current Computed Tomography. IEEE Trans. Med. Imaging 1986, 5, 91–95. [Google Scholar] [CrossRef] [PubMed]
- Hartov, A.; Mazzarese, R.A.; Reiss, F.R.; Kerner, T.E.; Osterman, K.S.; Williams, D.B.; Paulsen, K.D. A multichannel continuously selectable multifrequency electrical impedance spectroscopy measurement system. IEEE Trans. Biomed. Eng. 2000, 47, 49–58. [Google Scholar] [CrossRef] [PubMed]
- Assenheimer, M.; Laver-Moskovitz, O.; Malonek, D.; Manor, D.; Nahaliel, U.; Nitzan, R.; Saad, A. The T-SCANTM technology: Electrical impedance as a diagnostic tool for breast cancer detection. Physiol. Meas. 2001, 22, 1–8. [Google Scholar] [CrossRef]
- Scholz, B. Towards virtual electrical breast biopsy: Space-frequency MUSIC for trans-admittance data. IEEE Trans. Med. Imaging 2002, 21, 588–595. [Google Scholar] [CrossRef] [PubMed]
- Jin, K.S.; Kwon, O.; Ammari, H.; Eung, J.W. A mathematical model for breast cancer lesion estimation: Electrical impedance technique using TS2000 commercial system. IEEE Trans. Biomed. Eng. 2004, 51, 1898–1906. [Google Scholar] [CrossRef]
- Oh, T.I.; Lee, J.; Seo, J.K.; Kim, S.W.; Woo, E.J. Feasibility of breast cancer lesion detection using a multi-frequency trans-admittance scanner (TAS) with 10 Hz to 500 kHz bandwidth. Physiol. Meas. 2007, 28. [Google Scholar] [CrossRef] [PubMed]
- Karhunen, K.; Seppänen, A.; Lehikoinen, A.; Monteiro, P.J.M.; Kaipio, J.P. Electrical Resistance Tomography imaging of concrete. Cem. Concr. Res. 2010, 40, 137–145. [Google Scholar] [CrossRef]
- Kim, B.S.; Khambampati, A.K.; Jang, Y.J.; Kim, K.Y.; Kim, S. Image reconstruction using voltage-current system in electrical impedance tomography. Nucl. Eng. Des. 2014, 278, 134–140. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, G.; Xue, Q.; Wang, H.; Xu, Y. An iterative thresholding algorithm for the inverse problem of electrical resistance tomography. Flow Meas. Instrum. 2013, 33, 244–250. [Google Scholar] [CrossRef]
- Górski, J.; Siepak, M. Assessment of metal concentrations in tap-water—From source to the tap: A case study from Szczecin, Poland. Geologos 2014, 20, 25–33. [Google Scholar] [CrossRef]
- Taitel, Y.; Bornea, D.; Dukler, A.E. Modelling flow pattern transitions for steady upward gas-liquid flow in vertical tubes. AIChE J. 1980, 26, 345–354. [Google Scholar] [CrossRef]
- Banasiak, R.; Wajman, R.; Jaworski, T.; Fiderek, P.; Kapusta, P.; Sankowski, D. Two-Phase Flow Regime Three-Dimensonal Visualization Using Electrical Capacitance Tomography—Algorithms and Software. Inf. Control. Meas. Econ. Environ. Prot. 2017, 7, 11–16. [Google Scholar] [CrossRef]
- Oussar, Y.; Lucas, J.; Holé, S. One or two circular shapes? A binary detection for electrical capacitance tomography sensors. Int. J. Numer. Model. Electron. Netw. Dev. Fields 2018, 31, 1–7. [Google Scholar] [CrossRef]
- Kim, B.S.; Kim, K.Y. Estimation of conductivity distribution based on fast inversion using eigenvalue and eigenvector in electrical impedance tomography. Flow Meas. Instrum. 2015, 46, 276–283. [Google Scholar] [CrossRef]
- Wahab, Y.A.; Rahim, R.A.; Rahiman, M.H.F.; Ling, L.P.; Aw, S.R.; Pusppanathan, M.J.; Abd Shaib, M.F.; Rahim, H.A.; Mohamad, E.J. Image reconstruction for solid profile measurement in ERT using non-invasive approach. Telkomnika 2017, 15, 1554–1564. [Google Scholar] [CrossRef][Green Version]
- Hernandez-Alvarado, F.; Kleinbart, S.; Kalaga, D.V.; Banerjee, S.; Joshi, J.B.; Kawaji, M. Comparison of void fraction measurements using different techniques in two-phase flow bubble column reactors. Int. J. Multiph. Flow 2018, 102, 119–129. [Google Scholar] [CrossRef]
- Davidson, J.L.; Ruffino, L.S.; Stephenson, D.R.; Mann, R.; Grieve, B.D.; York, T.A. Three-dimensional electrical impedance tomography applied to a metal-walled filtration test platform. Meas. Sci. Technol. 2004, 15, 2263–2274. [Google Scholar] [CrossRef][Green Version]
- Brandstätter, B.; Hollaus, K.; Hutten, H.; Mayer, M.; Merwa, R.; Scharfetter, H. Direct estimation of Cole parameters in multifrequency EIT using a regularized Gauss-Newton method. Physiol. Meas. 2003, 24, 437–448. [Google Scholar] [CrossRef] [PubMed]
- Andy, A. EIDORS Version 3.10. In Proceedings of the 20th International Conference on Biomedical Applications of Electrical Impedance Tomography (EIT2019), London, UK, 1–5 July 2019; p. 63. [Google Scholar]
- Adler, A.; Lionheart, W.R.B. Uses and abuses of EIDORS: An extensible software base for EIT. Physiol. Meas. 2006, 27, 24–42. [Google Scholar] [CrossRef]
- Schöberl, J. An advancing front 2D/3D-mesh generator based on abstract rules. Comput. Vis. Sci. 1997, 1, 41–52. [Google Scholar] [CrossRef]
- Yu, J. Study on a Voidage Measurement Method Based on ERT System and Otsu Algorithm. In Proceedings of the Chinese Control and Decision Conference, Yantai, China, 2–4 July 2008; pp. 4939–4942. [Google Scholar]
- Khan, A.; Sanaullah, K.; Sobri Takriff, M.; Hussain, A.; Shah, A.; Rafiq Chughtai, I. Void fraction of supersonic steam jet in subcooled water. Flow Meas. Instrum. 2016, 47, 35–44. [Google Scholar] [CrossRef]
- Boykov, Y.; Funka-Lea, G. Graph cuts and efficient N-D image segmentation. Int. J. Comput. Vis. 2006, 70, 109–131. [Google Scholar] [CrossRef]
- Salah, M.B.; Mitiche, A.; Ayed, I. Ben Multiregion image segmentation by parametric kernel graph cuts. IEEE Trans. Image Process. 2011, 20, 545–557. [Google Scholar] [CrossRef]
- Yu, J.H. Study on Algorithm of ERT for Voidage Measurement of Two-Phase Flow. In Proceedings of the Sixth International Conference on Machine Learning and Cybernetics, ICMLC 2007; Curran Associates Inc.: New York, NY, USA, 2007; Volume 4, pp. 2401–2404. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man. Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Lowe, M.L.; Kutt, P.H. Refraction through cylindrical tubes. Exp. Fluids 1992, 13, 315–320. [Google Scholar] [CrossRef]
- Schiebener, P.; Straub, J.; Sengers, L.J.M.H.; Gallagher, J.S. RI of Water and Steam as a Function of Wavelength, Temperature and Density. J. Phys. Chem. 1990, 19, 677. [Google Scholar]
- Beadie, G.; Brindza, M.; Flynn, R.A.; Rosenberg, A.; Shirk, J.S. Refractive index measurements of poly(methyl methacrylate) (PMMA) from 0.4–1.6 μm. Appl. Opt. 2015, 54, 139–143. [Google Scholar] [CrossRef]
- Scott, D.W. Histograms: Theory and Practice. In Multivariate Density Estimation; John Wiley & Sons: New York, NY, USA, 1992; pp. 47–94. ISBN 9780470316849. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sattar, M.A.; Garcia, M.M.; Banasiak, R.; Portela, L.M.; Babout, L. Electrical Resistance Tomography for Control Applications: Quantitative Study of the Gas-Liquid Distribution inside A Cyclone. Sensors 2020, 20, 6069. https://doi.org/10.3390/s20216069
Sattar MA, Garcia MM, Banasiak R, Portela LM, Babout L. Electrical Resistance Tomography for Control Applications: Quantitative Study of the Gas-Liquid Distribution inside A Cyclone. Sensors. 2020; 20(21):6069. https://doi.org/10.3390/s20216069
Chicago/Turabian StyleSattar, Muhammad Awais, Matheus Martinez Garcia, Robert Banasiak, Luis M. Portela, and Laurent Babout. 2020. "Electrical Resistance Tomography for Control Applications: Quantitative Study of the Gas-Liquid Distribution inside A Cyclone" Sensors 20, no. 21: 6069. https://doi.org/10.3390/s20216069
APA StyleSattar, M. A., Garcia, M. M., Banasiak, R., Portela, L. M., & Babout, L. (2020). Electrical Resistance Tomography for Control Applications: Quantitative Study of the Gas-Liquid Distribution inside A Cyclone. Sensors, 20(21), 6069. https://doi.org/10.3390/s20216069









