In this section, the performance of our approach is evaluated in different ways and compared to other approaches. In
Section 4.1, we illustrate the performance using a simple architecture (LeNet [
31]) and dataset (MNIST [
42]). We compare the results we obtain with classical deep learning based on frequentist interpretation and the approach proposed by Gal and Ghahramani [
16] that uses Bernoulli dropout to define the variational distribution. Since we expect Bernoulli dropout to perform similar to Gaussian dropout [
17] due to the Central Limit Theorem, we do not include a comparison against the latter approach. We also analyze the uncertainty information obtained about the network parameters as well as the network predictions in detail. These results were obtained using the caffe implementation described above. In
Section 4.2, we compare our approach to the “Bayes by Backprop” algorithm [
30] and show that we can achieve comparable or better results despite giving up some flexibility in representing the true posterior uncertainty of the network parameters. Finally, in
Section 4.3, we illustrate the benefits of trading off flexibility for a lower number of parameters by showing that our approach can also be used for larger network architectures with larger input data vectors. This is illustrated by fine-tuning a GoogLeNet [
43] architecture with a custom dataset. The last two results were obtained with the pytorch implementation.
4.1. LeNet and the MNIST Dataset
Basis of the experiments in this section is the benchmark dataset MNIST [
42] together with the architecture LeNet [
31]. The MNIST dataset consists of 70,000 images of handwritten digits, from which 60,000 build up the training dataset and the remaining 10,000 build up the testing data. The specific version of LeNet used is the same described in Reference [
16]. Therefore the first convolutional layer generates 20 feature maps, while the second one extracts 50 features. Both layers use
kernels. Max-pooling with kernel size
and stride 2 is applied after both convolutional layers. The first fully connected layer consists of 500 neurons, the second one covers only 10 since there are 10 different digits. Moreover, the first fully connected layer uses the rectified linear unit as activation and the other ones the identity function.
In order to get an idea how well our Bayesian approach performs it should be compared to the classical, that is, the frequentist, approach. Therefore, LeNet is trained three times in the classical way. First, without dropout, then with dropout ( dropping rate ) applied after the first inner product layer, and finally, with dropout applied as before and exchanged training and testing datasets. Exchanging training and testing data results in a significant reduction of the training data from 60,000 to 10,000 and should give an intuition how well Bayesian models work for limited training data.
All three models are optimized the same way. To prevent overfitting, the Euclidean norm of the network weights is penalized with a factor of
. As usual in deep learning, the optimization procedure applied is mini-batch gradient descent. A batch size of 64 is chosen. The learning rate used in the
i-th iteration is given by
. Momentum is used and set to
. The accuracies for the test dataset are given in
Table 1 and are expressed by the corresponding test error defined as
where
is the number of correctly classified samples and
N is the total number of samples in the test dataset (here
10,000).
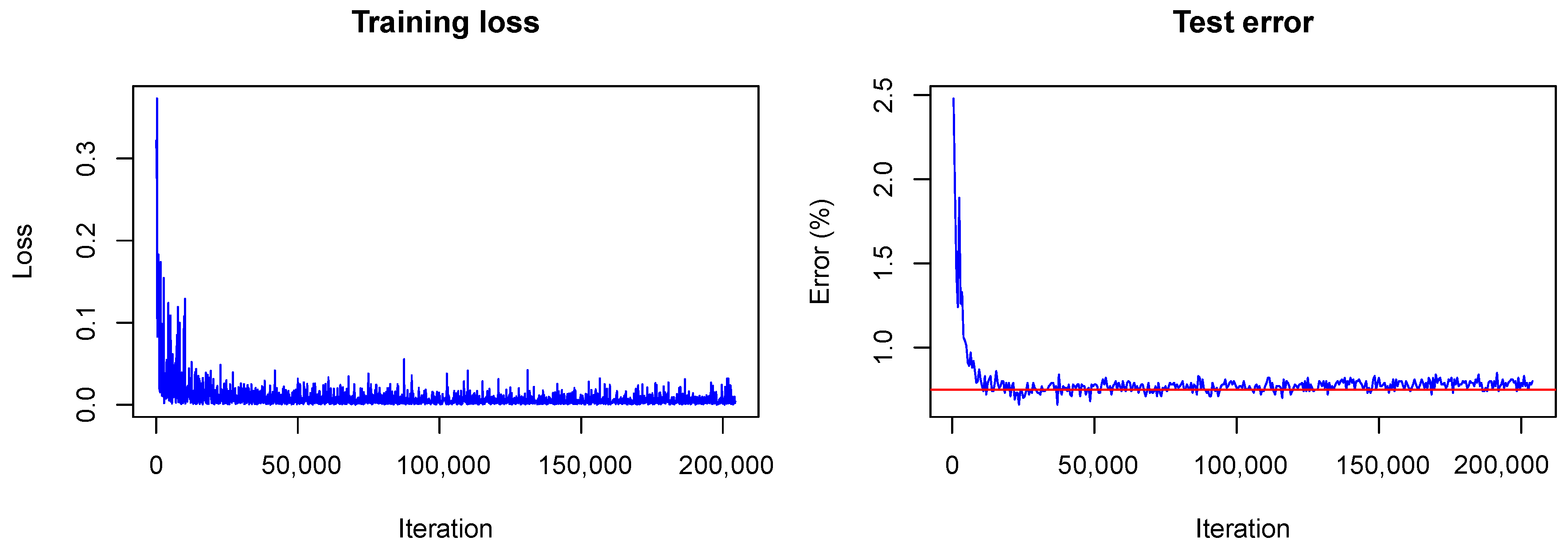
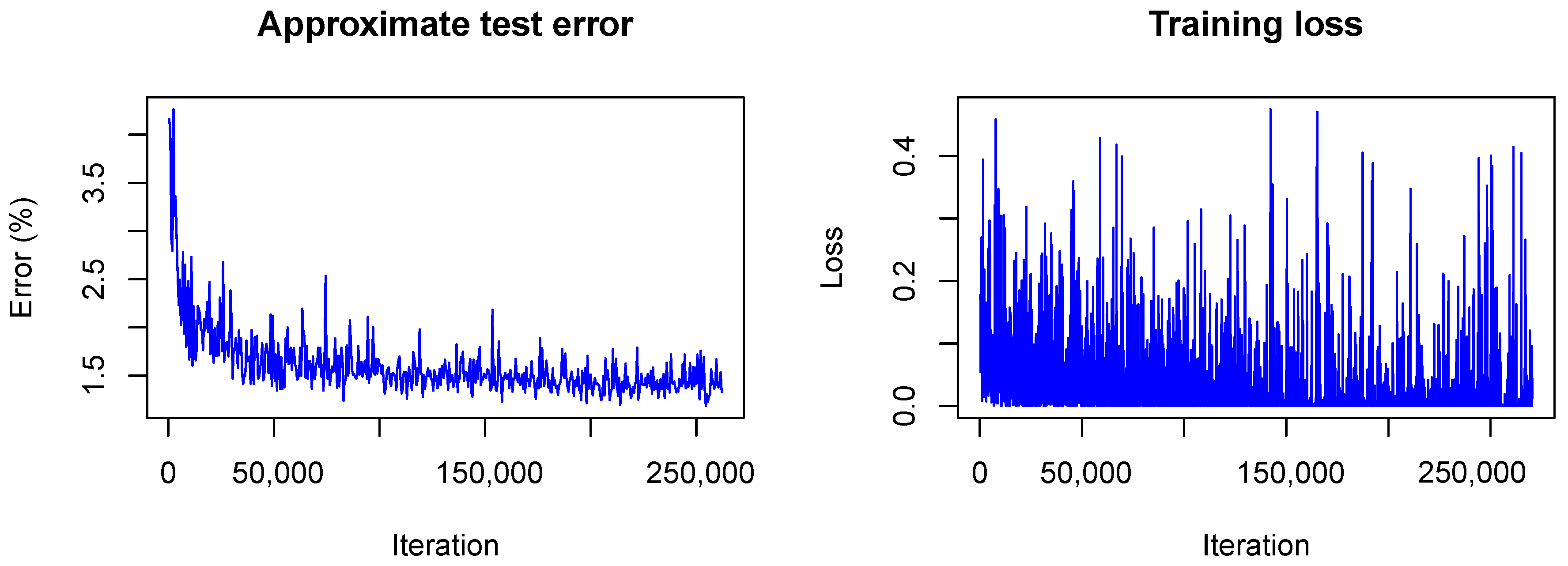
The training converged quite similarly in all three cases. A visualization of the training loss and test error for the second model, that is, the model trained with dropout, is shown in
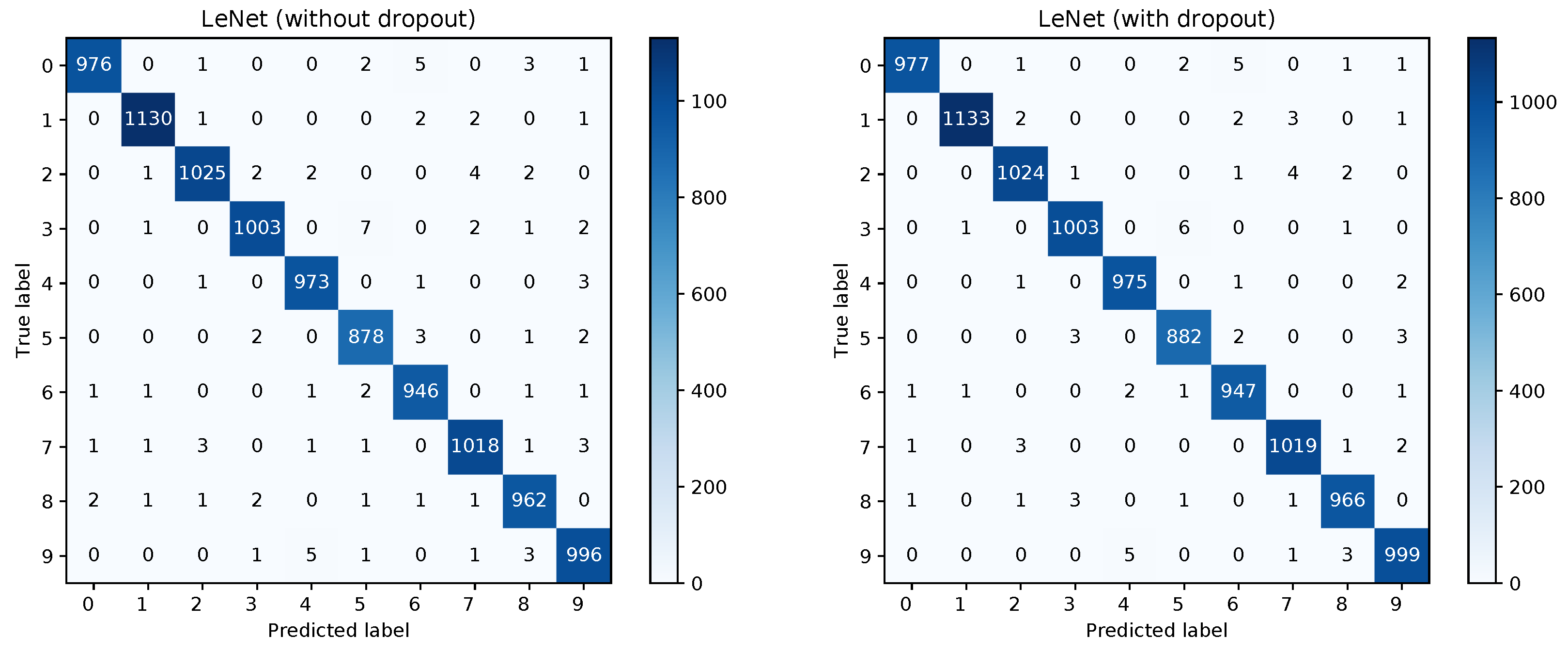
Figure 1. This figure will serve for comparison of the Bayesian and the frequentist training process. A plot of the confusion matrices is shown in
Figure 2 for the models without dropout (left) and with dropout (right) and in
Figure 3 (left) for the the model with dropout and exchanged training and testing data. The right side of
Figure 3 shows a zoomed in section of the ROC curves for the three models. Each ROC curve is the mean of the one-against-all ROC curves for each class. The results confirm the performance differences of the different models as indicated by
Table 1.
Similarly for our Bayesian approach, LeNet is trained three times with the MNIST dataset. In analogy to the frequentist training (see above), LeNet is trained first without dropout, then with dropout, and finally, with dropout and exchanged training and testing data. In contrast to Gal and Ghahramani, we interpret dropout training as simultaneous training of multiple Bayesian models and assume that combining multiple models will result in a better accuracy than using just one model. Thus, during testing, the weight scaling inference rule, which states that each neuron should be used but multiplied with the dropping ratio, is not applied. Rather in the testing phase, neurons are randomly dropped in order to sample from the set of simultaneously trained Bayesian models and combine their predictions to one overall prediction.
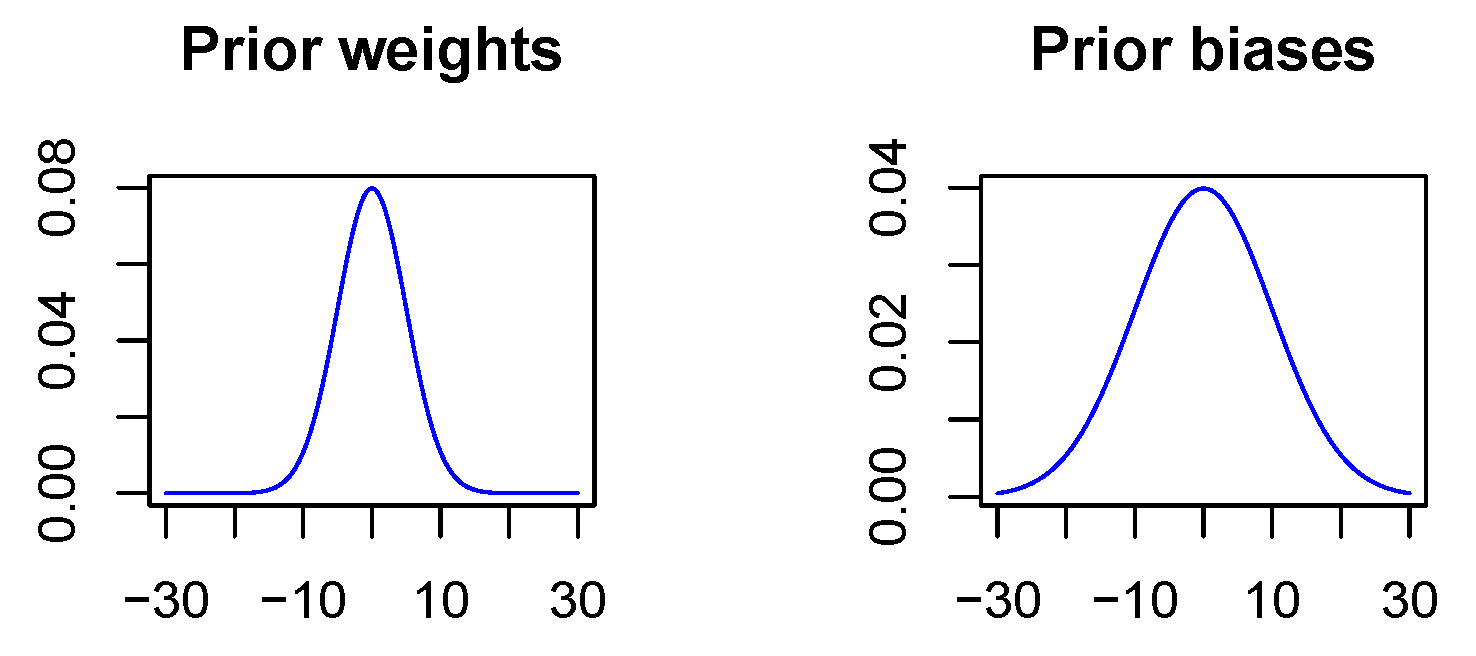
In contrast to the non-Bayesian case, a penalization of the Euclidean norm does not take place since in the Bayesian case deviations from the a priori distribution are penalized. As there is not really a priori information available, the prior is used to express the wish that values should not diverge. Thus, the a priori expectation value is specified as zero for all network parameters, and further, the a priori standard deviation is chosen to be 5 for all weights and 10 for all biases. The variance for the biases is chosen to be larger since biases act on linear combinations of neuron outputs with network weights as coefficients and therefore may take on larger values, see
Figure 4. It should be mentioned that the penalization strength of the KL-divergence between the variational distribution and the a priori distribution is chosen smaller than recommended in the theoretical considerations in
Section 3.1 because of convergence problems. Empirically, we found that we have to scale the penalization strength down by a factor of 100 to ensure convergence. While somewhat puzzling, this does not matter since there is not really a priori information available and the network parameters took small values in all experiments even with the reduced penalization. It should also be mentioned, that our implementation easily lends itself to ’Bayesian transfer learning’ in analogy to classical transfer learning [
44], where the results of a previous training run with a large dataset are optimized for a more targeted application by fine-tuning the network with a smaller but specific training dataset. In the Bayesian case, the information about the posterior distribution of the network parameters in the pre-trained network will then be used to specify a prior for the fine-tuning step. This is subject to future work.
In order for the Bayesian networks to converge, the parameters
and
(see
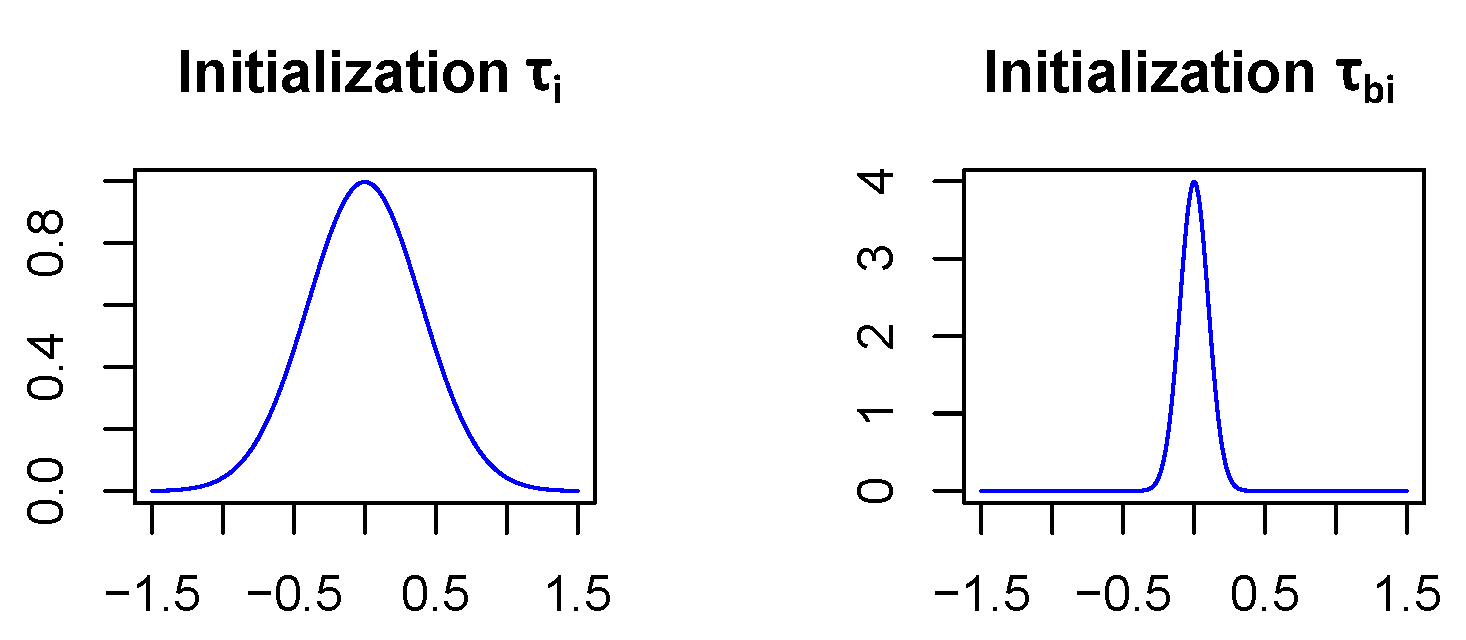
Section 3.1) which specify the standard deviations of the network weight and bias distributions, respectively, have to be initialized carefully. Therefore,
is initialized as
and
as
in all network layers except for the first fully connected one which is treated separately. In this initialization, it becomes highly unlikely (<0.7%) that the weights of the neural net differ by more than the size of their expectation value from their expectation value, see
Figure 5. This is a reasonable way to start since stronger deviations from the expectation values would mean that weights are even unsure about their algebraic sign, which might lead to convergence issues, if assumed for a majority of the network layers. In addition, assuming biases to vary less is not unusual since there are relatively few of them and they have a strong influence on the model since they act on sums. The reason why the first fully connected layer is treated differently is that it covers much more parameters than the other layers. Indeed it includes 400,000 weights, while all the other layers together only contain 30,500 weights. Due to the large number of parameters in the first fully connected layer, we assume that the model will be more uncertain in the network parameters of this layer. So
is initialized with 1 and
with
.
Finally, all Bayesian models are optimized with the same mini-batch optimization procedure as their frequentist analogues. For computing the model accuracies, each test example is propagated 100 times through the network using Caffe’s bindings to Python. The test errors computed on the test dataset (
10,000 samples) and the absolute and relative decreases in the error with respect to the non-Bayesian models are given in
Table 2. One can see that the Bayesian models always perform better than their frequentist analogues. For the first two models the accuracy is only slightly better, while the third model shows a significant improvement, especially if one considers the relative decrease of the test error. It is not surprising that the increase in accuracy is only small for the first two models since all models considered converge very well and do not suffer from overfitting because there is plenty of training data available. The third model which is trained using only 10,000 images shows signs of overfitting in the non-Bayesian case. The Bayesian network however is more robust towards overfitting and thus performs significantly better. This illustrates the advantage of Bayesian deep learning in the presence of only a limited number of training images.
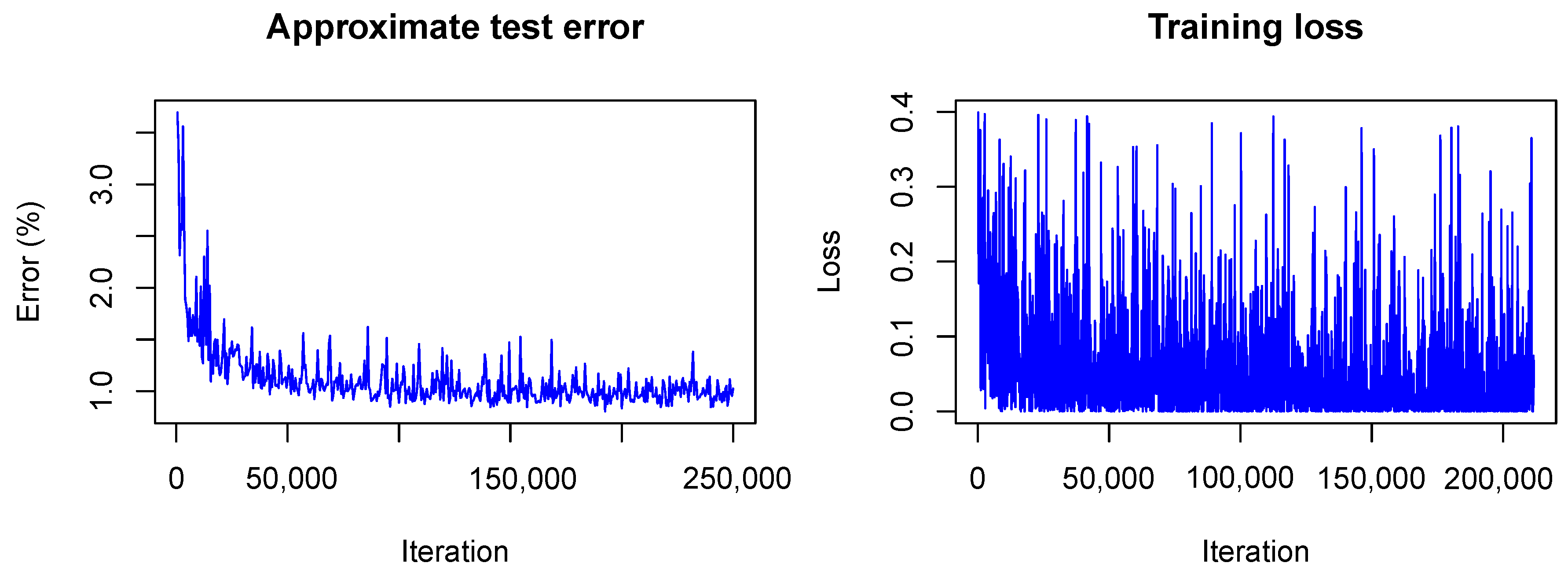
It is interesting to see how LeNet converges following our Bayesian approach. In
Figure 6 and
Figure 7 the training is visualized for the first and the second model, that is, the model trained without dropout and the model trained with dropout.
In contrast to the frequentist case, only the approximate test error is plotted. This means that only one sample of each testing image is used for predictions and that the weight scaling inference rule is applied. Currently, the Caffe framework does not provide other options for the testing phase during optimization. Nonetheless, the imprecise approximation of the test error gives a rough estimate of the real test error and therefore helps to understand what happens with the model accuracy during training. One can see that the loss
(plotted without the term due to the KL-divergence) fluctuates heavily during training due to the random samples drawn from the variational distribution. However, the test error decreases quickly as in the non-Bayesian case and seems to keep decreasing as training goes on. This is not the case for the frequentist model (see
Figure 1) for which the test error seems to increase slowly. This, again, indicates the strength of our approach against overfitting.
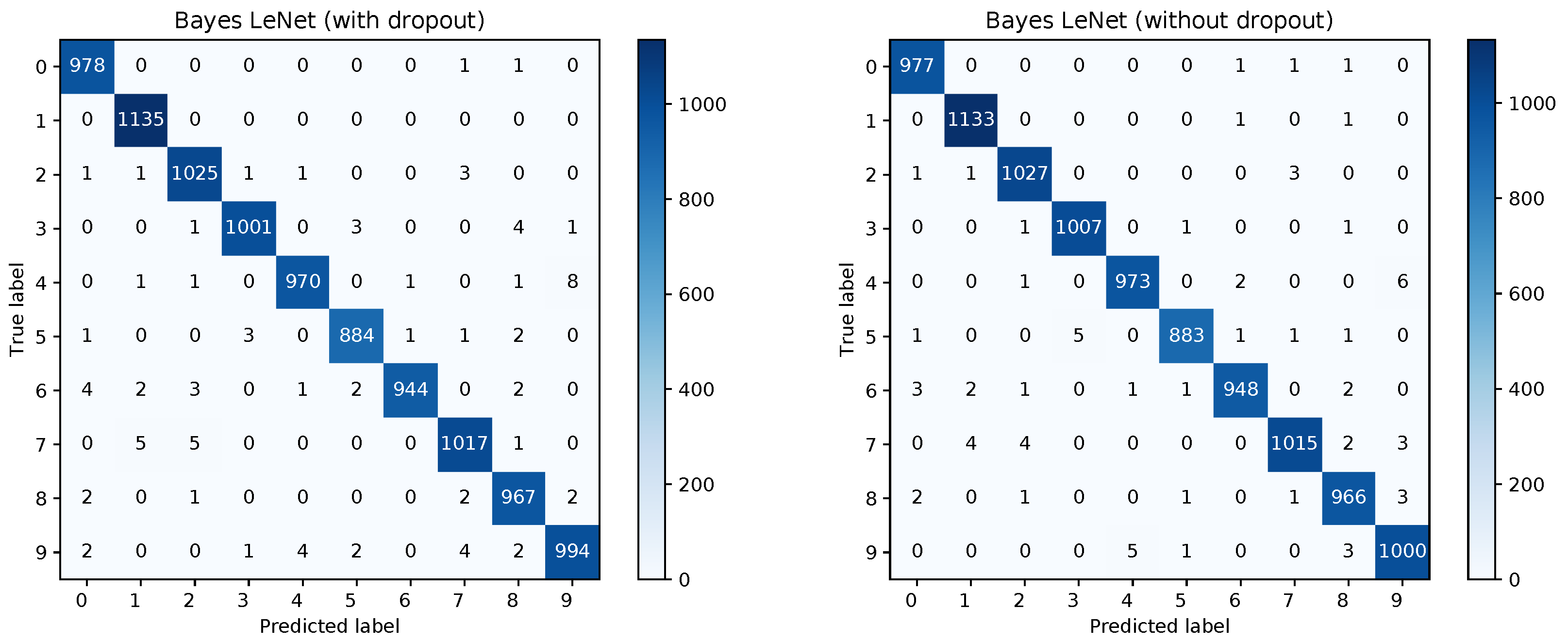
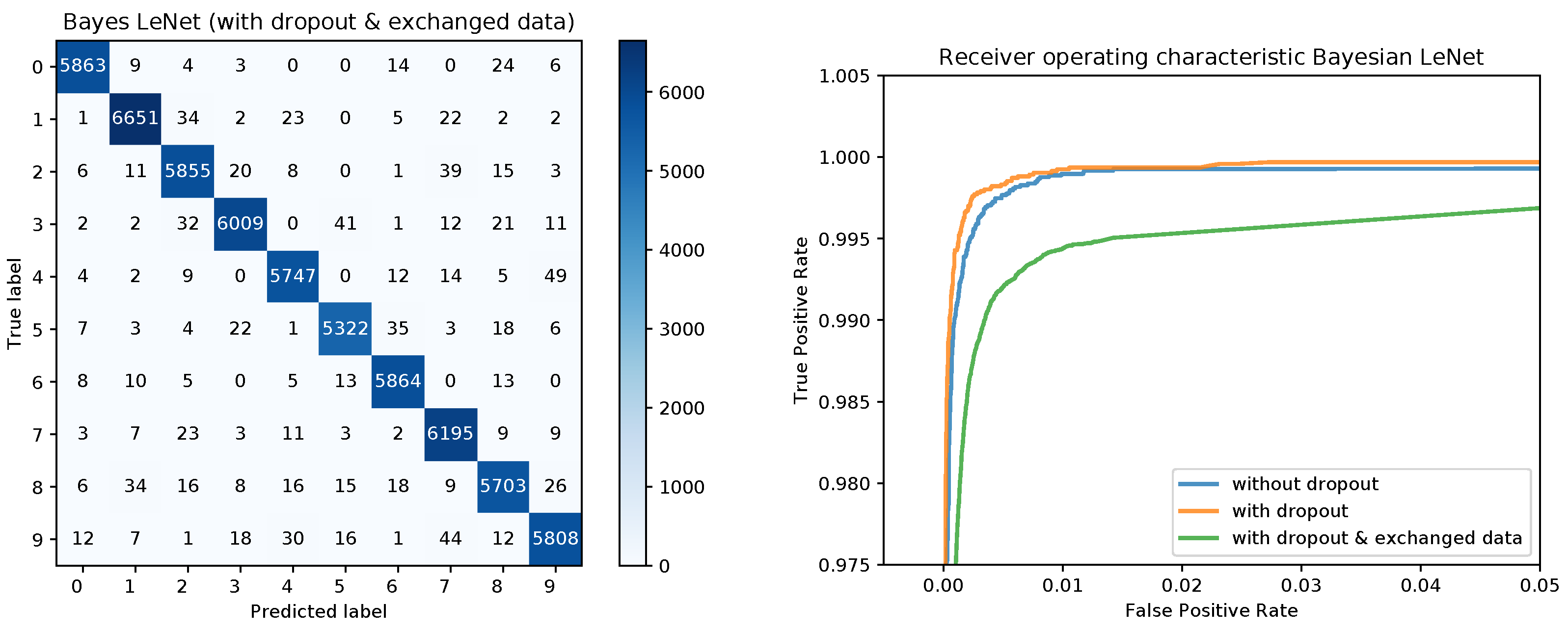
Figure 8 shows the confusion matrices for the Bayesian LeNet without dropout (left) and with dropout (right). The confusion matrix for the Bayesian LeNet with dropout and exchanged training and testing data is shown in
Figure 9 (left). In addition, the mean ROC curves for each of the Bayesian models is shown in
Figure 9 (right). Comparing these results to the results of the frequentists networks from
Figure 2 and
Figure 3 confirms the superior performance of the Bayesian models, especially for the model with exchanged training and testing data where the initial slope for the Bayesian model is much steeper.
The a posteriori uncertainties are quite the same for all three Bayesian models. In
Table 3, the uncertainties for the second model, that is, the model trained with dropout, are given. One can see that the model uncertainty is small for all layers except for the first fully connected one.
A value of
for
indicates that the network is not even sure about the algebraic sign of the weights in this layer. Therefore, we assume that the network architecture is not optimal and reduce the number of output neurons for the first fully connected layer from 500 to 250. In the Bayesian case, this does not lead to a significant increase of the network accuracy but the network uncertainty for the first fully connected layer decreases significantly as one can see in
Table 4.
This result indicates that the Bayesian approach can be used to optimize the model architecture both in terms of accuracy and model size for a given training and testing dataset. In this particular case, we were able to reduce the number of parameters by almost a factor of 2 while achieving the same accuracy. Even more interesting, when the reduced model is trained the classical way, the achieved accuracies become as good as for the Bayesian model, indicating again that the initial model was suffering from overfitting.
In addition to providing information about the model uncertainty, our approach can also be used to determine the uncertainties of the predictions. Due to the random sampling of the weights and biases during each forward pass, accurate credible intervals can be estimated by performing multiple forward passes per image. This information can be used in applications using our algorithm for classification. For example, a check for statistical significance for the classification result can be performed and the result can be used to decide about the next steps in the application (e.g., proceed autonomously, repeat classification, escalate to user, etc.).
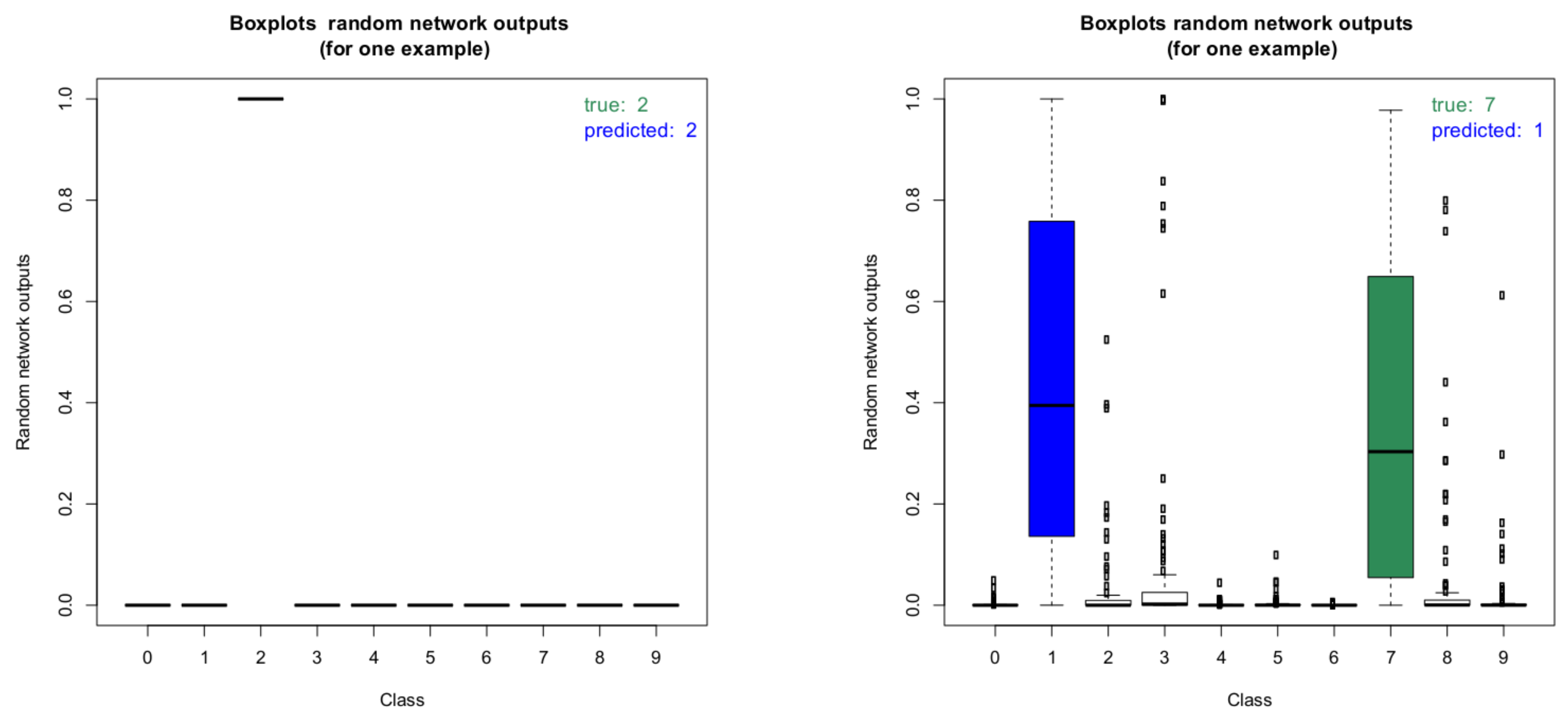
Figure 10 shows two boxplots of the random network outputs (model without dropout) for two representative images from the MNIST test data set. On the left, the boxplot for an image with correct classification result is shown. Clearly, the network is very certain about this classification result. On the right, the boxplot for an image with wrong classification result is shown. As can be seen, the result for the wrongly predicted label is not statistically significant as there is a clear overlap between the boxes of the true label and the predicted one.
These boxplots were computed by performing the inference 100 times for each image. It is interesting to note that in the case of the wrongly predicted image on the right, the network produces very high outlier probabilities for other classes besides the true and the predicted label. This illustrates the potential for deterministic networks to produce wrong classifications with very high class probabilities. Checking for all images if the estimated 95% credible intervals of the predicted classes overlap with the 95% intervals of the other classes gives further insight into the prediction capabilities of the network.
Table 5 summarizes the results for the model without dropout.
As can be seen, the overwhelming majority of classification results is correct and the network is also confident about these predictions. About 300 images are classified correctly, but the network is not sure within 95% credible intervals. A total of 94 images are classified incorrectly. In the vast majority of these cases, the network is unsure about the classification result. In only 14 cases, the network is quite sure about its wrong classification. Please note, that due to the random sampling of network parameters, the results are slightly different each time they are computed unless a very large number of forward passes is performed for each image. This is also the reason why the number of miss-classified images in this section differs from the one obtained above. The uncertainty analysis presented here was performed separately. From an application point of view, the latter case (quite certain about wrong results) is the most critical.
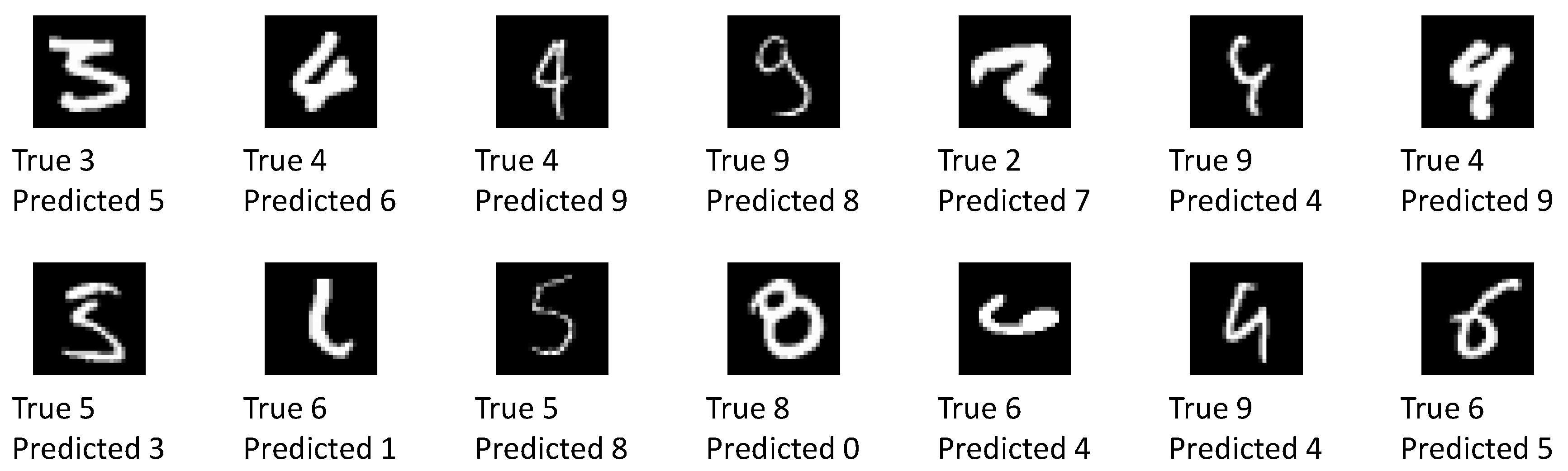
Figure 11 shows all of the 14 images which have been classified wrongly with confidence by the network.
More than half of these images visually resemble the predicted label at least as much as they resemble the true label. The remaining images are without a doubt wrongly classified. Some of these images can be excluded by raising the confidence level requirement. A detailed investigation into wrong yet confident classification results is left for further study.
4.3. GoogLeNet and Custom Dataset
To illustrate that our approach is also applicable to large, modern network architectures with many more hidden layers and network parameters and also larger size input vectors, we trained a GoogLeNet architecture [
43] on a custom dataset of 11 different classes of fruits and vegetables. This work was performed using the pytorch implementation (see
Section 3.2). The dataset consists of a total of 2437 images, randomly split into a training dataset of 1952 images and a validation dataset of 485 images. The 11 classes of fruits an vegetables were apple, avocado, banana, blackberry, blueberry, carrot, cucumber, grape, peach, pear, and strawberry. The dataset was compiled from freely available online resources. The images were chosen such that only items belonging to one particular class were present in each image. No restrictions were placed on the background scenery provided it did not show other types of fruits and vegetables. The number of images in the training and test split for each class is shown in
Table 7.
As the images are all of a different size, they are first randomly cropped and then resized to
pixels using the utility routine
RandomResizedCrop provided by pytorch. Similarly to
Section 4.1, we compare a frequentist model to our Bayesian approach. Both models are trained based on an Image-Net pre-trained version of GoogLeNet available from pytorch (
https://download.pytorch.org/models/googlenet-1378be20.pth). In both cases, the pre-trained model is fine-tuned for 100 epochs using a learning rate of
with momentum of
and a batch size of 32. For the Bayesian approach, the a posteriori uncertainties are initialized the same for all layers. As before they take on the values of 0.4 for
and 0.1 for
. The a priori variances are initialized to
for the biases and
for the weights. The regularization term of the Kullback-Leibler divergence was weighted with a factor of
. After 100 epochs, the frequentist model reaches an accuracy of
across the entire validation dataset. The Bayesian model reaches an accuracy of about
for a one-pass evaluation over the validation dataset (the exact number differs for each random forward pass). When averaging over the results of 100 forward passes for each image, the accuracy of the Bayesian model improves to
.
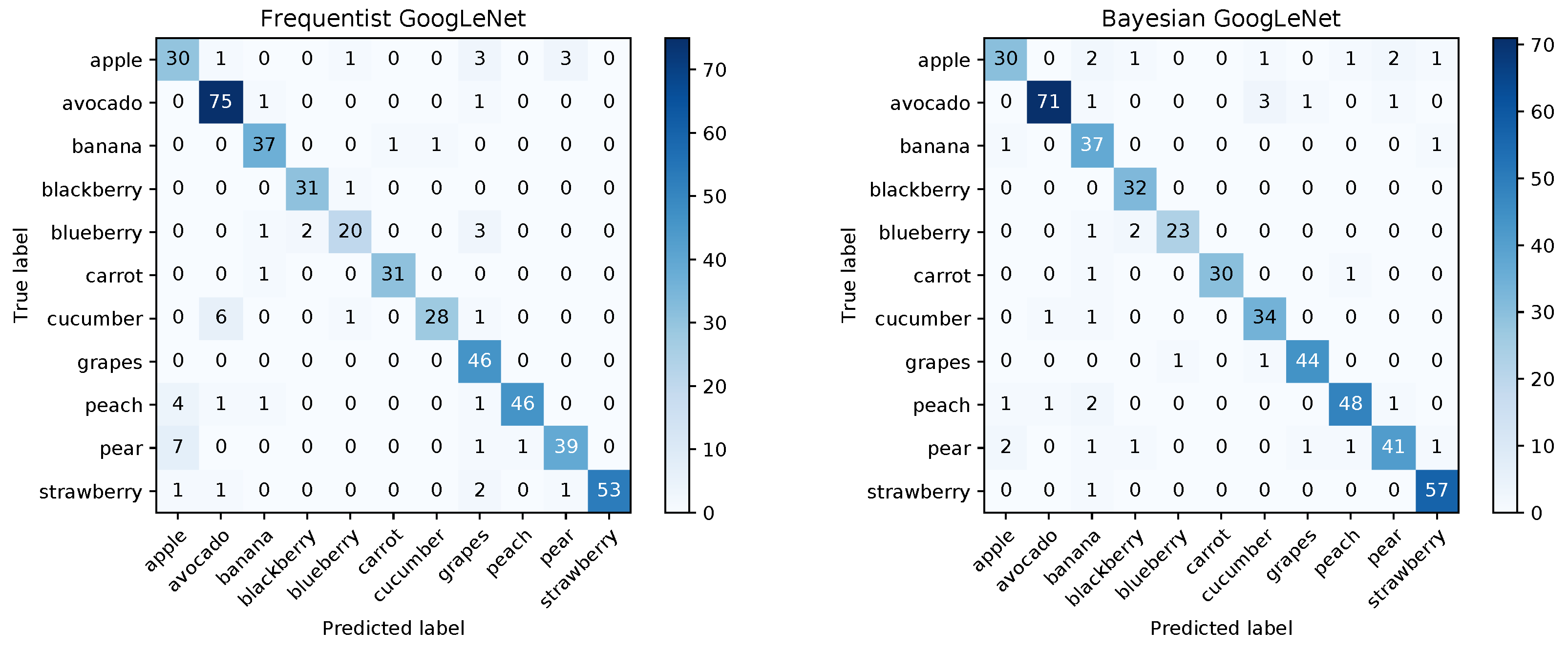
The confusion matrices for the frequentist and the Bayesian model are shown in
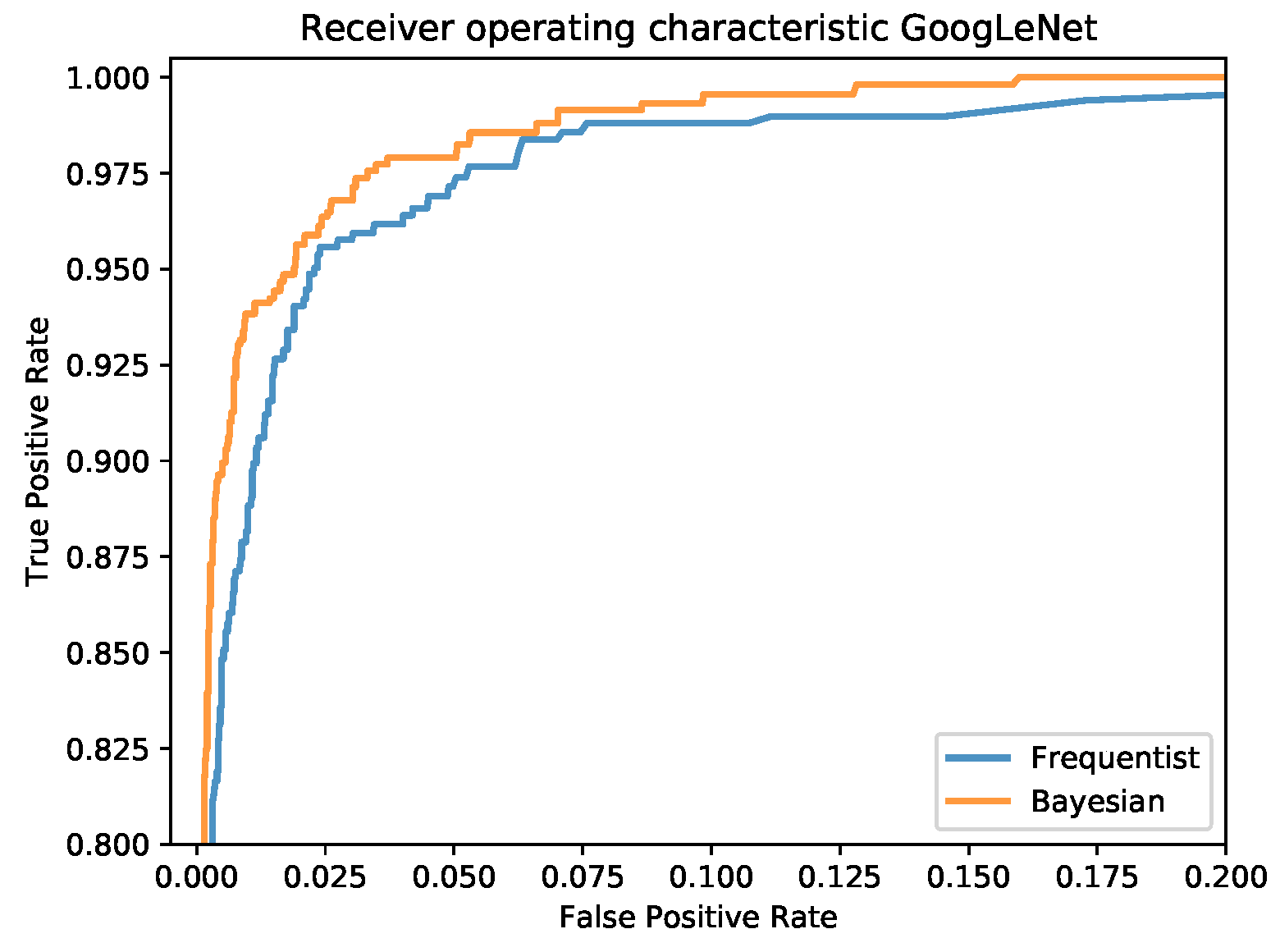
Figure 12 and a comparison of the mean ROC curves obtained in
Figure 13.
An analysis of the
credible intervals as before is summarized in
Table 8.
As before, the analysis shows that the network is quite certain about the majority of its correct results and quite uncertain about all but one of its wrong results. This indicates that with the proper settings for the credible intervals, the vast majority of wrong classification results can be detected. Although it comes at the expense of a larger number of uncertain but correct results, this may be important for applications where sensitivity is of utmost importance. An investigation into how the prediction uncertainty depends on network architecture, training and testing datasets as well as network optimization hyperparameters is subject to ongoing work.