Optimization of IMU Sensor Placement for the Measurement of Lower Limb Joint Kinematics
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
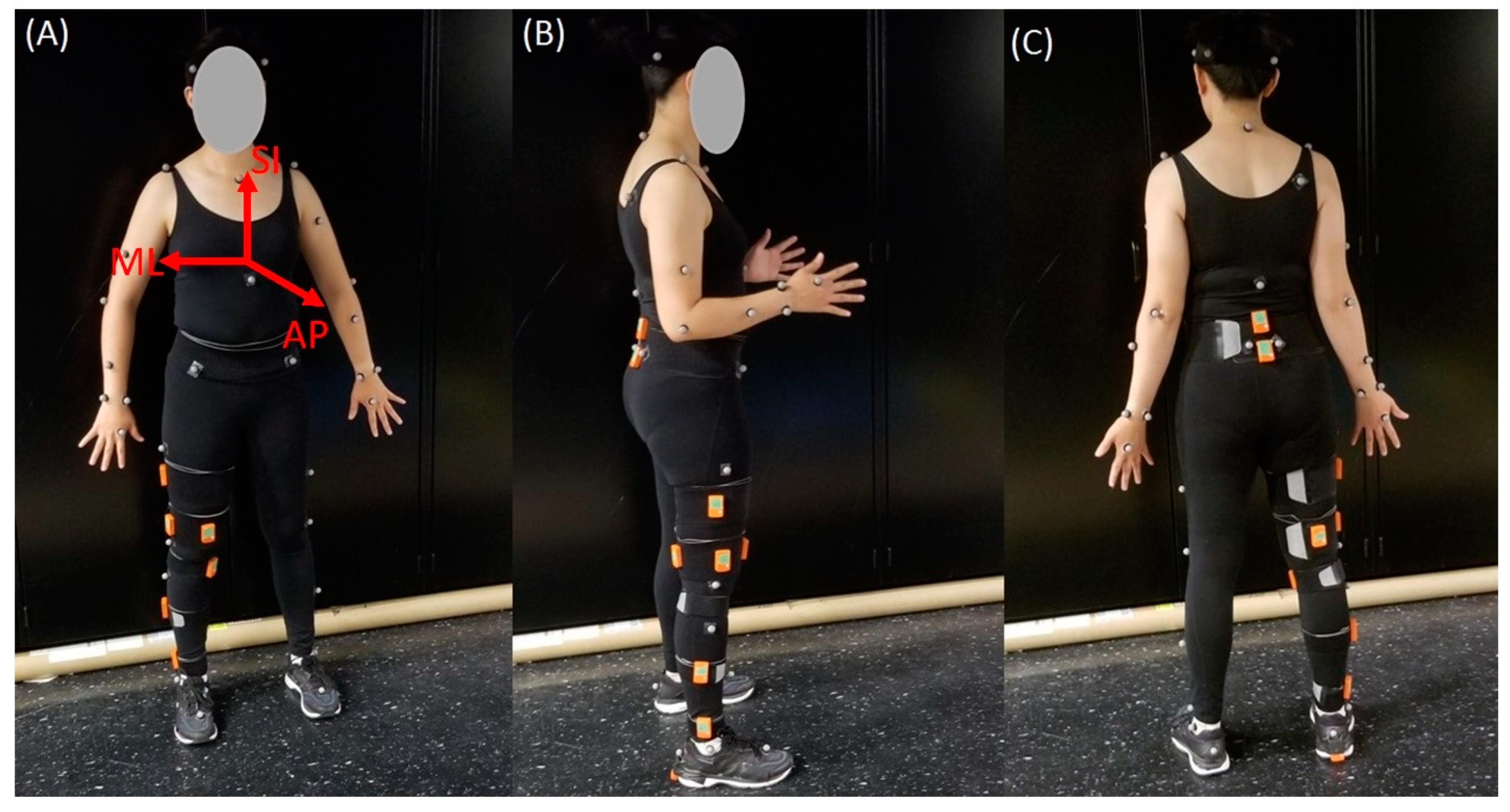
2.2. IMU System and Sensor Placements
2.3. MOCAP System and Marker Placement
2.4. Functional Task–TUG Test
2.5. IMU Joint Angle Calculations
2.6. MOCAP Joint Angle Calculations
2.7. Data Analysis
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hodgins, D. The importance of measuring human gait. Med. Device Technol. 2008, 19, 44–47. [Google Scholar]
- Muro-de-la-Herran, A.; Garcia-Zapirain, B.; Mendez-Zorrilla, A. Gait analysis methods: An overview of wearable and non-wearable systems, highlighting clinical applications. Sensors 2014, 14, 3362–3394. [Google Scholar] [CrossRef] [PubMed]
- Weygers, I.; Kok, M.; Konings, M.; Hallez, H.; De Vroey, H.; Claeys, K. Inertial sensor-based lower limb joint kinematics: A methodological systematic review. Sensors 2020, 20, 673. [Google Scholar] [CrossRef] [PubMed]
- Reinfelder, S.; Hauer, R.; Barth, J.; Klucken, J.; Eskofier, B.M. Timed Up-and-Go phase segmentation in Parkinson’s disease patients using unobtrusive inertial sensors. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 5171–5174. [Google Scholar]
- Maqbool, H.F.; Husman, M.A.B.; Awad, M.I.; Abouhossein, A.; Mehryar, P.; Iqbal, N.; Dehghani-Sanij, A.A. Real-time gait event detection for lower limb amputees using a single wearable sensor. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 5067–5070. [Google Scholar]
- Picerno, P. 25 years of lower limb joint kinematics by using inertial and magnetic sensors: A review of methodological approaches. Gait Posture 2017, 51, 239–246. [Google Scholar] [CrossRef]
- Bolink, S.; Naisas, H.; Senden, R.; Essers, H.; Heyligers, I.; Meijer, K.; Grimm, B. Validity of an inertial measurement unit to assess pelvic orientation angles during gait, sit–stand transfers and step-up transfers: Comparison with an optoelectronic motion capture system. Med. Eng. Phys. 2016, 38, 225–231. [Google Scholar] [CrossRef]
- Janssen, W.G.; Bussmann, H.B.; Stam, H.J. Determinants of the sit-to-stand movement: A review. Phys. Ther. 2002, 82, 866–879. [Google Scholar] [CrossRef]
- Adusumilli, G.; Lancia, S.; Levasseur, V.A.; Amblee, V.; Orchard, M.; Wagner, J.M.; Naismith, R.T. Turning is an important marker of balance confidence and walking limitation in persons with multiple sclerosis. PLoS ONE 2018, 13, e0198178. [Google Scholar] [CrossRef]
- Panebianco, G.P.; Bisi, M.C.; Stagni, R.; Fantozzi, S. Analysis of the performance of 17 algorithms from a systematic review: Influence of sensor position, analysed variable and computational approach in gait timing estimation from IMU measurements. Gait Posture 2018, 66, 76–82. [Google Scholar] [CrossRef]
- Anwary, A.R.; Yu, H.; Vassallo, M. Optimal foot location for placing wearable IMU sensors and automatic feature extraction for gait analysis. IEEE Sens. J. 2018, 18, 2555–2567. [Google Scholar] [CrossRef]
- Kianifar, R.; Joukov, V.; Lee, A.; Raina, S.; Kulić, D. Inertial measurement unit-based pose estimation: Analyzing and reducing sensitivity to sensor placement and body measures. J. Rehabil. Assist. Technol. Eng. 2019, 6. [Google Scholar] [CrossRef]
- Hafsteinsdóttir, T.B.; Rensink, M.; Schuurmans, M. Clinimetric properties of the timed up and go test for patients with stroke: A systematic review. Top. Stroke Rehabil. 2014, 21, 197–210. [Google Scholar] [CrossRef] [PubMed]
- Mollinedo, I.; Ma Cancela, J. Evaluation of the psychometric properties and clinical applications of the Timed Up and Go test in Parkinson disease: A systematic review. J. Exerc. Rehabil. 2020, 16, 302–312. [Google Scholar] [CrossRef]
- Long, J.; Cai, T.; Huang, X.; Zhou, Y.; Kuang, J.; Wu, L. Reference value for the TUGT in healthy older people: A systematic review and meta-analysis. Geriatr. Nurs. 2020, 41, 325–330. [Google Scholar] [CrossRef] [PubMed]
- Kong, W.; Sessa, S.; Cosentino, S.; Zecca, M.; Saito, K.; Wang, C.; Imtiaz, U.; Lin, Z.; Bartolomeo, L.; Ishii, H. Development of a real-time IMU-based motion capture system for gait rehabilitation. In Proceedings of the 2013 IEEE International Conference on Robotics and Biomimetics (ROBIO), Shenzhen, China, 12–14 December 2013; pp. 2100–2105. [Google Scholar]
- Kwakkel, S.; Godha, S.; Lachapelle, G. Foot and Ankle Kinematics during Gait Using Foot Mounted Inertial System; ION NTM: San Diego, CA, USA, 2007. [Google Scholar]
- Palermo, E.; Rossi, S.; Marini, F.; Patanè, F.; Cappa, P. Experimental evaluation of accuracy and repeatability of a novel body-to-sensor calibration procedure for inertial sensor-based gait analysis. Measurement 2014, 52, 145–155. [Google Scholar] [CrossRef]
- Laudanski, A.; Brouwer, B.; Li, Q. Measurement of lower limb joint kinematics using inertial sensors during stair ascent and descent in healthy older adults and stroke survivors. J. Healthc. Eng. 2013, 4, 555–576. [Google Scholar] [CrossRef]
- Barrois, R.; Gregory, T.; Oudre, L.; Moreau, T.; Truong, C.; Pulini, A.A.; Vienne, A.; Labourdette, C.; Vayatis, N.; Buffat, S. An automated recording method in clinical consultation to rate the limp in lower limb osteoarthritis. PLoS ONE 2016, 11, e0164975. [Google Scholar] [CrossRef]
- Spain, R.; George, R.S.; Salarian, A.; Mancini, M.; Wagner, J.; Horak, F.; Bourdette, D. Body-worn motion sensors detect balance and gait deficits in people with multiple sclerosis who have normal walking speed. Gait Posture 2012, 35, 573–578. [Google Scholar] [CrossRef]
- Mancini, M.; Chiari, L.; Holmstrom, L.; Salarian, A.; Horak, F.B. Validity and reliability of an IMU-based method to detect APAs prior to gait initiation. Gait Posture 2016, 43, 125–131. [Google Scholar] [CrossRef]
- Esser, P.; Dawes, H.; Collett, J.; Feltham, M.G.; Howells, K. Assessment of spatio-temporal gait parameters using inertial measurement units in neurological populations. Gait Posture 2011, 34, 558–560. [Google Scholar] [CrossRef]
- Esser, P.; Dawes, H.; Collett, J.; Howells, K. IMU: Inertial sensing of vertical CoM movement. J. Biomech. 2009, 42, 1578–1581. [Google Scholar] [CrossRef]
- Doheny, E.P.; McGrath, D.; Greene, B.R.; Walsh, L.; McKeown, D.; Cunningham, C.; Crosby, L.; Kenny, R.A.; Caulfield, B. Displacement of centre of mass during quiet standing assessed using accelerometry in older fallers and non-fallers. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 3300–3303. [Google Scholar]
- Vargas-Valencia, L.S.; Elias, A.; Rocon, E.; Bastos-Filho, T.; Frizera, A. An IMU-to-body alignment method applied to human gait analysis. Sensors 2016, 16, 2090. [Google Scholar] [CrossRef] [PubMed]
- Bourgeois, A.B.; Mariani, B.; Aminian, K.; Zambelli, P.; Newman, C. Spatio-temporal gait analysis in children with cerebral palsy using, foot-worn inertial sensors. Gait Posture 2014, 39, 436–442. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Wu, D.; Liu, G.; Zhao, G.; Huang, B.; Wang, L. A low-cost body inertial-sensing network for practical gait discrimination of hemiplegia patients. Telemed. e-Health 2012, 18, 748–754. [Google Scholar] [CrossRef] [PubMed]
- Hsu, Y.-L.; Chung, P.-C.; Wang, W.-H.; Pai, M.-C.; Wang, C.-Y.; Lin, C.-W.; Wu, H.-L.; Wang, J.-S. Gait and balance analysis for patients with Alzheimer’s disease using an inertial-sensor-based wearable instrument. IEEE J. Biomed. Health Inform. 2014, 18, 1822–1830. [Google Scholar] [CrossRef]
- Tadano, S.; Takeda, R.; Miyagawa, H. Three dimensional gait analysis using wearable acceleration and gyro sensors based on quaternion calculations. Sensors 2013, 13, 9321–9343. [Google Scholar] [CrossRef]
- Scapellato, S.; Cavallo, F.; Martelloni, C.; Sabatini, A.M. In-use calibration of body-mounted gyroscopes for applications in gait analysis. Sens. Actuators A Phys. 2005, 123, 418–422. [Google Scholar] [CrossRef]
- Khan, A.; Biddiss, E. Musical Stairs: A motivational therapy tool for children with disabilities featuring automated detection of stair-climbing gait events via inertial sensors. Med. Eng. Phys. 2017, 40, 95–102. [Google Scholar] [CrossRef]
- Lau, H.; Tong, K. The reliability of using accelerometer and gyroscope for gait event identification on persons with dropped foot. Gait Posture 2008, 27, 248–257. [Google Scholar] [CrossRef]
- Rebula, J.R.; Ojeda, L.V.; Adamczyk, P.G.; Kuo, A.D. Measurement of foot placement and its variability with inertial sensors. Gait Posture 2013, 38, 974–980. [Google Scholar] [CrossRef]
- Rampp, A.; Barth, J.; Schülein, S.; Gaßmann, K.-G.; Klucken, J.; Eskofier, B.M. Inertial sensor-based stride parameter calculation from gait sequences in geriatric patients. IEEE Trans. Biomed. Eng. 2014, 62, 1089–1097. [Google Scholar] [CrossRef]
- Sijobert, B.; Denys, J.; Coste, C.A.; Geny, C. IMU based detection of freezing of gait and festination in parkinson’s disease. In Proceedings of the 2014 IEEE 19th International Functional Electrical Stimulation Society Annual Conference (IFESS), Kuala Lumpur, Malaysia, 7–19 September 2014. [Google Scholar]
- Pacher, L.; Chatellier, C.; Vauzelle, R.; Fradet, L. Sensor-to-segment calibration methodologies for lower-body kinematic analysis with inertial sensors: A systematic review. Sensors 2020, 20, 3322. [Google Scholar] [CrossRef] [PubMed]
- Dorschky, E.; Nitschke, M.; Seifer, A.-K.; van den Bogert, A.J.; Eskofier, B.M. Estimation of gait kinematics and kinetics from inertial sensor data using optimal control of musculoskeletal models. J. Biomech. 2019, 95, 109278. [Google Scholar] [CrossRef] [PubMed]
- Takeda, R.; Tadano, S.; Natorigawa, A.; Todoh, M.; Yoshinari, S. Gait posture estimation using wearable acceleration and gyro sensors. J. Biomech. 2009, 42, 2486–2494. [Google Scholar] [CrossRef] [PubMed]
- Ohtaki, Y.; Sagawa, K.; Inooka, H. A method for gait analysis in a daily living environment by body-mounted instruments. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 2001, 44, 1125–1132. [Google Scholar] [CrossRef]
| Body Segment | Location | Number of Sources | Sources |
|---|---|---|---|
| Pelvis | L4-L5 | 8 | Laudanski 2013 [19], Panebianco 2018 [10], Barrois 2016 [20], Spain 2012 [21], Mancini 2016 [22], Esser 2011 [23], Esser 2009 [24], Doheny 2012 [25] |
| Sacrum | 2 * | Vargas-Valencia 2016 [26] | |
| Foot | Dorsal foot | 13 * | Laudanski 2013 [19], Panebianco 2018 [10], Barrois 2016 [20], Vargas-Valencia 2016 [26], Bourgeois 2014 [27], Guo 2012 [28], Hsu 2014 [29], Tadano 2013 [30], Kong 2013 [16], Scapellato 2005 [31], Kwakkel 2007 [17], Anwary 2018 [11] |
| Heel | 5 | Kwakkel 2007 [17], Anwary 2018 [11], Khan 2017 [32], Lau 2008 [33], Rebula 2013 [34] | |
| Lateral, below lateral malleolus | 3 | Anwary 2018 [11], Rampp 2014 [35], Reinfelder 2015 [4] | |
| Shank | Lateral mid-shank | 2 | Laudanski 2013 [19], Kong 2013 [16] |
| Flat surface of shin bone | 1 * | ||
| Lateral, just above lateral malleolus | 4 | Panebianco 2018 [10], Vargas-Valencia 2016, Guo 2012 [28], Sijobert 2014 [36] | |
| Anterior | 4 | Spain 2012 [21], Tadano 2013 [30], Kwakkel 2007 [17], Maqbool 2016 [5] | |
| Tibial tuberosity | 1 | Lau 2008 [33] | |
| Thigh | Lateral mid-thigh | 3 * | Laudanski 2013 [19], Kong 2013 [16] |
| Lateral near knee | 2 | Vargas-Valencia 2016 [26], Guo 2012 [28] | |
| Anterior near knee | 2 | Tadano 2013 [30], Lau 2008 [33] |
| Torso | L4-L5 | L4/L5 lumbar spine |
| Sacrum | on the sacrum | |
| Thigh | LAT | Lower Anterior Thigh: anterior thigh, 5 cm above the knee joint axis. |
| MLT | Middle Lateral Thigh: lateral thigh, halfway between the hip and knee joints. | |
| LLT | Lower Lateral Thigh: lateral thigh, 5 cm above the knee joint axis. | |
| LPT | Lower Posterior Thigh: posterior thigh, 5 cm above the knee joint axis. | |
| Shank | Shin | Shin Bone: hard surface of tibial bone, below the knee and above the thickest part of the calf. |
| MLS | Middle Lateral Shank: lateral shank, halfway between the knee and ankle. | |
| LLS | Lower Lateral Shank: lateral shank, 5 cm above the lateral malleolus. | |
| Foot | Heel | Adhered to heel on the back of participant’s shoe |
| DFoot | Dorsal Foot: under the tongue of the participant’s shoe, approximately over the distal end of the third and fourth metatarsal bones. |
| Sit-to-Stand | Starts when participant begins to lean forward; ends with first heel strike |
| Walk Pass 1 | Starts with first heel strike; ends with final toe off prior to participant turning |
| Turn 1 | Starts with final toe off prior to starting turn; ends with first heel strike out of turn |
| Walk Pass 2 | Starts with first heel strike out of turn; ends with final toe off prior to participant turning |
| Turn 2 | Starts with final toe off prior to starting turn; ends when participant begins to bend knees to sit |
| Stand-to-Sit | Starts when participant begins to bend knees to sit; ends when participant is seated upright |
| Sit to Stand | Shin | MLS | LLS | ||||
| Heel (n = 19 from 5 subs) | DFoot (n = 20 from 6 subs) | Heel (n = 19 from 5 subs) | DFoot (n = 20 from 6 subs) | Heel (n = 19 from 5 subs) | DFoot (n = 20 from 6 subs) | ||
| Bias | −1.98 (0.81) | −1.00 (0.93) | −1.44 (0.62) | −0.40 (0.85) | −1.30 (0.64) | 0.09 (0.96) | |
| p value * | 0.015 | 0.280 | 0.021 | 0.639 | 0.042 | 0.927 | |
| RMSE | 3.18 (0.66) | 2.86 (0.50) | 2.41 (0.48) | 2.33 (0.57) | 2.72 (0.25) | 2.69 (0.58) | |
| p value * | 0.332 | 0.271 | 0.866 | n/a | 0.351 | 0.265 | |
| Stand to Sit | Shin | MLS | LLS | ||||
| Heel (n = 16 from 5 subs) | DFoot (n = 17 from 6 subs) | Heel (n = 16 from 5 subs) | DFoot (n = 17 from 6 subs) | Heel (n = 16 from 5 subs) | DFoot (n = 17 from 6 subs) | ||
| Bias | −1.53 (1.19) | −1.87 (1.25) | −0.76 (1.13) | −0.83 (1.03) | −0.56 (1.41) | −0.43 (1.19) | |
| p value * | 0.200 | 0.135 | 0.498 | 0.418 | 0.691 | 0.717 | |
| RMSE | 3.80 (0.49) | 3.73 (0.68) | 2.71 (0.71) | 2.58 (0.61) | 3.31 (0.49) | 2.89 (0.57) | |
| p value # | 0.026 | 0.114 | 0.538 | n/a | 0.009 | 0.444 | |
| Turn 1 | Shin | MLS | LLS | ||||
| Heel (n = 19 from 5 subs) | DFoot (n = 20 from 6 subs) | Heel (n = 19 from 5 subs) | DFoot (n = 20 from 6 subs) | Heel (n = 19 from 5 subs) | DFoot (n = 20 from 6 subs) | ||
| Bias | −0.84 (0.60) | −1.10 (1.09) | −1.68 (0.39) | −1.96 (0.63) | 0.02 (1.11) | −1.58 (0.66) | |
| p value * | 0.167 | 0.316 | < 0.001 | 0.002 | 0.989 | 0.017 | |
| RMSE | 4.51 (0.66) | 4.56 (0.66) | 3.94 (0.45) | 4.13 (0.68) | 4.54 (0.71) | 4.21 (0.53) | |
| p value * | 0.124 | 0.070 | n/a | 0.762 | 0.311 | 0.647 | |
| Turn 2 | Shin | MLS | LLS | ||||
| Heel (n = 19 from 5 subs) | DFoot (n = 20 from 6 subs) | Heel (n = 19 from 5 subs) | DFoot (n = 20 from 6 subs) | Heel (n = 19 from 5 subs) | DFoot (n = 20 from 6 subs) | ||
| Bias | 0.79 (0.88) | −1.56 (0.73) | −1.09 (0.56) | −2.35 (0.54) | −1.49 (1.48) | −1.76 (0.75) | |
| p value * | 0.373 | 0.033 | 0.052 | < 0.001 | 0.314 | 0.020 | |
| RMSE | 3.93 (0.68) | 4.71 (0.70) | 3.85 (0.58) | 4.58 (0.77) | 5.49 (0.91) | 4.74 (0.59) | |
| p value # | 0.626 | 0.016 | n/a | 0.095 | 0.077 | 0.030 | |
| Walk (1 and 2) | Shin | MLS | LLS | ||||
| Heel (n = 38 from 5 subs) | DFoot (n = 40 from 6 subs) | Heel (n = 38 from 5 subs) | DFoot (n = 40 from 6 subs) | Heel (n = 38 from 5 subs) | DFoot (n = 40 from 6 subs) | ||
| Bias | 0.97 (0.84) | −0.39 (0.90) | −0.16 (0.65) | −1.10 (0.53) | 1.03(0.73) | −0.05 (0.52) | |
| p value * | 0.246 | 0.662 | 0.801 | 0.038 | 0.157 | 0.927 | |
| RMSE | 4.10 (0.56) | 4.44 (0.46) | 3.40 (0.32) | 3.90 (0.32) | 3.95 (0.51) | 3.59 (0.31) | |
| p value # | 0.035 | 0.005 | n/a | 0.238 | 0.118 | 0.532 | |
| Sit to Stand | Shin | MLS | LLS | ||||||||||
| LAT (n = 25 from 7 subs) | MLT (n = 25 from 7 subs) | LLT (n = 25 from 7 subs) | LPT (n = 25 from 7 subs) | LAT (n = 25 from 7 subs) | MLT (n = 25 from 7 subs) | LLT (n = 25 from 7 subs) | LPT (n = 25 from 7 subs) | LAT (n = 25 from 7 subs) | MLT (n = 25 from 7 subs) | LLT (n = 25 from 7 subs) | LPT (n = 25 from 7 subs) | ||
| Bias | −2.49 (1.21) | −3.19 (1.07) | −7.06 (1.52) | −0.87 (1.53) | −2.14 (1.36) | −2.75 (1.17) | −6.58 (1.62) | −0.51 (1.68) | −1.91 (1.21) | −2.62 (1.39) | −6.46 (1.68) | −0.24 (1.58) | |
| p value * | 0.039 | 0.003 | <0.001 | 0.569 | 0.114 | 0.019 | <0.001 | 0.763 | 0.114 | 0.060 | <0.001 | 0.881 | |
| RMSE | 5.51 (0.86) | 5.58 (1.04) | 9.31 (1.59) | 5.05 (1.29) | 5.23 (0.93) | 5.23 (1.08) | 8.64 (1.66) | 4.93 (1.42) | 4.82 (0.79) | 5.37 (1.15) | 8.32 (1.67) | 4.93 (1.23) | |
| p value # | 0.013 | 0.307 | <0.001 | 0.817 | 0.134 | 0.558 | 0.001 | 0.923 | n/a | 0.486 | 0.003 | 0.911 | |
| Stand to Sit | Shin | MLS | LLS | ||||||||||
| LAT (n = 21 from 7 subs) | MLT (n = 21 from 7 subs) | LLT (n = 21 from 7 subs) | LPT (n = 21 from 7 subs) | LAT (n = 21 from 7 subs) | MLT (n = 21 from 7 subs) | LLT (n = 21 from 7 subs) | LPT (n = 21 from 7 subs) | LAT (n = 21 from 7 subs) | MLT (n = 21 from 7 subs) | LLT (n = 21 from 7 subs) | LPT (n = 21 from 7 subs) | ||
| Bias | −1.27 (1.57) | −1.34 (1.41) | −7.00 (2.08) | 1.33 (1.41) | −0.76 (1.70) | −0.63 (1.61) | −6.27 (2.23) | 1.89 (1.63) | −0.75 (1.68) | −0.69 (1.89) | −6.35 (2.36) | 1.91 (1.62) | |
| p value * | 0.417 | 0.343 | 0.001 | 0.344 | 0.655 | 0.695 | 0.005 | 0.246 | 0.656 | 0.715 | 0.007 | 0.240 | |
| RMSE | 6.16 (0.54) | 5.13 (0.78) | 8.82 (2.07) | 5.67 (0.88) | 5.79 (0.69) | 4.74 (0.93) | 7.78 (2.2) | 5.75 (1.06) | 5.34 (0.72) | 4.78 (1.23) | 7.27 (2.49) | 5.56 (0.99) | |
| p value # | 0.072 | 0.262 | 0.010 | 0.512 | 0.148 | n/a | 0.047 | 0.538 | 0.178 | 0.935 | 0.140 | 0.621 | |
| Turn 1 | Shin | MLS | LLS | ||||||||||
| LAT (n = 25 from 7 subs) | MLT (n = 25 from 7 subs) | LLT (n = 25 from 7 subs) | LPT (n = 25 from 7 subs) | LAT (n = 25 from 7 subs) | MLT (n = 25 from 7 subs) | LLT (n = 25 from 7 subs) | LPT (n = 25 from 7 subs) | LAT (n = 25 from 7 subs) | MLT (n = 25 from 7 subs) | LLT (n = 25 from 7 subs) | LPT (n = 25 from 7 subs) | ||
| Bias | 1.19 (1.06) | 1.62 (1.25) | −0.53 (1.22) | 3.44 (0.76) | 0.08 (1.01) | 0.61 (1.12) | −1.59 (1.15) | 2.3 (0.95) | 1.19 (0.67) | 1.76 (0.70) | −0.49 (0.50) | 3.42 (0.78) | |
| p value * | 0.265 | 0.195 | 0.664 | <0.001 | 0.934 | 0.588 | 0.168 | 0.015 | 0.076 | 0.012 | 0.326 | <0.001 | |
| RMSE | 6.26 (0.56) | 6.81 (0.79) | 6.31 (0.86) | 6.76 (0.71) | 6.23 (0.60) | 6.64 (0.66) | 6.29 (0.90) | 6.32 (0.68) | 6.37 (0.64) | 6.81 (0.72) | 6.13 (0.77) | 6.94 (0.69) | |
| p value # | 0.765 | 0.327 | 0.489 | 0.405 | 0.814 | 0.428 | 0.493 | 0.840 | 0.611 | 0.292 | n/a | 0.217 | |
| Turn 2 | Shin | MLS | LLS | ||||||||||
| LAT (n = 25 from 7 subs) | MLT (n = 25 from 7 subs) | LLT (n = 25 from 7 subs) | LPT (n = 25 from 7 subs) | LAT (n = 25 from 7 subs) | MLT (n = 25 from 7 subs) | LLT (n = 25 from 7 subs) | LPT (n = 25 from 7 subs) | LAT (n = 25 from 7 subs) | MLT (n = 25 from 7 subs) | LLT (n = 25 from 7 subs) | LPT (n = 25 from 7 subs) | ||
| Bias | 1.77 (0.71) | 2.61 (0.93) | 0.10 (0.56) | 4.12 (1.05) | 0.11 (0.92) | 1.03 (0.94) | −1.51 (0.90) | 2.41 (0.88) | −0.52 (1.62) | 0.5 (1.46) | −2.2 (1.63) | 1.76 (1.29) | |
| p value * | 0.013 | 0.005 | 0.858 | <0.001 | 0.904 | 0.272 | 0.094 | 0.006 | 0.749 | 0.730 | 0.178 | 0.173 | |
| RMSE | 5.4 (0.54) | 4.84 (1.01) | 4.62 (0.63) | 5.68 (0.88) | 5.48 (0.58) | 4.63 (0.82) | 4.96 (0.92) | 4.98 (0.68) | 6.37(0.89) | 6.01 (1.17) | 5.96 (1.33) | 5.93 (0.86) | |
| p value # | 0.150 | 0.756 | n/a | 0.014 | 0.019 | 0.979 | 0.481 | 0.506 | <0.001 | 0.024 | 0.153 | 0.013 | |
| Walk (1 and 2) | Shin | MLS | LLS | ||||||||||
| LAT (n = 50 from 7 subs) | MLT (n = 50 from 7 subs) | LLT (n = 50 from 7 subs) | LPT (n = 50 from 7 subs) | LAT (n = 50 from 7 subs) | MLT (n = 50 from 7 subs) | LLT (n = 50 from 7 subs) | LPT (n = 50 from 7 subs) | LAT (n = 50 from 7 subs) | MLT (n = 50 from 7 subs) | LLT (n = 50 from 7 subs) | LPT (n = 50 from 7 subs) | ||
| Bias | −0.45 (0.79) 0.573 | 1.65 (0.76) | −0.80 (0.67) 0.234 | 2.76 (0.5) | −1.43 (1.07) 0.181 | 0.71 (0.94) 0.451 | −1.75 (0.97) 0.071 | 1.75 (0.94) 0.062 | −0.41(1.05) 0.697 | 1.78 (0.73) | −0.79 (0.89) 0.376 | 2.73 (0.86) | |
| p value * | 0.030 | <0.001 | 0.015 | 0.002 | |||||||||
| RMSE | 6.02 (0.34) | 6.48 (0.37) | 6.02 (0.56) | 6.05 (0.33) | 6.37 (0.50) | 6.53 (0.44) | 6.30 (0.66) | 5.83 (0.41) | 6.43 (0.41) | 7.24 (0.41) | 6.38 (0.59) | 6.51 (0.42) | |
| p value # | 0.717 | 0.226 | 0.785 | 0.276 | 0.428 | 0.230 | 0.566 | n/a | 0.319 | 0.014 | 0.468 | 0.001 | |
| Sit to Stand | Sacrum | L4–L5 | |||||||
| LAT (n = 25 from 7 subs) | MLT (n = 25 from 7 subs) | LLT (n = 25 from 7 subs) | LPT (n = 25 from 7 subs) | LAT (n = 25 from 7 subs) | MLT (n = 25 from 7 subs) | LLT (n = 25 from 7 subs) | LPT (n = 25 from 7 subs) | ||
| Bias | 0.41 (2.78) | −0.33 (2.79) | −4.11 (2.97) | 2.13 (2.85) | 9.50 (5.00) | 8.76 (4.27) | 4.98 (4.50) | 11.21 (5.31) | |
| p value * | 0.882 | 0.907 | 0.167 | 0.455 | 0.058 | 0.040 | 0.268 | 0.035 | |
| RMSE | 6.95 (1.53) | 6.76 (1.49) | 7.03 (1.41) | 8.44 (1.39) | 15.59 (3.70) | 14.39 (3.13) | 12.69 (2.57) | 17.89 (3.76) | |
| p value # | 0.759 | n/a | 0.839 | 0.124 | 0.045 | 0.043 | 0.067 | 0.014 | |
| Stand to Sit | Sacrum | L4–L5 | |||||||
| LAT (n = 21 from 7 subs) | MLT (n = 21 from 7 subs) | LLT (n = 21 from 7 subs) | LPT (n = 21 from 7 subs) | LAT (n = 21 from 7 subs) | MLT (n = 21 from 7 subs) | LLT (n = 21 from 7 subs) | LPT (n = 21 from 7 subs) | ||
| Bias | 1.55 (3.48) | 1.37 (3.50) | −4.23 (3.92) | 4.33 (3.29) | 13.53 (5.75) | 13.39 (5.14) | 7.75 (5.17) | 16.30 (6.43) | |
| p value * | 0.657 | 0.695 | 0.280 | 0.189 | 0.019 | 0.009 | 0.134 | 0.011 | |
| RMSE | 7.18 (2.01) | 6.95 (2.04) | 7.32 (1.40) | 9.31 (1.53) | 18.28 (4.06) | 17.31 (3.71) | 14.41 (2.80) | 21.46 (4.52) | |
| p value # | 0.790 | n/a | 0.863 | 0.036 | 0.026 | 0.025 | 0.054 | 0.012 | |
| Turn 1 | Sacrum | L4–L5 | |||||||
| LAT (n = 25 from 7 subs) | MLT (n = 25 from 7 subs) | LLT (n = 25 from 7 subs) | LPT (n = 25 from 7 subs) | LAT (n = 25 from 7 subs) | MLT (n = 25 from 7 subs) | LLT (n = 25 from 7 subs) | LPT (n = 25 from 7 subs) | ||
| Bias | −1.12 (1.65) | −0.38 (2.20) | −2.34 (2.06) | 1.38 (1.91) | 2.16 (1.75) | 2.84 (1.62) | 0.91 (1.55) | 4.65 (2.17) | |
| p value * | 0.497 | 0.862 | 0.255 | 0.471 | 0.219 | 0.081 | 0.558 | 0.032 | |
| RMSE | 5.36 (0.58) | 6.30 (0.95) | 5.34 (1.18) | 6.06 (0.74) | 6.22 (0.67) | 6.48 (0.77) | 5.20 (0.63) | 7.93 (1.11) | |
| p value # | 0.876 | 0.384 | 0.917 | 0.489 | 0.120 | 0.010 | n/a | 0.002 | |
| Turn 2 | Sacrum | L4–L5 | |||||||
| LAT (n = 25 from 7 subs) | MLT (n = 25 from 7 subs) | LLT (n = 25 from 7 subs) | LPT (n = 25 from 7 subs) | LAT (n = 25 from 7 subs) | MLT (n = 25 from 7 subs) | LLT (n = 25 from 7 subs) | LPT (n = 25 from 7 subs) | ||
| Bias | −1.00 (1.50) | 0.13 (2.24) | −2.31 (1.82) | 1.57 (1.93) | 2.93 (1.94) | 4.04 (2.14) | 1.59 (1.93) | 5.50 (2.71) | |
| p value * | 0.505 | 0.954 | 0.204 | 0.416 | 0.131 | 0.059 | 0.410 | 0.042 | |
| RMSE | 4.47 (0.64) | 5.21 (1.44) | 4.74 (0.87) | 5.34 (0.95) | 6.95 (0.99) | 7.14 (1.28) | 5.91 (1.04) | 8.75 (1.68) | |
| p value # | n/a | 0.399 | 0.615 | 0.095 | 0.078 | 0.070 | 0.316 | 0.039 | |
| Walk (1 and 2) | Sacrum | L4–L5 | |||||||
| LAT (n = 50 from 7 subs) | MLT (n = 50 from 7 subs) | LLT (n = 50 from 7 subs) | LPT (n = 50 from 7 subs) | LAT (n = 50 from 7 subs) | MLT (n = 50 from 7 subs) | LLT (n = 50 from 7 subs) | LPT (n = 50 from 7 subs) | ||
| Bias | −3.08 (1.65) | −0.89 (1.97) | −3.21 (1.85) | 0.14 (1.83) | −0.29 (1.57) | 1.86 (1.53) | −0.47 (1.45) | 2.92 (2.01) | |
| p value * | 0.062 | 0.652 | 0.082 | 0.939 | 0.852 | 0.225 | 0.747 | 0.147 | |
| RMSE | 5.95 (0.90) | 6.65 (0.80) | 5.37 (1.08) | 5.78 (0.87) | 5.74 (0.64) | 6.46 (0.64) | 4.35 (0.64) | 7.10 (0.76) | |
| p value # | 0.171 | 0.025 | 0.463 | 0.201 | <0.001 | 0.002 | n/a | 0.003 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niswander, W.; Wang, W.; Kontson, K. Optimization of IMU Sensor Placement for the Measurement of Lower Limb Joint Kinematics. Sensors 2020, 20, 5993. https://doi.org/10.3390/s20215993
Niswander W, Wang W, Kontson K. Optimization of IMU Sensor Placement for the Measurement of Lower Limb Joint Kinematics. Sensors. 2020; 20(21):5993. https://doi.org/10.3390/s20215993
Chicago/Turabian StyleNiswander, Wesley, Wei Wang, and Kimberly Kontson. 2020. "Optimization of IMU Sensor Placement for the Measurement of Lower Limb Joint Kinematics" Sensors 20, no. 21: 5993. https://doi.org/10.3390/s20215993
APA StyleNiswander, W., Wang, W., & Kontson, K. (2020). Optimization of IMU Sensor Placement for the Measurement of Lower Limb Joint Kinematics. Sensors, 20(21), 5993. https://doi.org/10.3390/s20215993




