Pervasive Lying Posture Tracking
Abstract
1. Introduction
2. Background & Related Studies
2.1. Multi-Sensor Lying Posture Tracking
2.2. Single-Sensor Lying Posture Tracking
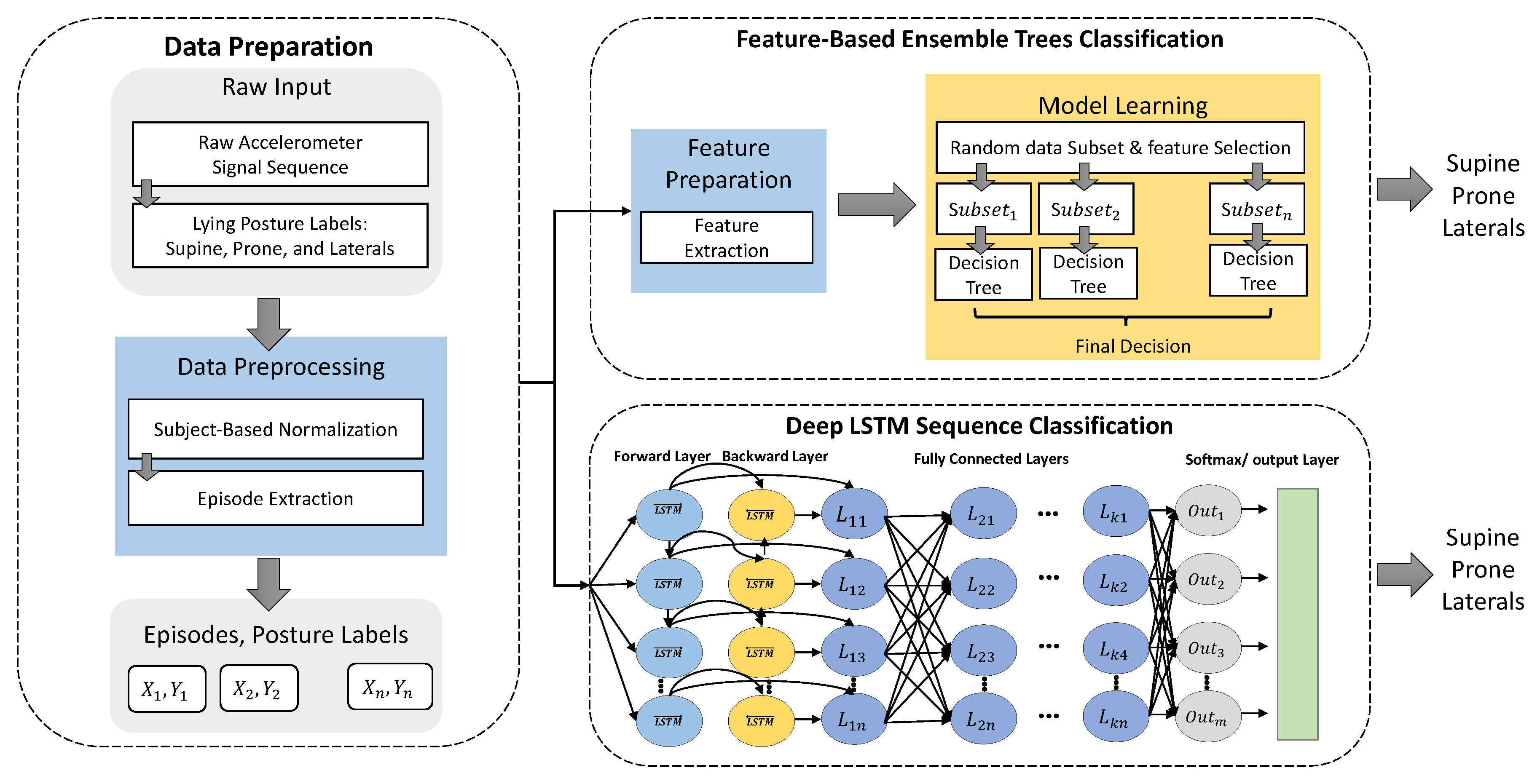
3. Methodologies
3.1. Data Preparation
3.2. Traditional Lying Posture Tracking
3.2.1. Feature Preparation
3.2.2. Ensemble Model Learning
3.3. Deep Lying Posture Tracking
4. Experimental Evaluation
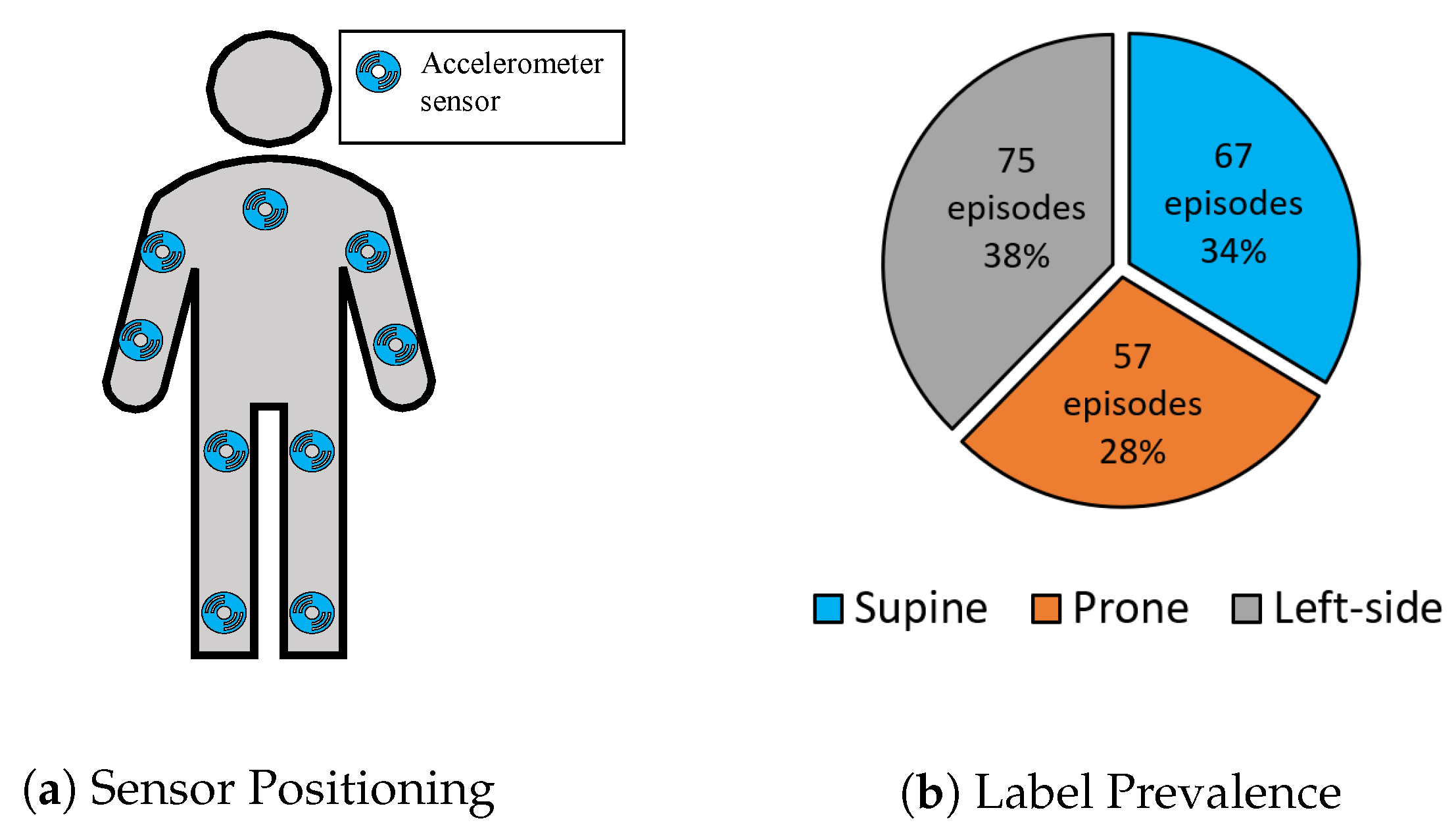
4.1. Datasets & Preprocessing
4.1.1. Class-Act: Datasets from a Human Posture/Activity Classification
4.1.2. Daily and Sports Activities Dataset (Das)
4.1.3. Integrated Dataset
4.2. Comparison Metrics and Implementation Details
5. Results
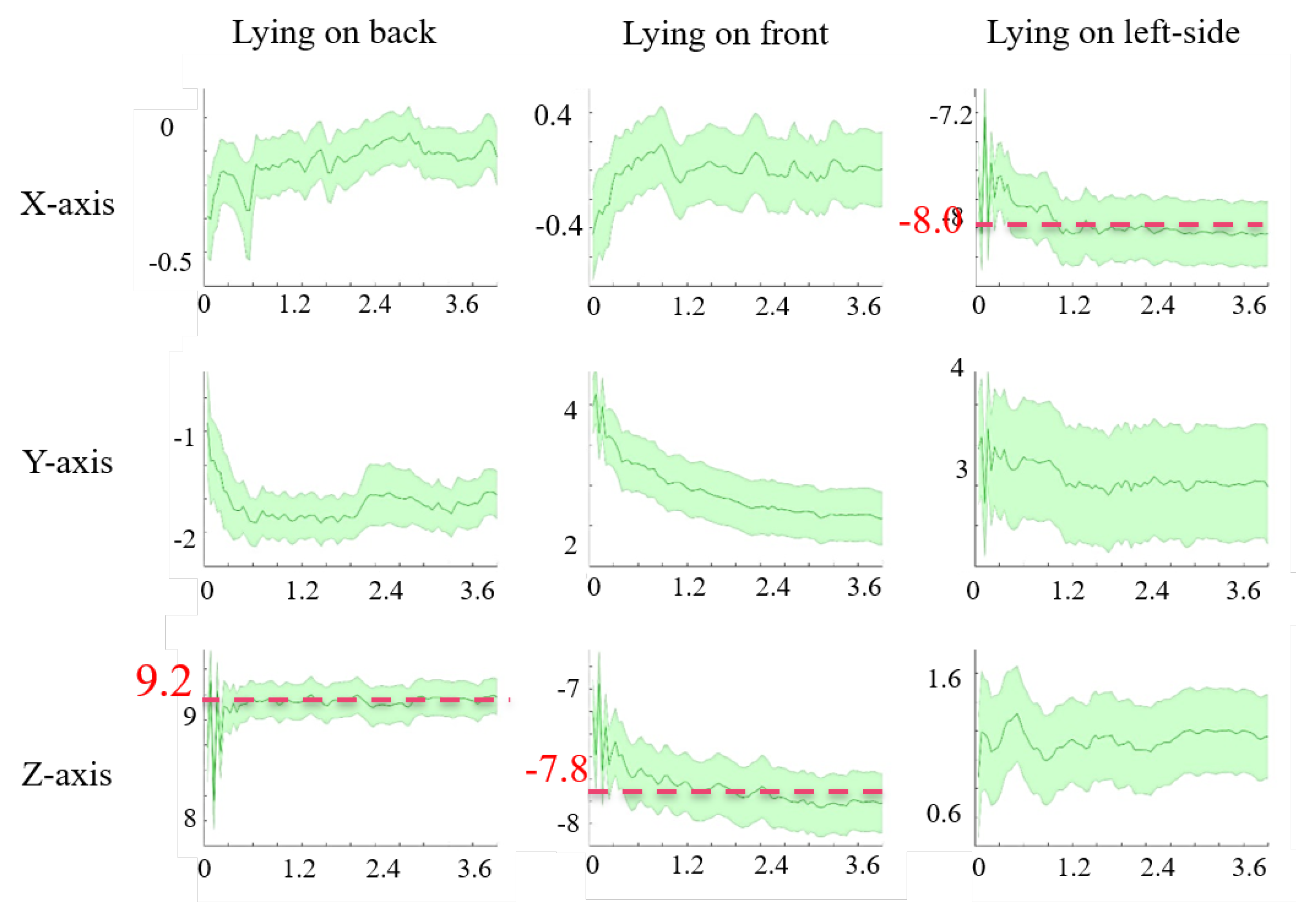
5.1. Raw Data Inspection
5.2. Traditional Machine Learning
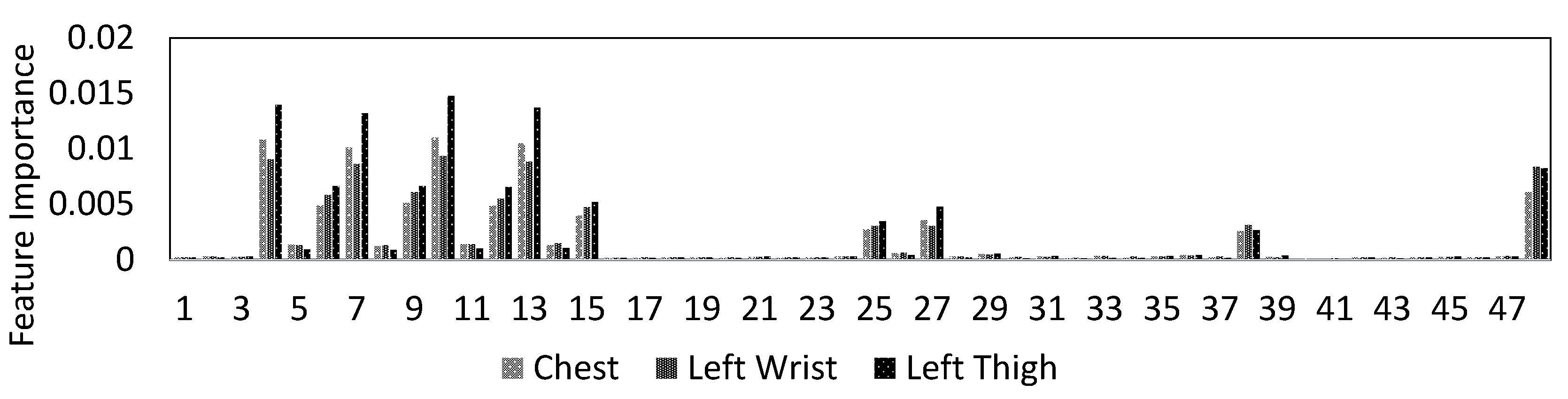
5.2.1. Feature Engineering
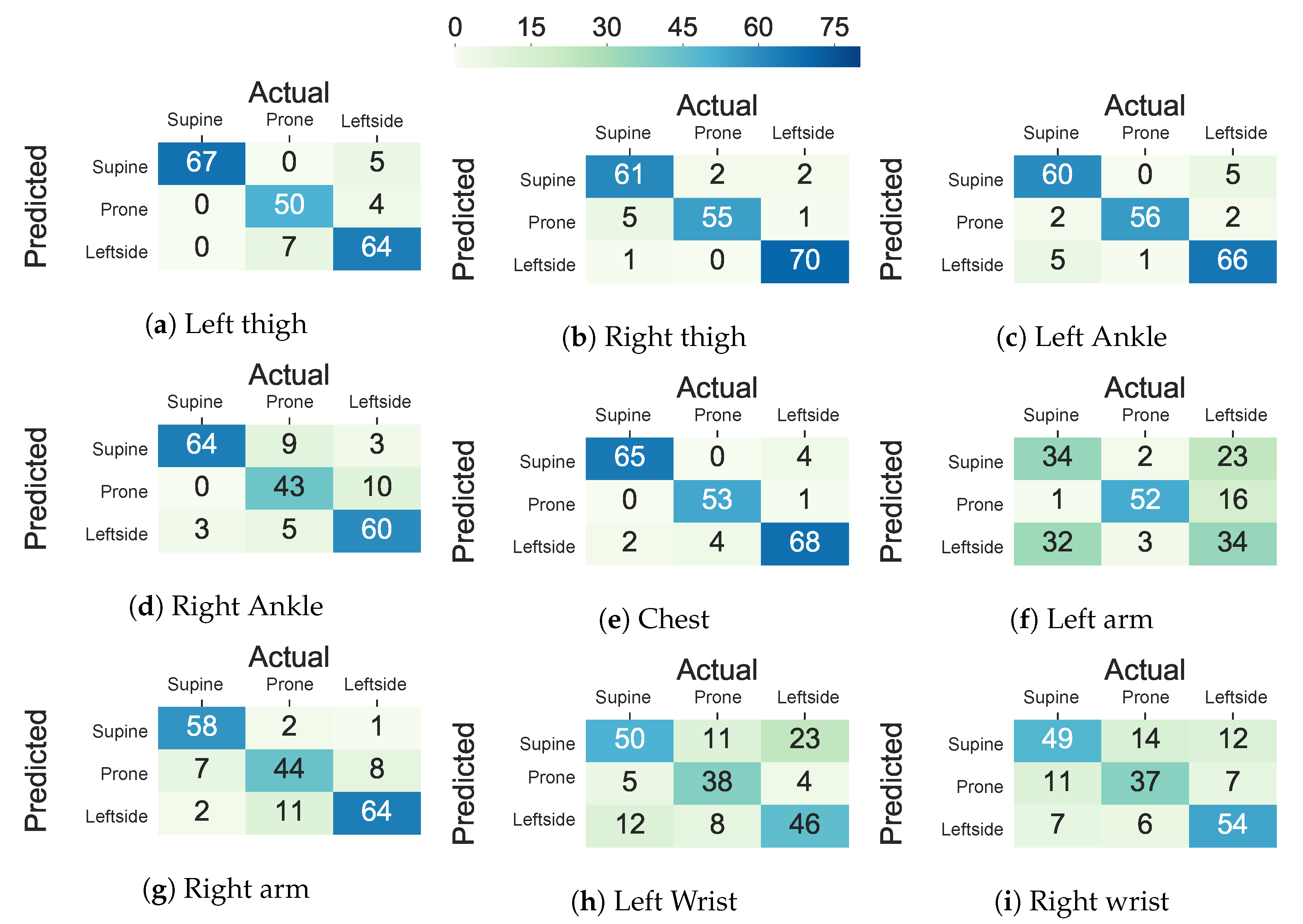
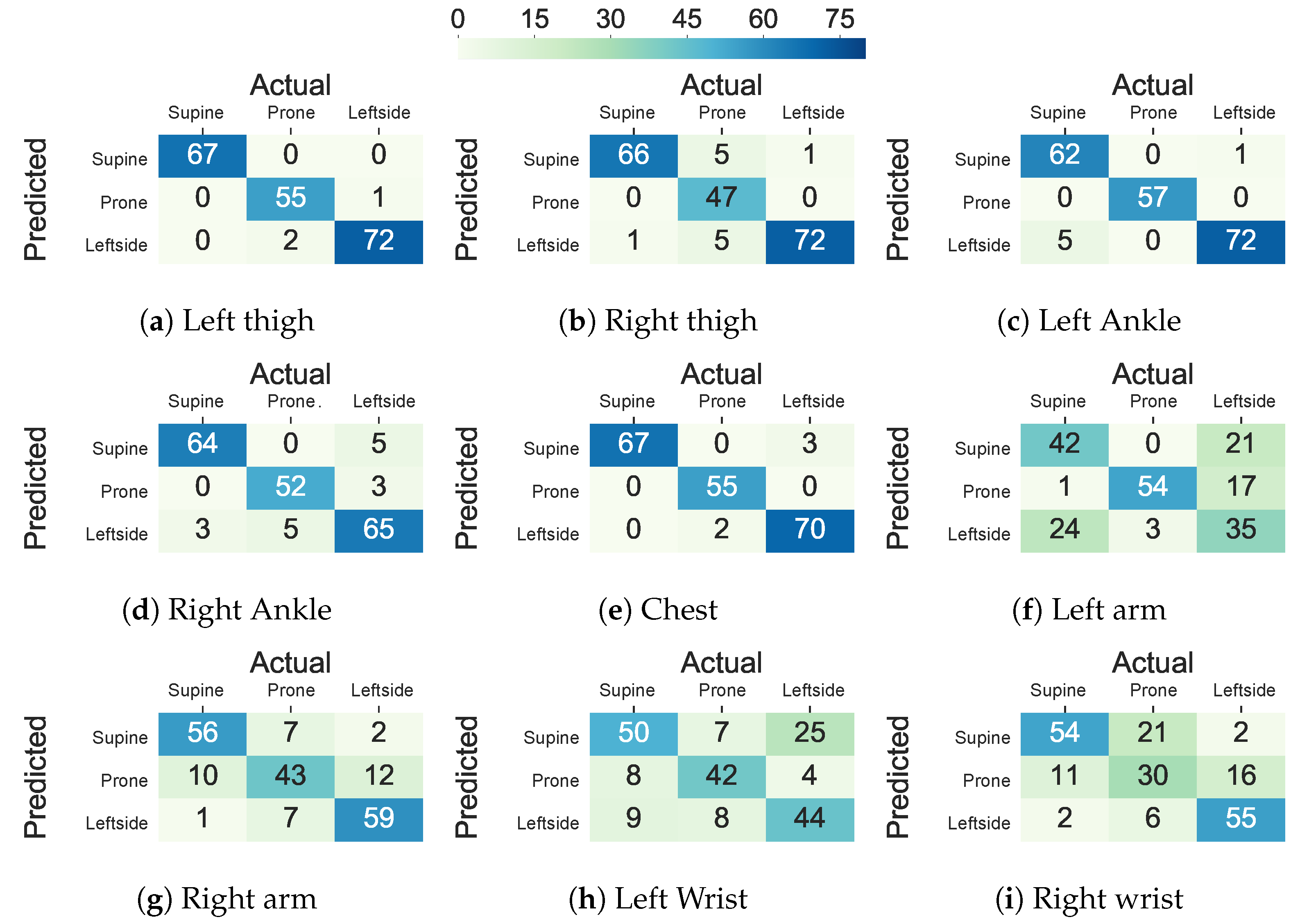
5.2.2. Lying Posture Detection
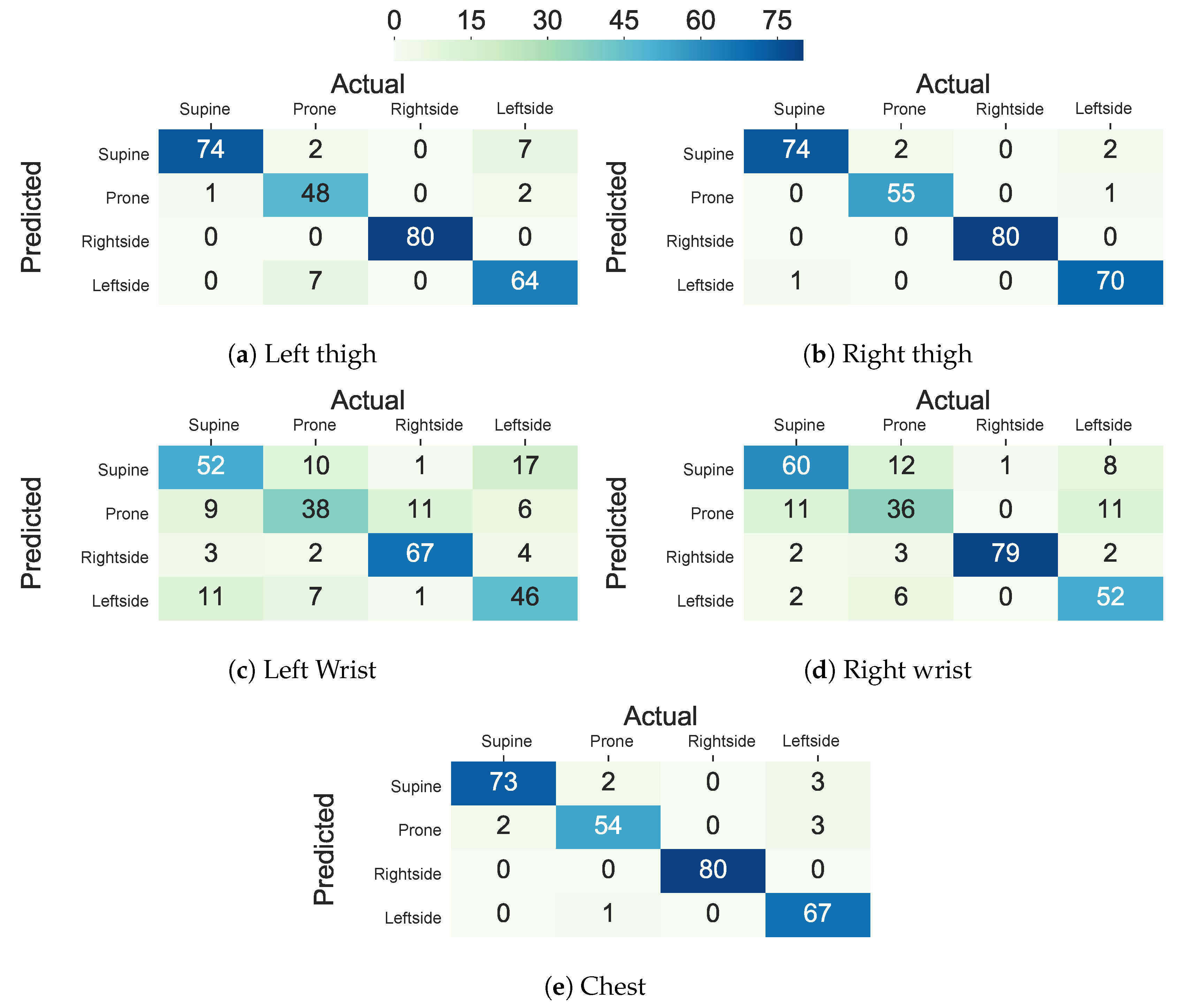
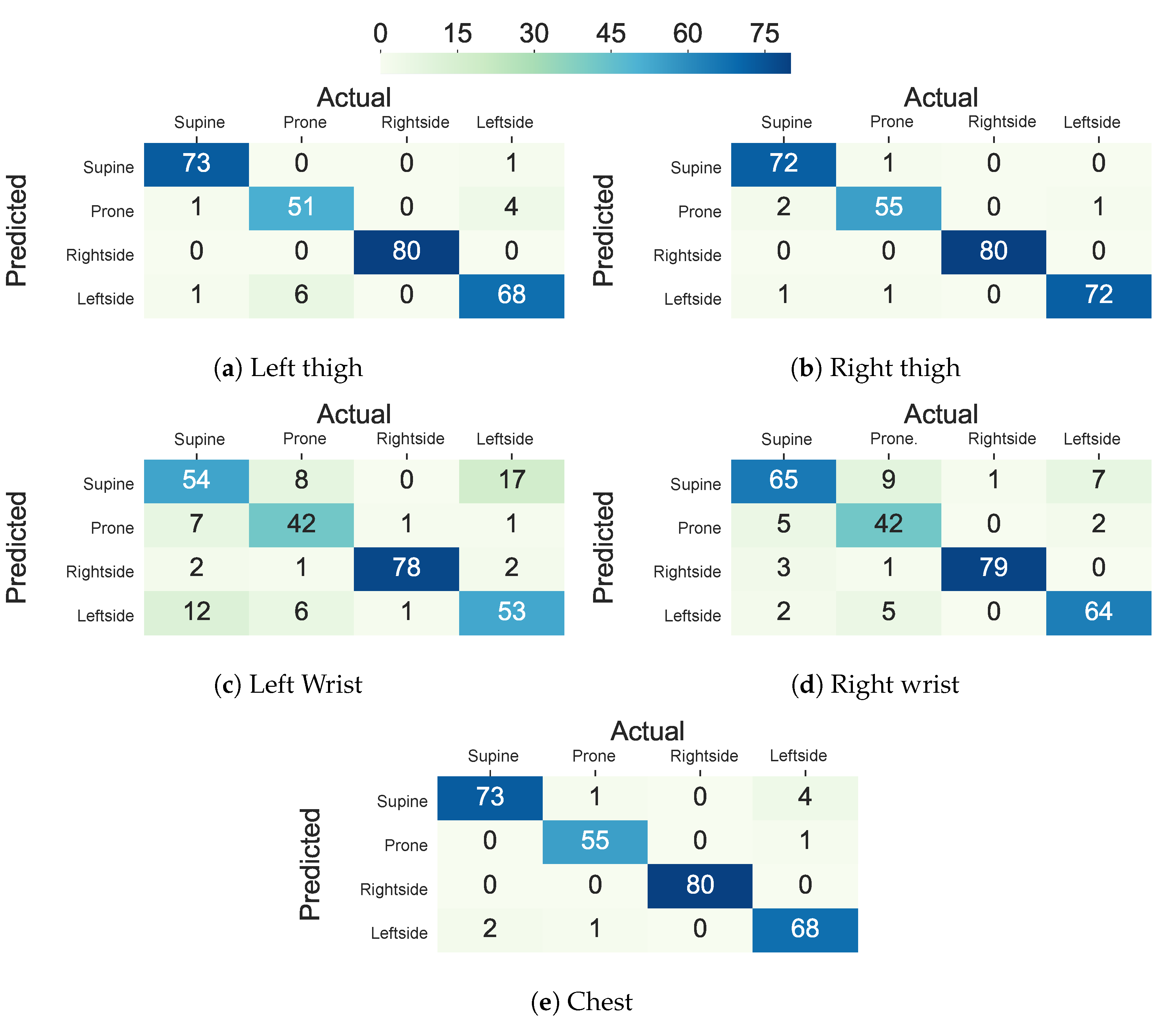
5.3. Deep Sequence Learning
5.4. Deep Learning vs. Traditional Machine Learning
5.5. Comparison with the State-Of-The-Art
- ET is the proposed feature-based classifier, which is an ensemble of decision trees trained on 48 time-domain features.
- AdaLSTM is the proposed deep learning model, which is an adaptive long short-term memory network with Adam optimizer and decaying learning rate.
- LDA, as proposed by Zhang et al., is a linear discriminate analysis (LDA) classifier trained on the mean value of the signal [11].
- SVM, as proposed by Jeng et al., is a multi-class linear kernel support vector machine classifier trained on the mean value of the tri-axial accelerometer signal [31].
- LSTM is a long short-term memory network with the same structure as the AdaLSTM, but with a fixed learning rate of 0.01.
5.5.1. Class-Act Dataset
5.5.2. Integrated Dataset
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LSTM | Long Short-Term Memory |
| Bi-LSTM | Bidirectional Long Short-Term Memory |
| AdaLSTM | Adaptive Long Short-Term Memory |
| ML | Machine Learning |
| DL | Deep Learning |
| RNN | Recurrent Neural Network |
| DAS | Daily and Sports |
References
- Azuh, O.; Gammon, H.; Burmeister, C.; Frega, D.; Nerenz, D.; DiGiovine, B.; Siddiqui, A. Benefits of early active mobility in the medical intensive care unit: A pilot study. Am. J. Med. 2016, 129, 866–871. [Google Scholar] [CrossRef] [PubMed]
- Hoyer, E.H.; Friedman, M.; Lavezza, A.; Wagner-Kosmakos, K.; Lewis-Cherry, R.; Skolnik, J.L.; Byers, S.P.; Atanelov, L.; Colantuoni, E.; Brotman, D.J.; et al. Promoting mobility and reducing length of stay in hospitalized general medicine patients: A quality-improvement project. J. Hosp. Med. 2016, 11, 341–347. [Google Scholar] [CrossRef] [PubMed]
- Neilson, J.; Avital, L.; Willock, J.; Broad, N. Using a national guideline to prevent and manage pressure ulcers. Nurs. Manag. 2014, 21, 18–21. [Google Scholar] [CrossRef][Green Version]
- Kloster, R.; Engelskjøn, T. Sudden unexpected death in epilepsy (SUDEP): A clinical perspective and a search for risk factors. J. Neurol. Neurosurg. Psychiatry 1999, 67, 439–444. [Google Scholar] [CrossRef]
- Venkateshiah, S.B.; Collop, N.A. Sleep and sleep disorders in the hospital. Chest 2012, 141, 1337–1345. [Google Scholar] [CrossRef]
- Dwyer, T.; Ponsonby, A.L.; Newman, N.M.; Gibbons, L.E. Prospective cohort study of prone sleeping position and sudden infant death syndrome. Lancet 1991, 337, 1244–1247. [Google Scholar] [CrossRef]
- Lee, M.; Choh, A.; Demerath, E.; Knutson, K.; Duren, D.; Sherwood, R.; Sun, S.; Chumlea, W.C.; Towne, B.; Siervogel, R.; et al. Sleep disturbance in relation to health-related quality of life in adults: The Fels Longitudinal Study. J. Nutr. Health Aging 2009, 13, 576–583. [Google Scholar] [CrossRef]
- Lindgren, M.; Unosson, M.; Fredrikson, M.; Ek, A.C. Immobility—A major risk factor for development of pressure ulcers among adult hospitalized patients: A prospective study. Scand. J. Caring Sci. 2004, 18, 57–64. [Google Scholar] [CrossRef] [PubMed]
- Mador, M.J.; Kufel, T.J.; Magalang, U.J.; Rajesh, S.; Watwe, V.; Grant, B.J. Prevalence of positional sleep apnea in patients undergoing polysomnography. Chest 2005, 128, 2130–2137. [Google Scholar] [CrossRef]
- Wrzus, C.; Brandmaier, A.M.; Von Oertzen, T.; Müller, V.; Wagner, G.G.; Riediger, M. A new approach for assessing sleep duration and postures from ambulatory accelerometry. PLoS ONE 2012, 7, e48089. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Yang, G.Z. Monitoring cardio-respiratory and posture movements during sleep: What can be achieved by a single motion sensor. In Proceedings of the 2015 IEEE 12th International Conference on Wearable and Implantable Body Sensor Networks (BSN), Cambridge, MA, USA, 9–12 June 2015; pp. 1–6. [Google Scholar]
- Kwasnicki, R.M.; Cross, G.W.; Geoghegan, L.; Zhang, Z.; Reilly, P.; Darzi, A.; Yang, G.Z.; Emery, R. A lightweight sensing platform for monitoring sleep quality and posture: A simulated validation study. Eur. J. Med Res. 2018, 23, 28. [Google Scholar] [CrossRef] [PubMed]
- Austin, D.; Beattie, Z.T.; Riley, T.; Adami, A.M.; Hagen, C.C.; Hayes, T.L. Unobtrusive classification of sleep and wakefulness using load cells under the bed. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 5254–5257. [Google Scholar]
- Pouyan, M.B.; Ostadabbas, S.; Farshbaf, M.; Yousefi, R.; Nourani, M.; Pompeo, M. Continuous eight-posture classification for bed-bound patients. In Proceedings of the 2013 6th International Conference on Biomedical Engineering and Informatics, Hangzhou, China, 16–18 December 2013; pp. 121–126. [Google Scholar]
- Yousefi, R.; Ostadabbas, S.; Faezipour, M.; Farshbaf, M.; Nourani, M.; Tamil, L.; Pompeo, M. Bed posture classification for pressure ulcer prevention. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 7175–7178. [Google Scholar]
- Cary, D.; Collinson, R.; Sterling, M.; Briffa, K. Examining the relationship between sleep posture and morning spinal symptoms in the habitual environment using infrared cameras. J. Sleep Disord. Treat. Care 2016. [Google Scholar] [CrossRef]
- Lee, H.J.; Hwang, S.H.; Lee, S.M.; Lim, Y.G.; Park, K.S. Estimation of body postures on bed using unconstrained ECG measurements. IEEE J. Biomed. Health Inform. 2013, 17, 985–993. [Google Scholar] [PubMed]
- Chang, K.M.; Liu, S.H. Wireless portable electrocardiogram and a tri-axis accelerometer implementation and application on sleep activity monitoring. Telemed. e-Health 2011, 17, 177–184. [Google Scholar] [CrossRef] [PubMed]
- Wai, A.A.P.; Huang, W.; Fook, V.F.S.; Biswas, J.; Chi-Chun, H.; Koujuch, L. Situation-aware patient monitoring in and around the bed using multimodal sensing intelligence. In Proceedings of the 2010 Sixth International Conference on Intelligent Environments, Kuala Lumpur, Malaysia, 19–21 July 2010; pp. 128–133. [Google Scholar]
- Huang, W.; Wai, A.A.P.; Foo, S.F.; Biswas, J.; Hsia, C.C.; Liou, K. Multimodal sleeping posture classification. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 4336–4339. [Google Scholar]
- Lee, J.; Hong, M.; Ryu, S. Sleep monitoring system using kinect sensor. Int. J. Distrib. Sens. Netw. 2015, 11, 875371. [Google Scholar] [CrossRef]
- Goodfellow, S.D.; Goodwin, A.; Greer, R.; Laussen, P.C.; Mazwi, M.; Eytan, D. Atrial fibrillation classification using step-by-step machine learning. Biomed. Phys. Eng. Express 2018, 4, 045005. [Google Scholar] [CrossRef]
- Yongxiang, J.; Jingle, D.; Sanpeng, D.; Yuming, Q.; Peng, W.; Zijing, W.; Tianjiang, Z. Sitting posture recognition by body pressure distribution and airbag regulation strategy based on seat comfort evaluation. J. Eng. 2019, 2019, 8910–8914. [Google Scholar] [CrossRef]
- Yang, X.; Ren, X.; Chen, M.; Wang, L.; Ding, Y. Human Posture Recognition in Intelligent Healthcare. J. Phys. Conf. Ser. 2020, 1437, 012014. [Google Scholar] [CrossRef]
- Otoda, Y.; Mizumoto, T.; Arakawa, Y.; Nakajima, C.; Kohana, M.; Uenishi, M.; Yasumoto, K. Census: Continuous posture sensing chair for office workers. In Proceedings of the 2018 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 12–14 January 2018; pp. 1–2. [Google Scholar]
- Fallmann, S.; van Veen, R.; Chen, L.; Walker, D.; Chen, F.; Pan, C. Wearable accelerometer based extended sleep position recognition. In Proceedings of the 2017 IEEE 19th International Conference on e-Health Networking, Applications and Services (Healthcom), Dalian, China, 12–15 October 2017; pp. 1–6. [Google Scholar]
- Berridge, C.; Wetle, T.F. Why older adults and their children disagree about in-home surveillance technology, sensors, and tracking. Gerontologist 2020, 60, 926–934. [Google Scholar] [CrossRef]
- Coravos, A.; Doerr, M.; Goldsack, J.; Manta, C.; Shervey, M.; Woods, B.; Wood, W.A. Modernizing and designing evaluation frameworks for connected sensor technologies in medicine. NPJ Digit. Med. 2020, 3, 37. [Google Scholar] [CrossRef]
- Razjouyan, J.; Lee, H.; Parthasarathy, S.; Mohler, J.; Sharafkhaneh, A.; Najafi, B. Improving sleep quality assessment using wearable sensors by including information from postural/sleep position changes and body acceleration: A comparison of chest-worn sensors, wrist actigraphy, and polysomnography. J. Clin. Sleep Med. 2017, 13, 1301–1310. [Google Scholar] [CrossRef] [PubMed]
- Chang, L.; Lu, J.; Wang, J.; Chen, X.; Fang, D.; Tang, Z.; Nurmi, P.; Wang, Z. SleepGuard: Capturing rich sleep information using smartwatch sensing data. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2018, 2, 98. [Google Scholar] [CrossRef]
- Jeng, P.Y.; Wang, L.C.; Hu, C.J.; Wu, D. A Wrist Sensor Sleep Posture Monitoring System: An Automatic Labeling Approach. Available online: https://www.preprints.org/manuscript/201907.0060/v1 (accessed on 20 October 2020).
- Mannini, A.; Sabatini, A.M. Machine learning methods for classifying human physical activity from on-body accelerometers. Sensors 2010, 10, 1154–1175. [Google Scholar] [CrossRef]
- Saeedi, R.; Schimert, B.; Ghasemzadeh, H. Cost-sensitive feature selection for on-body sensor localization. In Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing: Adjunct Publication, Seattle, WA, USA, 13–17 September 2014; pp. 833–842. [Google Scholar]
- Baskin, I.I.; Marcou, G.; Horvath, D.; Varnek, A. Bagging and boosting of classification models. Tutorials Chemoinform. 2017, 241–247. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Fang, X.; Yuan, Z. Performance enhancing techniques for deep learning models in time series forecasting. Eng. Appl. Artif. Intell. 2019, 85, 533–542. [Google Scholar]
- Lefebvre, G.; Berlemont, S.; Mamalet, F.; Garcia, C. BLSTM-RNN based 3D Gesture Classification. In Artificial Neural Networks and Machine Learning—ICANN 2013, Proceedings of the International Conference on Artificial Neural Networks, Sofia, Bulgaria, 10–13 September 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 381–388. [Google Scholar]
- Graves, A.; Mohamed, A.R.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar]
- Gamboa, J.C.B. Deep learning for time-series analysis. arXiv 2017, arXiv:1701.01887. [Google Scholar]
- Sun, S.; Xie, Z. Bilstm-based models for metaphor detection. In Proceedings of the National CCF Conference on Natural Language Processing and Chinese Computing, Dalian, China, 8–12 November 2017; pp. 431–442. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Olguın, D.O.; Pentland, A.S. Human activity recognition: Accuracy across common locations for wearable sensors. In Proceedings of the 2006 10th IEEE International Symposium on Wearable Computers, Montreux, Switzerland, 11–14 October 2006; pp. 11–14. [Google Scholar]
- Altun, K.; Barshan, B.; Tunçel, O. Comparative study on classifying human activities with miniature inertial and magnetic sensors. Pattern Recognit. 2010, 43, 3605–3620. [Google Scholar]
- Taborri, J.; Palermo, E.; Masiello, D.; Rossi, S. Factorization of EMG via muscle synergies in walking task: Evaluation of intra-subject and inter-subject variability. In Proceedings of the 2017 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Turin, Italy, 22–25 May 2017; pp. 1–6. [Google Scholar]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Brodersen, K.H.; Ong, C.S.; Stephan, K.E.; Buhmann, J.M. The balanced accuracy and its posterior distribution. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 3121–3124. [Google Scholar]
- Ronao, C.A.; Cho, S.B. Human activity recognition using smartphone sensors with two-stage continuous hidden Markov models. In Proceedings of the 2014 10th International Conference on Natural Computation (ICNC), Xiamen, China, 19–21 August 2014; pp. 681–686. [Google Scholar]
- Skarpsno, E.S.; Mork, P.J.; Nilsen, T.I.L.; Holtermann, A. Sleep positions and nocturnal body movements based on free-living accelerometer recordings: Association with demographics, lifestyle, and insomnia symptoms. Nat. Sci. Sleep 2017, 9, 267. [Google Scholar] [CrossRef] [PubMed]
- Münzner, S.; Schmidt, P.; Reiss, A.; Hanselmann, M.; Stiefelhagen, R.; Dürichen, R. CNN-based sensor fusion techniques for multimodal human activity recognition. In Proceedings of the 2017 ACM International Symposium on Wearable Computers, Maui, HI, USA, 11–15 September 2017; pp. 158–165. [Google Scholar]
- Xue, Y.; Ju, Z.; Xiang, K.; Chen, J.; Liu, H. Multimodal human hand motion sensing and analysis—A review. IEEE Trans. Cogn. Dev. Syst. 2018, 11, 162–175. [Google Scholar]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Data augmentation using synthetic data for time series classification with deep residual networks. arXiv 2018, arXiv:1808.02455. [Google Scholar]
- DeVries, T.; Taylor, G.W. Dataset augmentation in feature space. arXiv 2017, arXiv:1702.05538. [Google Scholar]
- Wang, J.; Chen, Y.; Gu, Y.; Xiao, Y.; Pan, H. SensoryGANs: An Effective Generative Adversarial Framework for Sensor-based Human Activity Recognition. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]


| Feature | Description | Computation for Signal S | Number |
|---|---|---|---|
| AMP | Peak amplitude | 1–3 | |
| MED | Median | median(S) | 4–6 |
| MEAN | Mean value | 7–9 | |
| MAX | Maximum value | 10–12 | |
| MIN | Minimum value | 13–15 | |
| VAR | Variance | 16–18 | |
| STD | Standard deviation | 19–21 | |
| RMS | Root mean square | 22–24 | |
| P2P | Peak to peak | 25–27 | |
| ZCR | Zero crossing rate | 28–30 | |
| ENT | Entropy | 31–33 | |
| SKN | Skewness | 34–36 | |
| KRT | kurtosis | 37–39 | |
| MAG | Mean Magnitude | 40 | |
| ENG | Energy | 41 | |
| RNG | Range | 42–44 | |
| ANG | Angle | 45 | |
| MAD | Mean absolute deviation | 46–48 |
| Location | Accuracy | Balanced Accuracy | Score |
|---|---|---|---|
| Left Thigh | 94.5± 6.9 | 91.3 ± 10.3 | 90.7 ± 11.8 |
| Right Thigh | 96.2 ± 8.1 | 94.4 ± 12.0 | 93.5 ± 14.4 |
| Left Ankle | 94.9 ± 8.5 | 92.1 ± 12.8 | 91.4 ± 15.6 |
| Right Ankle | 89.8 ± 13.5 | 82.9 ± 19.9 | 82.8 ± 22.7 |
| Chest | 96.2 ± 9.1 | 93.6 ± 13.7 | 93.6 ± 16.2 |
| Left Arm | 78.6 ± 11.7 | 62.9 ± 15.1 | 60.9 ± 16.6 |
| Right Arm | 89.5 ± 12.1 | 84.0 ± 18.3 | 81.6 ± 21.7 |
| Left Wrist | 78.6 ± 12.5 | 67.1 ± 19.1 | 64.1 ± 21.7 |
| Right Wrist | 80.7 ± 14.1 | 79.7 ± 21.3 | 67.9 ± 23.8 |
| Location | Accuracy | Balanced Accuracy | Score |
|---|---|---|---|
| Left Thigh | 98.9 ± 8.2 | 98.4 ± 5.2 | 98.2 ± 6.2 |
| Right Thigh | 95.9 ± 7.3 | 93.4 ± 11.8 | 91.5 ± 15.6 |
| Left Ankle | 97.9 ± 4.2 | 96.8 ± 6.3 | 96.9 ± 6.4 |
| Right Ankle | 94.5 ± 6.3 | 92.4 ± 9.4 | 91.7 ± 10.7 |
| Chest | 98.3 ± 7.1 | 97.4 ± 7.1 | 97.3 ± 7.3 |
| Left Arm | 77.6 ± 11.7 | 68.8 ± 14.1 | 66.3 ± 16.5 |
| Right Arm | 86.8 ± 9.2 | 79.0 ± 14.5 | 75.7±17.3 |
| Left Wrist | 64.8 ± 22.9 | 64.9 ± 24.8 | 62.9 ± 23.2 |
| Right Wrist | 66.8 ± 26.7 | 67.6 ± 26.2 | 66.9 ± 28.9 |
| Location | ET | LDA | SVM | LSTM | AdaLSTM | |
|---|---|---|---|---|---|---|
| Mean Value (%) | Left thigh | 90.7 | 95.4 | 95.4 | 92.5 | 98.2 |
| Right thigh | 93.5 | 96.1 | 93.2 | 84.8 | 91.5 | |
| Left ankle | 92.1 | 88.3 | 94.8 | 90.2 | 96.9 | |
| Right ankle | 82.9 | 90.0 | 89.5 | 83.7 | 91.7 | |
| Chest | 97.0 | 94.8 | 90.1 | 88.3 | 97.3 | |
| Left arm | 60.9 | 58.1 | 53.3 | 53.7 | 66.3 | |
| Right arm | 81.6 | 82.2 | 76.1 | 75.5 | 75.7 | |
| Left wrist | 64.1 | 55.0 | 50.7 | 51.6 | 64.0 | |
| Right wrist | 67.9 | 65.5 | 59.2 | 54.1 | 69.4 | |
| Coefficient of variation | Left thigh | 0.13 | 0.15 | 0.13 | 0.22 | 0.06 |
| Right thigh | 0.15 | 0.16 | 0.17 | 0.28 | 0.17 | |
| Left ankle | 0.17 | 0.18 | 0.16 | 0.24 | 0.06 | |
| Right ankle | 0.27 | 0.18 | 0.12 | 0.27 | 0.11 | |
| Chest | 0.17 | 0.16 | 0.26 | 0.15 | 0.07 | |
| Left arm | 0.27 | 0.33 | 0.29 | 0.36 | 0.24 | |
| Right arm | 0.26 | 0.22 | 0.24 | 0.23 | 0.22 | |
| Left wrist | 0.33 | 0.36 | 0.36 | 0.50 | 0.25 | |
| Right wrist | 0.35 | 0.32 | 0.29 | 0.36 | 0.31 |
| Location | ET | LDA | SVM | LSTM | AdaLSTM | |
|---|---|---|---|---|---|---|
| Mean Value(%) | Left thigh | 90.6 | 94.6 | 91.4 | 92.9 | 93.7 |
| Right thigh | 97.3 | 96.9 | 91.4 | 93.2 | 94.0 | |
| Chest | 95.4 | 95.4 | 96.7 | 90.7 | 95.0 | |
| Left wrist | 65.9 | 42.1 | 58.4 | 54.1 | 63.3 | |
| Right wrist | 78.6 | 66.7 | 74.3 | 42.1 | 69.2 | |
| Coefficient of variation | Left thigh | 0.19 | 0.14 | 0.25 | 0.09 | 0.21 |
| Right thigh | 0.13 | 0.15 | 0.20 | 0.16 | 0.17 | |
| Chest | 0.13 | 0.13 | 0.24 | 0.25 | 0.12 | |
| Left wrist | 0.39 | 0.50 | 0.50 | 0.53 | 0.42 | |
| Right wrist | 0.34 | 0.38 | 0.32 | 0.40 | 0.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alinia, P.; Samadani, A.; Milosevic, M.; Ghasemzadeh, H.; Parvaneh, S. Pervasive Lying Posture Tracking. Sensors 2020, 20, 5953. https://doi.org/10.3390/s20205953
Alinia P, Samadani A, Milosevic M, Ghasemzadeh H, Parvaneh S. Pervasive Lying Posture Tracking. Sensors. 2020; 20(20):5953. https://doi.org/10.3390/s20205953
Chicago/Turabian StyleAlinia, Parastoo, Ali Samadani, Mladen Milosevic, Hassan Ghasemzadeh, and Saman Parvaneh. 2020. "Pervasive Lying Posture Tracking" Sensors 20, no. 20: 5953. https://doi.org/10.3390/s20205953
APA StyleAlinia, P., Samadani, A., Milosevic, M., Ghasemzadeh, H., & Parvaneh, S. (2020). Pervasive Lying Posture Tracking. Sensors, 20(20), 5953. https://doi.org/10.3390/s20205953





