Error-Robust Distributed Denial of Service Attack Detection Based on an Average Common Feature Extraction Technique
Abstract
:1. Introduction
- The proposal of a novel technique in which the average value of the common features among instances is filtered out from the dataset by applying the HOSVD low-rank approximation scheme, improving the performance of the intrusion detection system.
- The comparison with different state-of-the-art low-rank approximation techniques in order to show the higher performance and error-robustness of the proposed approach.
2. Related Works
3. Data Model
3.1. Mathematical Notation
3.2. Data Modeling
4. Theoretical Background
4.1. Taxonomy of DDoS Attacks
- Application-Layer Attack: in this type of attack, vulnerabilities present in the application are used by an attacker, making it inaccessible by legitimate users [19]. Instead of depleting the network bandwidth, the server resources, such as CPU, database, socket connections or memory, are exhausted by application-layer DDoS attacks. In addition, such attacks present some subtleties which make them harder to detect and mitigate: they are performed through legitimate HTTP packets, with a low traffic volume, presenting high resemblance to flash crowds [17]. HTTP and Domain Name System (DNS)-based DDoS attacks are examples of application-layer attacks.
- Resource Exhaustion Attack: In this category, hardware resources of servers, such as memory, CPU, and storage, are depleted. Consequently, they become unavailable for legitimate accesses. Resource exhaustion attacks are also known as protocol-based attacks, since vulnerabilities in protocols are exploited. For example, in an SYN flood attack, a hacker exploits the TCP three-way handshake process. After receiving a high volume of SYN packets, the targeted server responds with SYN/ACK packets and leaves open ports to receive the final ACK packets, which never arrive. This process continues until all ports of the server are unavailable.
- Volumetric Attack: In this type of attack, the bandwidth of the target system is exhausted by a massive amount of traffic. Since such attacks are launched by using amplification and reflection techniques, they are considered as the simplest DDoS attacks to be employed [18]. UDP flood and Internet Control Message Protocol (ICMP) flood can be cited as volumetric attacks.
4.2. CICDDoS2019 and CICIDS2017 Datasets
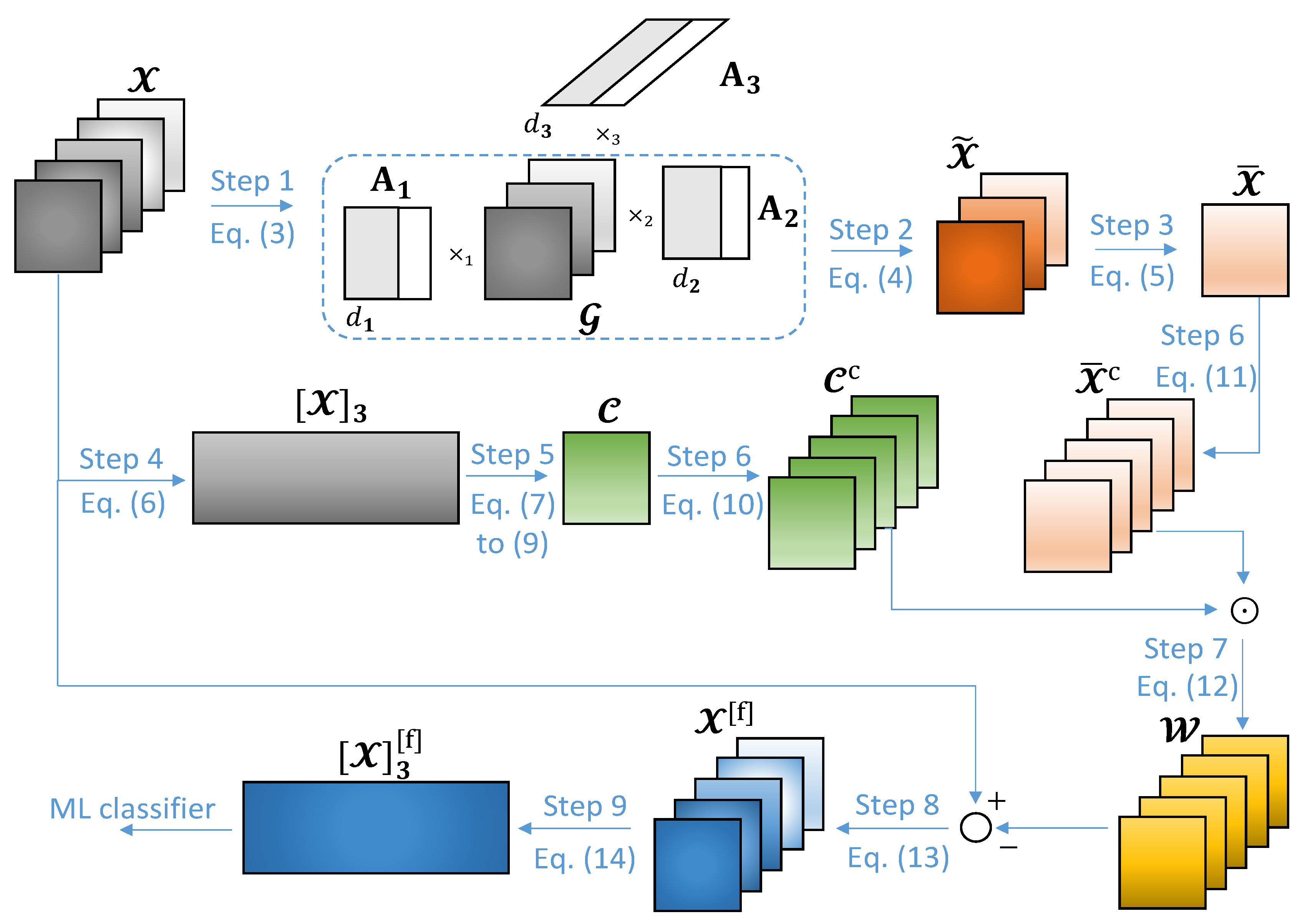
5. Proposed Average Common Feature Extraction Technique for DDoS Attack Detection in Cyber–Physical Systems
- Dataset Splitting: First, the DDoS attack dataset is split into the training and testing tensors and , where and are the number of training and testing instances, respectively, with .
- Dataset Pre-Processing: The training and testing datasets, and , are submitted to a preprocessing step, which includes data cleansing, feature scaling and label encoding. Initially, several rows containing missing values (NaN) and infinity values (Inf) are removed from the dataset. Next, all features are normalized to the range such that features with a higher order of magnitude do not dominate lower variables. Then, since we are dealing with binary classification, legitimate and DDoS attack instances are labeled as 0 and 1, respectively.
- Multilinear Rank Estimation: Finally, we estimate the multilinear ranks and corresponding to the tensors and , respectively. The parameters and for are estimated by using multidimensional model order selection (MOS) schemes, such as the R-D Minimum Description Length [25].
- Step 1: Computing the HOSVD of .In Step 1 of Figure 1, we compute the Higher-Order Singular Value Decomposition (HOSVD) of the dataset tensor . Here, we intend to obtain the core tensor, , as well as the first R factor matrices, for , where is the multilinear rank of . Such tensors are used in Step 2 to compute the common feature tensor, .The HOSVD of is given by:Usually, the number of common features among the dataset instances is obtained empirically. However, a considerable performance is achieved by considering as an estimate of the number of common features, as shown in the simulations of Section 6. We refer here to [25] to estimate the number of common features.
- Step 2: Computing the common feature tensor, .
- Step 3: Computing the average common feature tensor, .Next, in Step 3 of Figure 1, we compute , which corresponds to averaged along the -th dimension, i.e.,
- Step 4: Obtaining the -th mode unfolding matrix, .Following, in Step 4 of Figure 1, we obtain the -th mode unfolding matrix of , given by . In general, the r-th unfolding matrix is obtained after each element in is mapped to the element in as follows:Such a matrix is used in Step 5 in order to compute the weights to be applied on for dataset filtering.
- Step 5: Computing the weight tensor, .In Step 5 of Figure 1, we compute the weight tensor , which is used for dataset filtering in Step 7. First, the covariance matrix of the -th mode unfolding matrix , as well as its eigenvalue decomposition, are obtained as follows:where is the eigenvector matrix of and contains the eigenvalues of in its diagonal. Such eigenvalues are sorted in descending order so that is the largest one.Before subtracting the average common features from , we have to multiply each one of the elements of by a positive number smaller than 1. This can be done by computing the Hadamard product between and a weight tensor . The tensor can be obtained empirically or by some adaptive technique such that the errors between the expected and predicted classifications during the training phase of a ML classifier are minimized. In this paper, we adopt the following empirical approximation: all elements of are equal to the average eigenvalue of , i.e.,where for are the eigenvalues of .
- Step 6: Obtain the concatenated tensors, and .In Step 6 of Figure 1, M copies of are concatenated along the -th dimension, generating the tensor . The same procedure is adopted for in order to obtain . Both computations can be expressed as L:By doing this, we can compute the Hadamard product between and in Step 7, and then subtract the result from in Step 8, in a direct way.
- Step 7: Applying the weights on the tensor .Next, in Step 7 of Figure 1, we compute the Hadamard product between and such that the weights computed in Step 5 are applied to each element of the average common feature tensor, i.e.,
- Step 8: Computing the filtered dataset tensor, .Then, in Step 8 of Figure 1, the filtered dataset tensor can be computed as follows:
- Step 9: Obtaining the -th mode unfolding matrix, .Finally, in Step 9 of Figure 1, we obtain the -th mode unfolding matrix of , given by . Similarly to Equation (6), each element of the r-th unfolding matrix is computed as follows:Such a matrix is forwarded to the ML classification algorithm for classification tasks, where the predicted class label vector is computed. Since decision tree, random forest and gradient boosting algorithms present considerable results in network intrusion detection problems, they are adopted in this paper for classifying the network traffic data [14].
| Algorithm 1: Proposed average common feature extraction technique for DDoS attack detection. |
| Input: - Dataset tensor - Multilinear rank Output: - Filtered dataset matrix Algorithm Steps: 1 Compute the HOSVD of , with multilinear rank , as in (3) 2 Compute the common feature tensor as in (4) 3 Compute the average common feature tensor as in (5) 4 Convert into the -th mode unfolding matrix as in (6) 5 Obtain the weight tensor , whose elements are computed as in (7) to (9) 6 Obtain the concatenated tensors and as in (10) and (11) 7 Compute the Hadamard product between and as in (12) 8 Compute the filtered dataset tensor as in (13) 9 Convert into the -th mode unfolding matrix as in (14) |
6. Simulation Results
6.1. Results
- Accuracy (Acc): the ratio between the correctly predicted instances and the total number of instances,
- Detection Rate (DR): the ratio between the correctly predicted positive instances and the total number of actual positive instances,
- False Alarm Rate (FAR): the ratio between the number of negative instances wrongly classified as positives and the total number of actual negative instances,
- Area Under the Precision–Recall Curve (AUPRC): reflects a trade-off between the precision and recall. Precision is the ability of a classifier not to label as positive a sample that is negative, defined as . On the other hand, recall corresponds to the ability of a classifier to find all positive samples, given by . The AUPRC corresponds to the area under the curve obtained by plotting the precision and recall on the y and x axes, respectively, for different probability thresholds. By applying the trapezoidal rule, the AUPRC can be defined as:where and are the precision and recall values for the k-th threshold, and K is the total number of probability thresholds.Matthews Correlation Coefficient (MCC): measures the quality of binary classifications. It ranges from to such that higher values represent better performance. The MCC is defined as:
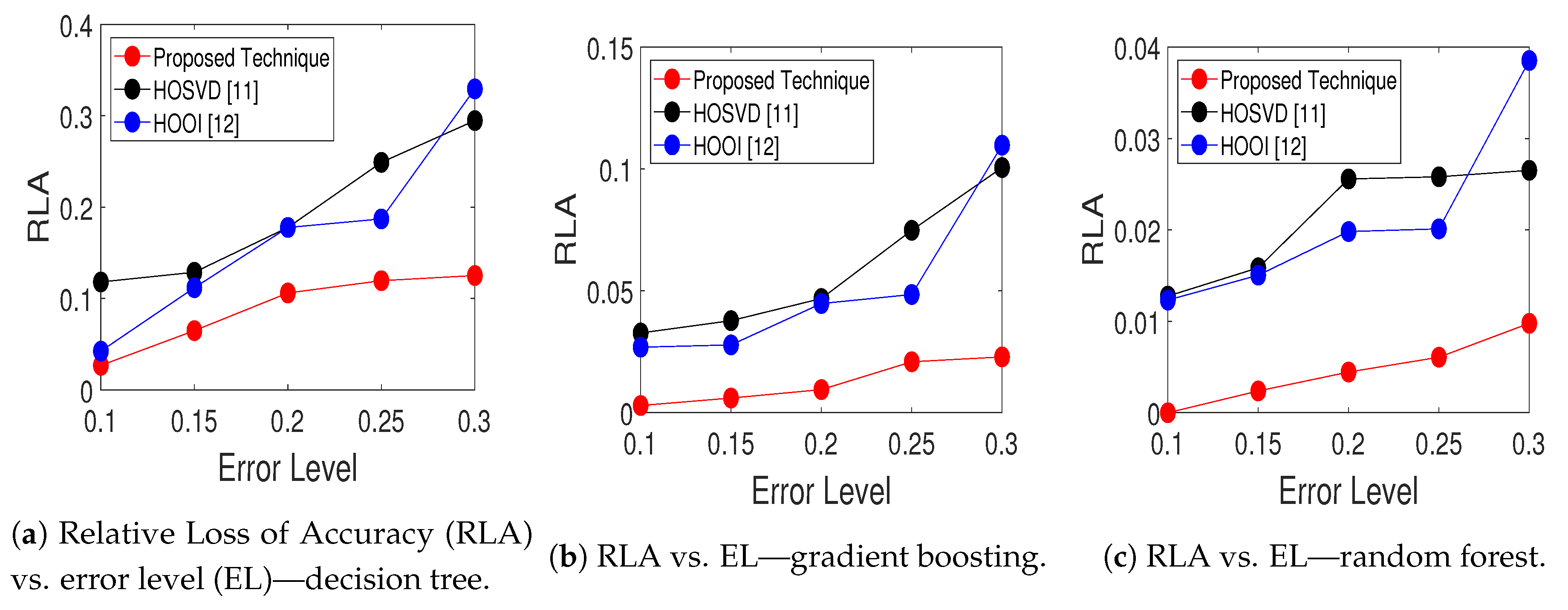
- Relative Loss of Accuracy (RLA): measures the percentage of variation of the accuracy of the classifiers at the error level , , with respect to the original case with no additional error, ,
6.2. Discussion
6.3. Performance Comparison with Related Works
6.4. Computational Complexity
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Acc | Accuracy |
| AUPRC | Area Under the Precision-Recall Curve |
| CIC | Canadian Institute for Cybersecurity |
| CNN | Convolutional Neural Network |
| CPS | Cyber-Physical System |
| CPU | Central Processing Unit |
| DDoS | Distributed Denial of Service |
| DoS | Denial of Service |
| DNS | Domain Name System |
| DR | Detection Rate |
| DT | Decision Tree |
| FAR | False Alarm Rate |
| GB | Gradient Boosting |
| HOOI | Higher Order Orthogonal Iteration |
| HOSVD | Higher Order Singular Value Decomposition |
| HTTP | HyperText Transfer Protocol |
| ICMP | Internet Control Message Protocol |
| IDS | Intrusion Detection System |
| IoT | Internet of Things |
| IP | Internet Protocol |
| LDAP | Lightweight Directory Access Protocol |
| LSTM | Long Short Term Memory |
| MCC | Matthews Correlation Coefficient |
| MDL | Minimum Description Length |
| ML | Machine Learning |
| MOS | Model Order Selection |
| MSSQL | Microsoft Structured Query Language |
| NaN | Not a Number |
| NetBIOS | Network Basic Input/Output System |
| NTP | Network Time Protocol |
| N/A | Not Available |
| OSI | Open System Interconnection |
| R-D MDL | R-Dimensional Minimum Description Length |
| RF | Random Forest |
| RLA | Relative Loss of Accuracy |
| SNMP | Simple Network Management Protocol |
| SQL Injection | Structured Query Language Injection |
| SSDP | Simple Service Discovery Protocol |
| TCP | Transmission Control Protocol |
| TFTP | Trivial File Transfer Protocol |
| TSP | Training Size Proportion |
| UDP | User Datagram Protocol |
| XSS | Cross-Site Scripting |
References
- Han, S.; Xie, M.; Chen, H.; Ling, Y. Intrusion detection in Cyber-Physical Systems: Techniques and challenges. IEEE Syst. J. 2014, 8, 1052–1062. [Google Scholar] [CrossRef]
- Lee, E.A. CPS Foundations. In Proceedings of the 47th Design Automation Conference, Anaheim, CA, USA, 13–18 June 2010; pp. 737–742. [Google Scholar] [CrossRef]
- Sadreazami, H.; Mohammadi, A.; Asif, A.; Plataniotis, K.N. Distributed-graph-based statistical approach for intrusion detection in Cyber-Physical Systems. IEEE Trans. Signal Inf. Process. Netw. 2018, 4, 137–147. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, H.; Zhang, J.; Ma, D.; Li, J.; Wei, J. Survey on Unmanned Aerial Vehicle networks: A Cyber Physical System prspective. IEEE Commun. Surv. Tutor. 2020, 22, 1027–1070. [Google Scholar] [CrossRef] [Green Version]
- Vieira, T.P.B.; Tenório, D.F.; da Costa, J.P.C.L.; de Freitas, E.P.; Del Galdo, G.; de Sousa, R.T., Jr. Model order selection and eigen similarity based framework for detection and identification of network attacks. J. Netw. Comput. Appl. 2017, 90, 26–41. [Google Scholar] [CrossRef]
- Wang, M.; Lu, Y.; Qin, J. A dynamic MLP-based DDoS attack detection method using feature selection and feedback. Comput. Secur. 2020, 88, 101645. [Google Scholar] [CrossRef]
- Jiang, J.; Yu, Q.; Yu, M.; Li, G.; Chen, J.; Liu, K.; Liu, C.; Huang, W. ALDD: A hybrid traffic-user behavior detection method for application layer DDoS. In Proceedings of the 2018 17th IEEE International Conference on Trust, Security and Privacy in Computing and Communications/12th IEEE International Conference on Big Data Science and Engineering (TrustCom/BigDataSE), New York, NY, USA, 1–3 August 2018; pp. 1565–1569. [Google Scholar] [CrossRef]
- Saez, J.A.; Galar, M.; Luengo, J.; Herrera, F. Tackling the problem of classification with noisy data using Multiple Classifier Systems: Analysis of the performance and robustness. Inf. Sci. 2013, 247, 1–20. [Google Scholar] [CrossRef]
- Li, F.; Tang, Y. False Data Injection Attack for Cyber-Physical Systems With Resource Constraint. IEEE Trans. Cybern. 2020, 50, 729–738. [Google Scholar] [CrossRef]
- Kisil, I.; Calvi, G.G.; Mandic, D.P. Tensor valued common and individual feature extraction: Multi-dimensional perspective. arXiv 2017, arXiv:1711.00487. [Google Scholar]
- Rajwade, A.; Rangarajan, A.; Banerjee, A. Image denoising using the Higher Order Singular Value Decomposition. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 849–862. [Google Scholar] [CrossRef]
- Lathauwer, L.D.; Moor, B.D.; Vandewalle, J. On the best rank-1 and rank-(R1,R2,…,RN) approximation of higher-order tensors. SIAM J. Matrix Anal. Appl. 2000, 21, 1324–1342. [Google Scholar] [CrossRef]
- Hosseini, S.; Azizi, M. The hybrid technique for DDoS detection with supervised learning algorithms. Comput. Netw. 2019, 158, 35–45. [Google Scholar] [CrossRef]
- Lima Filho, F.S.; Silveira, F.A.F.; Brito, A.M., Jr.; Vargas-Solar, G.; Silveira, L.F. Smart Detection: An online approach for DoS/DDoS attack detection using machine learning. Secur. Commun. Netw. 2019, 2019, 1574749. [Google Scholar] [CrossRef]
- Amouri, A.; Alaparthy, V.T.; Morgera, S.D. A machine learning based intrusion detection system for mobile Internet of Things. Sensors 2020, 20, 461. [Google Scholar] [CrossRef] [Green Version]
- Galeano-Brajones, J.; Carmona-Murillo, J.; Valenzuela-Valdés, J.F.; Luna-Valero, F. Detection and mitigation of DoS and DDoS attacks in IoT-based stateful SDN: An experimental approach. Sensors 2020, 20, 816. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Praseed, A.; Thilagam, P.S. DDoS attacks at the application layer: Challenges and research perspectives for safeguarding web applications. IEEE Commun. Surv. Tutor. 2019, 21, 661–685. [Google Scholar] [CrossRef]
- Vishwakarma, R.; Jain, A.K. A survey of DDoS attacking techniques and defence mechanisms in the IoT network. Telecommun. Syst. 2020, 73, 3–25. [Google Scholar] [CrossRef]
- Dantas Silva, F.S.; Silva, E.; Neto, E.P.; Lemos, M.; Neto, A.J.V.; Esposito, F. A taxonomy of DDoS attack mitigation approaches featured by SDN technologies in IoT scenarios. Sensors 2020, 20, 3078. [Google Scholar] [CrossRef]
- Canadian Institute for Cybersecurity. DDoS Evaluation Dataset (CICDDoS2019). 2019. Available online: https://www.unb.ca/cic/datasets/ddos-2019.html (accessed on 10 June 2020).
- Canadian Institute for Cybersecurity. Intrusion Detection Evaluation Dataset (CICIDS2017). 2017. Available online: https://www.unb.ca/cic/datasets/ids-2017.html (accessed on 10 June 2020).
- Sharafaldin, I.; Lashkari, A.H.; Hakak, S.; Ghorbani, A.A. Developing realistic Distributed Denial of Service (DDoS) attack dataset and taxonomy. In Proceedings of the 2019 International Carnahan Conference on Security Technology (ICCST), Chennai, India, 1–3 October 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Sharafaldin, I.; Lashkari, A.H.; Ghorbani, A.A. Toward generating a new intrusion detection dataset and intrusion traffic characterization. In Proceedings of the 4th ICISSP, Madeira, Portugal, 22–24 January 2018; pp. 108–116. [Google Scholar] [CrossRef]
- Zhou, G.; Cichocki, A.; Zhang, Y.; Mandic, D.P. Group component analysis for multiblock data: Common and individual feature extraction. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 2426–2439. [Google Scholar] [CrossRef] [Green Version]
- Da Costa, J.P.C.L.; Roemer, F.; Haardt, M.; de Sousa, R.T., Jr. Multi-dimensional model order selection. EURASIP J. Adv. Signal Process. 2011, 2011, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Kisil, I.; Calvi, G.; Cichocki, A.; Mandic, D.P. Common and individual feature extraction using tensor decompositions: A remedy for the curse of dimensionality? In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 6299–6303. [Google Scholar] [CrossRef]
- Kossaifi, J.; Panagakis, Y.; Anandkumar, A.; Pantic, M. TensorLy: Tensor learning in Python. arXiv 2016, arXiv:1610.09555. [Google Scholar]
- Elsayed, M.S.; Le-Khac, N.A.; Dev, S.; Jurcut, A.D. DDoSNet: A deep-learning model for detecting network attacks. arXiv 2020, arXiv:2006.13981. [Google Scholar]
- Doriguzzi-Corin, R.; Millar, S.; Scott-Hayward, S.; Martínez-del-Rincón, J.; Siracusa, D. LUCID: A practical, lightweight deep learning solution for DDoS attack detection. IEEE Trans. Netw. Serv. Manag. 2020, 17, 876–889. [Google Scholar] [CrossRef] [Green Version]
- Roopak, M.; Yun Tian, G.; Chambers, J. Deep learning models for cyber security in IoT networks. In Proceedings of the 2019 IEEE 9th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 7–9 January 2019; pp. 452–457. [Google Scholar] [CrossRef]
- Lopez, A.D.; Alma, D.; Mohan, A.P.; Nair, S. Network traffic behavioral analytics for detection of DDoS attacks. SMU Data Sci. Rev. 2019, 2, 1–24. Available online: https://scholar.smu.edu/datasciencereview/vol2/iss1/14 (accessed on 12 May 2020).
- Aamir, M.; Zaidi, S.M.A. Clustering based semi-supervised machine learning for DDoS attack classification. J. King Saud Univ. Comput. Inf. Sci. 2019. [Google Scholar] [CrossRef]
- Minster, R.; Saibaba, A.K.; Kilmer, M.E. Randomized algorithms for low-rank tensor decompositions in the Tucker format. arXiv 2019, arXiv:1905.07311. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
| Works related to multilinear algebra | ||||
| Paper | Aim | Proposed Solution | Pros | Cons |
| Kisil et al. [10] | - Image classification. | - Common and individual feature extraction technique based on LL1 tensor decomposition. | - Flexible - Not restricted to images of the same dimensions. - Tensor-based solution. | - High computational complexity. - Corrupted datasets are not considered. |
| Rajwade et al. [11] | - Image denoising and classification. | - Patch-based ML technique for image denoising by applying HOSVD. | - Outstanding performance on grayscale and color images. - Tensor-based solution. | - Limited denoising performance. |
| Lathauwer et al. [12] | - Estimation of the best rank- approximation of tensors. | - HOOI low-rank approximation algorithm. | - Outperforms HOSVD in the estimation of singular matrices and core tensor. - Tensor-based solution. | - High computational complexity. |
| Works related to DDoS attack detection | ||||
| Paper | Aim | Proposed Solution | Pros | Cons |
| Vieira et al. [5] | - Detection and identification of network attacks, including DDoS. | - Framework for detecting and identifying network attacks using model order selection, eigenvalues and similarity analysis. | - Outstanding accuracy for timely detection and identification of TCP and UDP ports under attack. | - Corrupted datasets are not considered. - Not based on ML techniques. |
| Hosseini and Azizi [13] | - DDoS attack detection. | - Hybrid framework based on data stream approach for detecting DDoS attacks. | - Computational process divided between client and proxy. - Early attack detection. | - Corrupted datasets are not considered. |
| Lima Filho et al. [14] | - DDoS attack detection. | - RF based DDoS detection system for early identification of TCP flood, UDP flood and HTTP flood. | - Early identification of volumetric attacks. - Packet inspection is not required. | - Corrupted datasets are not considered. |
| Wang et al. [6] | - DDoS attack detection. | - Feature selection combined with MLP. - Feedback mechanism to reconstruct the IDS according to detection errors. | - Feedback mechanism perceives errors based on recent detection results. | - Global optimal features are not necessarily found. - Corrupted datasets are not considered. |
| Symbol | Definition | Symbol | Definition |
|---|---|---|---|
| Dataset matrix | Core tensor | ||
| Error-free dataset matrix | Common feature tensor | ||
| Error matrix | Average common feature tensor | ||
| m-th dataset instance | Weight tensor | ||
| n-th dataset feature | Filtered dataset tensor | ||
| r-th factor matrix | r-th mode unfolding matrix of | ||
| Covariance matrix | Class label of | ||
| Eigenvector matrix | M | Number of instances | |
| Eigenvalue matrix | Number of training instances | ||
| Class label vector | Number of testing instances | ||
| Predicted class label vector | N | Number of features | |
| Dataset tensor | Number of features along the r-th dimension | ||
| Training dataset tensor | Order of | ||
| Testing dataset tensor | Multilinear rank of | ||
| Error-free dataset tensor | Multilinear rank of | ||
| Error tensor | Eigenvalues of |
| Dataset | Traffic File | Traffic Type | Total |
|---|---|---|---|
| Legitimate | 32,000 | ||
| DNS-based DDoS | 800 | ||
| LDAP-based DDoS | 800 | ||
| MSSQL-based DDoS | 800 | ||
| NetBIOS-based DDoS | 800 | ||
| CICDDoS2019 | 12 January 2019 | NTP-based DDoS | 800 |
| SNMP-based DDoS | 800 | ||
| SSDP-based DDoS | 800 | ||
| UDP flood | 800 | ||
| TCP SYN flood | 800 | ||
| TFTP-based DDoS | 800 | ||
| CICIDS2017 | 3 July 2017 | Legitimate | 32,000 |
| 7 July 2017 | DDoS LOIC | 8000 |
| EL | Model | Acc | FAR | MCC | AUPRC | DR | ||||||||||
| DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | ||
| Proposed | 0.9492 | 0.9958 | 0.9959 | 0.1308 | 0.0172 | 0.0147 | 0.8407 | 0.9866 | 0.9871 | 0.8855 | 0.9983 | 0.9975 | 0.9188 | 0.9909 | 0.9919 | |
| 10% | HOSVD [11] | 0.8605 | 0.9659 | 0.9839 | 0.1701 | 0.0949 | 0.0766 | 0.6311 | 0.8922 | 0.9485 | 0.7405 | 0.9484 | 0.9908 | 0.8490 | 0.9429 | 0.9611 |
| HOOI [12] | 0.9343 | 0.9707 | 0.9843 | 0.1313 | 0.0587 | 0.0722 | 0.7996 | 0.9098 | 0.9499 | 0.8542 | 0.9395 | 0.9946 | 0.9097 | 0.9596 | 0.9630 | |
| EL | Model | Acc | FAR | MCC | AUPRC | DR | ||||||||||
| DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | ||
| Proposed | 0.9121 | 0.9892 | 0.9857 | 0.2201 | 0.0294 | 0.0681 | 0.7272 | 0.9666 | 0.9545 | 0.8076 | 0.9944 | 0.9974 | 0.8585 | 0.9822 | 0.9654 | |
| 15% | HOSVD [11] | 0.8501 | 0.9608 | 0.9808 | 0.2916 | 0.0808 | 0.0925 | 0.5606 | 0.8820 | 0.9386 | 0.6855 | 0.9368 | 0.9902 | 0.7966 | 0.9451 | 0.9531 |
| HOOI [12] | 0.8666 | 0.9501 | 0.9768 | 0.2324 | 0.1464 | 0.1049 | 0.6195 | 0.8405 | 0.9257 | 0.7279 | 0.8491 | 0.9837 | 0.8331 | 0.9137 | 0.9460 | |
| EL | Model | Acc | FAR | MCC | AUPRC | DR | ||||||||||
| DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | ||
| Proposed | 0.9039 | 0.9844 | 0.9929 | 0.2398 | 0.0695 | 0.0284 | 0.6986 | 0.9502 | 0.9774 | 0.7829 | 0.9937 | 0.9966 | 0.8496 | 0.9640 | 0.9849 | |
| 20% | HOSVD [11] | 0.8023 | 0.9517 | 0.9708 | 0.5040 | 0.2231 | 0.1348 | 0.3932 | 0.8427 | 0.9063 | 0.5699 | 0.9665 | 0.9795 | 0.6867 | 0.8858 | 0.9310 |
| HOOI [12] | 0.6543 | 0.9538 | 0.9582 | 0.4227 | 0.1544 | 0.0930 | 0.2264 | 0.8521 | 0.8700 | 0.5019 | 0.9176 | 0.9617 | 0.6252 | 0.9130 | 0.9389 | |
| EL | Model | Acc | FAR | MCC | AUPRC | DR | ||||||||||
| DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | ||
| Proposed | 0.8719 | 0.9927 | 0.9931 | 0.3125 | 0.0258 | 0.0240 | 0.6268 | 0.9768 | 0.9781 | 0.7413 | 0.9954 | 0.9966 | 0.8023 | 0.9857 | 0.9866 | |
| 25% | HOSVD [11] | 0.6882 | 0.8981 | 0.9711 | 0.6180 | 0.1365 | 0.0942 | 0.1280 | 0.7245 | 0.9083 | 0.3906 | 0.7081 | 0.9722 | 0.5726 | 0.8850 | 0.9465 |
| HOOI [12] | 0.8023 | 0.8889 | 0.9816 | 0.4281 | 0.3198 | 0.0857 | 0.4198 | 0.6585 | 0.9412 | 0.5884 | 0.7804 | 0.9877 | 0.7154 | 0.8102 | 0.9562 | |
| EL | Model | Acc | FAR | MCC | AUPRC | DR | ||||||||||
| DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | ||
| Proposed | 0.8532 | 0.9759 | 0.9894 | 0.1782 | 0.0655 | 0.0435 | 0.6179 | 0.9266 | 0.9663 | 0.7335 | 0.9801 | 0.9937 | 0.8414 | 0.9602 | 0.9770 | |
| 30% | HOSVD [11] | 0.7328 | 0.9238 | 0.9701 | 0.5221 | 0.2647 | 0.1449 | 0.2554 | 0.7496 | 0.9042 | 0.4796 | 0.8675 | 0.9878 | 0.6366 | 0.8527 | 0.9267 |
| HOOI [12] | 0.7932 | 0.9717 | 0.9765 | 0.6998 | 0.0868 | 0.1152 | 0.2765 | 0.9102 | 0.9250 | 0.4818 | 0.9287 | 0.9906 | 0.6072 | 0.9496 | 0.9419 | |
| TSP | Model | Acc | FAR | MCC | AUPRC | DR | ||||||||||
| DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | ||
| Proposed | 0.8267 | 0.9890 | 0.9918 | 0.1938 | 0.0457 | 0.0171 | 0.5935 | 0.9654 | 0.9746 | 0.7804 | 0.9953 | 0.9976 | 0.8190 | 0.9760 | 0.9885 | |
| 20% | HOSVD [11] | 0.8833 | 0.8868 | 0.9755 | 0.4785 | 0.2786 | 0.0871 | 0.6108 | 0.6514 | 0.9227 | 0.7437 | 0.8168 | 0.9845 | 0.7478 | 0.8249 | 0.9520 |
| HOOI [12] | 0.7805 | 0.9360 | 0.9740 | 0.3457 | 0.1151 | 0.0422 | 0.4296 | 0.8115 | 0.9207 | 0.6099 | 0.9336 | 0.9869 | 0.7332 | 0.9168 | 0.9679 | |
| TSP | Model | Acc | FAR | MCC | AUPRC | DR | ||||||||||
| DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | ||
| Proposed | 0.8595 | 0.9855 | 0.9895 | 0.0660 | 0.0660 | 0.0454 | 0.6336 | 0.8405 | 0.9671 | 0.7817 | 0.9915 | 0.9948 | 0.8399 | 0.9662 | 0.9764 | |
| 30% | HOSVD [11] | 0.7831 | 0.9565 | 0.9703 | 0.2618 | 0.0856 | 0.1141 | 0.4664 | 0.8709 | 0.9057 | 0.6382 | 0.8804 | 0.9705 | 0.7663 | 0.9408 | 0.9387 |
| HOOI [12] | 0.7596 | 0.9287 | 0.9558 | 0.4072 | 0.2352 | 0.2182 | 0.3550 | 0.7704 | 0.8592 | 0.5534 | 0.9072 | 0.9841 | 0.6971 | 0.8673 | 0.8906 | |
| TSP | Model | Acc | FAR | MCC | AUPRC | DR | ||||||||||
| DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | ||
| Proposed | 0.8252 | 0.9847 | 0.9845 | 0.1977 | 0.0542 | 0.0494 | 0.5860 | 0.9518 | 0.9513 | 0.7743 | 0.9882 | 0.9922 | 0.8166 | 0.9701 | 0.9718 | |
| 40% | HOSVD [11] | 0.7588 | 0.9170 | 0.9735 | 0.4338 | 0.0728 | 0.1194 | 0.3411 | 0.7769 | 0.9154 | 0.5416 | 0.9022 | 0.9801 | 0.6864 | 0.9209 | 0.9385 |
| HOOI [12] | 0.5839 | 0.8913 | 0.9610 | 0.6249 | 0.2576 | 0.1760 | 0.6635 | 0.6638 | 0.8747 | 0.3484 | 0.8263 | 0.9575 | 0.5054 | 0.8353 | 0.9095 | |
| TSP | Model | Acc | FAR | MCC | AUPRC | DR | ||||||||||
| DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | ||
| Proposed | 0.9026 | 0.9814 | 0.9903 | 0.2605 | 0.0784 | 0.0396 | 0.6963 | 0.9418 | 0.9696 | 0.8087 | 0.9663 | 0.9972 | 0.8417 | 0.9591 | 0.9791 | |
| 50% | HOSVD [11] | 0.7211 | 0.9471 | 0.9834 | 0.4713 | 0.1930 | 0.0750 | 0.2729 | 0.8325 | 0.9479 | 0.5047 | 0.9435 | 0.9936 | 0.6493 | 0.8948 | 0.9615 |
| HOOI [12] | 0.8395 | 0.9319 | 0.9698 | 0.3490 | 0.0844 | 0.0839 | 0.5238 | 0.8121 | 0.9060 | 0.6614 | 0.7812 | 0.9758 | 0.7691 | 0.9258 | 0.9498 | |
| TSP | Model | Acc | FAR | MCC | AUPRC | DR | ||||||||||
| DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | ||
| Proposed | 0.9062 | 0.9815 | 0.9943 | 0.2103 | 0.0439 | 0.0209 | 0.7180 | 0.9420 | 0.9820 | 0.8523 | 0.9833 | 0.9972 | 0.8515 | 0.9587 | 0.9886 | |
| 60% | HOSVD [11] | 0.8134 | 0.9623 | 0.9623 | 0.2432 | 0.0673 | 0.0543 | 0.5353 | 0.8898 | 0.8882 | 0.6820 | 0.9330 | 0.9781 | 0.8035 | 0.9571 | 0.9561 |
| HOOI [12] | 0.8199 | 0.9251 | 0.9558 | 0.3815 | 0.2714 | 0.2154 | 0.4862 | 0.7651 | 0.8598 | 0.6417 | 0.8730 | 0.9838 | 0.7446 | 0.8516 | 0.8918 | |
| TSP | Model | Acc | FAR | MCC | AUPRC | DR | ||||||||||
| DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | DT | GB | RF | ||
| Proposed | 0.9065 | 0.9826 | 0.9937 | 0.2817 | 0.0427 | 0.0287 | 0.6928 | 0.9458 | 0.9800 | 0.8323 | 0.9658 | 0.9978 | 0.9277 | 0.9731 | 0.9853 | |
| 70% | HOSVD [11] | 0.7527 | 0.8902 | 0.9578 | 0.1265 | 0.0490 | 0.0781 | 0.4885 | 0.7391 | 0.8708 | 0.6699 | 0.8573 | 0.9688 | 0.7982 | 0.9131 | 0.9443 |
| HOOI [12] | 0.7727 | 0.9455 | 0.9599 | 0.2222 | 0.1584 | 0.0594 | 0.4668 | 0.8259 | 0.8791 | 0.6421 | 0.9407 | 0.9736 | 0.7746 | 0.9064 | 0.9526 | |
| Dataset | Paper | ML Algorithm | Acc | DR | FAR |
|---|---|---|---|---|---|
| Proposed scheme | DT | 0.9754 | 0.9509 | 0.0895 | |
| CICDDoS2019 | Proposed scheme | GB | 0.9987 | 0.9986 | 0.0016 |
| Proposed scheme | RF | 0.9955 | 0.9896 | 0.0201 | |
| Elsayed et al. [28] | RNN+AutoEncoder | 0.9900 | 0.9900 | N/A | |
| Proposed scheme | DT | 0.9994 | 0.9993 | 0.0007 | |
| Proposed scheme | GB | 0.9995 | 0.9995 | 0.0005 | |
| Proposed scheme | RF | 0.9996 | 0.9989 | 0.0022 | |
| Lopez et al. [31] | RF | 0.9900 | N/A | N/A | |
| Doriguzzi–Corin et al. [29] | LUCID | 0.9967 | 0.9994 | 0.0059 | |
| CICIDS2017 | Lima Filho et al. [14] | RF | N/A | 0.8000 | 0.0020 |
| Aamir and Ali Zaidi [32] | RF | 0.9666 | N/A | N/A | |
| Roopak et al. [30] | MLP | 0.8634 | 0.8625 | N/A | |
| Roopak et al. [30] | 1D-CNN | 0.9514 | 0.9017 | N/A | |
| Roopak et al. [30] | LSTM | 0.9624 | 0.8989 | N/A | |
| Roopak et al. [30] | 1D-CNN+LSTM | 0.9716 | 0.9910 | N/A |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abreu Maranhão, J.P.; Carvalho Lustosa da Costa, J.P.; Pignaton de Freitas, E.; Javidi, E.; Timóteo de Sousa Júnior, R. Error-Robust Distributed Denial of Service Attack Detection Based on an Average Common Feature Extraction Technique. Sensors 2020, 20, 5845. https://doi.org/10.3390/s20205845
Abreu Maranhão JP, Carvalho Lustosa da Costa JP, Pignaton de Freitas E, Javidi E, Timóteo de Sousa Júnior R. Error-Robust Distributed Denial of Service Attack Detection Based on an Average Common Feature Extraction Technique. Sensors. 2020; 20(20):5845. https://doi.org/10.3390/s20205845
Chicago/Turabian StyleAbreu Maranhão, João Paulo, João Paulo Carvalho Lustosa da Costa, Edison Pignaton de Freitas, Elnaz Javidi, and Rafael Timóteo de Sousa Júnior. 2020. "Error-Robust Distributed Denial of Service Attack Detection Based on an Average Common Feature Extraction Technique" Sensors 20, no. 20: 5845. https://doi.org/10.3390/s20205845
APA StyleAbreu Maranhão, J. P., Carvalho Lustosa da Costa, J. P., Pignaton de Freitas, E., Javidi, E., & Timóteo de Sousa Júnior, R. (2020). Error-Robust Distributed Denial of Service Attack Detection Based on an Average Common Feature Extraction Technique. Sensors, 20(20), 5845. https://doi.org/10.3390/s20205845








