Proposed Orbital Products for Positioning Using Mega-Constellation LEO Satellites
Abstract
:1. Introduction
2. Processing Procedures
2.1. Level A Products
- The GNSS data collected onboard the LEO satellites are downlinked to the GMSs with a time interval ∆T between subsequent downloads, and then transferred to the MPC.
- High-accuracy reduced-dynamic orbits are then processed with comprehensive dynamic models (as will be described in Section 2.1.2), having the Keplerian elements at the initial condition and certain dynamic parameters estimated to compensate for the deficiencies in the dynamic models.
- The orbits are then predicted for several hours into the future with numerical integration, which will be discussed in Section 2.1.1. The prediction interval should cover at least a period of ∆T + ∆tp, where ∆tp is the time needed for the data downloading, processing and uploading during the next GMS–LEO contact.
- Next, LEO-specific ephemeris parameters (Section 2.1.3) are estimated using the least-squares adjustment to describe the predicted orbits within a pre-defined fitting interval ∆tF (Section 2.1.3), where ∆tF is normally selected much shorter than the prediction interval.
- The fitted ephemeris parameters are updated with an interval of ∆tU < ∆tF, so that overlapping time exists between two subsequent sets of ephemeris parameters.
- All the estimated ephemeris parameters are then uplinked to the LEO satellites, and the LEO satellites broadcast their ephemeris parameters to the users.
2.1.1. Prediction Interval
2.1.2. Orbit Estimation and Prediction
2.1.3. Ephemeris Parameters
2.1.4. Alternative Approaches
- Upload the initial conditions and the estimated dynamic parameters with the numerical integration performed onboard, or directly uplink the predicted orbits to the LEO satellite [12].
- With enough computational power onboard the LEO satellites, it is also possible to make use of the GNSS broadcast ephemeris and observations, directly compute the real-time LEO orbits onboard, and extrapolate them for a short time in the future—i.e., tens of seconds [27].
- Make use of the GNSS broadcast ephemeris and observations, directly compute the SPP solutions onboard in real time, and broadcast the epoch-wise positions to the users.
- No heavy burden on the LEO onboard computational power, where fast processing is carried out using high-performance computers in the MPC.
- Comprehensive dynamic models can be used for the POD.
- High-accuracy real-time GNSS products can be continuously obtained via Internet links.
- Only a limited amount of parameters (for each LEO satellite) are transferred during the uploading process.
- The navigation information can be downlinked to users with a relatively low sampling rate—e.g., 10 min.
- The LEO orbits derived from the broadcast ephemeris are smooth, which is suitable for the polynomial fitting of the precise Level B orbits (see Section 2.2).
- Multiple GMSs might be needed to guarantee the upload intervals of several hours.
- With the rapidly increasing number of the LEO satellites, a heavy burden is put on the downlink and uplink systems at the GMSs.
- A high-grade GNSS receiver is required onboard the LEO satellite.
2.2. Level B Products
Alternative Approaches
- No heavy burden on the LEO onboard computational power; comprehensive dynamic models can be used for the POD; fast processing with high-performance computers.
- High-accuracy real-time GNSS products can be continuously obtained with Internet links free of charge.
3. Test Results
3.1. Level A Products
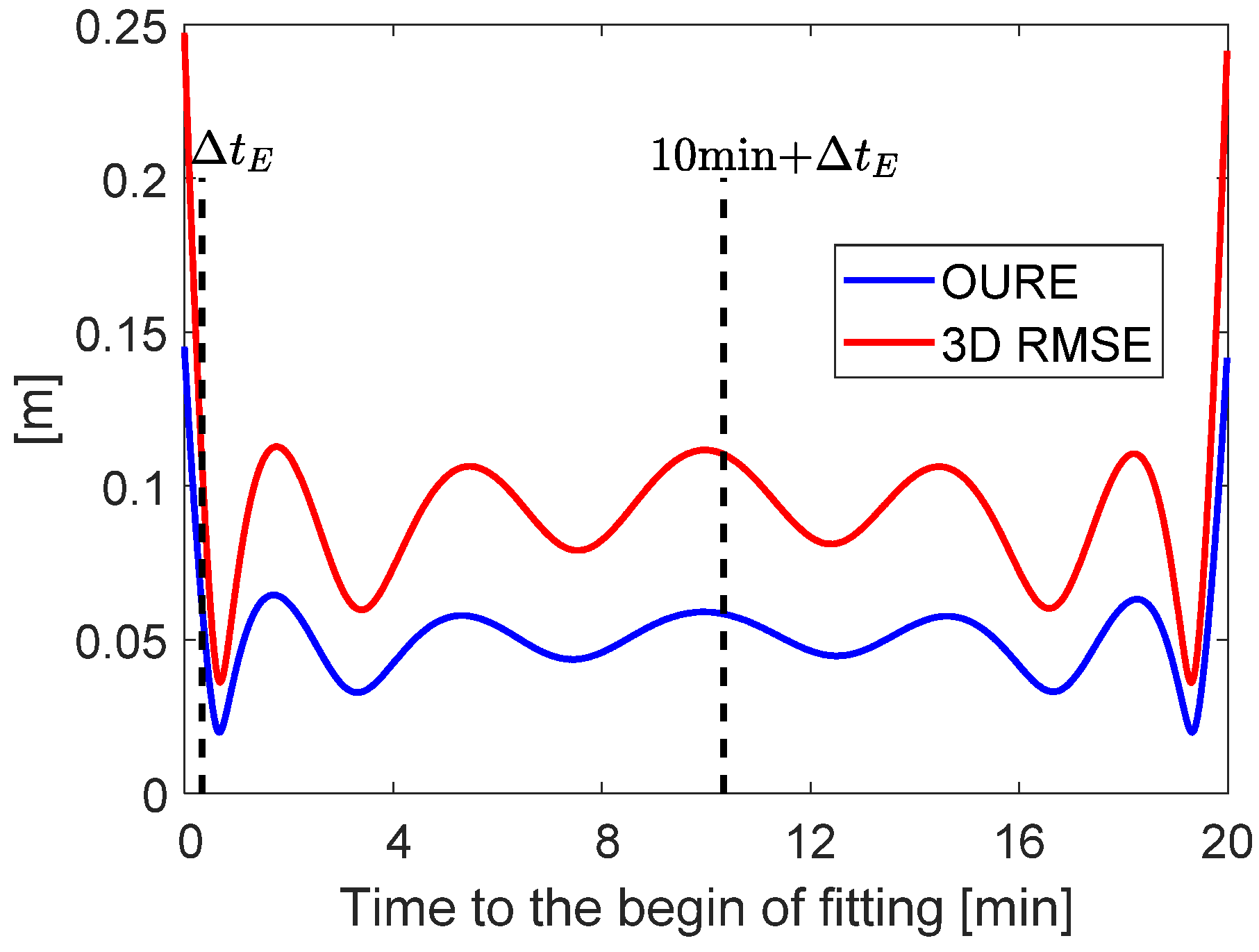
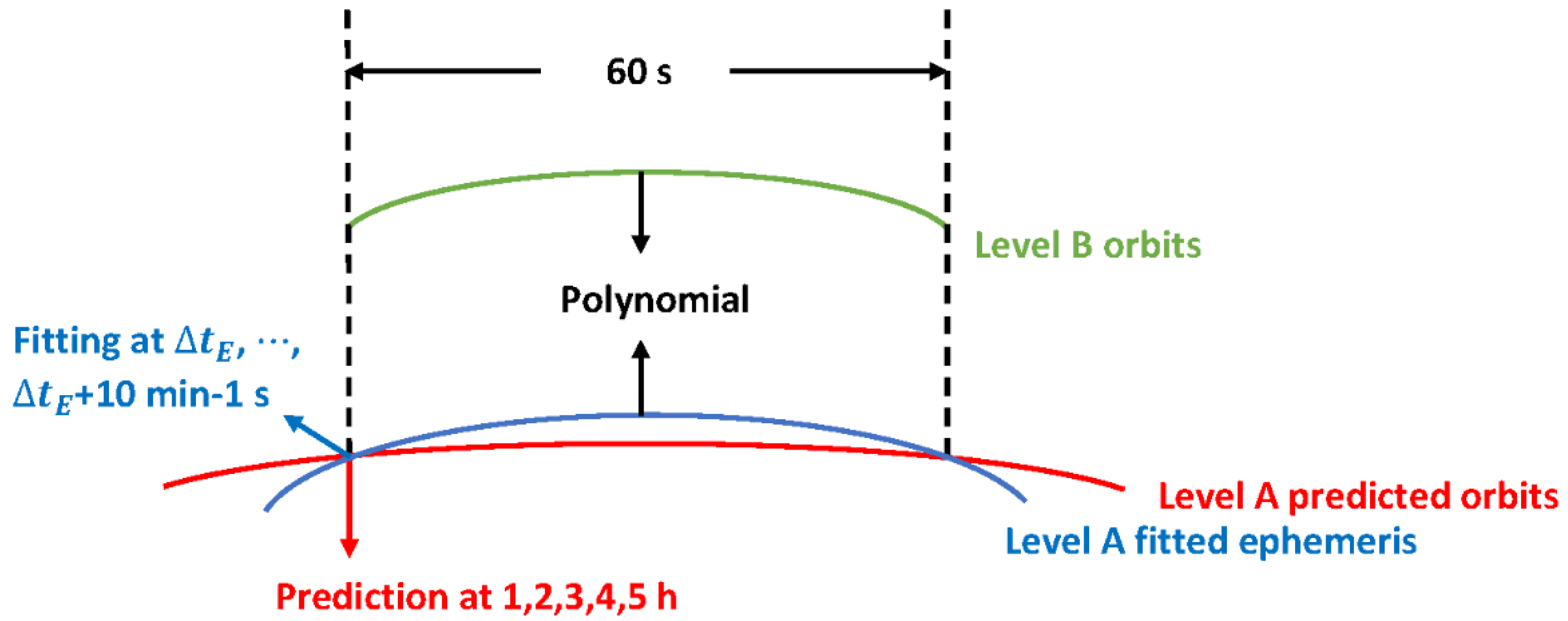
3.2. Level B Products
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Coluccia, A.; Ricciato, F.; Ricci, G. Positioning based on signals of opportunity. IEEE Commun. Lett. 2014, 18, 356–359. [Google Scholar] [CrossRef]
- Montenbruck, O.; Gill, E. Around the world in a hundred minutes. In Satellite Orbits, 1st ed.; Springer: Berlin, Germany, 2000; pp. 1–13. [Google Scholar]
- Reid, T.G.R.; Neish, A.M.; Walter, T.; Enge, P.K. Broadband LEO Constellations for Navigation. Navig. J. Inst. Navig. 2018, 65, 205–220. [Google Scholar] [CrossRef]
- Ge, H.; Li, B.; Ge, M.; Zang, N.; Nie, L.; Shen, Y.; Schuh, H. Initial Assessment of Precise Point Positioning with LEO Enhanced Global Navigation Satellite Systems (LeGNSS). Remote Sens. 2018, 10, 984. [Google Scholar] [CrossRef] [Green Version]
- Khalife, J.; Neinavaie, M.; Kassas, Z.M. Navigation with differential carrier phase measurements from Megaconstellation LEO satellites. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 1393–1404. [Google Scholar]
- Vetter, J.R. Fifty Years of Orbit Determination: Development of Modern Astrodynamics Methods. J. Hopkins APL Tech. Dig. 2007, 27, 239–252. [Google Scholar]
- Danchik, R.J.; Pryor, L.L. The NAVY navigation satellite system (TRANSIT). J. Hopkins APL Tech. Dig. 1990, 11, 97–104. [Google Scholar]
- Wolf, R. Satellite Orbit and Ephemeris Determination Using Inter Satellite Links. Ph.D. Thesis, Faculty of Civil Engineering and Surveying, Bundeswehr University Munich, Munich, Germany, 2000. [Google Scholar]
- Wang, F.; Gong, X.; Sang, J.; Zhang, X. A novel method for precise onboard real-time orbit determination with a standalone GPS receiver. Sensors 2015, 15, 30403–30418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, K.; Zhou, X.; Guo, N.; Zhao, G.; Xu, K.; Lei, W. Comparison of precise orbit determination methods of zero-difference kinematic, dynamic and reduced-dynamic of GRACE-A satellite using SHORDE software. J. Appl. Geodesy 2017, 11, 157–165. [Google Scholar] [CrossRef]
- Xie, X.; Geng, T.; Zhao, Q.; Liu, X.; Zhang, Q.; Liu, J. Design and validation of broadcast ephemeris for low Earth orbit satellites. GPS Solut. 2018, 22, 54. [Google Scholar] [CrossRef]
- Ge, H.; Li, B.; Ge, M.; Nie, L.; Schuh, H. Improving low Earth orbit (LEO) prediction with accelerometer data. Remote Sens. 2020, 12, 1599. [Google Scholar] [CrossRef]
- Johnston, G.; Riddell, A.; Hausler, G. The International GNSS Service. In Springer Handbook of Global Navigation Satellite Systems, 1st ed.; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer: Cham, Switzerland, 2017; pp. 967–982. [Google Scholar]
- Hadas, T.; Bosy, J. IGS RTS precise orbits and clocks verification and quality degradation over time. GPS Solut. 2015, 19, 93–105. [Google Scholar] [CrossRef] [Green Version]
- Global Positioning System Standard Positioning Service Performance Standard 5th Edition. Available online: https://www.gps.gov/technical/ps/2020-SPS-performance-standard.pdf (accessed on 13 October 2020).
- Flechtner, F.; Morton, P.; Watkins, M.; Webb, F. Status of the GRACE follow-on mission. In Gravity, Geoid and Height Systems; Marti, U., Ed.; Springer: Cham, Switzerland, 2014; Volume 141, pp. 117–121. [Google Scholar]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software Version 5.2; Astronomical Institute, University of Bern: Bern, Switzerland, 2015. [Google Scholar]
- Montenbruck, O.; Gill, E. Linearization. In Satellite Orbits; Springer: Berlin, Germany, 2000. [Google Scholar]
- Wang, K.; Allahvirdi-Zadeh, A.; El-Mowafy, A.; Gross, J.N. A sensitivity study of POD using dual-frequency GPS for CubeSats data limitation and resources. Remote Sens. 2020, 12, 2107. [Google Scholar] [CrossRef]
- Laurichesse, D.; Cerri, L.; Berthias, J.P.; Mercier, F. Real time precise GPS constellation and clocks estimation by means of a Kalman filter. In Proceedings of the the 26th international technical meeting of the satellite division of the institute of navigation (ION GNSS+ 2013), Nashville, TN, USA, 16–20 September 2013; pp. 1155–1163. [Google Scholar]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. An Earth gravitational model to degree 2160: EGM2008. In Proceedings of the European Geosciences Union General Assembly, Vienna, Austria, 13–18 April 2008. [Google Scholar]
- Standish, E.M. The JPL Planetary and Lunar Ephemerides, DE405/LE405. Available online: ftp://ssd.jpl.nasa.gov/pub/eph/planets/ioms/de405.iom.pdf (accessed on 13 October 2020).
- Petit, G.; Luzum, B. IERS Conventions. IERS Technical Note, 36. Verl. Bundesamts Kartogr. Geodäsie Frankfurt Main 2010, 179, 58. [Google Scholar]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Beutler, G. Variational equations. In Methods of Celestial Mechanics; Springer: Berlin, Germany, 2005; pp. 175–207. [Google Scholar]
- Kwan, R.E.P. Navstar GPS Space Segment/Navigation User Segment Interfaces, 2019. IS-GPS-200K. Available online: https://www.gps.gov/technical/icwg/IS-GPS-200K.pdf (accessed on 13 October 2020).
- Wang, L.; Chen, R.; Li, D.; Zhang, G.; Shen, X.; Yu, B.; Wu, C.; Xie, S.; Zhang, P.; Li, M.; et al. Initial assessment of the LEO based navigation signal augmentation system from Luojia-1A satellite. Sensors 2018, 18, 3919. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- El-Mowafy, A.; Deo, M.; Kubo, N. Maintaining real-time precise point positioning during outages of orbit and clock corrections. GPS Solut. 2017, 21, 937–947. [Google Scholar] [CrossRef]
- Hauschild, A.; Tegedor, J.; Montenbruck, O.; Visser, H.; Markgraf, M. Precise onboard orbit determination for LEO satellites with real-time orbit and clock corrections. In Proceedings of the ION GNSS+ 2016, Portland, OR, USA, 12–16 September 2016; pp. 3715–3723. [Google Scholar]
- Zhang, S.; Du, S.; Li, W.; Wang, G. Evaluation of the GPS precise orbit and clock corrections from MADOCA real-time products. Sensors 2019, 19, 2580. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sobreira, H.; Bougard, B.; Barrios, J.; Calle, J.D. SBAS Australian-NZ Test Bed: Exploring New Services. In Proceedings of the ION GNSS+ 2018, Miami, FL, USA, 24–28 September 2018; pp. 2119–2133. [Google Scholar]
- El-Mowafy, A.; Cheung, N.; Rubinov, E. First results of using the second generation SBAS in Australian urban and suburban road environments. J. Spat. Sci. 2020, 65, 99–121. [Google Scholar] [CrossRef]
- Wen, H.Y.; Kruizinga, G.; Paik, M.; Landerer, F.; Bertiger, W.; Sakumura, C.; Bandikova, T.; Mccullough, C. Gravity Recovery and Climate Experiment Follow-on (GRACE-FO) Level-1 Data Product User Handbook; JPL D-56935 (URS270772); NASA Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 2019. [Google Scholar]
- Chen, L.; Jiao, W.; Huang, X.; Geng, C.; Ai, L.; Lu, L.; Hu, Z. Study on signal-in-space errors calculation method and statistical characterization of BeiDou navigation satellite system. In Proceedings of the China Satellite Navigation Conference (CSNC), Wuhan, China, 15–17 May 2013; pp. 423–434. [Google Scholar]
- Montenbruck, O.; Gill, E.; Kroes, R. Rapid orbit determination of LEO satellites using IGS clock and ephemeris products. GPS Solut. 2005, 9, 226–235. [Google Scholar] [CrossRef]







| Latitude (B) Range | ||||
|---|---|---|---|---|
| 8 | 5 | 2 | 2 | |
| 5 | 2 | 2 | 1 | |
| 2 | 1 | 1 | 1 | |
| All | 2 | 1 | 1 | 1 |
| Category | Parameters | Estimation Interval | |
|---|---|---|---|
| Keplerian elements | , , , , , | 24 h | |
| Dynamic parameters | Option A | , , | 24 h 6/15/30 min |
| Option B | , , , , , , , , | 24 h 15/30 min, 1/2/3/4/6/12/24 h | |
| Parameters/Models | Details |
|---|---|
| Observations | GPS IF combination (L1/L2), code + phase |
| Sampling interval | Observations: 30 s; Prediction: 1 s |
| Estimation interval | 24 h |
| Prediction interval | 6 h |
| Elevation mask | 5° |
| GPS orbits/clocks | CNES real-time products [20] |
| Dynamic models | Earth gravity terms: EGM2008 (degree: 120) [21] |
| Gravity terms of other planets: JPL DE405 [22] | |
| Solid Earth tides, Pole tides: IERS 2010 [23] | |
| Ocean tides: FES2004 [24] | |
| General relativistic effects |
| Category | Ephemeris Parameters |
|---|---|
| GPS LNAV ephemeris parameters | , , , , , , , , , , , , |
| Transformed GPS LNAV ephemeris parameters | , , |
| Additional ephemeris parameters | , , , |
| Parameters/Models | Details |
|---|---|
| Strategy of orbit estimation | Reduced-dynamic orbits (Section 2.1.2) |
| Sampling interval of the observations | 30 s |
| Strategy of orbit prediction | Dynamic orbits (Table 2 and Table 3) |
| Prediction sampling interval | 1 s |
| Prediction interval | 60 s |
| Polynomial degree | 1, 2, 3 |
| Prediction Interval | RMSE Radial (m) | RMSE Along-Track (m) | RMSE Cross-Track (m) | 3D RMSE (m) | OURE (m) |
|---|---|---|---|---|---|
| 0.5 h | 0.035 | 0.131 | 0.028 | 0.138 | 0.086 |
| 1 h | 0.042 | 0.156 | 0.033 | 0.165 | 0.102 |
| 2 h | 0.052 | 0.359 | 0.039 | 0.365 | 0.228 |
| 3 h | 0.070 | 0.560 | 0.047 | 0.566 | 0.355 |
| 4 h | 0.072 | 0.829 | 0.055 | 0.834 | 0.523 |
| 5 h | 0.083 | 1.203 | 0.064 | 1.207 | 0.758 |
| 6 h | 0.105 | 1.599 | 0.082 | 1.605 | 1.008 |
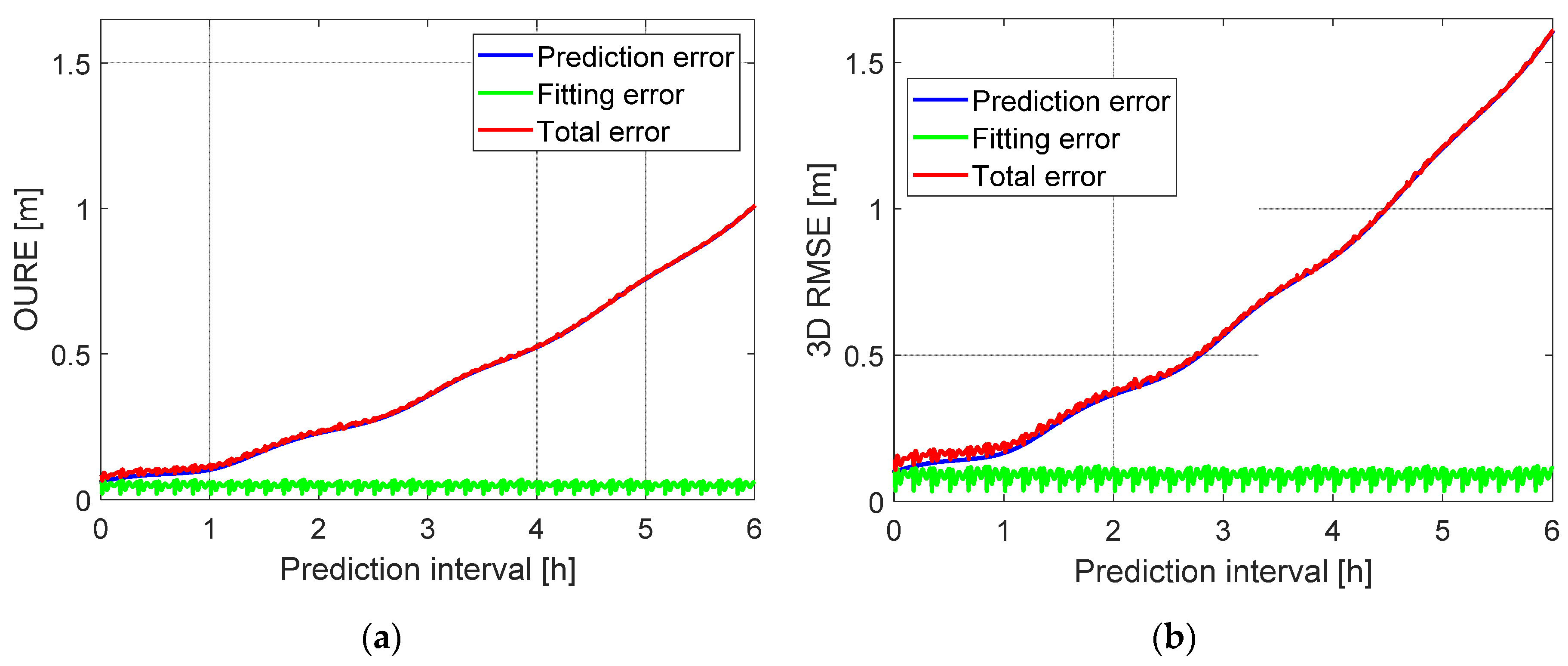
| Prediction Interval | OURE (m) | 3D RMSE (m) | ||||
|---|---|---|---|---|---|---|
| Prediction | Fitting | Total | Prediction | Fitting | Total | |
| 0.5 h | 0.086 | 0.059 | 0.101 | 0.138 | 0.111 | 0.173 |
| 1 h | 0.102 | 0.058 | 0.118 | 0.165 | 0.112 | 0.200 |
| 2 h | 0.228 | 0.059 | 0.236 | 0.365 | 0.113 | 0.383 |
| 3 h | 0.355 | 0.059 | 0.360 | 0.566 | 0.102 | 0.579 |
| 4 h | 0.523 | 0.059 | 0.527 | 0.834 | 0.114 | 0.842 |
| 5 h | 0.758 | 0.059 | 0.760 | 1.207 | 0.114 | 1.213 |
| 6 h | 1.008 | 0.060 | 1.010 | 1.605 | 0.114 | 1.609 |
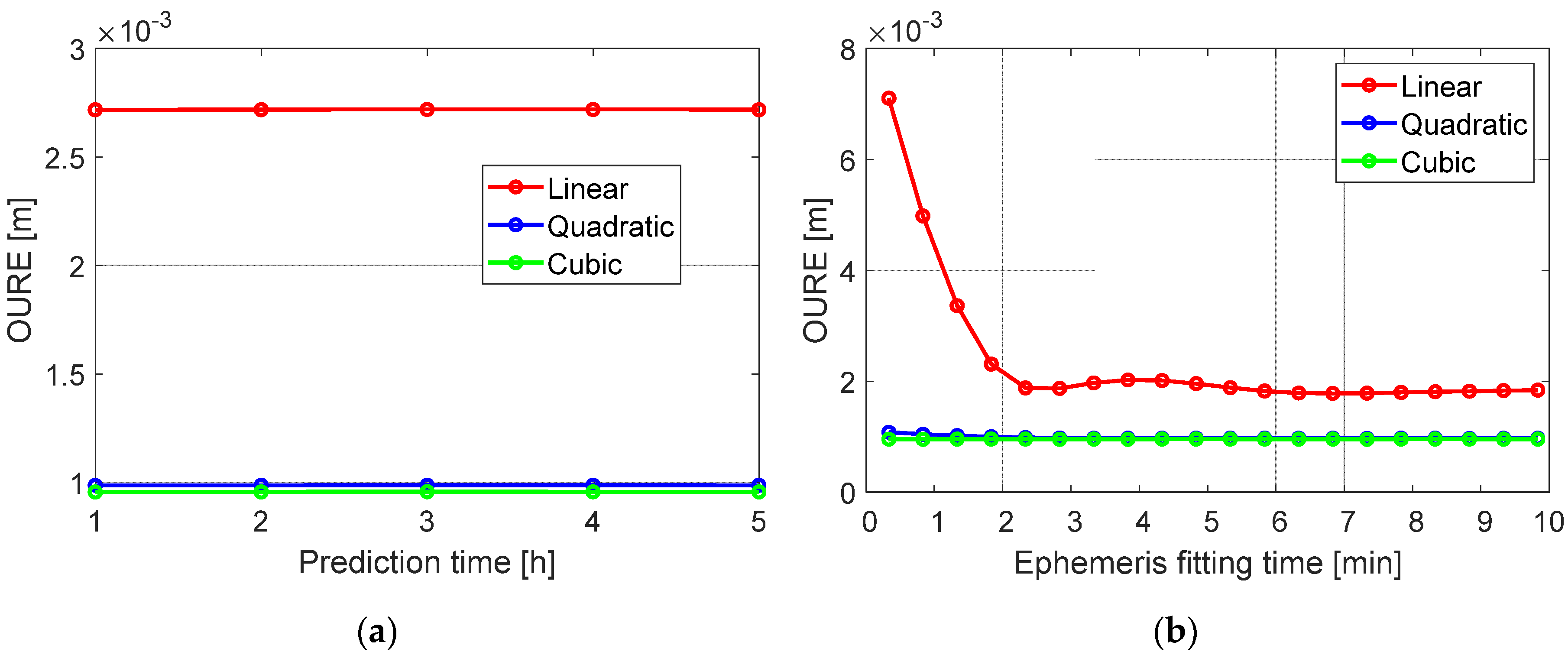
| Fitting Type | Prediction Errors [cm] | Fitting Errors [cm] | Total Errors [cm] | |||
|---|---|---|---|---|---|---|
| OURE | 3D RMSE | OURE | 3D RMSE | OURE | 3D RMSE | |
| Linear polynomial | 2.4/2.5 | 4.3/4.4 | 0.6/0.5 | 1.0/0.9 | 2.52/2.59 | 4.43/4.56 |
| Quadratic polynomial | 0.1/0.1 | 0.2/0.2 | 2.45/2.53 | 4.29/4.44 | ||
| Cubic polynomial | 0.1/0.1 | 0.2/0.2 | 2.45/2.54 | 4.28/4.45 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; El-Mowafy, A. Proposed Orbital Products for Positioning Using Mega-Constellation LEO Satellites. Sensors 2020, 20, 5806. https://doi.org/10.3390/s20205806
Wang K, El-Mowafy A. Proposed Orbital Products for Positioning Using Mega-Constellation LEO Satellites. Sensors. 2020; 20(20):5806. https://doi.org/10.3390/s20205806
Chicago/Turabian StyleWang, Kan, and Ahmed El-Mowafy. 2020. "Proposed Orbital Products for Positioning Using Mega-Constellation LEO Satellites" Sensors 20, no. 20: 5806. https://doi.org/10.3390/s20205806
APA StyleWang, K., & El-Mowafy, A. (2020). Proposed Orbital Products for Positioning Using Mega-Constellation LEO Satellites. Sensors, 20(20), 5806. https://doi.org/10.3390/s20205806





