Efficient Privacy-Preserving Data Sharing for Fog-Assisted Vehicular Sensor Networks
Abstract
1. Introduction
1.1. Our Contributions
- First, the proposed EPDS scheme exploits the super-increasing sequence [20] for achieving multi-dimensional data aggregation, while calculating the average sensory data in each road segment, greatly saving on the resources of communication and computation.
- Secondly, by utilizing the modified oblivious transfer [28], the proposed EPDS scheme is able to query about the road conditions of the potential moving routes without disclosing the query location.
- Thirdly, an analysis of security indicates that the proposed EPDS scheme is proven to be secure under elliptic curve discrete logarithm (ECDL) assumption in the random oracle model and satisfies all the requirements for security and privacy.
- Finally, the performances of computation and communication in costs are evaluated through quantitative calculations, with the results that the proposed EPDS scheme is of more efficiency than others.
1.2. Organization
2. Related Works
3. Background
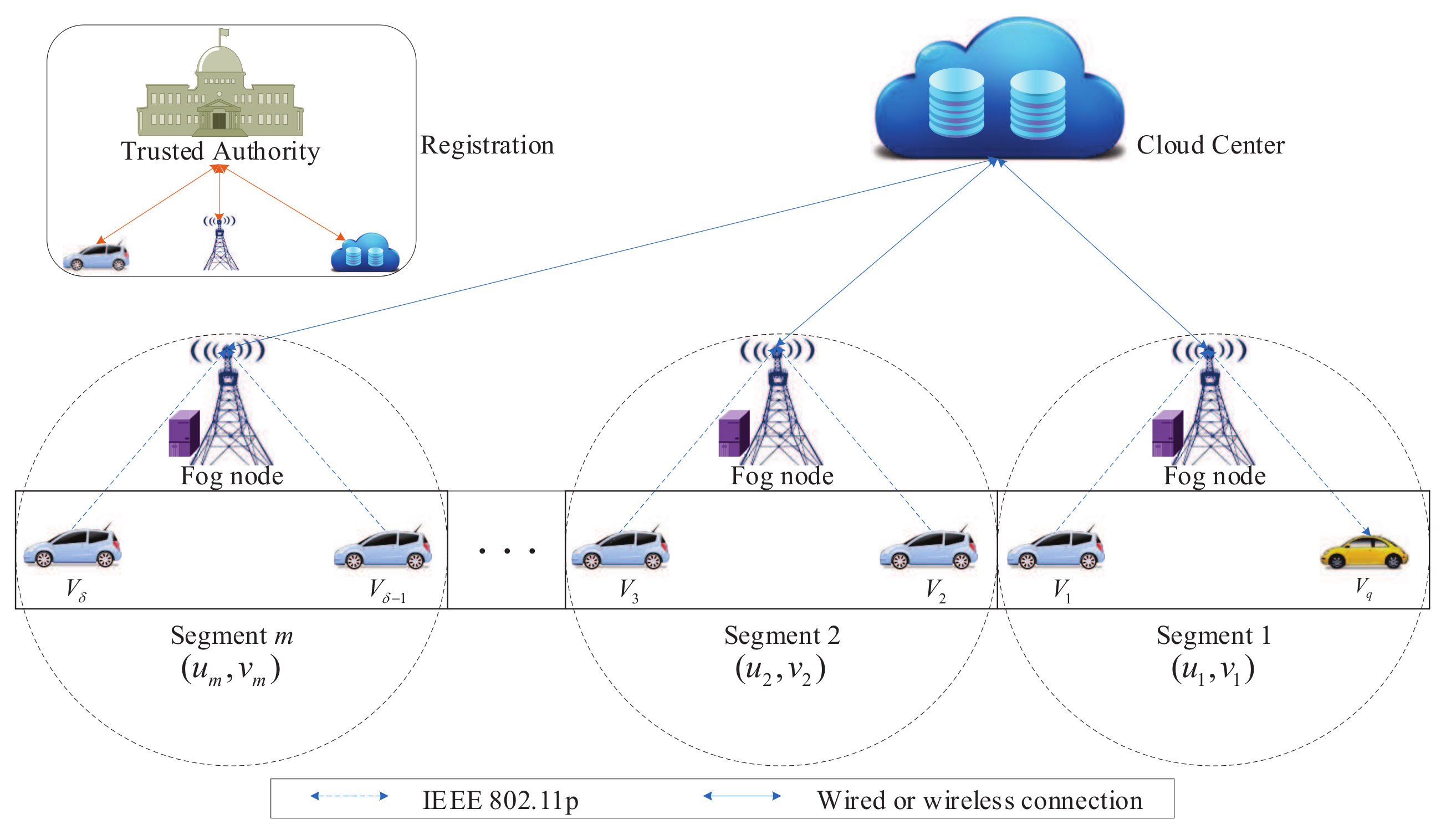
3.1. System Model
3.2. Security Requirement
3.3. Elliptic Curve
3.4. Security Assumption
4. The Proposed Scheme
4.1. System Initialization
- (1)
- randomly chooses a large prime number p, and selects a non-singular elliptic curve E defined by , where .
- (2)
- picks a group of E with the prime order q and a generator P.
- (3)
- randomly chooses as its master key and computes its public key .
- (4)
- chooses eight one-way hash functions , , .
- (5)
- chooses a super-increasing sequence , such that , (), where are large prime numbers and d is the maximum value of the data. Then, assigns prime number towards segment k.
- (6)
- publishes the system parameters .
4.2. Registration
4.2.1. Registers with
- (1)
- sends the identity to the in secure channel.
- (2)
- After confirming the identity , randomly chooses and computesand sets , where represents the valid period of .
- (3)
- randomly chooses and computes
- (4)
- randomly chooses a sharing key , and transmits the pseudo identity , the private key and the sharing key to in a secure channel.
4.2.2. Registers with
- (1)
- sends the identity to the in a secure channel.
- (2)
- randomly chooses and computes
- (3)
- sends the private key to in a secure channel.
4.2.3. Registers with
- (1)
- randomly chooses and computes .
- (2)
- sends the private key x and public key to in a secure channel.
4.3. Data Collection
4.3.1. Data Gathering
- (1)
- formats and into and .
- (2)
- randomly selects , and computes
- (3)
- randomly picks and calculateswhere is current timestamp.
- (4)
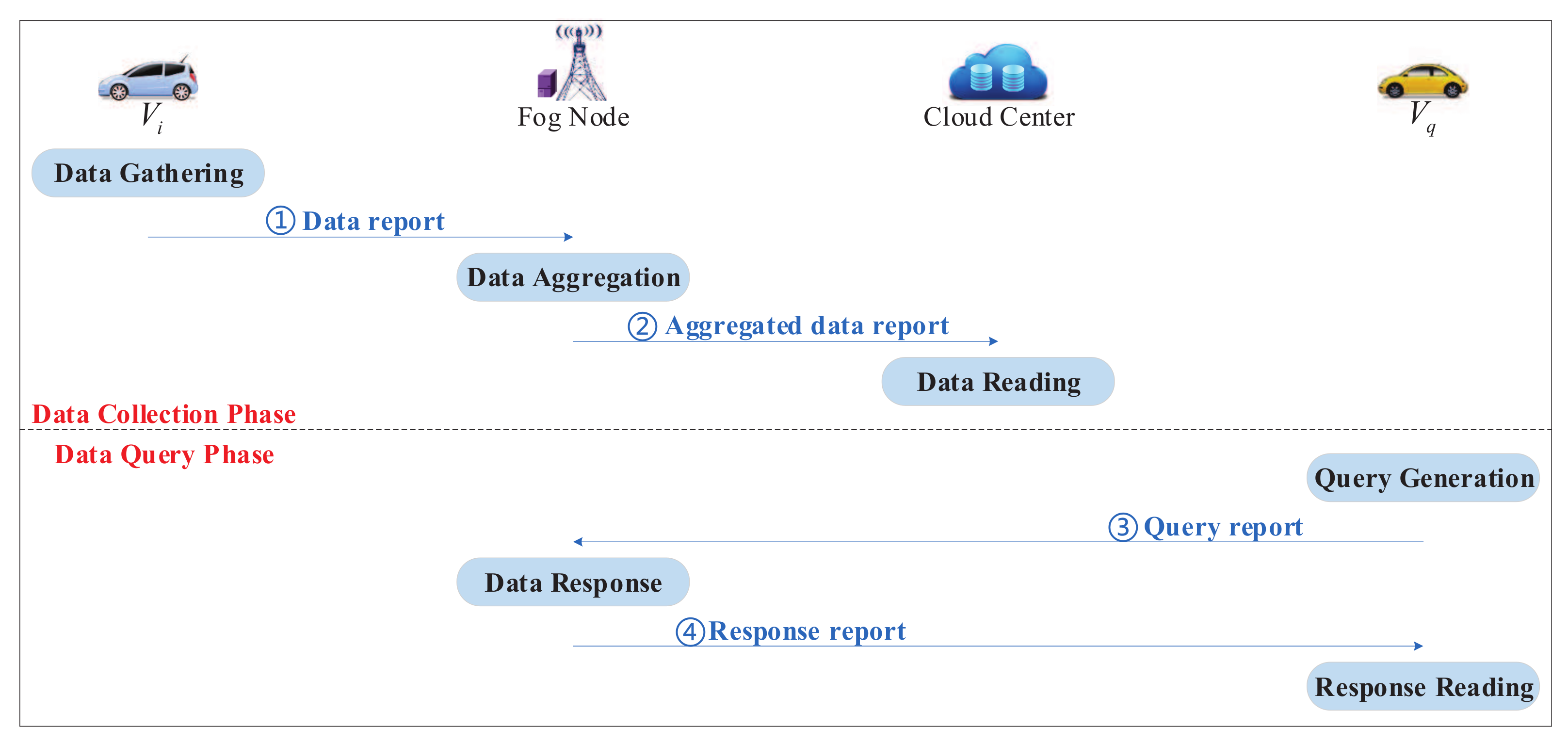
- transmits the data report towards , as shown in Figure 2 (①).
4.3.2. Data Aggregation
- (1)
- checks whether is valid and is fresh for each . If is not valid or is not fresh, will be rejected. Otherwise, performs the batch verification using small exponent test [36]. randomly selects a set of small numbers and checks whether the following equation holdsIf it does hold, computes
- (2)
- randomly picks and calculateswhere is current timestamp.
- (3)
- transmits the aggregated data report towards , as shown in Figure 2 (②).
4.3.3. Data Reading
- (1)
- checks whether is fresh for each . If is not fresh, will be rejected. Otherwise, randomly chooses a set of small numbers and performs the batch verification using small exponent test [36]. verifies whether the following equation holdsIf it does hold, calculatesBy solving the discrete log of and with the base P, utilizing the Pollard’s lambda algorithm [37], can obtain
- (2)
- distributes and to all fog nodes for further sharing with vehicles.
4.4. Data Query
4.4.1. Query Generation
- (1)
- selects two random numbers and calculates
- (2)
- randomly picks and calculateswhere is the current timestamp.
- (3)
- transmits the query report towards , as shown in Figure 2 (③).
4.4.2. Data Response
- (1)
- After receiving , checks whether is valid and is fresh. If is not valid or is not fresh, will be rejected. Otherwise, verifies whether the following equation holdsIf it does hold, selects two random numbers and calculates
- (2)
- randomly picks and calculateswhere is the current timestamp.
- (3)
- transmits the response report towards , as shown in Figure 2 (④).
4.4.3. Response Reading
- (1)
- After receiving , checks whether is fresh. If is not fresh, will be rejected. Otherwise, verifies whether the following equation holdsIf it does hold, calculatesBy solving the discrete log of with the base P, utilizing the Pollard’s lambda algorithm [37], can obtain .
- (2)
- By calling the Algorithm 1, can achieve the average sensing data captured at segment c.
| Algoruthm 1 Recovery captured at segment c |
| Input: , , , , and |
| Output: |
| begin: |
| set , ; |
| for to c do |
| , ; |
| , ; |
| return . |
| end |
5. Security
5.1. Security Model
5.2. Security Proof
5.3. Analysis and Comparison of Security Requirement
- Modification attack: Based on Theorem 2, any polynomial attacker is unable to forge a valid data report with modification on data reports found.
- Replay attack: On the basis of the proposed EPDS scheme, the timestamp is contained in the data report. By examining freshness of the timestamp, the verifier is able to bear any replay attacks.
- Impersonation attack: From Theorem 2, no attacker can fabricate a legal data report without vehicle’s private key.
- Man-in-the-middle attack: The analysis of the modification attack shows that any modification of the data reports on transmission is able to be found.
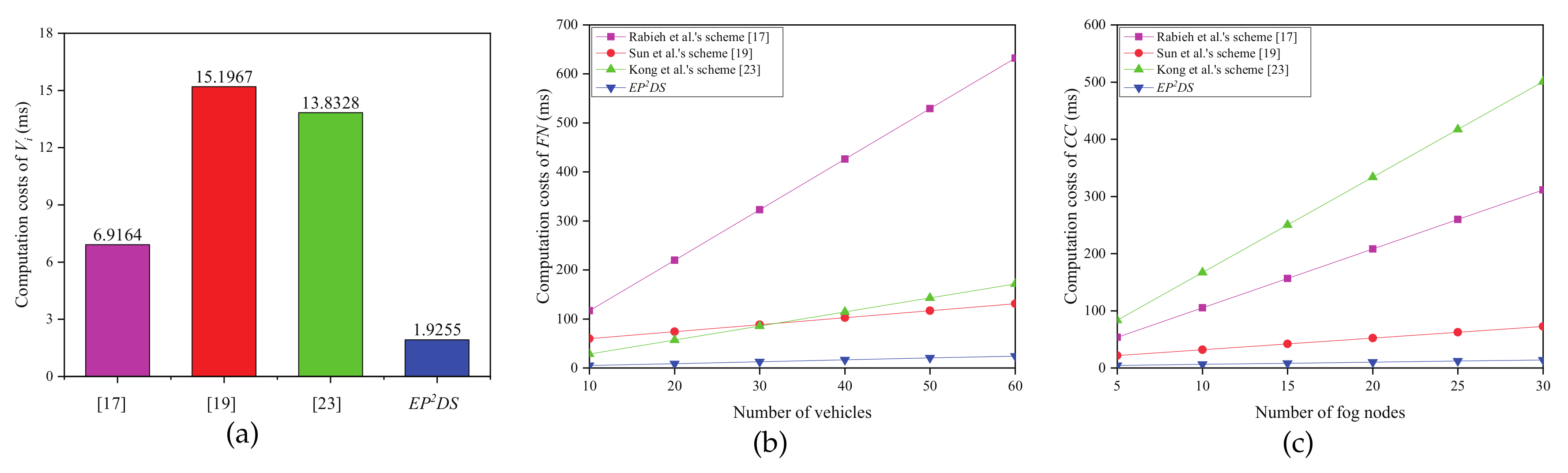
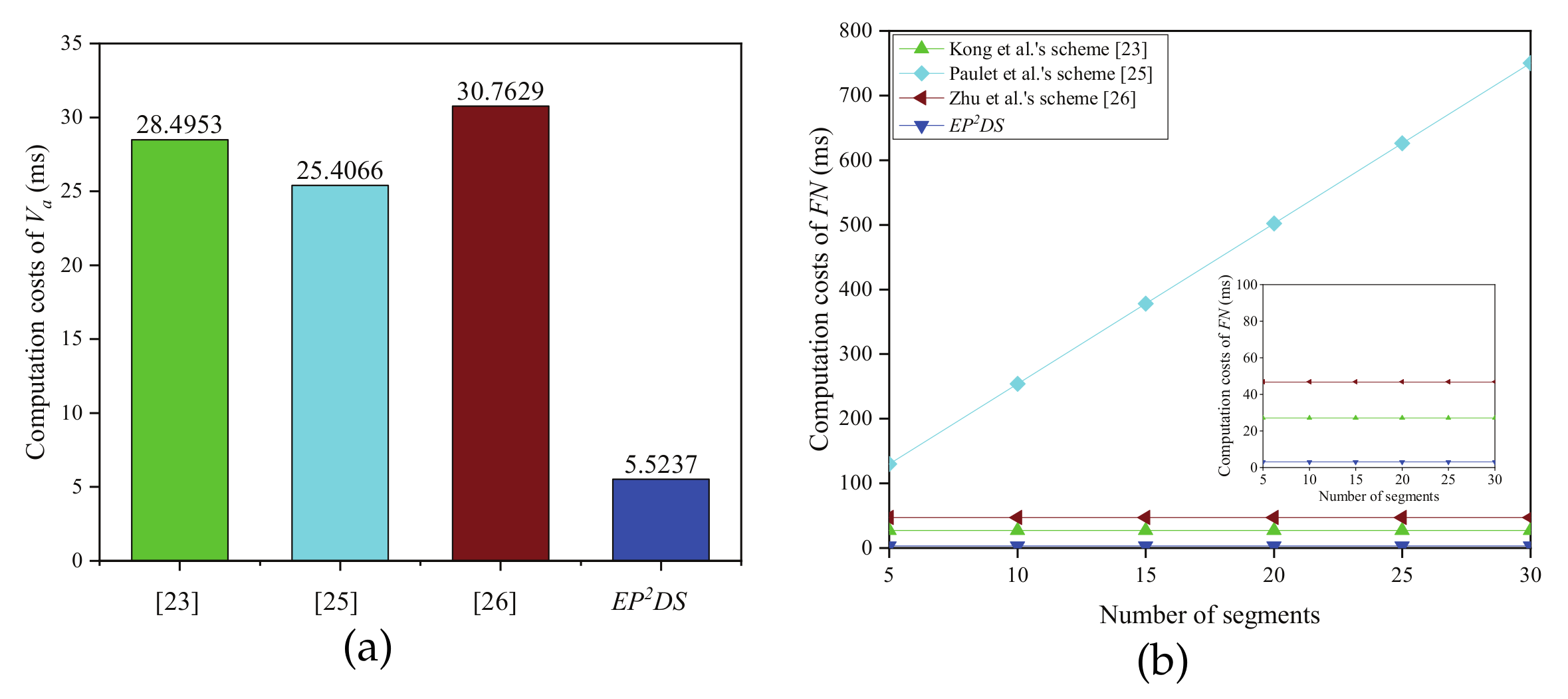
6. Performance Evaluation
6.1. Computation Costs
6.2. Communication Costs
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- Hash queries: Upon receiving the query, returns a random value to .
- Extract queries: Upon receiving the query on the pseudo identity , returns a private key to .
- Signcryption queries: Upon receiving the query on the message under , returns a ciphertext to .
- The ciphertext on under is valid.
- has not been requested in the extract queries.
Appendix B
- : It consists of tuples .
- : It consists of tuples .
- : It consists of tuples .
- If contains , responds with the previous value to .
- If does not contain , randomly chooses a number , adds into and returns to .
- If contains , responds with the previous value to .
- If does not contain , randomly chooses a number , adds into and returns to .
- If , aborts the game.
- If , executes:
- -
- If contains , returns to .
- -
- If does not contain , randomly chooses and makes . If already appear in , chooses another and tries again. inserts and into and , respectively. Finally, returns the to .
- : does not abort above game in extract queries.
- : is able to correctly output the value of b.
- If , randomly selects and calculates , , . If the already appears in or already appears in , chooses another and tries again. Then, returns the ciphertext to , and inserts and into and , respectively.
- If , generates a ciphertext in accordance with the proposed scheme. Then, returns the ciphertext to .
- : never abort above game in extract and signcryption queries.
- : is able to output a valid ciphertext.
- : .
References
- Lee, U.; Magistretti, E.; Zhou, B.; Gerla, M.; Bellavista, P.; Corradi, A. MobEyes: Smart mobs for urban monitoring with a vehicular sensor network. IEEE Trans. Commun. Mag. 2006, 13, 52–57. [Google Scholar] [CrossRef]
- Placzek, B. Selective data collection in vehicular networks for traffic control applications. Transp. Res. Part C Emerging Technol. 2012, 23, 14–28. [Google Scholar] [CrossRef]
- Mednis, A.; Elsts, A.; Selavo, L. Embedded solution for road condition monitoring using vehicular sensor networks. In Proceedings of the 2012 6th International Conference on Application of Information and Communication Technologies (AICT), Tbilisi, Georgia, 17–19 October 2012; pp. 1–5. [Google Scholar]
- Fiebig, B. European traffic accidents and purposed solutions. In Proceedings of the ITU-Workshop on Standardization in Telecommunication for Motor Vehicles, Geneva, Switzerland, 24–25 November 2003; pp. 24–25. [Google Scholar]
- Yu, R.; Huang, X.; Kang, J.; Ding, J.; Maharjan, S.; Gjessing, S.; Zhang, Y. Cooperative resource management in cloud-enabled vehicular networks. IEEE Trans. Ind. Electron. 2015, 62, 7938–7951. [Google Scholar] [CrossRef]
- Ni, J.; Lin, X.; Zhang, K.; Shen, X.M. Privacy-preserving real-time navigation system using vehicular crowdsourcing. In Proceedings of the IEEE 84th Vehicular Technology Conference: VTC2016-Fall, Montreal, QC, Canada, 18–21 September 2016; pp. 1–5. [Google Scholar]
- Bonomi, F.; Milito, R.; Zhu, J.; Addepalli, S. Fog computing and its role in the internet of things. In Proceedings of the Mobile Cloud Computing Workshop, Helsinki, Finland, 13–17 August 2012; pp. 13–16. [Google Scholar]
- Armbrust, M.; Fox, A.; Griffith, R.; Joseph, A.D.; Katz, R.H.; Konwinski, A.; Lee, G.; Patterson, D.A.; Rabkin, A.; Stoica, I.; et al. A view of cloud computing. Commun. ACM 2010, 53, 50–58. [Google Scholar] [CrossRef]
- Dai, Y.; Xu, D.; Maharjan, S.; Zhang, Y. Joint offloading and resource allocation in vehicular edge computing and networks. In Proceedings of the IEEE Global Communications Conference, Abu Dhabi, UAE, 9–13 December 2018; pp. 1–7. [Google Scholar]
- Ni, J.; Zhang, K.; Yu, Y.; Lin, X.; Shen, X.S. Privacy-preserving smart parking navigation supporting efficient driving guidance retrieval. IEEE Trans. Veh. Technol. 2018, 67, 6504–6517. [Google Scholar] [CrossRef]
- Basudan, S.; Lin, X.; Sankaranarayanan, K. A privacy-preserving vehicular crowdsensing based road surface condition monitoring system using fog computing. IEEE Internet Things J. 2017, 4, 772–782. [Google Scholar] [CrossRef]
- Chun, S.; Shin, S.; Seo, S.; Eom, S.; Jung, J.; Lee, K. A pubsub-based fog computing architecture for Internet-of-vehicles. In Proceedings of the 8th International Conference on Cloud Computing Technology and Science, Luxembourg, 12–15 December 2016; pp. 90–93. [Google Scholar]
- Ni, J.; Zhang, A.; Lin, X.; Shen, X.S. Security, privacy, and fairness in fog-based vehicular crowdsensing. IEEE Commun. Mag. 2017, 55, 146–152. [Google Scholar] [CrossRef]
- Wei, J.; Wang, X.; Li, N. A privacy-preserving fog computing framework for vehicular crowdsensing betworks. IEEE Access 2018, 6, 43776–43784. [Google Scholar] [CrossRef]
- Omoniwa, B.; Hussain, R.; Javed, M.A. Fog/Edge computing-based IoT (FECIoT): Architecture, applications, and research issues. IEEE Internet Things 2019, 6, 4118–4149. [Google Scholar] [CrossRef]
- Zhuo, G.; Jia, Q.; Guo, L.; Li, M.; Li, P. Privacy-preserving verifiable data aggregation and analysis for cloud-assisted mobile crowdsourcing. In Proceedings of the 35th IEEE International Conference on Computer Communications, San Francisco, CA, USA, 10–14 April 2016; pp. 1–9. [Google Scholar]
- Rabieh, K.; Mahmoud, M.M.E.A.; Younis, M. Privacy-preserving route reporting schemes for traffic management systems. IEEE Trans. Veh. Technol. 2017, 66, 2703–2713. [Google Scholar] [CrossRef]
- Xu, C.; Lu, R.; Wang, H.; Zhu, L.; Huang, C. PAVS: A new privacy-preserving data aggregation scheme for vehicle sensing systems. Sensors 2017, 17, 500. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.; Sun, S.; Sun, J.; Yu, H.; Du, X.; Guizani, M. Security and privacy preservation in fog-based crowd sensing on the internet of vehicles. J. Network Comput. Appl. 2019, 134, 89–99. [Google Scholar] [CrossRef]
- Lin, X.; Lu, R.; Shen, X. MDPA: Multidimensional privacy-preserving aggregation scheme for wireless sensor networks. Wirel. Commun. Mob. Comput. 2010, 10, 843–856. [Google Scholar] [CrossRef]
- Lu, R.; Heung, K.; Lashkari, A.H.; Ghorbani, A.A. A light-weight privacy-preserving data aggregation scheme for fog computing-enhanced IoT. IEEE Access 2017, 5, 3302–3312. [Google Scholar] [CrossRef]
- Wang, B.; Chang, Z.; Zhou, Z.; Ristaniemi, T. Reliable and privacy-preserving task recomposition for crowdsensing in vehicular fog computing. In Proceedings of the 87th Vehicular Technology Conference, Porto, Portugal, 3–6 June 2018; pp. 6–11. [Google Scholar]
- Kong, Q.; Lu, R.; Ma, M.; Bao, H. A privacy-preserving sensory data sharing scheme in internet of vehicles. Future Gener. Comput. Syst. 2019, 92, 644–655. [Google Scholar] [CrossRef]
- Ghinita, G.; Kalnis, P.; Kantarcioglu, M.; Bertino, E. A hybrid technique for private location-based queries with database protection. In Proceedings of the 11th International Symposium on Spatial and Temporal Databases, Aalborg, Denmark, 8–10 July 2009; pp. 98–116. [Google Scholar]
- Paulet, R.; Kaosar, M.G.; Yi, X.; Bertino, E. Privacy-preserving and content protecting location based queries. IEEE Trans. Knowl. Data Eng. 2014, 26, 1200–1210. [Google Scholar] [CrossRef]
- Zhu, H.; Lu, R.; Huang, C.; Chen, L.; Li, H. An efficient privacy-preserving location-based services query scheme in outsourced cloud. IEEE Trans. Veh. Technol. 2016, 65, 7729–7739. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, F.; Li, H. Efficient and privacy-preserving polygons spatial query framework for location-based services. IEEE Internet Things J. 2017, 4, 536–545. [Google Scholar] [CrossRef]
- Naor, M.; Pinkas, B. Oblivious transfer with adaptive queries. In Proceedings of the Advances in Cryptology-CRYPTO’99, Santa Barbara, CA, USA, 15–19 August 1999; pp. 573–590. [Google Scholar]
- IEEE, 802.11p-2010-IEEE Standard for Information technology. Available online: https://ieeexplore.ieee.org/document/5514475/versions#versions (accessed on 14 January 2020).
- Jiang, S.; Liu, J.; Duan, M.; Wang, L.; Fang, L. Secure and privacy-preserving report de-duplication in the fog-based vehicular crowdsensing system. In Proceedings of the IEEE Global Communications Conference, Abu Dhabi, UAE, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Zhu, L.; Li, M.; Zhang, Z. Secure fog-assisted crowdsensing with collusion resistance: From data reporting to data requesting. IEEE Internet Things J. 2019, 6, 5473–5484. [Google Scholar] [CrossRef]
- Miller, V.S. Use of elliptic curves in cryptography. In Proceedings of the Advances in Cryptology-CRYPTO’85, Santa Barbara, CA, USA, 18–22 August 1985; pp. 417–426. [Google Scholar]
- Koblitz, N. Elliptic curve cryptosystem. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Ming, Y.; Zhang, X.; Shen, X. Efficient privacy-preserving multi-dimensional data aggregation scheme in smart grid. IEEE Access 2019, 7, 32907–32921. [Google Scholar] [CrossRef]
- He, D.; Zeadally, S.; Xu, B.; Huang, X. An efficient identity-based conditional privacy-preserving authentication scheme for vehicular ad hoc networks. IEEE Trans. Inf. Forensics Secur. 2015, 10, 2681–2690. [Google Scholar] [CrossRef]
- Liu, J.K.; Yuen, T.H.; Au, M.H.; Susilo, W. Improvements on an authentication scheme for vehicular sensor networks. Expert Syst. Appl. 2014, 41, 2559–2564. [Google Scholar] [CrossRef]
- Boneh, D.; Goh, E.; Nissim, K. Evaluating 2-DNF formulas on ciphertexts. In Proceedings of the 2nd Theory of Cryptography Conference, Cambridge, MA, USA, 10–12 February 2005; pp. 325–341. [Google Scholar]
- Ming, Y.; Cheng, H. Efficient certificateless conditional privacy-preserving authentication scheme in VANETs. Mob. Inf. Syst. 2019, 2019, 1–19. [Google Scholar] [CrossRef]
- Shamus Software Ltd. Multi precision integer and rational arithmetic cryptographic library (MIRACL). Available online: http://www.certivox.com/miracl/ (accessed on 1 December 2019).
- Pointcheval, D.; Stern, J. Security proofs for signature schemes. In Proceedings of the Advances in Cryptology-EUROCRYPT’96, Saragossa, Spain, 12–16 May 1996; pp. 387–398. [Google Scholar]
- Ming, Y.; Shen, X. PCPA: A practical certificateless conditional privacy preserving authentication scheme for vehicular ad hoc networks. Sensors 2018, 18, 1573. [Google Scholar] [CrossRef] [PubMed]
- He, D.; Kumar, N.; Zeadally, S.; Vinel, A.; Yang, L.T. Efficient and privacy-preserving data aggregation scheme for smart grid against internal adversaries. IEEE Trans. Smart Grid 2017, 13, 1–9. [Google Scholar] [CrossRef]
| Symbol | Definition |
|---|---|
| Trusted authority | |
| Cloud center | |
| ’s public key and private key | |
| ’s public key and private key | |
| The i-th data collection vehicle | |
| ’s real identity and pseudo identity | |
| ’s private key | |
| The j-th fog node | |
| ’s identity | |
| ’s private key | |
| The data query vehicle | |
| ’s real identity and pseudo identity | |
| ’s private key | |
| Identifier of the segment k | |
| d | Maximum value of sensory data |
| m | The total number of segments |
| n | The total number of fog nodes |
| The total number of vehicles | |
| Maximum length of sensory data | |
| The vehicles’ sharing key | |
| The sensory data captured by at segment k under | |
| If , then ; If , then . | |
| Eight one-way hash functions, . | |
| ⊕ | The exclusive OR operation |
| Two large prime numbers | |
| The finite field over p | |
| An additive group with the order q on the elliptic curve E over | |
| P | A generator of |
| Security | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Rabieh et al.’s scheme [17] | √ | √ | × | × | × | √ | √ | √ | √ | √ |
| Sun et al.’s scheme [19] | √ | √ | × | √ | √ | √ | √ | √ | √ | √ |
| Kong et al.’s scheme [23] | √ | √ | √ | × | × | √ | √ | × | √ | × |
| Paulet et al.’s scheme [25] | × | √ | √ | × | × | √ | × | × | × | × |
| Zhu et al.’s scheme [26] | √ | √ | √ | × | × | √ | √ | × | √ | × |
| EPDS | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Notations | Descriptions | Runtime |
|---|---|---|
| Scalar multiplication operation in | 0.3851 | |
| Solving the DL operation mod p | 0.6438 | |
| The exponentiation operation in | 2.0289 | |
| The multiplication operation in | 1.4293 | |
| Map to point hash function operation | 3.5819 | |
| Bilinear pairing operation in | 10.3092 |
| Scheme | Data Collection Phase | Data Query Phase | |||
|---|---|---|---|---|---|
| [17] | + | +++ | ++ | − | − |
| = 6.9164 ms | = 10.3092w+13.7674 ms | =10.3092n+2.0289 ms | |||
| [19] | ++ | ++ | ++ | − | − |
| = 15.1967 ms | = 1.4293w+45.5247 ms | =2.0289n+11.7385 ms | |||
| [23] | + | + | + | + | |
| = 13.8328 ms | = 2.8586w ms | =16.6914n ms | =28.4953 ms | =27.0660 ms | |
| [25] | − | − | − | + | 6m+m+ )Te |
| =25.4066 ms | =24.8070m+6.0867 ms | ||||
| [26] | − | − | − | + | + |
| =30.7629 ms | =46.9540 ms | ||||
| EPDS | + | ++ | + | ||
| =1.9255 ms | =0.3851w+1.1553 ms | =0.3851n+2.4429 ms | =5.5237 ms | =3.0808 ms | |
| Scheme | Data Collection Phase | Data Query Phase | |
|---|---|---|---|
| Data Report Size | Query Report Size | Response Report Size | |
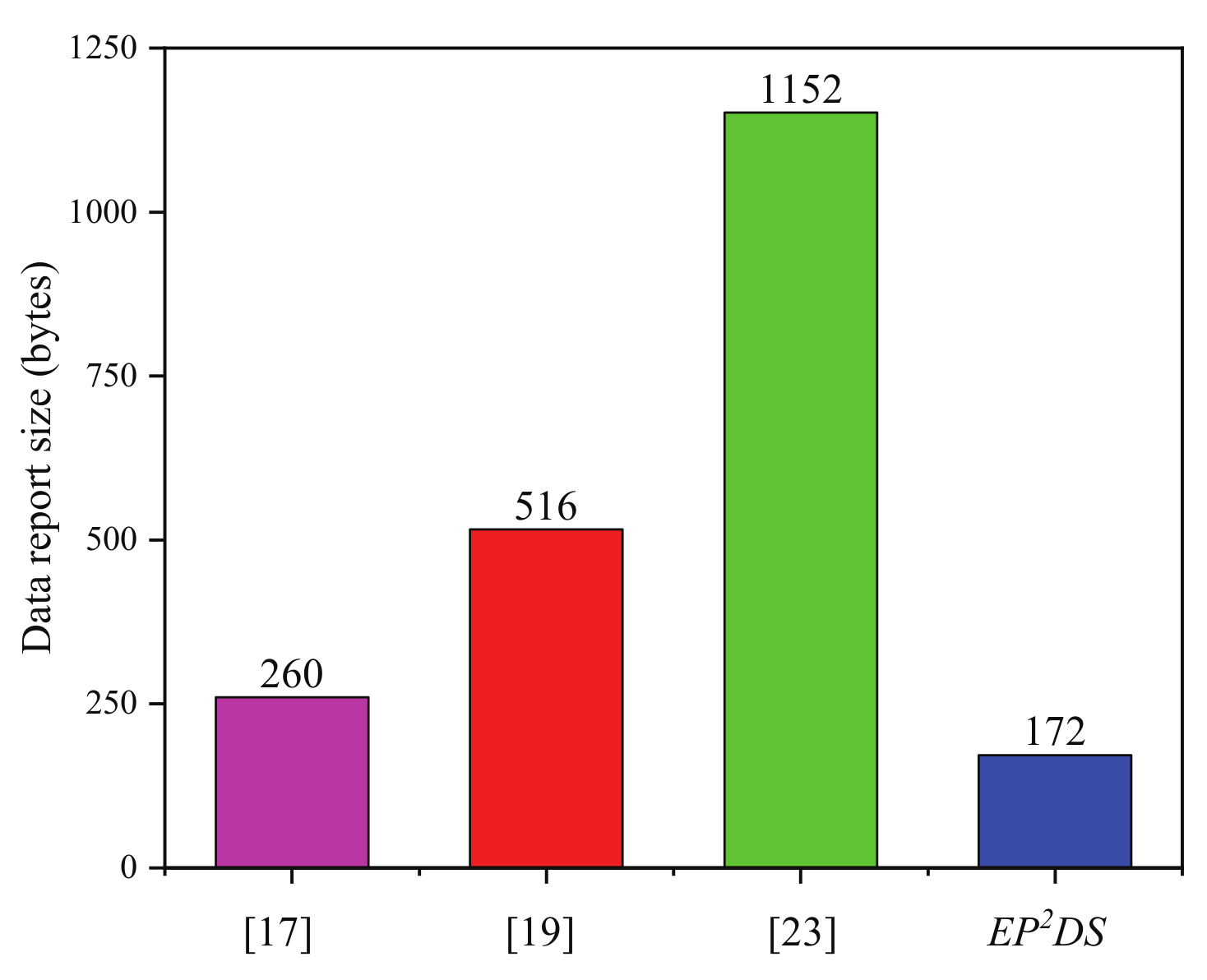
| Rabieh et al.’s scheme [17] | 260 bytes | − | − |
| Sun et al.’s scheme [19] | 516 bytes | − | − |
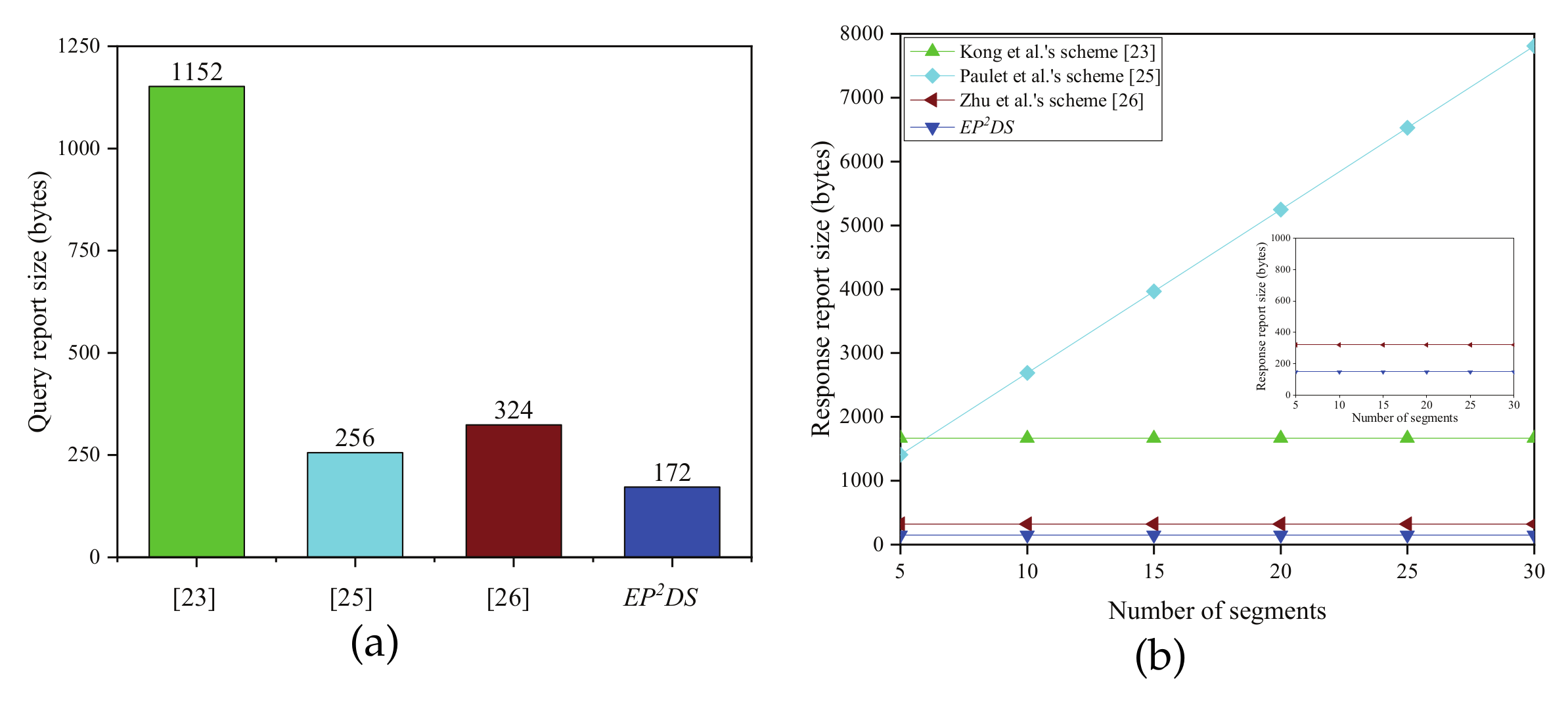
| Kong et al.’s scheme [23] | 1152 bytes | 1152 bytes | 1664 bytes |
| Paulet et al.’s scheme [25] | − | 256 bytes | 256m+128 bytes |
| Zhu et al.’s scheme [26] | − | 324 bytes | 320 bytes |
| EPDS | 172 bytes | 172 bytes | 148 bytes |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ming, Y.; Yu, X. Efficient Privacy-Preserving Data Sharing for Fog-Assisted Vehicular Sensor Networks. Sensors 2020, 20, 514. https://doi.org/10.3390/s20020514
Ming Y, Yu X. Efficient Privacy-Preserving Data Sharing for Fog-Assisted Vehicular Sensor Networks. Sensors. 2020; 20(2):514. https://doi.org/10.3390/s20020514
Chicago/Turabian StyleMing, Yang, and Xiaopeng Yu. 2020. "Efficient Privacy-Preserving Data Sharing for Fog-Assisted Vehicular Sensor Networks" Sensors 20, no. 2: 514. https://doi.org/10.3390/s20020514
APA StyleMing, Y., & Yu, X. (2020). Efficient Privacy-Preserving Data Sharing for Fog-Assisted Vehicular Sensor Networks. Sensors, 20(2), 514. https://doi.org/10.3390/s20020514





