Adaptive Sampling of the Electrocardiogram Based on Generalized Perceptual Features
Abstract
1. Introduction
2. Materials and Methods
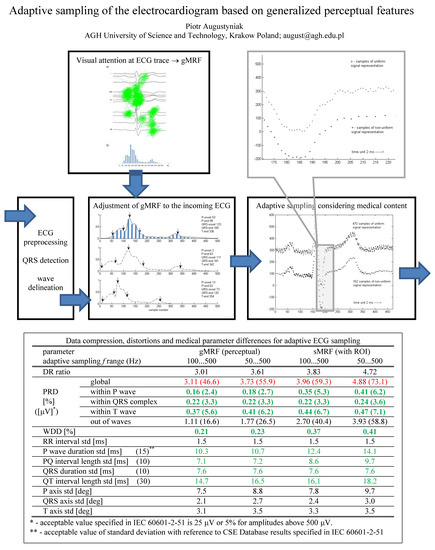
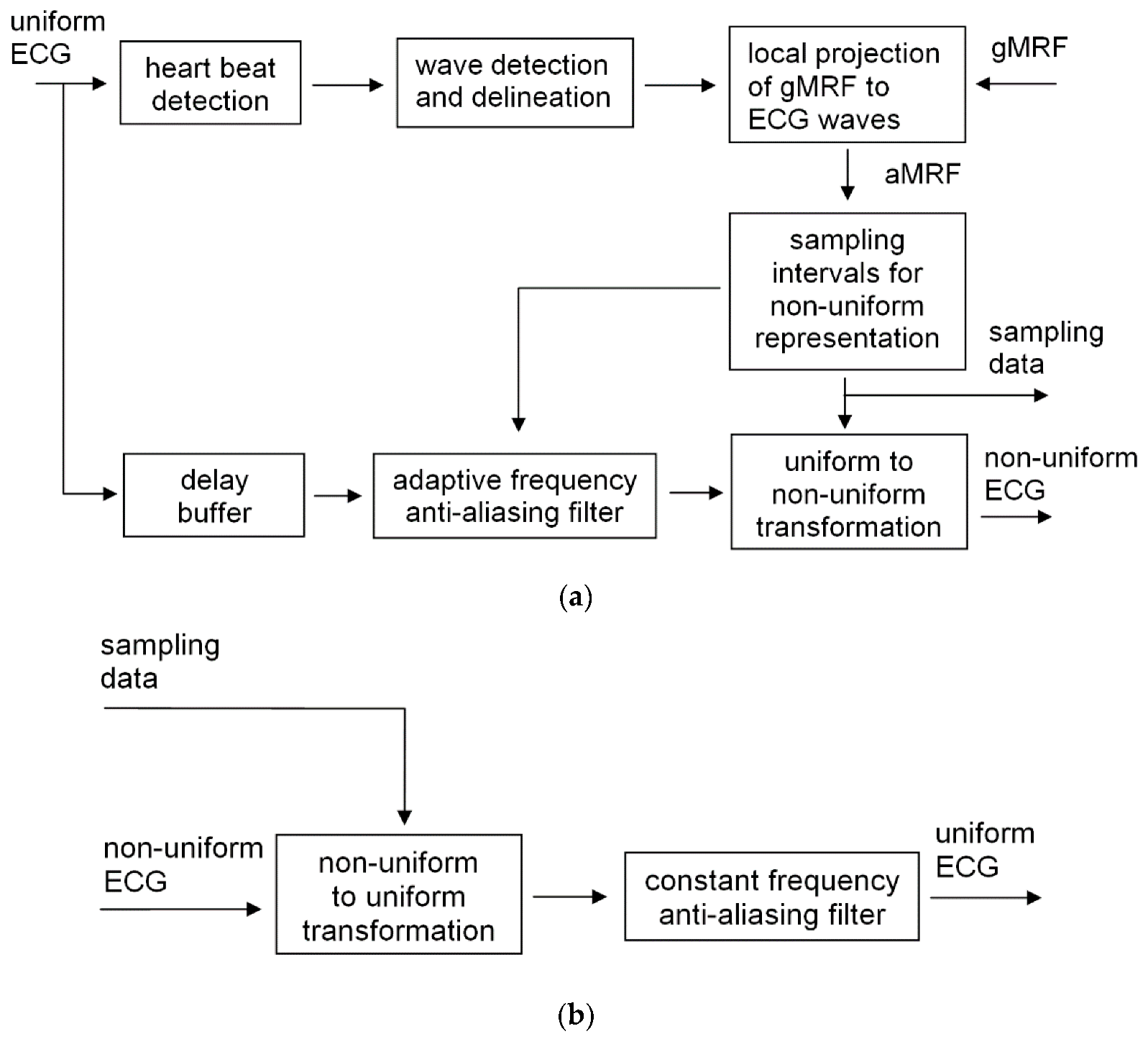
2.1. The Idea and Processing Scheme
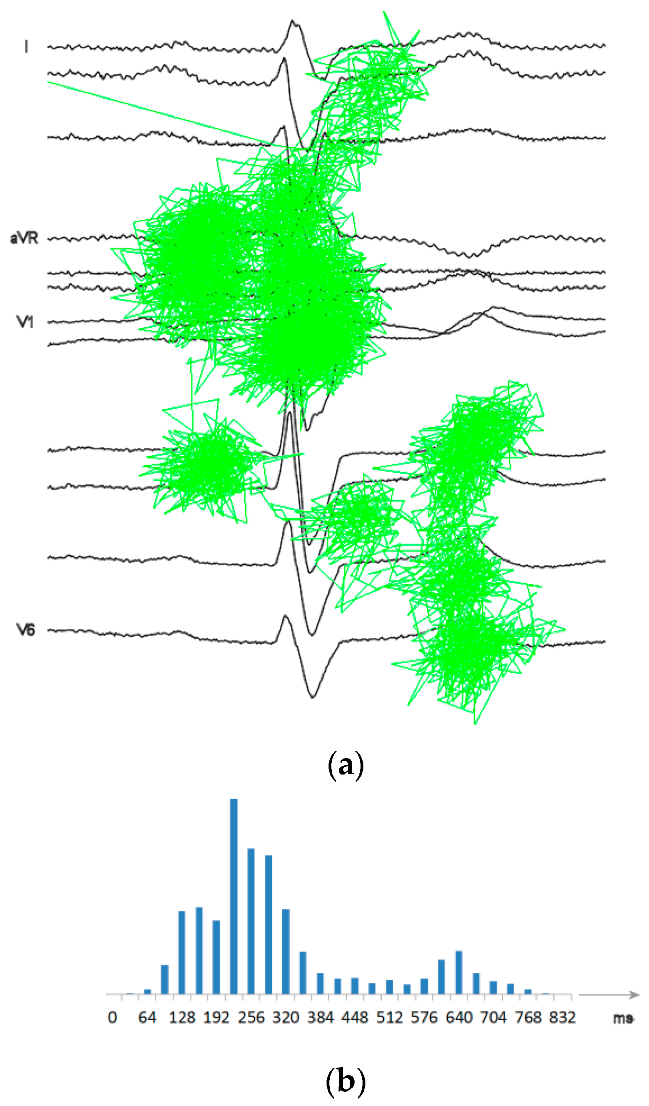
2.2. The ECG Trace Conspicuity as an Estimate of Local Information Density
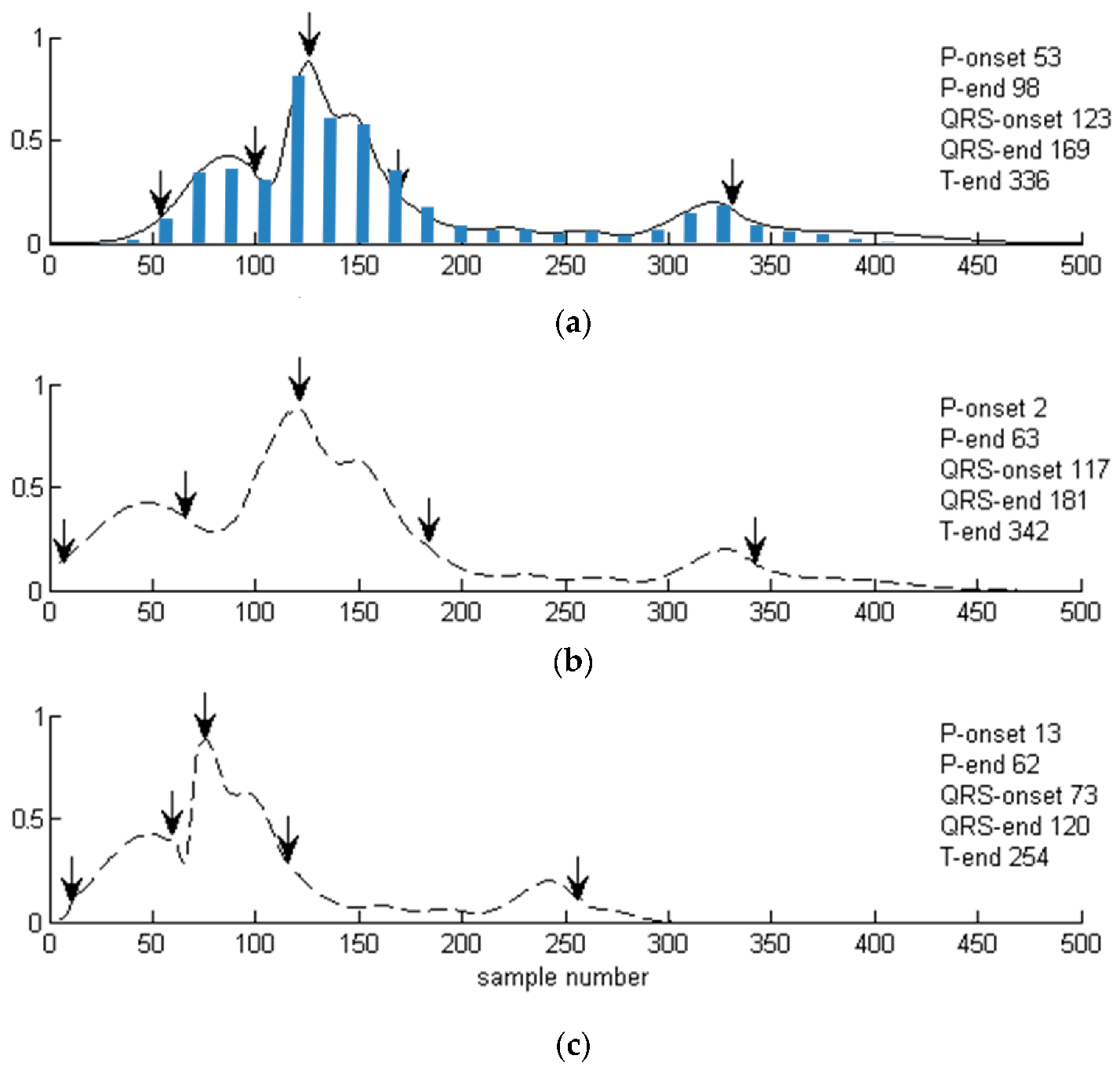
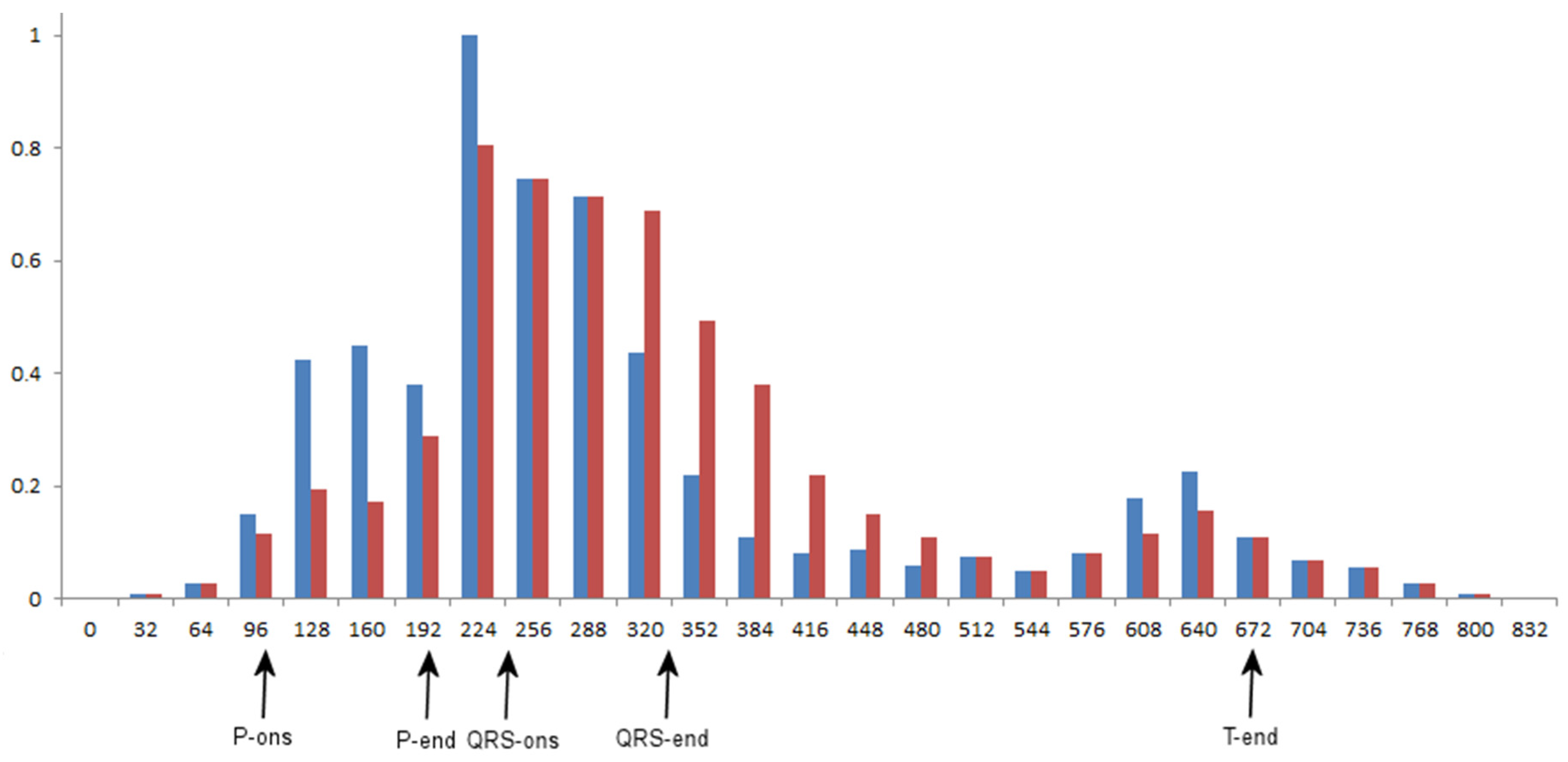
2.3. ECG Waves Delineation
2.4. Piecewise Adaptation of the Local Relevance Function
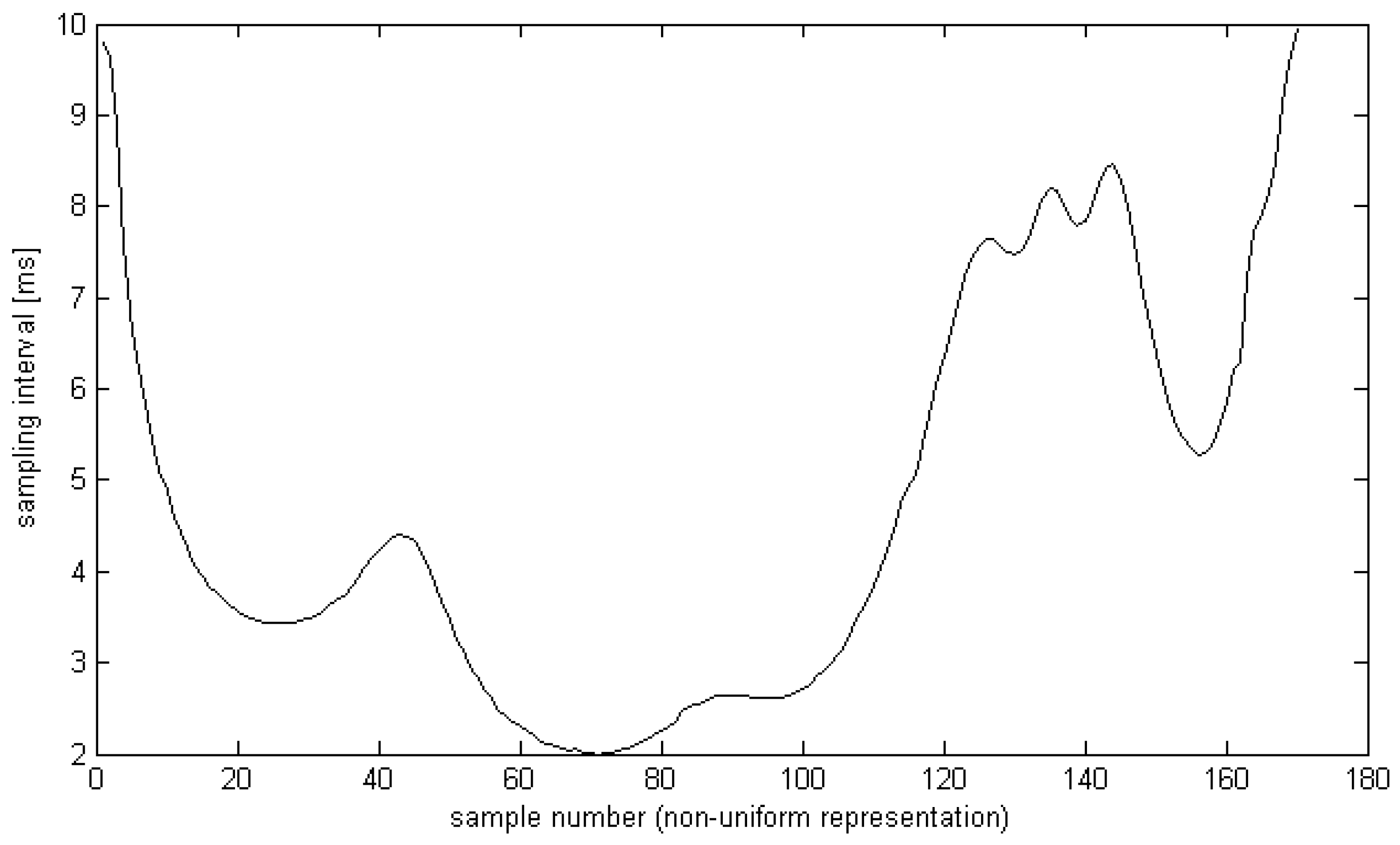
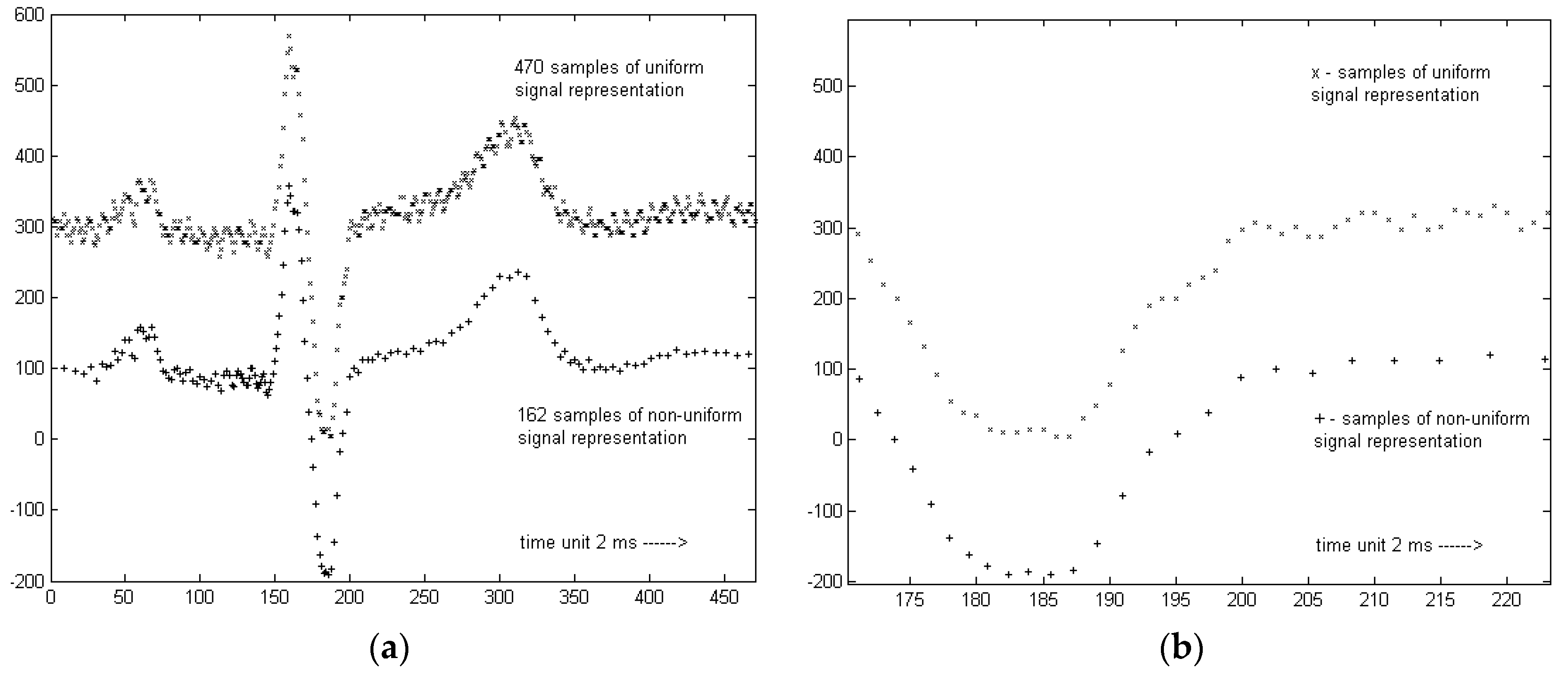
2.5. ECG Signal Resampling
- Given a generator φ, conditions on X have to be defined, usually in the form of a density, such that the norm equivalence (6) holds.Then, at least in principle, is uniquely and stably determined by .
- Reconstruction procedures useful and efficient in practical applications have to be designed as fast numerical algorithms which recover f from its samples , when (6) is satisfied.
2.6. Implementation Details
3. Evaluation of the Method
- Selecting a set of test signals complying with international standards (the CSE Database);
- Selecting tools (the ECG interpretive software) and error measures (PRD, local PRD and WDD);
- Selecting the range of method parameters (gMRF, sMRF, sampling interval);
- Comparing differences between original and processed records with error measures (PRD compares discrete values of samples, whereas the WDD compares values of diagnostic results);
- Statistical processing of error values estimated for each file with each combination of parameters.
3.1. The Test Signal Set
3.2. The Error Metrics
3.3. Performance Assessment
4. Discussion
- On a PC platform i7 3770 (® Intel, Santa Clara, CA, USA), 3400 MHz, 8 GB RAM—0.943% (i.e., 106 times faster than the ECG acquisition);
- on a mobile platform PXA-270 (® Toradex AG., Horw, Switzerland), 624 MHz, 64 MB RAM—7.518% (i.e., 13.3 times faster than the ECG acquisition).
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, J.; Itoh, S. A wavelet transform-based ECG compression method guaranteeing desired signal quality. IEEE Trans. Biomed. Eng. 1998, 45, 1414–1419. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Kim, D.Y.; Pearlman, W.A. Wavelet compression of ECG signals by the set partitioning in hierarchical trees (SPIHT) algorithm. IEEE Trans. Biomed. Eng. 2000, 47, 849–856. [Google Scholar] [PubMed]
- Miaou, S.G.; Chao, S.N. Wavelet-based lossy-to-lossless ECG compression in a unified vector quantization framework. IEEE Trans. Biomed. Eng. 2005, 52, 539–543. [Google Scholar] [CrossRef] [PubMed]
- Rajoub, B.A. An efficient coding algorithm for the compression of ECG signals using the wavelet transform. IEEE Trans. Biomed. Eng. 2002, 49, 355–362. [Google Scholar] [CrossRef] [PubMed]
- Zigel, Y.; Cohen, A.; Katz, A. The weighted diagnostic distortion (WDD) measure for ECG signal compression. IEEE Trans. Biomed. Eng. 2000, 47, 1422–1430. [Google Scholar]
- Alesanco, S.; Olmos, R.S.H.; Garcıa, I.J. Enhanced Real-Time ECG Coder for Packetized Telecardiology Applications. IEEE Trans. Inf. Tech. Biomed. 2006, 10, 229–236. [Google Scholar] [CrossRef][Green Version]
- Huang, C.Y.; Miaou, S.G. Transmitting SPIHT compressed ECG data over a next-generation mobile telecardiology testbed. In Proceedings of the 23rd IEEE EMBS Annual International Conference, Istanbul, Turkey, 25–28 October 2001; pp. 3525–3528. [Google Scholar]
- Kannan, R.; Eswaran, C. Lossless compression schemes for ECG signals using neural network predictors. EURASIP J. Adv. Signal Process. 2007, 2007, 035641. [Google Scholar] [CrossRef]
- Bradie, B. Wavelet Packet-Based Compression of Single Lead ECG. IEEE Trans. Biomed. Eng. 1996, 43, 493–501. [Google Scholar] [CrossRef]
- Duda, K.; Turcza, P.; Zielinski, T.P. Lossless ECG compression with lifting wavelet transform. In Proceedings of the IEEE Instrumentation and Measurement Technology Conference, Budapest, Hungary, 21–23 May 2001; pp. 640–644. [Google Scholar]
- Augustyniak, P. Time-frequency modelling and discrimination of noise in the electrocardiogram. Physiol. Meas. 2003, 24, 753–767. [Google Scholar] [CrossRef]
- Liji, C.A.; Indiradevi, K.P.; Babu, K.A. Integer-to-integer wavelet transform based ECG steganography for securing patient confidential information. Procedia Technol. 2016, 24, 1039–1047. [Google Scholar] [CrossRef]
- Craven, D.; McGinley, B.; Kilmartin, L.; Glavin, M.; Jones, E. Adaptive Dictionary Reconstruction for Compressed Sensing of ECG Signals. IEEE J. Biomed. Health Inform. 2017, 21, 645–654. [Google Scholar] [CrossRef] [PubMed]
- Mamaghanian, H.; Khaled, N.; Atienza, D.; Vandergheynst, P. Compressed Sensing for Real-Time Energy-Efficient ECG Compression on Wireless Body Sensor Nodes. IEEE Trans. Biomed. Eng. 2011, 58, 2456–2466. [Google Scholar] [CrossRef]
- Polanía, L.F.; Carrillo, R.E.; Blanco-Velasco, M.; Barner, K.E. Exploiting Prior Knowledge in Compressed Sensing Wireless ECG Systems. IEEE J. Biomed. Health Inform. 2015, 19, 508–519. [Google Scholar] [CrossRef] [PubMed]
- Rieger, R.; Taylor, J.T. An adaptive sampling system for sensor nodes in body area networks. IEEE Trans. Neural Syst. Rehabil. Eng. 2009, 17, 183–189. [Google Scholar] [CrossRef] [PubMed]
- Yazicioglu, R.F.; Kim, S.; Torfs, T.; Kim, H.; van Hoof, C. A 30 µW analog signal processor ASIC for portable biopotential signal monitoring. IEEE J. Solid-State Circuits 2011, 46, 209–223. [Google Scholar] [CrossRef]
- Augustyniak, P. Moving window signal concatenation for spectral analysis of ECG waves. Comput. Cardiol. 2010, 37, 665–668. [Google Scholar]
- Augustyniak, P. How a Human Perceives the Electrocardiogram. Comput. Cardiol. 2003, 30, 601–604. [Google Scholar]
- Augustyniak, P.; Tadeusiewicz, R. Assessment of electrocardiogram visual interpretation strategy based on scanpath analysis. Physiol. Meas. 2006, 27, 597–608. [Google Scholar] [CrossRef]
- Almeida, R.; Martınez, J.P.; Rocha, A.P.; Laguna, P. Multilead ECG delineation using spatially projected leads from wavelet transform loops. IEEE Trans. Biomed. Eng. 2009, 56, 1996–2005. [Google Scholar] [CrossRef]
- Martınez, J.P.; Almeida, R.; Olmos, S.; Rocha, A.P.; Laguna, P. A wavelet-based ECG delineator: Evaluation on standard databases. IEEE Trans. Biomed. Eng. 2004, 51, 570–581. [Google Scholar] [CrossRef]
- Dumont, J.; Hernandez, A.I.; Carrault, G. ECG beat delineation with an evolutionary optimization process. IEEE Trans. Biomed. Eng. 2010, 57, 607–615. [Google Scholar] [CrossRef] [PubMed]
- Yochum, M.; Renaud, C.; Jacquir, S. Automatic detection of P, QRS and T patterns in 12 leads ECG signal based on CWT. Biomed. Signal Process. Control 2016. [Google Scholar] [CrossRef]
- Kohler, B.; Hennig, C.; Orglmeister, R. The principles of software QRS detection. IEEE Eng. Med. Biol. Mag. 2002, 21, 42–57. [Google Scholar] [CrossRef] [PubMed]
- IEC 60601-2-51. Medical Electrical Equipment Part 2-51: Particular Requirements for Safety, Including Essential Performance, of Recording and Analyzing Single Channel and Multichannel Electrocardiographs; IEC: Geneva, Switzerland, 2003; ISBN 2-8318-6880-7. [Google Scholar]
- Chen, F.; Chandrakasan, A.P.; Stojanovic, V.M. Design and analysis of a hardware-efficient compressed sensing architecture for data compression in wireless sensors. IEEE J. Solid-State Circuits 2012, 47, 744–756. [Google Scholar] [CrossRef]
- Malik, M.; Camm, A.J. Dynamic Electrocardiography; Futura; Blackwell: Oxford, UK, 2004; pp. 112–177. [Google Scholar]
- Boccignone, G. An information-theoretic approach to active vision. In Proceedings of the 11th International Conference on Image Analysis and Processing (ICIAP ’01), Palermo, Italy, 26–28 September 2001. [Google Scholar]
- Pelz, J.B.; Canosa, R. Oculomotor behavior and perceptual strategies in complex tasks. Vis. Res. 2001, 41, 3587–3596. [Google Scholar] [CrossRef]
- Morlet, D. Contribution a L’analyse Automatique des Electrocardiogrammes—Algorithmes de Localisation, Classification et Delimitation Precise des Ondes dans le Systeme de Lyon. Ph.D. Thesis, INSA-Lyon, Lyon, France, 1986. (In French). [Google Scholar]
- Willems, J.L. Common Standards for Quantitative Electrocardiography 10-th CSE Progress Report; ACCO Publication: Leuven, Belgium, 1990. [Google Scholar]
- Aldroubi, A.; Groechenig, K. Non-Uniform Sampling and Reconstruction in Shift-Invariant Spaces. SIAM Rev. 2001, 43, 585–620. [Google Scholar] [CrossRef]
- Aldroubi, A.; Feichtinger, H. Exact iterative reconstruction algorithm for multivariate irregularly sampled functions in spline-like spaces: The Lp theory. Proc. Am. Math. Soc. 1998, 126, 2677–2686. [Google Scholar] [CrossRef]
- Landau, H. Necessary density conditions for sampling and interpolation of certain entire functions. Acta Math. 1967, 117, 37–52. [Google Scholar] [CrossRef]
- Candés, E.; Romberg, J.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 2006, 59, 1207–1223. [Google Scholar] [CrossRef]
- Needell, D.; Tropp, J.A. COSAMP: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 2008, 26, 301–321. [Google Scholar] [CrossRef]
- Pei, S.-C.; Lin, H.-S. Tunable FIR and IIR Fractional-Delay Filter Design and Structure Based on Complex Cepstrum. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 56, 2195–2206. [Google Scholar]
- Wei, X.; Anyu, L.; Boya, S.; Jiaxiang, Z. A Novel Design of Sparse FIR Multiple Notch Filters with Tunable Notch Frequencies. Math. Probl. Eng. 2018, 2018, 3490830. [Google Scholar] [CrossRef]
- Senthilkumar, E.; Manikandan, J.; Agrawa, V.K. FPGA Implementation of Dynamically Tunable Filters. In Proceedings of the International Conference on Advances in Computing, Communications and Informatics (ICACCI), Greater Noida, India, 24–27 September 2014; pp. 1852–1857. [Google Scholar]
- Al-Fahoum, S. Quality Assessment of ECG Compression Techniques Using a Wavelet-Based Diagnostic Measure. IEEE Trans. Inf. Technol Biomed. 2006, 10, 182–191. [Google Scholar] [CrossRef] [PubMed]
- Sayadi, O.; Shamsollahi, M.-B. ECG Denoising and Compression Using a Modified Extended Kalman Filter Structure. IEEE Trans. Biomed. Eng. 2008, 55, 2240–2248. [Google Scholar] [CrossRef] [PubMed]
- Miaou, S.G.; Yen, H.L.; Lin, C.L. Wavelet-based ECG compression using dynamic vector quantization with tree codevectors in single codebook. IEEE Trans. Biomed. Eng. 2002, 49, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Filho, E.B.L.; Rodrigues, N.M.M.; da Silva, E.A.B.; de Faria, S.M.M.; da Silva, V.M.M.; de Carvalho, M.B. ECG signal compression based on DC equalization and complexity sorting. IEEE Trans. Biomed. Eng. 2008, 55, 1923–1926. [Google Scholar] [CrossRef]
- Fira, C.M.; Goras, L. An ECG signals compression method and its validation using NNs. IEEE Trans. Biomed. Eng. 2008, 55, 1319–1326. [Google Scholar] [CrossRef]
- Ku, C.-T.; Wang, H.-S.; Hung, K.-C.; Hung, Y.-S. A novel ECG data compression method based on nonrecursive discrete periodized wavelet transform. IEEE Trans. Biomed. Eng. 2006, 53, 2577–2583. [Google Scholar]
- Sun, C.-C.; Tai, S.-C. Beat-based ECG compression using gain-shape vector quantization. IEEE Trans. Biomed. Eng. 2005, 52, 1882–1888. [Google Scholar] [CrossRef] [PubMed]
- Tai, S.-C.; Sun, C.-C.; Yan, W.-C. A 2-D ECG compression method based on wavelet transform and modified SPIHT. IEEE Trans. Biomed. Eng. 2005, 52, 999–1008. [Google Scholar] [CrossRef] [PubMed]
- MIT-BIH Arrhythmia Database. Available online: https://www.physionet.org/content/mitdb/1.0.0/ (accessed on 21 December 2019).
- Kim, H.; Yazicioglu, R.F.; Merken, P.; Van Hoof, C.; Yoo, H.J. ECG signal compression and classification algorithm with quad level vector for ECG Holter system. IEEE Trans. Inf. Technol. Biomed. 2010, 14, 93–100. [Google Scholar] [PubMed]
- Polania, L.F.; Plaza, R.I. Compressed Sensing ECG using Restricted Boltzmann Machines. Biomed. Signal Process. Control 2018, 45, 237–245. [Google Scholar] [CrossRef]
- Parkale, Y.V.; Nalbalwar, S.L. Application of compressed sensing (CS) for ECG signal compression: A Review. In Advances in Intelligent Systems and Computing, Proceedings of the International Conference on Data Engineering and Communication Technology, Pune, India, 15–16 December 2017; Satapathy, S., Bhateja, V., Joshi, A., Eds.; Springer: Singapore, 2017; Volume 469. [Google Scholar]
- Mishra, A.; Thakkar, F.; Modi, C.; Kher, R. ECG Signal Compression using Compressive Sensing and Wavelet Transform. In Proceedings of the 34th Annual International Conference of the IEEE EMBS, San Diego, CA, USA, 28 August–1 September 2012; pp. 3402–3407. [Google Scholar]
- Chen, J.; Xing, J.; Zhang, L.Y.; Qi, L. Compressed sensing for electrocardiogram acquisition in wireless body sensor network: A comparative analysis. Int. J. Distrib. Sens. Netw. 2019, 15, 1550147719864884. [Google Scholar] [CrossRef]
- Luo, K.; Cai, Z.; Du, K.; Zou, F.; Zhang, X.; Li., J. A digital compressed sensing-based energy-efficient single-spot Bluetooth ECG node. J. Healthc. Eng. 2018. [Google Scholar] [CrossRef]
- Kim, H.; Van Hoof, C.; Yazicioglu, R.F. A mixed signal ECG processing platform with an adaptive sampling ADC for portable monitoring applications. In Proceedings of the 33rd Annual International Conference of the IEEE EMBS, Boston, MA, USA, 30 August–3 September 2011; pp. 2196–2199. [Google Scholar]
- Zywietz, C.; Fischer, R. Integrated content and format checking for processing of SCP ECG records. In Proceedings of the Computers in Cardiology, Chicago, IL, USA, 19–22 September 2004; pp. 37–40. [Google Scholar]
| Parameter | gMRF (Perceptual) | sMRF (with ROI) | |||
|---|---|---|---|---|---|
| fs Range (Hz) | 100 … 500 | 50 … 500 | 100 … 500 | 50 … 500 | |
| Compression ratio | 3.01 | 3.61 | 3.83 | 4.72 | |
| PRD [%] ([μV] *) | global | 3.11 (46.6) | 3.73 (55.9) | 3.96 (59.3) | 4.88 (73.1) |
| within P-wave | 0.16 (2.4) | 0.18 (2.7) | 0.35 (5.3) | 0.41 (6.2) | |
| within QRS complex | 0.22 (3.3) | 0.22 (3.3) | 0.22 (3.3) | 0.24 (3.6) | |
| within T-wave | 0.37 (5.6) | 0.41 (6.2) | 0.44 (6.7) | 0.47 (7.1) | |
| out of waves | 1.11 (16.6) | 1.77 (26.5) | 2.70 (40.4) | 3.93 (58.8) | |
| WDD [%] | 0.21 | 0.23 | 0.37 | 0.41 | |
| RR interval std [ms] | 1.5 | 1.5 | 1.5 | 1.5 | |
| P-wave duration std [ms] (15) ** | 10.3 | 10.7 | 12.4 | 14.1 | |
| PQ interval length std [ms] (10) | 7.1 | 7.2 | 8.6 | 9.7 | |
| QRS duration std [ms] (10) | 7.6 | 7.6 | 7.6 | 7.6 | |
| QT interval length std [ms] (30) | 14.7 | 16.5 | 16,1 | 18.2 | |
| P axis std [deg] | 7.5 | 8.8 | 7.8 | 9.7 | |
| QRS axis std [deg] | 2.1 | 2.7 | 2.4 | 3.0 | |
| T axis std [deg] | 3.1 | 3.5 | 3.3 | 3.5 | |
| Work (Test Set) | Method | Scenario 1 | Scenario 2 | ||
|---|---|---|---|---|---|
| CR | PRD [%] | CR | PRD [%] | ||
| Mamaghanian [14] (MIT-BIH) | wavelet db10 | 3.70 | 2.00 | 10.00 | 9.00 |
| CS | 2.04 | 2.00 | 3.45 | 9.00 | |
| Mishra [53] (10 ECGs custom set) | db | 2.00 | 1.31 | 6.00 | 17.37 |
| rbio3.9 | 2.00 | 0.32 | 6.00 | 10.84 | |
| Craven [13] (MIT-BIH) | SPIHT | 6.10 | 1.95 | 12.00 | 4.00 |
| AD-Q6 | 6.75 | 3.20 | 11.10 | 4.50 | |
| Polania [15] (subset of MIT–BIH) | MMB–IHT | 6.40 | 3.76 | ||
| MMB–CoSaMP | 6.40 | 3.96 | |||
| Polania [51] (European QT DB) | RBM-OMP-like | 2.00 | 1.20 | 5.00 | 6.30 |
| BPON | 2.00 | 1.30 | 5.00 | 8.90 | |
| Chen [54] (MIT-BIH) | rbio5.5 | 2.00 | 10.03 | 5.00 | 46.63 |
| rbio5.5-JBHI | 2.00 | 3.85 | 5.00 | 9.10 | |
| this work (CSE) | perceptual | 3.01 | 3.11 | 4.72 | 4.88 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Augustyniak, P. Adaptive Sampling of the Electrocardiogram Based on Generalized Perceptual Features. Sensors 2020, 20, 373. https://doi.org/10.3390/s20020373
Augustyniak P. Adaptive Sampling of the Electrocardiogram Based on Generalized Perceptual Features. Sensors. 2020; 20(2):373. https://doi.org/10.3390/s20020373
Chicago/Turabian StyleAugustyniak, Piotr. 2020. "Adaptive Sampling of the Electrocardiogram Based on Generalized Perceptual Features" Sensors 20, no. 2: 373. https://doi.org/10.3390/s20020373
APA StyleAugustyniak, P. (2020). Adaptive Sampling of the Electrocardiogram Based on Generalized Perceptual Features. Sensors, 20(2), 373. https://doi.org/10.3390/s20020373