Force Shadows: An Online Method to Estimate and Distribute Vertical Ground Reaction Forces from Kinematic Data
Abstract
1. Introduction
2. Methods
2.1. Force Shadow Method
2.1.1. Ground Reaction Force
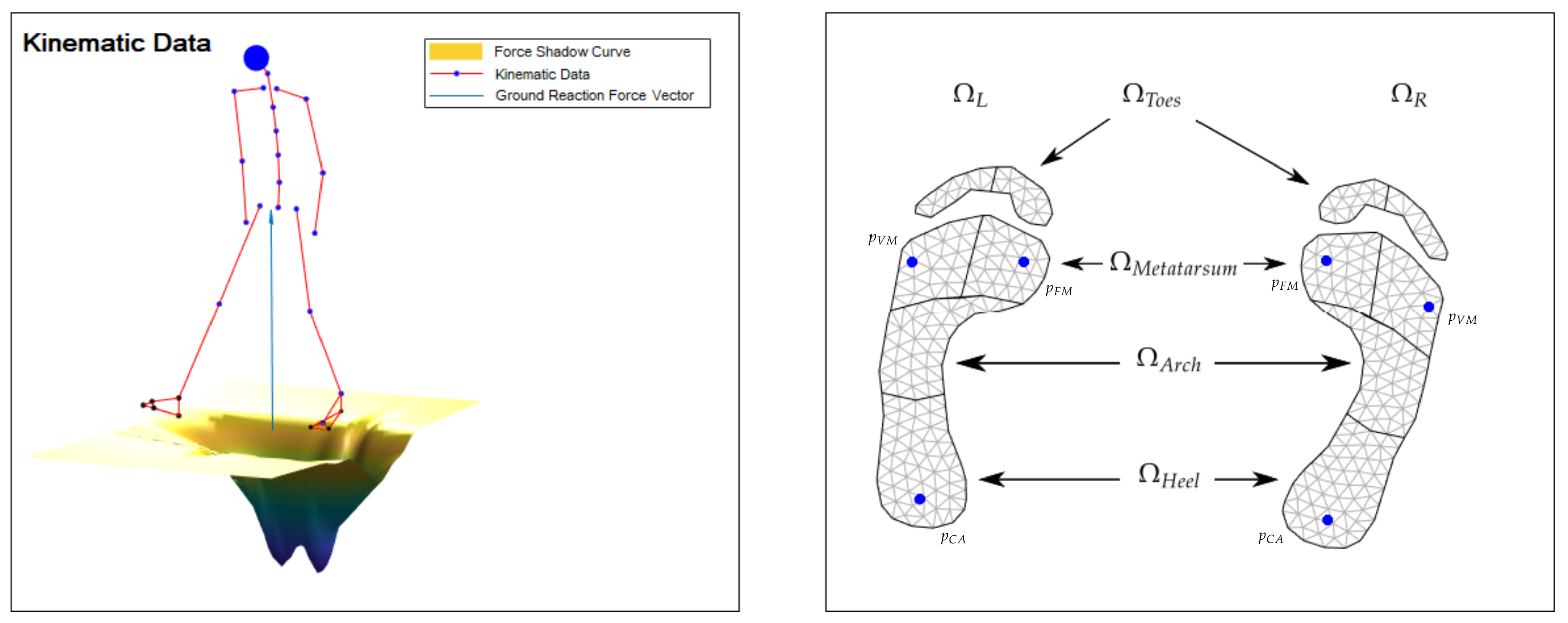
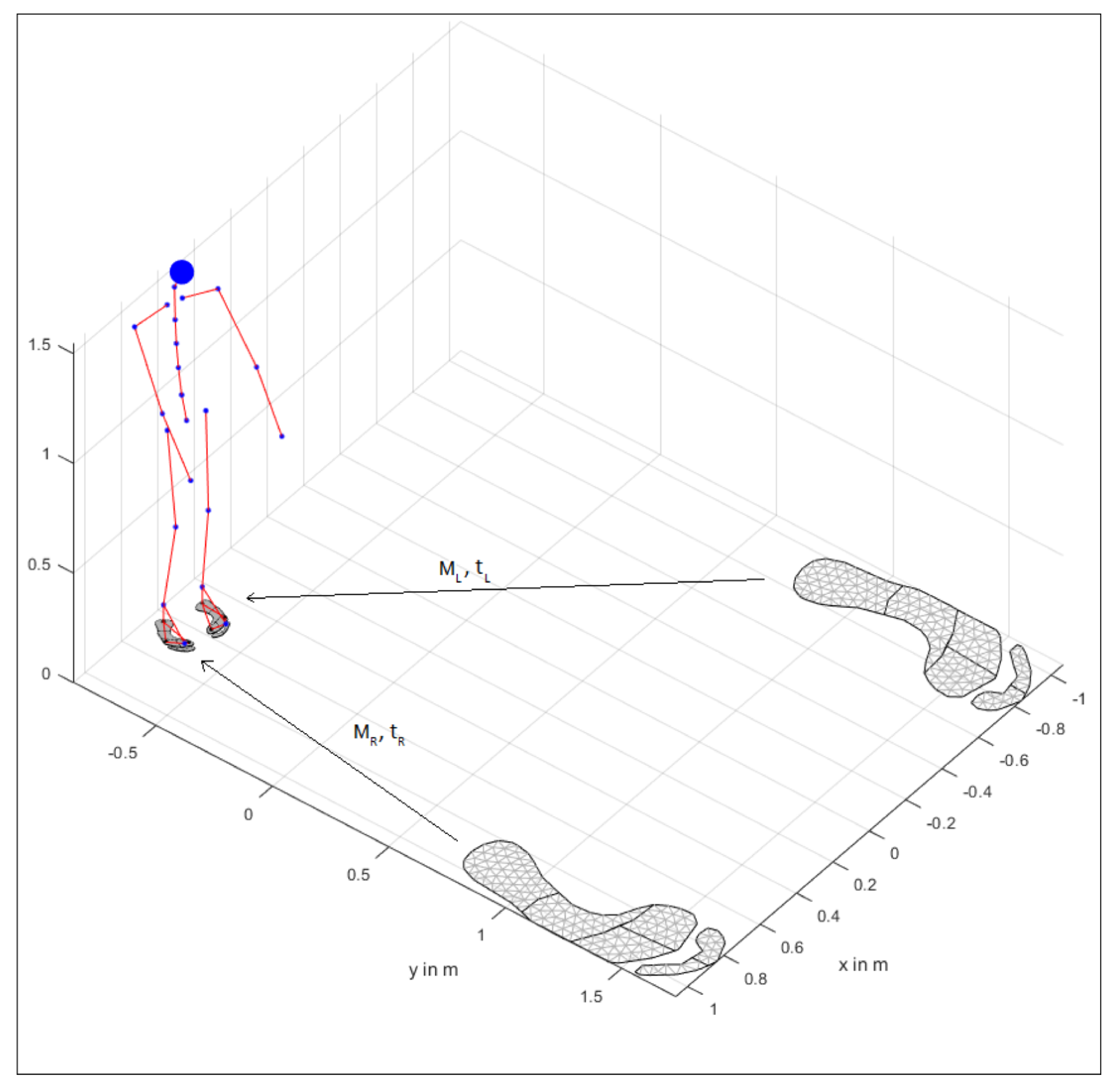
2.1.2. Construction of Force Shadows for a Human Body
2.1.3. Contact Region Estimation
2.1.4. Force Distribution
2.2. Anatomical Models
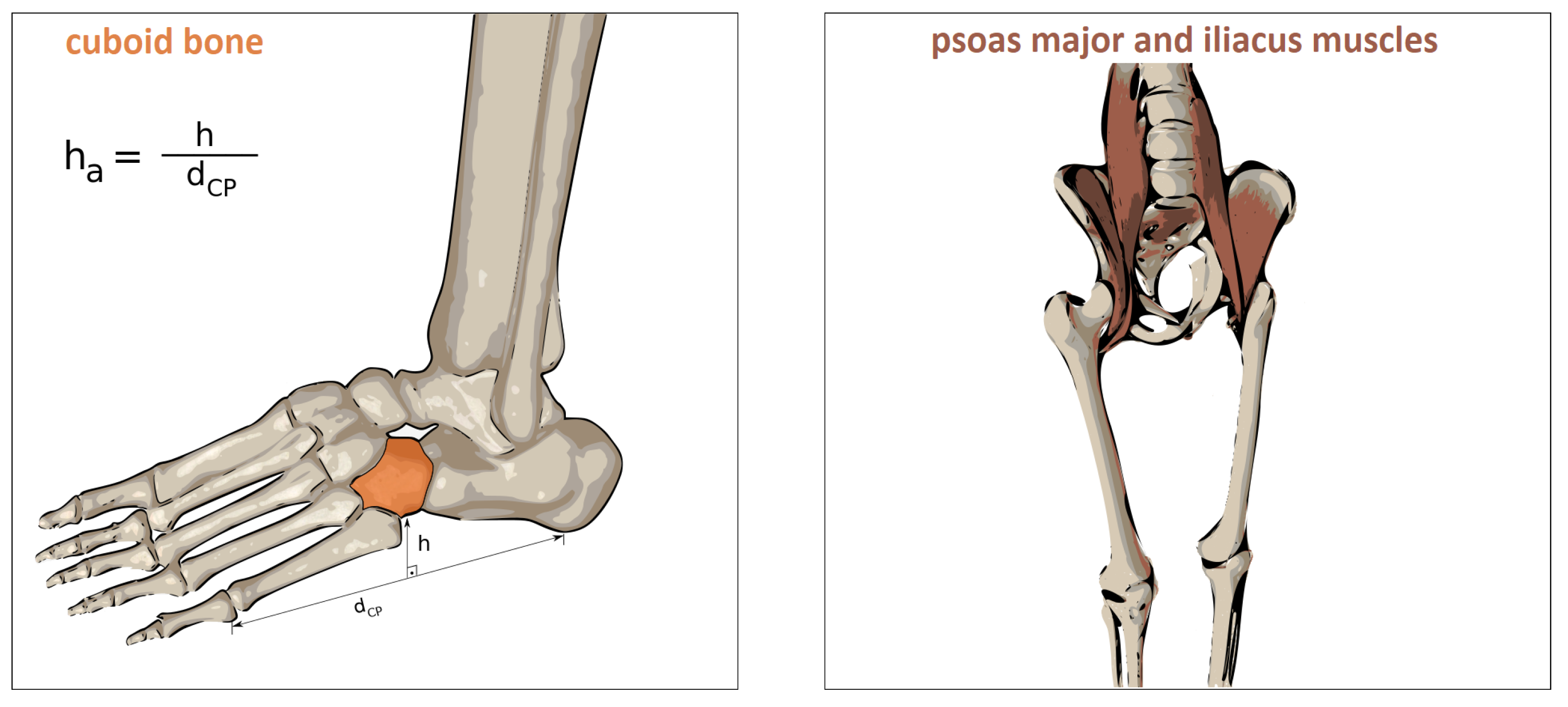
2.2.1. Arch of Foot
2.2.2. Hip Flexion Muscles
2.2.3. Anatomy Aware Load Estimation
2.3. Utilized Hyper Parameters
2.4. FSM Algorithm
3. Experimental Results and Discussion
3.1. Materials
3.2. Experiments
| Algorithm 1 Force Shadow Method (FSM) |
Require:, (cf. (19)), set of hyper parameters ;
|
3.3. Registration of the Pressure Plate Data
3.4. Error Metrics
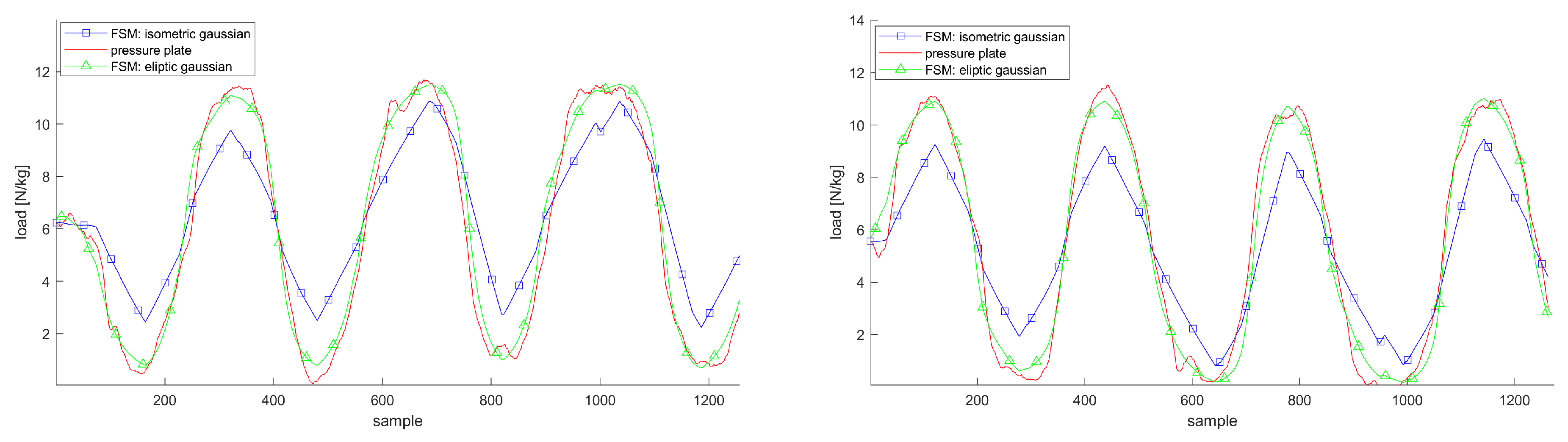
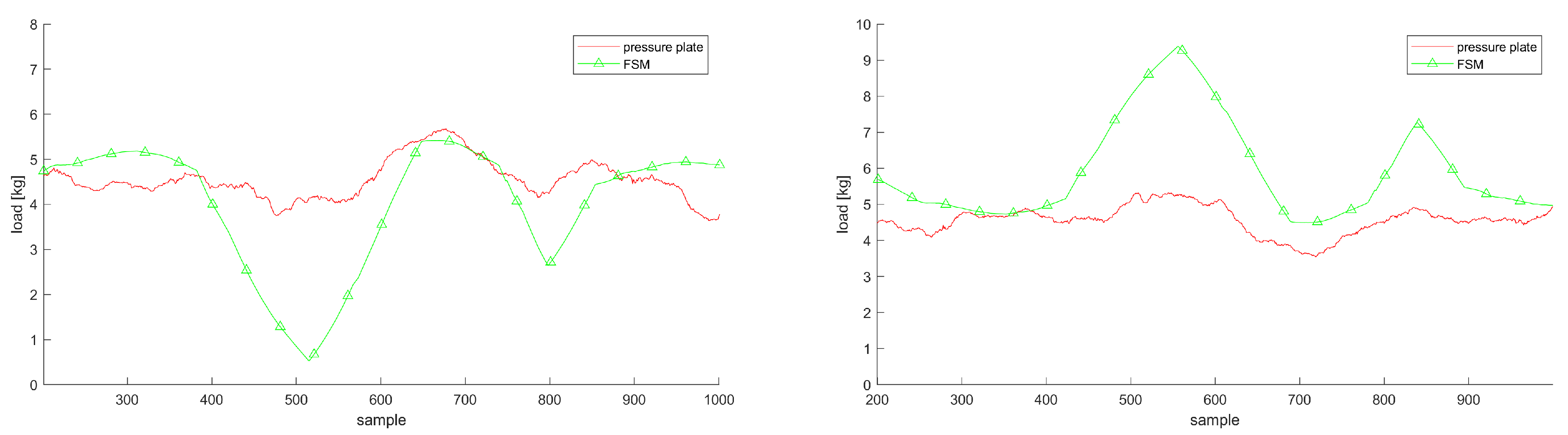
3.5. Subregions
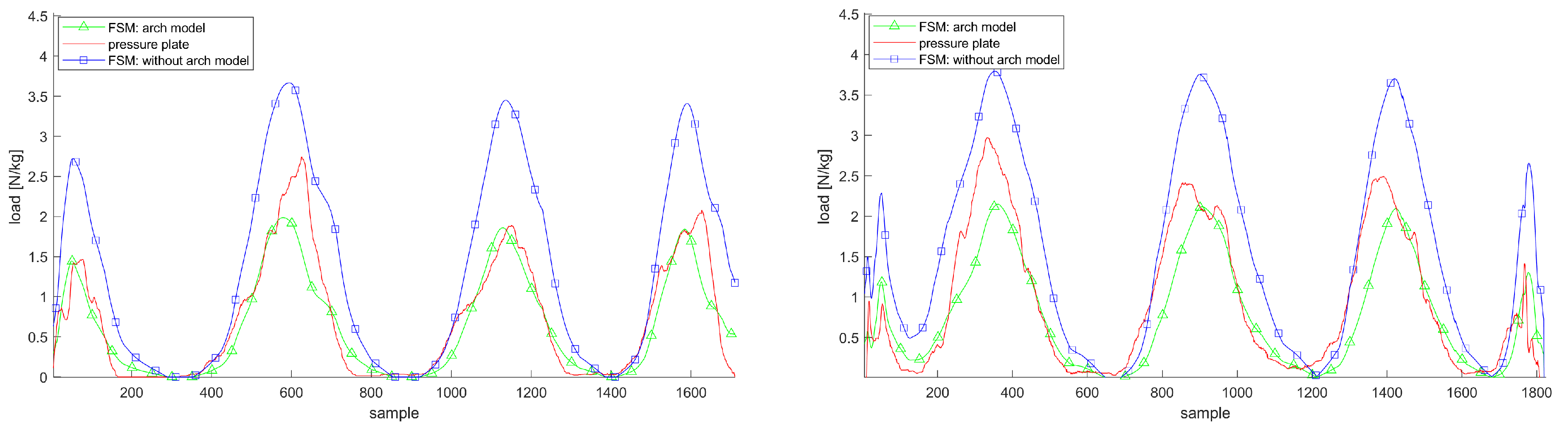
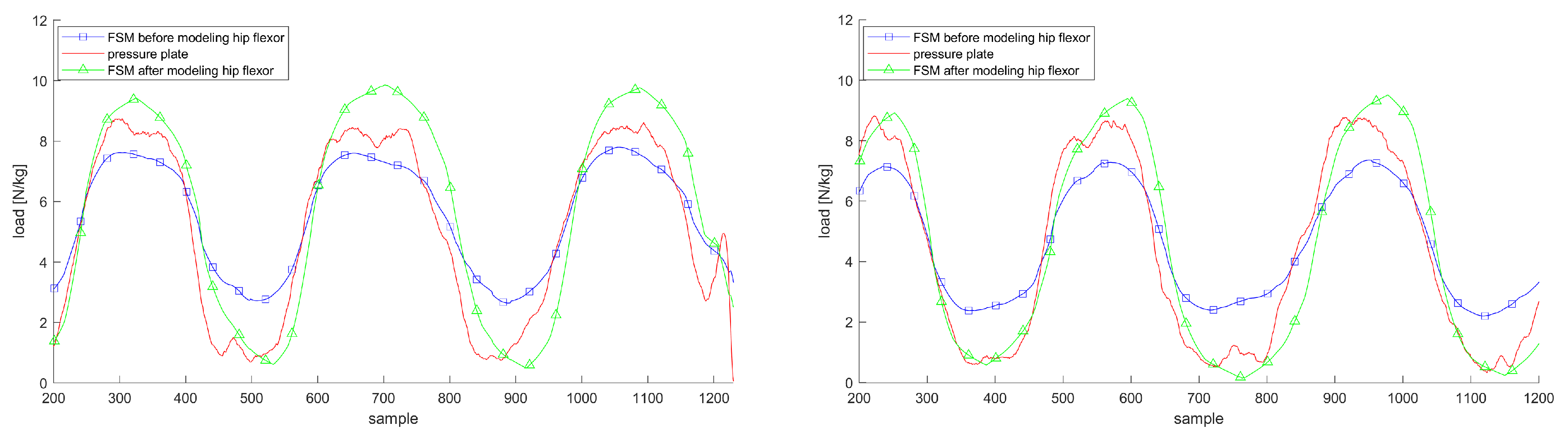
3.6. Justification of Arch and Hip Flexion Model
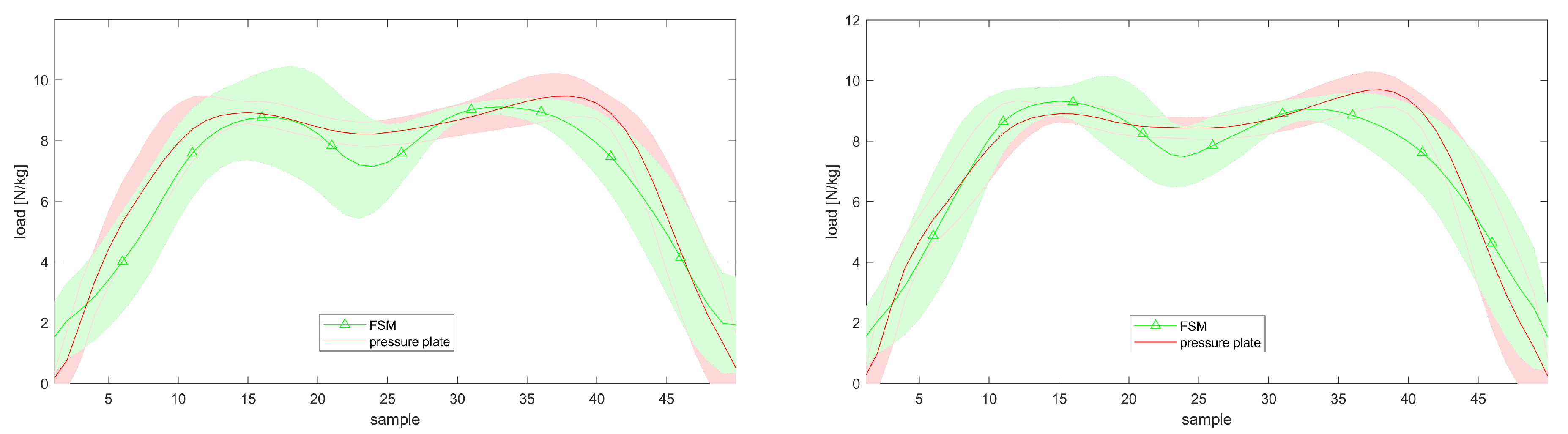
3.7. Gait Cycle Trajectories
3.8. Execution Time
3.9. Discussion on Application Scenarios and Accuracy
3.10. Main Limitations
4. Conclusions and Future Work
4.1. Conclusions
4.2. Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| proposed force shadow method | |
| set of real numbers | |
| set of natural numbers | |
| three dimensional ground reaction force | |
| third, vertical component of | |
| set of all segments of a human body | |
| number of segments | |
| m | mass in kilogram |
| mass of segment in kilogram | |
| total mass in kilogram | |
| position vector, or , respectively | |
| acceleration vector | |
| center of mass | |
| location of total mass center | |
| location of segment’s center of mass, | |
| g | acceleration of gravity |
| R | rotation matrix |
| bell-shaped probability density function representing a normal distribution with mean value , covariance , evaluated at | |
| general region specifier ( and indicate the regions for the left and right foot) | |
| p | position vector regarding the landmarks of the foot model |
| absolute value function | |
| estimated load on region | |
| difference between two measured time frames | |
| convex hull of region | |
| weighting functions evaluated at | |
| set of hyper parameters | |
| p-norm or -norm | |
| root mean square error | |
| relative root mean square error | |
| mean absolute error | |
| standard deviation | |
| r | Pearson correlation coefficient; |
| motion indicator: shifting the weight all around | |
| motion indicator: shifting the weight from side to side | |
| motion indicator: shifting the weight back and forth | |
| motion indicator: performing squats | |
| motion indicator: walking with normal speed |
References
- Zhou, H.; Hu, H. Human motion tracking for rehabilitation—A survey. Biomed. Signal Process. Control 2008, 3, 1–18. [Google Scholar] [CrossRef]
- Muro-de-la Herran, A.; Garcia-Zapirain, B.; Mendez-Zorrilla, A. Gait Analysis Methods: An Overview of Wearable and Non-Wearable Systems, Highlighting Clinical Applications. Sensors 2014, 14, 3362–3394. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Na, Y.; Gu, G.; Kim, J. Flexible insole ground reaction force measurement shoes for jumping and running. In Proceedings of the 2016 6th IEEE International Conference on Biomedical Robotics and Biomechatronics (BioRob), Singapore, 26–29 June 2016; pp. 1062–1067. [Google Scholar] [CrossRef]
- Cordova, M.L.; Armstrong, C.W. Reliability of ground reaction forces during a vertical jump: Implications for functional strength assessment. J. Athl. Train. 1996, 31, 342–345. [Google Scholar] [PubMed]
- Bobbert, M.F.; Schamhardt, H.C.; Nigg, B.M. Calculation of vertical ground reaction force estimates during running from positional data. J. Biomech. 1991, 24, 1095–1105. [Google Scholar] [CrossRef]
- Karhu, O.; Kansi, P.; Kuorinka, I. Correcting working postures in industry: A practical method for analysis. Appl. Ergon. 1977, 8, 199–201. [Google Scholar] [CrossRef]
- Kant, I.; Notermans, J.H.V.; Borm, P.J.A. Observations of working postures in garages using the Ovako Working Posture Analysing System (OVVAS) and consequent workload reduction recommendations. Ergonomics 1990, 33, 209–220. [Google Scholar] [CrossRef] [PubMed]
- Kivi, P.; Mattila, M. Analysis and improvement of work postures in the building industry: Application of the computerised OWAS method. Appl. Ergon. 1991, 22, 43–48. [Google Scholar] [CrossRef]
- Chen, B.; Bates, B.T. Comparison of F-Scan in-sole and AMTI forceplate system in measuring vertical ground reaction force during gait. Physiother. Theory Pract. 2000, 16, 43–53. [Google Scholar] [CrossRef]
- Oh, S.E.; Choi, A.; Mun, J.H. Prediction of ground reaction forces during gait based on kinematics and a neural network model. J. Biomech. 2013, 46, 2372–2380. [Google Scholar] [CrossRef]
- Karatsidis, A.; Bellusci, G.; Schepers, H.; de Zee, M.; Andersen, M.; Veltink, P. Estimation of Ground Reaction Forces and Moments During Gait Using Only Inertial Motion Capture. Sensors 2016, 17, 75. [Google Scholar] [CrossRef]
- Ren, L.; Jones, R.K.; Howard, D. Dynamic analysis of load carriage biomechanics during level walking. J. Biomech. 2005, 38, 853–863. [Google Scholar] [CrossRef] [PubMed]
- Ren, L.; Jones, R.K.; Howard, D. Whole body inverse dynamics over a complete gait cycle based only on measured kinematics. J. Biomech. 2008, 41, 2750–2759. [Google Scholar] [CrossRef] [PubMed]
- Fluit, R.; Andersen, M.; Kolk, S.; Verdonschot, N.; Koopman, H. Prediction of ground reaction forces and moments during various activities of daily living. J. Biomech. 2014, 47, 2321–2329. [Google Scholar] [CrossRef] [PubMed]
- Vaughan, C.L.; Hay, J.G.; Andrews, J.G. Closed loop problems in biomechanics. Part I—A classification system. J. Biomech. 1982, 15, 197–200. [Google Scholar] [CrossRef]
- Bernstein, N.A. The Coordination and Regulation of Movements; Pergamon Press: London, UK, 1967; pp. 60–113. [Google Scholar]
- Forner Cordero, A.; Koopman, H.; van der Helm, F. Use of pressure insoles to calculate the complete ground reaction forces. J. Biomech. 2004, 37, 1427–1432. [Google Scholar] [CrossRef] [PubMed]
- Winiarski, S.; Rutkowska-Kucharska, A. Estimated ground reaction force in normal and pathological gait. Acta Bioeng. Biomech. 2009, 11, 53–60. [Google Scholar]
- Gross, D.; Hauger, W.; Schröder, J.; Wall, W.A. Technische Mechanik 1 Statik; Springer: Berlin/Heidelberg, Germany, 2019; Chapter 4; pp. 87–109, OCLC: 1103690329. [Google Scholar]
- Zatsiorsky, V.M. Kinetics of Human Motion; Human Kinetics: Champaign, IL, USA, 2002; p. 309. [Google Scholar]
- Van Alsenoy, K.; Thomson, A.; Burnett, A. Reliability and validity of the Zebris FDM-THQ instrumented treadmill during running trials. Sports Biomech. 2018, 18. [Google Scholar] [CrossRef]
- Golyanik, V.; Taetz, B.; Reis, G.; Stricker, D. Extended coherent point drift algorithm with correspondence priors and optimal subsampling. In Proceedings of the 2016 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Placid, NY, USA, 7–10 March 2016; pp. 1–9. [Google Scholar]
- Barnett, S.; Cunningham, J.L.; West, S. A Comparison of vertical force and temporal parameters produced by an in-shoe pressure measuring system and a force platform. Clin. Biomech. 2001, 16, 353–357. [Google Scholar] [CrossRef]
- Mariani, B.; Rouhani, H.; Crevoisier, X.; Aminian, K. Quantitative estimation of foot-flat and stance phase of gait using foot-worn inertial sensors. Gait Posture 2013, 37, 229–234. [Google Scholar] [CrossRef]
- Miezal, M.; Taetz, B.; Bleser, G. On Inertial Body Tracking in the Presence of Model Calibration Errors. Sensors 2016, 16, 1132. [Google Scholar] [CrossRef] [PubMed]
- Krüger, D.; Wartzack, S. A contact model to simulate human–artifact interaction based on force optimization: Implementation and application to the analysis of a training machine. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Pishchulin, L.; Wuhrer, S.; Helten, T.; Theobalt, C.; Schiele, B. Building Statistical Shape Spaces for 3D Human Modeling. Pattern Recognit. 2017, 67, 276–286. [Google Scholar] [CrossRef]
- Taetz, B.; Teufl, W.; Weidmann, A.; Pietschmann, J.; Jöllenbeck, T.; Bleser, G. Depth camera based statistical shape fitting approach for the creation of an individualized lower body biomechanical model: Validity and reliability. Comput. Methods Biomech. Biomed. Eng. 2020, 23, 12–22. [Google Scholar] [CrossRef] [PubMed]
- Bogo, F.; Black, M.J.; Loper, M.; Romero, J. Detailed Full-Body Reconstructions of Moving People from Monocular RGB-D Sequences. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 2300–2308. [Google Scholar]
- Taetz, B.; Bleser, G.; Miezal, M. Towards self-calibrating inertial body motion capture. In Proceedings of the 2016 19th International Conference on Information Fusion (FUSION), Heidelberg, Germany, 5–8 July 2016; pp. 1751–1759. [Google Scholar]
- Zimmermann, T.; Taetz, B.; Bleser, G. IMU-to-Segment Assignment and Orientation Alignment for the Lower Body Using Deep Learning. Sensors 2018, 18, 302. [Google Scholar] [CrossRef] [PubMed]
- Vignais, N.; Miezal, M.; Bleser, G.; Mura, K.; Gorecky, D.; Marin, F. Innovative system for real-time ergonomic feedback in industrial manufacturing. Appl. Ergon. 2013, 44, 566–574. [Google Scholar] [CrossRef]
- Alberto, R.; Draicchio, F.; Varrecchia, T.; Silvetti, A.; Iavicoli, S. Wearable Monitoring Devices for Biomechanical Risk Assessment at Work: Current Status and Future Challenges-A Systematic Review. Int. J. Environ. Res. Public Health 2018, 15, 2001. [Google Scholar]
| AR | (Left Foot) | (Right Foot) | ||||||
| vGRF | vGRF | |||||||
| RMSE [N/kg] | 1.46 | 0.59 | 1.18 | 1.28 | 1.50 | 0.60 | 1.26 | 1.25 |
| rRMSE [%] | 18.04 | 20.63 | 14.83 | 13.28 | 20.39 | 20.53 | 17.04 | 13.15 |
| MAE [N/kg] | 1.03 | 0.39 | 0.89 | 1.01 | 1.03 | 0.41 | 0.92 | 1.03 |
| SD [N/kg] | 1.03 | 0.44 | 0.78 | 0.78 | 1.09 | 0.44 | 0.86 | 0.71 |
| r | 0.87 | 0.85 | 0.84 | 0.94 | 0.84 | 0.80 | 0.81 | 0.94 |
| S2S | (Left Foot) | (Right Foot) | ||||||
| vGRF | vGRF | |||||||
| RMSE [N/kg] | 2.00 | 0.64 | 1.48 | 1.31 | 2.36 | 0.76 | 1.64 | 1.41 |
| rRMSE [%] | 31.41 | 24.12 | 22.45 | 13.56 | 38.88 | 25.45 | 25.81 | 14.39 |
| MAE [N/kg] | 1.57 | 0.44 | 1.18 | 1.03 | 1.81 | 0.51 | 1.21 | 1.12 |
| SD [N/kg] | 1.23 | 0.46 | 0.90 | 0.81 | 1.52 | 0.57 | 1.10 | 0.86 |
| r | 0.76 | 0.85 | 0.66 | 0.93 | 0.78 | 0.80 | 0.68 | 0.93 |
| BF | (Left Foot) | (Right Foot) | ||||||
| vGRF | vGRF | |||||||
| RMSE [N/kg] | 1.33 | 0.34 | 1.23 | 0.75 | 1.30 | 0.49 | 1.18 | 0.60 |
| rRMSE [%] | 26.76 | 30.28 | 28.32 | 27.65 | 24.79 | 33.28 | 26.69 | 16.20 |
| MAE [N/kg] | 1.14 | 0.29 | 0.97 | 0.56 | 1.10 | 0.38 | 0.98 | 0.48 |
| SD [N/kg] | 0.68 | 0.19 | 0.76 | 0.50 | 0.69 | 0.31 | 0.67 | 0.36 |
| r | 0.91 | 0.47 | 0.92 | 0.65 | 0.86 | 0.17 | 0.92 | 0.75 |
| SQ | (Left Foot) | (Right Foot) | ||||||
| vGRF | vGRF | |||||||
| RMSE [N/kg] | 1.07 | 0.31 | 0.98 | 0.78 | 1.54 | 0.42 | 0.98 | 1.01 |
| rRMSE [%] | 22.93 | 20.07 | 27.54 | 14.96 | 32.14 | 20.97 | 16.74 | 18.82 |
| MAE [N/kg] | 0.87 | 0.21 | 0.77 | 0.61 | 1.31 | 0.31 | 0.82 | 0.77 |
| SD [N/kg] | 0.62 | 0.22 | 0.60 | 0.48 | 0.82 | 0.28 | 0.55 | 0.65 |
| r | 0.55 | 0.37 | 0.14 | 0.39 | 0.19 | 0.43 | 0.71 | 0.45 |
| NW | (Left Foot) | (Right Foot) | ||||||
| vGRF | vGRF | |||||||
| RMSE [N/kg] | 2.13 | 1.03 | 1.91 | 1.64 | 1.86 | 1.00 | 1.79 | 1.42 |
| rRMSE [%] | 24.77 | 33.19 | 20.67 | 15.94 | 22.71 | 31.42 | 19.40 | 13.60 |
| MAE [N/kg] | 1.51 | 0.74 | 1.55 | 1.22 | 1.36 | 0.75 | 1.42 | 1.09 |
| SD [N/kg] | 1.49 | 0.71 | 1.12 | 1.11 | 1.28 | 0.66 | 1.09 | 0.91 |
| r | 0.64 | 0.53 | 0.79 | 0.83 | 0.75 | 0.60 | 0.81 | 0.87 |
| Code Line | Procedure | Execution Time |
|---|---|---|
| 5: | Determine | |
| 6–7: | Determine and | |
| 9: | Register foot models | |
| 10: | Determine weights | |
| 11–12: | Determine weights | |
| 14: | Integration and Normalization | |
| 4–15: | One complete iteration |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weidmann, A.; Taetz, B.; Andres, M.; Laufer, F.; Bleser, G. Force Shadows: An Online Method to Estimate and Distribute Vertical Ground Reaction Forces from Kinematic Data. Sensors 2020, 20, 5709. https://doi.org/10.3390/s20195709
Weidmann A, Taetz B, Andres M, Laufer F, Bleser G. Force Shadows: An Online Method to Estimate and Distribute Vertical Ground Reaction Forces from Kinematic Data. Sensors. 2020; 20(19):5709. https://doi.org/10.3390/s20195709
Chicago/Turabian StyleWeidmann, Alexander, Bertram Taetz, Matthias Andres, Felix Laufer, and Gabriele Bleser. 2020. "Force Shadows: An Online Method to Estimate and Distribute Vertical Ground Reaction Forces from Kinematic Data" Sensors 20, no. 19: 5709. https://doi.org/10.3390/s20195709
APA StyleWeidmann, A., Taetz, B., Andres, M., Laufer, F., & Bleser, G. (2020). Force Shadows: An Online Method to Estimate and Distribute Vertical Ground Reaction Forces from Kinematic Data. Sensors, 20(19), 5709. https://doi.org/10.3390/s20195709






