UVIRT—Unsupervised Virtual Try-on Using Disentangled Clothing and Person Features
Abstract
1. Introduction
- We are the first to propose a fully unsupervised virtual try-on method. Conventional virtual try-on methods use inputs such as paired images, clothing parsing semantic segmentation maps, and human dense image maps, as ground truth data or some kind of additional information. On the other hand, we do not need any additional data by employing the concept of disentanglement.
- We are the first to apply real-world C2C market data to virtual try-on. This is demonstrated through experiments on a real-world C2C market dataset. This is particularly challenging because the C2C market dataset has images that come from a wide variety of RGB camera types. We show that it is still possible to fuse disentangled components (person vs. clothing) features despite these challenges.
- Despite being completely unsupervised, our approach achieves competitive results with existing supervised approaches.
- Our approach is 13 times faster than the supervised method (i.e., Characteristic-Preserving Virtual Try-On Network (CP-VTON) [4]) because ours does not use additional networks, such as the human pose detector and human parser.
2. Related Work
2.1. Supervised Virtual Try-on
2.2. Image-to-Image Translation
2.3. Weakly-Supervised Virtual Try-ony
3. Methods
| Algorithm 1: Unsupervised Virtual Try-on (UVIRT) |
| Require: The weight of latent loss , the weight of pixel loss , the weight of whitening regularization loss , the weight of coloring regularization loss , the batchsize m, Adam hyperparameters |
| Require: Initial style and content encoder parameters in domain and , initial decoder parameters in domain and , initial discriminator parameters in domain and |
| while has not converged do |
| fordo |
| Sample each domain real data |
| end for |
| end while |
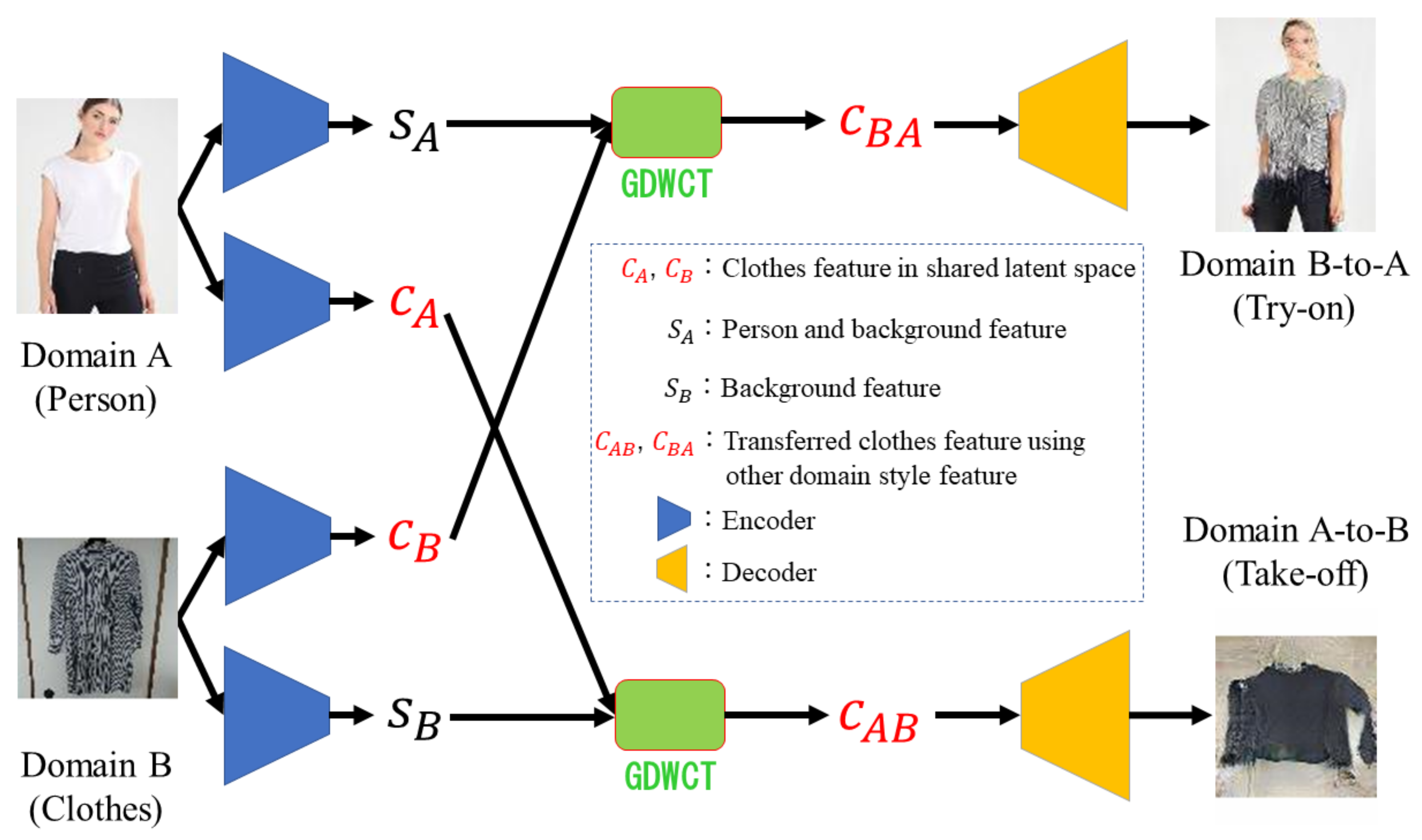
3.1. Model
3.2. Loss Functions
3.2.1. Adversarial Loss
3.2.2. Reconstruction Loss
3.2.3. Regularization
3.2.4. Total Loss
3.3. Collecting C2C Market Datasets
4. Experiments
4.1. Evaluation Criteria
4.1.1. Learned Perceptual Image Patch Similarity (LPIPS)
4.1.2. Fréchet Inception Distance (FID)
4.2. Implementation Details
4.2.1. Conventional Dataset
4.2.2. Setting
4.2.3. Architecture
4.3. Baseline
4.4. Comparison with Conventional Supervised Methods
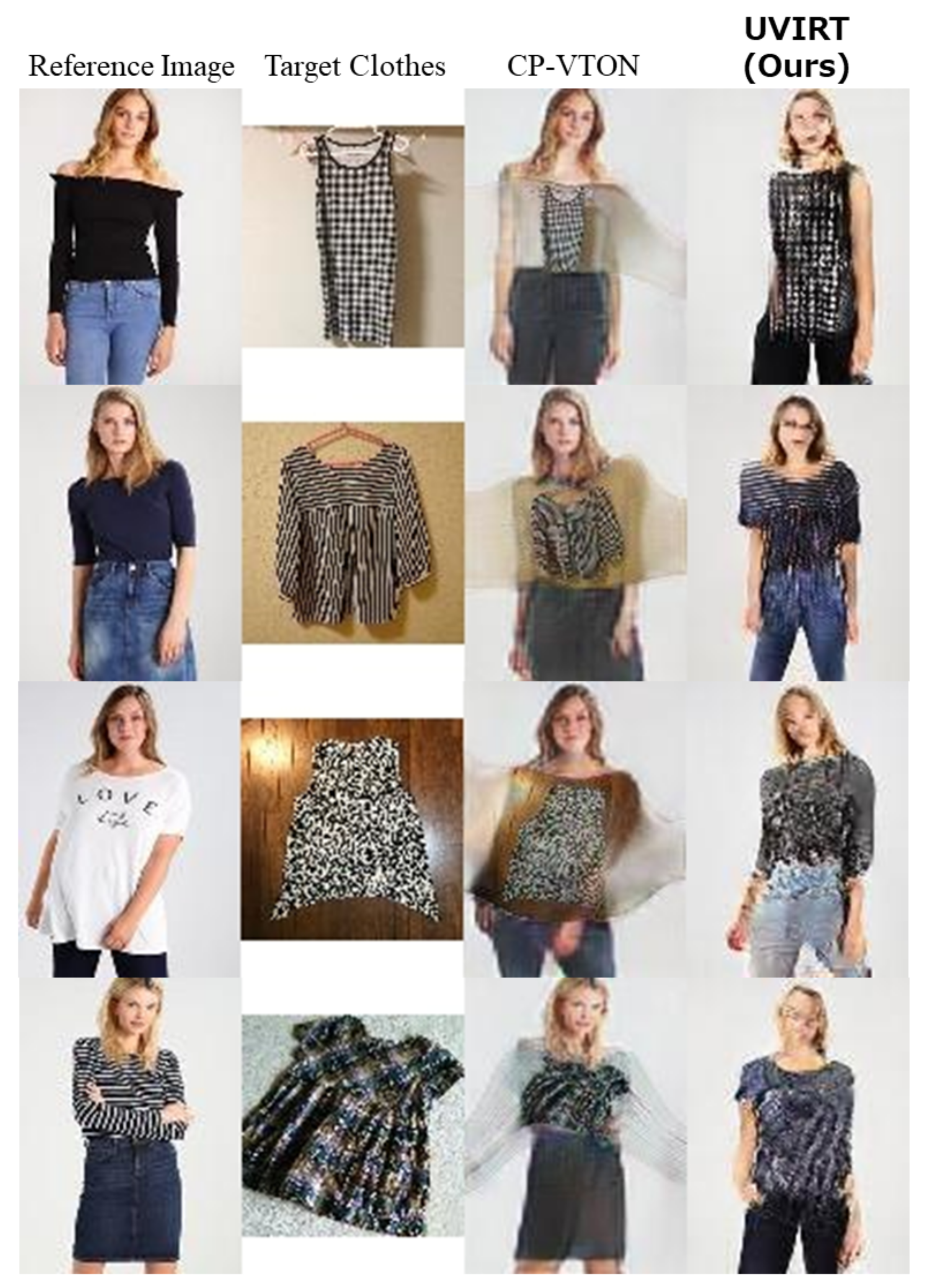
4.4.1. Qualitative Results
4.4.2. Quantitative Results
4.5. Virtual Try-on on C2C Market Dataset
4.5.1. Qualitative Results
4.5.2. Quantitative Results
4.6. Ablation Study
4.7. Testing Time Comparison
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Statista. eBay: Annual Net Revenue 2013–2019. 2020. Available online: https://www.statista.com/statistics/507881/ebays-annual-net-revenue/ (accessed on 4 August 2020).
- Amazon. Prime Wardrobe. 2020. Available online: https://www.amazon.co.jp/b/?ie=UTF8&bbn=5429200051&node=5425661051&tag=googhydr-22&ref=pd_sl_pn6acna5m_b&adgrpid=60466354043&hvpone=&hvptwo=&hvadid=338936031340&hvpos=&hvnetw=g&hvrand=9233286119764777328&hvqmt=b&hvdev=c&hvdvcmdl=&hvlocint=&hvlocphy=1009310&hvtargid=kwd-327794409245&hydadcr=3627_11172809&gclid=Cj0KCQjw6_vzBRCIARIsAOs54z7lvkoeDTmckFM2Vakdras4uWdqWSe2ESCzS6dRoX_fTNLNE8Y5p-8aAq1REALw_wcB (accessed on 4 August 2020).
- Han, X.; Wu, Z.; Wu, Z.; Yu, R.; Davis, L.S. VITON: An Image-based Virtual Try-on Network. In Proceedings of the CVPR 2021: IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 19–21 June 2018; pp. 7543–7552. [Google Scholar]
- Wang, B.; Zheng, H.; Liang, X.; Chen, Y.; Lin, L. Toward Characteristic-Preserving Image-based Virtual Try-On Network. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 589–604. [Google Scholar]
- Hsieh, C.; Chen, C.; Chou, C.; Shuai, H.; Cheng, W. Fit-me: Image-Based Virtual Try-on With Arbitrary Poses. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 4694–4698. [Google Scholar]
- Yildirim, G.; Jetchev, N.; Vollgraf, R.; Bergmann, U. Generating High-Resolution Fashion Model Images Wearing Custom Outfits. In Proceedings of the IEEE International Conference on Computer Vision (ICCV) Workshops, Seoul, Korea, 27 October–2 November 2019. [Google Scholar] [CrossRef]
- Yu, R.; Wang, X.; Xie, X. VTNFP: An Image-Based Virtual Try-On Network With Body and Clothing Feature Preservation. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 10511–10520. [Google Scholar]
- Jae Lee, H.; Lee, R.; Kang, M.; Cho, M.; Park, G. LA-VITON: A Network for Looking-Attractive Virtual Try-On. In Proceedings of the IEEE International Conference on Computer Vision (ICCV) Workshops, Seoul, Korea, 27 October–2 November 2019; pp. 3129–3132. [Google Scholar]
- Issenhuth, T.; Mary, J.; Calauzènes, C. End-to-End Learning of Geometric Deformations of Feature Maps for Virtual Try-On. arXiv 2019, arXiv:cs.CV/1906.01347. [Google Scholar]
- Dong, H.; Liang, X.; Shen, X.; Wang, B.; Lai, H.; Zhu, J.; Hu, Z.; Yin, J. Towards Multi-Pose Guided Virtual Try-On Network. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 9026–9035. [Google Scholar]
- Pumarola, A.; Goswami, V.; Vicente, F.; De la Torre, F.; Moreno-Noguer, F. Unsupervised Image-to-Video Clothing Transfer. In Proceedings of the IEEE International Conference on Computer Vision (ICCV) Workshops, Seoul, Korea, 27 October–2 November 2019. [Google Scholar] [CrossRef]
- Wang, K.; Ma, L.; Oramas, J.; Gool, L.V.; Tuytelaars, T. Unsupervised shape transformer for image translation and cross-domain retrieval. arXiv 2018, arXiv:cs.CV/1812.02134. [Google Scholar]
- Jetchev, N.; Bergmann, U. The Conditional Analogy GAN: Swapping Fashion Articles on People Images. In Proceedings of the IEEE International Conference on Computer Vision (ICCV) Workshops, Venice, Italy, 22–29 October 2017; pp. 2287–2292. [Google Scholar]
- Mercari. The Total Merchandise Number of C2C Market Application “Mercari” Goes Beyond 10 Billion (Japanese Website). 2018. Available online: https://about.mercari.com/press/news/article/20180719_billionitems/ (accessed on 4 August 2020).
- Bengio, Y.; Courville, A.; Vincent, P. Representation Learning: A Review and New Perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Higgins, I.; Matthey, L.; Pal, A.; Burgess, C.; Glorot, X.; Botvinick, M.; Mohamed, S.; Lerchner, A. beta-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Chen, X.; Duan, Y.; Houthooft, R.; Schulman, J.; Sutskever, I.; Abbeel, P. InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems 29, Centre Convencions Internacional Barcelona, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Kim, H.; Mnih, A. Disentangling by Factorising. In Proceedings of the 35th International Conference on Machine Learning, Stockholmsmässan, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Mathieu, E.; Rainforth, T.; Siddharth, N.; Teh, Y.W. Disentangling Disentanglement in Variational Autoencoders. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Kumar, A.; Sattigeri, P.; Balakrishnan, A. Variational Inference of Disentangled Latent Concepts from Unlabeled Observations. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Esmaeili, B.; Wu, H.; Jain, S.; Bozkurt, A.; Siddharth, N.; Paige, B.; Brooks, D.H.; Dy, J.; van de Meent, J.W. Structured Disentangled Representations. In Proceedings of the Machine Learning Research, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Karras, T.; Laine, S.; Aila, T. A Style-Based Generator Architecture for Generative Adversarial Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-To-Image Translation With Conditional Adversarial Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Zhu, J.Y.; Zhang, R.; Pathak, D.; Darrell, T.; Efros, A.A.; Wang, O.; Shechtman, E. Toward Multimodal Image-to-Image Translation. In Proceedings of the Advances in Neural Information Processing Systems 30, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Cordts, M.; Omran, M.; Ramos, S.; Rehfeld, T.; Enzweiler, M.; Benenson, R.; Franke, U.; Roth, S.; Schiele, B. The Cityscapes Dataset for Semantic Urban Scene Understanding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Liu, M.Y.; Breuel, T.; Kautz, J. Unsupervised Image-to-Image Translation Networks. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Huang, X.; Liu, M.Y.; Belongie, S.; Kautz, J. Multimodal Unsupervised Image-to-image Translation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Choi, Y.; Choi, M.; Kim, M.; Ha, J.; Kim, S.; Choo, J. StarGAN: Unified Generative Adversarial Networks for Multi-domain Image-to-Image Translation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8789–8797. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation Using Cycle-Consistent Adversarial Networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2242–2251. [Google Scholar]
- Cho, W.; Choi, S.; Park, D.K.; Shin, I.; Choo, J. Image-To-Image Translation via Group-Wise Deep Whitening-And-Coloring Transformation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 10631–10639. [Google Scholar]
- Güler, R.A.; Neverova, N.; Kokkinos, I. Densepose: Dense human pose estimation in the wild. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7297–7306. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Huang, X.; Belongie, S. Arbitrary Style Transfer in Real-Time with Adaptive Instance Normalization. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Mao, X.; Li, Q.; Xie, H.; Lau, R.Y.; Wang, Z.; Paul Smolley, S. Least Squares Generative Adversarial Networks. Proeedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Mercari, I. Mercari (Japanese Website). 2020. Available online: https://www.mercari.com/jp/ (accessed on 4 August 2020).
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X.; Chen, X. Improved Techniques for Training GANs. In Proceedings of the Advances in Neural Information Processing Systems 29, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The Unreasonable Effectiveness of Deep Features as a Perceptual Metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems 25, Lake Tahoe, CA, USA, 3–8 December 2012. [Google Scholar]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium. In Proceedings of the Advances in Neural Information Processing Systems 30, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Dowson, D.C.; Landau, B.V. The frechet distance between multivariate normal distributions. J. Multivar. Anal. 1982, 12, 450–455. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representation (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Wang, T.; Liu, M.; Zhu, J.; Tao, A.; Kautz, J.; Catanzaro, B. High-Resolution Image Synthesis and Semantic Manipulation with Conditional GANs. In Proceedings of the 2018 the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8798–8807. [Google Scholar]
- Zhu, X.; Xu, C.; Tao, D. Learning Disentangled Representations with Latent Variation Predictability. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Cao, Z.; Hidalgo Martinez, G.; Simon, T.; Wei, S.; Sheikh, Y.A. OpenPose: Realtime Multi-Person 2D Pose Estimation using Part Affinity Fields. IEEE Trans. Pattern Anal. Mach. Intell. 2019. [CrossRef] [PubMed]
- Cao, Z.; Simon, T.; Wei, S.E.; Sheikh, Y. Realtime Multi-Person 2D Pose Estimation using Part Affinity Fields. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Simon, T.; Joo, H.; Matthews, I.; Sheikh, Y. Hand Keypoint Detection in Single Images using Multiview Bootstrapping. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Wei, S.E.; Ramakrishna, V.; Kanade, T.; Sheikh, Y. Convolutional pose machines. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Gong, K.; Liang, X.; Zhang, D.; Shen, X.; Lin, L. Look Into Person: Self-Supervised Structure-Sensitive Learning and a New Benchmark for Human Parsing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Liang, X.; Gong, K.; Shen, X.; Lin, L. Look into Person: Joint Body Parsing & Pose Estimation Network and a New Benchmark. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 871–885. [Google Scholar]



| Method | LPIPS ↓ | FID ↓ |
|---|---|---|
| CP-VTON (Supervised) | 0.191 | 25.23 () |
| UVIRT (ours) (Unsupervised) | 0.442 |
| Method | FID ↓ |
|---|---|
| CP-VTON * (Supervised) | 122.83 (±0.51) |
| UVIRT * (ours) (Unsupervised) | 245.25 (±0.77) |
| UVIRT (ours) (Unsupervised) | 92.55 (±0.29) |
| Training Data Scale | FID ↓ |
|---|---|
| 5% (33,721 images) | 95.01 (±0.26) |
| 10% (67,443 images) | 98.97 (±0.41) |
| 25% (134,886 images) | 99.31 (±0.60) |
| 50% (269,773 images) | 92.55(±0.29) |
| 100% (539,546 images) | 95.13 (±0.24) |
| Method | Testing Time [msec] ↓ |
|---|---|
| CP-VTON (Supervised) | 662.81 |
| UVIRT (Unsupervised) | 53.94 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsunashima, H.; Arase, K.; Lam, A.; Kataoka, H. UVIRT—Unsupervised Virtual Try-on Using Disentangled Clothing and Person Features. Sensors 2020, 20, 5647. https://doi.org/10.3390/s20195647
Tsunashima H, Arase K, Lam A, Kataoka H. UVIRT—Unsupervised Virtual Try-on Using Disentangled Clothing and Person Features. Sensors. 2020; 20(19):5647. https://doi.org/10.3390/s20195647
Chicago/Turabian StyleTsunashima, Hideki, Kosuke Arase, Antony Lam, and Hirokatsu Kataoka. 2020. "UVIRT—Unsupervised Virtual Try-on Using Disentangled Clothing and Person Features" Sensors 20, no. 19: 5647. https://doi.org/10.3390/s20195647
APA StyleTsunashima, H., Arase, K., Lam, A., & Kataoka, H. (2020). UVIRT—Unsupervised Virtual Try-on Using Disentangled Clothing and Person Features. Sensors, 20(19), 5647. https://doi.org/10.3390/s20195647






