The Feasibility of Longitudinal Upper Extremity Motor Function Assessment Using EEG
Abstract
1. Introduction
2. Materials and Methods
2.1. Inclusion Criteria
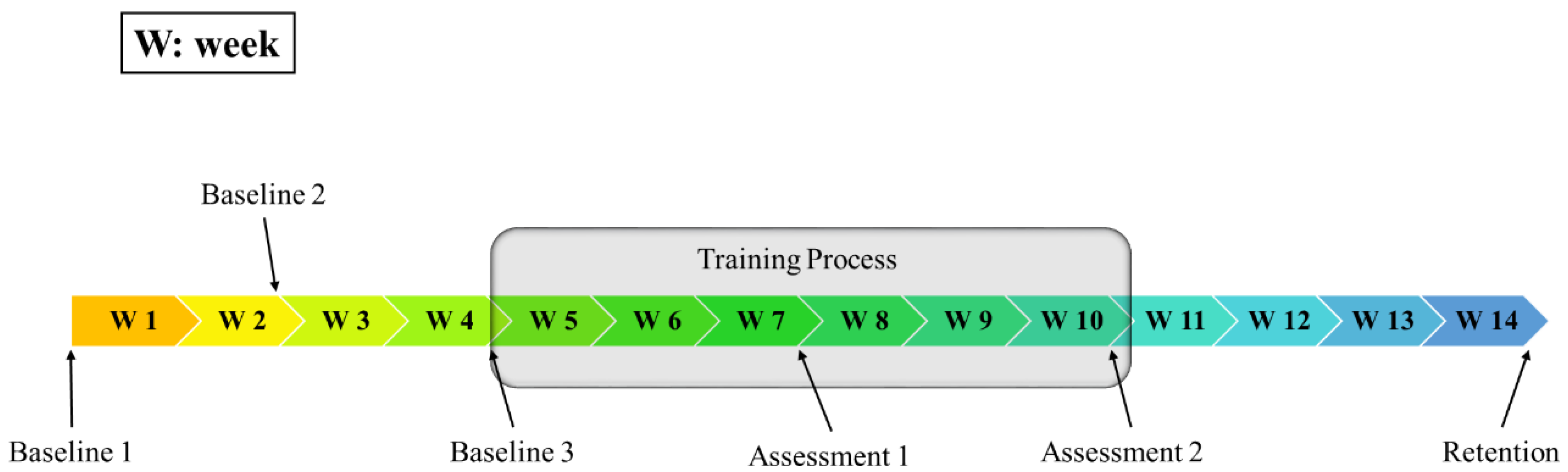
2.2. Participation Protocol
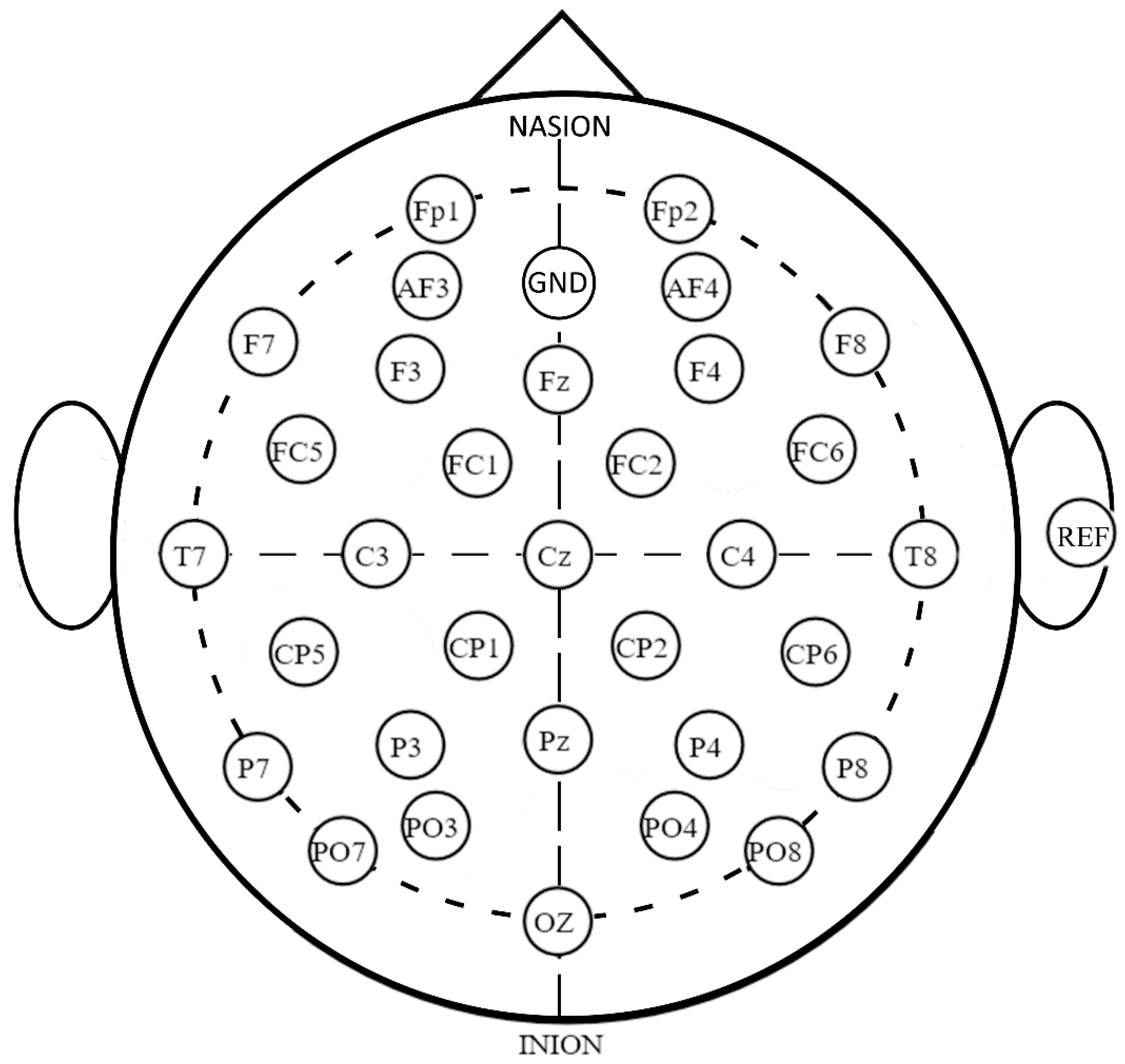
2.3. EEG Data Acquisition
2.4. Data Pre-Processing
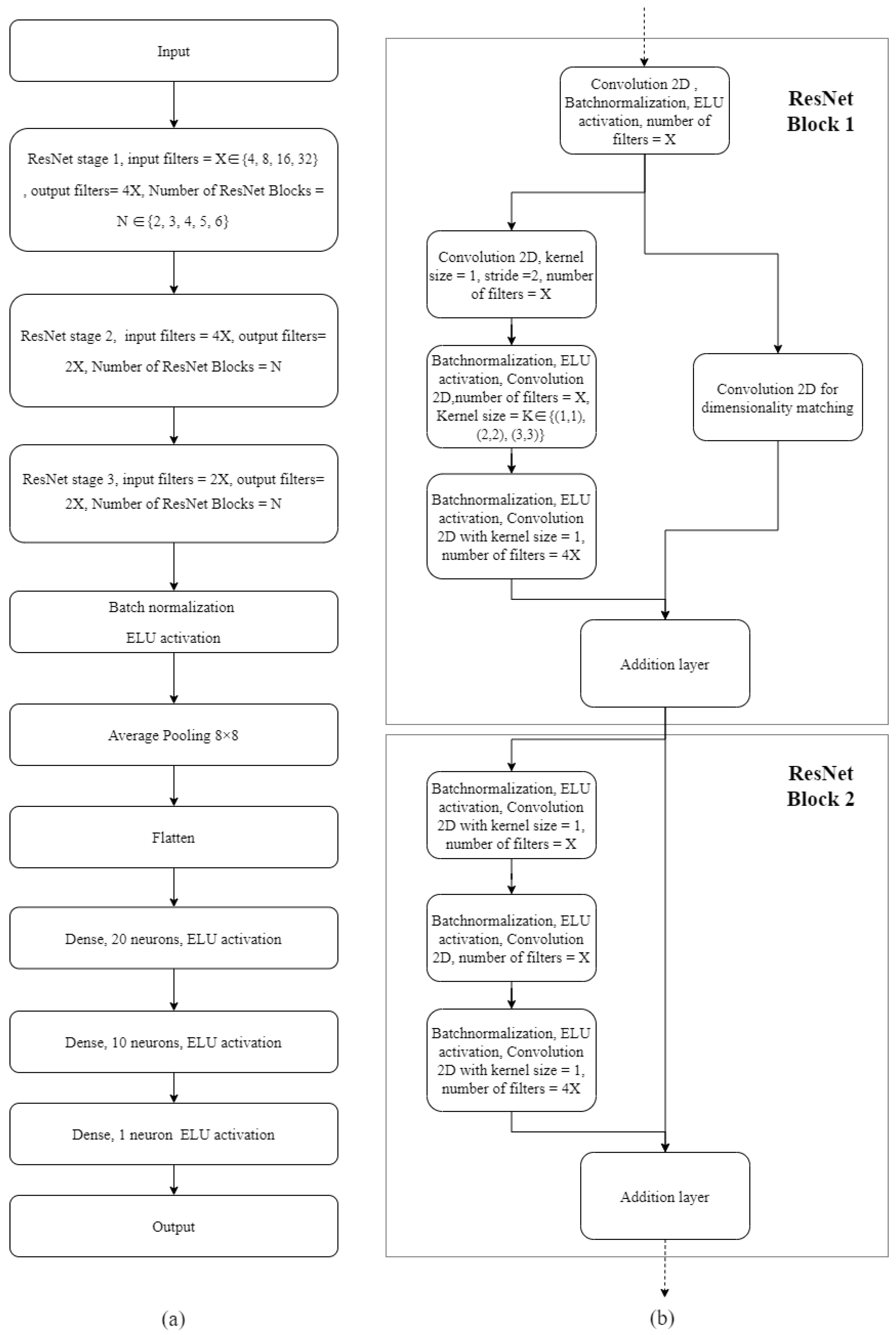
2.5. Neural Network Model Configuration, Hyperparameter Optimization and Testing
2.6. Statistical Analysis
3. Results
3.1. Demographic Data
3.2. ANN Model Training and Hyperparameter Optimization
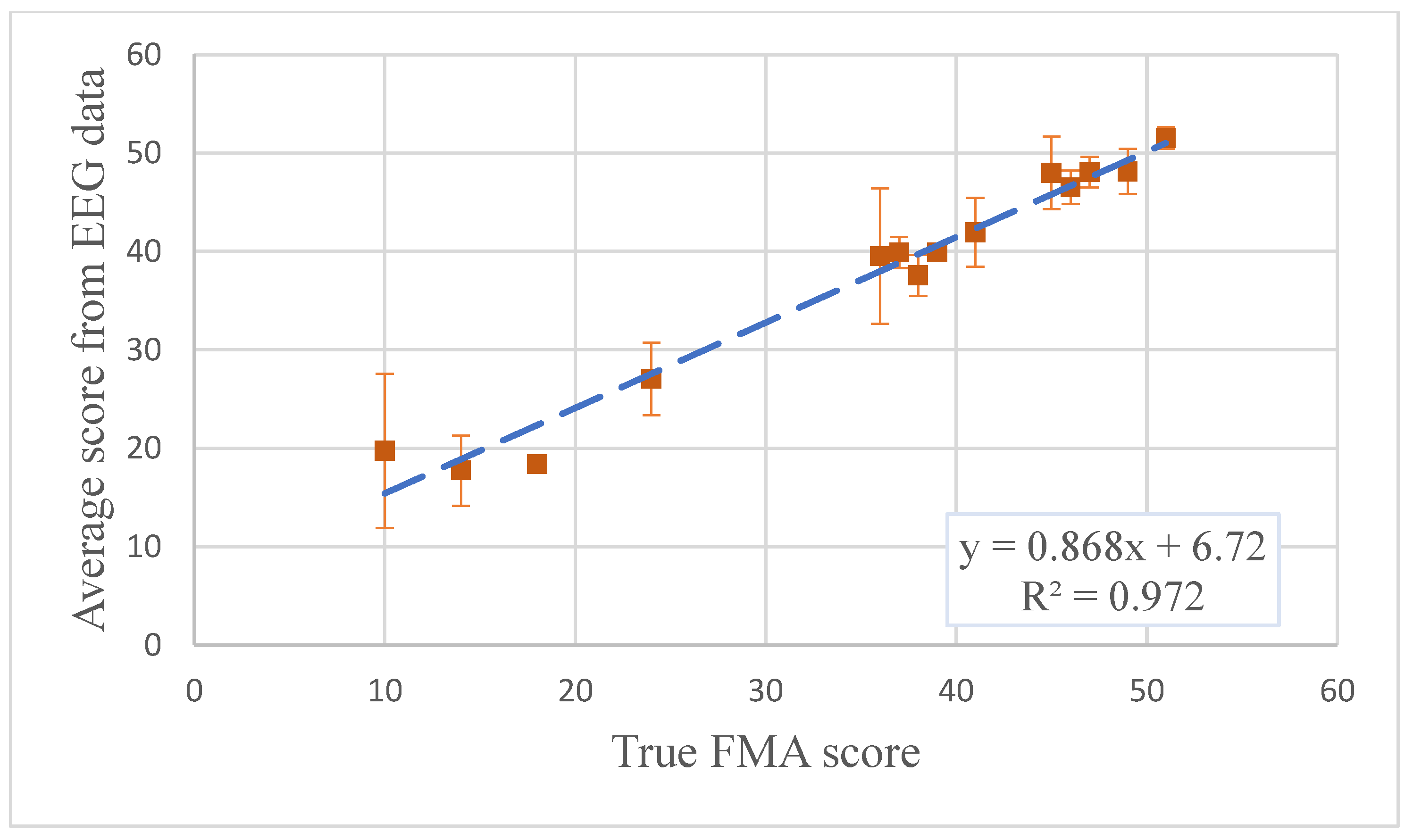
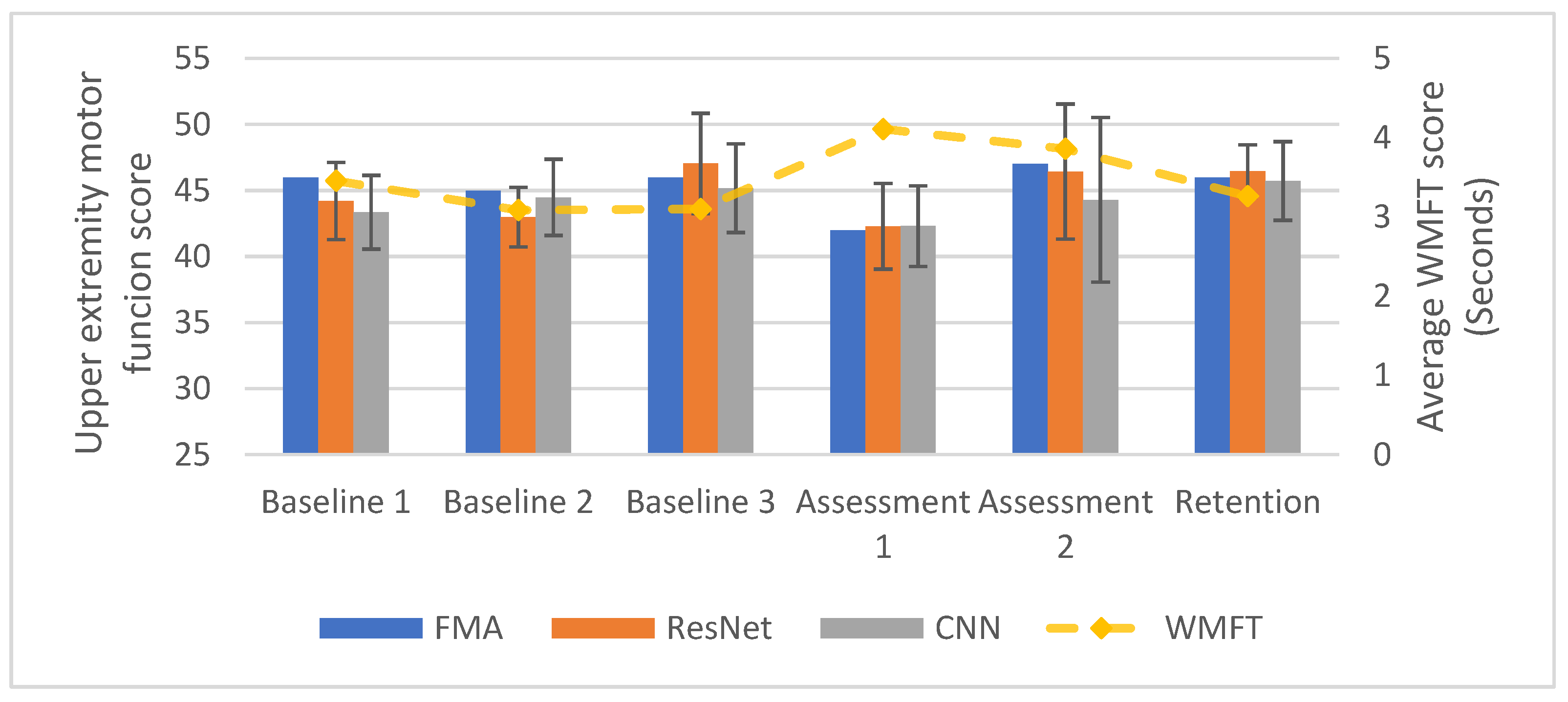
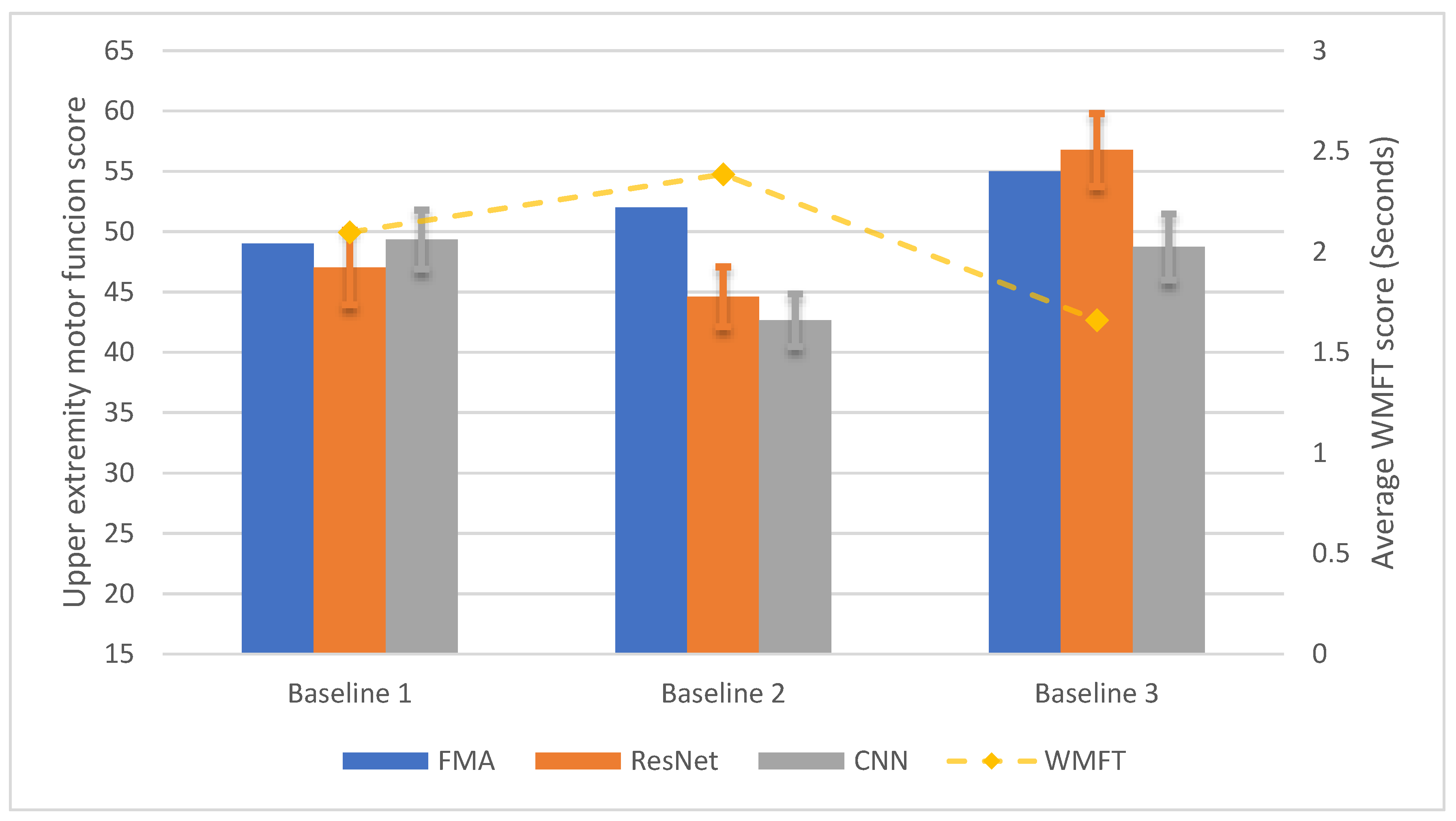
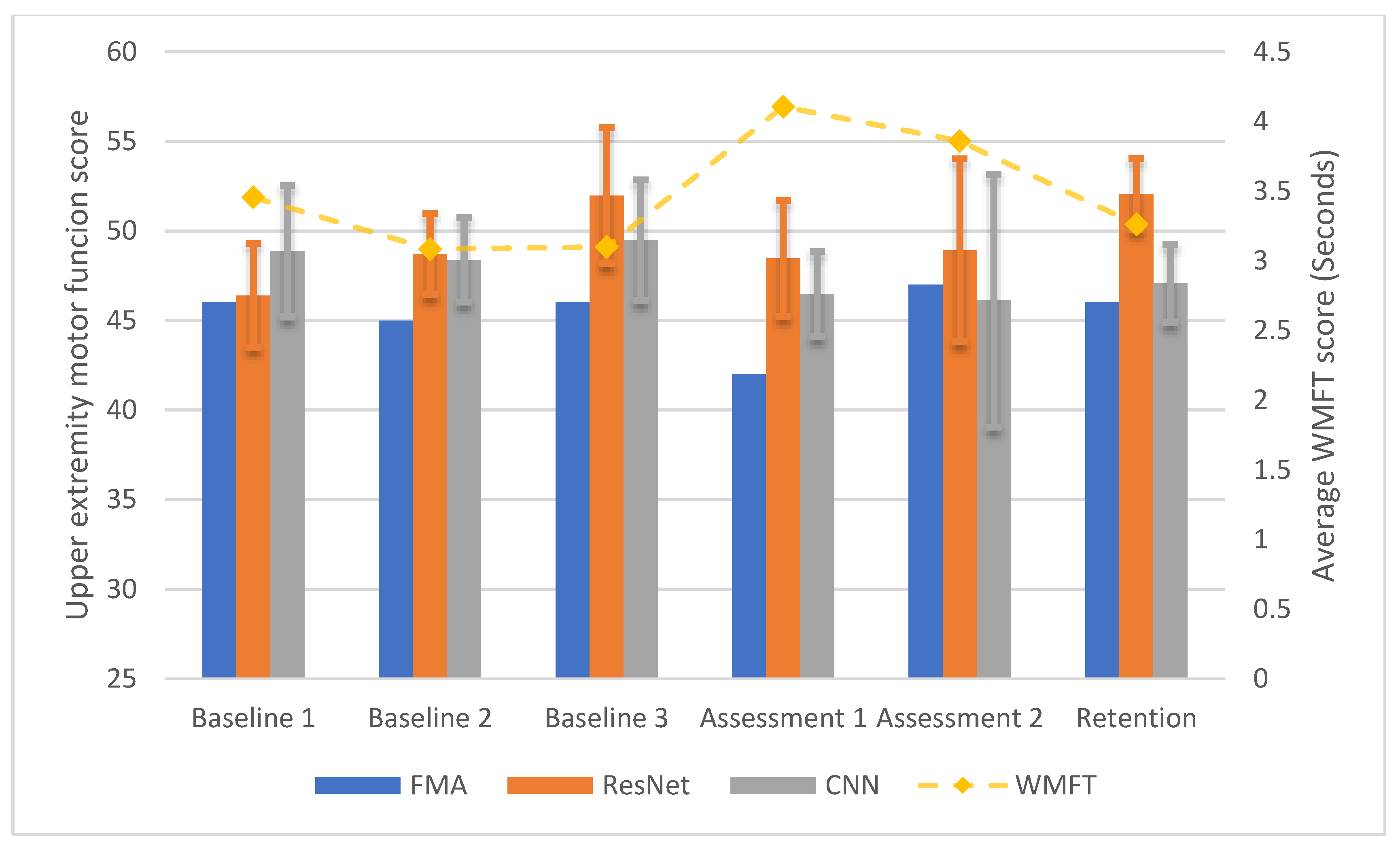
3.3. Longitudinal Within-Participant Test Result and Prediction
3.4. Longitudinal Cross-Participant Test Result and Prediction
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fugl-Meyer, A.R.; Jääskö, L.; Leyman, I.; Olsson, S.; Steglind, S. The post-stroke hemiplegic patient. 1. a method for evaluation of physical performance. Scand. J. Rehabil. Med. 1975, 7, 13–31. [Google Scholar] [CrossRef] [PubMed]
- Kwah, L.K.; Diong, J. National Institutes of Health Stroke Scale (NIHSS). J. Physiother. 2014, 60, 61. [Google Scholar] [CrossRef] [PubMed]
- Keith, R.; Granger, C.; Hamilton, B.; Sherwin, F. The functional independence measure: A new tool for rehabilitation. Adv. Clin. Rehabil. 1987, 1, 6–18. [Google Scholar]
- Pfurtscheller, G.; Lopes Da Silva, F.H. Event-related EEG/MEG synchronization and desynchronization: Basic principles. Clin. Neurophysiol. 1999, 110, 1842–1857. [Google Scholar] [CrossRef]
- Neuper, C.; Pfurtscheller, G. Event-related dynamics of cortical rhythms: Frequency-specific features and functional correlates. Int. J. Psychophysiol. 2001, 43, 41–58. [Google Scholar] [CrossRef]
- Anastasi, A.A.; Falzon, O.; Camilleri, K.; Vella, M.; Muscat, R. Brain Symmetry Index in Healthy and Stroke Patients for Assessment and Prognosis. Stroke Res. Treat. 2017, 2017, 1–9. [Google Scholar] [CrossRef]
- Leon-Carrion, J.; Martin-Rodriguez, J.F.; Damas-Lopez, J.; Barroso y Martin, J.M.; Dominguez-Morales, M.R. Delta-alpha ratio correlates with level of recovery after neurorehabilitation in patients with acquired brain injury. Clin. Neurophysiol. 2009, 120, 1039–1045. [Google Scholar] [CrossRef] [PubMed]
- Kawano, T.; Hattori, N.; Uno, Y.; Kitajo, K.; Hatakenaka, M.; Yagura, H.; Fujimoto, H.; Yoshioka, T.; Nagasako, M.; Otomune, H.; et al. Large-Scale Phase Synchrony Reflects Clinical Status after Stroke: An EEG Study. Neurorehabil. Neural Repair 2017, 31, 561–570. [Google Scholar] [CrossRef]
- Kawano, T.; Hattori, N.; Uno, Y.; Hatakenaka, M.; Yagura, H.; Fujimoto, H.; Yoshioka, T.; Nagasako, M.; Otomune, H.; Kitajo, K.; et al. Electroencephalographic Phase Synchrony Index as a Biomarker of Poststroke Motor Impairment and Recovery. Neurorehabil. Neural Repair 2020, 34, 711–722. [Google Scholar] [CrossRef]
- Zhang, X.; D’Arcy, R.; Menon, C. Scoring upper-extremity motor function from EEG with artificial neural networks: A preliminary study. J. Neural Eng. 2019, 16, 036013. [Google Scholar] [CrossRef]
- Riahi, N.; Vakorin, V.A.; Menon, C. Estimating Fugl-Meyer Upper Extremity Motor Score from Functional-Connectivity Measures. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 860–868. [Google Scholar] [CrossRef] [PubMed]
- Liyanage, S.R.; Guan, C.; Zhang, H.; Ang, K.K.; Xu, J.; Lee, T.H. Dynamically weighted ensemble classification for non-stationary EEG processing. J. Neural Eng. 2013, 10, 036007. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, A.; Raza, H.; Meena, Y.K.; Dutta, A.; Prasad, G. Online Covariate Shift Detection based Adaptive Brain-Computer Interface to Trigger Hand Exoskeleton Feedback for Neuro-Rehabilitation. IEEE Trans. Cogn. Dev. Syst. 2017, XX, 1–11. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity Mappings in Deep Residual Networks. Eur. Conf. Comput. Vis. 2016, 630–645. [Google Scholar] [CrossRef]
- Orand, A.; Aksoy, E.E.; Miyasaka, H.; Levy, C.; Zhang, X.; Menon, C. Bilateral tactile feedback-enabled training for stroke survivors using microsoft kinecttm. Sens. Switz. 2019, 19, 3474. [Google Scholar] [CrossRef]
- Carson, N.; Leach, L.; Murphy, K.J. A re-examination of Montreal Cognitive Assessment (MoCA) cutoff scores. Int. J. Geriatr. Psychiatry 2017, 33, 379–388. [Google Scholar] [CrossRef]
- Stancák, A.; Pfurtscheller, G. Event-related desynchronisation of central beta-rhythms during brisk and slow self-paced finger movements of dominant and nondominant hand. Cogn. Brain Res. 1996, 4, 171–183. [Google Scholar] [CrossRef]
- Gao, L.; Wang, J.; Chen, L. Event-related desynchronization and synchronization quantification in motor-related EEG by Kolmogorov entropy. J. Neural Eng. 2013, 10, 036023. [Google Scholar] [CrossRef]
- Pfurtscheller, G.; Neuper, C. Simultaneous EEG 10 Hz desynchronization and 40 Hz synchronization during finger movements. Neuroreport 1992, 3, 1057–1060. [Google Scholar] [CrossRef]
- Pfurtscheller, G.; Brunner, C.; Schlögl, A.; Lopes da Silva, F.H. Mu rhythm (de)synchronization and EEG single-trial classification of different motor imagery tasks. Neuroimage 2006, 31, 153–159. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. arXiv 2015, arXiv:1512.00567. [Google Scholar]
- Schirrmeister, R.T.; Springenberg, J.T.; Fiederer, L.D.J.; Glasstetter, M.; Eggensperger, K.; Tangermann, M.; Hutter, F.; Burgard, W.; Ball, T. Deep learning with convolutional neural networks for brain mapping and decoding of movement-related information from the human EEG. arXiv 2017, arXiv:1703.05051. [Google Scholar]
- Chollet, F. Keras. Github Repos. Available online: https://github.com/keras-team/keras (accessed on 25 September 2020).
- Tensorflow. TensorFlow. Available online: https://medium.com/tensorflow/tensorflow-at-google-i-o-2018-b6612840f59d (accessed on 25 September 2020).
- Apache Spark. Apache SparkTM—Lightning-Fast Cluster Computing. Available online: http://spark.apache.org/ (accessed on 25 September 2020).
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for Hyper-Parameter Optimization. In Proceedings of the 24th International Conference on Neural Information Processing Systems, Granada, Spain, 12 December 2011; pp. 2546–2554. [Google Scholar]
- Gladstone, D.J.; Danells, C.J.; Black, S.E. The Fugl-Meyer Assessment of Motor Recovery after Stroke: A Critical Review of Its Measurement Properties. Neurorehabil. Neural Repair 2002, 16, 232–240. [Google Scholar] [CrossRef] [PubMed]
- Van Der Lee, J.H.; Beckerman, H.; Lankhorst, G.J.; Bouter, L.M. The responsiveness of the Action Research Arm test and the Fugl-Meyer Assessment scale in chronic stroke patients. J. Rehabil. Med. 2001, 33, 110–113. [Google Scholar] [CrossRef]
- Sanford, J.; Moreland, J.; Swanson, L.R.; Stratford, P.W.; Gowland, C. Reliability of the Fugl-Meyer assessment for testing motor performance in patients following stroke. Phys. Ther. 1993, 73, 447–454. [Google Scholar] [CrossRef]
- Hsueh, I.-P.; Hsu, M.-J.; Sheu, C.-F.; Lee, S.; Hsieh, C.-L.; Lin, J.-H. Psychometric Comparisons of 2 Versions of the Fugl-Meyer Motor Scale and 2 Versions of the Stroke Rehabilitation Assessment of Movement. Neurorehabil. Neural Repair 2008, 22, 737–744. [Google Scholar] [CrossRef]
- Hiragami, S.; Inoue, Y.; Harada, K. Minimal clinically important difference for the Fugl-Meyer assessment of the upper extremity in convalescent stroke patients with moderate to severe hemiparesis. J. Phys. Sci. 2019, 31, 917–921. [Google Scholar] [CrossRef]
| Layer Name | Parameters |
|---|---|
| Input Layer | Shape = (None, 270, 32, 2) |
| 2D Convolutional Layer 1 | Number of Filters ∈ {25, 50, 100}, Kernel Size ∈ {(2,2), (2,4), (2,6), … (10,8), (10,10)} |
| Max Pooling Layer 1 | Pooling Size = (2, 2) |
| 2D Convolutional Layer 2 | Number of Filters ∈ {25, 50, 100}, Kernel Size = (2, 2) |
| Max Pooling Layer 2 | Pooling Size = (2, 2) |
| Flatten Layer | N/A |
| Dense Layer 1 | Number of neurons = 100 |
| Dropout Layer | Dropout rate∈ {0 to 1 with 0.05 as step size} |
| Dense Layer 2 | Number of neurons = 25 |
| Dense Layer 3 | Number of neurons = 10 |
| Dense Layer 4 | Number of neurons = 5 |
| Output Layer | Number of neurons = 1 |
| ID | Age | Gender | Years after Stroke | Affected Side | MOCA | Handedness before Stroke |
|---|---|---|---|---|---|---|
| P1 | 65 | Male | 7 | Left | 27 | Right |
| P2 | 51 | Female | 7 | Right | 23 | Right |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; D’Arcy, R.; Chen, L.; Xu, M.; Ming, D.; Menon, C. The Feasibility of Longitudinal Upper Extremity Motor Function Assessment Using EEG. Sensors 2020, 20, 5487. https://doi.org/10.3390/s20195487
Zhang X, D’Arcy R, Chen L, Xu M, Ming D, Menon C. The Feasibility of Longitudinal Upper Extremity Motor Function Assessment Using EEG. Sensors. 2020; 20(19):5487. https://doi.org/10.3390/s20195487
Chicago/Turabian StyleZhang, Xin, Ryan D’Arcy, Long Chen, Minpeng Xu, Dong Ming, and Carlo Menon. 2020. "The Feasibility of Longitudinal Upper Extremity Motor Function Assessment Using EEG" Sensors 20, no. 19: 5487. https://doi.org/10.3390/s20195487
APA StyleZhang, X., D’Arcy, R., Chen, L., Xu, M., Ming, D., & Menon, C. (2020). The Feasibility of Longitudinal Upper Extremity Motor Function Assessment Using EEG. Sensors, 20(19), 5487. https://doi.org/10.3390/s20195487






