1. Introduction
The current generation of robotic manipulators has triggered new application scenarios in which robots can enter into direct interactions with unknown environments or humans to perform complex tasks [
1]. The theory of impedance control [
2] has played an important role in this direction, to control the dynamic interactions between a manipulator and the external world. In fact, due to its implementation simplicity and the robustness to the external disturbances, it has found several significant areas of application [
3,
4,
5]. Nevertheless, the choice of impedance parameters in this control framework is not intuitive for a given task, especially for the tasks that require continuously varying interaction patterns [
6,
7,
8].
To address the impedance planning problem from a machine learning point of view, previous works proposed the use of model-free reinforcement learning (RL) algorithms. In [
6], a policy improvement with path integrals (PI
2) algorithm was proposed to accomplish variable impedance control for a given task. In [
8], the authors propose exploiting the end-effector space for RL to learn the reference position and impedance profile for contact-rich tasks. Although these works demonstrated the potential of the RL approach to fulfill the impedance requirements of a task, they demanded a large number of trials (hundreds in [
6] and even more in [
8]) to train the models.
An alternative approach to the impedance learning through RL is learning from demonstration (LfD). In [
9], a LfD-based algorithm was proposed to collaboratively assemble a wooden table with a human subject and a robot. The desired trajectory was retrieved through a task-parametrized Gaussian mixture model (TPGMM). In addition, by taking into account the sensed force information, a weighted least-squares (WLS) method was employed to estimate the stiffness matrix, which was used in the task reproduction. In [
10], the authors used a similar framework but adopted a sliding window technique to carry out local stiffness estimation instead of WLS. However, in both methods, a first estimation of the stiffness matrix does not comply with the symmetric and positive-definite (SPD) constraints. In [
11], benefiting from estimations of both the mean and the variance from kernelized movement primitives (KMP) [
12], the authors consider the variance of the positional demonstrations as the task-related uncertainty, whose inverse then is used as the stiffness parameters in the controller. Force sensing is not required in this approach, and the assumption that variability of position and stiffness are directly related may not always be reasonable [
7].
It is well known that human arm endpoint stiffness can be adapted to different task requirements and instabilities through changing posture [
13] and muscle contractions [
14]. In fact, human interaction skills can be defined by the ability to exploit the two mechanisms to match the arm endpoint stiffness to the task requirements. A preliminary investigation of this concept was carried out by the authors in [
15], where a virtual tennis system was developed to estimate the readiness impedance of the skilled players. In another work [
16], the authors studied the hand impedance measurements comparatively across professional and novice manual welders when they performed tungsten inert gas (TIG) welding interactively with the KUKA lightweight robot arm (LWR). The result showed that hand impedance profiles differed across professional and novice welders, demonstrating the superior capability of the skilled workers in regulating the arm endpoint impedance.
Inspired by the stiffness regulation capability of the human arm, some studies have made an attempt to transfer such an ability to robotic manipulators. In that direction, the first problem to address was the estimation of the human arm endpoint stiffness or joint stiffness, so that either the real-time stiffness profiles or the underlying impedance-regulation principles can be transferred to robotic manipulators. In [
17], a practical approach to estimating human wrist stiffness during tooling tasks was proposed, and the joint stiffness information was pre-programmed to allow transferring skills from expert human operators to an impedance-controlled industrial robot. Instead of only modeling the wrist stiffness, modeling human arm endpoint stiffness based on a complete arm skeleton model is more useful in practice. The methods to estimate the human arm endpoint stiffness can be divided into offline and online categories. Stochastic [
18] or deterministic [
19] perturbation techniques, for instance, are among the offline methods to identify discrete human arm endpoint stiffness in certain arm postures. The alternative offline techniques make use of human upper extremity musculoskeletal models [
20], which can generate appropriate muscle activities to repeat a movement recorded from a human demonstration. In such models, human arm joint stiffness is calculated according to the generated muscle activities, and consequently, the endpoint stiffness is formulated through a conservative congruence transformation [
21]. The latter technique is suitable for the continuous stiffness profile estimation’ however, the process is very complex, which makes it hardly suitable for applications that require personalized human models.
The online human impedance estimation techniques were first proposed under the concept of teleimpedance control [
22], for real-time transferring of human arm stiffness to teleoperated robots. To extend this model to a larger arm workspace, the theory of the common mode stiffness (CMS) and configuration dependent stiffness (CDS) was proposed in [
23]. The CMS, which reflected the effect of muscular co-activation in synchronous modulation of the stiffness ellipsoid’s major axes, and the CDS, which reflected the geometric contribution of the arm Jacobian, were used for the estimation of the arm endpoint stiffness projected from joint stiffness in real-time. However, the joint stiffness matrix is a symmetric and non-diagonal matrix, which means for a 7-DOF human arm, there are 28 unknown parameters in this matrix (30 in total, two for the muscular co-activation model). Furthermore, to reduce the open parameters in the model, the muscle Jacobian was introduced in [
24]; it leads to a diagonal muscle stiffness matrix. The number of unknown parameters in this matrix depends on the number of selected muscles (11 muscles were selected and 13 unknown parameters in total in [
24]). Although this resulted in an less parameterized and accurate model, calculating the muscle Jacobian can be quite complex, hindering its widespread use in practice.
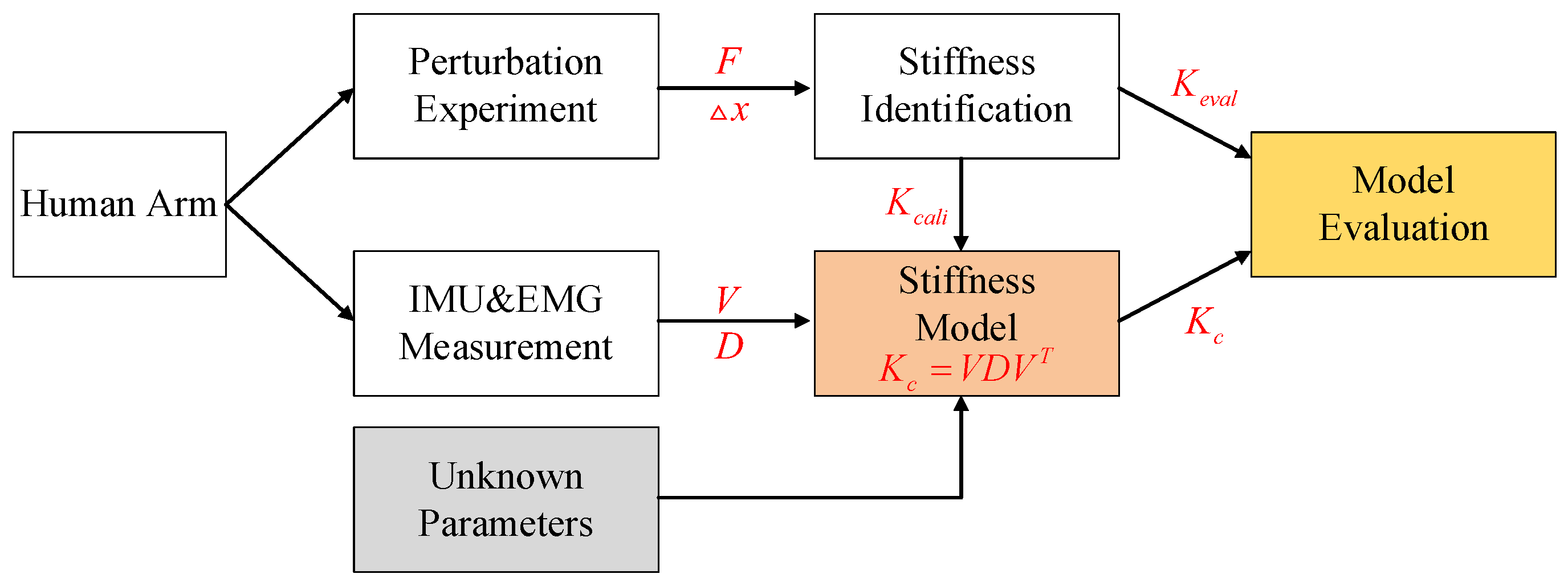
As a continuation of our developments in this direction, in this work, we proposed a new, principally simplified, and intuitive online model of the human arm endpoint stiffness which significantly reduces the total unknown parameters to 4 and without computation of above Jacobians. The new model is based on the large dependency of the shape and orientation of the stiffness ellipsoid on the arm configuration. In fact, previous studies [
19,
25] indicate that (i) the major principal axis of the arm endpoint stiffness ellipse passes close to the hand-shoulder vector, and (ii) when the arm is extended and the hand moves further from the shoulder, the ellipse becomes more elongated, and conversely, it becomes more isotropic. Inspired by those findings, in this work, we propose a new model in 3D formed by constructing the ellipsoids’ principal axes and their lengths, namely, the eigenvectors and eigenvalues, based on the arm configuration. Compared with the recent model proposed in our previous work [
24], we exploit the basic human arm motion data to retrieve arm geometry information, from which the CDS part is constructed. This is in contrast to our previous models that exploited human arm and muscle Jacobians, with the latter being quite complex. This consideration can significantly increase its integration and personalization potential in various application scenarios, such as teleoperation and human kinodynamics tracking for ergonomic assessment. The main blocks of this work are illustrated in
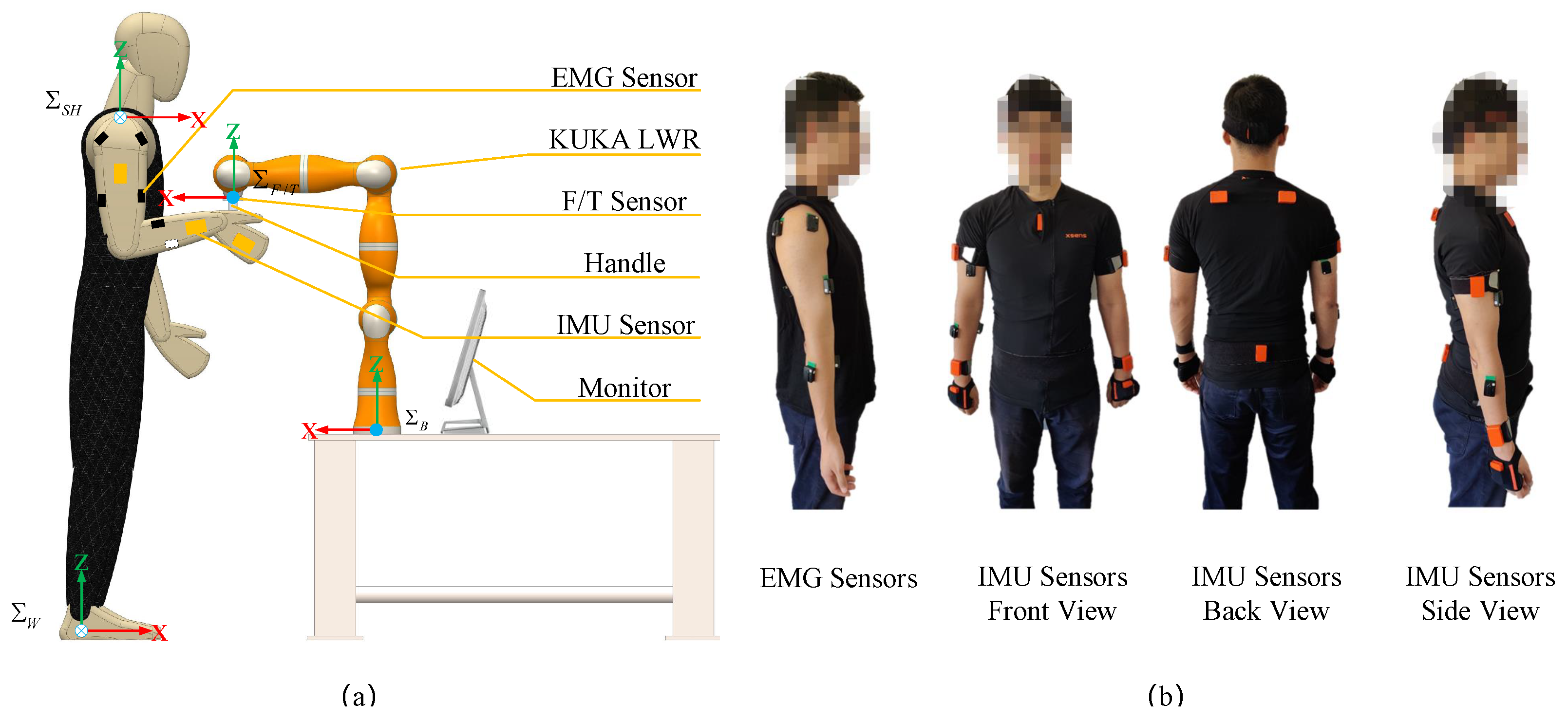
Figure 1. Under our experimental setup, through a deterministic perturbation experiment, perturbed force
and displacement
were recorded and from which the separate human arm endpoint stiffness samples were collected. The elements
and
in the human arm endpoint stiffness estimation model were constructed based on inertial measurement unit (IMU) and electromyography (EMG) sensors’ measurements and a few unknown parameters. Then, the model’s unknown parameters were calibrated by using the collected stiffness samples for calibration
. Finally, the accuracy of the proposed model
was evaluated by using the collected stiffness samples for evaluation
.
The remainder of this paper is structured as follows:
Section 2 elaborates on the theory of the new model.
Section 3 starts with the identification of human arm endpoint stiffness, which is then followed by the optimization of the model parameters. In
Section 4, the accuracy of the model across several subjects is evaluated. Finally, the discussions and conclusions are presented in
Section 5.
2. Formulation
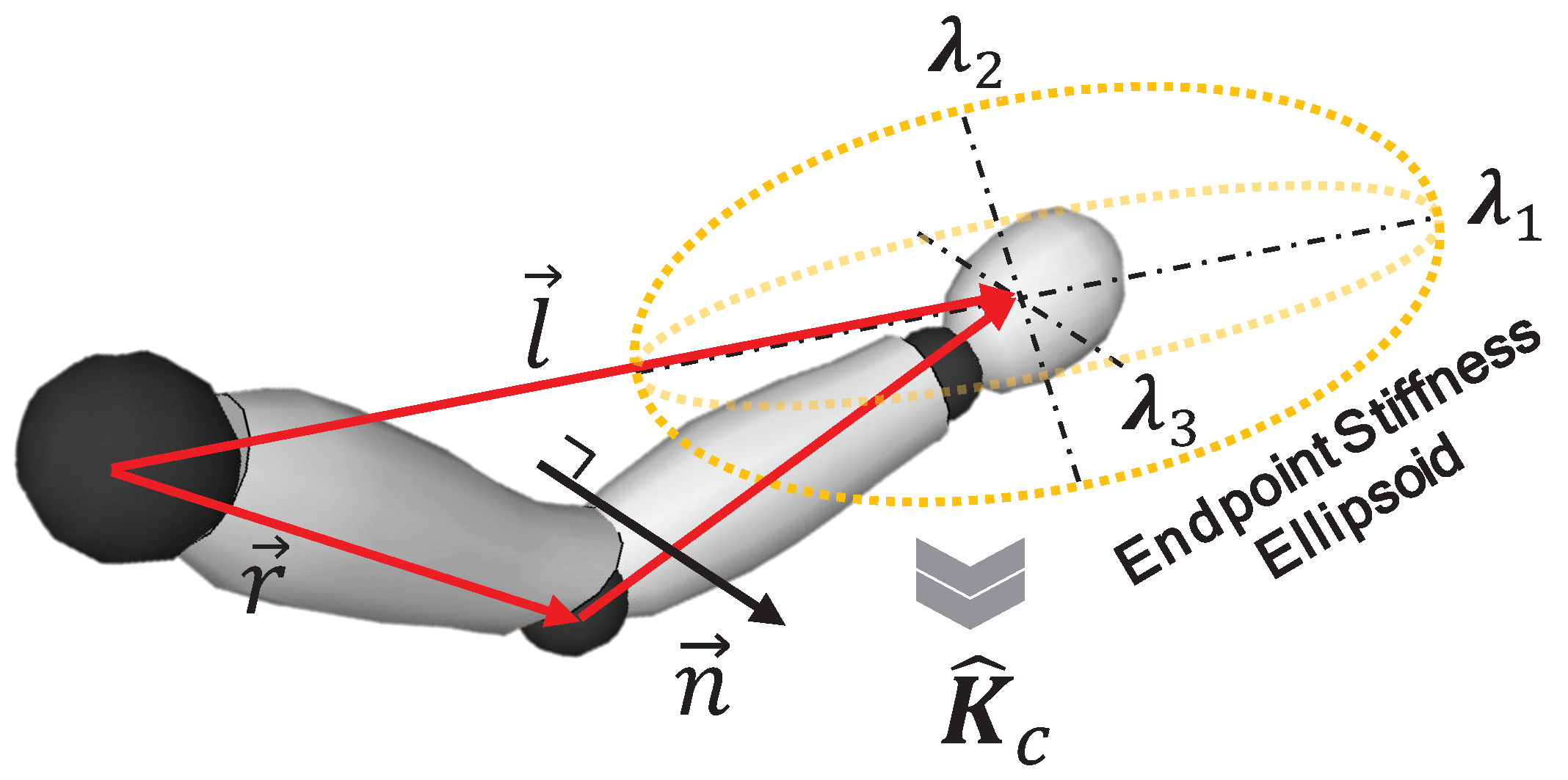
As shown in
Figure 2, in this work, we use a two-segment human arm skeleton structure in 3D space. The hand–forearm and upper arm segments in this model permit us to form an arm triangle [
26] at any non-singular configuration. Relying on the dominant contribution of the arm configuration to the endpoint stiffness geometry, we propose to use the vector from the center of shoulder joint to the position of the hand (
), to identify the major principal direction of the human arm endpoint stiffness ellipsoid. The minor principal axis direction (
), instead, is defined to be perpendicular to the arm triangle plane
where
represents the vector from the center of shoulder to the center of elbow.
The remaining principal axis of the stiffness ellipsoid (
), which lies on the arm triangle plane, is calculated based on the orthogonality of the three principal axes
Hence, the orthonormal matrix
can be constructed as
From the equation above, when the arm is extended and the hand moves further from the shoulder, the ellipse becomes more elongated, and conversely, it becomes more isotropic. Hence, we assume that the ratio of the length of median principal axis to the major principal axis of the stiffness ellipsoid is inversely proportional to the distance
from the hand position to the center of shoulder.
where
and
represent the eigenvalues corresponding to the major and median principal axes, respectively.
is the scale factor and
The ratio of the length of the minor principal axis to the major principal axis is assumed to be proportional to the distance
from the center of the elbow to the major principal axis.
where
represents the eigenvalue corresponding to the minor principal axis,
is the scale factor, and
Previous works indicate that human arm muscles contribute to the endpoint stiffness in a synergistic way. The findings in [
19] show the magnitude of the stiffness is coordinately increased but only minor changes occur in shape and orientation when a disturbance occurred to the arm. A force regulation task was introduced in [
27] to examine the human arm’s abilities (especially the muscles) regarding voluntary control of static endpoint stiffness with a fixed arm configuration; it turned out that individuals can voluntarily change stiffness orientation but that the magnitude of these changes is small. Therefore, in this work, we built the model based on the assumption of the synergistic contribution of the arm muscle co-contractions to the endpoint ellipsoid’s volume. This contribution is represented by the active component
.
which is in a linear relation with the muscle activation level
p.
and
are two coefficients to be identified.
The diagonal matrix
is formed by the length of the principal axes, i.e., the eigenvalues,
where
is set to
, and
represents the shape of the stiffness ellipsoid. Finally, the estimated endpoint stiffness matrix
is formulated by
In this formulation, only four parameters (, , and ) must be personalized to match an individual’s physical interaction characteristics. Note that this formulation guarantees the symmetry and positive definiteness of the endpoint stiffness matrix, as long as the eigenvalues are positive. The number of dimensions of the input space of this model is six, which are composed of (1) a one-dimensional vector for the EMG signal, and (2) a three-dimensional vector and three-dimensional vector ; we use with the elbow-hand vector length constraints which reduce the number of dimensions to five. The output space, which includes the translational Cartesian stiffness components of the endpoint stiffness matrix, has six dimensions as well. The following chapter explains the procedure for the identification and personalization of the model parameters.
4. Results
The identified model parameters for the four subjects are listed in
Table 1. The average (AVG), standard deviation (SD) and coefficient of variation (CV) of the parameters were calculated across subjects. From the CV values of different parameters, it can been seen
and
exhibit large difference while
and
are similar within subjects. The reason behind is that
and
are closely related to the arm skeleton dimensions and which do not have much difference within the subjects in our experiment.
and
are closely related to the strength of the muscles, which may have large difference across the subjects.
To evaluate the accuracy of the proposed model, the following function (
13), where
represents the 3 × 3 identity matrix, was calculated:
By utilising the test data set (
) from different subjects, the model error was within
, and the average error was around 20%.
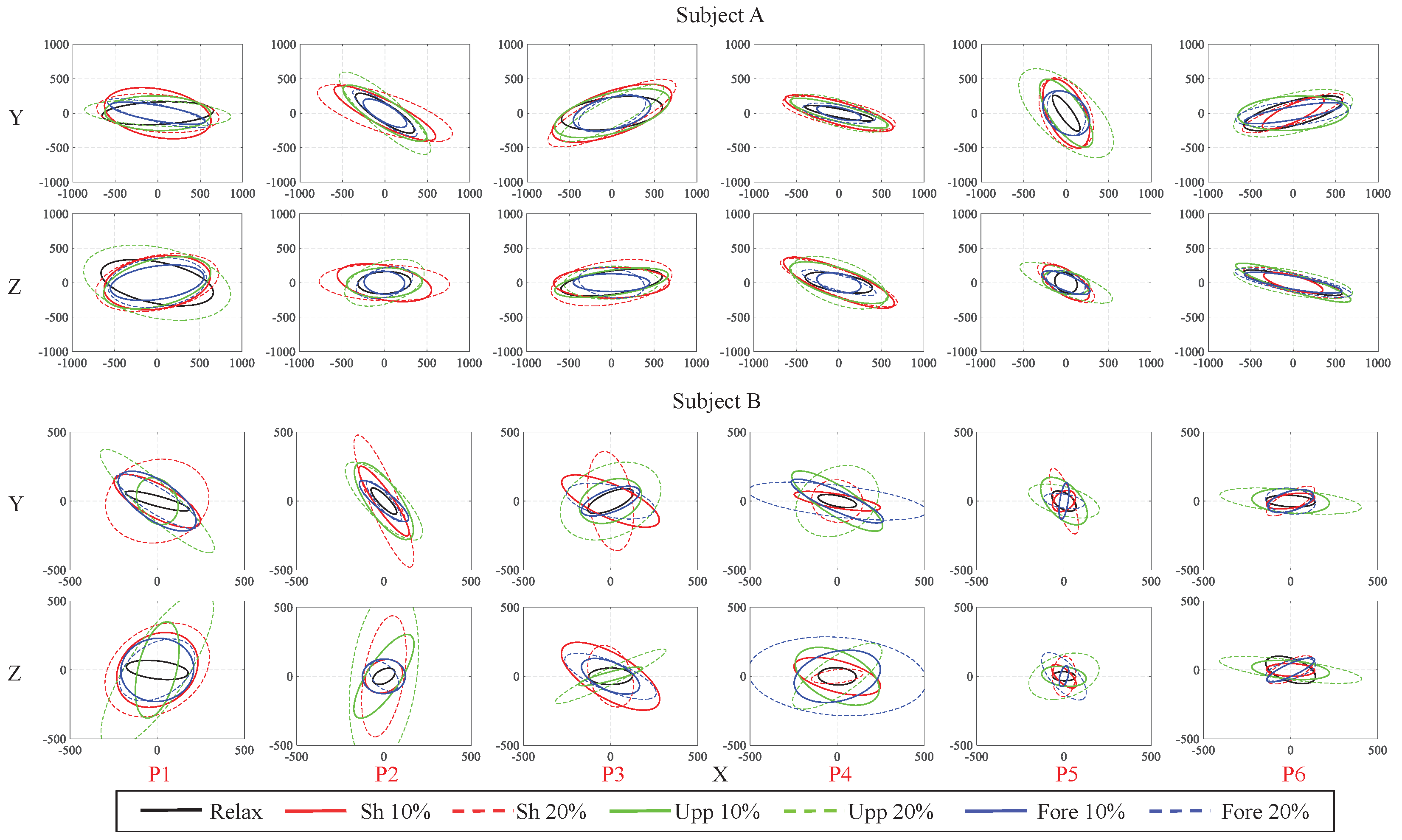
Figure 8 demonstrates the typical results across subjects of the measured (solid line) and the predicted (dashed line) endpoint stiffness ellipses on X–Y and X–Z planes for the subjects A and B in 10% MVC of the shoulder, upper arm and forearm muscles. As illustrated, the principal axis directions of the reconstructed (from model) ellipses largely match the estimated (from experiments) ones.
To provide a quantified comparison, the angle between the major principal axes of the measured and the predicted endpoint stiffness ellipsoids is used to evaluate the directional mismatch between the two. In addition, the relative error of the volume of the measured and the predicted endpoint stiffness ellipsoids is used to evaluate the size difference. To keep in line with the data depicted in
Figure 8, the above two indexes were separately analyzed on X–Y and X–Z planes. For the principal axes difference, the average angle errors on X–Y plane across test data set for subjects A, B, C and D were
rad (the data are reported as: mean ± standard deviation),
rad,
rad, and
rad, respectively, resulting in a total average angle error of
rad across all subjects. On X–Z plane, the average angle errors for subjects A, B, C and D were
rad,
rad,
rad, and
rad, respectively, resulting in a total average angle error of
rad across all subjects. Compared with the error on X–Y plane, the error on X–Z plane is a bit higher due to more uncertainty existing in Z direction caused by the neglected gravitational effect of the human arm. This confirms and gives credibility to our geometric approach in constructing the eigenvectors of the stiffness model.
On the other hand, for the size difference, the average relative error of ellipses area
is defined by (
14) for each subject. It resulted in
equal to
and
for subjects A, B, C and D on X–Y plane, respectively, and therefore a total average error is
across all subjects. On X–Z plane, the average relative error
was equal to
and
for subjects A, B, C and D, respectively; the total average error therefore, was
across all subjects. Regarding the shape/volume, the reconstructed ellipses were more circular than the measured ones and because of this, the volumes cannot match each other very well after the optimization. Most of the reconstructed ellipses were smaller than the measured ones mainly in
x direction. One potential limitation is that the shape/volume mismatch may cause the reducing of modeling accuracy because of the movement of subject’s trunk was rigidly constrained only in
x direction, where is in the experimental setup. In fact, in [
30], the effects of unconstrained trunk and shoulder movements on arm endpoint stiffness were examined, it showed that the compliance associated with unrestrained trunk and shoulder decreased the static endpoint stiffness of the arm. Thus, the true human arm endpoint stiffness values in
y and
z directions should be larger than the measured ones. It means that the true stiffness ellipses could be more circular and the shape/volume mismatch problem could be relieved.
where
is the average relative error of the measured and the predicted ellipses area across the test data set for each subject,
and
are respectively the
i-th predicted and measured ellipses area on X–Y or X–Z plane.
5. Discussion and Conclusions
In this paper, we proposed a new human arm endpoint stiffness model, in which the stiffness matrix was decomposed as through eigendecomposition. The unitary basis and the singular values of were extracted directly from a reduced human arm skeleton structure in 3D and a muscular co-contraction index, respectively.
The proposed model offers several advantages. Firstly, the calibration and personalization of the model to an individual can be achieved through the identification of only four parameters. This implies that a small-scale experiment’s data would be sufficient to calibrate this model to match an individual’s physical characteristics. As it was shown in the last column of
Table 1, the average values of
and
were used to re-evaluate the model accuracy. It turns out that minor error is increased compared with the personalized
and
which means in some specific applications where only CDS is considered, the average value could be used even without parameter identification process for a new individual who shares a similar arm skeleton dimensions with the subjects in our experiment. Secondly, the SPD properties of the calculated arm endpoint stiffness are guaranteed, which is due to the underlying eigendecomposition. Thirdly, and relying on the above two advantages, the log-frobenius, which is the geodesic length between two elements in
, can be used in the optimization procedure to speed up the convergence rate. Lastly, due to the above advantages, the implementation of this model requires less programming work compared with previous models. The main difference appears in the CDS part. In [
23,
24], the input for CDS is the joint angles which means an inverse kinematics process has to be preprogrammed based on the raw data from the IMU, and a 3 by 7 matrix of arm Jacobian has to be constructed in [
23] and besides that, a 7 by 11 matrix of muscle Jacobian is also needed in [
24] which requires the forward kinematics of the length of relative muscles respect to the joint angles and it is hard to develop from scratch for most researchers. However, in the proposed model, the input for CDS is the raw data from IMU without any inverse kinematic process. Meanwhile, the construction the eigenvectors and eigenvalues is much easier compared with the Jacobians, especially the muscle Jacobian. This advantage makes our model more suitable for human–robot interaction and collaboration, and teleoperation (teleimpedance) applications. In robot learning from demonstration scenarios, by employing this model, one can enrich the demonstrated data by adding human stiffness profile to the kinodynamic data that can be measured by external sensory systems.
The price paid for the above substantial advantages is the average model error of around 20% evaluated by (
13) which mainly catches the nonlinear structure of SPD stiffness matrix, although the average size difference evaluated by (
14) is around 50% which is closely related to the linear part of the stiffness matrix. This error is mainly introduced by neglecting the effect of external forces [
14] and probably by our assumption on muscle synergies [
31]. Therefore, the error is imposed by the trade-off between simplicity and accuracy of the model. Noteworthy is that the influence of the external forces on human arm stiffness is also ignored in [
24].
The model error is still acceptable for most applications mentioned before. In particular, for what concerns the stiffness ellipsoid’s geometry, according to the quantitative comparison in principal axes difference between the measured and predicted stiffness in last section, the constructed principal axes coincide with the experimentally measured ones with a limited error. In most applications, the stiffness geometry plays a dominant role compared to its volume. In fact, some tasks do not require specific stiffness values to be executed, but stiffness ranges along principal axes. An example is the assembly tasks (e.g., peg-in-hole), where the stiffness profile along the insertion must be higher than the others to comply with the environmental constraints. For this kind of application, the measurement error in the proposed model may not result in task failure. However, there are other applications that are more sensitive to the variation of stiffness values, which means that the task may fail because of the existence of a similar error. In this case, only relying on the task-related stiffness information recorded from human arm may be not sufficient. Nonetheless, by combining adaptive control approaches or reinforcement learning algorithms, a fine modulation of the modeled stiffness profile is expected to compensate for such an error.