Noise Suppression in Compressive Single-Pixel Imaging
Abstract
1. Introduction
2. Compressive Imaging Theory
3. Multiplicative Noise
4. Additive Noise
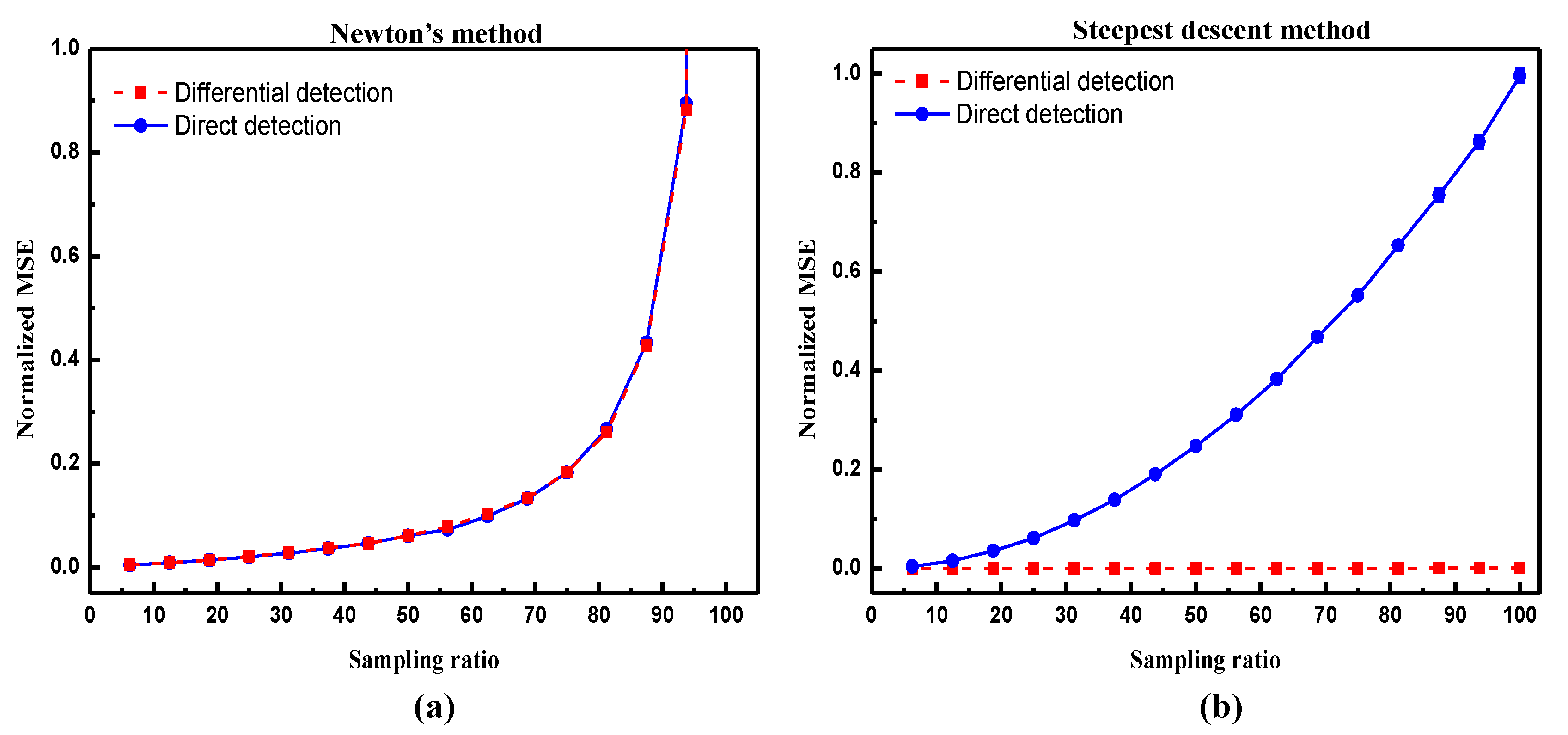
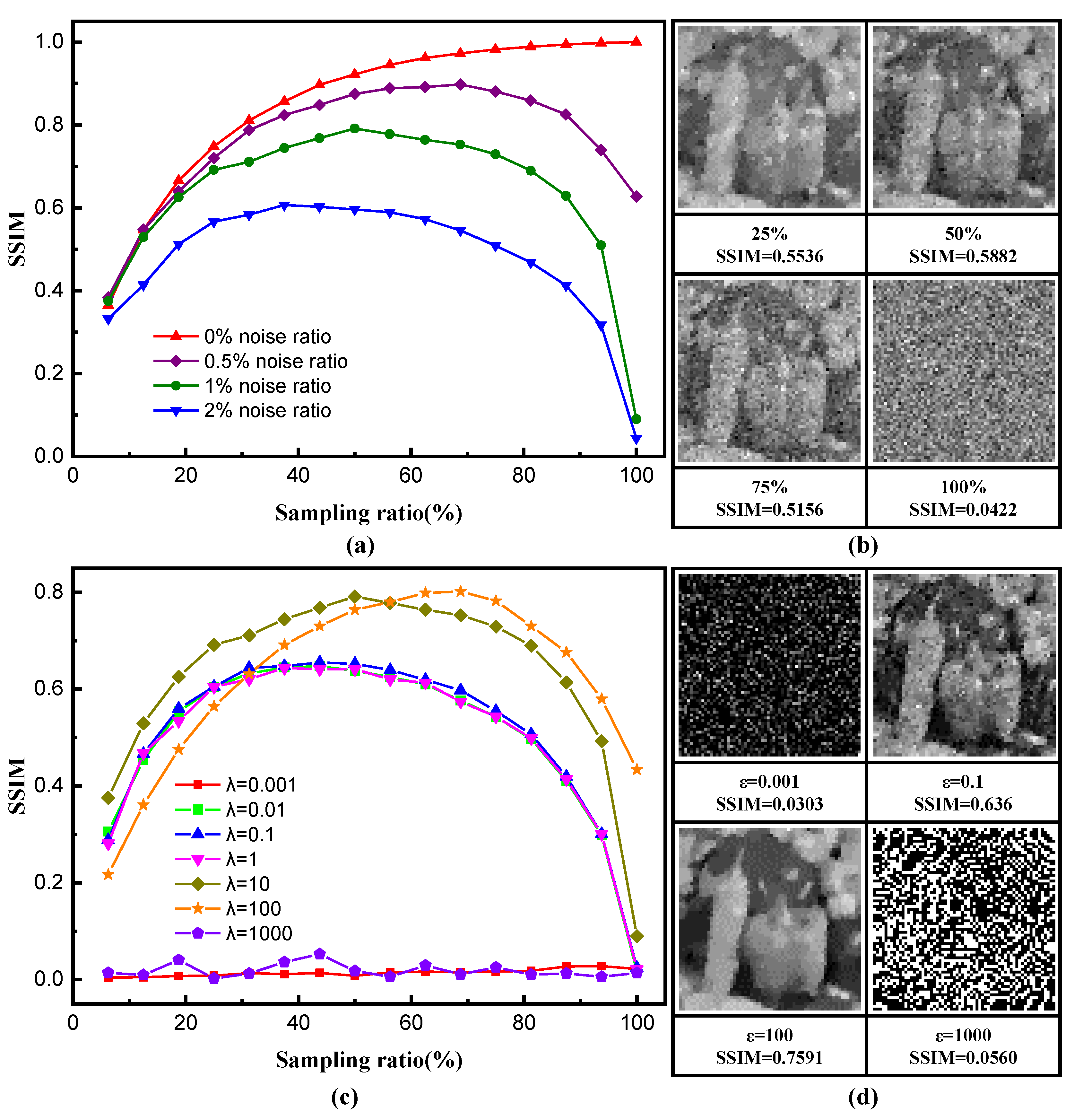
4.1. The Influence of Additive Noise
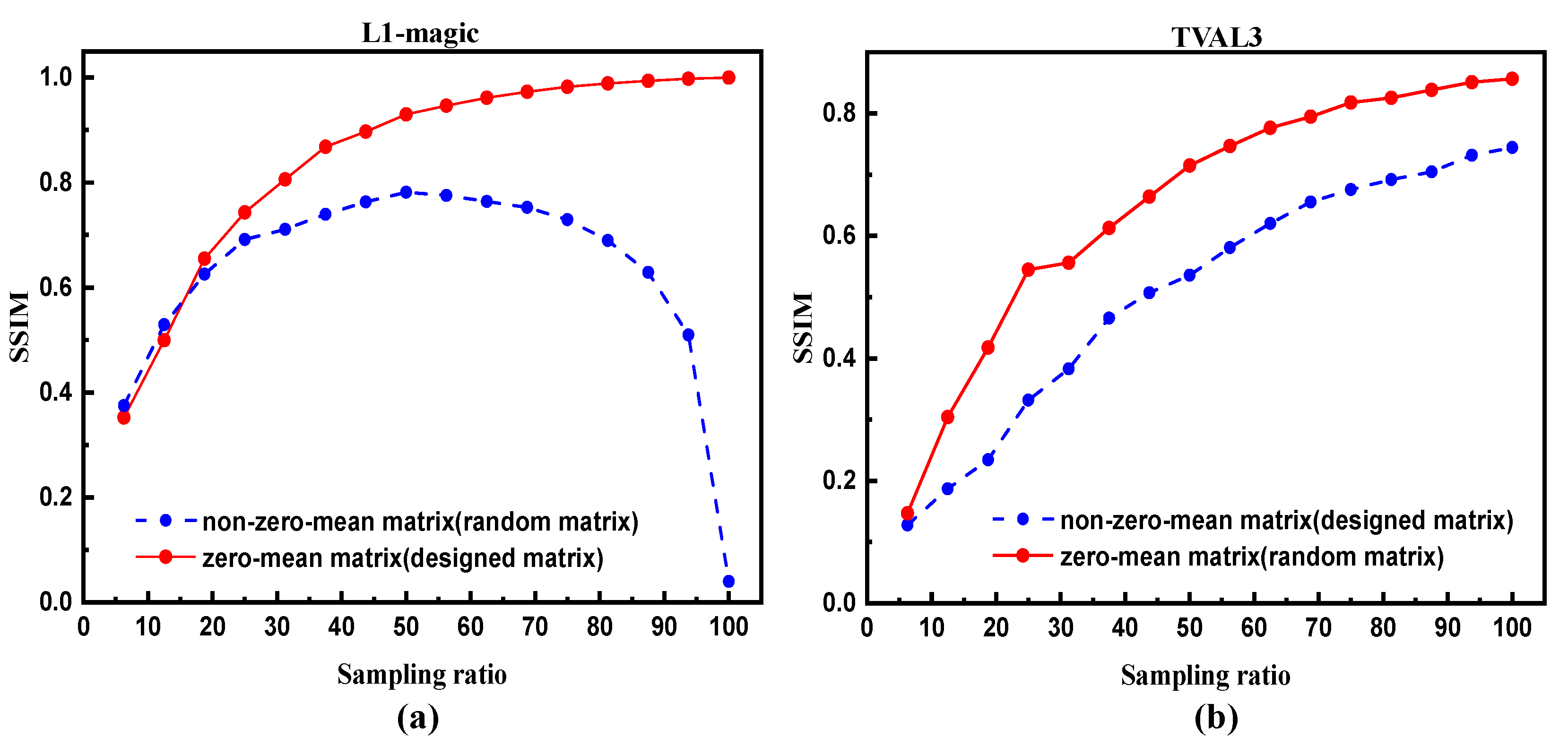
4.2. Theoretical Explanations
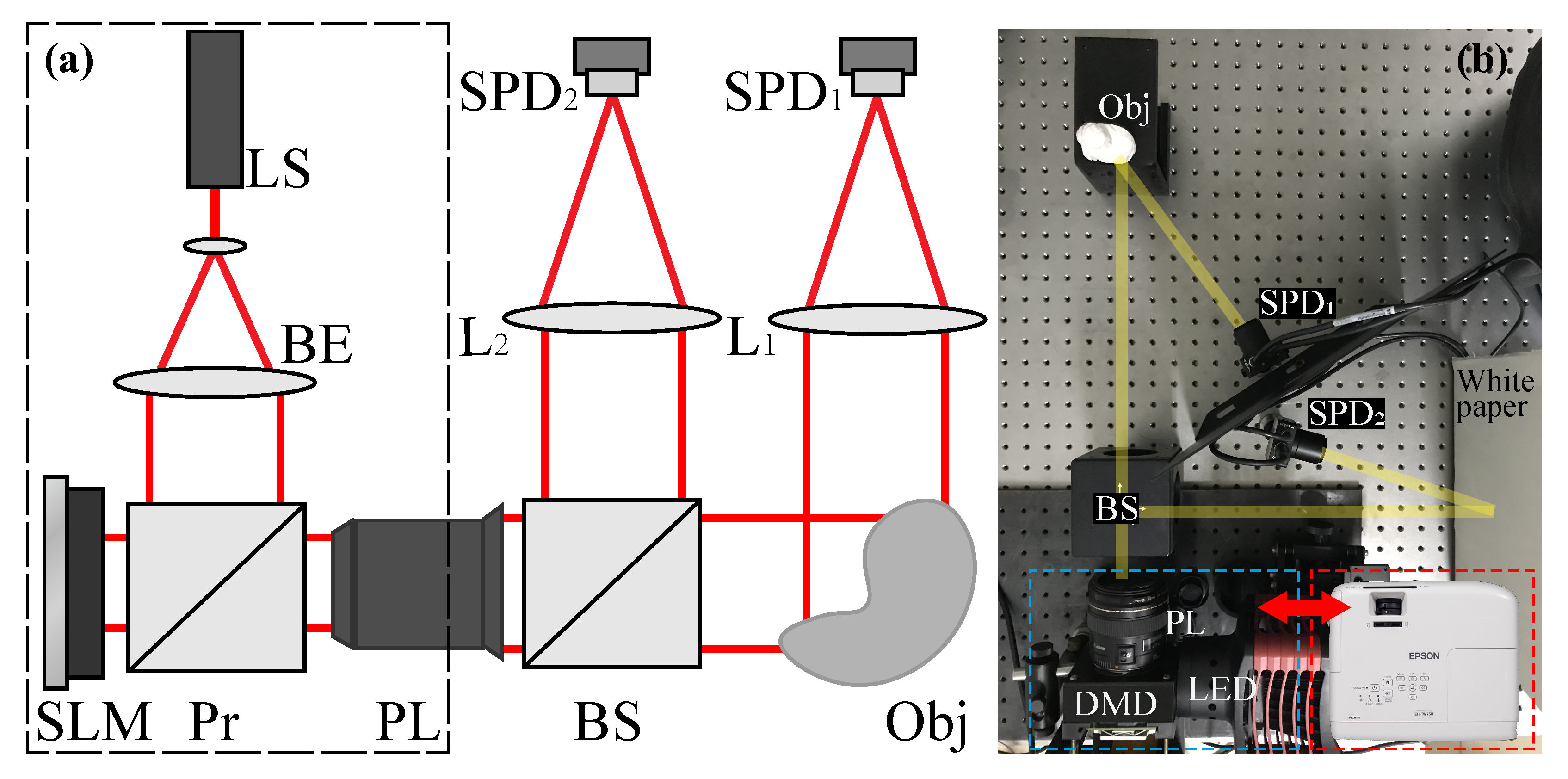
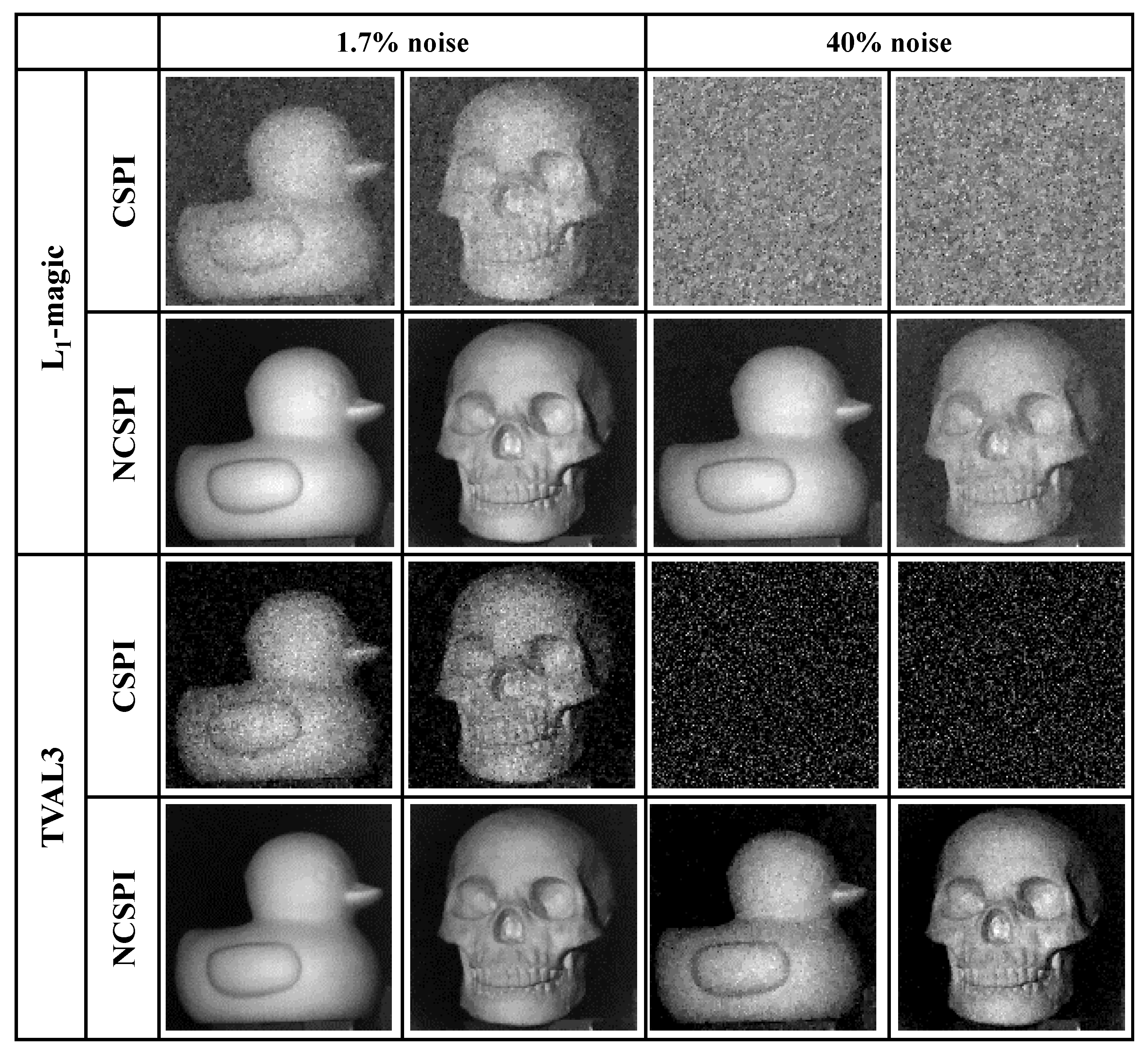
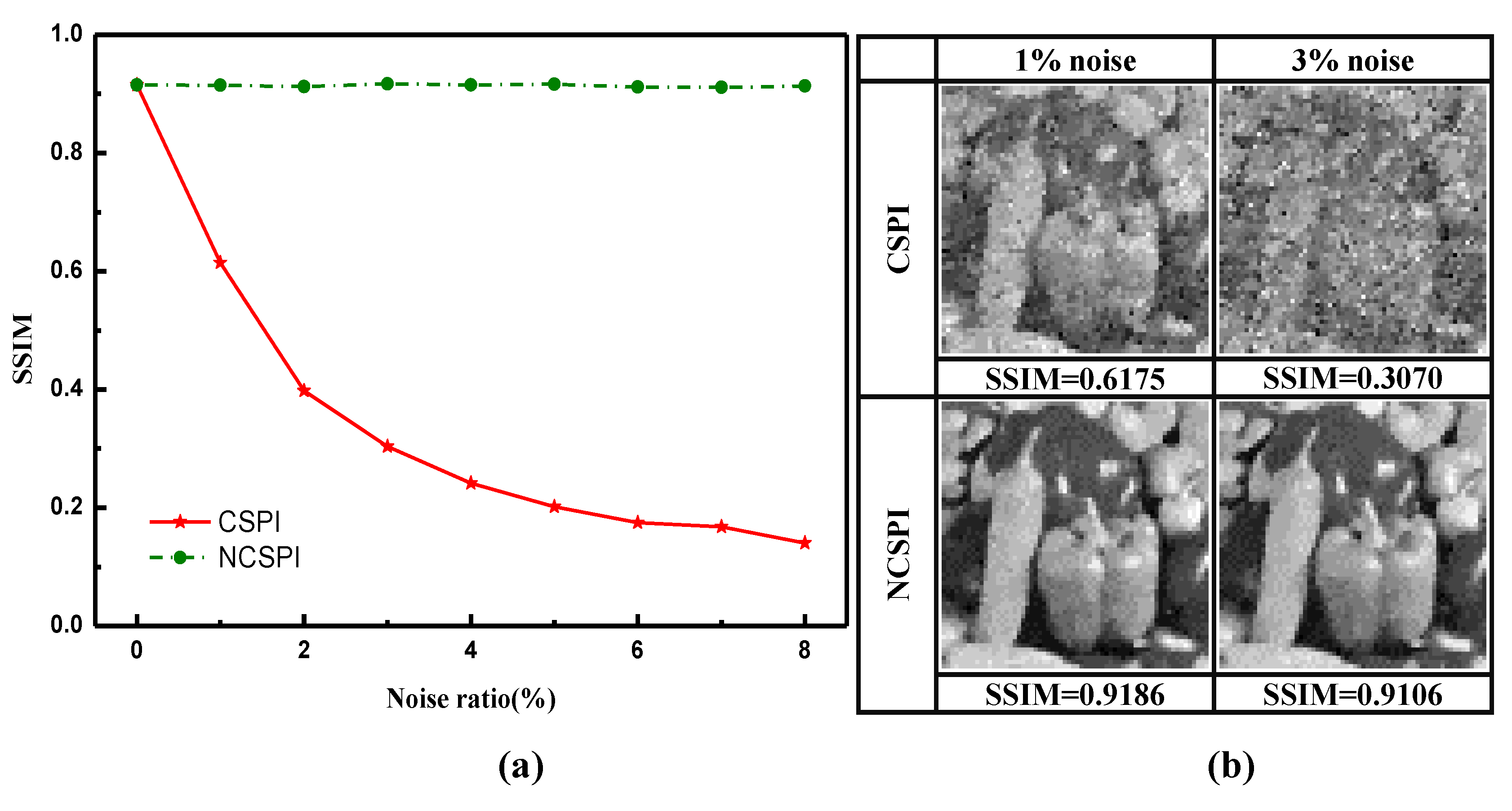
4.3. Experimental Verifications and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Candès, E.J. Compressive sampling. In Proceedings of the International Congress of Mathematicians, Madrid, Spain, 22–30 August 2006; Volume 3, pp. 1433–1452. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Rauhut, H.; Schnass, K.; Vandergheynst, P. Compressed Sensing and Redundant Dictionaries; IEEE Press: Piscataway Township, NJ, USA, 2008; pp. 2210–2219. [Google Scholar]
- Chan, W.L.; Charan, K.; Takhar, D.; Kelly, K.F.; Baraniuk, R.G.; Mittleman, D.M. A single-pixel terahertz imaging system based on compressed sensing. Appl. Phys. Lett. 2008, 93, 121105. [Google Scholar] [CrossRef]
- Gehm, M.; John, R.; Brady, D.; Willett, R.; Schulz, T. Single-shot compressive spectral imaging with a dual-disperser architecture. Opt. Express 2007, 15, 14013–14027. [Google Scholar] [CrossRef]
- Baraniuk, R.; Steeghs, P. Compressive Radar Imaging. In Proceedings of the 2007 IEEE Radar Conference, Boston, MA, USA, 17–20 April 2007; pp. 128–133. [Google Scholar]
- Sun, B.; Edgar, M.P.; Bowman, R.; Vittert, L.E.; Welsh, S.; Bowman, A.; Padgett, M. 3D computational imaging with single-pixel detectors. Science 2013, 340, 844–847. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Liang, J.; Li, C.; Wang, L.V. Single-shot compressed ultrafast photography at one hundred billion frames per second. Nature 2014, 516, 74. [Google Scholar] [CrossRef]
- Liu, Y.; Yuan, X.; Suo, J.; Brady, D.; Dai, Q. Rank Minimization for Snapshot Compressive Imaging. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 1–18. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhou, L.; Chen, W. Fourier spectrum retrieval in single-pixel imaging. IEEE Photonics J. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhou, L.; Chen, W. Single-Pixel Imaging Authentication Using Sparse Hadamard Spectrum Coefficients. IEEE Photonics Technol. Lett. 2019, 31, 1975–1978. [Google Scholar] [CrossRef]
- Chartrand, R.; Yin, W. Iteratively reweighted algorithms for compressive sensing. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 3869–3872. [Google Scholar]
- Shapiro, J.H. Computational ghost imaging. Phys. Rev. A 2008, 78, 061802. [Google Scholar] [CrossRef]
- Sun, M.J.; Edgar, M.P.; Phillips, D.B.; Gibson, G.M.; Padgett, M.J. Improving the signal-to-noise ratio of single-pixel imaging using digital microscanning. Opt. Express 2016, 24, 10476–10485. [Google Scholar] [CrossRef]
- Jauregui-Sánchez, Y.; Clemente, P.; Latorre-Carmona, P.; Tajahuerce, E.; Lancis, J. Signal-to-noise ratio of single-pixel cameras based on photodiodes. Appl. Opt. 2018, 57, B67–B73. [Google Scholar] [CrossRef] [PubMed]
- Tuzlukov, V. Signal Processing Noise; CRC Press: Boca Raton, FL, USA, 2002; Volume 8. [Google Scholar]
- Sun, B.; Welsh, S.S.; Edgar, M.P.; Shapiro, J.H.; Padgett, M.J. Normalized ghost imaging. Opt. Express 2012, 20, 16892–16901. [Google Scholar] [CrossRef]
- Garg, R.; Khandekar, R. Gradient descent with sparsification: An iterative algorithm for sparse recovery with restricted isometry property. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; ACM: New York, NY, USA, 2009; pp. 337–344. [Google Scholar]
- Li, C. An Efficient Algorithm for Total Variation Regularization with Applications to the Single Pixel Camera and Compressive Sensing. Ph.D. Thesis, Rice University, Houston, TX, USA, 2010. [Google Scholar]
- Emmanuel Candés and Justin Romberg, Caltech. L1-Magic. 2018. Available online: https://statweb.stanford.edu/~candes/software/l1magic/ (accessed on 15 Auguest 2020).
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Candes, E.J. The restricted isometry property and its implications for compressed sensing. C. R. Math. 2008, 346, 589–592. [Google Scholar] [CrossRef]
- Figueiredo, M.A.; Nowak, R.D.; Wright, S.J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G. Online dictionary learning for sparse coding. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; ACM: New York, NY, USA, 2009; pp. 689–696. [Google Scholar]
- Zhang, A.X.; He, Y.H.; Wu, L.A.; Chen, L.M.; Wang, B.B. Tabletop x-ray ghost imaging with ultra-low radiation. Optica 2018, 5, 374–377. [Google Scholar] [CrossRef]
- Ota, S.; Horisaki, R.; Kawamura, Y.; Ugawa, M.; Sato, I.; Hashimoto, K.; Kamesawa, R.; Setoyama, K.; Yamaguchi, S.; Fujiu, K.; et al. Ghost cytometry. Science 2018, 360, 1246–1251. [Google Scholar] [CrossRef]
- Sun, B.; Edgar, M.; Bowman, R.; Vittert, L.; Welsh, S.; Bowman, A.; Padgett, M. Differential computational ghost imaging. In Computational Optical Sensing and Imaging; Optical Society of America: Washington, DC, USA, 2013; p. CTu1C.4. [Google Scholar]
- Pfeffer, Y.; Zibulevsky, M. Sampling and Noise in Compressive Sensing; Technical Report; Technion: Haifa, Israel, 2010. [Google Scholar]
- Czajkowski, K.M.; Pastuszczak, A.; Kotyński, R. Real-time single-pixel video imaging with Fourier domain regularization. Opt. Express 2018, 26, 20009–20022. [Google Scholar] [CrossRef]
- Yin, P.; Yin, L.; Luo, B.; Wu, G.; Guo, H. Ghost imaging with Gram-Schmidt orthogonalization. In Computational Optical Sensing and Imaging; Optical Society of America: Washington, DC, USA, 2018; p. CTh4A–2. [Google Scholar]
- Czajkowski, K.M.; Pastuszczak, A.; Kotyński, R. Single-pixel imaging with sampling distributed over simplex vertices. Opt. Lett. 2019, 44, 1241–1244. [Google Scholar] [CrossRef]
- Dokmanić, I.; Kolundžija, M.; Vetterli, M. Beyond Moore-Penrose: Sparse pseudoinverse. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6526–6530. [Google Scholar]
- Pati, Y.C.; Rezaiifar, R.; Krishnaprasad, P.S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–3 November 1993; Volume 1, pp. 40–44. [Google Scholar] [CrossRef]
- Do, T.T.; Gan, L.; Nguyen, N.; Tran, T.D. Sparsity adaptive matching pursuit algorithm for practical compressed sensing. In Proceedings of the 2008 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 26–29 October 2008; pp. 581–587. [Google Scholar] [CrossRef]
- Gong, W. High-resolution pseudo-inverse ghost imaging. Photon. Res. 2015, 3, 234–237. [Google Scholar] [CrossRef]
- Miao, J.; Ishikawa, T.; Robinson, I.K.; Murnane, M.M. Beyond crystallography: Diffractive imaging using coherent x-ray light sources. Science 2015, 348, 530–535. [Google Scholar] [CrossRef] [PubMed]
- Hitomi, Y.; Gu, J.; Gupta, M.; Mitsunaga, T.; Nayar, S.K. Video from a single coded exposure photograph using a learned over-complete dictionary. In Proceedings of the 2011 IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 287–294. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Qi, N.; Jiang, S.; Wang, Y.; Li, X.; Sun, B. Noise Suppression in Compressive Single-Pixel Imaging. Sensors 2020, 20, 5341. https://doi.org/10.3390/s20185341
Li X, Qi N, Jiang S, Wang Y, Li X, Sun B. Noise Suppression in Compressive Single-Pixel Imaging. Sensors. 2020; 20(18):5341. https://doi.org/10.3390/s20185341
Chicago/Turabian StyleLi, Xianye, Nan Qi, Shan Jiang, Yurong Wang, Xun Li, and Baoqing Sun. 2020. "Noise Suppression in Compressive Single-Pixel Imaging" Sensors 20, no. 18: 5341. https://doi.org/10.3390/s20185341
APA StyleLi, X., Qi, N., Jiang, S., Wang, Y., Li, X., & Sun, B. (2020). Noise Suppression in Compressive Single-Pixel Imaging. Sensors, 20(18), 5341. https://doi.org/10.3390/s20185341





