Evaluation of Bonding Quality with Advanced Nondestructive Testing (NDT) and Data Fusion †
Abstract
1. Introduction
2. Materials and Methods
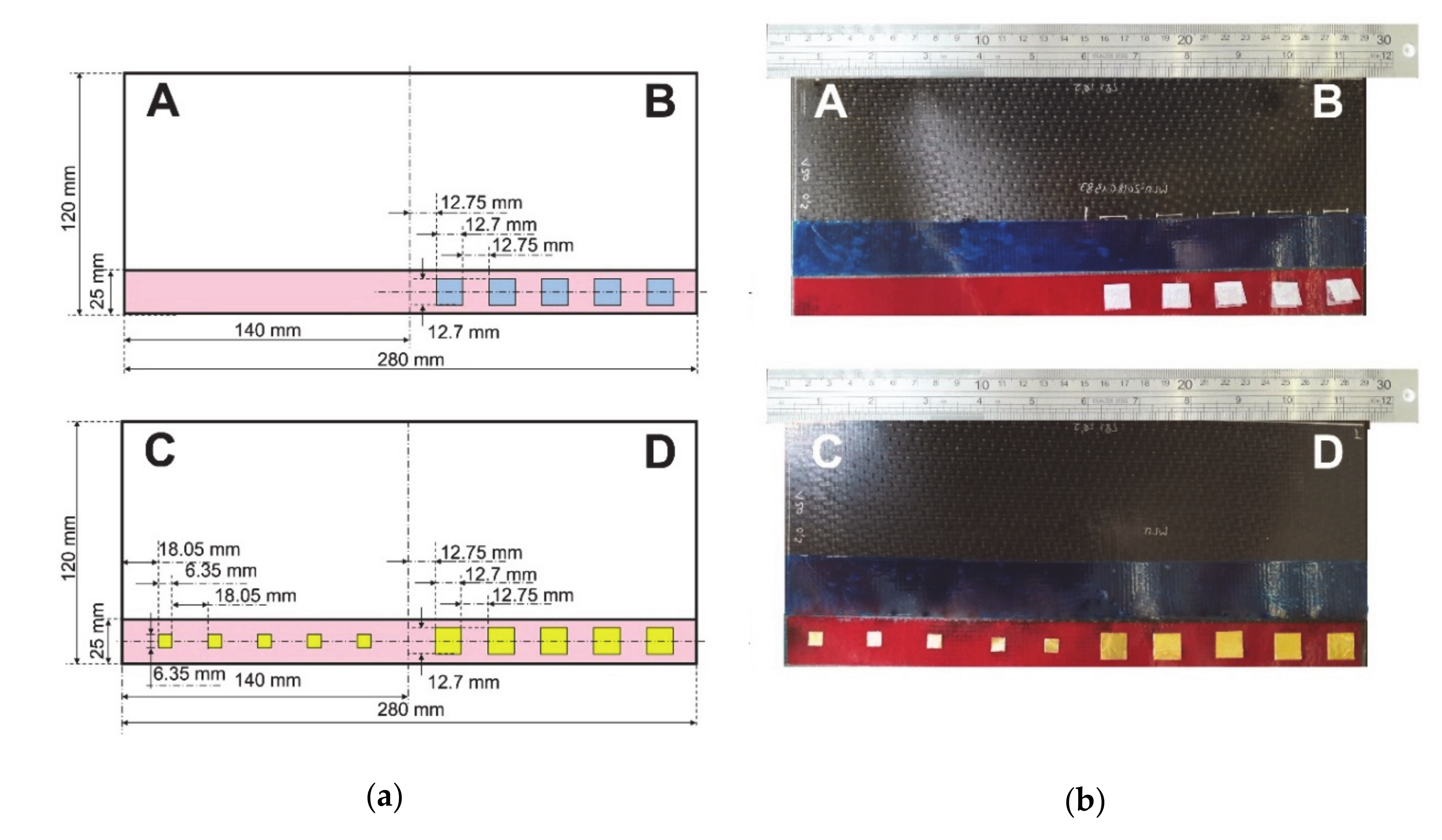
2.1. Sample Description
2.2. Nondestructive Testing
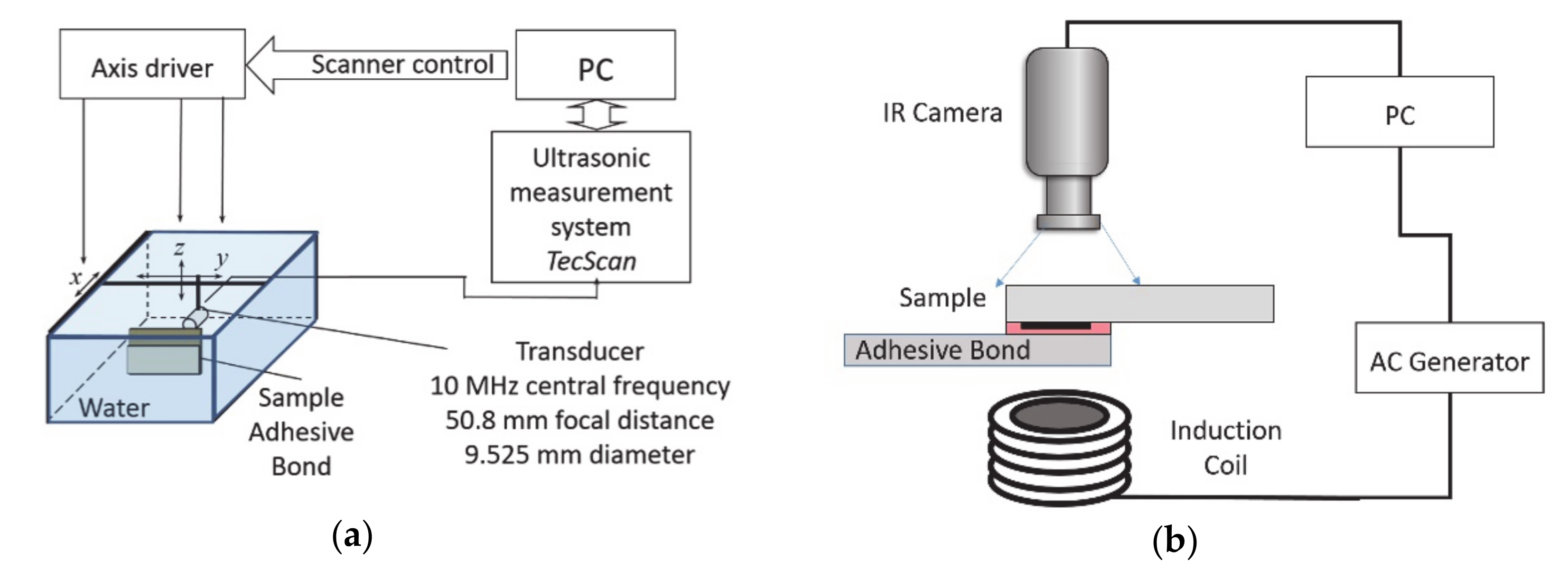
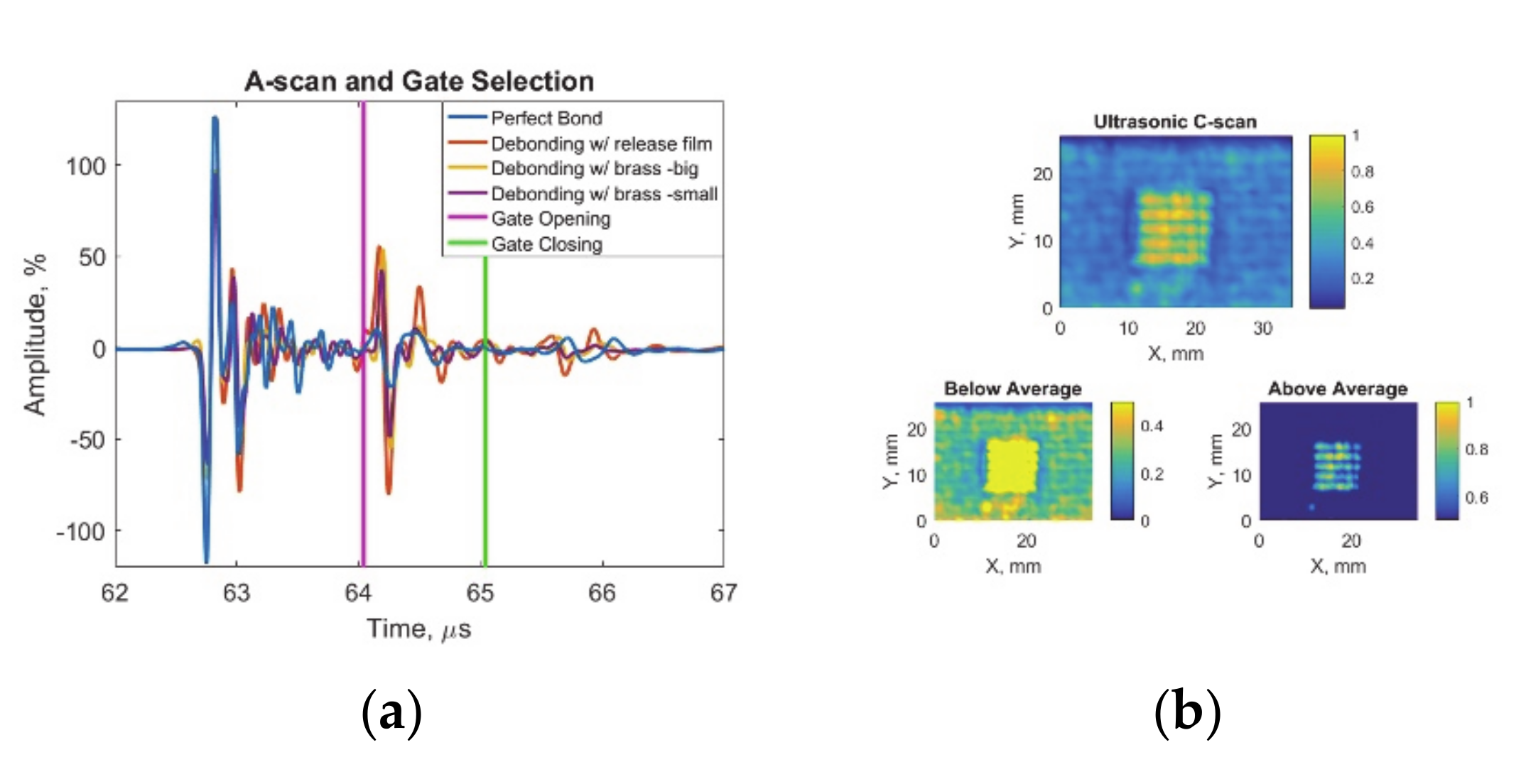
2.2.1. Ultrasonic Inspection
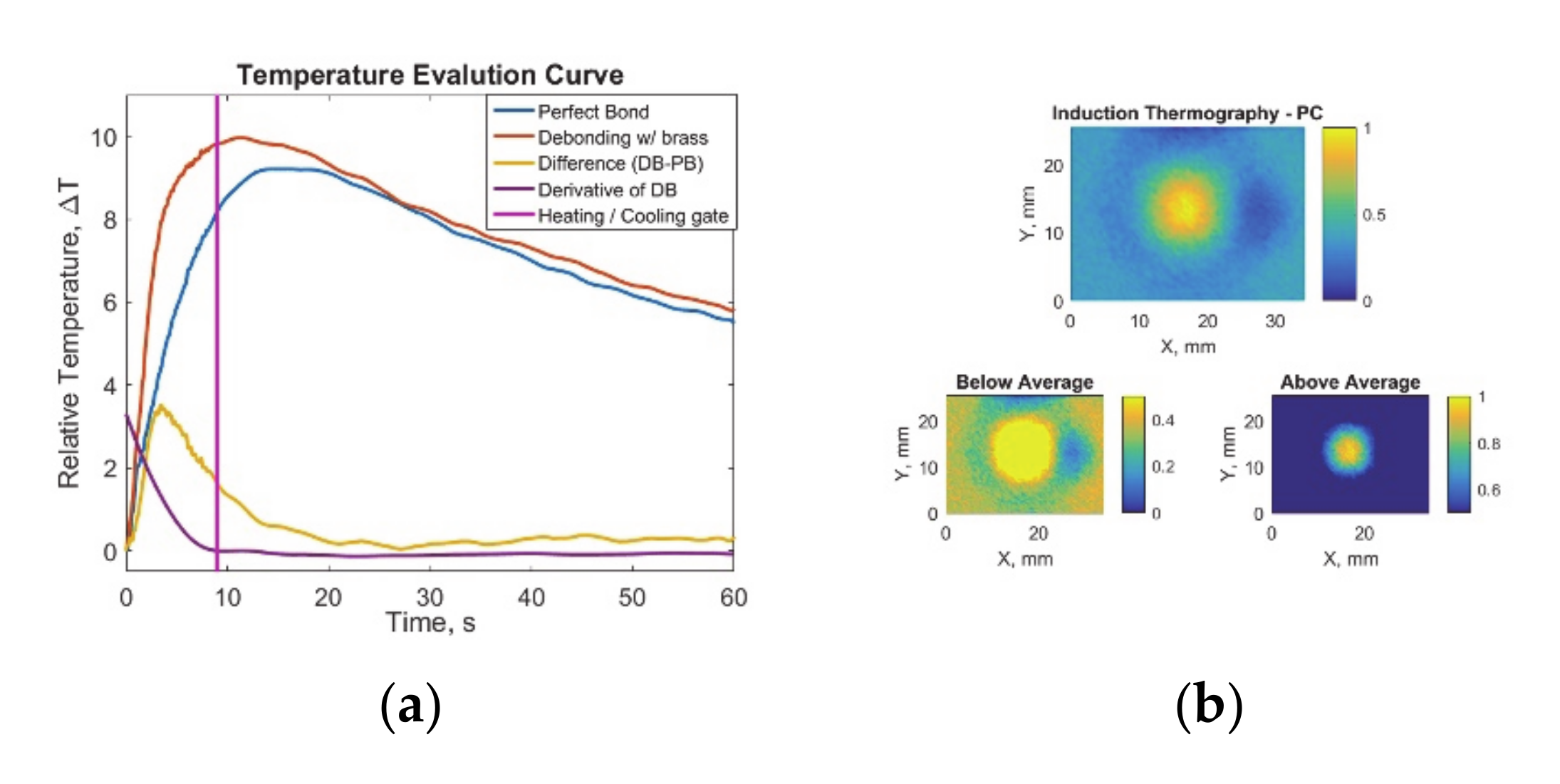
2.2.2. Induction Thermography
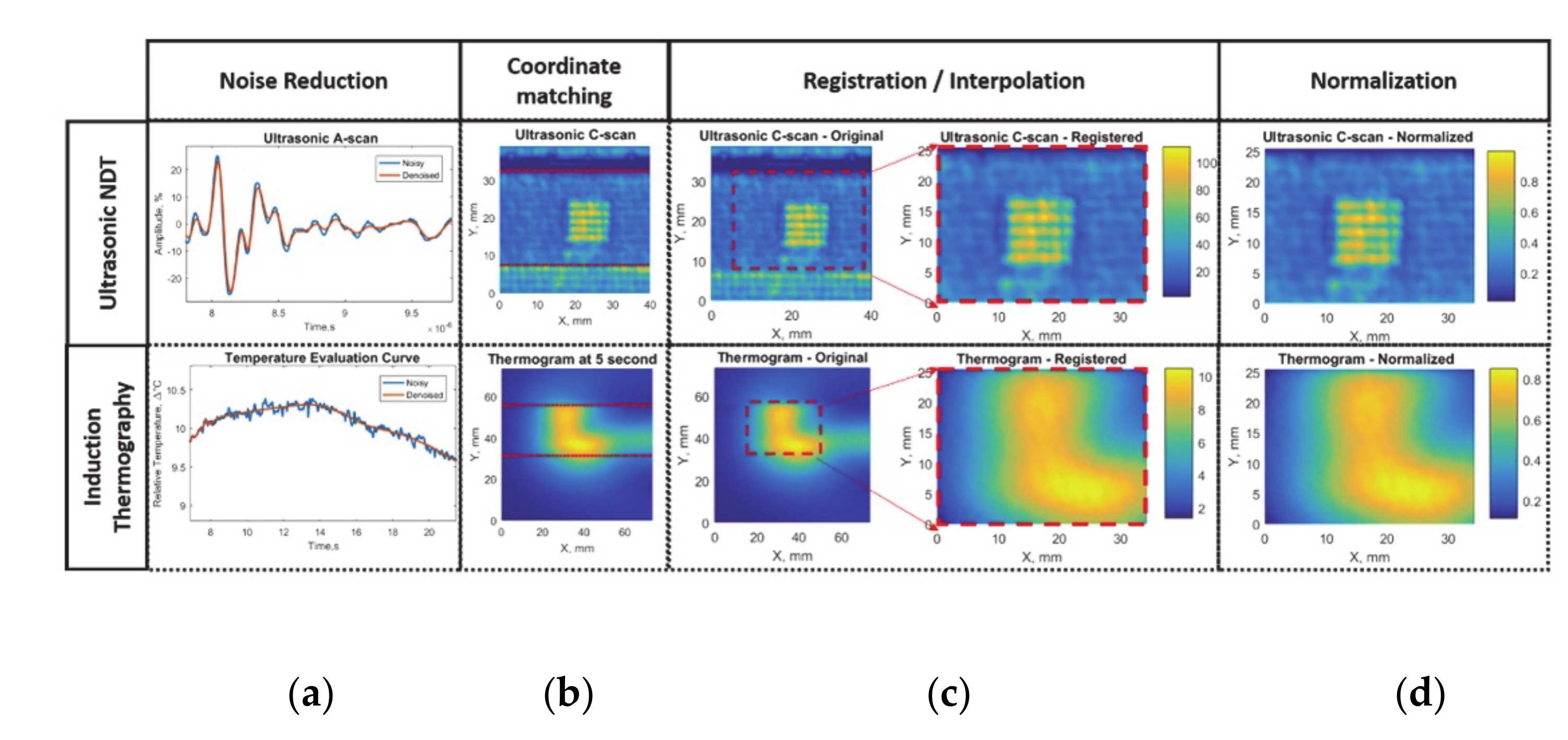
2.3. Feature-Based Data Fusion
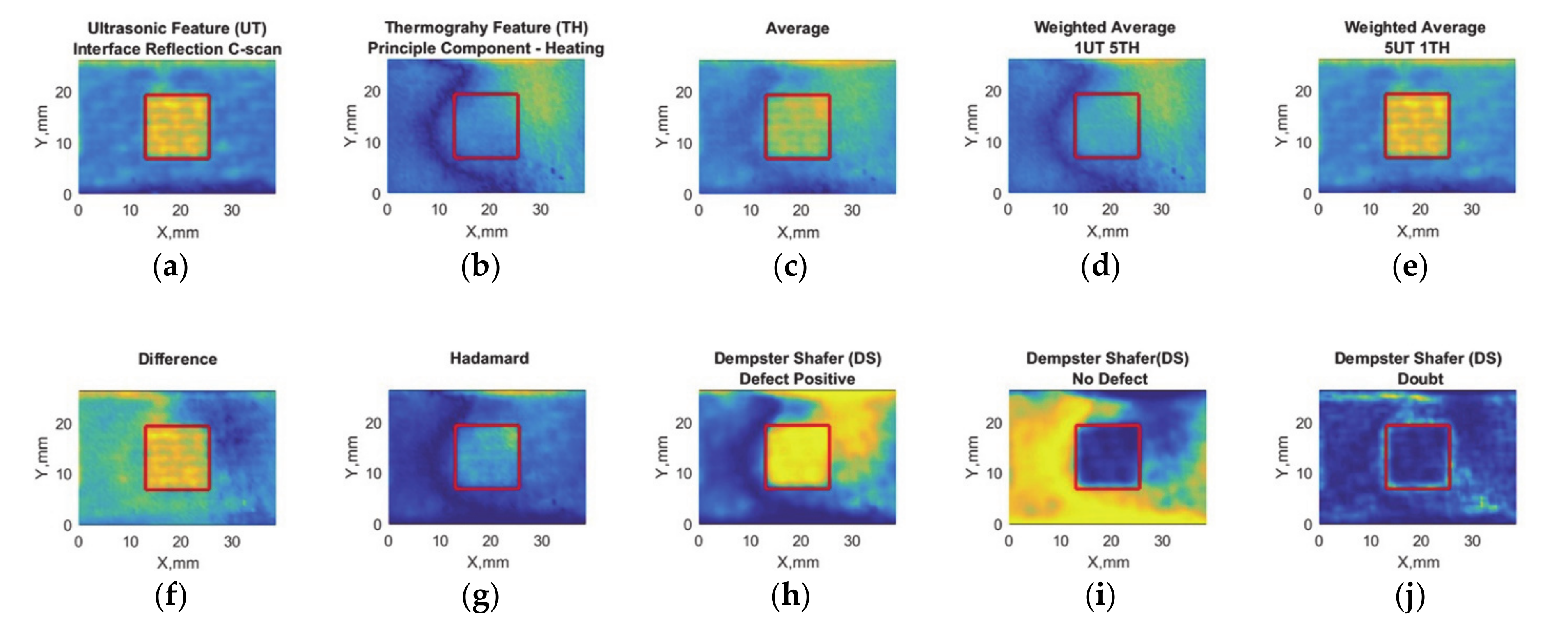
2.4. Data Fusion Algorithms
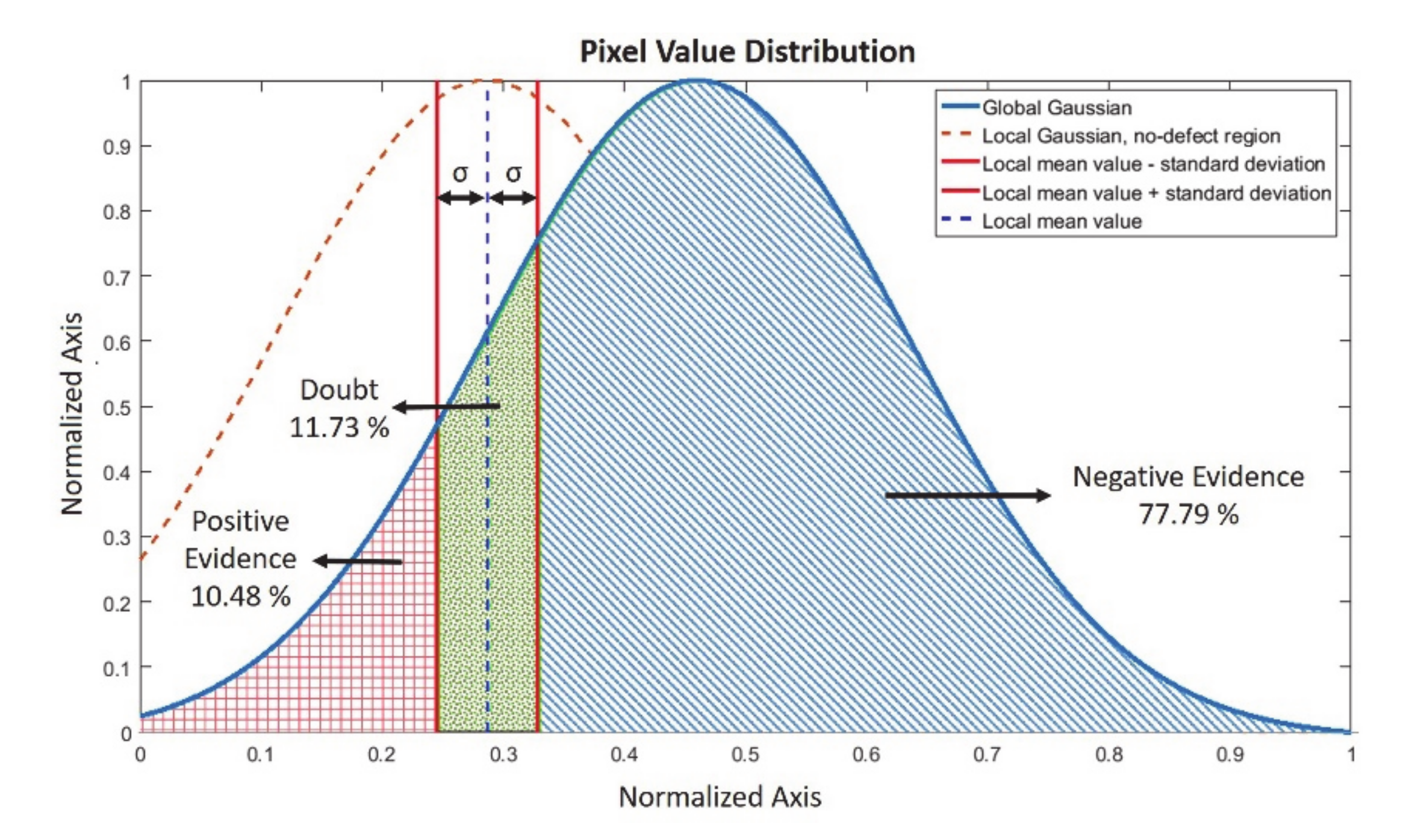
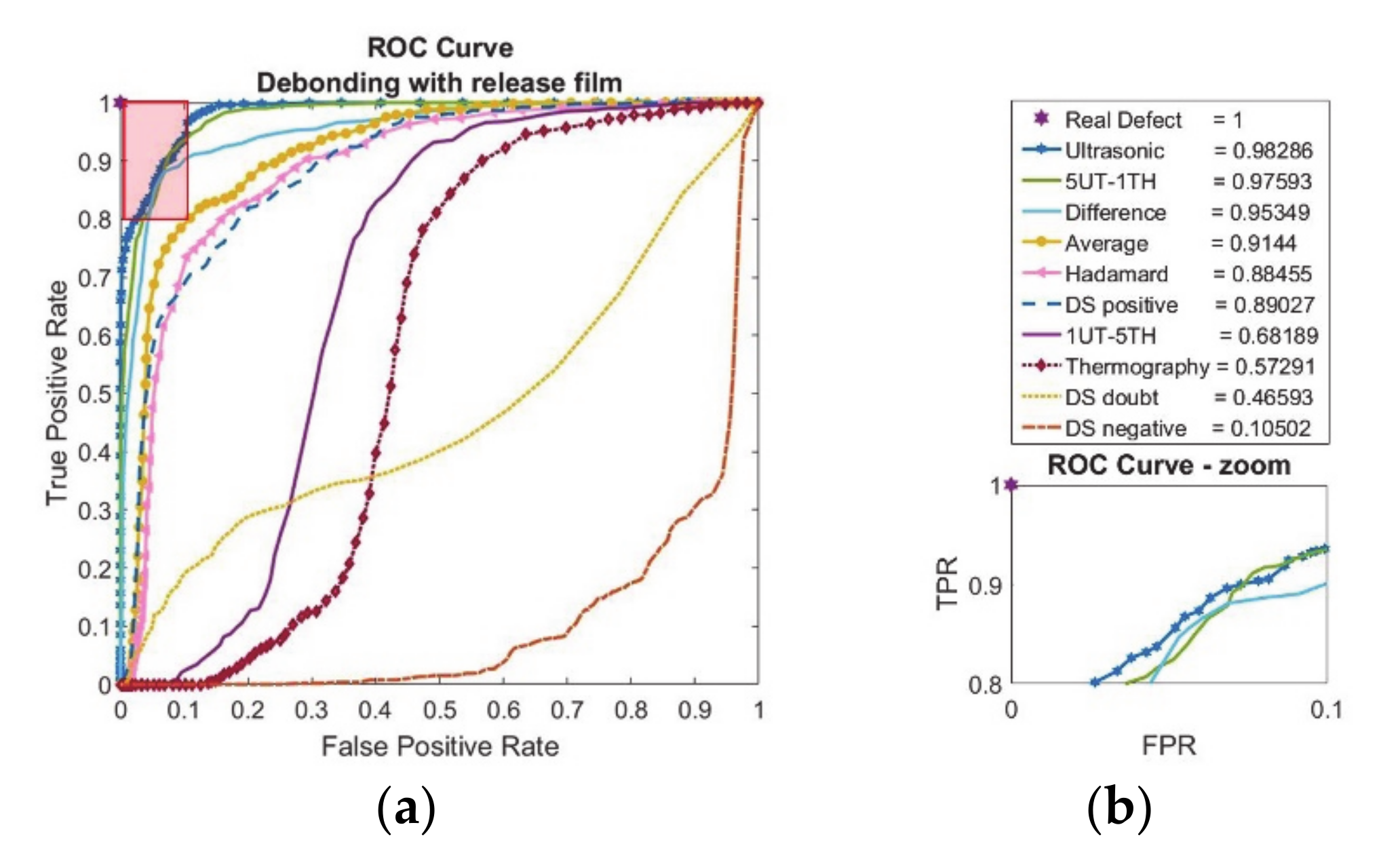
2.5. Evaluation of Different Techniques
3. Results
3.1. Case 1: Debonding with Release Film Inclusions (12.7 mm Edge Size)
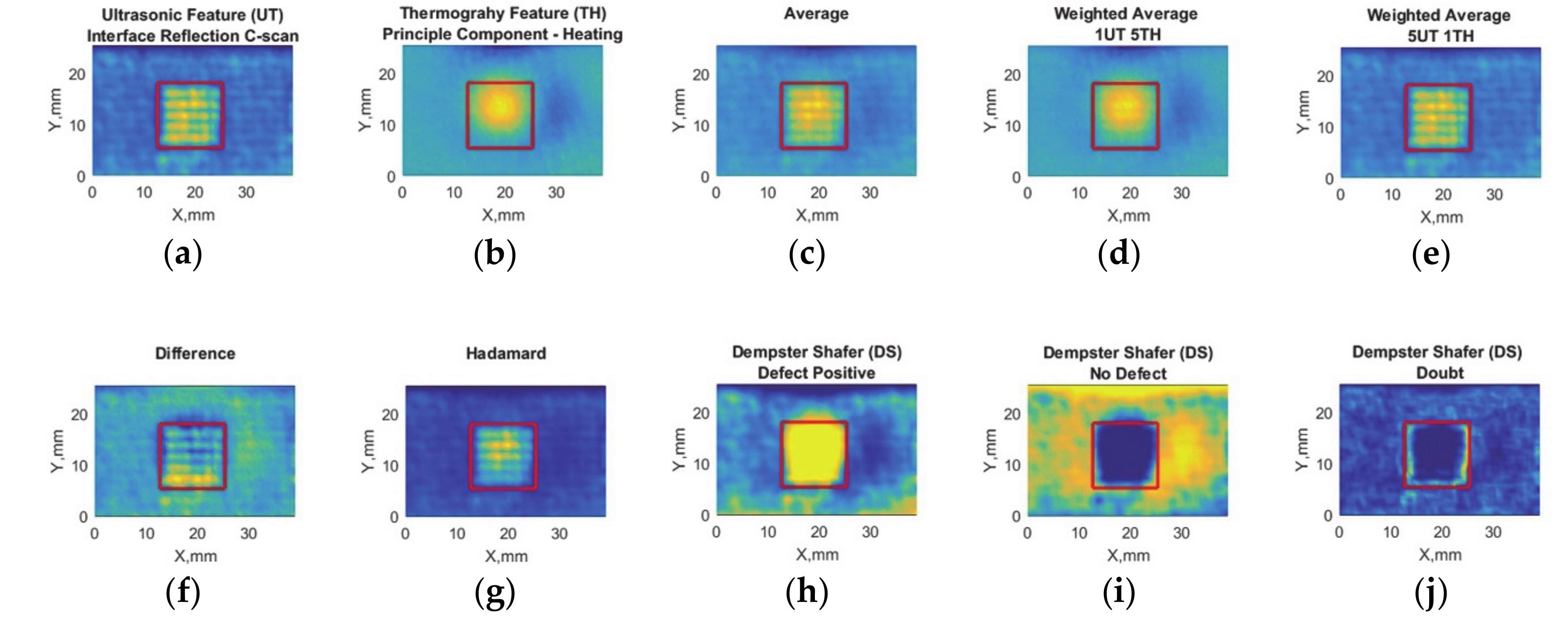
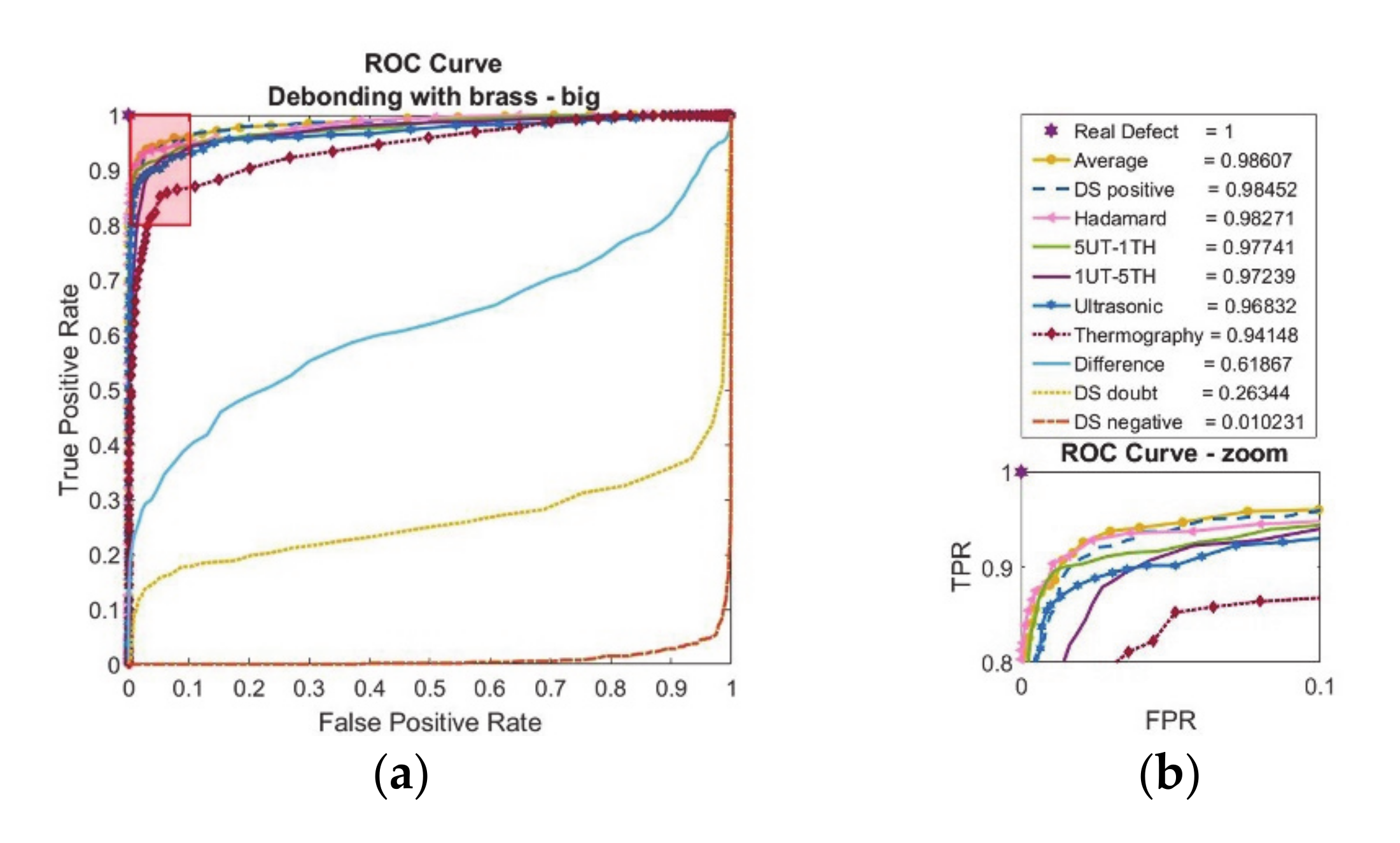
3.2. Case 2: Debonding with Brass Inclusion—Large (12.7 mm Edge Size)
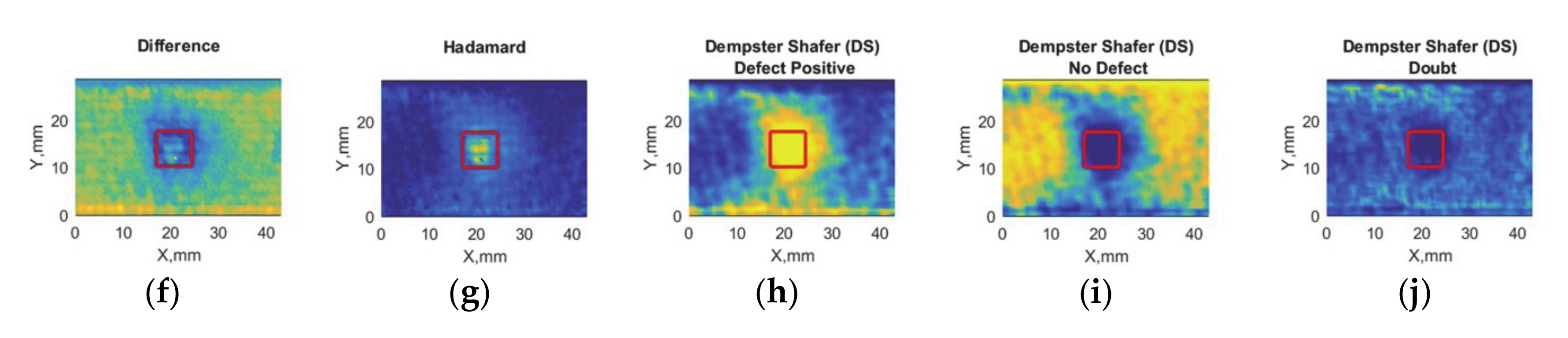
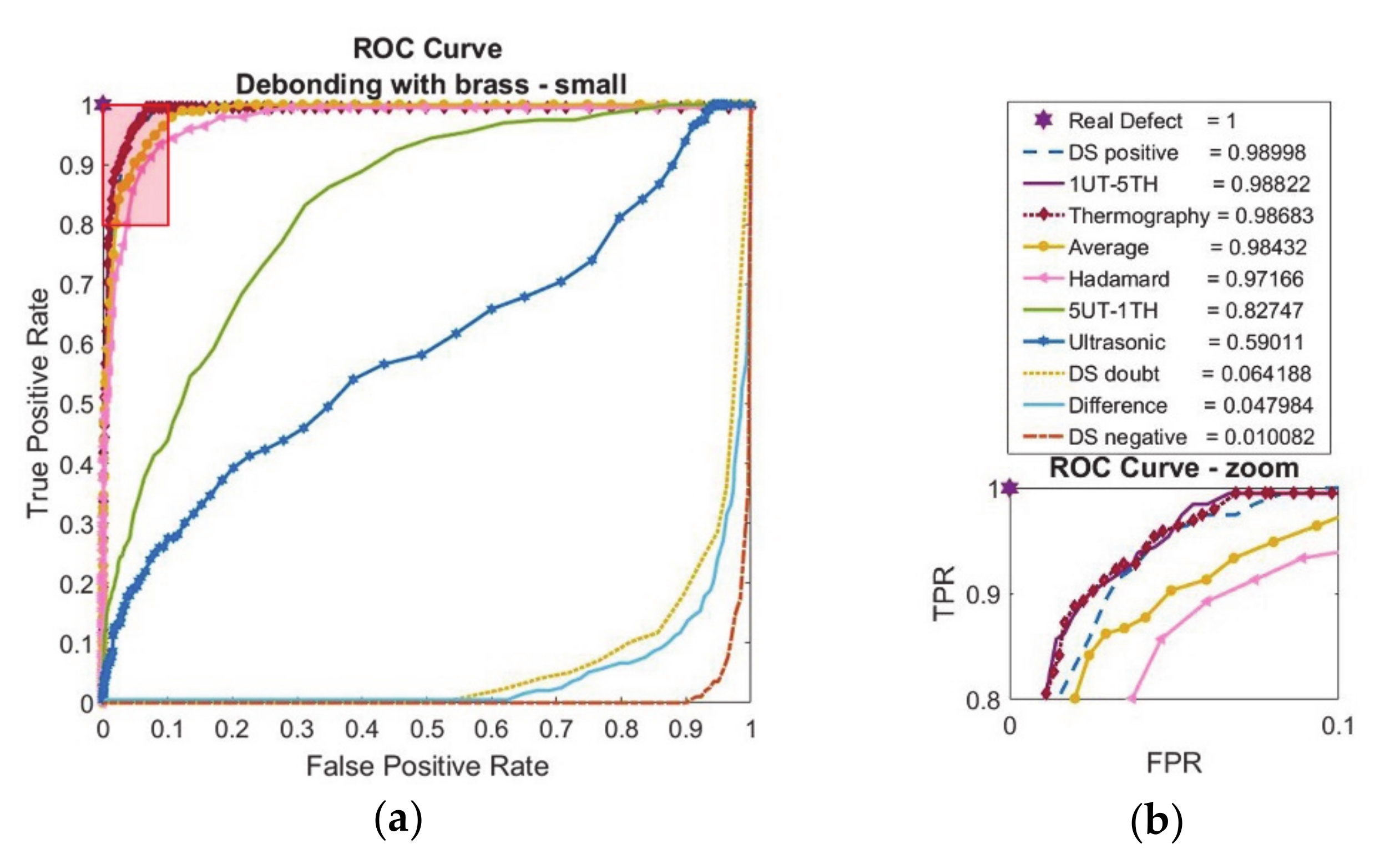
3.3. Case 3: Debonding with Brass Inclusion—Small (6.35 mm Edge Size)
4. Discussion
5. Conclusions
- Ultrasonic immersion pulse-echo NDT technique is an advantageous method for debonding detection.
- Induction thermography NDT performs well with electrically conductive inclusion detection; however, it is not sensitive to nonconductive inclusions.
- While ultrasonic NDT performs better in release film inclusion, obvious fact that brass inclusion (or any inclusion with high electrical conductivity) is detected better with induction thermography.
- Data fusion performs well only if the sensors are not in contradiction.
- While the information theory-based fusion algorithm, the Dempster-Shafer rule of combination and Hadamard shows high performance, basic data fusion techniques such as averaging should not be disregarded.
- NDT of adhesive bonding is challenging, but as long as the sources do not contradict, data fusion increases the sensitivity and specificity of the inspection.
Author Contributions
Funding
Conflicts of Interest
References
- Daryabor, P.; Safizadeh, M.S. Image fusion of ultrasonic and thermographic inspection of carbon/epoxy patches bonded to an aluminum plate. NDT E Int. 2017, 90, 1–10. [Google Scholar] [CrossRef]
- Yi, Q.; Tian, G.Y.; Yilmaz, B.; Malekmohammadi, H.; Laureti, S.; Ricci, M.; Jasiuniene, E. Evaluation of debonding in CFRP-epoxy adhesive single-lap joints using eddy current pulse-compression thermography. Compos. Part B Eng. 2019, 178, 107461. [Google Scholar] [CrossRef]
- Yilmaz, B.; Ba, A.; Jasiuniene, E.; Bui, H.K.; Berthiau, G. Comparison of different nondestructive testing techniques for bonding quality evaluation. In Proceedings of the 2019 IEEE 5th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Torino, Italy, 19–21 June 2019; pp. 92–97. [Google Scholar] [CrossRef]
- Galy, J.; Moysan, J.; El Mahi, A.; Ylla, N.; Massacret, N. Controlled reduced-strength epoxy-aluminium joints validated by ultrasonic and mechanical measurements. Int. J. Adhes. Adhes. 2017, 72, 139–146. [Google Scholar] [CrossRef]
- Scarselli, G.; Nicassio, F. Analysis of debonding in single lap joints based on employment of ultrasounds. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, Portland, OR, USA, 25–29 March 2017; p. 1017020. [Google Scholar] [CrossRef]
- Tamborrino, R.; Palumbo, D.; Galietti, U.; Aversa, P.; Chiozzi, S.; Luprano, V.A.M. Assessment of the effect of defects on mechanical properties of adhesive bonded joints by using non destructive methods. Compos. Part B Eng. 2016, 91, 337–345. [Google Scholar] [CrossRef]
- Katsiropoulos, C.V.; Pantelakis, S.G. Assessment of the imperfect bonding of adhesively bonded U-joints using ultrasonic inspection. Plast. Rubber Compos. 2014, 43, 316–321. [Google Scholar] [CrossRef]
- Bhanushali, R.; Ayre, D.; Nezhad, H.Y. Tensile Response of Adhesively Bonded Composite-to-composite Single-lap Joints in the Presence of Bond Deficiency. Procedia CIRP 2017, 59, 139–143. [Google Scholar] [CrossRef]
- Jasiūnienė, E.; Mažeika, L.; Samaitis, V.; Cicėnas, V.; Mattsson, D. Ultrasonic nondestructive testing of complex titanium/carbon fibre composite joints. Ultrasonics 2019, 95, 13–21. [Google Scholar] [CrossRef]
- Jiao, D.; Rose, J.L. An ultrasonic interface layer model for bond evaluation. J. Adhes. Sci. Technol. 1991, 5, 631–646. [Google Scholar] [CrossRef]
- Brotherhood, C.J.; Drinkwater, B.W.; Guild, F.J. The effect of compressive loading on the ultrasonic detectability of kissing bonds in adhesive joints. J. Nondestruct. Eval. 2002, 21, 95–104. [Google Scholar] [CrossRef]
- Ding, J.; Wu, B.; He, C.-F. Longitudinal wave propagation in adhesive structure under different forms of interfaces. In Proceedings of the 2015 Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA), Jinan, China, 30 October–2 November 2015. [Google Scholar]
- Kazys, R.; Demcenko, A.; Zukauskas, E.; Mazeika, L. Air-coupled ultrasonic investigation of multi-layered composite materials. Ultrasonics 2006, 44, 819–822. [Google Scholar] [CrossRef] [PubMed]
- Gaal, M.; Dohse, E.; Bartusch, J.; Köppe, E.; Kreutzbruck, M.; Hillger, W.; Amos, J. Ultrasonic Testing of Adhesively Bonded Joints Using Air-Coupled Cellular Polypropylene Transducers 1. Cellular polypropylene transducers for air-coupled ultrasonic testing. In Proceedings of the ECNDT 2014 - 11th European Conference on Non-Destructive Testing, Prague, Czech Republic, 6–10 October 2014. [Google Scholar]
- Marks, R.; Clarke, A.; Featherston, C.; Paget, C.; Pullin, R. Lamb Wave Interaction with Adhesively Bonded Stiffeners and Disbonds Using 3D Vibrometry. Appl. Sci. 2016, 6, 12. [Google Scholar] [CrossRef]
- Sherafat, M.H.; Guitel, R.; Quaegebeur, N.; Lessard, L.; Hubert, P.; Masson, P. Guided wave scattering behavior in composite bonded assemblies. Compos. Struct. 2016, 136, 696–705. [Google Scholar] [CrossRef]
- Cho, H.; Hara, Y.; Matsuo, T. Evaluation of the thickness and bond quality of three-layered media using zero-group-velocity lamb waves. J. Phys. Conf. Ser. 2014, 520. [Google Scholar] [CrossRef]
- Leiderman, R.; Braga, A.M.B. Scattering of guided waves by defective adhesive bonds in multilayer anisotropic plates. Wave Motion 2017, 74, 93–104. [Google Scholar] [CrossRef]
- Nagy; Jeenjitkaew, C.; Stein, N.; Felger, J.; Becker, W.; Jeenjitkaew, C.; Luklinska, Z.; Guild, F.J.; Argust, G.; Hazimeh, R.; et al. Kissing bond detection in structural adhesive joints using nonlinear dynamic characteristics. Int. J. Adhes. Adhes. 2015, 70, 46–56. [Google Scholar] [CrossRef]
- Yan, D.; Drinkwater, B.W.; Neild, S.A. Measurement of the ultrasonic nonlinearity of kissing bonds in adhesive joints. NDT E Int. 2009, 42, 459–466. [Google Scholar] [CrossRef]
- Scarselli, G.; Ciampa, F.; Ginzburg, D.; Meo, M. Nondestructive testing techniques based on nonlinear methods for assessment of debonding in single lap joints. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 8–12 March 2015. [Google Scholar] [CrossRef]
- Solodov, I.; Kreutzbruck, M.; Ségur, D. Monitoring of bonding quality in CFRP composite laminates by measurements of local vibration nonlinearity. In Proceedings of the 12th International Workshop on Structural Health Monitoring: Enabling Intelligent Life-Cycle Health Management for Industry Internet of Things (IIOT), Stanford, CA, USA, 10–12 September 2019. [Google Scholar]
- Asif, M.; Khan, M.A.; Khan, S.Z.; Choudhry, R.S.; Khan, K.A. Identification of an effective nondestructive technique for bond defect determination in laminate composites—A technical review. J. Compos. Mater. 2018, 52, 3589–3599. [Google Scholar] [CrossRef]
- Gauthier, C.; Ech-Cherif El-Kettani, M.; Galy, J.; Predoi, M.; Leduc, D.; Izbicki, J.L. Lamb waves characterization of adhesion levels in aluminum/epoxy bi-layers with different cohesive and adhesive properties. Int. J. Adhes. Adhes. 2017, 74, 15–20. [Google Scholar] [CrossRef]
- Grosso, M.; Marinho, C.A.; Nesteruk, D.A.; Rebello, J.M.A.; Soares, S.D.; Vavilov, V.P. Evaluating quality of adhesive joints in glass fiber plastic piping by using active thermal NDT. In Proceedings of the SPIE Defense, Security, and Sensing, Baltimore, MD, USA, 29 April–3 May 2013; Volume 8705, pp. 1–11. [Google Scholar] [CrossRef]
- Hung, M.Y.Y. Review and comparison of shearography and pulsed thermography for adhesive bond evaluation. Opt. Eng. 2007, 46, 051007. [Google Scholar] [CrossRef]
- Genest, M.; Martinez, M.; Mrad, N.; Renaud, G.; Fahr, A. Pulsed thermography for nondestructive evaluation and damage growth monitoring of bonded repairs. Compos. Struct. 2009, 88, 112–120. [Google Scholar] [CrossRef]
- Shin, P.H.; Webb, S.C.; Peters, K.J. Pulsed phase thermography imaging of fatigue-loaded composite adhesively bonded joints. NDT E Int. 2016, 79, 7–16. [Google Scholar] [CrossRef]
- Bui, H.K.; Wasselynck, G.; Trichet, D.; Ramdane, B.; Berthiau, G.; Fouladgar, J. 3-D modeling of thermo inductive non destructive testing method applied to multilayer composite. IEEE Trans. Magn. 2013, 49, 1949–1952. [Google Scholar] [CrossRef]
- Cheng, L.; Gao, B.; Tian, G.Y.; Woo, W.L.; Berthiau, G. Impact damage detection and identification using eddy current pulsed thermography through integration of PCA and ICA. IEEE Sens. J. 2014, 14, 1655–1663. [Google Scholar] [CrossRef]
- Ehrhart, B.; Valeske, B.; Bockenheimer, C. Nondestructive evaluation (NDE) of aerospace composites. In Nondestructive Evaluation (NDE) of Polymer Matrix Composites: Techniques and Applications; Woodhead Publishing: Cambridge, UK, 2013. [Google Scholar] [CrossRef]
- Kiziltaş, G.; Papila, M.; Yilmaz, B.; Bilge, K. Challenges in Micro-CT Characterization of Composites. Micro-Computed Tomogr. Med. Eng. 2020, 225–246. [Google Scholar] [CrossRef]
- Bossi, R.; Lahrman, D.; Sokol, D.; Walters, C. Laser Bond Inspection for adhesive bond strength. In Proceedings of the International SAMPE Technical Conference, Paris, France, 28–29 March 2011. [Google Scholar]
- Ecault, R.; Boustie, M.; Touchard, F.; Pons, F.; Berthe, L.; Chocinski-Arnault, L.; Ehrhart, B.; Bockenheimer, C. A study of composite material damage induced by laser shock waves. Compos. Part A Appl. Sci. Manuf. 2013, 53, 54–64. [Google Scholar] [CrossRef]
- Marty, P.; Desai, N.; Andersson, J. NDT of kissing bond in aeronautical structures. In Proceedings of the 16th World Conference on NDT, Montreal, QC, Canada, 30 August–3 September 2004. [Google Scholar]
- Gros, X.E.; Strachan, P.; Lowden, D.W. Theory and implementation of NDT data fusion. Res. Nondestruct. Eval. 1995, 6, 227–236. [Google Scholar] [CrossRef]
- Jasiūnienė, E.; Žukauskas, E.; Dragatogiannis, D.A.; Koumoulos, E.P.; Charitidis, C.A. Investigation of dissimilar metal joints with nanoparticle fillers. NDT E Int. 2017, 92, 122–129. [Google Scholar] [CrossRef]
- Dong, J.; Zhuang, D.; Huang, Y.; Fu, J. Advances in multi-sensor data fusion: Algorithms and applications. Sensors 2009, 9, 7771–7784. [Google Scholar] [CrossRef]
- Liu, Z.; Forsyth, D.S.; Komorowski, J.P.; Hanasaki, K.; Kirubarajan, T. Survey: State of the art in NDE data fusion techniques. IEEE Trans. Instrum. Meas. 2007, 56, 2435–2451. [Google Scholar] [CrossRef]
- Ploix, M.; Garnier, V.; Breysse, D.; Moysan, J. NDE data fusion to improve the evaluation of concrete structures. NDT E Int. 2011, 44, 442–448. [Google Scholar] [CrossRef]
- Völker, C.; Shokouhi, P. Clustering Based Multi Sensor Data Fusion for Honeycomb Detection in Concrete. J. Nondestruct. Eval. 2015, 34, 1–10. [Google Scholar] [CrossRef]
- Cotič, P.; Jagličić, Z.; Niederleithinger, E.; Stoppel, M.; Bosiljkov, V. Image Fusion for Improved Detection of Near-Surface Defects in NDT-CE Using Unsupervised Clustering Methods. J. Nondestruct. Eval. 2014, 33, 384–397. [Google Scholar] [CrossRef]
- Völker, C.; Shokouhi, P. Multi sensor data fusion approach for automatic honeycomb detection in concrete. NDT E Int. 2015, 71, 54–60. [Google Scholar] [CrossRef]
- Gusenbauer, C.; Reiter, M.; Plank, B.; Salaberger, D.; Senck, S.; Kastner, J. Porosity Determination of Carbon and Glass Fibre Reinforced Polymers Using Phase-Contrast Imaging. J. Nondestruct. Eval. 2019, 38, 1–10. [Google Scholar] [CrossRef]
- Cuadra, J.; Vanniamparambil, P.A.; Hazeli, K.; Bartoli, I.; Kontsos, A. Damage quantification in polymer composites using a hybrid NDT approach. Compos. Sci. Technol. 2013, 83, 11–21. [Google Scholar] [CrossRef]
- Cao, Y.; Dong, Y.; Cao, Y.; Yang, J.; Yang, M.Y. Two-stream convolutional neural network for nondestructive subsurface defect detection via similarity comparison of lock-in thermography signals. NDT E Int. 2020, 112, 102246. [Google Scholar] [CrossRef]
- Horn, R.A.; Zhang, F. Basic Properties of the Schur Complement. In The Schur Complement and Its Applications; Springer-Verlag: Boston, MA, USA, 2005; pp. 17–46. [Google Scholar]
- Smith, A.F.M.; Shafer, G. A Mathematical Theory of Evidence. Biometrics 1976, 32, 703–704. [Google Scholar] [CrossRef]
- Dempster, A.P. Upper and Lower Probabilities Induced by a Multivalued Mapping. Ann. Math. Stat. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Brierley, N.; Tippetts, T.; Cawley, P. Data fusion for automated nondestructive inspection. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 470. [Google Scholar] [CrossRef]

| Fusion Algorithm | Description | Mathematical Formula | |
|---|---|---|---|
| average | on pixel level, the average from two sources: UT1 and TH2 | (1) | |
| difference | on pixel level, differentiating one matrix (TH) from the other (UT) | (2) | |
| Weighted average | on pixel level, weighted average when one matrix has four times higher weight than the other | (3) | |
| Hadamard product | pixel-wise multiplication of same-size matrices | (4) | |
| Dempster–Shafer rule of combination | evidence theory based on mass, belief, and plausibility functions | (5) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yilmaz, B.; Ba, A.; Jasiuniene, E.; Bui, H.-K.; Berthiau, G. Evaluation of Bonding Quality with Advanced Nondestructive Testing (NDT) and Data Fusion. Sensors 2020, 20, 5127. https://doi.org/10.3390/s20185127
Yilmaz B, Ba A, Jasiuniene E, Bui H-K, Berthiau G. Evaluation of Bonding Quality with Advanced Nondestructive Testing (NDT) and Data Fusion. Sensors. 2020; 20(18):5127. https://doi.org/10.3390/s20185127
Chicago/Turabian StyleYilmaz, Bengisu, Abdoulaye Ba, Elena Jasiuniene, Huu-Kien Bui, and Gérard Berthiau. 2020. "Evaluation of Bonding Quality with Advanced Nondestructive Testing (NDT) and Data Fusion" Sensors 20, no. 18: 5127. https://doi.org/10.3390/s20185127
APA StyleYilmaz, B., Ba, A., Jasiuniene, E., Bui, H.-K., & Berthiau, G. (2020). Evaluation of Bonding Quality with Advanced Nondestructive Testing (NDT) and Data Fusion. Sensors, 20(18), 5127. https://doi.org/10.3390/s20185127





