Spectral Efficiency Augmentation in Uplink Massive MIMO Systems by Increasing Transmit Power and Uniform Linear Array Gain
Abstract
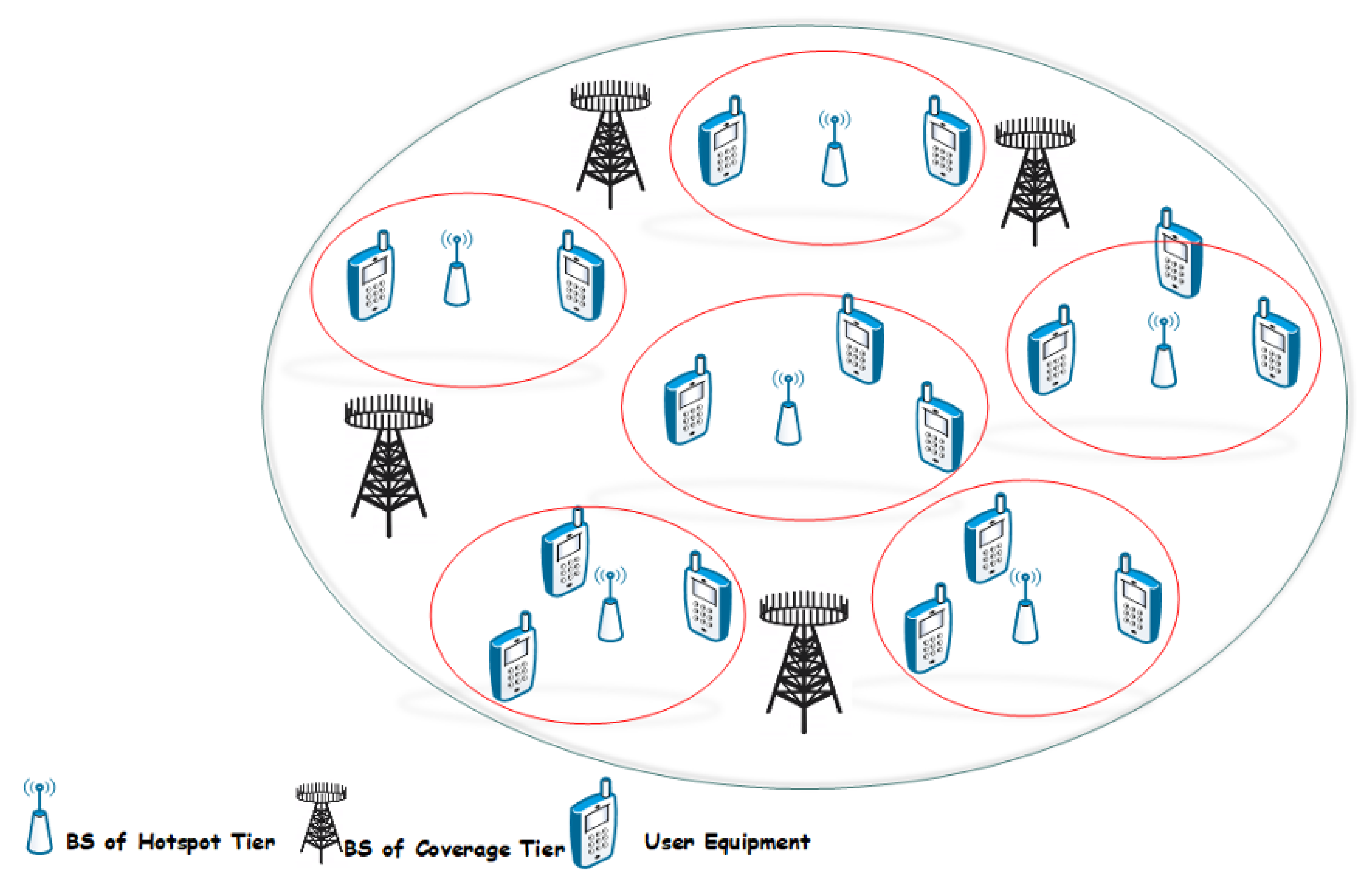
1. Introduction
Preliminaries
2. System Model and Proposed Methods to Enhance Se
2.1. Increase the Transmit Power
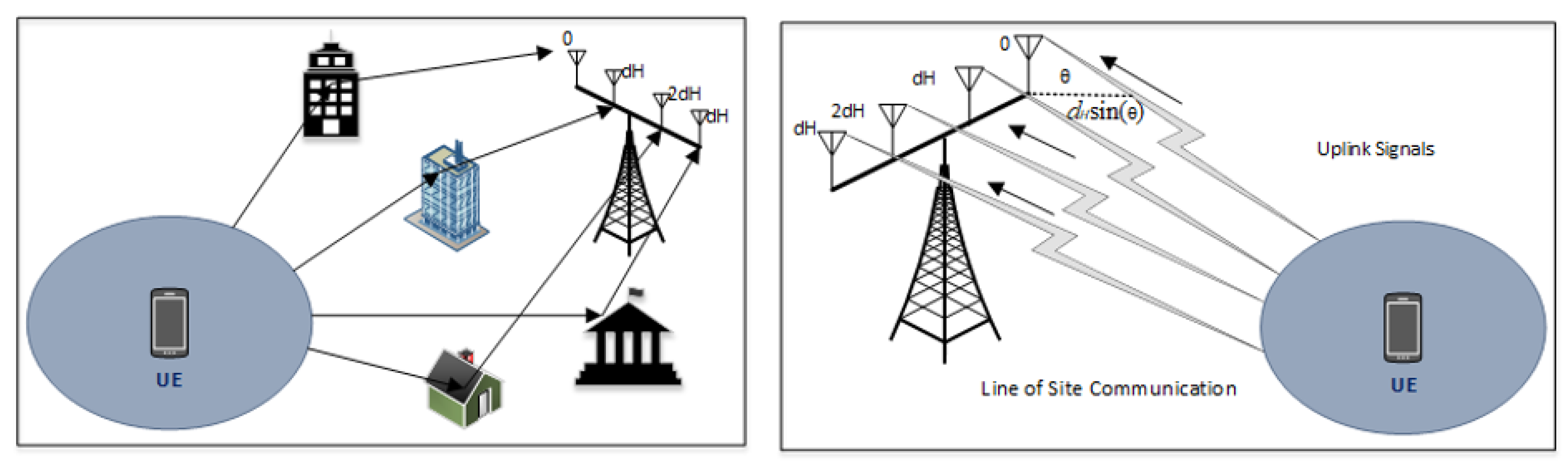
2.2. Enhanced Se by Enhancing Array Gain
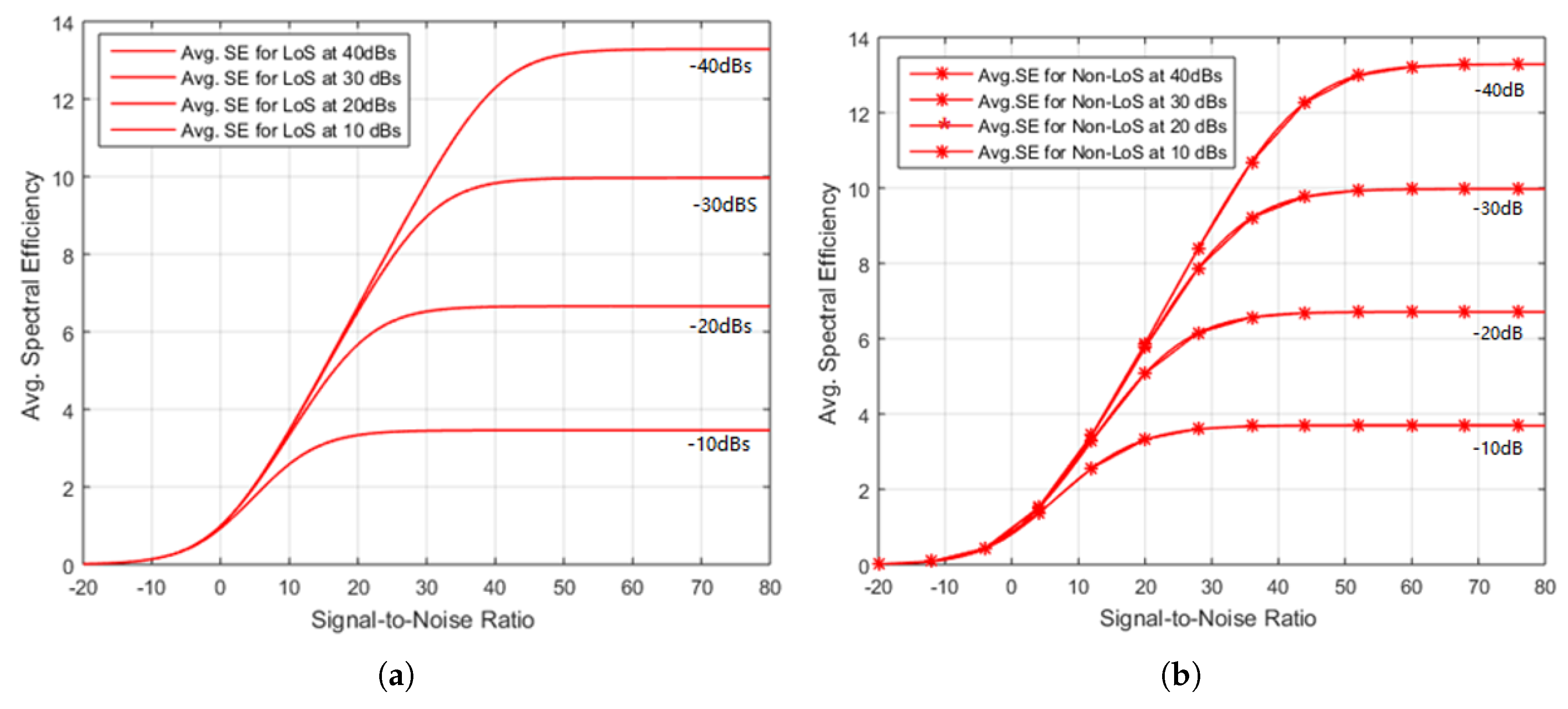
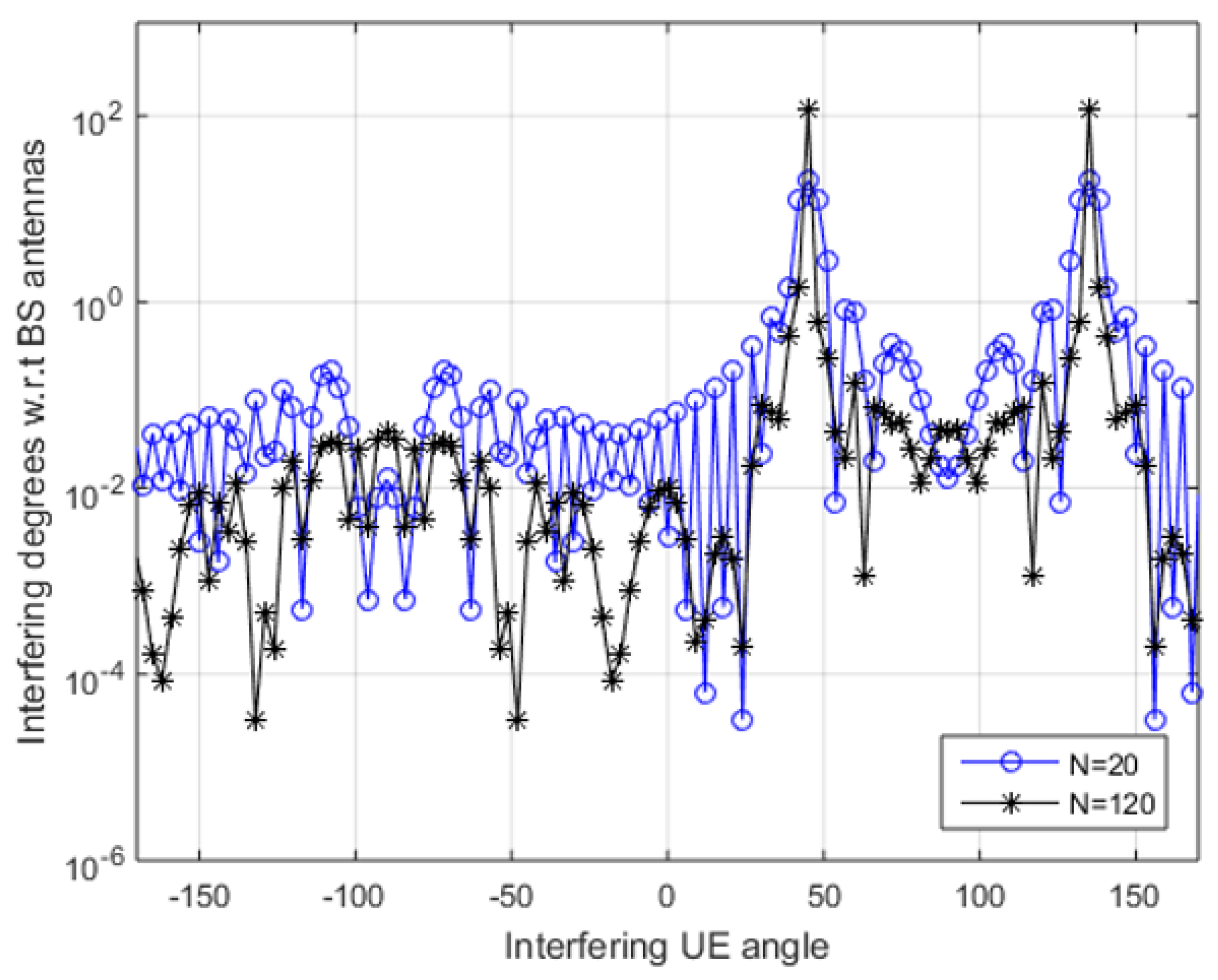
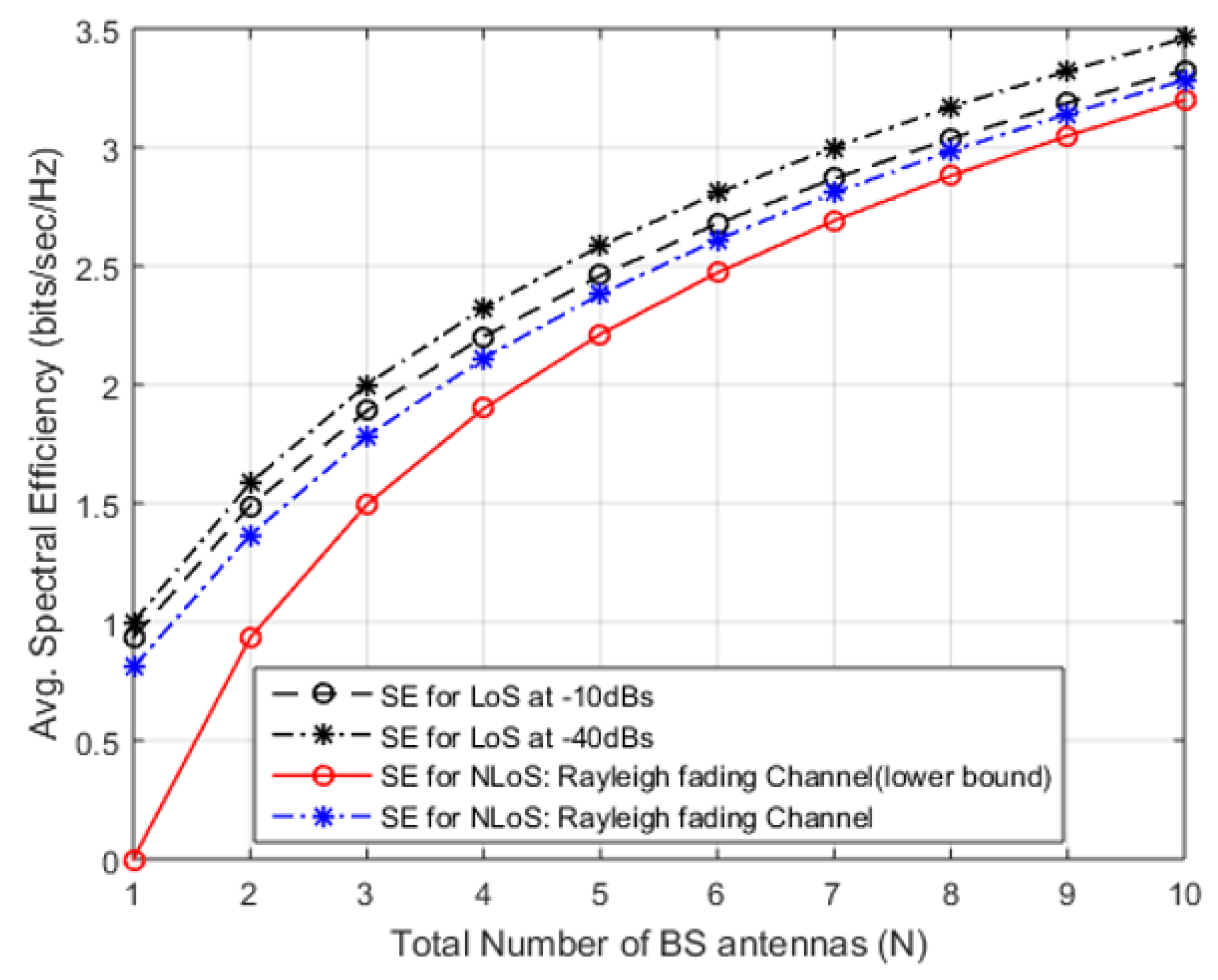
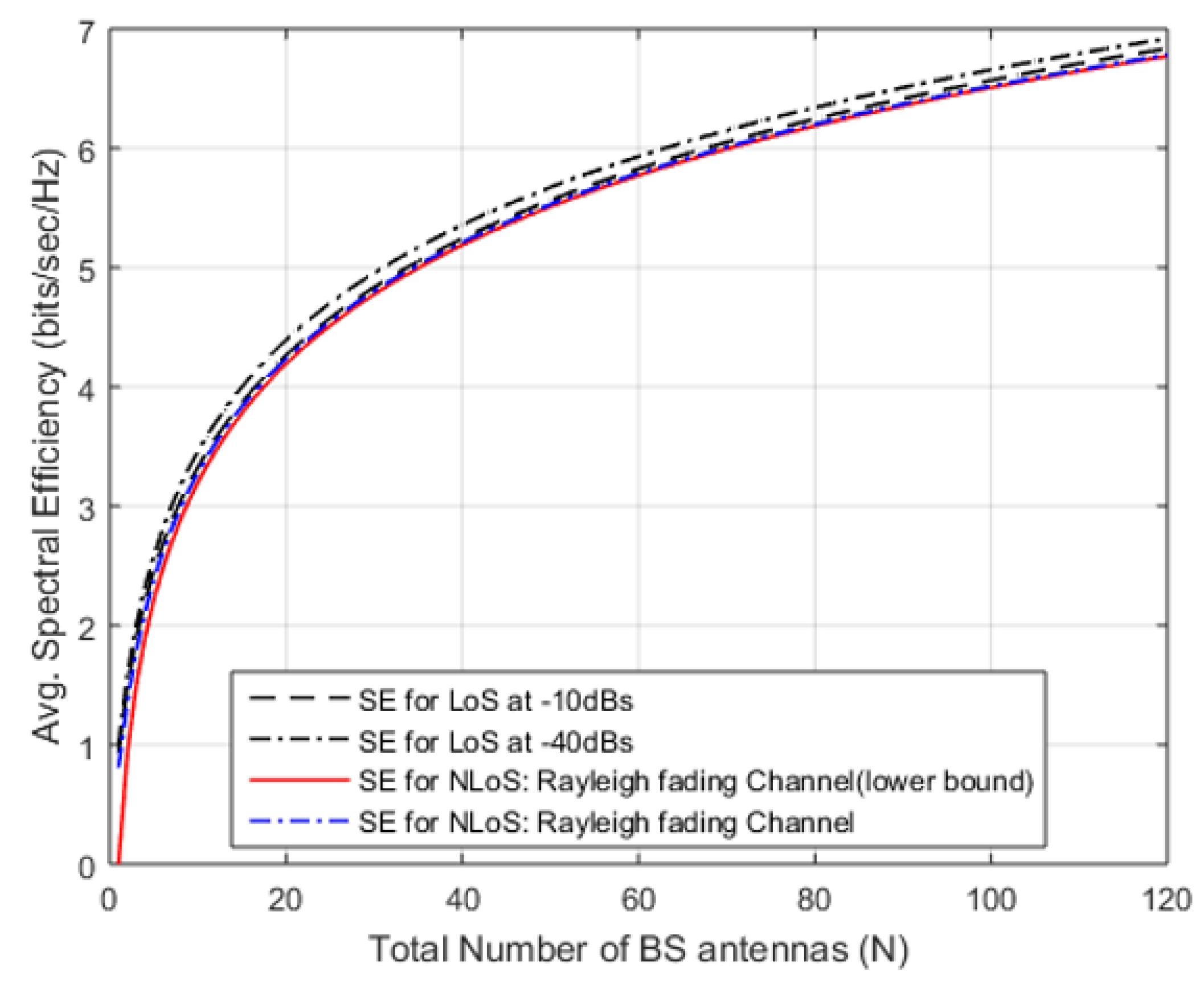
3. Results And Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hazlett, T.W. The Wireless Craze, the Unlimited Bandwidth Myth, the Spectrum Auction Faux Pas, and the Punchline to Ronald Coase’s Big Joke: An Essay on Airwave Allocation Policy. Harv. J. Law Technol. 2000, 14, 335. [Google Scholar] [CrossRef]
- Obile, W. Ericsson Mobility Report; Ericsson: Stockholm, Sweden, 2016. [Google Scholar]
- Update, I. Ericsson Mobility Report; Ericsson: Stockholm, Sweden, 2018. [Google Scholar]
- Rehman, A.; Din, S.; Paul, A.; Ahmad, W. An algorithm for alleviating the effect of hotspot on throughput in wireless sensor networks. In Proceedings of the 2017 IEEE 42nd Conference on Local Computer Networks Workshops (LCN Workshops), Singapore, 9 October 2017; pp. 170–174. [Google Scholar]
- Index, C.V.N. Global Mobile Data Traffic Forecast Update. Cisco White Paper [Online]. 2014. Available online: http://www.cisco.com/en/US/solutions/collateral/ns341/ns525/ns537/ns705/ns827/white_paper_c11-520862.pdf (accessed on 5 August 2020).
- Björnson, E.; Hoydis, J.; Sanguinetti, L. Massive MIMO networks: Spectral, energy, and hardware efficiency. Found. Trends Signal Process. 2017, 11, 154–655. [Google Scholar] [CrossRef]
- Björnson, E.; Sanguinetti, L. Power scaling laws and near-field behaviors of massive MIMO and intelligent reflecting surfaces. arXiv 2020, arXiv:2002.04960. [Google Scholar] [CrossRef]
- Dahlman, E.; Mildh, G.; Parkvall, S.; Peisa, J.; Sachs, J.; Selén, Y.; Sköld, J. 5G wireless access: Requirements and realization. IEEE Commun. Mag. 2014, 52, 42–47. [Google Scholar] [CrossRef]
- Uchoa, A.G.; Healy, C.T.; de Lamare, R.C. Iterative detection and decoding algorithms for MIMO systems in block-fading channels using LDPC codes. IEEE Trans. Veh. Technol. 2015, 65, 2735–2741. [Google Scholar] [CrossRef]
- Fang, Y.; Chen, P.; Cai, G.; Lau, F.C.; Liew, S.C.; Han, G. Outage-limit-approaching channel coding for future wireless communications: Root-protograph low-density parity-check codes. IEEE Veh. Technol. Mag. 2019, 14, 85–93. [Google Scholar] [CrossRef]
- Arshad, J.; Younas, T.; Jiandong, L.; Suryani, A. Study on MU-MIMO Systems in the Perspective of Energy Efficiency with Linear Processing. In Proceedings of the 2018 10th International Conference on Communication Software and Networks (ICCSN), Chengdu, China, 6–9 July 2018; pp. 168–172. [Google Scholar]
- Björnson, E.; Larsson, E.G.; Marzetta, T.L. Massive MIMO: Ten myths and one critical question. IEEE Commun. Mag. 2016, 54, 114–123. [Google Scholar] [CrossRef]
- Farahani, H.S.; Veysi, M.; Kamyab, M.; Tadjalli, A. Mutual coupling reduction in patch antenna arrays using a UC-EBG superstrate. IEEE Antennas Wirel. Propag. Lett. 2010, 9, 57–59. [Google Scholar] [CrossRef]
- Islam, M.T.; Alam, M.S. Compact EBG structure for alleviating mutual coupling between patch antenna array elements. Prog. Electromagn. Res. 2013, 137, 425–438. [Google Scholar] [CrossRef]
- OuYang, J.; Yang, F.; Wang, Z. Reducing mutual coupling of closely spaced microstrip MIMO antennas for WLAN application. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 310–313. [Google Scholar] [CrossRef]
- Yu, A.; Zhang, X. A novel method to improve the performance of microstrip antenna arrays using a dumbbell EBG structure. IEEE Antennas Wirel. Propag. Lett. 2003, 2, 170–172. [Google Scholar]
- Alibakhshikenari, M.; See, C.H.; Virdee, B.; Abd-Alhameed, R.A. Meta-surface wall suppression of mutual coupling between microstrip patch antenna arrays for THz-band applications. Electromagn. Res. Lett. 2018, 75, 105–111. [Google Scholar] [CrossRef]
- Zhu, F.G.; Xu, J.D.; Xu, Q. Reduction of mutual coupling between closely-packed antenna elements using defected ground structure. Electron. Lett. 2009, 45, 601–602. [Google Scholar] [CrossRef]
- Hein, M. High-Temperature-Superconductor Thin Films at Microwave Frequencies; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999; Volume 155. [Google Scholar]
- Chen, Z.; Bjornson, E.; Larsson, E.G. Dynamic scheduling and power control in uplink massive MIMO with random data arrivals. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar]
- Rehman, A.U.; Jiang, A.; Rehman, A.; Paul, A.; Sadiq, M.T. Identification and role of opinion leaders in information diffusion for online discussion network. J. Ambient. Intell. Humaniz. Comput. 2020, 1–13. [Google Scholar] [CrossRef]
- Rehman, A.U.; Naqvi, R.A.; Rehman, A.; Paul, A.; Sadiq, M.T.; Hussain, D. A Trustworthy SIoT Aware Mechanism as an Enabler for Citizen Services in Smart Cities. Electronics 2020, 9, 918. [Google Scholar] [CrossRef]
- Arshad, J.; Li, J.; Younas, T.; Sheng, M.; Hongyan, L. Analysis of Energy Efficiency and Area Throughput in Large Scale MIMO Systems with MRT and ZF Precoding. Wirel. Pers. Commun. 2017, 96, 23–46. [Google Scholar] [CrossRef]
- Rehman, A.; Paul, A.; Ahmad, A.; Jeon, G. A novel class based searching algorithm in small world internet of drone network. Comput. Commun. 2020, 157, 329–335. [Google Scholar] [CrossRef]
- Abdul, R.; Paul, A.; Gul, M.J.; Hong, W.H.; Seo, H. Exploiting small world problems in a SIoT environment. Energies 2018, 11, 2089. [Google Scholar] [CrossRef]
- Kocharlakota, A.K.; Upadhya, K.; Vorobyov, S.A. On the Spectral Efficiency for Massive MIMO Systems With Imperfect Spacial Covariance Information. arXiv 2019, arXiv:1903.11807. [Google Scholar]
- Kong, C.; Zhong, C.; Matthaiou, M.; Björnson, E.; Zhang, Z. Spectral efficiency of multipair massive MIMO two-way relaying with imperfect CSI. IEEE Trans. Veh. Technol. 2019, 68, 6593–6607. [Google Scholar] [CrossRef]
- Marzetta, T.L. Fundamentals of Massive MIMO; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Larsson, E.G.; Edfors, O.; Tufvesson, F.; Marzetta, T.L. Massive MIMO for next generation wireless systems. IEEE Commun. Mag. 2014, 52, 186–195. [Google Scholar] [CrossRef]
- Parida, P.; Dhillon, H.S. Stochastic geometry-based uplink analysis of massive MIMO systems with fractional pilot reuse. IEEE Trans. Wirel. Commun. 2019, 18, 1651–1668. [Google Scholar] [CrossRef]
- Soomro, H.; Habib, A.; Akhtar, M.W. Spectral Efficiency Enhancement using Clustered LTV Channel Model in mmWave Doubly Massive MIMO System. In Proceedings of the 2019 16th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 8–12 January 2019; pp. 1050–1052. [Google Scholar]
- Xin, Y.; Zhang, R.; Shi, P.; Su, X.; Zhang, X. Spectral efficiency analysis for massive MIMO systems in Ricean fading channels. IET Commun. 2019, 13, 3193–3200. [Google Scholar]
- Yang, H.; Larsson, E.G. Can massive MIMO support uplink intensive applications? In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019; pp. 1–6. [Google Scholar]
- Younas, T.; Li, J.; Arshad, J. On bandwidth efficiency analysis for LS-MIMO with hardware impairments. IEEE Access 2017, 5, 5994–6001. [Google Scholar] [CrossRef]
- Rice, S. Communication in the presence of noise—Probability of error for two encoding schemes. Bell Syst. Tech. J. 1950, 29, 60–93. [Google Scholar] [CrossRef]
- Younas, T.; Mekonnen, M.; Farid, G.; Tahir, S.; Younas, O.; Wattoo, W.A.; Farhan, M.; Liaqat, M. Investigation of LS-MIMO systems with channel aging effects. Phys. Commun. 2020, 40, 101088. [Google Scholar] [CrossRef]
- Li, J.; Lv, Q.; Yang, J.; Zhu, P.; You, X. Spectral and Energy Efficiency of Distributed Massive MIMO with Low-Resolution ADC. Electronics 2018, 7, 391. [Google Scholar] [CrossRef]
- Dai, H.; Poor, H.V. Asymptotic spectral efficiency of multicell MIMO systems with frequency-flat fading. IEEE Trans. Signal Process. 2003, 51, 2976–2988. [Google Scholar] [CrossRef]
- Galiotto, C.; Gomez-Miguelez, I.; Marchetti, N.; Doyle, L. Effect of LOS/NLOS propagation on area spectral efficiency and energy efficiency of small-cells. In Proceedings of the 2014 IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 3471–3476. [Google Scholar]
- Kamga, G.N.; Xia, M.; Aïssa, S. Spectral-efficiency analysis of massive MIMO systems in centralized and distributed schemes. IEEE Trans. Commun. 2016, 64, 1930–1941. [Google Scholar] [CrossRef]
- Xin, Y.; Wang, D.; Li, J.; Zhu, H.; Wang, J.; You, X. Area spectral efficiency and area energy efficiency of massive MIMO cellular systems. IEEE Trans. Veh. Technol. 2015, 65, 3243–3254. [Google Scholar] [CrossRef]
- Björnson, E.; Larsson, E.G.; Debbah, M. Massive MIMO for maximal spectral efficiency: How many users and pilots should be allocated? IEEE Trans. Wirel. Commun. 2015, 15, 1293–1308. [Google Scholar] [CrossRef]
- Lv, Q.; Li, J.; Zhu, P.; Wang, D.; You, X. Downlink Spectral Efficiency Analysis in Distributed Massive MIMO with Phase Noise. Electronics 2018, 7, 317. [Google Scholar] [CrossRef]
- Tan, W.; Jin, S.; Wen, C.K.; Jing, Y. Spectral efficiency of mixed-ADC receivers for massive MIMO systems. IEEE Access 2016, 4, 7841–7846. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Z.; Shen, M.; Xia, B. Spectral and energy efficiency of multipair two-way full-duplex relay systems with massive MIMO. IEEE J. Sel. Areas Commun. 2016, 34, 848–863. [Google Scholar] [CrossRef]
- Tan, W.; Matthaiou, M.; Jin, S.; Li, X. Spectral efficiency of DFT-based processing hybrid architectures in massive MIMO. IEEE Wirel. Commun. Lett. 2017, 6, 586–589. [Google Scholar] [CrossRef]
- Gunnarsson, S.; Flordelis, J.; Van der Perre, L.; Tufvesson, F. Channel hardening in massive MIMO-A measurement based analysis. In Proceedings of the 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Kalamata, Greece, 25–28 June 2018; pp. 1–5. [Google Scholar]

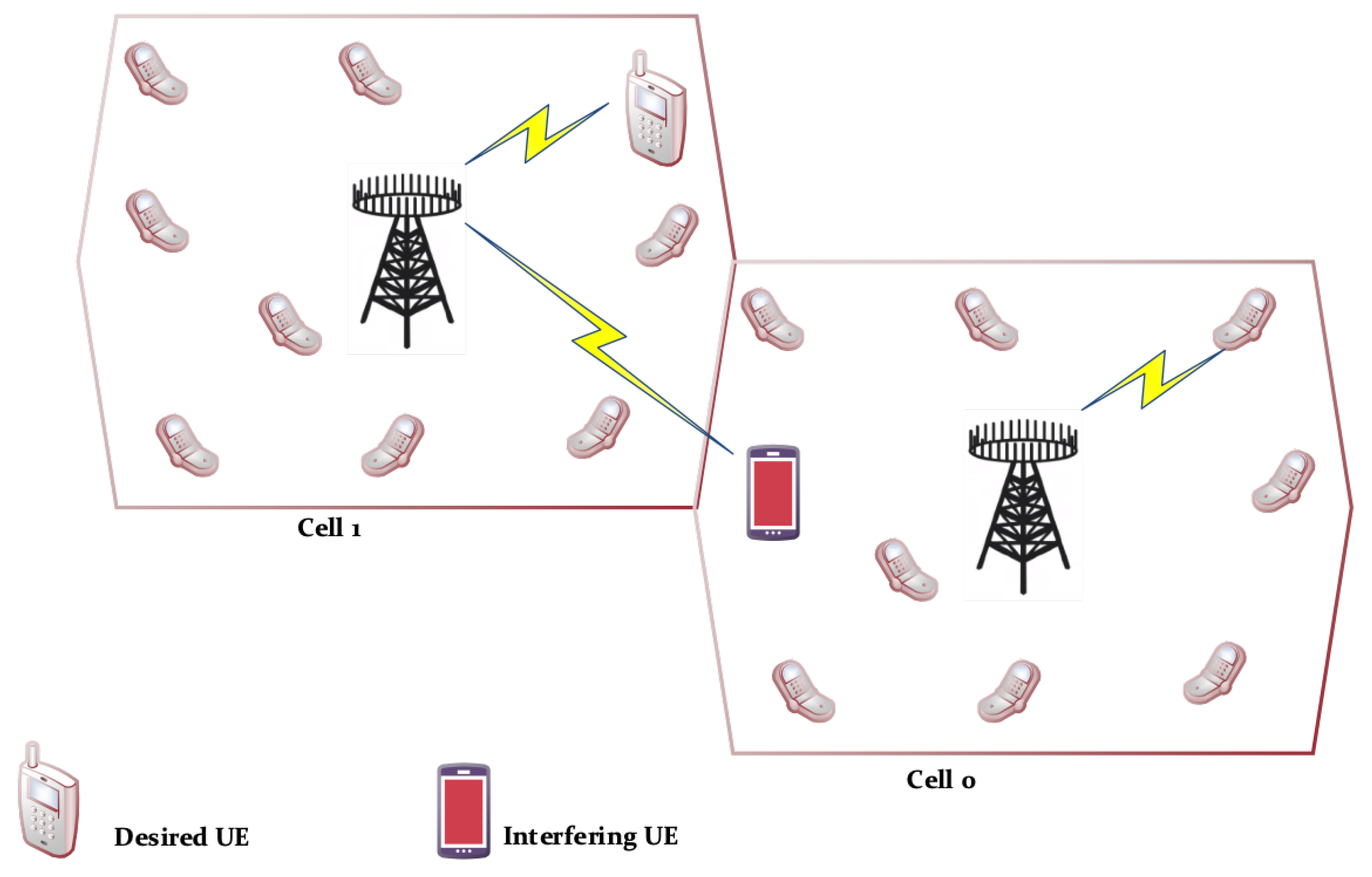
| Symbols | Description |
|---|---|
| Average Channel Gain in Cell 0 | |
| Average Channel Gain in Cell 1 | |
| Avg. Interference Signal Channel Gain of UEs in Cell 1 | |
| Avg. Interference Signal Channel Gain of UEs in Cell 0 | |
| The ratio of inter and intra cell Gain [14] | |
| Antenna Spacing | |
| Wavelength | |
| Signal received at Output (UL Communication) | |
| , | Information Symbols |
| and | Channel Responses |
| Large-Scale Fading Coefficient |
| Simulation Symbols | Parameter Values |
|---|---|
| Antennas in an array (N) | 120 |
| The angle of Desired UE | |
| Range of Angle of Interfering UE | Varies from |
| Antenna spacing | 1/2 |
| No. of cells | 2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arshad, J.; Rehman, A.; Rehman, A.U.; Ullah, R.; Hwang, S.O. Spectral Efficiency Augmentation in Uplink Massive MIMO Systems by Increasing Transmit Power and Uniform Linear Array Gain. Sensors 2020, 20, 4982. https://doi.org/10.3390/s20174982
Arshad J, Rehman A, Rehman AU, Ullah R, Hwang SO. Spectral Efficiency Augmentation in Uplink Massive MIMO Systems by Increasing Transmit Power and Uniform Linear Array Gain. Sensors. 2020; 20(17):4982. https://doi.org/10.3390/s20174982
Chicago/Turabian StyleArshad, Jehangir, Abdul Rehman, Ateeq Ur Rehman, Rehmat Ullah, and Seong Oun Hwang. 2020. "Spectral Efficiency Augmentation in Uplink Massive MIMO Systems by Increasing Transmit Power and Uniform Linear Array Gain" Sensors 20, no. 17: 4982. https://doi.org/10.3390/s20174982
APA StyleArshad, J., Rehman, A., Rehman, A. U., Ullah, R., & Hwang, S. O. (2020). Spectral Efficiency Augmentation in Uplink Massive MIMO Systems by Increasing Transmit Power and Uniform Linear Array Gain. Sensors, 20(17), 4982. https://doi.org/10.3390/s20174982









