1. Introduction
In the era of Deep Learning (DL), research in many domains has shown that bigger datasets can result in better models, since, in general, training on more data allows better generalization. The problem with some small datasets is that they have been collected under different conditions, thus merging them is not an option. When a task involves the analysis of biomedical signals, e.g., electroencephalography (EEG), electromyography (EMG), electrocardiography (ECG), etc., acquiring bigger datasets is a complicated task, and it can be an unpleasant experience for the patients due to tiredness and patient’s limitations or physical impairments. In addition, manual effort might be needed for cleaning and labeling the data. Consequently, the absence of a sufficient amount of data makes analyzing these signals quite a challenging task. In this work, we address the problem of limited data for the task of hand gesture recognition based on surface electromyography (sEMG) using data augmentation—a promising approach for enhancing existing datasets, which could allow further research and analysis.
Data augmentation comprises a set of approaches that aim at inflating the amount and diversity of available data for training models for a target task without the need to collect new data. This family of techniques builds synthetic/artificial data by transforming existing labeled samples so as to help the model learn the range of intra-class variation that one could possibly observe. A key challenge for data augmentation is to generate new data that maintain the correct label. In many tasks, this requires domain knowledge, which in the case of sEMG can be difficult to exploit due to high within-subject variability (i.e., the same person can perform the same gesture in many different ways, while factors such as fatigue and sweat affect the properties of the recorded signal). Data augmentation is also one of the approaches to deal with the problem of overfitting because the augmented data are expected to represent a more extensive set of possible data points, thus reducing the dissimilarity between the training and validation/testing sets.
Over the last few years, the subject of data augmentation has attracted many researchers and considerable progress has been made especially in the domain of computer vision, which influences many other research areas. Augmentation methods can be divided into two big categories [
1]: Basic image manipulations (e.g., kernel filters, geometric and color transformations [
2]) and DL approaches (e.g., neural style transfer [
3] and Generative Adversarial Network (GAN) [
4,
5]). Furthermore, meta-learning methods (e.g., Smart Augmentation [
6], AutoAugment [
7]) can utilize neural networks in order to learn a set of appropriate augmentations for a given dataset and task, while the RandAugment strategy [
8] manages to reduce the augmentation search space without reducing the performance of the model.
In the area of biosignal processing, augmentation methods have been developed as well. In the work of [
9], a set of simple sequence manipulations (e.g., warping, time shuffling, additive noise) are evaluated on a Parkinson’s disease dataset recorded with accelerometer sensors. For brain computer interfaces, [
10] investigates the possibility of electrode shifts of an EEG cap as a means of generating augmented data that correspond to spatial distortions. An extensive review of augmentation methods for EEG-related tasks is performed in [
11]. The authors evaluate a wide range of augmentations that includes data manipulations such as additive noise and sliding windows as well as deep learning approaches based on GANs. Their results showed that additive noise and sliding windows provided the highest accuracy increase across different tasks. Furthermore, the authors of [
12] have developed a method based on sub-optimally aligned sequences for generating augmented data. Their approach evaluated across different datasets, including EEG and ECG signals, yielded better or equivalent performance compared to existing methods.
Various augmentation strategies have been applied to sEMG-based gesture recognition. Basic data manipulations like the addition of Gaussian noise [
13,
14] and the electrode shift of a high density electrode grid [
15] have provided limited gains. In [
16], a set of domain specific augmentations are evaluated. These include the simulation of sensor noise, electrode displacement, and fatigue. Additionally, a sliding window approach is used instead of non-overlapping signal segments. Their analysis showed that the sliding window approach results in significant improvement, while the additive noise performed the worst. The fact that domain-specific approaches like electrode displacement and muscle fatigue approximation failed to improve the classification accuracy confirms the difficulty of generating appropriate sEMG signals. On the other hand, electrode displacement has been successful as an augmentation method for the problem of user authentication based on sEMG. The authors of [
17] apply a circular rotation of the eight electrodes of the Myo armband, thus expanding the original data up to 8×. In this case, the electrode displacement augmentation improves the performance of the model because the enhanced dataset still belongs to one person, while a specific hand gesture is not required for the successful authentication. Finally, DL-based approaches have shown great potential for enhancing EMG datasets. In [
18], the authors utilize a GAN architecture combined with Style Transfer to augment sEMG signals recorded from Parkinson’s disease patients. Specifically, their model learns the tremor patterns of a patient and applies them to signals acquired from healthy subjects. Thus, they can use able-bodied subjects to investigate how patients’ movements are affected by the disease.
Despite the research progress in many fields, there are very few studies that provide an extensive evaluation of the augmentation methods applied to a specific task. In this work, we investigate the application of data augmentation to the problem of hand gesture recognition based on sEMG signals, while providing a thorough assessment of the proposed methods. The training dataset is enhanced with synthetic data in order to improve the recognition accuracy of Convolutional Neural Network (CNN) classifiers. The main contributions are:
the presentation of common (i.e., additive noise, overlapping windows) and novel (i.e., magnitude warping, wavelet decomposition, synthetic sEMG models) data augmentation methods for sEMG signals
an extensive and systematic evaluation of the aforementioned augmentation methods
an improvement in classification accuracy of the state-of-the-art model [
19].
The rest of the paper is organized as follows. In
Section 2, we give the details of the proposed approaches and the CNN architectures used in the experimentation. The experiments are presented in
Section 3. Next, the results are shown in
Section 4 and the discussion follows in
Section 5. Finally,
Section 6 summarizes the outcomes and outlines future work.
3. Experiments
The first step of the experimentation consists of determining the proper values for the parameters of the augmentation methods. This is achieved through a grid search performed for the
AtzoriNet* on each dataset separately. Specifically for the WD, MW, and GN methods, the values shown in
Table A4 are evaluated. In the case of WD, the
and
l correspond to the mother wavelet and the decomposition level used to compute the wavelet coefficients
and
(i.e., average and details coefficients, respectively), while
b is the multiplication factor that modifies the details coefficients (Equation (
3)). In the cases of MW and GN, there is a single hyper-parameter that controls the variance,
, of the smoothing curve (Equation (
2)) and the amount of additive noise, characterised by
(Equation (
1)), respectively. For these experiments, only the first 20 subjects are used. During training the validation repetitions shown in
Table A3 are held out from the training set.
At a next step, two experiments are carried out: (a) the evaluation of the augmentation methods with the optimized augmentations using the complete datasets, and (b) the improvement of the state-of-the-art model (WeiNet). In the first case (a), the augmentation methods (i.e., SS1, SS2, WD, MW, GN) are compared against each other, and in the latter (b) the methods that performed best are applied to the WeiNet model. For the Augmentor methods, the top-3 best performing augmentations as evaluated on Ninapro-DB1 are used setting in the case of AR.
For the AtzoriNet* model, the input images of size , where L the segment duration and C the number of electrodes, are generated using 150 ms segments, i.e., . In the augmentation hyper-parameter selection step, the images are generated without overlap, i.e., , and the size of the augmented training set is 10 times the size of the original, i.e., . For the rest of the experiments, window overlaps and augmentation ratios are evaluated.
In the case of WeiNet, the input images are generated using 200 ms segments and maximum overlap, i.e., , as proposed by the authors of the model. Window overlap is held constant for the investigated augmentation ratios .
Augmentation methods are indicated by their name with the window step in parentheses. For example, corresponds to SS1 augmentation with window step (no overlap), while is the MW method with maximum overlap. In the following experimentation, we consider as a first baseline the case without any augmentation () and window step denoted as . Taking into account that there is no consensus in literature concerning the use of sliding windows (SW) as an augmentation method, we also consider the maximum overlap approach as a second baseline, i.e., .
Data preparation and training of the models are carried out on a workstation with an Intel i9-7920X 2.90 GHz processor, 128 GB RAM and an Nvidia GeForce RTX 2080Ti 11GB GPU. The implementation is based on the Tensorflow Python library.
3.1. Metrics
The performance metrics used for the evaluation are the accuracy and the loss values computed on the validation/test set averaged across the subjects. Specifically, the metrics values for a given dataset, CNN model and augmentation method are compared with the corresponding values of the other methods as well as the baseline of the same dataset and model. Additionally, the average across subjects f1-score for each gesture is shown. Statistical significance is analysed through an Analysis of Variance (ANOVA) followed by post-hoc pairwise tests. To assess the quality of the generated data, a low dimensional tSNE embedding [
26] of the CNN features computed on the real and the augmented sEMGs is provided. Furthermore, metrics that evaluate the gesture clusters in the high-dimensional feature space are provided. These are:
the Silhouette Coefficient (SC) [
27]:
where
N is the total number of points,
is the mean distance between point
i and all other data points in the same cluster and
is the smallest mean distance of
i to all points in any other cluster, of which
i is not a member.
the Davies–Bouldin (DB) index [
28]:
where
K is the number of clusters,
the average distance of all points in cluster
i from the cluster centroid
and
the distance between the two centroids.
SC values are in the range [−1, 1], where a high value indicates that the points are well matched to their own clusters. DB index values are positive numbers and the optimal clustering solution has the smallest DB value.
3.2. Model Optimization
Optimization hyper-parameters for the two CNN models are reported in
Table A2. Specifically, the
AtzoriNet* models were trained with the Adam [
29] optimizer using a constant learning rate of 0.001 and a batch size of 512 for 100 epochs. Furthermore, to avoid overfitting the models, an early stopping strategy was adopted and a weight decay (
) regularization of 0.0005 was used. In the case of
WeiNet, the networks were optimized following the guidelines of the authors [
19], i.e., using stochastic gradient descent (SGD) with momentum for 28 epochs with a learning rate of 0.1 divided by 10 after epochs 16 and 24, a batch size of 1024 and
regularization equal to 0.0001.
5. Discussion
For the Discussion and the Conclusions sections, we always base the comparative performance analysis of the various methods on significance tests. No significant difference implies equal performance. In this discussion, we add to this quantitative approach some qualitative analyses of the behaviour of several methods on both datasets, supported by more intuitive reasoning or corroborated by different viewpoints.
The hyper-parameter selection conducted for the WD, MW, and GN augmentation methods provided some useful results (
Table A5). For the SNR parameter of GN, a value of
was selected by the greedy search, which is different compared to previous works on the
AtzoriNet and Ninapro dataset [
13,
22]. In the case of the putEMG dataset, a higher SNR is chosen (
) for the GN augmentation since the signals in this dataset are already much noisier. The value of
determines the degree of deformation applied to the sEMG, so a small value (
) is selected to avoid synthetic signals that could represent a signal of a different gesture. In the case of WD, the parameter values are different in the two datasets.
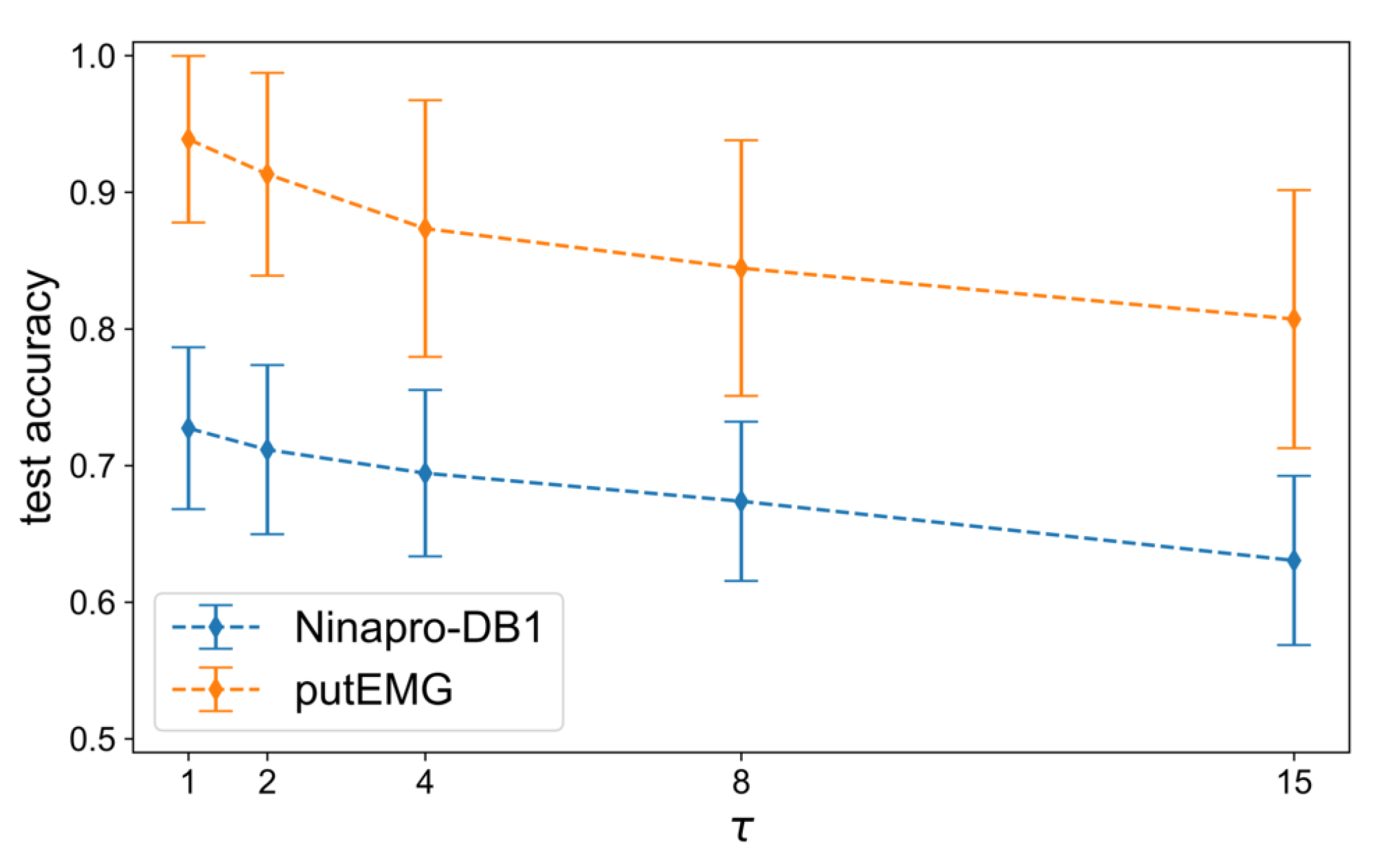
The main evaluation of the methods is performed next, using the best hyper-parameters selected in the previous step. Firstly, we assess the effect of overlapping windows, since many works in the literature do not clarify whether it is used or not. The analysis of [
16] showed that among the investigated methods the SW augmentation approach performed significantly better. In
Figure A3, we can see the declining trend of the average accuracy when the window step,
, increases. Specifically, with densely overlapping windows, the size of the training set increases more than with the augmentation ratio
R, which translates to higher gain in classification accuracy. For example, when
, there are 6038 training samples and when
there are 10× more samples, i.e., 60,380. On the other hand, when
the training size consists of 87,936 samples and when
there are 879,360. This confirms that using overlapping windows is an important factor of a DL pipeline for sEMG signal processing.
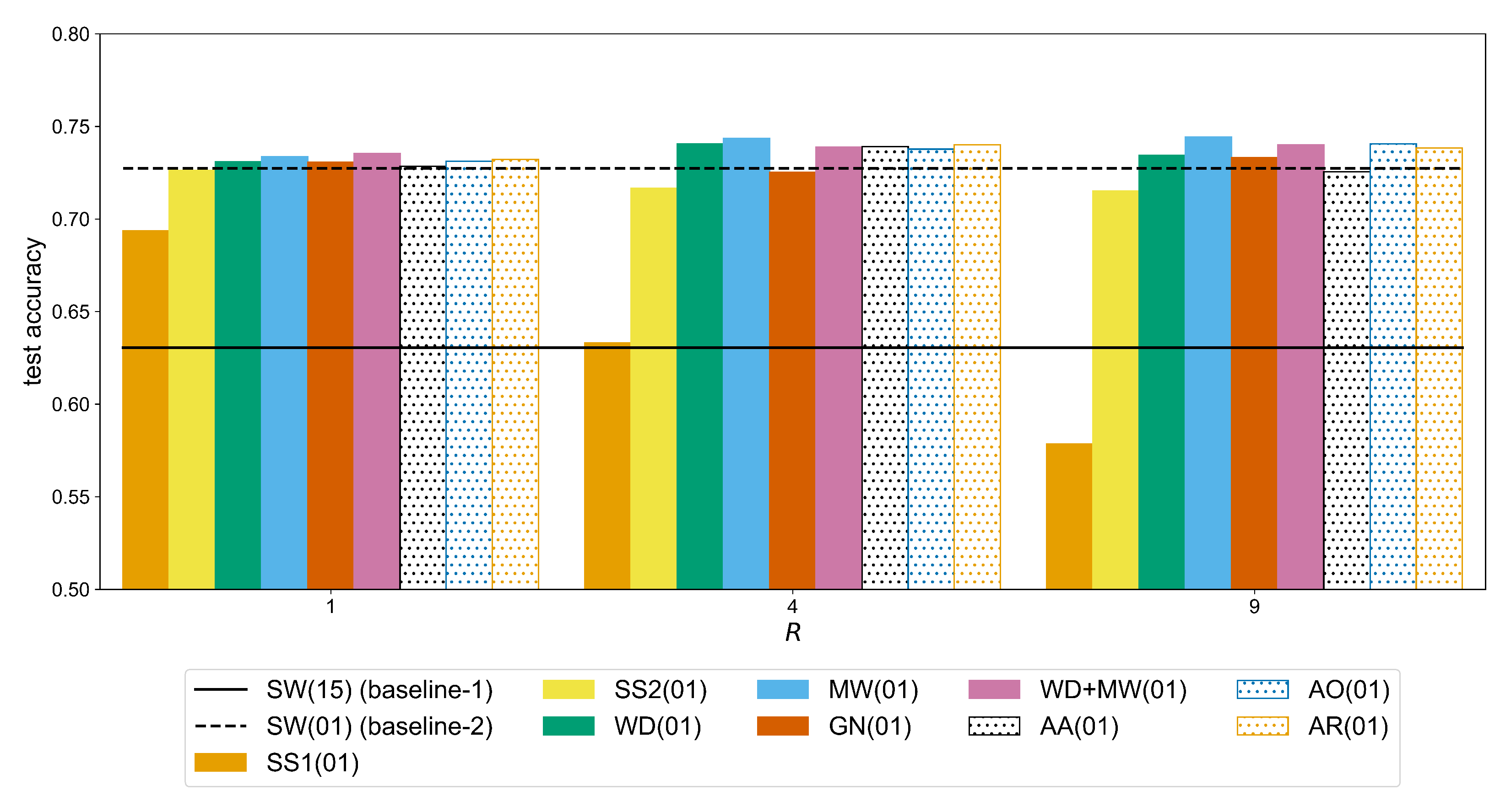
The second factor that affects the performance of the CNN model with respect to both baselines is the amount of augmentation expressed with the augmentation ratio
R. In
Figure A4, we can see that for the Ninapro-DB1 dataset a statistically significant improvement (observed through the following
p-values,
for GN,
for WD+MW,
for the remaining methods) can be measured for a ratio up to
. For example, the accuracy of the MW method (
Table A6) improves from 0.7337 (
) to 0.7436 (
) (significant difference with a
p-value of
), while the additional improvement when using
is not significant (i.e., +0.0007 with
p-value equal to
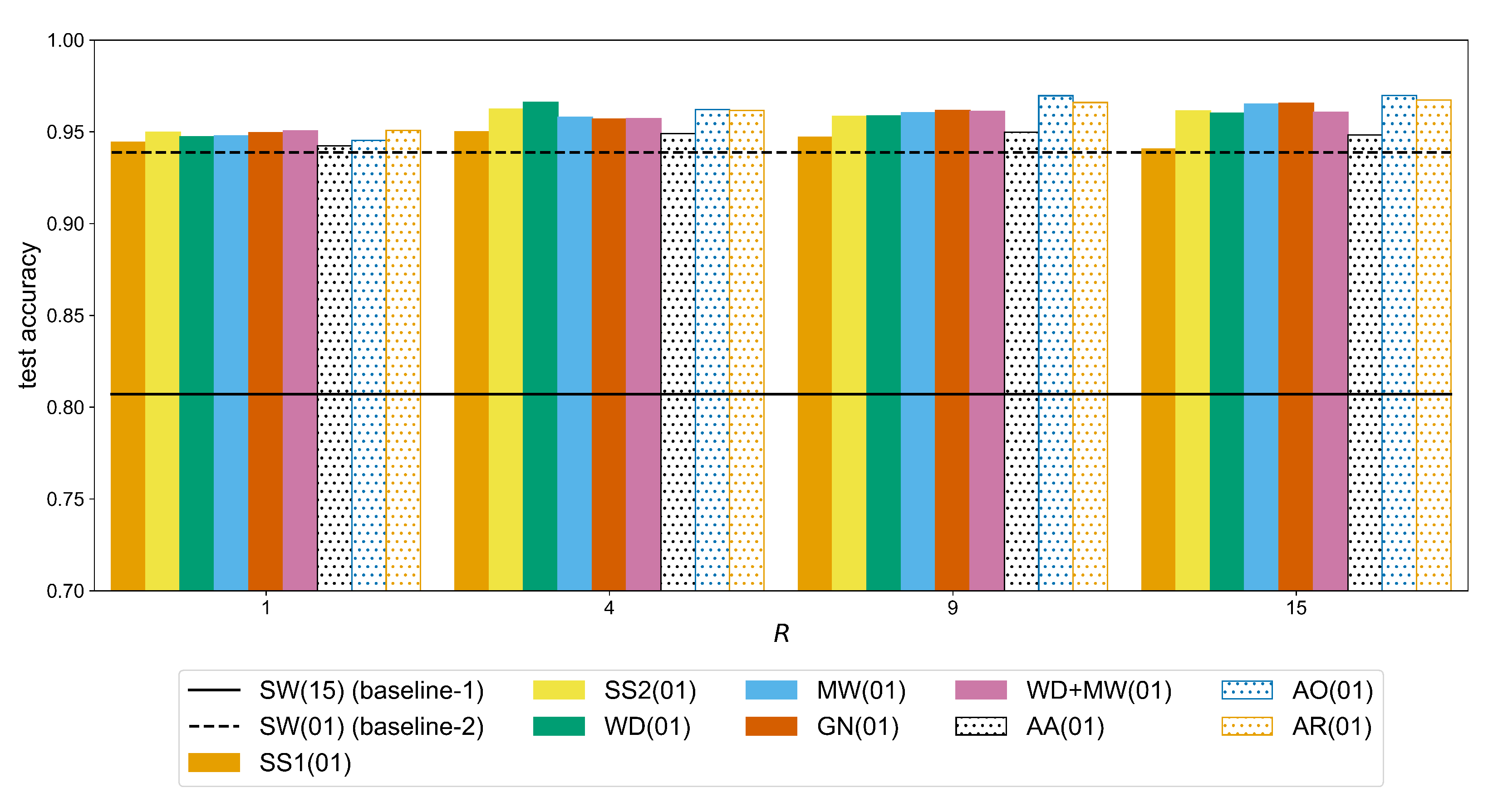
). In the case of putEMG (
Figure A5), the accuracy continues to improve for bigger values of R. For the same augmentation method (MW), there is an increase from 0.9477 (
) to 0.9580 (
) (significant difference with a
p-value of
) and then 0.9650 (
) (significant difference with a
p-value of
). This is due to the fact that in putEMG there are less repetitions per gesture and also their duration is shorter than in Ninapro, so the number of sEMG windows is generally smaller. Therefore, a larger amount of augmented signals is required to train a given CNN model.
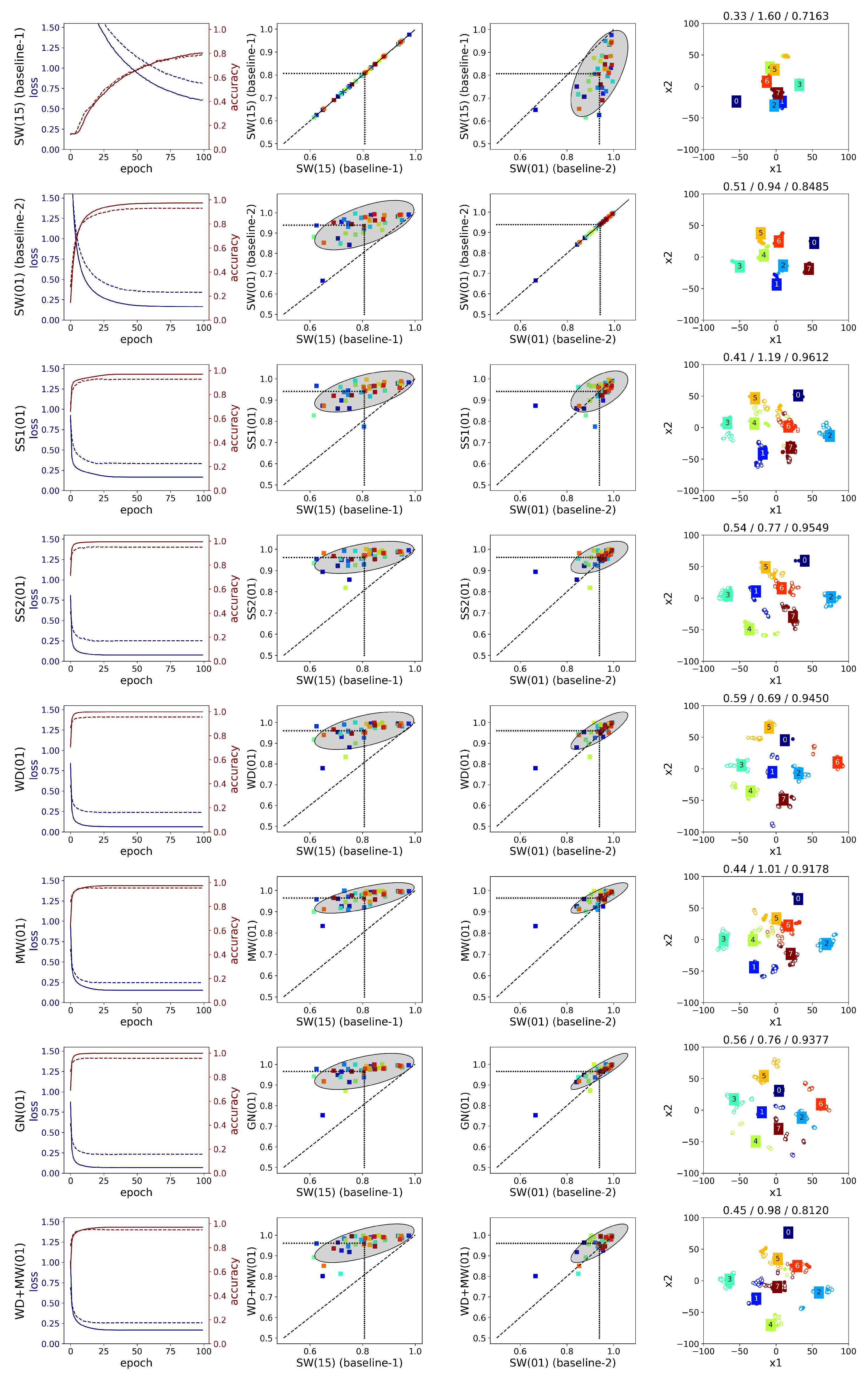
A detailed comparison is given below (
Figure A6 and
Figure A7) considering the following points: the average loss/accuracy graphs, the accuracy improvement per subject relative to the baselines (i.e., SW(15) and SW(01)), and the 2D embeddings. Regarding the use of overlapping windows, the loss graphs show that with maximum overlap the network weights are trained more efficiently. The performance for every subject is improved, though the high variance in the results remains as we can see from the spread of the points in the second column of
Figure A6 and
Figure A7. Additionally, the average SC and DB metrics for the SW(15) and SW(01) methods remain low. This is also illustrated in the embedding graphs which do not show any improvement in distinguishing the features of different gestures.
Comparing the two augmentation methods based on sEMG simulation, i.e., SS1 and SS2, we can see that the latter outperforms the former in both datasets regardless the value of augmentation ratio R. On the other hand, SS1 does not improve the accuracy in any of the subjects of Ninapro, since the ellipse in the second and third columns of
Figure A6 is below the diagonal. An explanation for the difference in the performance of these two methods can be given by the corresponding clustering metrics of the CNN features (
Table A8), where SS1 has the lowest SC value, i.e., 0.1535, and SS2 the highest, i.e., 0.2980 (the difference is significant with
as shown in
Table A12). These observations are visualized in the t-SNE graphs shown in the last column of
Figure A6 and
Figure A7 for a single subject. In the case of SS2, a few clusters of similar gestures appear, whereas the features of the augmented signals lie far away from the real data in SS1. As a result, when generating more augmented signals with SS1 by increasing the ratio R, the classification accuracy deteriorates rapidly (
Table A6). In Ninapro, the accuracy deteriorates for bigger augmentation ratios when SS2 is used (the difference between
and
is significant with
), but for putEMG there is an improvement of 0.0124 from
to
(
). The difference between the two simulation methods lies in the calculation of the sEMG variance. In SS2, it is better estimated through an inverse Gaussian distribution using the EM algorithm. However, this leads to an increased computational demand which only affects the training time of the CNN.
In general, WD and MW followed by GN yield higher accuracy results so, these augmentations are considered in the Augmentor variants, i.e., AO, AA, AR. In Ninapro-DB1, the Augmentor methods are slightly below the other approaches while the best result is achieved with MW (
Table A6). The WD and MW score higher accuracies in putEMG as well, but equally good results can be obtained with the AO and AR methods. Overall, the best performance in Ninapro-DB1 is achieved by the MW with an accuracy of 0.7443 (equally good to GN, WD+MW, AO, and AR (
Table A10)), while in putEMG by the Augmentor AO with 0.9697 accuracy (equally good to other augmentations except SS1 where
(
Table A11)). When compared to SW(15) (baseline-1), these accuracy scores correspond to an improvement of over 11% on Ninapro (
Table A6) and over 16% on putEMG (
Table A7).
The learning curves averaged across subjects (first column of
Figure A6 and
Figure A7) can be used to assess the degree of overfitting by the difference between the training and testing curves. In the case of the Ninapro dataset (first column of
Figure A6), MW performs better in reducing overfitting. On the other hand, in WD and GN, there is a great degree of overfitting, which can be explained by the fact that the features of the augmented signals remain close to the corresponding original ones. Although their combination, WD+MW, does not yield higher accuracy than MW alone, overfitting is further decreased. In general, from the first column of
Figure A6, we may conclude that the investigated augmentations do not provide an adequate variety in the generated signals of
all the 52 gestures in Ninapro-DB1, since the difference in the loss values between train and test is considerable. Similarly in the putEMG dataset, MW and WD+MW yield the best performance in terms of reduced overfitting (first column of
Figure A7).
A few differences are observed between the learning curves of the two datasets. Specifically, in Ninapro, the gap between the training and testing loss curve is bigger than in putEMG. In addition, the final loss values are much lower in putEMG across every method. A possible explanation could be the fact that the classification task is easier in putEMG which contains less gestures compared to Ninapro-DB1. This is also depicted in the t-SNE embeddings (last column of
Figure A6 and
Figure A7) where some clear clusters are formed in the case of putEMG. Regardless of the differences in the learning curves, the behaviour of the augmentation methods is largely the same in the two datasets as described above.
A difference in the classification performance of the two datasets is observed in the middle plots of
Figure A6 and
Figure A7. For Ninapro (
Figure A6), we observe a more consistent behaviour across the subjects since the accuracy variance in the augmentation methods (
y-axis) is similar to the variance in the two baselines (
x-axis), though a slightly lower variance is observed in the MW method. In the third column, we can see that almost all the subjects are above the diagonal when MW method is used, whereas in the case of SS2 the points are slightly below the diagonal. Furthermore, the classification accuracy changes the same way across the subjects. On the other hand, in putEMG (
Figure A7), there is a high variance in the SW(15) (baseline-1) approach, which is minimized in the MW method. In addition, many subjects perform very well without any augmentation, thus there is a smaller margin for improvement in these cases compared to the subjects that score poorly without augmentation. This is more clear when the augmentation methods are compared to SW(01) (baseline-2), where the ellipses are less elongated and the angle between the ellipses and the diagonal is smaller. Overall, apart from the different hardware used in the two datasets, which has a dominant effect on the quality of the recorded signal, another reason that can explain these differences is the amount of gestures in the two datasets. Ninapro contains a huge variety of gestures where the subtle differences between them make the classification a much harder problem than in the case of putEMG with fewer gestures. The results of the augmentation methods on putEMG show that augmentation techniques are beneficial to improving the accuracy when there are too few data.
Regarding the clustering metrics and the t-SNE embeddings, the following can be observed. Between the two datasets, we see larger SC values and smaller DB values in putEMG (
Table A9) compared to Ninapro-DB1 (
Table A8). This is expected since the classification task is easier in putEMG, thus the CNN features of the same gesture can be clustered together as can be seen in the example t-SNE embeddings (last column of
Figure A7). From the low dimensional visualizations of the CNN features for a single subject, we can see that for the augmentation methods with higher accuracy (e.g., SS2, GN), there is better separability between the clusters. This is in agreement with the cluster metrics, since the SC value is greater than in the baseline-1 and the DB is smaller (the differences are significant with
in both datasets as shown in
Table A12 and
Table A14). Eventually, the average clustering metrics (
Table A8) show significantly better separation (
) of the SS2 method compared to all the other augmentation methods in the Ninapro dataset (the differences are significant with
for the SC and
for the DB metric (
Table A12)). In putEMG, (
Table A9), the AR augmentation offers better separation (
) than the baselines, SS1, MW, WD+MW, and AA, but it is equally good to SS2, WD, GN, and AO (with
p-values shown in the last column and last row of
Table A13 for the SC and DB metric, respectively). Another observation is that in general there is an agreement between the SC/DB metrics and the accuracy score. For example, a high SC value corresponds to higher accuracy (Pearson’s correlation
with
for Ninapro and
with
for putEMG) and a large DB value to lower accuracy (Pearson’s correlation
with
for Ninapro and
with
for putEMG). However, ordering the augmentation methods with respect to metrics SC/DB might be different than a ranking based on the accuracy values (e.g., in
Table A9, the AR method has the best values for the SC and DB metrics, but the highest accuracy is achieved by AO).
To assess the improvement for each individual gesture, the average f1-score is provided in
Figure A8 and
Figure A9. With the exception of the SS1 method in Ninapro, the remaining augmentation approaches improve the classification of every gesture. This improvement is mostly clear in the more complex gestures of Ninapro, e.g., labels 21–29 (wrist rotations) and labels 38, 40, 50 (variations of tripod grasp), where the difference between the baseline-1 and the WD, MW augmentations is bigger. Similarly, in putEMG the most gain in classification is observed in labels 4–7 that correspond to a subject performing a pinch grasp using the thumb and any of the other fingers. This indicates that the augmentation methods investigated in this study improve the performance on difficult gestures.
Considering that the
WeiNet model has far more weights than the
AtzoriNet*, we did not perform a grid search for the optimum augmentation hyper-parameters. Rather, based on the results from
AtzoriNet*, the best augmentation methods, namely the WD and MW, are applied. As reported in [
19], the performance of the model on the Ninapro dataset when maximum overlap is used, i.e., SW(01), is 0.85. Due to differences in the development tools, the baseline accuracy we achieved is 0.8480.
Table A14 shows that, with the MW augmentation, the baseline performance is improved by 1% when the augmentation ratio is set to
. A repeated measures ANOVA test showed that this change in accuracy is significant (
). Additionally, the WD method performed worse than the baseline, which consequently had a negative effect on the accuracy of WD+MW.