Multidirectional Cylindrical Piezoelectric Force Sensor: Design and Experimental Validation
Abstract
1. Introduction
2. Simulation
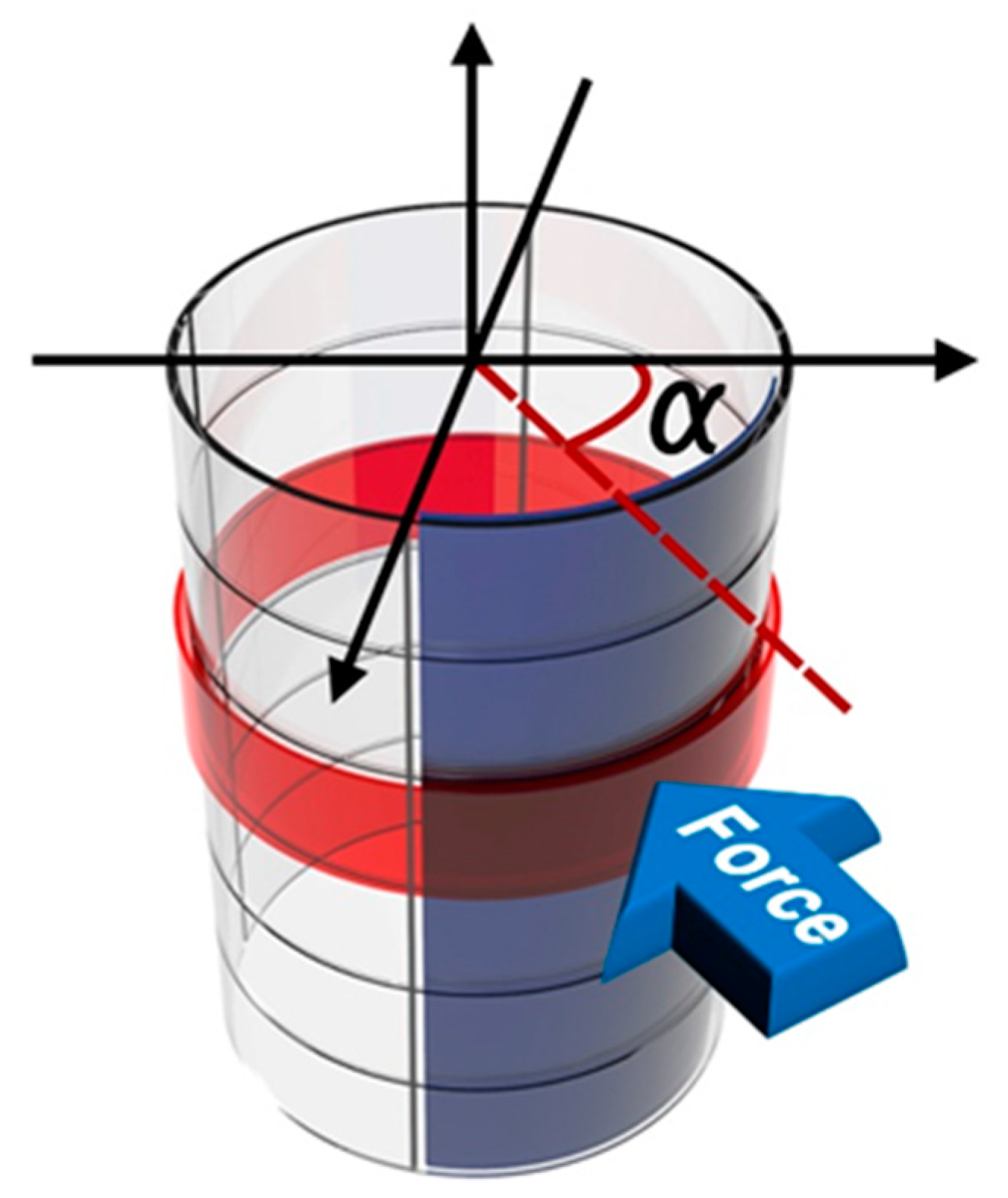
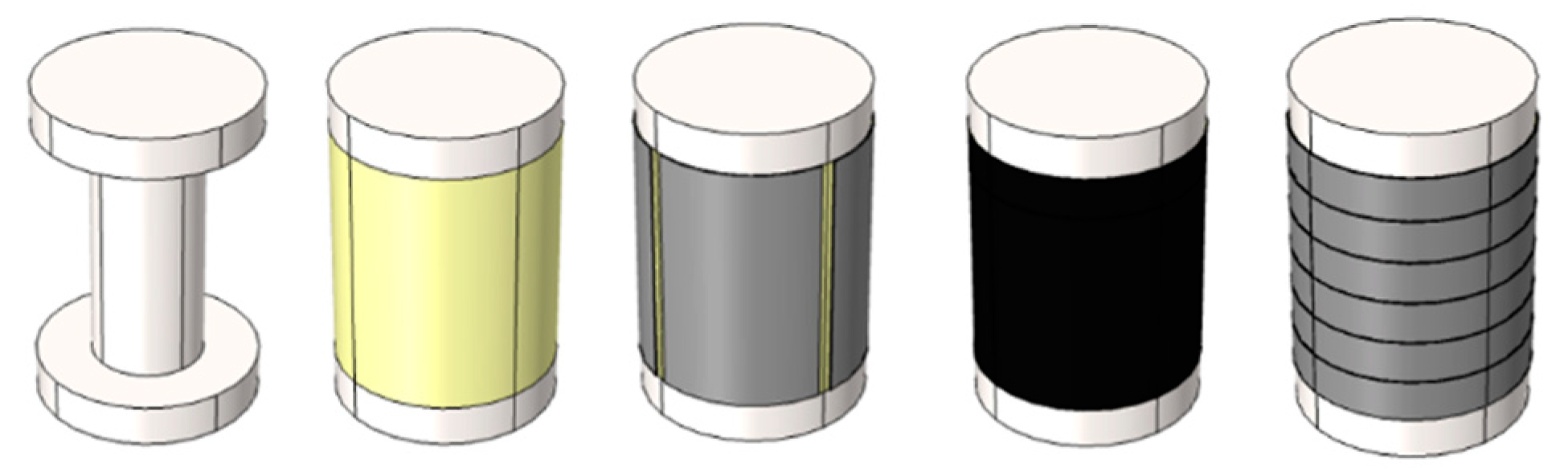
2.1. Modeling Structure
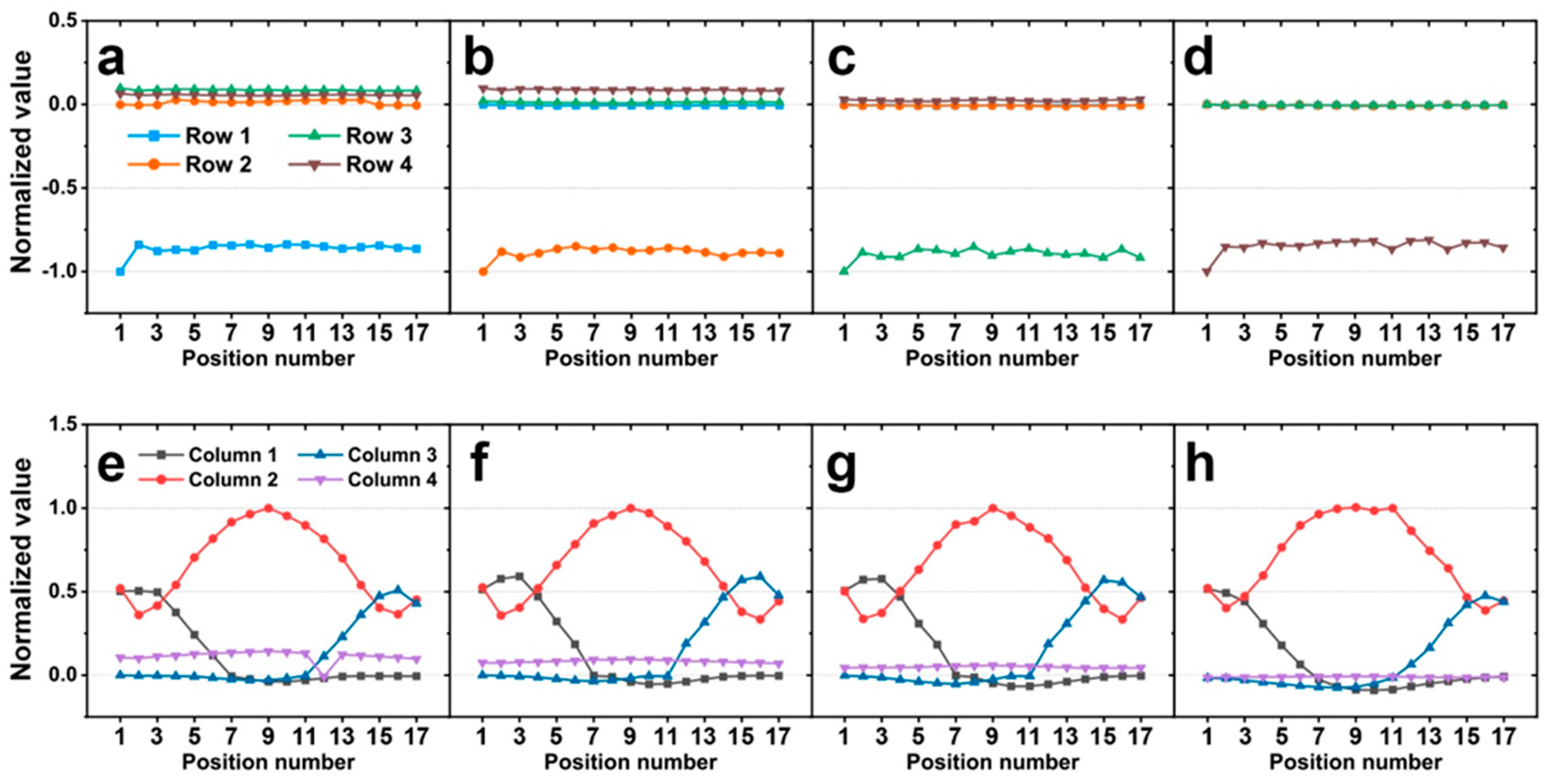
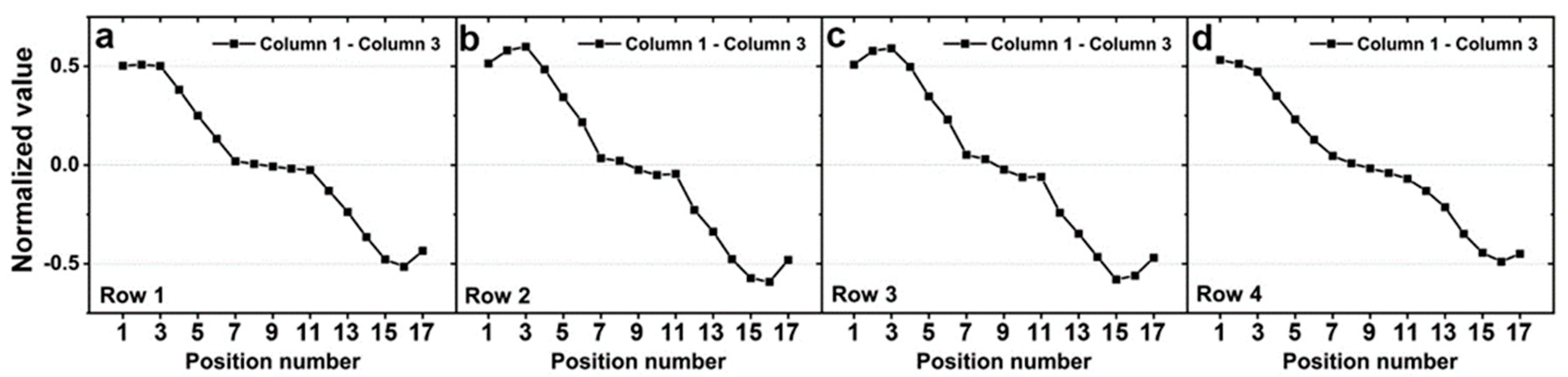
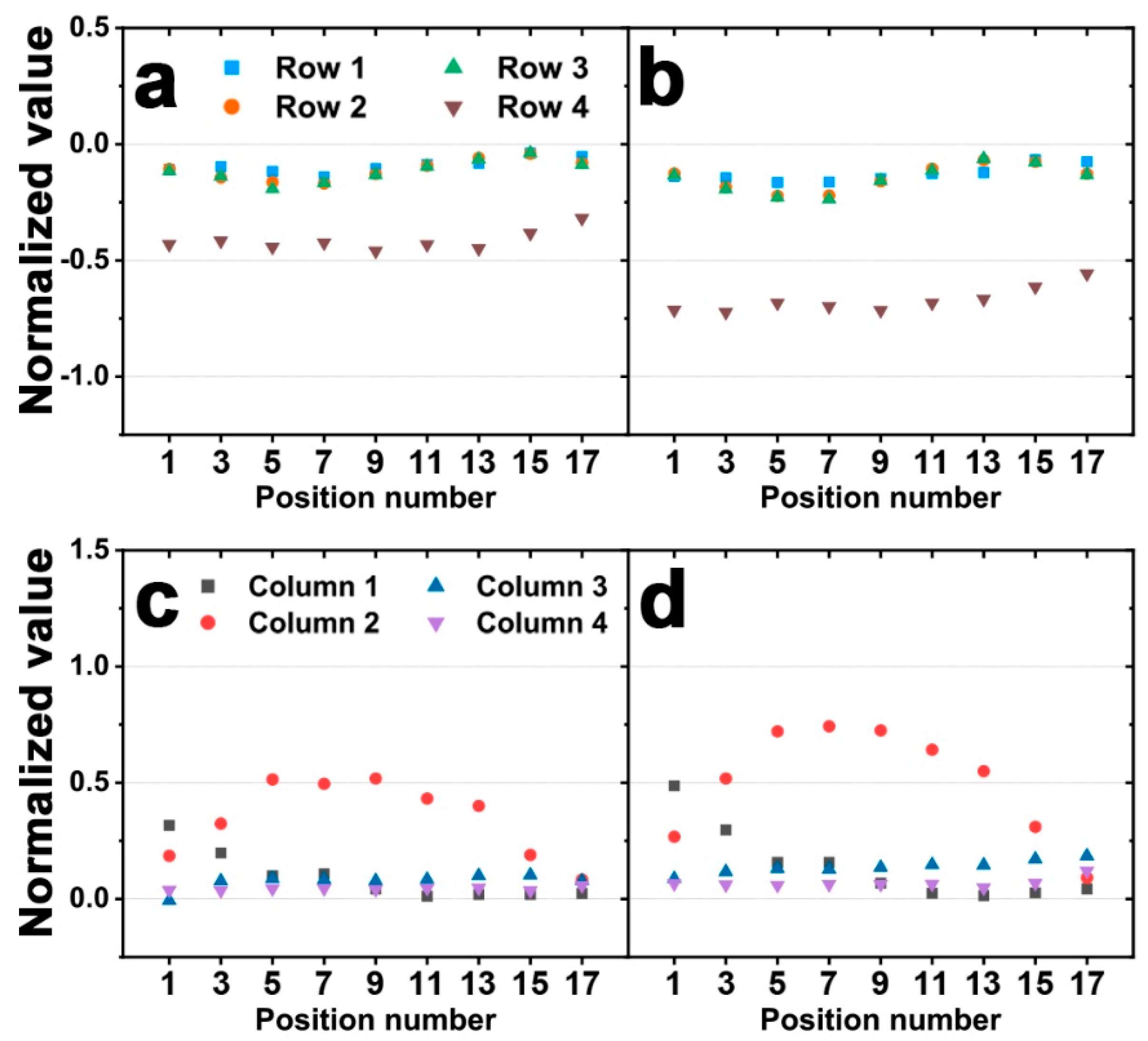
2.2. Simulation Results and Discussion
3. Experimental Validation
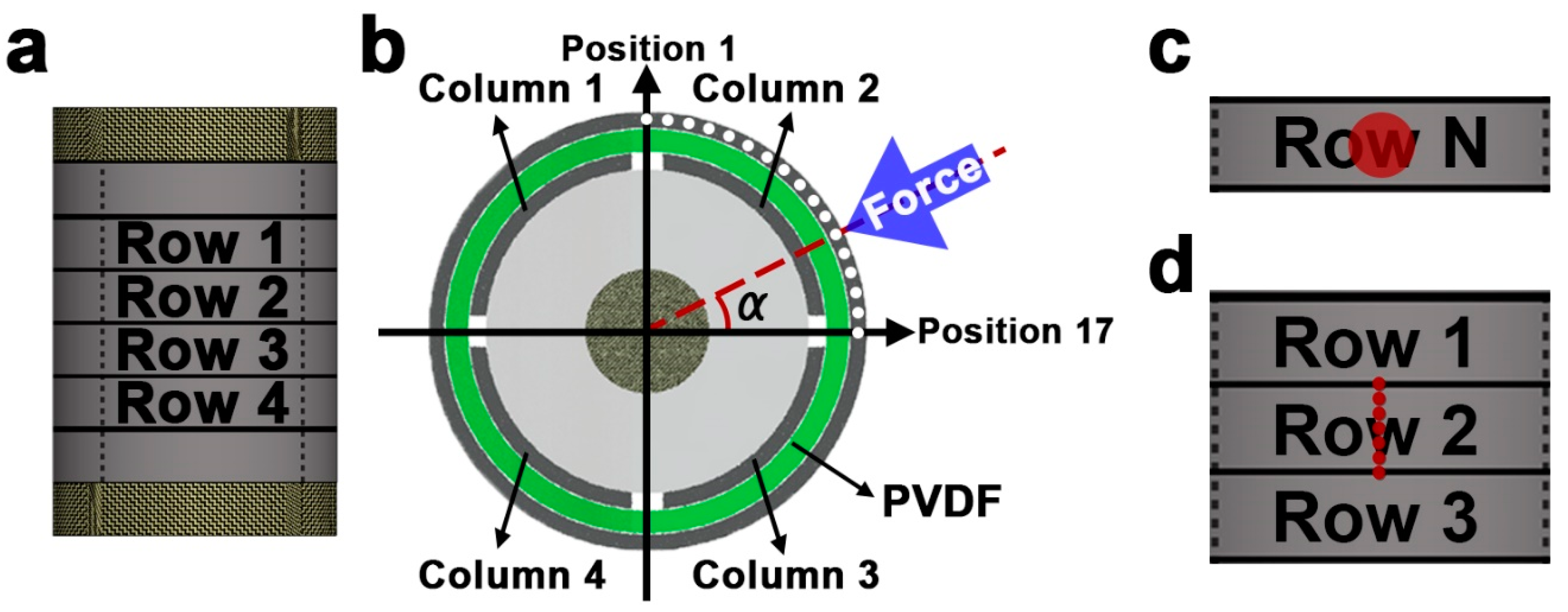
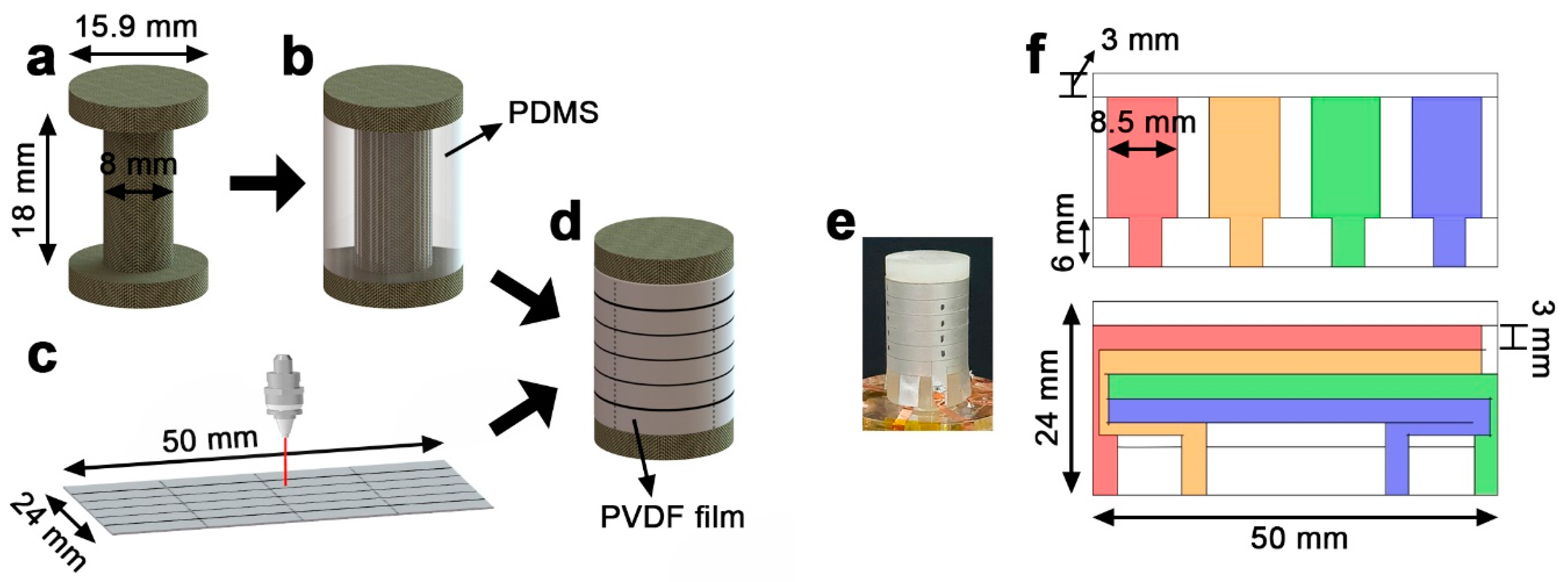
3.1. Fabrication of Cylindrical Piezoelectric Force Sensor
3.2. Experimental Setup
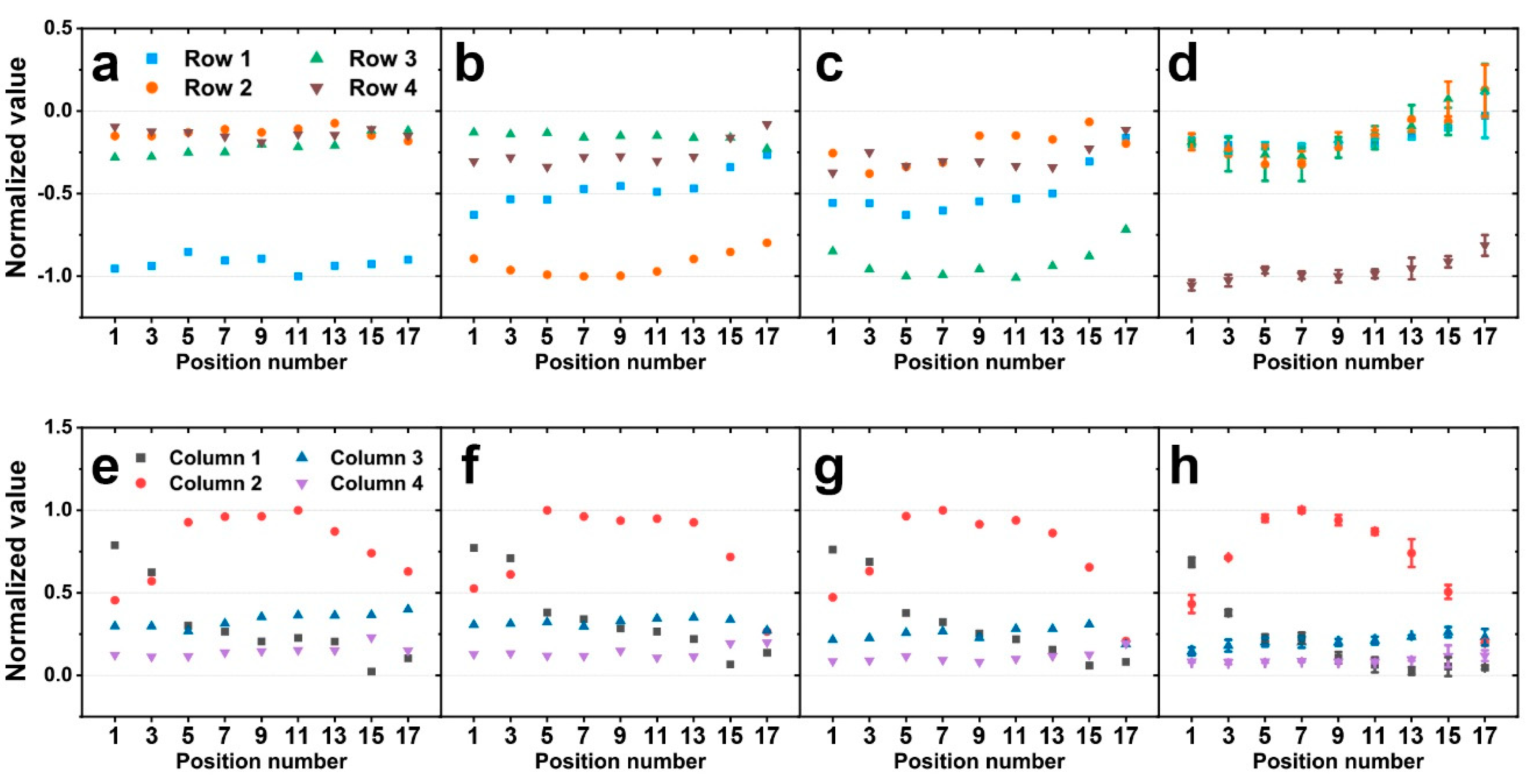
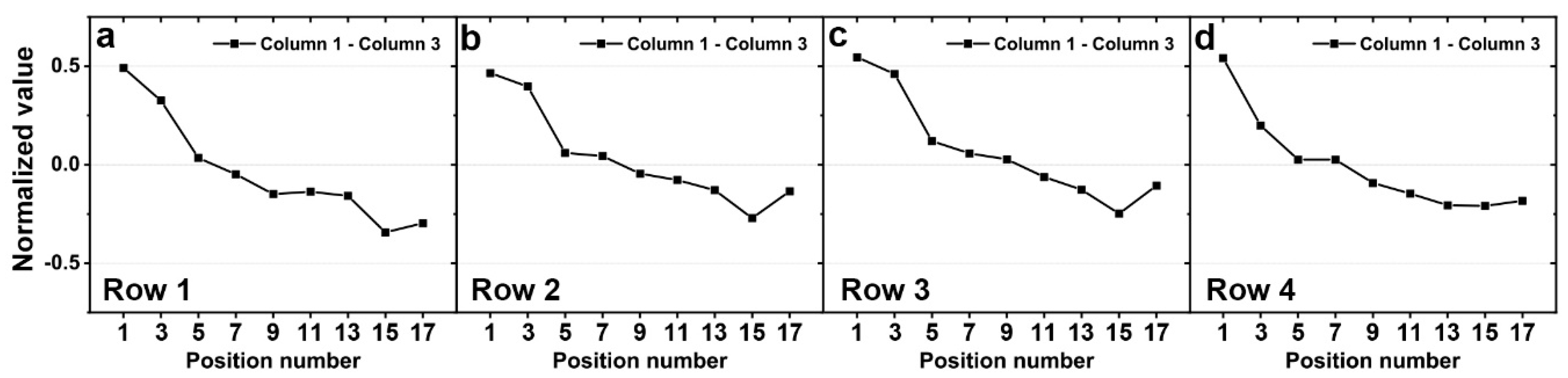
3.3. Model Validation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cha, Y.; Kim, H.; Kim, D. Flexible Piezoelectric Sensor-Based Gait Recognition. Sensors 2018, 18, 468. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Li, X.; Shao, J.; An, N.; Tian, H.; Wang, C.; Han, T.; Wang, L.; Lu, B. High-Performance Piezoelectric Nanogenerators with Imprinted P(VDF-TrFE)/BaTiO3 Nanocomposite Micropillars for Self-Powered Flexible Sensors. Small 2017, 13, 1604245. [Google Scholar] [CrossRef] [PubMed]
- Song, K.; Kim, S.H.; Jin, S.; Kim, S.; Lee, S.; Kim, J.-S.; Park, J.-M.; Cha, Y. Pneumatic actuator and flexible piezoelectric sensor for soft virtual reality glove system. Sci. Rep. 2019, 9, 8988. [Google Scholar] [CrossRef] [PubMed]
- Cha, Y.; Seo, J. Energy harvesting from a piezoelectric slipper during walking. J. Intell. Mater. Syst. Struct. 2018, 29, 1456–1463. [Google Scholar] [CrossRef]
- Kim, Y.; Song, K.; Song, J.-B.; Cha, Y. Energy harvesting from flexible piezoelectric ring. Smart Mater. Struct. 2019, 28, 084007. [Google Scholar] [CrossRef]
- Fan, F.R.; Tang, W.; Wang, Z.L. Flexible Nanogenerators for Energy Harvesting and Self-Powered Electronics. Adv. Mater. 2016, 28, 4283–4305. [Google Scholar] [CrossRef]
- Jaffe, B. Piezoelectric Ceramics; Elsevier: Amsterdam, The Netherlands, 2012; Volume 3. [Google Scholar]
- Ramadan, K.S.; Sameoto, D.; Evoy, S. A review of piezoelectric polymers as functional materials for electromechanical transducers. Smart Mater. Struct. 2014, 23, 033001. [Google Scholar] [CrossRef]
- Lu, K.; Huang, W.; Guo, J.; Gong, T.; Wei, X.; Lu, B.-W.; Liu, S.-Y.; Yu, B. Ultra-Sensitive Strain Sensor Based on Flexible Poly(vinylidene fluoride) Piezoelectric Film. Nanoscale Res. Lett. 2018, 13, 83. [Google Scholar] [CrossRef]
- Yamashita, T.; Takamatsu, S.; Okada, H.; Itoh, T.; Kobayashi, T. Ultra-Thin Piezoelectric Strain Sensor Array Integrated on a Flexible Printed Circuit Involving Transfer Printing Methods. IEEE Sens. J. 2016, 16, 8840–8846. [Google Scholar] [CrossRef]
- Morales, A.R.R.; Zaghloul, M.E. Highly Sensitive Wearable Piezoelectric Force Sensor with Quasi-Static Load Testing. IEEE Sens. J. 2018, 18, 9910–9918. [Google Scholar] [CrossRef]
- Yi, Z.; Yang, H.; Tian, Y.; Dong, X.; Liu, J.; Yang, B. Self-Powered Force Sensor Based on Thinned Bulk PZT for Real-Time Cutaneous Activities Monitoring. IEEE Electron Device Lett. 2018, 39, 1226–1229. [Google Scholar] [CrossRef]
- Hubbard, J.J.; Fleming, M.; Palmre, V.; Pugal, D.; Kim, K.J.; Leang, K.K. Monolithic IPMC Fins for Propulsion and Maneuvering in Bioinspired Underwater Robotics. IEEE J. Ocean. Eng. 2014, 39, 540–551. [Google Scholar] [CrossRef]
- Cho, K.H.; Jin, Y.H.; Kim, H.M.; Moon, H.; Koo, J.C.; Choi, H.R. Multifunctional Robotic Crawler for Inspection of Suspension Bridge Hanger Cables: Mechanism Design and Performance Validation. IEEE/ASME Trans. Mechatron. 2017, 22, 236–246. [Google Scholar] [CrossRef]
- Kim, U.; Kim, Y.B.; So, J.; Seok, D.; Choi, H.R. Sensorized Surgical Forceps for Robotic-Assisted Minimally Invasive Surgery. IEEE Trans. Ind. Electron. 2018, 65, 9604–9613. [Google Scholar] [CrossRef]
- Behbahani, S.B.; Tan, X. Role of Pectoral Fin Flexibility in Robotic Fish Performance. J. Nonlinear Sci. 2017, 27, 1155. [Google Scholar] [CrossRef]
- Zhang, B.; Fan, Y.; Yang, P.; Cao, T.; Liao, H. Worm-Like Soft Robot for Complicated Tubular Environments. Soft Robot. 2019, 6, 399–413. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Kashiwagi, T.; Arie, T.; Akita, S.; Takei, K. Human-Like Electronic Skin-Integrated Soft Robotic Hand. Adv. Intell. Syst. 2019, 1, 1900018. [Google Scholar] [CrossRef]
- Lee, D.; Park, J.; Park, S.; Baeg, M.; Bae, J. KITECH-Hand: A Highly Dexterous and Modularized Robotic Hand. IEEE/ASME Trans. Mechatron. 2017, 22, 876–887. [Google Scholar] [CrossRef]
- Liu, H.; Nguyen, K.C.; Perdereau, V.; Bimbo, J.; Back, J.; Godden, M.; Seneviratne, L.D.; Althoefer, K. Finger contact sensing and the application in dexterous hand manipulation. Auton. Robots 2015, 39, 25. [Google Scholar] [CrossRef]
- Wijayarathne, L.; Blaise, B.; Ward, D.; Hammond, F.L. Force Feedback-Enabled Dexterous Robotic Micromanipulation Platform for Surgical Tasks. In In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 2297–2303. [Google Scholar]
- Drimus, A.; Kootstra, G.; Bilberg, A.; Kragic, D. Design of a flexible tactile sensor for classification of rigid and deformable objects. Robot. Auton. Syst. 2014, 62, 3–15. [Google Scholar] [CrossRef]
- Liang, G.; Wang, Y.; Mei, D.; Xi, K.; Chen, Z. Flexible Capacitive Tactile Sensor Array With Truncated Pyramids as Dielectric Layer for Three-Axis Force Measurement. J. Microelectromech. Syst. 2015, 24, 1510–1519. [Google Scholar] [CrossRef]
- Viry, L.; Levi, A.; Totaro, M.; Mondini, A.; Mattoli, V.; Mazzolai, B.; Beccai, L. Flexible Three-Axial Force Sensor for Soft and Highly Sensitive Artificial Touch. Adv. Mater. 2014, 26, 2659–2664. [Google Scholar] [CrossRef] [PubMed]
- Dobrzynska, J.A.; Gijs, M.A.M. Polymer-based flexible capacitive sensor for three-axial force measurements. J. Micromech. Microeng. 2012, 23, 015009. [Google Scholar] [CrossRef]
- Vogt, D.M.; Park, Y.; Wood, R.J. Design and Characterization of a Soft Multi-Axis Force Sensor Using Embedded Microfluidic Channels. IEEE Sens. J. 2013, 13, 4056–4064. [Google Scholar] [CrossRef]
- Thanh-Vinh, N.; Binh-Khiem, N.; Takahashi, H.; Matsumoto, K.; Shimoyama, I. High-sensitivity triaxial tactile sensor with elastic microstructures pressing on piezoresistive cantilevers. Sens. Actuators A Phys. 2014, 215, 167–175. [Google Scholar] [CrossRef]
- Yang, J.; Li, X.; X, L.; Bao, W.; Chen, R. Three-Dimensional Interfacial Stress Sensor Based on Graphene Foam. IEEE Sens. J. 2018, 18, 7956–7963. [Google Scholar] [CrossRef]
- Ting, Y.; Suprapto; Nugraha, A.; Chiu, C.W.; Gunawan, H. Design and characterization of one-layer PVDF thin film for a 3D force sensor. Sens. Actuators A Phys. 2016, 250, 129–137. [Google Scholar] [CrossRef]
- Kim, M.-S.; Ahn, H.-R.; Lee, S.; Kim, C.; Kim, Y.-J. A dome-shaped piezoelectric tactile sensor arrays fabricated by an air inflation technique. Sens. Actuators A Phys. 2014, 212, 151–158. [Google Scholar] [CrossRef]
- Yang, J.C.; Kim, J.O.; Oh, J.; Kwon, S.Y.; Sim, J.Y.; Kim, D.W.; Choi, H.B.; Park, S. Microstructured Porous Pyramid-Based Ultrahigh Sensitive Pressure Sensor Insensitive to Strain and Temperature. ACS Appl. Mater. Inter. 2019, 11, 19472–19480. [Google Scholar] [CrossRef]
- Park, J.; Kim, J.; Hong, J.; Lee, H.; Lee, Y.; Cho, S.; Kim, S.W.; Kim, J.J.; Kim, S.Y.; Ko, H. Tailoring force sensitivity and selectivity by microstructure engineering of multidirectional electronic skins. NPG Asia Mater. 2018, 10, 163–176. [Google Scholar] [CrossRef]
- Li, B.; Gil, B.; Power, M.; Gao, A.Z.; Treratanakulchai, S.; Anastasova, S.; Yang, G.Z. Carbon-Nanotube-Coated 3D Microspring Force Sensor for Medical Applications. ACS Appl. Mater. Int. 2019, 11, 35577–35586. [Google Scholar] [CrossRef] [PubMed]
- Yu, P.; Liu, W.; Gu, C.; Cheng, X.; Fu, X. Flexible Piezoelectric Tactile Sensor Array for Dynamic Three-Axis Force Measurement. Sensors 2016, 16, 819. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Shao, J.; Tian, H.; Li, X.; Tian, Y.; Wang, C. Flexible three-axial tactile sensors with microstructure-enhanced piezoelectric effect and specially-arranged piezoelectric arrays. Smart Mater. Struct. 2018, 27, 025018. [Google Scholar] [CrossRef]
- Cha, Y.; Nam, K.; Kim, D. Patient Posture Monitoring System Based on Flexible Sensors. Sensors 2017, 17, 584. [Google Scholar] [CrossRef] [PubMed]
- Cha, Y.; Hong, S. Energy harvesting from walking motion of a humanoid robot using a piezoelectric composite. Smart Mater. Struct. 2016, 25, 10LT01. [Google Scholar] [CrossRef]
- Lei, H.; Sharif, M.A.; Tan, X.B. Dynamics of Omnidirectional IPMC Sensor: Experimental Characterization and Physical Modeling. IEEE/ASME Trans. Mechatron. 2016, 21, 601–612. [Google Scholar] [CrossRef]
- Lee, H.B.; Kim, Y.W.; Yoon, J.; Lee, N.K.; Park, S.H. 3D customized and flexible tactile sensor using a piezoelectric nanofiber mat and sandwich-molded elastomer sheets. Smart Mater. Struct. 2017, 26, 045032. [Google Scholar] [CrossRef]
- Yin, J.Z.; Santos, V.J.; Posner, J.D. Bioinspired flexible microfluidic shear force sensor skin. Sens. Actuators A Phys 2017, 264, 289–297. [Google Scholar] [CrossRef]



| Standard Mesh (the Preceding Data) | Fine Mesh | Finer Mesh | |
|---|---|---|---|
| Domain elements | 82,820 | 153,217 | 292,355 |
| Boundary elements | 35,383 | 55,905 | 103,672 |
| Standard Mesh (the Preceding Data) | Fine Mesh | Finer Mesh | |
|---|---|---|---|
| row 1 | 1.000 | 1.020 | 0.896 |
| column 1 | 0.504 | 0.509 | 0.444 |
| column 2 | 0.521 | 0.518 | 0.436 |
| column 3 | 0.106 | 0.117 | 0.120 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.R.; Neubauer, J.; Kim, K.J.; Cha, Y. Multidirectional Cylindrical Piezoelectric Force Sensor: Design and Experimental Validation. Sensors 2020, 20, 4840. https://doi.org/10.3390/s20174840
Lee YR, Neubauer J, Kim KJ, Cha Y. Multidirectional Cylindrical Piezoelectric Force Sensor: Design and Experimental Validation. Sensors. 2020; 20(17):4840. https://doi.org/10.3390/s20174840
Chicago/Turabian StyleLee, Ye Rim, Justin Neubauer, Kwang Jin Kim, and Youngsu Cha. 2020. "Multidirectional Cylindrical Piezoelectric Force Sensor: Design and Experimental Validation" Sensors 20, no. 17: 4840. https://doi.org/10.3390/s20174840
APA StyleLee, Y. R., Neubauer, J., Kim, K. J., & Cha, Y. (2020). Multidirectional Cylindrical Piezoelectric Force Sensor: Design and Experimental Validation. Sensors, 20(17), 4840. https://doi.org/10.3390/s20174840







