Structural Model Identification Using a Modified Electromagnetism-Like Mechanism Algorithm
Abstract
1. Introduction
2. Optimization Formulation of Structural Model Identification
3. Electromagnetism-Like Mechanism Algorithm
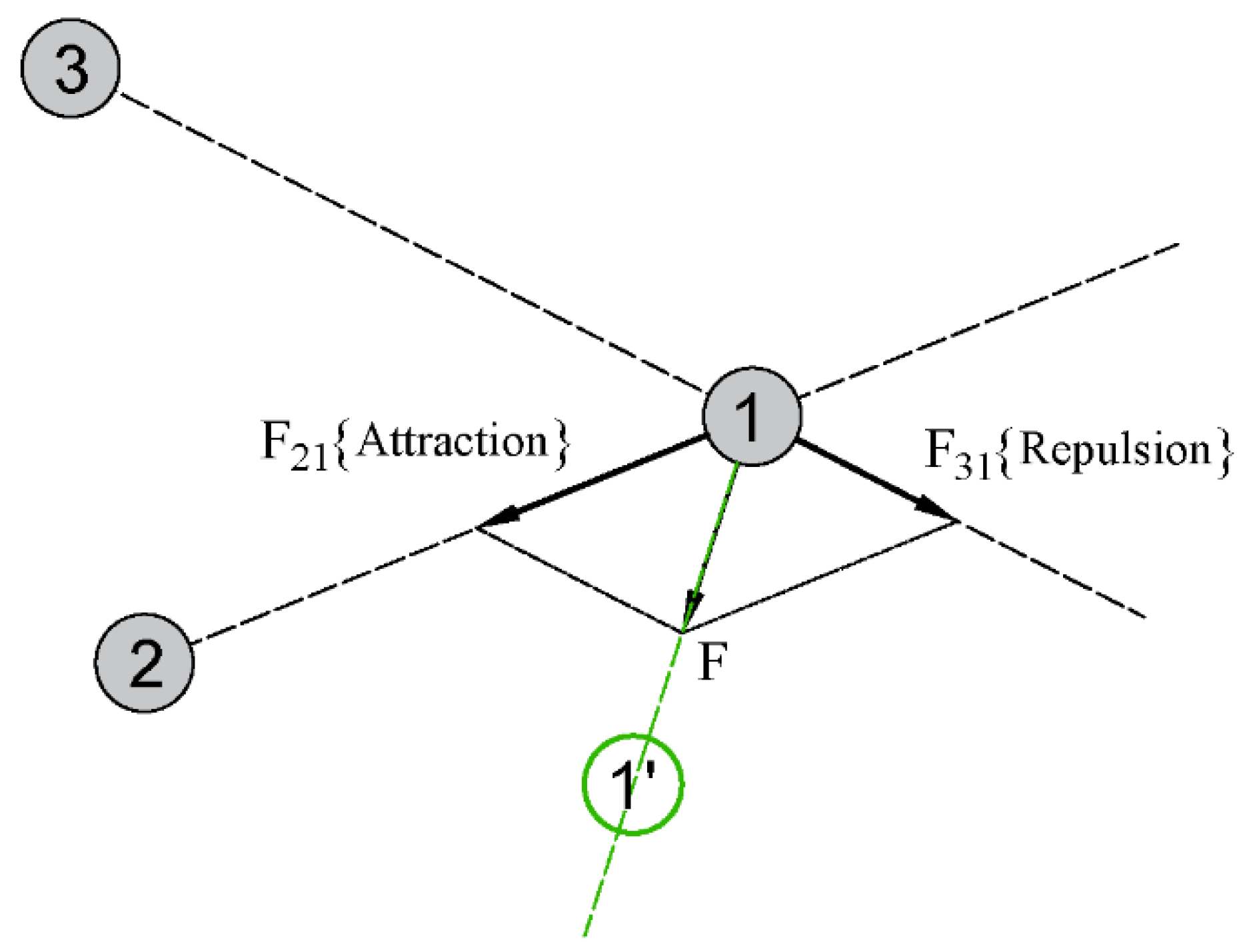
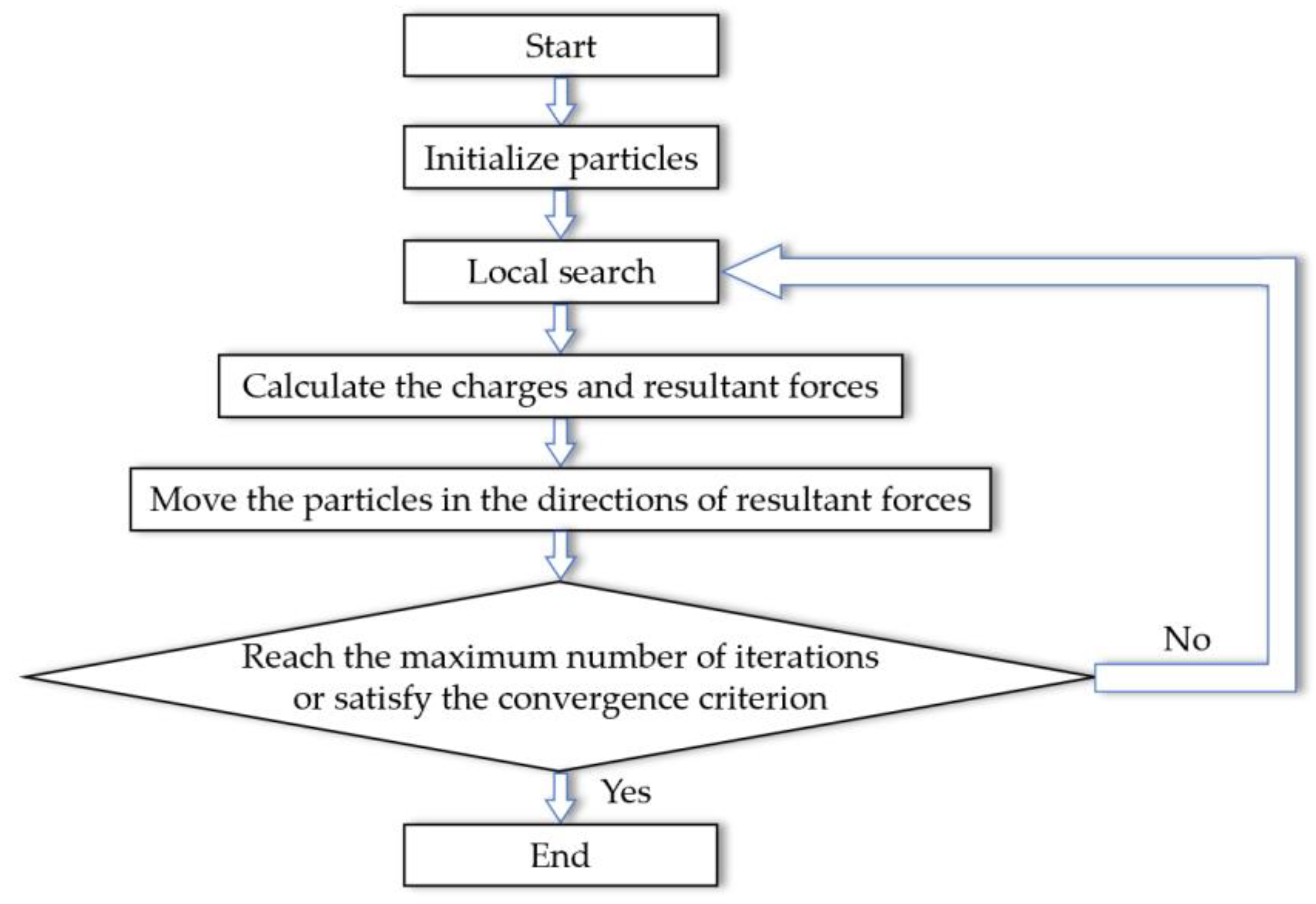
3.1. The Original EM Algorithm
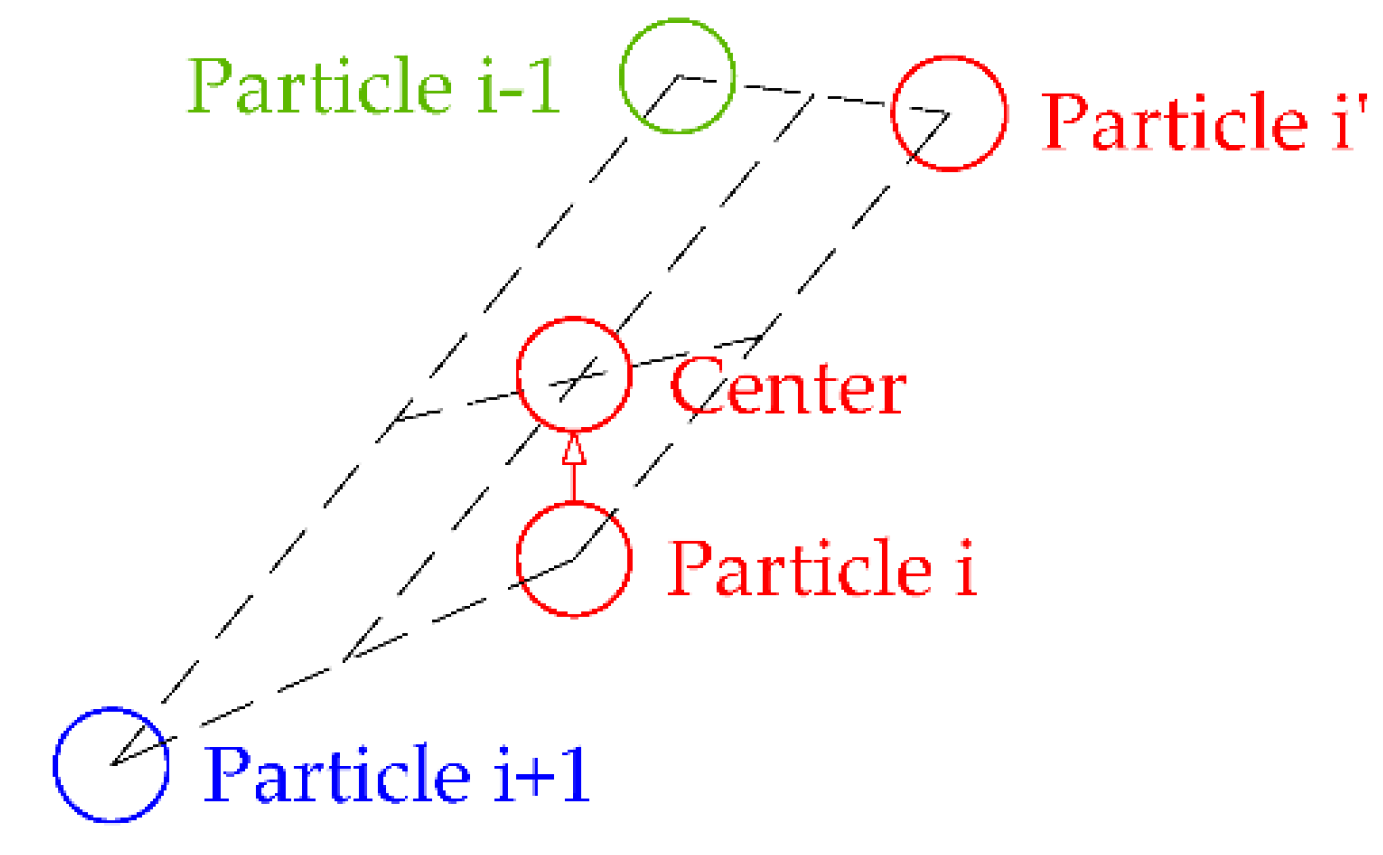
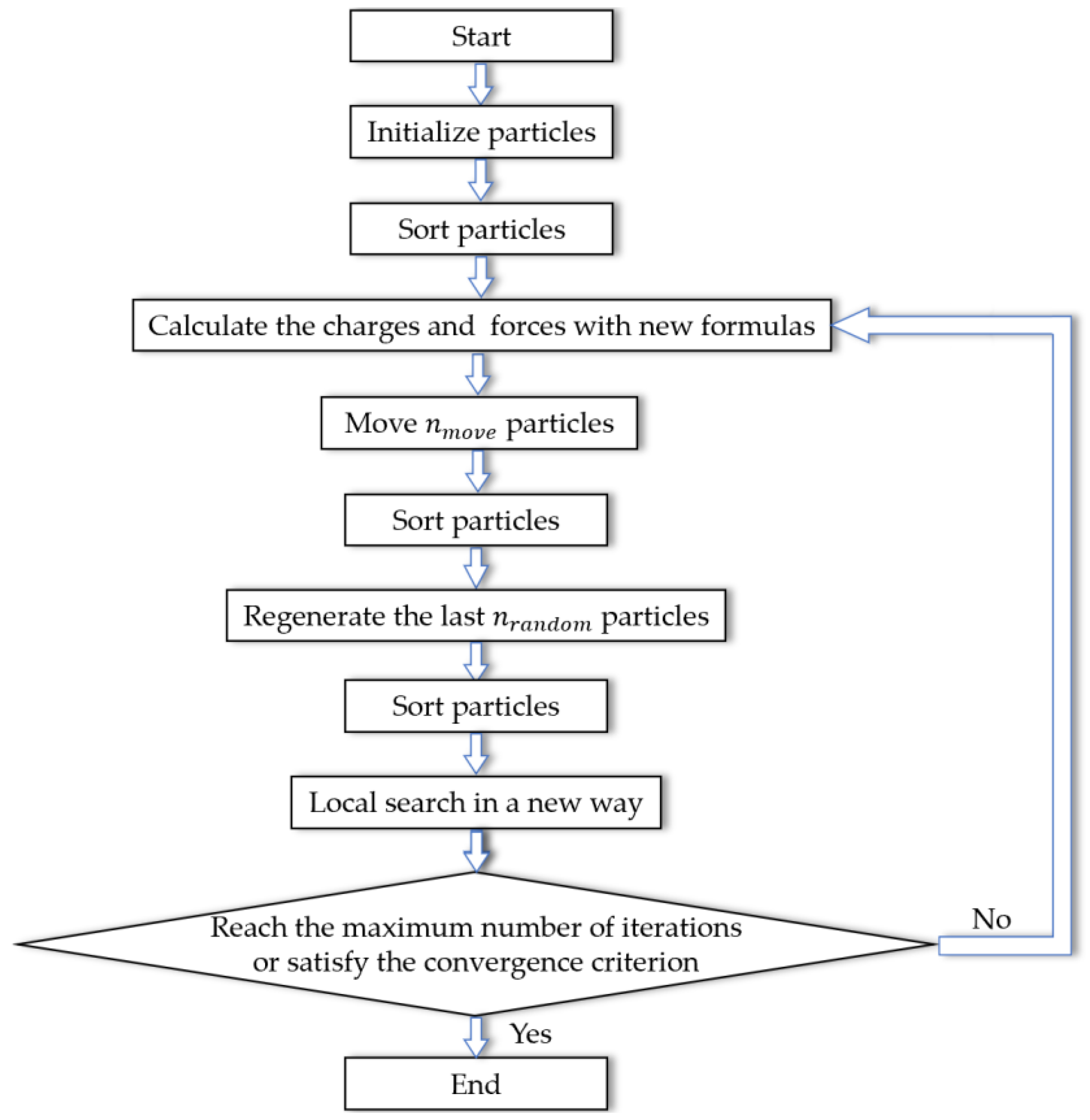
3.2. The Modified EM Algorithm
4. Illustrative Examples
4.1. Benchmark Functions
4.2. Numerical Truss Model
- Case 1: 1% noise for frequency, 5% noise for mode shape, 11 measurements and 8 modes.
- Case 2: 2% noise for frequency, 10% noise for mode shape, 11 measurements and 8 modes.
- Case 3: 1% noise for frequency, 5% noise for mode shape, 7 measurements and 8 modes.
- Case 4: 1% noise for frequency, 5% noise for mode shape, 11 measurements and 5 modes.
4.3. Experimental Shear-Building Model
5. Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A scaling factor of the predicted mode shape with respect to | |
| DOFs | Degrees of freedom |
| Objective function to be minimized | |
| Attraction force | |
| Repulsion force | |
| The resultant force on particle i of the original EM algorithm | |
| The measured modal frequency of jth mode in the ith data set | |
| The predicted modal frequency of jth mode | |
| M | Global mass matrix |
| MAC | Modal Assurance Criterion |
| m | The number of particles in the original EM algorithm |
| max_iter | The number of maximum iterations |
| N | The number of DOFs |
| The dimension of the problem | |
| The number of particles | |
| The number of particles regenerated randomly in each iteration | |
| Nθ | The number of parameters |
| Ne | The total number of finite elements |
| Nm | The number of modes |
| Ns | The number of data sets of measured modal data |
| The charge quantity of particle i | |
| K | Global stiffness matrix |
| kei | The stiffness matrix of the ith element |
| RNG | The feasible step size vector |
| Movement vector | |
| Particle i | |
| The particle with the optimal objective function value | |
| The particle with the second best objective function value | |
| The particle with the third best objective function value | |
| Rate of repulsion uniformly distributed in | |
| Upper bound of in each iteration | |
| Step size in the local search of the original EM algorithm | |
| θ | Parameters of the stiffness matrix K |
| The random step of movement used in the original EM algorithm | |
| The measured mode shape of jth mode in the ith data set | |
| The predicted mode shape of jth mode |
Appendix A
| Algorithm A1. |
| 1: % and are row vectors 2: 3: 4: for do 5: % f_vals is a column vector 6: end for 7: % 8: |
| Algorithm A2. |
| 1: % |
| Algorithm A3. |
| 1: % if 2: % if |
| Algorithm A4. |
| 1: for do 2: % 3: end for |
| AlgorithmA5. |
| 1: 2: 3: 4: 5: % 6: for do 7: 8: 9: 10: 11: 12: if 13: % Center of four particles 14: end if 15: % 16: end for |
| AlgorithmA6. |
| 1: for do 2: 3: 4: end for |
| AlgorithmA7. |
| 1: % or 2: for do 3: 4: 5: if % is 6: % 7: % 8: else if 9: % 10: end if 11: for do 12: 13: 14: if 15: % 16: % 17: break 18: elseif 19: % 20: end if 21: end for 22: end for |
Appendix B
| AlgorithmA8. Complete pseudocode |
| 1: 2: 3: for do 4: 5: 6: 7: 8: 9: 10: 11: if 12: 13: 14: end if 15: end for 16: |
References
- Alvin, K.F.; Robertson, A.N.; Reich, G.W.; Park, K.C. Structural system identification: From reality to models. Comput. Struct. 2003, 81, 1149–1176. [Google Scholar] [CrossRef]
- Tang, H.; Xue, S.; Fan, C. Differential evolution strategy for structural system identification. Comput. Struct. 2008, 86, 2004–2012. [Google Scholar] [CrossRef]
- Sun, H.; Luş, H.; Betti, R. Identification of structural models using a modified Artificial Bee Colony algorithm. Comput. Struct. 2013, 116, 59–74. [Google Scholar] [CrossRef]
- Xu, B.; Chen, G.; Wu, Z.S. Parametric Identification for a Truss Structure Using Axial Strain. Comput. Civ. Infrastruct. Eng. 2007, 22, 210–222. [Google Scholar] [CrossRef]
- Feng, Z.; Lin, Y.; Wang, W.; Hua, X.; Chen, Z. Probabilistic Updating of Structural Models for Damage Assessment Using Approximate Bayesian Computation. Sensors 2020, 20, 3197. [Google Scholar] [CrossRef]
- Mao, J.-X.; Wang, H.; Feng, D.-M.; Tao, T.-Y.; Zheng, W.-Z. Investigation of dynamic properties of long-span cable-stayed bridges based on one-year monitoring data under normal operating condition. Struct. Control Health Monit. 2018, 25, e2146. [Google Scholar] [CrossRef]
- Chudzikiewicz, A.; Bogacz, R.; Kostrzewski, M.; Konowrocki, R. Condition monitoring of railway track systems by using acceleration signals on wheelset axle-boxes. Transport 2017, 33, 555–566. [Google Scholar] [CrossRef]
- Bogoevska, S.; Spiridonakos, M.; Chatzi, E.; Dumova-Jovanoska, E.; Höffer, R. A Data-Driven Diagnostic Framework for Wind Turbine Structures: A Holistic Approach. Sensors 2017, 17, 720. [Google Scholar] [CrossRef]
- Kostrzewski, M. Sensitivity Analysis of Selected Parameters in the Order Picking Process Simulation Model, with Randomly Generated Orders. Entropy 2020, 22, 423. [Google Scholar] [CrossRef]
- Ambroziak, T.; Malesa, A.; Kostrzewski, M. Analysis of multicriteria transportation problem connected to minimization of means of transport number applied in a selected example. Pr. Nauk. Politech. Warsz. Transp. 2018, 123, 5–20. [Google Scholar]
- Mottershead, J.E.; Link, M.; Friswell, M.I. The sensitivity method in finite element model updating: A tutorial. Mech. Syst. Signal Process. 2011, 25, 2275–2296. [Google Scholar] [CrossRef]
- Yan, W.-J.; Katafygiotis, L.S. A novel Bayesian approach for structural model updating utilizing statistical modal information from multiple setups. Struct. Saf. 2015, 52, 260–271. [Google Scholar] [CrossRef]
- Brownjohn, J.M.W.; Xia, P.-Q. Dynamic Assessment of Curved Cable-Stayed Bridge by Model Updating. J. Struct. Eng. 2000, 126, 252–260. [Google Scholar] [CrossRef]
- Teughels, A.; De Roeck, G. Structural damage identification of the highway bridge Z24 by FE model updating. J. Sound Vib. 2004, 278, 589–610. [Google Scholar] [CrossRef]
- Jaishi, B.; Ren, W.-X. Structural Finite Element Model Updating Using Ambient Vibration Test Results. J. Struct. Eng. 2005, 131, 617–628. [Google Scholar] [CrossRef]
- Bakir, P.G.; Reynders, E.; De Roeck, G. Sensitivity-based finite element model updating using constrained optimization with a trust region algorithm. J. Sound Vib. 2007, 305, 211–225. [Google Scholar] [CrossRef]
- Hua, X.G.; Ni, Y.Q.; Ko, J.M. Adaptive regularization parameter optimization in output-error-based finite element model updating. Mech. Syst. Signal Process. 2009, 23, 563–579. [Google Scholar] [CrossRef]
- Sarmadi, H.; Karamodin, A.; Entezami, A. A new iterative model updating technique based on least squares minimal residual method using measured modal data. Appl. Math. Model. 2016, 40, 10323–10341. [Google Scholar] [CrossRef]
- Perera, R.; Ruiz, A.; Manzano, C. Performance assessment of multicriteria damage identification genetic algorithms. Comput. Struct. 2009, 87, 120–127. [Google Scholar] [CrossRef]
- Shabbir, F.; Omenzetter, P. Particle Swarm Optimization with Sequential Niche Technique for Dynamic Finite Element Model Updating. Comput. Civ. Infrastruct. Eng. 2015, 30, 359–375. [Google Scholar] [CrossRef]
- Seyedpoor, S.M.; Shahbandeh, S.; Yazdanpanah, O. An efficient method for structural damage detection using a differential evolution algorithm-based optimisation approach. Civ. Eng. Environ. Syst. 2015, 32, 230–250. [Google Scholar] [CrossRef]
- Xu, H.; Liu, J.; Lu, Z. Structural damage identification based on cuckoo search algorithm. Adv. Struct. Eng. 2016, 19, 849–859. [Google Scholar] [CrossRef]
- Mishra, M.; Barman, S.K.; Maity, D.; Maiti, D.K. Performance Studies of 10 Metaheuristic Techniques in Determination of Damages for Large-Scale Spatial Trusses from Changes in Vibration Responses. J. Comput. Civ. Eng. 2020, 34, 04019052. [Google Scholar] [CrossRef]
- Birbil, Ş.I.; Fang, S.-C. An electromagnetism-like mechanism for global optimization. J. Glob. Optim. 2003, 25, 263–282. [Google Scholar] [CrossRef]
- Birbil, Ş.I.; Fang, S.-C.; Sheu, R.-L. On the Convergence of a Population-Based Global Optimization Algorithm. J. Glob. Optim. 2004, 30, 301–318. [Google Scholar] [CrossRef]
- Rocha, A.M.A.C.; Fernandes, E.M.G.P. Modified movement force vector in an electromagnetism-like mechanism for global optimization. Optim. Methods Softw. 2009, 24, 253–270. [Google Scholar] [CrossRef]
- Zhang, C.; Li, X.; Gao, L.; Wu, Q. An improved electromagnetism-like mechanism algorithm for constrained optimization. Expert Syst. Appl. 2013, 40, 5621–5634. [Google Scholar] [CrossRef]
- Tan, J.-D.; Dahari, M.; Koh, S.-P.; Koay, Y.-Y.; Abed, I.-A. An improved electromagnetism-like algorithm for numerical optimization. Theor. Comput. Sci. 2016, 641, 75–84. [Google Scholar] [CrossRef]
- Tan, J.D.; Dahari, M.; Koh, S.P.; Koay, Y.Y.; Abed, I.A. A new experiential learning electromagnetism-like mechanism for numerical optimization. Expert Syst. Appl. 2017, 86, 321–333. [Google Scholar] [CrossRef]
- Debels, D.; De Reyck, B.; Leus, R.; Vanhoucke, M. A hybrid scatter search/electromagnetism meta-heuristic for project scheduling. Eur. J. Oper. Res. 2006, 169, 638–653. [Google Scholar] [CrossRef]
- Yurtkuran, A.; Emel, E. A new Hybrid Electromagnetism-like Algorithm for capacitated vehicle routing problems. Expert Syst. Appl. 2010, 37, 3427–3433. [Google Scholar] [CrossRef]
- Abdullah, S.; Turabieh, H.; McCollum, B.; McMullan, P. A hybrid metaheuristic approach to the university course timetabling problem. J. Heuristics 2012, 18, 1–23. [Google Scholar] [CrossRef]
- Guan, X.; Dai, X.; Qiu, B.; Li, J. A revised electromagnetism-like mechanism for layout design of reconfigurable manufacturing system. Comput. Ind. Eng. 2012, 63, 98–108. [Google Scholar] [CrossRef]
- Wang, K.-J.; Adrian, A.M.; Chen, K.-H.; Wang, K.-M. An improved electromagnetism-like mechanism algorithm and its application to the prediction of diabetes mellitus. J. Biomed. Inform. 2015, 54, 220–229. [Google Scholar] [CrossRef] [PubMed]
- El-Hana Bouchekara, H.R.; Abido, M.A.; Chaib, A.E. Optimal Power Flow Using an Improved Electromagnetism-like Mechanism Method. Electr. Power Compon. Syst. 2016, 44, 434–449. [Google Scholar] [CrossRef]
- Le, D.T.; Bui, D.-K.; Ngo, T.D.; Nguyen, Q.-H.; Nguyen-Xuan, H. A novel hybrid method combining electromagnetism-like mechanism and firefly algorithms for constrained design optimization of discrete truss structures. Comput. Struct. 2019, 212, 20–42. [Google Scholar] [CrossRef]
- Hosseinzadeh, Y.; Taghizadieh, N.; Jalili, S. Hybridizing electromagnetism-like mechanism algorithm with migration strategy for layout and size optimization of truss structures with frequency constraints. Neural Comput. Appl. 2016, 27, 953–971. [Google Scholar] [CrossRef]
- Vanik, M.W.; Beck, J.L.; Au, S.K. Bayesian Probabilistic Approach to Structural Health Monitoring. J. Eng. Mech. 2000, 126, 738–745. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks—Conference Proceedings, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Chang, C.C.; Poon, C.W. Nonlinear Identification of Lumped-Mass Buildings Using Empirical Mode Decomposition and Incomplete Measurement. J. Eng. Mech. 2010, 136, 273–281. [Google Scholar] [CrossRef]
- Feng, Z.Q.; Zhao, B.; Hua, X.G.; Chen, Z.Q. Enhanced EMD-RDT Method for Output-Only Ambient Modal Identification of Structures. J. Aerosp. Eng. 2019, 32, 04019046. [Google Scholar] [CrossRef]
- Feng, Z.; Shen, W.; Chen, Z. Consistent Multilevel RDT-ERA for Output-Only Ambient Modal Identification of Structures. Int. J. Struct. Stab. Dyn. 2017, 17, 1750106. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification of output-only systems using frequency domain decomposition. Smart Mater. Struct. 2001, 10, 441–445. [Google Scholar] [CrossRef]
- Katafygiotis, L.S.; Beck, J.L. Updating Models and Their Uncertainties. II: Model Identifiability. J. Eng. Mech. 1998, 124, 463–467. [Google Scholar] [CrossRef]


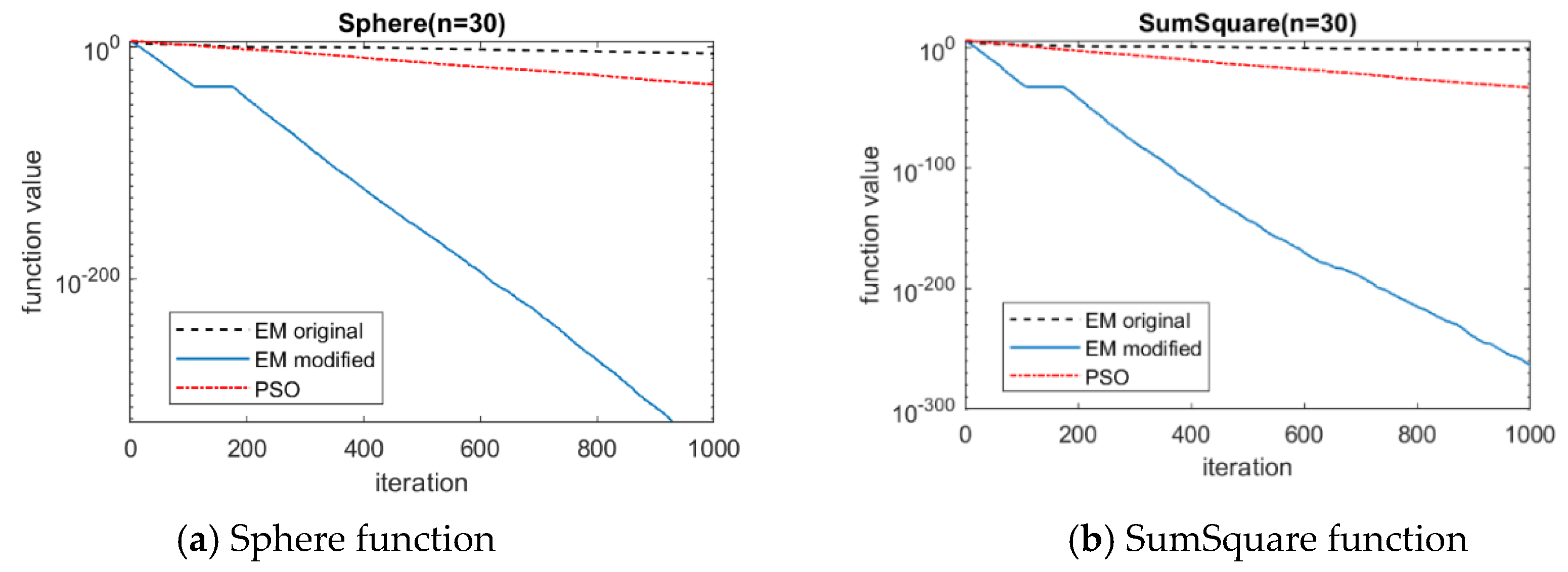
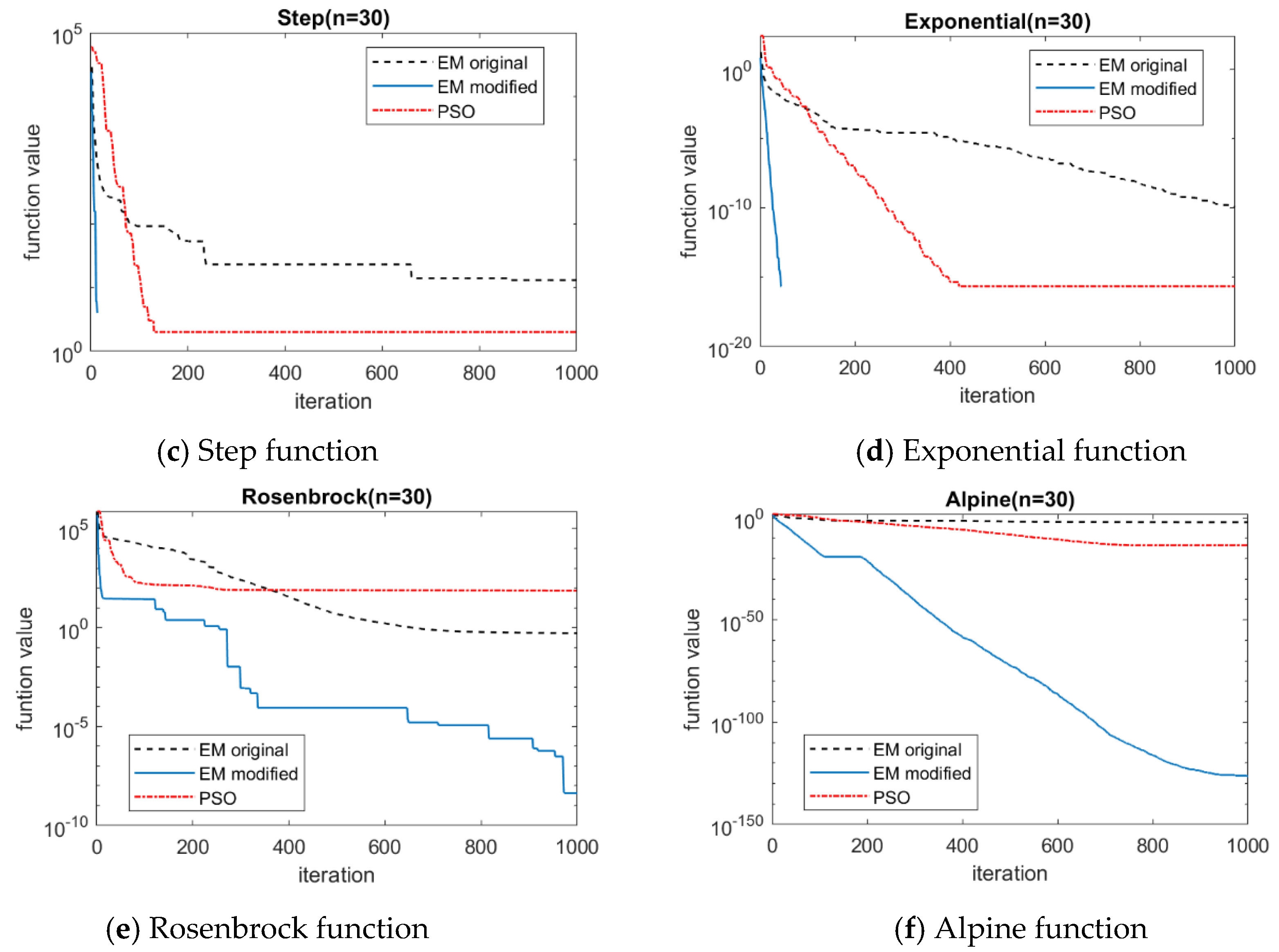



| Name | Function | Search Range | Accepted Accuracy |
|---|---|---|---|
| Sphere | |||
| SumSquare | |||
| Step | |||
| Exponential | |||
| Rosenbrock | |||
| Alpine |
| Function | Sphere | SumSquare | Step | Exponential | Rosenbrock | Alpine | |
|---|---|---|---|---|---|---|---|
| Original EM | mean | 1.20 × 10−6 | 0.0089 | 13.64 | 1.03 × 10−10 | 21.28 | 0.0031 |
| max | 1.74 × 10−6 | 0.12 | 22 | 1.45 × 10−10 | 140.65 | 0.015 | |
| min | 6.89 × 10−7 | 2.93 × 10−5 | 6 | 6.66 × 10−11 | 7.33 × 10−4 | 5.32 × 10−5 | |
| avg time | 9.24 s | 9.60 s | 9.51 s | 9.38 s | 9.03 s | 9.46 s | |
| Modified EM | mean | 0 | 7.10 × 10−239 | 0 | 0 | 0.0038 | 5.04 × 10−107 |
| max | 0 | 3.55 × 10−237 | 0 | 0 | 0.053 | 2.52 × 10−105 | |
| min | 0 | 5.08 × 10−241 | 0 | 0 | 1.15 × 10−9 | 2.79 × 10−141 | |
| avg time | 2.78 s | 2.88 s | 4.89 s | 2.65 s | 3.66 s | 3.01 s | |
| PSO | mean | 2.93 × 10−34 | 2.25 × 10−29 | 2.68 | 4.22 × 10−16 | 30.19 | 1.07 × 10−14 |
| max | 7.04 × 10−33 | 1.12 × 10−27 | 19 | 1.78 × 10−15 | 138.04 | 3.86 × 10−14 | |
| min | 2.02 × 10−37 | 6.76× 10−37 | 0 | 2.22 × 10−16 | 0.21 | 1.33 × 10−15 | |
| avg time | 3.10 s | 3.24 s | 2.51 s | 2.71 s | 2.96 s | 2.97 s | |
| Case 1 | Case 2 | Case 3 | Case 4 | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Standard Deviation | Mean | Standard Deviation | Mean | Standard Deviation | Mean | Standard Deviation | |
| θ19 | −0.1502 | 2.401 × 10−4 | −0.1510 | 4.082 × 10−4 | −0.1515 | 5.380 × 10−3 | −0.1501 | 7.174 × 10−4 |
| θ20 | −0.2006 | 6.237 × 10−4 | −0.2021 | 6.321 × 10−4 | −0.2013 | 4.450 × 10−3 | −2.005 | 7.855 × 10−4 |
| Mode | Identified Frequency | Nominal Frequency | MACn−e | Updated Frequency | MACu−e |
|---|---|---|---|---|---|
| 1 | 4.246 | 4.545 (7%) | 0.9975 | 4.258 (0.3%) | 0.9997 |
| 2 | 12.809 | 13.023 (1.6%) | 0.9842 | 12.783 (0.2%) | 0.9949 |
| 3 | 18.685 | 18.21 (−2.5%) | 0.9589 | 18.607 (0.4%) | 0.9698 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Z.; Ye, Z.; Wang, W.; Lin, Y.; Chen, Z.; Hua, X. Structural Model Identification Using a Modified Electromagnetism-Like Mechanism Algorithm. Sensors 2020, 20, 4789. https://doi.org/10.3390/s20174789
Feng Z, Ye Z, Wang W, Lin Y, Chen Z, Hua X. Structural Model Identification Using a Modified Electromagnetism-Like Mechanism Algorithm. Sensors. 2020; 20(17):4789. https://doi.org/10.3390/s20174789
Chicago/Turabian StyleFeng, Zhouquan, Zhengtao Ye, Wenzan Wang, Yang Lin, Zhengqing Chen, and Xugang Hua. 2020. "Structural Model Identification Using a Modified Electromagnetism-Like Mechanism Algorithm" Sensors 20, no. 17: 4789. https://doi.org/10.3390/s20174789
APA StyleFeng, Z., Ye, Z., Wang, W., Lin, Y., Chen, Z., & Hua, X. (2020). Structural Model Identification Using a Modified Electromagnetism-Like Mechanism Algorithm. Sensors, 20(17), 4789. https://doi.org/10.3390/s20174789






