5G SLAM Using the Clustering and Assignment Approach with Diffuse Multipath
Abstract
:1. Introduction
- The description of an end-to-end framework for SLAM harnessing diffuse multipath and its performance evaluation.
- The evaluation of clustering and assignment methods, which is suitable for estimated channel parameters under both specular and diffuse multipath, as well as a method to utilize the estimated channel gains for improving the clustering in the 5G SLAM problem.
- The extension of the 5G SLAM likelihood function, in order to harness both specular and diffuse multipath components and to classify different object types according to their roughness, while accounting for clustering errors.
Notations
2. System Model
2.1. User Model
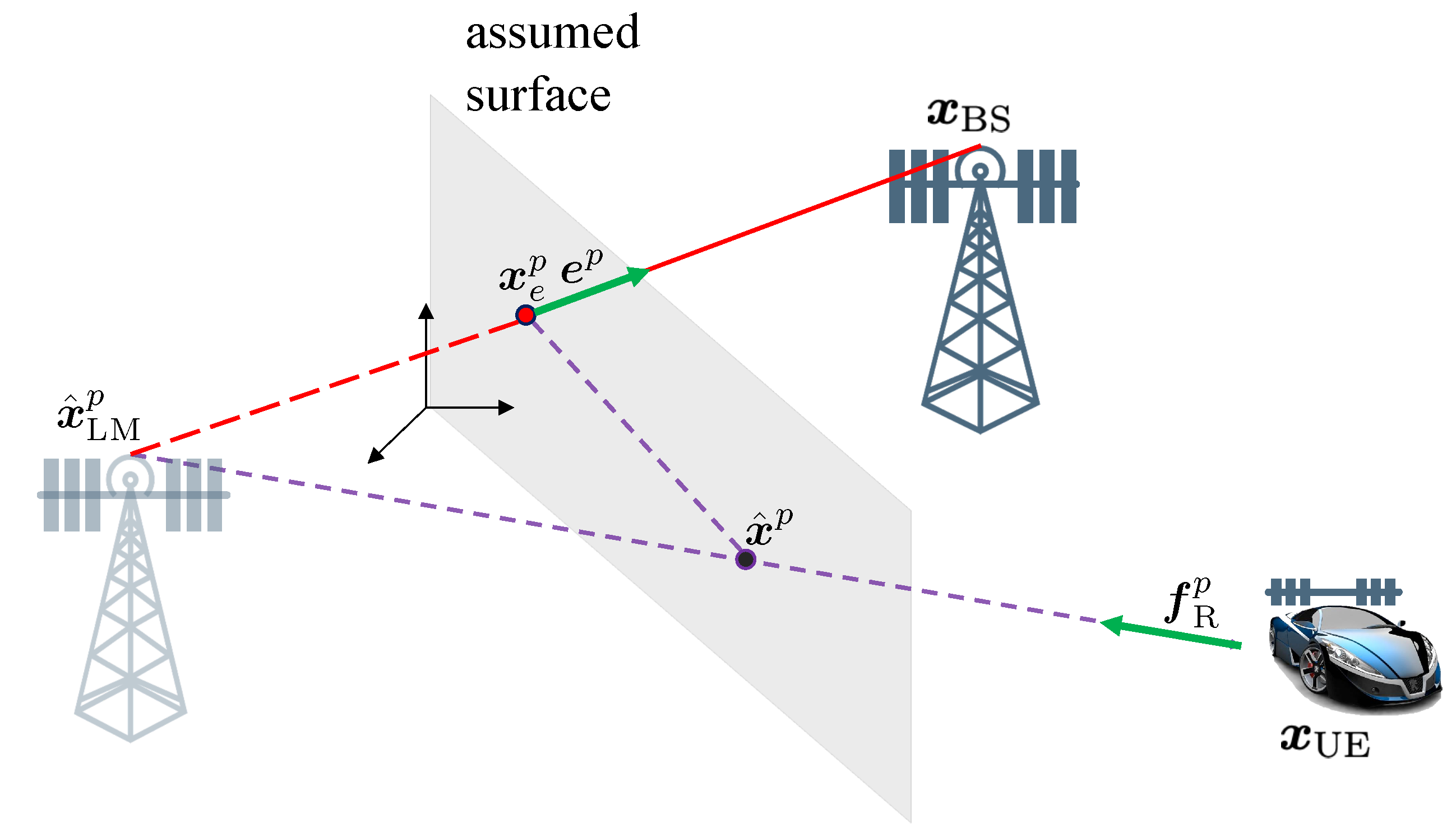
2.2. Environment Model
- A point on a corner of the surface and a vector normal to the surface.
- The size of the surface in length l and height h. The width w is not relevant.
- The smoothness of the surface, denoted by .
- The scattering attenuation and reflection attenuation , with , in which the remaining power is absorbed in the surface.
2.3. Channel Model
- LOS path: When , , the gain has uniform phase and has powerwhere is the wavelength, and the TOA, AOA, and AOD follow the geometric relations between the BS and the UE. They are given in Appendix A.
- Specular path from surface i: For , , the point of incidence on the i-th surface (denoted by with virtual anchor ) is the intersection of the surface and the line between the i-th virtual anchor and the UE . The specular path gain has uniform phase and powerThe TOA, AOA, and AOD follow the relative position of the UE, BS, and the incidence point on the surface. They are given in Appendix A.
- Diffuse paths from surface i: For , , the number of paths per surface and their spread in angle and delay, as well as the channel gains, depend on the roughness of that surface. These paths can be interpreted as coming from random points on the surface, with a spatial distribution that depends on the roughness, where is the random variable that describes the position of the diffuse point. The diffuse points are generated from the distribution ([43],Chapter 3)where denotes the set of points that make the i-th surface, is the deviation of the scattering angle with respect to the angle of the specular path (i.e,. when is the incidence point of the specular path), is the angle between the impinging ray (i.e., from the transmitter to ) and the surface normal, and is the angle between the departing ray and the surface normal. The diffuse paths have uniform and independent phases and equal powerThe locations of the diffuse points fully determine their corresponding TOA, AOA, and AOD, provided in Appendix A.
2.4. Signal Model
3. Methodology and End-to-End Framework
- First of all, channel estimation is performed to recover the channel parameters (angles, delays, gains). Due to the finite resolution at the receiver side, not all paths are resolvable. Hence, the number of estimated paths (denoted by ) will be much smaller than . The channel estimator thus provides a set of channel parameter estimates at time k, . Each element is either a clutter, which is caused by noise peaks that are detected as paths during channel estimation, with clutter intensity or followswhere denotes the measurement noise; is for LOS, the incidence point of the deterministic specular components, or a (random) point on the surface for a NLOS component. We recall that the underlying geometric relation can be found in Appendix A. We describe the channel estimator in Section 4.
- After channel estimation, we group the unordered elements in in clusters , where each cluster should correspond to one landmark. This removes the need to consider all possible partitions of the measurements in the SLAM method, drastically reducing overall complexity. Clustering is challenging as measurement clusters may be non-convex. In addition, diffuse paths may be far away from the specular paths, leading to possible miss-classifications. The proposed clustering method is described in Section 5.
- Finally, after clustering, the SLAM method requires a likelihood function that expresses the statistical relation between the state and the clustered measurements, . The SLAM method is deferred to Appendix B, while in the main text we focus on the proposed likelihood function in Section 6. The SLAM filter follows a Rao-Blackwellized approach, where we use a set of particles (indexed by n) to represent the user state, and use PMBM densities conditioned on each particle to represent the map. Clustering and likelihood computation are conditioned in the user state and are thus performed per particle.
4. Channel Estimation
4.1. Background
4.2. ESPRIT Channel Estimator
4.2.1. Observations in Tensor Form
4.2.2. Shift Invariance
4.2.3. Tensor-ESPRIT
5. Channel Parameter Clustering
5.1. Background
5.2. Modified DBSCAN
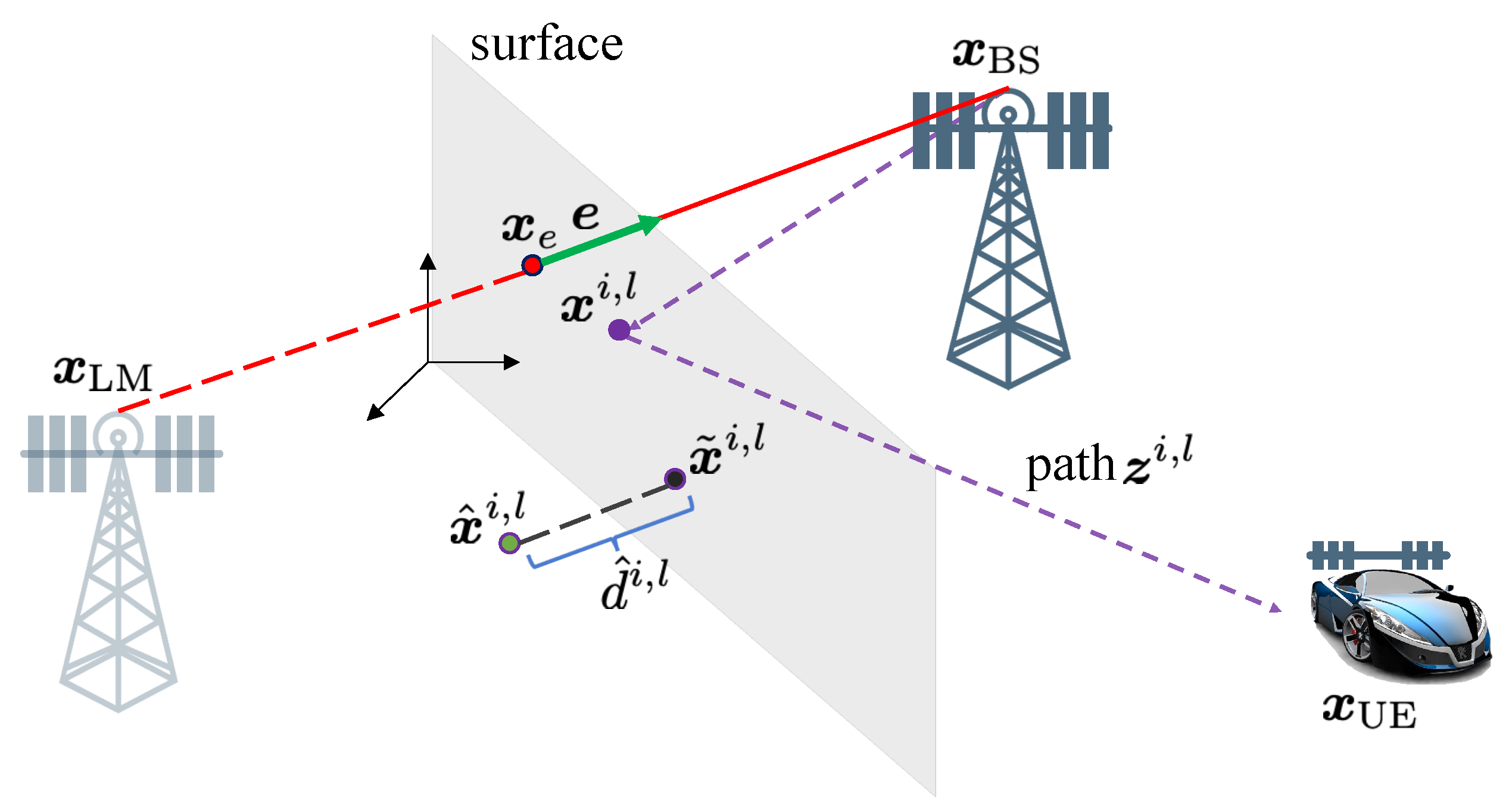
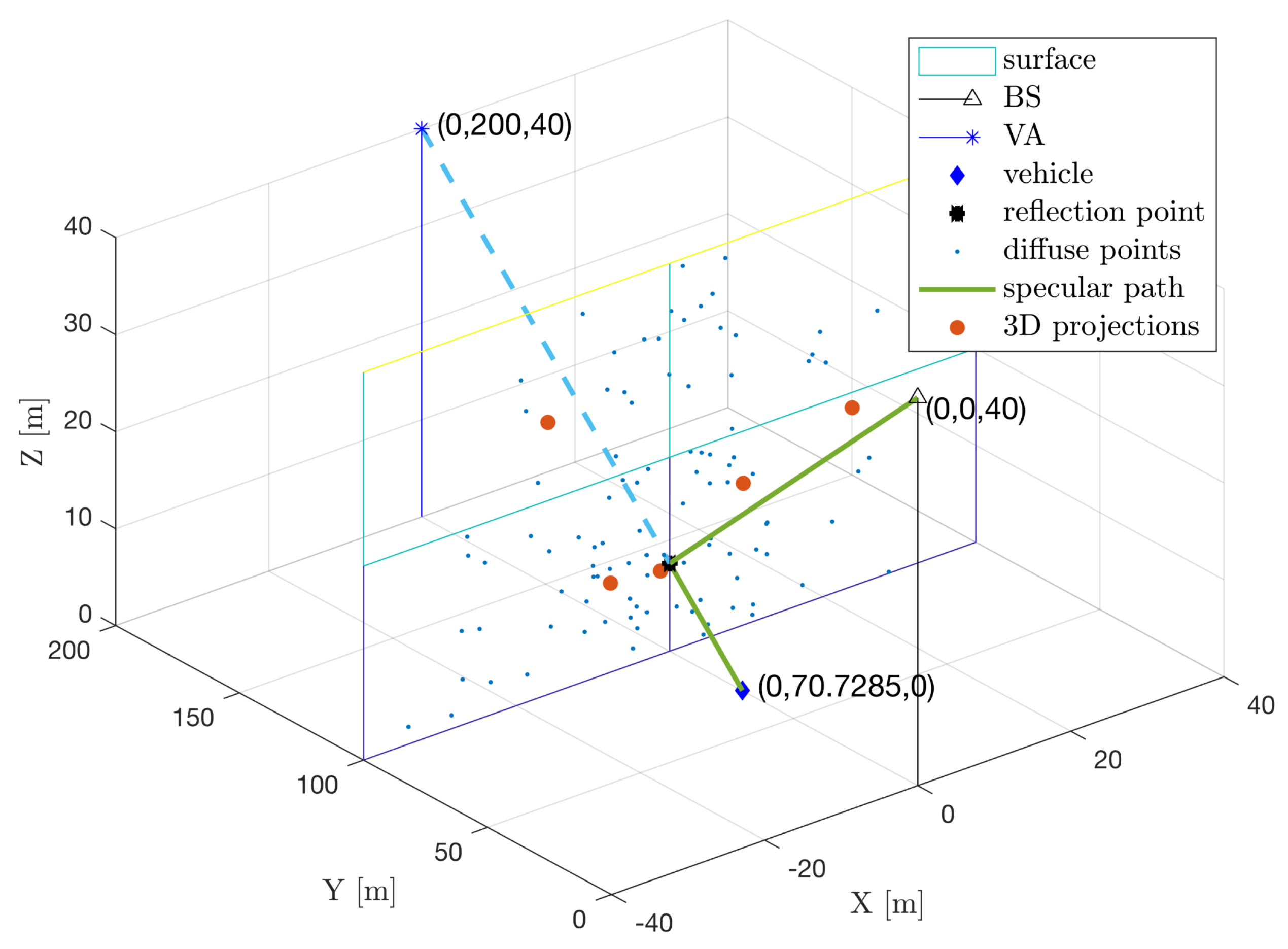
5.2.1. Phase 1: 5D to 3D Mapping
5.2.2. Phase 2: Clustering with DBSCAN
| Algorithm 1: DBSCAN for Clustering |
| Input: Points , threshold , and ; |
| Output: All clusters and the associated points. |
|
| Algorithm 2: Find All Points in Cluster l |
| Input: Cluster index l, point index p and its -neighbourhood ; |
| Output: The associated points in cluster l. |
|
5.2.3. Phase 3: Extract Isolated Specular Paths and Outliers Using Channel Gain
- The tensor ESPRIT channel estimator from Section 4 can generate estimates, whose 3D points (as obtained in Section 5.2.1) are still on or near the corresponding surfaces, but are far away from the cluster centers. Hence, they are informative for the SLAM algorithm, but are part of , so they are not clustered correctly. We have observed that the channel gains of these paths are very small.
- The LOS path and specular paths from smooth surfaces are not part of any cluster, as such landmarks have one or few associated paths. We have observed that the channel gains of these paths are very large (approximately following the path loss models from Section 2.3).
6. Likelihood Function for SLAM
6.1. Background
6.2. Likelihood Function
6.2.1. Likelihood for Diffuse Paths
6.2.2. Clustering Errors and Marginal Likelihood Function
7. Results
7.1. Simulation Parameters
7.2. Channel Estimation Results
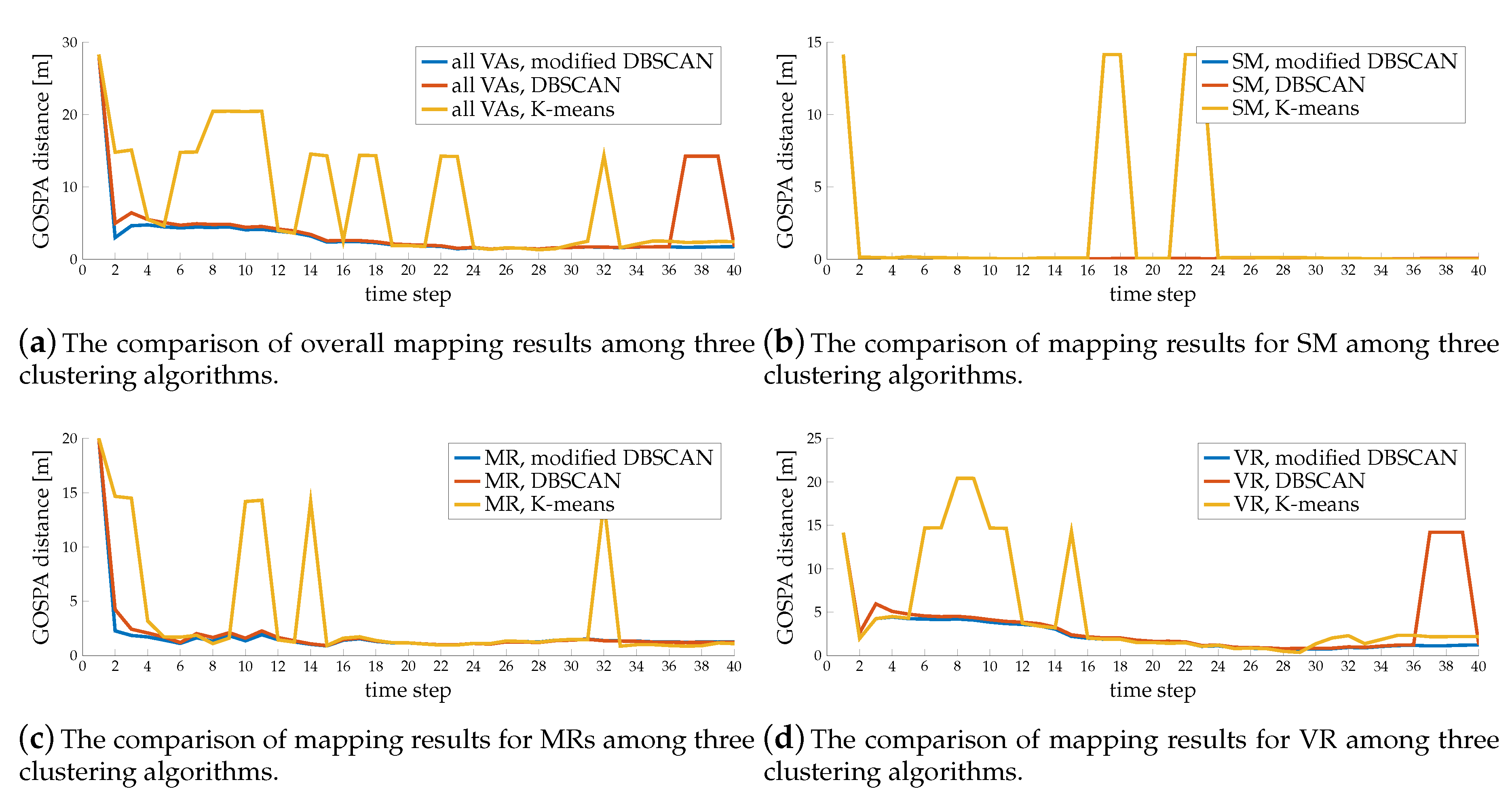
7.3. Clustering Performance Evaluation
7.4. Estimated Likelihoods
7.5. SLAM Performance Evaluation
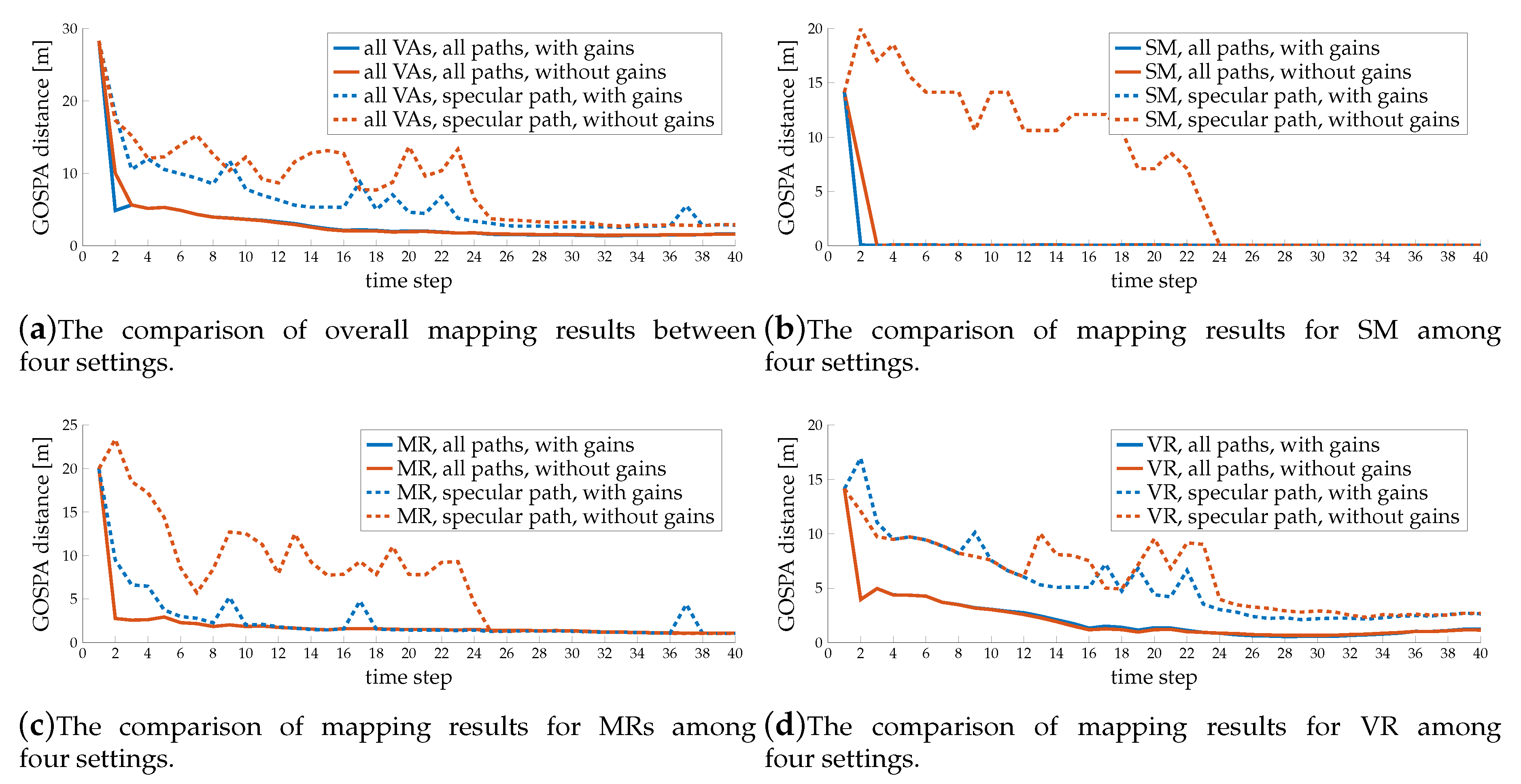
7.5.1. Mapping Performance
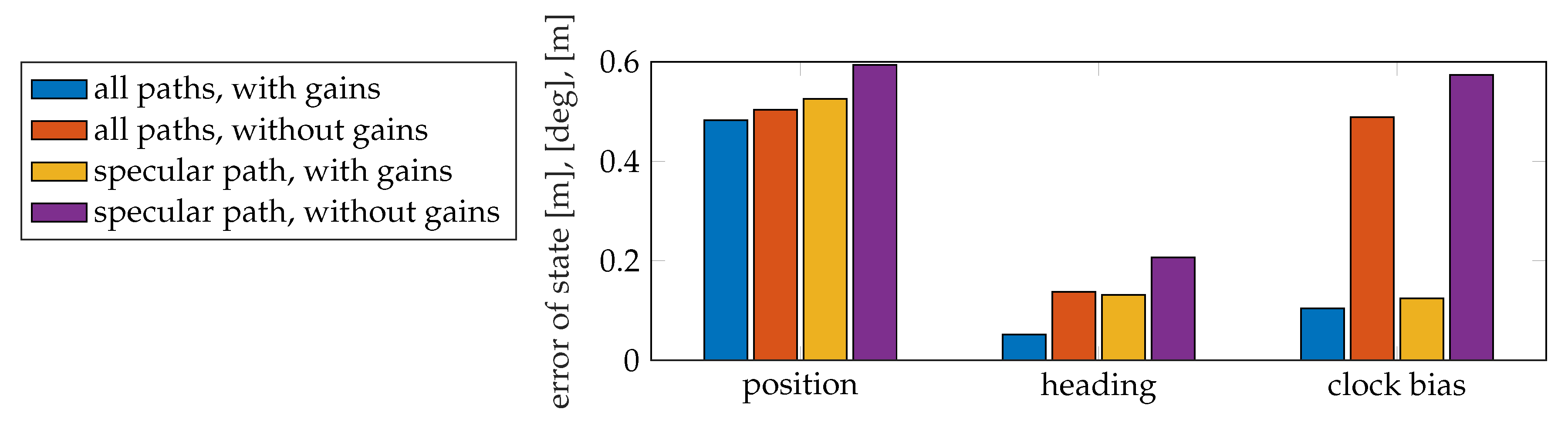
7.5.2. Localization Performance
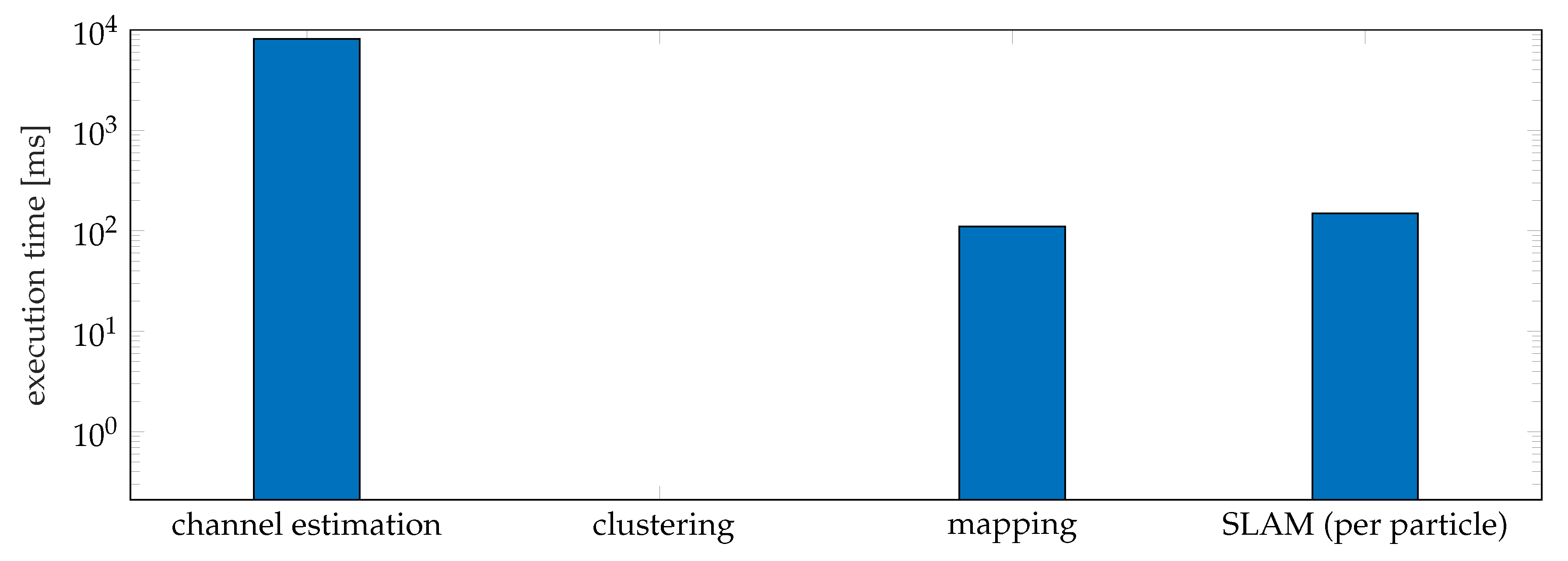
7.5.3. Complexity Evaluation
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Geometric Relations
- TOA:
- AOD pair: ,
- AOA pair: ,
- TOA:
- AOD pair: ,
- AOA pair: , .
- TOA:
- AOD pair: ,
- AOA pair: , .
Appendix B. PMBM SLAM Filter
Appendix B.1. Representation of PMBM Density
Appendix B.2. Implementation of PMBM SLAM Filter
- User Prediction: Using (1), the user particle is predicted as , where and .
- Map Prediction: Since the targets are static, the PPP parameter is predicted as , where is the survival probability, is the birth intensity. For the MBM components, , , and .
- Map Update: The map update is divided into the following four cases [65]
- (a)
- Missed detections for undetected objects: The undetected objects remain as the undetected objects, and thus is given bywhere indicates the detection probability.
- (b)
- Detections for the first time: Using the grouped measurement and the PPP parameter , we newly generate the MBM parameters aswhere .
- (c)
- Missed detections for the previously detected objects: The detected objects also remain as the detected objects, and then the MBM parameters have no measurement update
- (d)
- Detections for the previously detected objects: Using , the MBM parameters are computed as
- User Update: Each particle weight is updated aswhere is the weight for the updated global hypothesis h and particle n. Then, the user state is estimated by .
Appendix B.3. Map Fusion
References
- Narayanan, A.; Ramadan, E.; Carpenter, J.; Liu, Q.; Liu, Y.; Qian, F.; Zhang, Z.L. A first look at commercial 5G performance on smartphones. In Proceedings of the Web Conference, Taipei, Taiwan, 20–24 April 2020; pp. 894–905. [Google Scholar]
- Del Peral-Rosado, J.A.; Raulefs, R.; López-Salcedo, J.A.; Seco-Granados, G. Survey of cellular mobile radio localization methods: From 1G to 5G. IEEE Commun. Surv. Tutorials 2017, 20, 1124–1148. [Google Scholar] [CrossRef]
- 3GPP TR 38.855 V16.0.0; Study on NR Positioning Support; Technical Report. Available online: https://www.3gpp.org (accessed on 18 August 2020).
- Del Peral-Rosado, J.; Granados, G.; Raulefs, R.; Leitinger, E.; Grebien, S.; Wilding, T.; Dardari, D.; Lohan, E.; Wymeersch, H.; Floch, J.; et al. White Paper on New Localization Methods for 5G Wireless Systems and the Internet-of-Things. In COST Action CA15104. Available online: http://www.iracon.org/wp-content/uploads/2018/03/IRACON-WP2.pdf (accessed on 18 August 2020).
- Witrisal, K.; Meissner, P.; Leitinger, E.; Shen, Y.; Gustafson, C.; Tufvesson, F.; Haneda, K.; Dardari, D.; Molisch, A.F.; Conti, A.; et al. High-accuracy localization for assisted living: 5G systems will turn multipath channels from foe to friend. IEEE Signal Process. Mag. 2016, 33, 59–70. [Google Scholar] [CrossRef]
- Talvitie, J.; Valkama, M.; Destino, G.; Wymeersch, H. Novel algorithms for high-accuracy joint position and orientation stimation in 5G mmWave systems. In Proceedings of the IEEE Globecom Workshops (GC Wkshps), Singapore, 4–8 December 2017. [Google Scholar]
- Mendrzik, R.; Wymeersch, H.; Bauch, G. Joint localization and mapping through millimeter wave MIMO in 5G systems. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, UAE, 9–13 December 2018. [Google Scholar]
- Li, X.; Leitinger, E.; Oskarsson, M.; Åström, K.; Tufvesson, F. Massive MIMO-based localization and mapping exploiting phase information of multipath components. IEEE Trans. Wirel. Commun. 2019, 18, 4254–4267. [Google Scholar] [CrossRef] [Green Version]
- Fascista, A.; Coluccia, A.; Wymeersch, H.; Seco-Granados, G. Millimeter-wave downlink positioning with a single-antenna receiver. IEEE Trans. Wirel. Commun. 2019, 18, 4479–4490. [Google Scholar] [CrossRef] [Green Version]
- Fascista, A.; Coluccia, A.; Wymeersch, H.; Seco-Granados, G. Downlink single-snapshot localization and mapping with a single-antenna receiver. arXiv 2020, arXiv:2007.14679. [Google Scholar]
- Richter, A. Estimation of Radio Channel Parameters: Models and Algorithms. Ph.D. Thesis, Ilmenau University of Technology, Ilmenau, Germany, 2005. [Google Scholar]
- Alkhateeb, A.; El Ayach, O.; Leus, G.; Heath, R.W. Channel estimation and hybrid precoding for millimeter wave cellular systems. IEEE J. Sel. Top. Signal Process. 2014, 8, 831–846. [Google Scholar] [CrossRef] [Green Version]
- Venugopal, K.; Alkhateeb, A.; Prelcic, N.G.; Heath, R.W. Channel estimation for hybrid architecture-based wideband millimeter wave systems. IEEE J. Sel. Areas Commun. 2017, 35, 1996–2009. [Google Scholar] [CrossRef]
- Gershman, A.B.; Rübsamen, M.; Pesavento, M. One- and two-dimensional direction-of-arrival estimation: An overview of search-free techniques. Signal Process. 2010, 90, 1338–1349. [Google Scholar] [CrossRef]
- Wen, F.; Garcia, N.; Kulmer, J.; Witrisal, K.; Wymeersch, H. Tensor decomposition based beamspace ESPRIT for millimeter wave MIMO channel estimation. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, UAE, 9–13 December 2018. [Google Scholar]
- Zhou, Z.; Fang, J.; Yang, L.; Li, H.; Chen, Z.; Blum, R.S. Low-rank tensor decomposition-aided channel estimation for millimeter wave MIMO-OFDM systems. IEEE J. Sel. Areas Commun. 2017, 35, 1524–1538. [Google Scholar] [CrossRef]
- Mullane, J.; Vo, B.N.; Adams, M.D.; Vo, B.T. A random-finite-set approach to Bayesian SLAM. IEEE Trans. Robot. 2011, 27, 268–282. [Google Scholar] [CrossRef]
- Williams, J.L. Marginal multi-Bernoulli filters: RFS derivation of MHT, JIPDA, and association-based MeMBer. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1664–1687. [Google Scholar] [CrossRef] [Green Version]
- Leitinger, E.; Meyer, F.; Hlawatsch, F.; Witrisal, K.; Tufvesson, F.; Win, M.Z. A belief propagation algorithm for multipath-based SLAM. IEEE Trans. Wirel. Commun. 2019, 18, 5613–5629. [Google Scholar] [CrossRef] [Green Version]
- Gentner, C.; Jost, T.; Wang, W.; Zhang, S.; Dammann, A.; Fiebig, U.C. Multipath assisted positioning with simultaneous localization and mapping. IEEE Trans. Wirel. Commun. 2016, 15, 6104–6117. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Wymeersch, H.; Garcia, N.; Seco-Granados, G.; Kim, S. 5G mmWave vehicular tracking. In Proceedings of the 52nd IEEE Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 28–31 October 2018; pp. 541–547. [Google Scholar]
- Meyer, F.; Braca, P.; Willett, P.; Hlawatsch, F. A scalable algorithm for tracking an unknown number of targets using multiple sensors. IEEE Trans. Signal Process. 2017, 65, 3478–3493. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Granström, K.; Gao, L.; Battistelli, G.; Kim, S.; Wymeersch, H. 5G mmWave cooperative positioning and mapping using multi-model PHD filter and map fusion. IEEE Trans. Wirel. Commun. 2020. [Google Scholar] [CrossRef] [Green Version]
- Ge, Y.; Kim, H.; Wen, F.; Svensson, L.; Kim, S.; Wymeersch, H. Exploiting diffuse multipath in 5G SLAM. arXiv 2020, arXiv:2006.15603. [Google Scholar]
- Granström, K.; Baum, M.; Reuter, S. Extended object tracking: Introduction, overview and applications. arXiv 2016, arXiv:1604.00970. [Google Scholar]
- Aubry, A.; De Maio, A.; Foglia, G.; Orlando, D. Diffuse multipath exploitation for adaptive radar detection. IEEE Trans. Signal Process. 2015, 63, 1268–1281. [Google Scholar] [CrossRef]
- Setlur, P.; Negishi, T.; Devroye, N.; Erricolo, D. Multipath exploitation in non-LOS urban synthetic aperture radar. IEEE J. Sel. Top. Signal Process. 2013, 8, 137–152. [Google Scholar] [CrossRef] [Green Version]
- Wen, F.; Kulmer, J.; Witrisal, K.; Wymeersch, H. 5G positioning and mapping with diffuse multipath. arXiv 2019, arXiv:1912.08697. [Google Scholar]
- Fatemi, M.; Granström, K.; Svensson, L.; Ruiz, F.J.; Hammarstrand, L. Poisson multi-Bernoulli mapping using Gibbs sampling. IEEE Trans. Signal Process. 2017, 65, 2814–2827. [Google Scholar] [CrossRef] [Green Version]
- Granström, K.; Svensson, L.; Reuter, S.; Xia, Y.; Fatemi, M. Likelihood-based data association for extended object tracking using sampling methods. IEEE Trans. Intell. Veh. 2017, 3, 30–45. [Google Scholar] [CrossRef]
- Granström, K.; Lundquist, C.; Orguner, O. Extended target tracking using a Gaussian-mixture PHD filter. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3268–3286. [Google Scholar] [CrossRef] [Green Version]
- Czink, N.; Cera, P.; Salo, J.; Bonek, E.; Nuutinen, J.P.; Ylitalo, J. A framework for automatic clustering of parametric MIMO channel data including path powers. In Proceedings of the IEEE Vehicular Technology Conference, Melbourne, Australia, 7–10 May 2006. [Google Scholar]
- 5GPPP Association. 5G Automotive Vision, 5GPPP; White Paper. Available online: https://5g-ppp.eu (accessed on 18 August 2020).
- Ahvar, E.; Daneshgar-Moghaddam, N.; Ortiz, A.M.; Lee, G.M.; Crespi, N. On analyzing user location discovery methods in smart homes: A taxonomy and survey. J. Netw. Comput. Appl. 2016, 76, 75–86. [Google Scholar] [CrossRef] [Green Version]
- Yaeli, A.; Bak, P.; Feigenblat, G.; Nadler, S.; Roitman, H.; Saadoun, G.; Ship, H.J.; Cohen, D.; Fuchs, O.; Ofek-Koifman, S.; et al. Understanding customer behavior using indoor location analysis and visualization. IBM J. Res. Dev. 2014, 58, 1–3. [Google Scholar] [CrossRef]
- Hwangbo, H.; Kim, Y.S.; Cha, K.J. Use of the smart store for persuasive marketing and immersive customer experiences: A case study of Korean apparel enterprise. Mob. Inform. Syst. 2017, 2017, 4738340. [Google Scholar]
- Taranto, R.D.; Muppirisetty, S.; Raulefs, R.; Slock, D.; Svensson, T.; Wymeersch, H. Location-aware communications for 5G networks. IEEE Signal Process. Mag. 2014, 31, 102–112. [Google Scholar] [CrossRef] [Green Version]
- Guidi, F.; Guerra, A.; Dardari, D. Personal mobile radars with millimeter-wave massive arrays for indoor mapping. IEEE Trans. Mob. Comput. 2015, 15, 1471–1484. [Google Scholar] [CrossRef]
- Bourdoux, A.; Barreto, A.N.; van Liempd, B.; de Lima, C.; Dardari, D.; Belot, D.; Lohan, E.S.; Seco-Granados, G.; Sarieddeen, H.; Wymeersch, H.; et al. 6G white paper on localization and sensing. arXiv 2020, arXiv:2006.01779. [Google Scholar]
- Kim, H.; Granström, K.; Kim, S.; Wymeersch, H. Low-complexity 5G SLAM with CKF-PHD filter. In IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); IEEE: Piscataway, NJ, USA, 2020; pp. 5220–5224. [Google Scholar]
- Ferre, R.M.; Seco-Granados, G.; Lohan, E.S. Positioning Reference Signal Design for Positioning Via 5G; National Committee for Radiology in Finland: Tampere, Finland, 2019. [Google Scholar]
- 3GPP TS 38.211 NR V15.8.0; Physical Channels and Modulation; Technical Report. Available online: https://www.3gpp.org (accessed on 18 August 2020).
- Kulmer, J. High-Accuracy Positioning Exploiting Multipath for Reducing the Infrastructure. Ph.D. Thesis, Graz University of Technology, Graz, Austria, 2019. [Google Scholar]
- Heath, R.W.; Gonzalez-Prelcic, N.; Rangan, S.; Roh, W.; Sayeed, A.M. An overview of signal processing techniques for millimeter wave MIMO systems. IEEE J. Sel. Top. Signal Process. 2016, 10, 436–453. [Google Scholar] [CrossRef]
- Vukmirović, N.; Erić, M.; Janjić, M.; Djurić, P.M. Direct wideband coherent localization by distributed antenna arrays. Sensors 2019, 19, 4582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, P.; Pajovic, M.; Koike-Akino, T.; Sun, H.; Orlik, P.V. Fingerprinting-based indoor localization with commercial mmWave WiFi-part II: Spatial beam SNRs. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019. [Google Scholar]
- Guerra, A.; Guidi, F.; Dardari, D. Single-anchor localization and orientation performance limits using massive arrays: Mimovs. beamforming. IEEE Trans. Wirel. Commun. 2018, 17, 5241–5255. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Sidiropoulos, N.D.; Jiang, T.; Gershman, A. Multidimensional harmonic retrieval with applications in MIMO wireless channel sounding. In Space-Time Processing for MIMO Communications; Wiley Online Library: Hoboken, NJ, USA, 2005; pp. 41–75. [Google Scholar]
- Yang, Z.; Li, J.; Stoica, P.; Xie, L. Sparse methods for direction-of-arrival estimation. In Academic Press Library in Signal Processing; Elsevier: Amsterdam, The Netherlands, 2018; Volume 7, pp. 509–581. [Google Scholar]
- Haardt, M.; Pesavento, M.; Roemer, F.; El Korso, M.N. Subspace methods and exploitation of special array structures. In Academic Press Library in Signal Processing; Elsevier: Amsterdam, The Netherlands, 2014; Volume 3, pp. 651–717. [Google Scholar]
- Haardt, M.; Roemer, F.; Del Galdo, G. Higher-order SVD-based subspace estimation to improve the parameter estimation accuracy in multidimensional harmonic retrieval problems. IEEE Trans. Signal Process. 2008, 56, 3198–3213. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Liu, K.; da Costa, J.P.C.; So, H.C.; Huang, L.; Ye, J. Detection of number of components in CANDECOMP/PARAFAC models via minimum description length. Digit. Signal Process. 2016, 51, 110–123. [Google Scholar] [CrossRef]
- Phan, A.; Tichavský, P.; Cichocki, A. CANDECOMP/PARAFAC decomposition of high-order tensors through tensor reshaping. IEEE Trans. Signal Process. 2013, 61, 4847–4860. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Pei, J. Data Mining, Concepts and Techniques; Morgan Kaufmann Publishers: San Mateo, CA, USA, 2011. [Google Scholar]
- Foerster, J.R.; Pendergrass, M.; Molisch, A.F. A UWB channel model for ultra wideband indoor communications. In Proceedings of the International Symposium on Wireless Personal Multimedia Communications, Yokosuka, Japan, 19–22 October 2003. [Google Scholar]
- Czink, N. The Random-Cluster Model. Ph.D. Thesis, Technische Universitäat Wien, Vienna, Austria, 2007. [Google Scholar]
- Wyne, S.; Czink, N.; Karedal, J.; Almers, P.; Tufvesson, F.; Molisch, A.F. A cluster-based analysis of outdoor-to-indoor office MIMO measurements at 5.2 GHz. In Proceedings of the IEEE Vehicular Technology Conference, Melbourne, Australia, 7–10 May 2006. [Google Scholar]
- Salo, J.; Salmi, J.; Czink, N.; Vainikainen, P. Automatic clustering of nonstationary MIMO channel parameter estimates. In Proceedings of the Information and Communications Technologies, Cape Town, South Africa, 3–6 May 2005. [Google Scholar]
- Czink, N.; Yin, X.; Ozcelik, H.; Herdin, M.; Bonek, E.; Fleury, B.H. Cluster characteristics in a MIMO indoor propagation environment. IEEE Trans. Wirel. Commun. 2007, 6, 1465–1475. [Google Scholar] [CrossRef]
- He, R.; Ai, B.; Molisch, A.F.; Stuber, G.L.; Li, Q.; Zhong, Z.; Yu, J. Clustering enabled wireless channel modeling using big data algorithms. IEEE Commun. Mag. 2018, 56, 177–183. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Frey, B.J.; Dueck, D. Clustering by passing messages between data points. Science 2007, 315, 972–976. [Google Scholar] [CrossRef] [Green Version]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- García-Fernández, Á.F.; Williams, J.L.; Granström, K.; Svensson, L. Poisson multi-Bernoulli mixture filter: Direct derivation and implementation. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1883–1901. [Google Scholar] [CrossRef] [Green Version]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B Stat. Methodol. 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Rahmathullah, A.S.; García-Fernández, Á.F.; Svensson, L. Generalized optimal sub-pattern assignment metric. In Proceedings of the 20th IEEE International Conference on Information Fusion (Fusion), Xi’an, China, 10–13 July 2017. [Google Scholar]
- Mitsis, G.; Tsiropoulou, E.E.; Papavassiliou, S. Data offloading in UAV-assisted multi-access edge computing systems: A resource-based pricing and user risk-awareness approach. Sensors 2020, 20, 2434. [Google Scholar] [CrossRef] [PubMed]
- Mitsis, G.; Apostolopoulos, P.A.; Tsiropoulou, E.E.; Papavassiliou, S. Intelligent dynamic data offloading in a competitive mobile edge computing market. Future Internet 2019, 11, 118. [Google Scholar] [CrossRef] [Green Version]
- Ferdowsi, A.; Challita, U.; Saad, W. Deep learning for reliable mobile edge analytics in intelligent transportation systems: An overview. IEEE Veh. Technol. Mag. 2019, 14, 62–70. [Google Scholar] [CrossRef]
- Mahler, R.P. Advances in Statistical Multisource-Multitarget Information Fusion; Artech House: Norwood, MA, USA, 2014. [Google Scholar]
- Mahler, R.P. Multitarget Bayes filtering via first-order multitarget moments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Murty, K.G. An algorithm for ranking all the assignments in order of increasing cost. Oper. Res. 1968, 16, 682–687. [Google Scholar] [CrossRef]





| Notation | Definition | Notation | Definition |
|---|---|---|---|
| state of the user | landmark location | ||
| m | landmark type | angle of arrival (AOA) pair | |
| angle of departure (AOD) pair | time of arrival (TOA) | ||
| g | channel gain | measurement set | |
| single measurement | c | speed of light | |
| detection probability | k | time index | |
| i | surface index | path index | |
| s | subcarrier index | r | dimension index |
| Clustering Method | Clustering Accuracy | Impurity |
|---|---|---|
| Modified DBSCAN | 99.61% | 0 |
| DBSCAN | 99.07% | 0 |
| K-means | 94.63% | 5.37% |
| Gap Statistics (GS) | 68.64% | 27.19% |
| Affinity Propagation (AP) | 84.35% | 12.54% |
| Type m | ||
|---|---|---|
| BS | N/A | |
| SM | N/A | |
| MR | ||
| VR | ||
| BS | ||
| SM | ||
| MR | ||
| VR | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, Y.; Wen, F.; Kim, H.; Zhu, M.; Jiang, F.; Kim, S.; Svensson, L.; Wymeersch, H. 5G SLAM Using the Clustering and Assignment Approach with Diffuse Multipath. Sensors 2020, 20, 4656. https://doi.org/10.3390/s20164656
Ge Y, Wen F, Kim H, Zhu M, Jiang F, Kim S, Svensson L, Wymeersch H. 5G SLAM Using the Clustering and Assignment Approach with Diffuse Multipath. Sensors. 2020; 20(16):4656. https://doi.org/10.3390/s20164656
Chicago/Turabian StyleGe, Yu, Fuxi Wen, Hyowon Kim, Meifang Zhu, Fan Jiang, Sunwoo Kim, Lennart Svensson, and Henk Wymeersch. 2020. "5G SLAM Using the Clustering and Assignment Approach with Diffuse Multipath" Sensors 20, no. 16: 4656. https://doi.org/10.3390/s20164656
APA StyleGe, Y., Wen, F., Kim, H., Zhu, M., Jiang, F., Kim, S., Svensson, L., & Wymeersch, H. (2020). 5G SLAM Using the Clustering and Assignment Approach with Diffuse Multipath. Sensors, 20(16), 4656. https://doi.org/10.3390/s20164656





