Integrity Monitoring of Multimodal Perception System for Vehicle Localization
Abstract
1. Introduction
2. Problem Statement
Contributions
- Defining a common reference frame and formalizing a common model to represent all data sources in all scenarios.
- Prototyping an integrity assessment framework using the common model and providing proof of concept.
- Analyzing the performance of the proposed framework using publicly available datasets and comparison with other state-of-the-art integrity monitoring solutions from the literature.
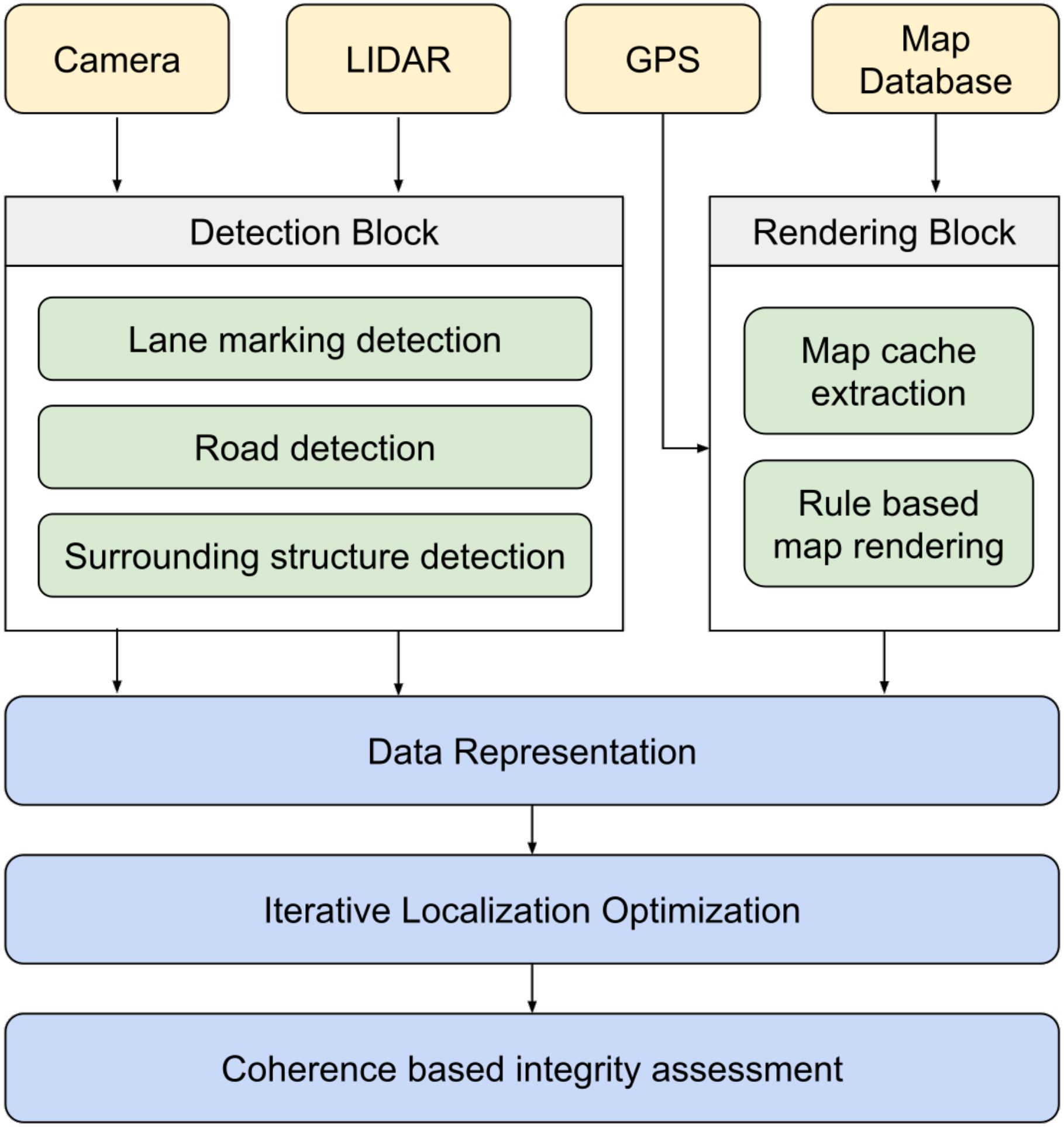
3. Methodology
3.1. Detection
3.1.1. Vision
3.1.2. LiDAR
3.2. Map Handling
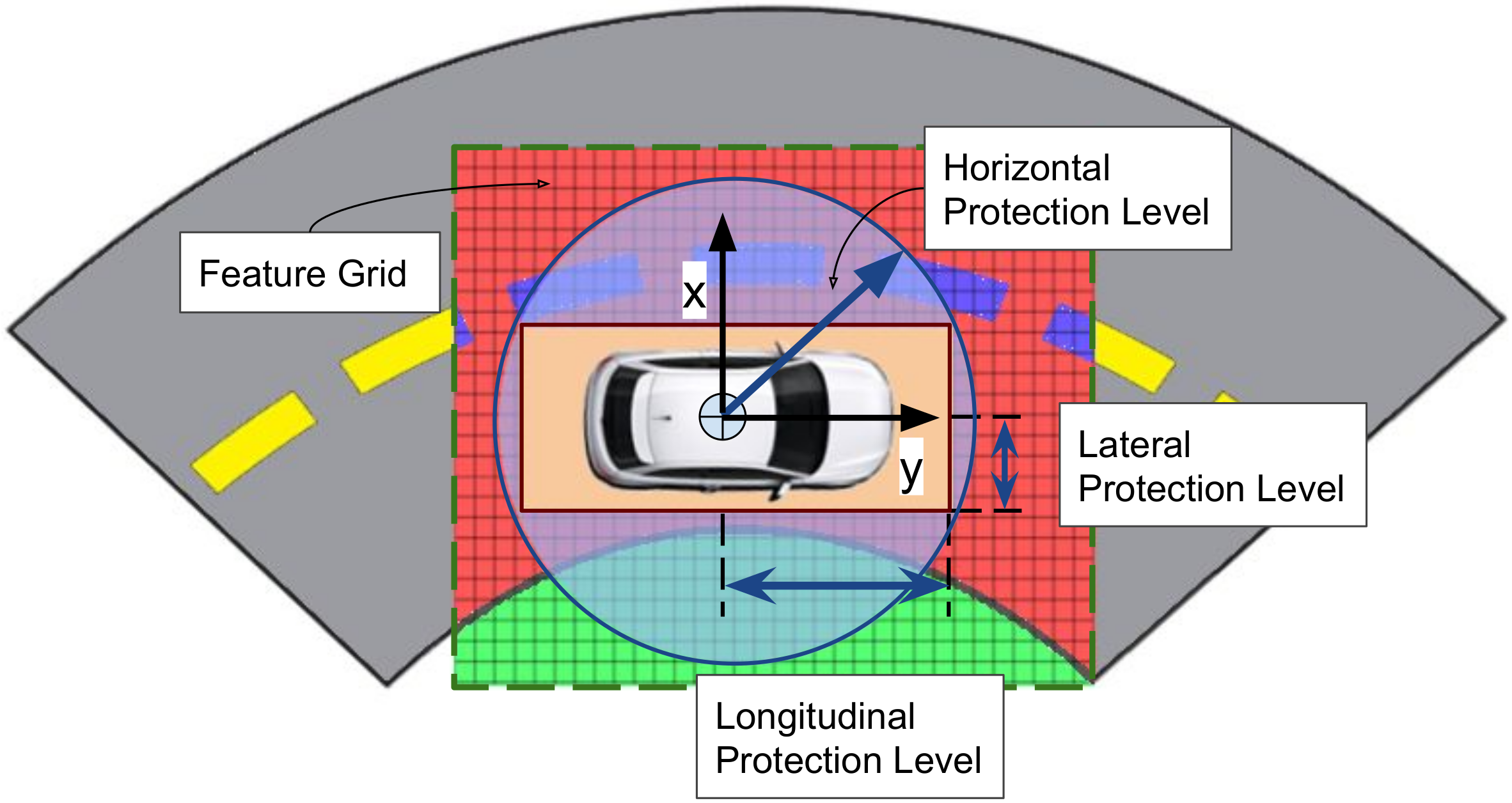
3.3. Representation
3.4. Integrity Analysis
3.5. Localization Optimization
| Algorithm 1 Algorithm for localization optimization. |
| Inputs: Localization: , GPS+IMU localization measurement: , FG of LiDAR: L, FG of Vision: C, FG of Map: M, Minimum coherence limit: |
| if and are consistent then |
| if and then |
| Output: Integrity markers |
| Update |
| else |
| Compute: |
| if and are consistent then |
| Output Integrity values |
| Update |
| else |
| if then |
| Output: Integrity markers |
| else |
| Output: Error in map |
| end if |
| end if |
| end if |
| else |
| Output: Error in GPS |
| end if |
4. Experiments and Discussions
- : Not enough nodes in the map for model fitting;
- : Not enough lane markings for model fitting;
- : GPS measurement is not available or an outlier;
- : Vehicle not moving or moving very slowly;
- : Vehicle performing a hard turn.
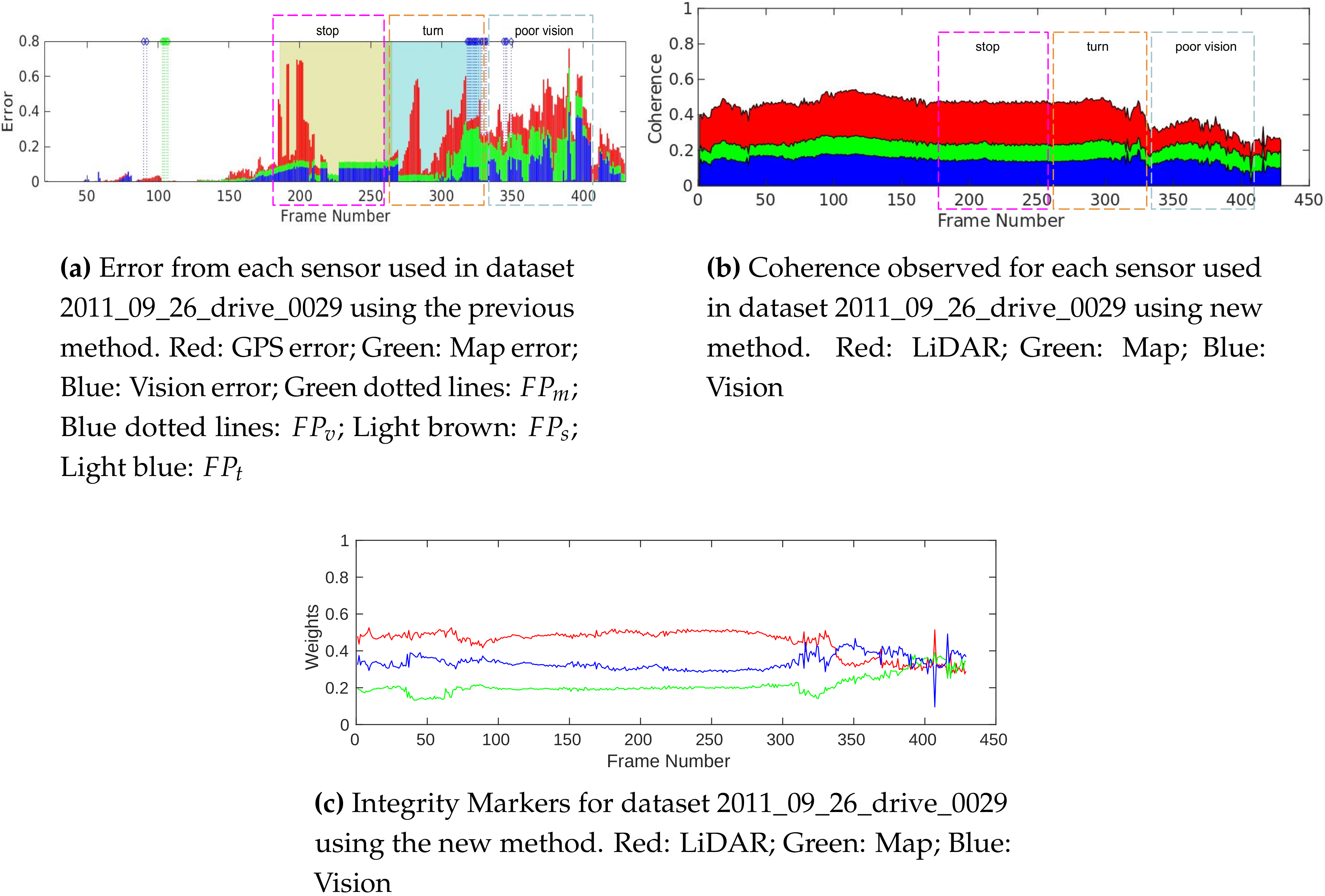
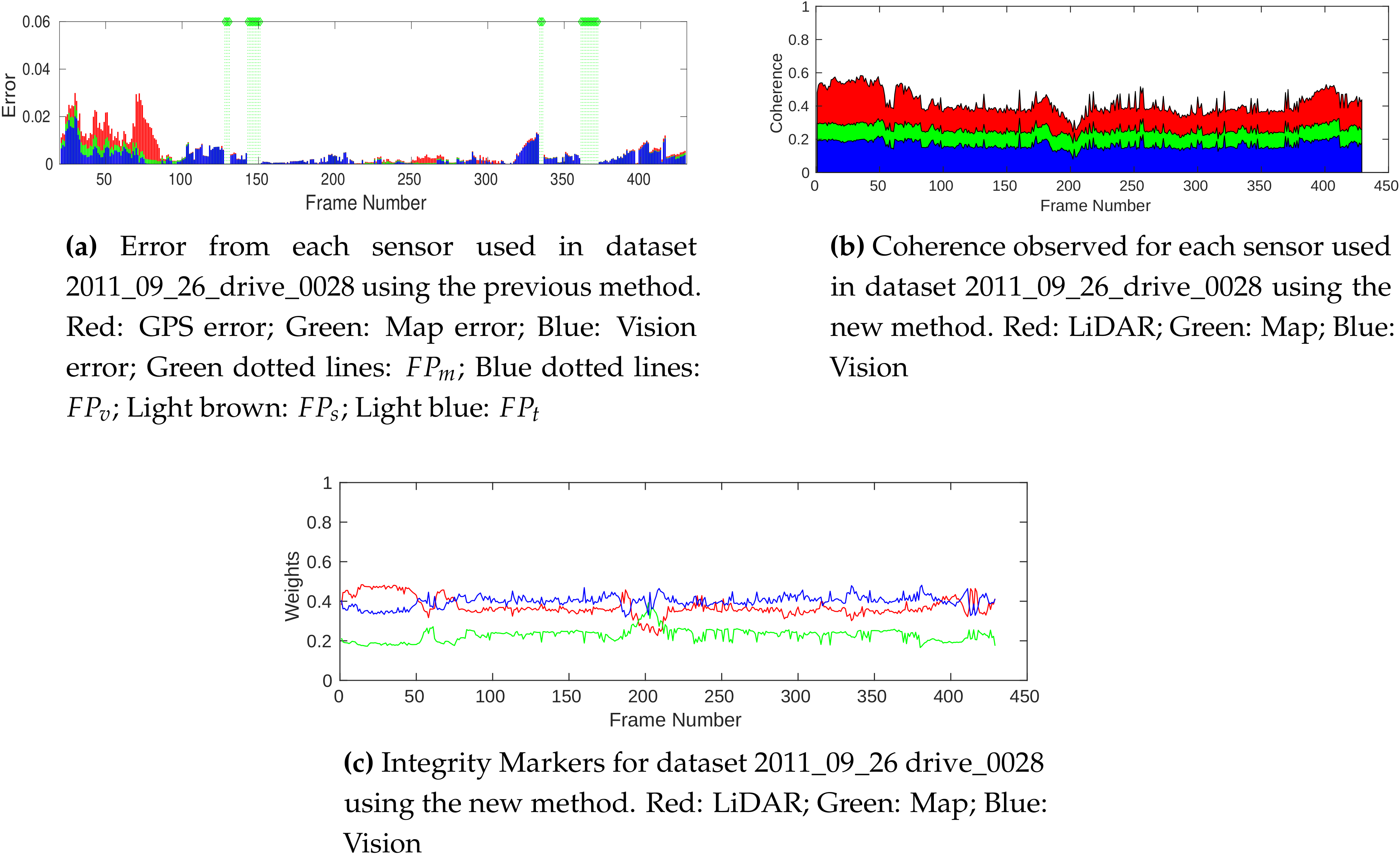
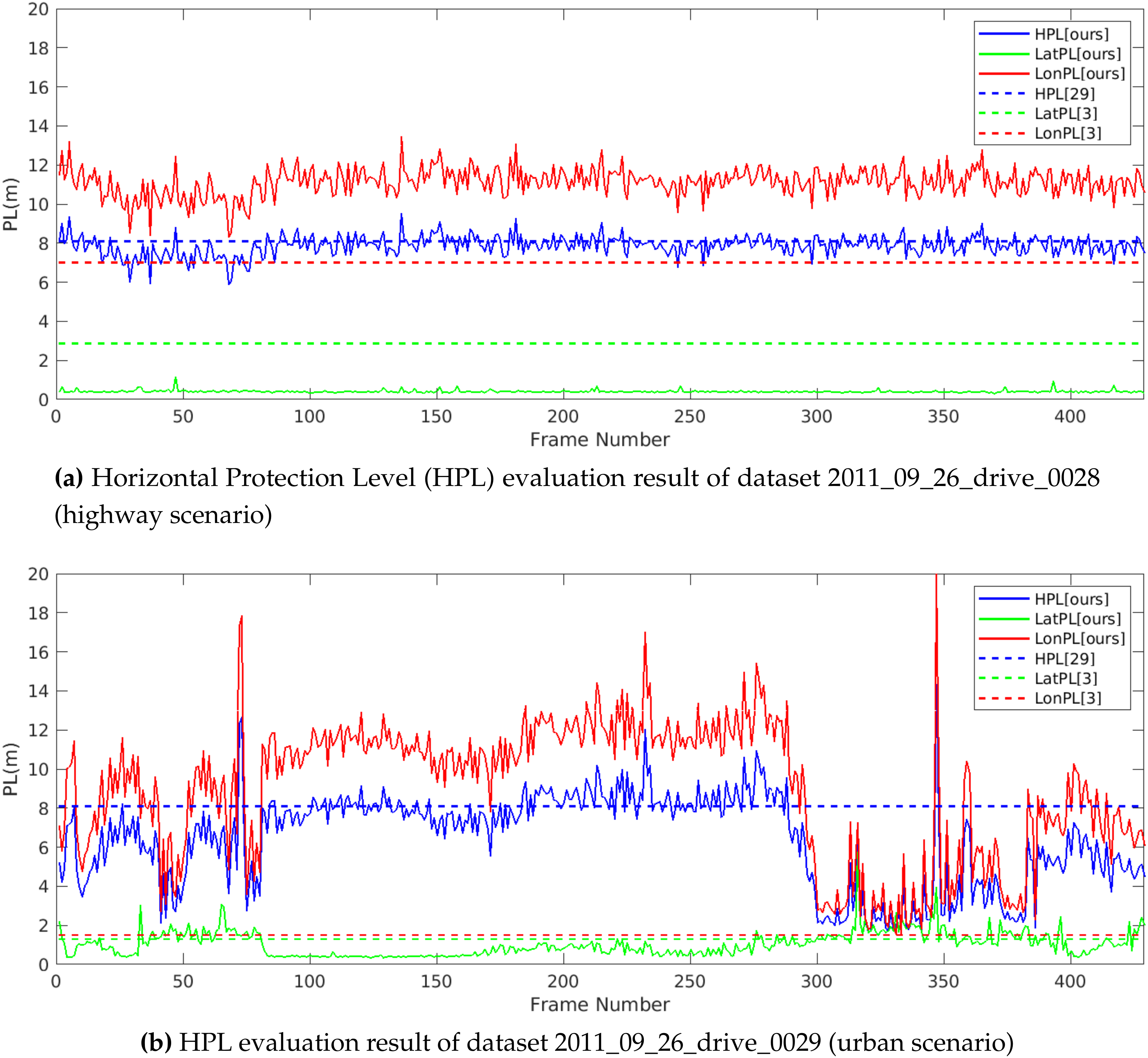
4.1. Integrity Marker Comparison
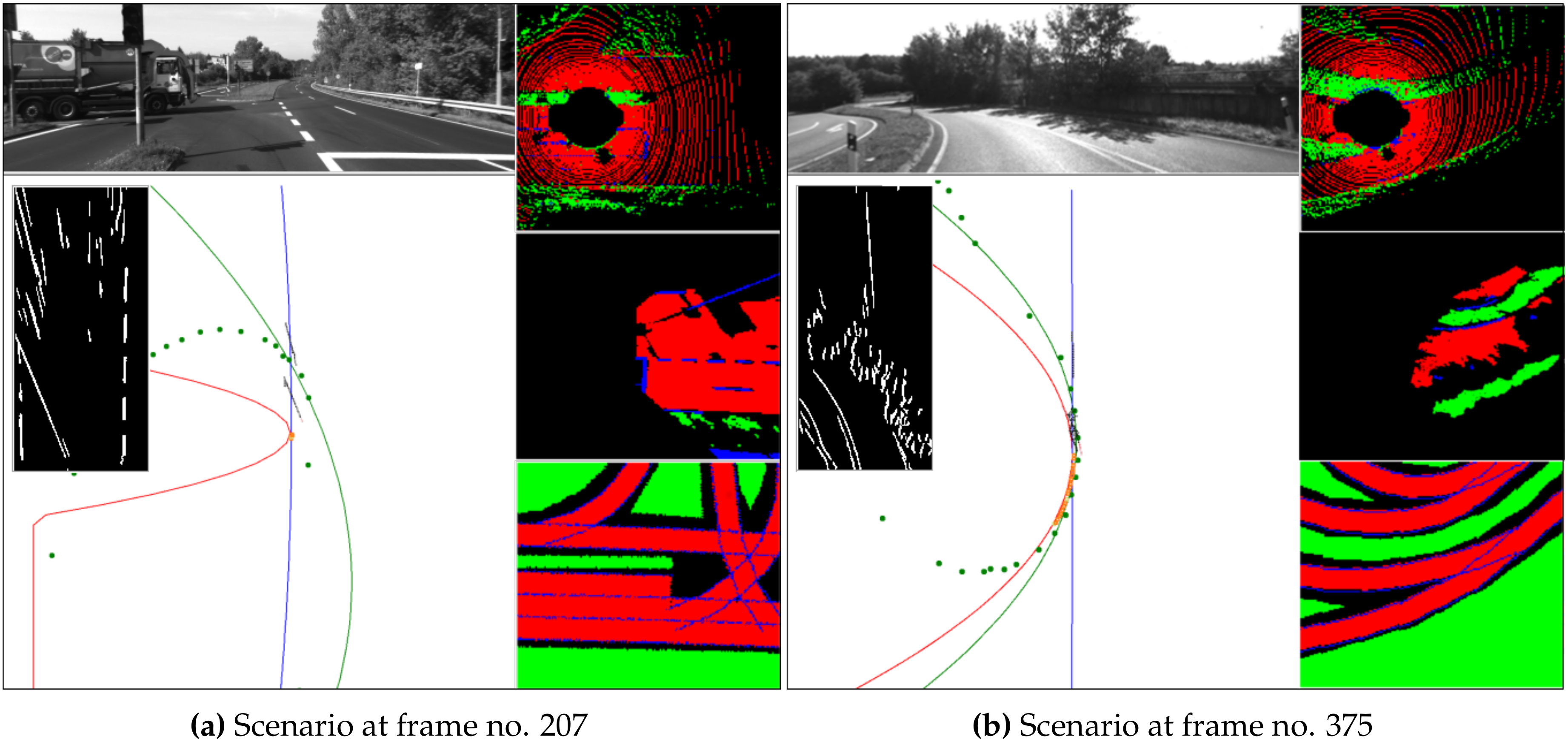
4.2. Complex Situations
4.3. Performance of Integrity Monitoring
5. Conclusions
6. Future Works
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- International SAE Taxonomy and Definitions for Terms Related to Driving Automation Systems for On-Road Motor Vehicles. 2018. Available online: https://www.sae.org/standards/content/j3016_201806/ (accessed on 16 July 2020).
- Velaga, N.R.; Quddus, M.A.; Bristow, A.L.; Zheng, Y. Map-aided integrity monitoring of a land vehicle navigation system. IEEE Trans. Intelligent Transp. Syst. 2012, 13, 848–858. [Google Scholar] [CrossRef]
- Reid, T.G.; Houts, S.E.; Cammarata, R.; Mills, G.; Agarwal, S.; Vora, A.; Pandey, G. Localization Requirements for Autonomous Vehicles. SAE Int. J. Connect. Autom. Veh. 2019, 2, 2574–2590. [Google Scholar] [CrossRef]
- Palmqvist, J. Integrity Monitoring of Integrated Satellite/Inertial Navigation Systems Using the Likelihood Ratio. In Proceedings of the 9th International Technical Meeting of the Satellite Division of The Institute of Navigation, Kansas City, MO, USA, 17–20 September 1996; pp. 1687–1696. [Google Scholar]
- Zinoune, C.; Bonnifait, P.; Ibañez-Guzmán, J. Integrity monitoring of navigation systems using repetitive journeys. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings, Ypsilanti, MI, USA, 8–11 June 2014; pp. 274–280. [Google Scholar]
- Yang, Y.; Xu, J. GNSS receiver autonomous integrity monitoring (RAIM) algorithm based on robust estimation. Geod. Geodyn. 2016, 7, 117–123. [Google Scholar] [CrossRef]
- Zinoune, C.; Bonnifait, P.; Ibañez-Guzmán, J. Sequential FDIA for autonomous integrity monitoring of navigation maps on board vehicles. IEEE Trans. Intell. Transp. Syst. 2016, 17, 143–155. [Google Scholar] [CrossRef][Green Version]
- Worner, M.; Schuster, F.; Dolitzscher, F.; Keller, C.G.; Haueis, M.; Dietmayer, K. Integrity for autonomous driving: A survey. In Proceedings of the 2016 IEEE/ION Position, Location and Navigation Symposium, Savannah, GA, USA, 11–14 April 2016; pp. 666–671. [Google Scholar]
- Le Marchand, O.; Bonnifait, P.; Ibañez-Guzmán, J.; Betaille, D. Automotive localization integrity using proprioceptive and pseudo-ranges measurements. In Proceedings of the Accurate Localization for Land Transportation, Paris, France, 16 June 2009. [Google Scholar]
- Li, L.; Quddus, M.; Zhao, L. High accuracy tightly-coupled integrity monitoring algorithm for map-matching. Transp. Res. Part C Emerg. Technol. 2013, 36, 13–26. [Google Scholar] [CrossRef]
- Ballardini, A.L.; Cattaneo, D.; Fontana, S.; Sorrenti, D.G. Leveraging the OSM building data to enhance the localization of an urban vehicle. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems, Rio de Janeiro, Brazil, 1–4 November 2016; pp. 622–628. [Google Scholar]
- Ballardini, A.L.; Cattaneo, D.; Sorrenti, D.G. Visual Localization at Intersections with Digital Maps. In Proceedings of the 2019 International Conference on Robotics and Automation, Montreal, QC, Canada, 20–24 May 2019; pp. 6651–6657. [Google Scholar]
- Kang, J.M.; Yoon, T.S.; Kim, E.; Park, J.B. Lane-Level Map-Matching Method for Vehicle Localization Using GPS and Camera on a High-Definition Map. Sensors 2020, 20, 2166. [Google Scholar] [CrossRef] [PubMed]
- Nedevschi, S.; Popescu, V.; Danescu, R.; Marita, T.; Oniga, F. Accurate Ego-Vehicle Global Localization at Intersections Through Alignment of Visual Data With Digital Map. IEEE Trans. Intell. Transp. Syst. 2013, 14, 673–687. [Google Scholar] [CrossRef]
- Liu, H.; Ye, Q.; Wang, H.; Chen, L.; Yang, J. A Precise and Robust Segmentation-Based Lidar Localization System for Automated Urban Driving. Remote. Sens. 2019, 11, 1348. [Google Scholar] [CrossRef]
- Liang, W.; Zhang, Y.; Wang, J. Map-Based Localization Method for Autonomous Vehicles Using 3D-LIDAR. IFAC Pap. Online 2017, 50, 276–281. [Google Scholar]
- Mueller, A.; Himmelsbach, M.; Luettel, T.; Hundelshausen, F.; Wuensche, H.J. GIS-based topological robot localization through LIDAR crossroad detection. In Proceedings of the 2011 14th International IEEE Conference on Intelligent Transportation Systems (ITSC), Washington, DC, USA, 5–7 October 2011; pp. 2001–2008. [Google Scholar]
- Balakrishnan, A.; Rodríguez , F.S.A.; Reynaud, R. An Integrity Assessment Framework for multimodal Vehicle Localization. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference, Auckland, New Zealand, 27–30 October 2019; pp. 2976–2983. [Google Scholar]
- Toth, C.; Jozkow, G.; Koppanyi, Z.; Grejner-Brzezinska, D. Positioning Slow-Moving Platforms by UWB Technology in GPS-Challenged Areas. J. Surv. Eng. 2017, 143, 04017011. [Google Scholar] [CrossRef]
- Pusztai, Z.; Eichhardt, I.; Hajder, L. Accurate Calibration of Multi-LiDAR-Multi-Camera Systems. Sensors 2018, 18, 2139. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.; Chen, L.; Lou, J.; Ren, M. A real-time road detection method based on reorganized lidar data. PLoS ONE 2019, 14, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Ye, J.; Shi, W.; Yang, C. Robust smooth fitting method for LIDAR data using weighted adaptive mapping LS-SVM. Proc. SPIE 2008, 7144, 5669–5683. [Google Scholar]
- Feng, R.; Li, X.; Zou, W.; Shen, H. Registration of multitemporal GF-1 remote sensing images with weighting perspective transformation model. In Proceedings of the 2017 IEEE International Conference on Image Processing, Beijing, China, 17–20 September 2017; pp. 2264–2268. [Google Scholar]
- Boritz, J.E. IS practitioners’ views on core concepts of information integrity. Int. J. Account. Inf. Syst. 2005, 6, 260–279. [Google Scholar] [CrossRef]
- Sandhu, R.; Dambreville, S.; Tannenbaum, A. Particle filtering for registration of 2D and 3D point sets with stochastic dynamics. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Roysdon, P.F.; Farrell, J.A. GPS-INS outlier detection elimination using a sliding window filter. In Proceedings of the 2017 American Control Conference, Seattle, WA, USA, 24–26 May 2017; pp. 1244–1249. [Google Scholar]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets robotics: The KITTI dataset. Int. J. Robot. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef]
- Backman, J.; Kaivosoja, J.; Oksanen, T.; Visala, A. Simulation Environment for Testing Guidance Algorithms with Realistic GPS Noise Model. IFAC Proc. Vol. 2010, 43, 139–144. [Google Scholar] [CrossRef]
- Zhu, N.; Marais, J.; Betaille, D.; Berbineau, M. GNSS Position Integrity in Urban Environments: A Review of Literature. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2762–2778. [Google Scholar] [CrossRef]
- PROTECTION LEVEL (specific location). Available online: https://egnos-user-support.essp-sas.eu/new_egnos_ops/protection_levels. (accessed on 16 July 2020).


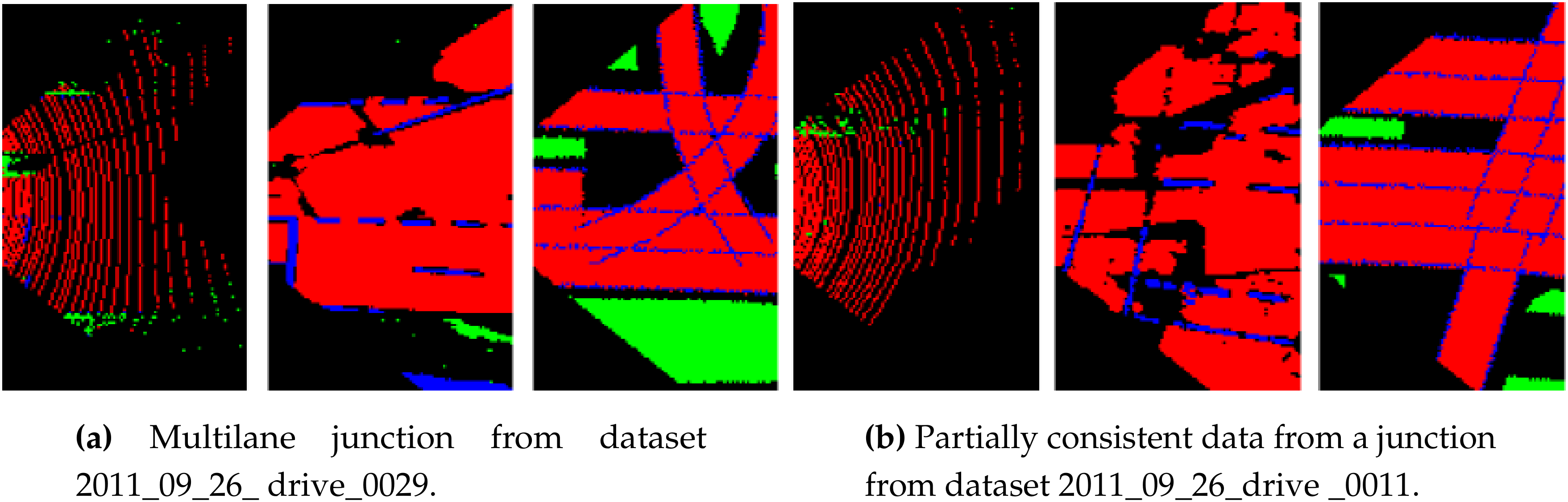
| Dataset–Frames | Integrity [18] | Integrity (Ours) | Situation |
|---|---|---|---|
| Dataset 1–150 | map-0.422 | not enough nodes from the map | |
| Dataset 1–21 | vision-0.175 | vision-0.612 | no good quality lane markings |
| Dataset 2–390 | map-0.087 | map-0.374 | road with multiple curvatures |
| Dataset 3–562 | vision-0.573 | partial occulusion in vision due to vehicles | |
| Dataset 3–1117 | map-0.006 | map-0.381 | wrong map extraction |
| Dataset 4-22 | vision-0.214 | vision-0.681 | road with multiple curvatures |
| Dataset 4-260 | vision-0.651 | vision-0.629 | highway road with single curvature |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balakrishnan, A.; Florez, S.R.; Reynaud, R. Integrity Monitoring of Multimodal Perception System for Vehicle Localization. Sensors 2020, 20, 4654. https://doi.org/10.3390/s20164654
Balakrishnan A, Florez SR, Reynaud R. Integrity Monitoring of Multimodal Perception System for Vehicle Localization. Sensors. 2020; 20(16):4654. https://doi.org/10.3390/s20164654
Chicago/Turabian StyleBalakrishnan, Arjun, Sergio Rodriguez Florez, and Roger Reynaud. 2020. "Integrity Monitoring of Multimodal Perception System for Vehicle Localization" Sensors 20, no. 16: 4654. https://doi.org/10.3390/s20164654
APA StyleBalakrishnan, A., Florez, S. R., & Reynaud, R. (2020). Integrity Monitoring of Multimodal Perception System for Vehicle Localization. Sensors, 20(16), 4654. https://doi.org/10.3390/s20164654







