Application of Artificial Neural Networks for Accurate Determination of the Complex Permittivity of Biological Tissue
Abstract
1. Introduction
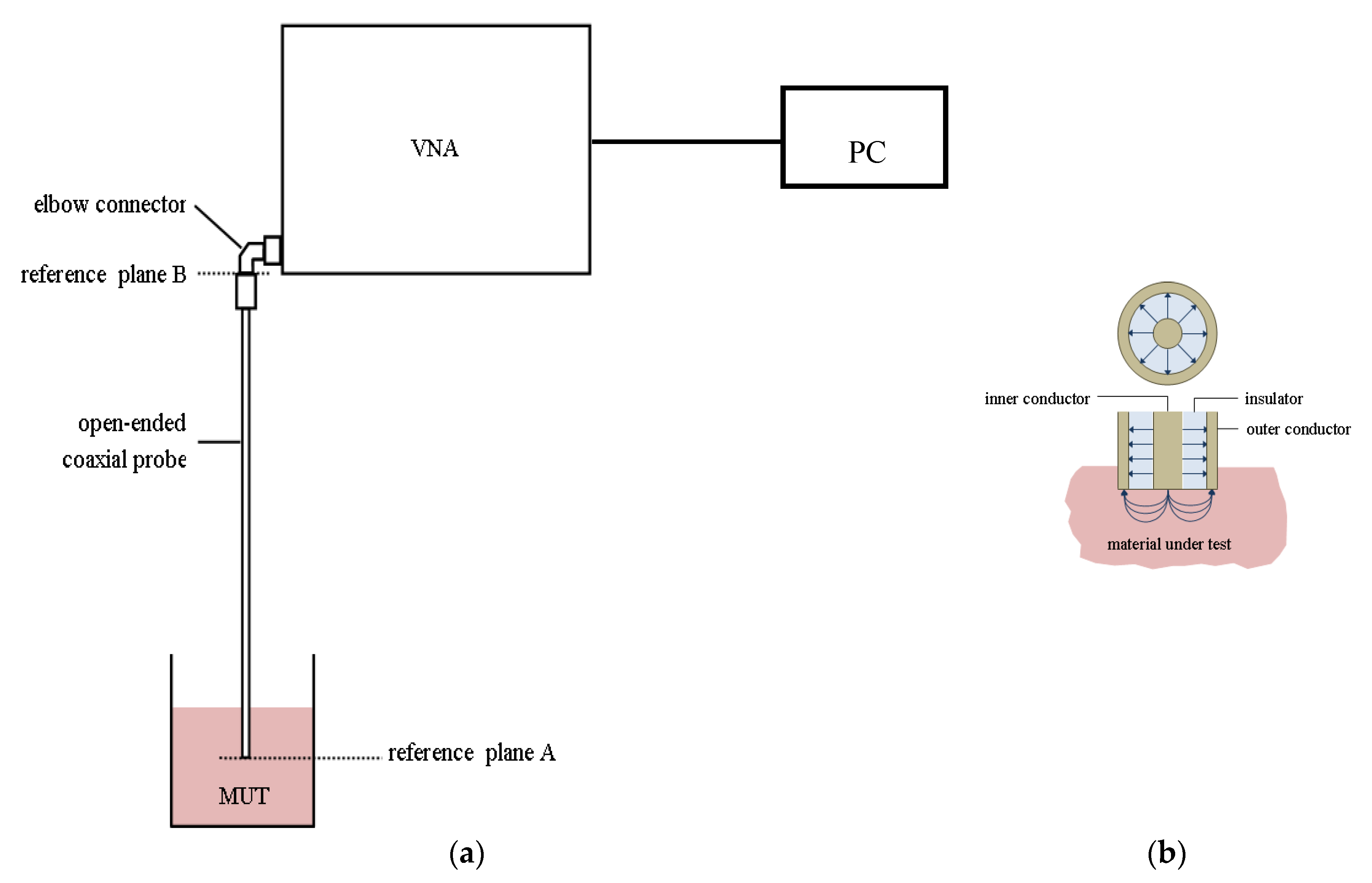
Measurement Methods
2. Materials and Methods
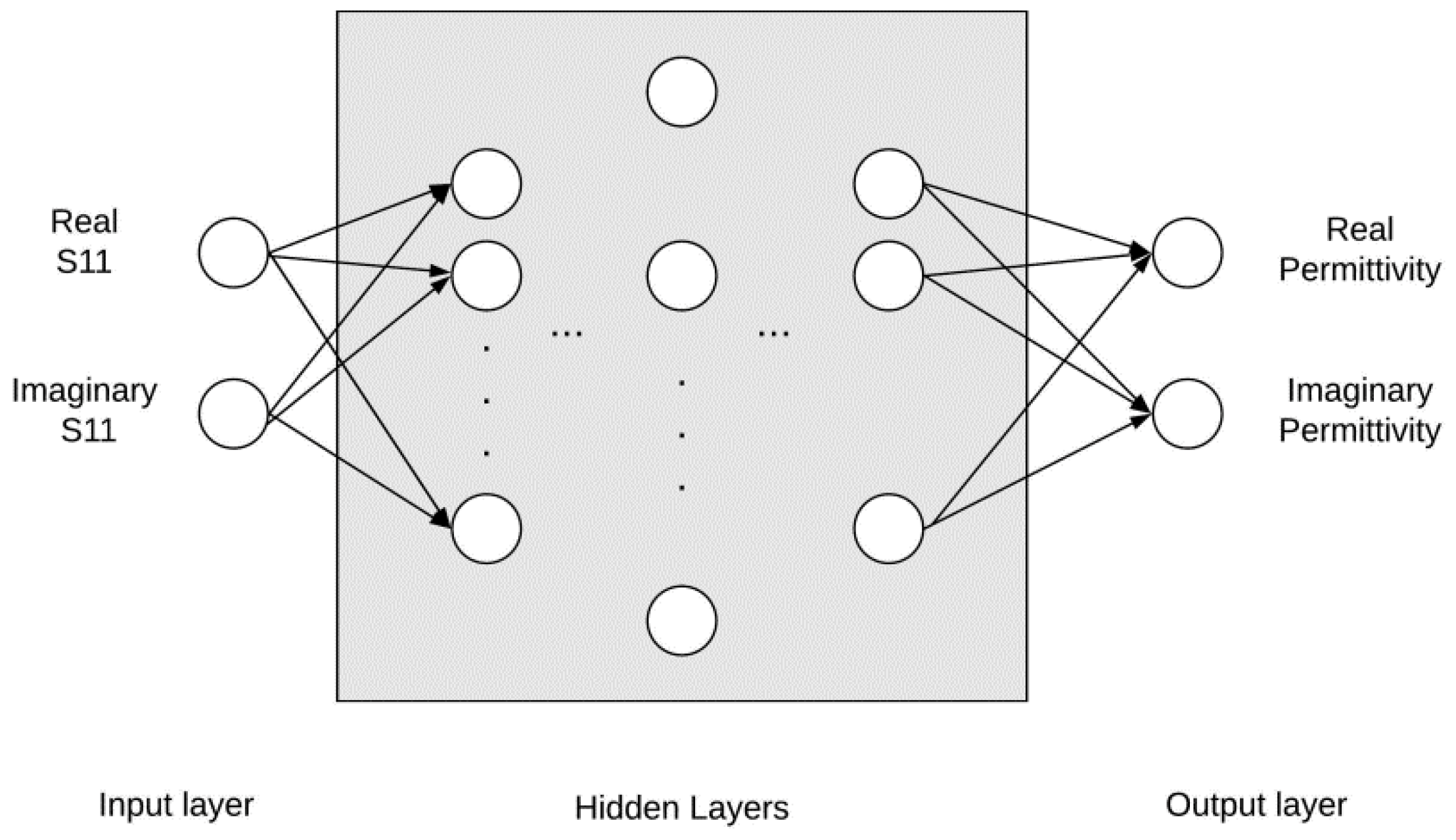
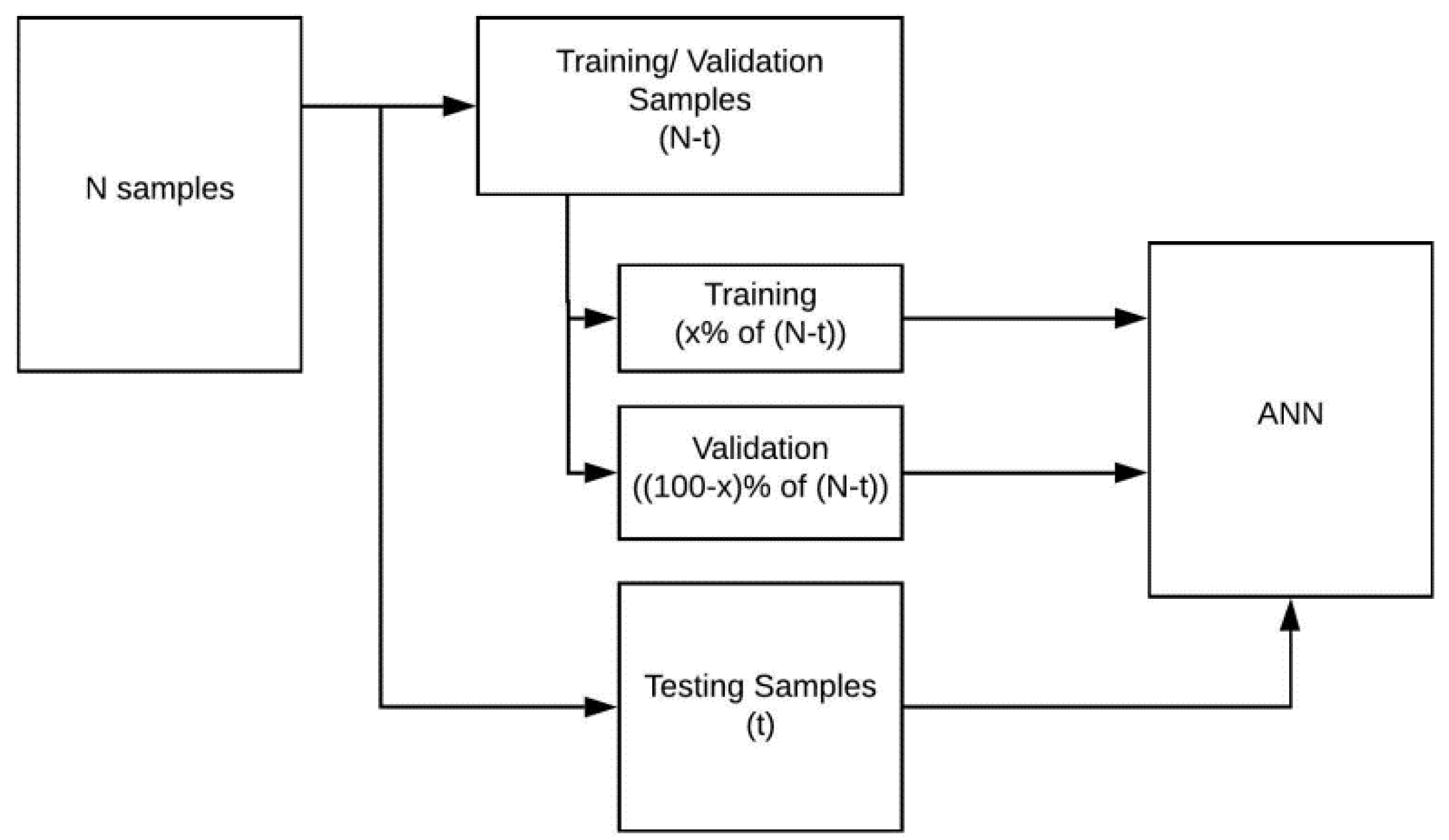
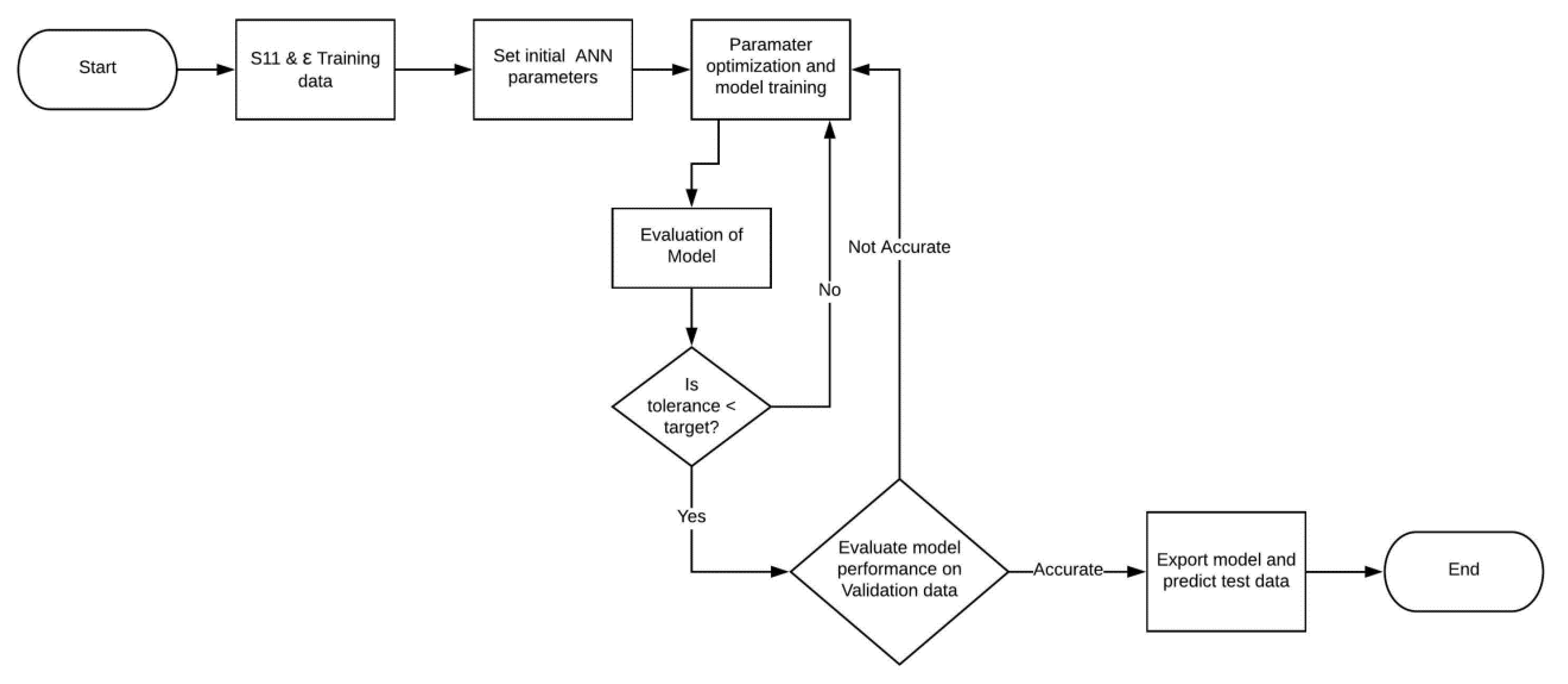
Implementation of the ANN
3. Results
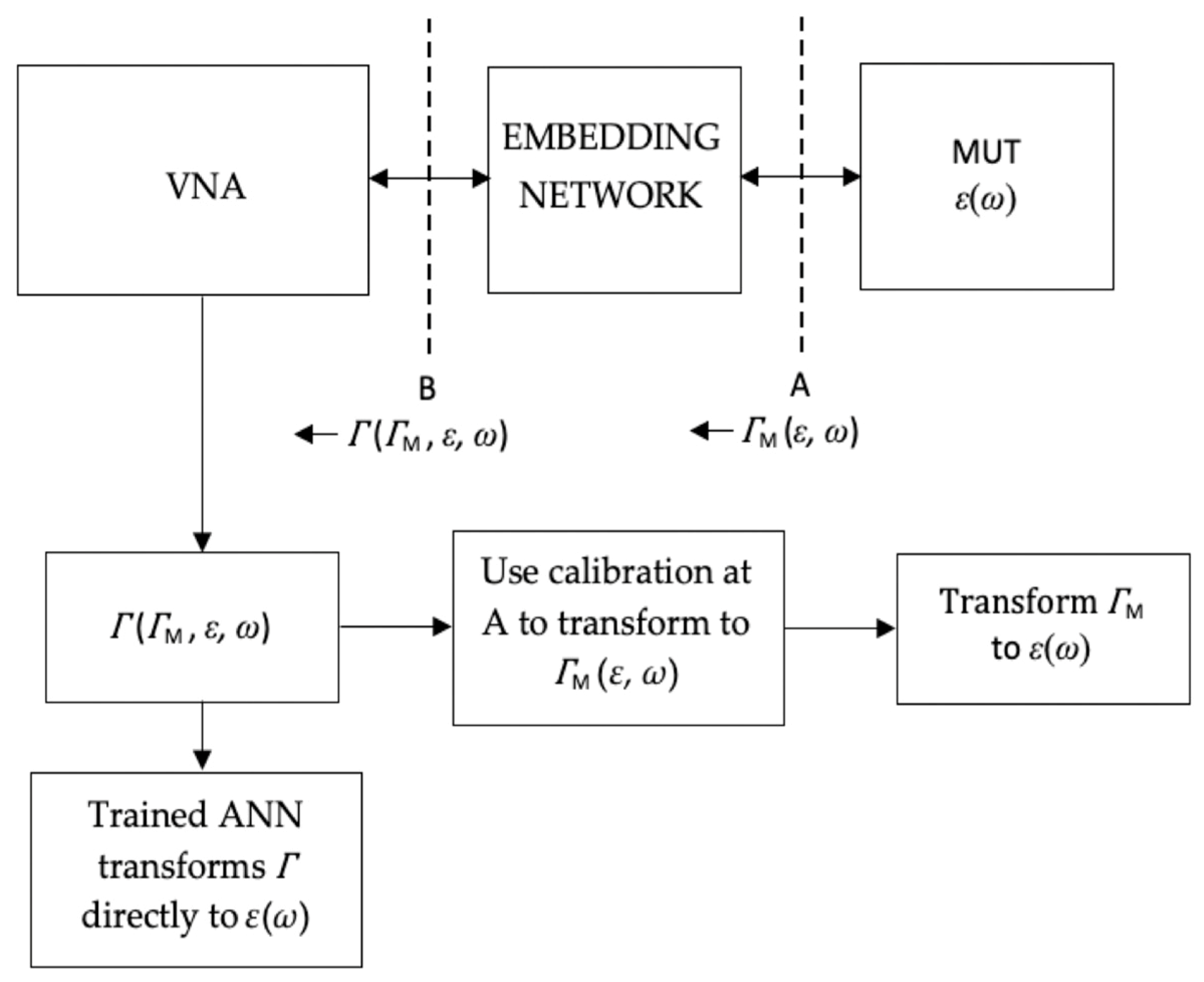
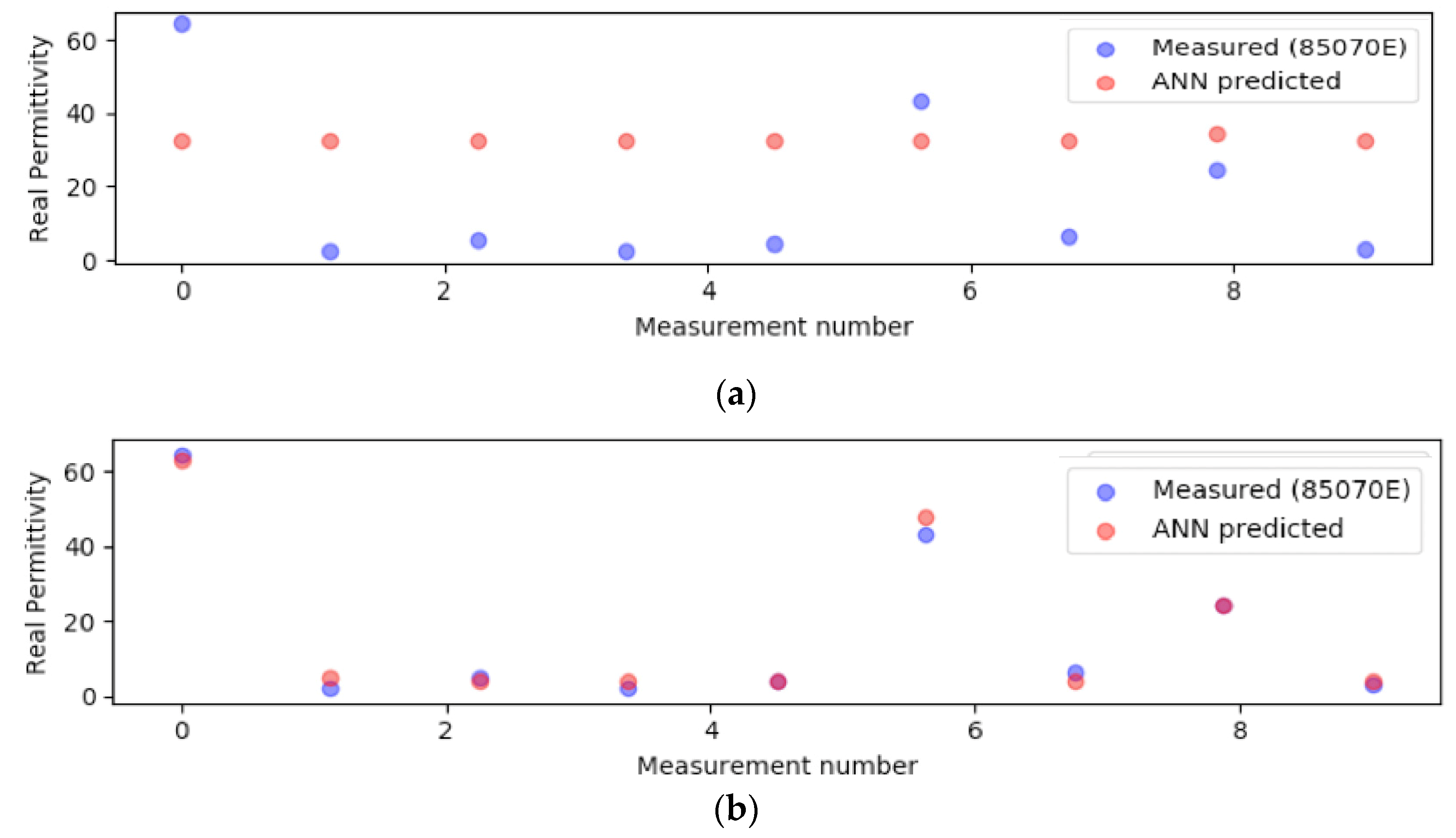
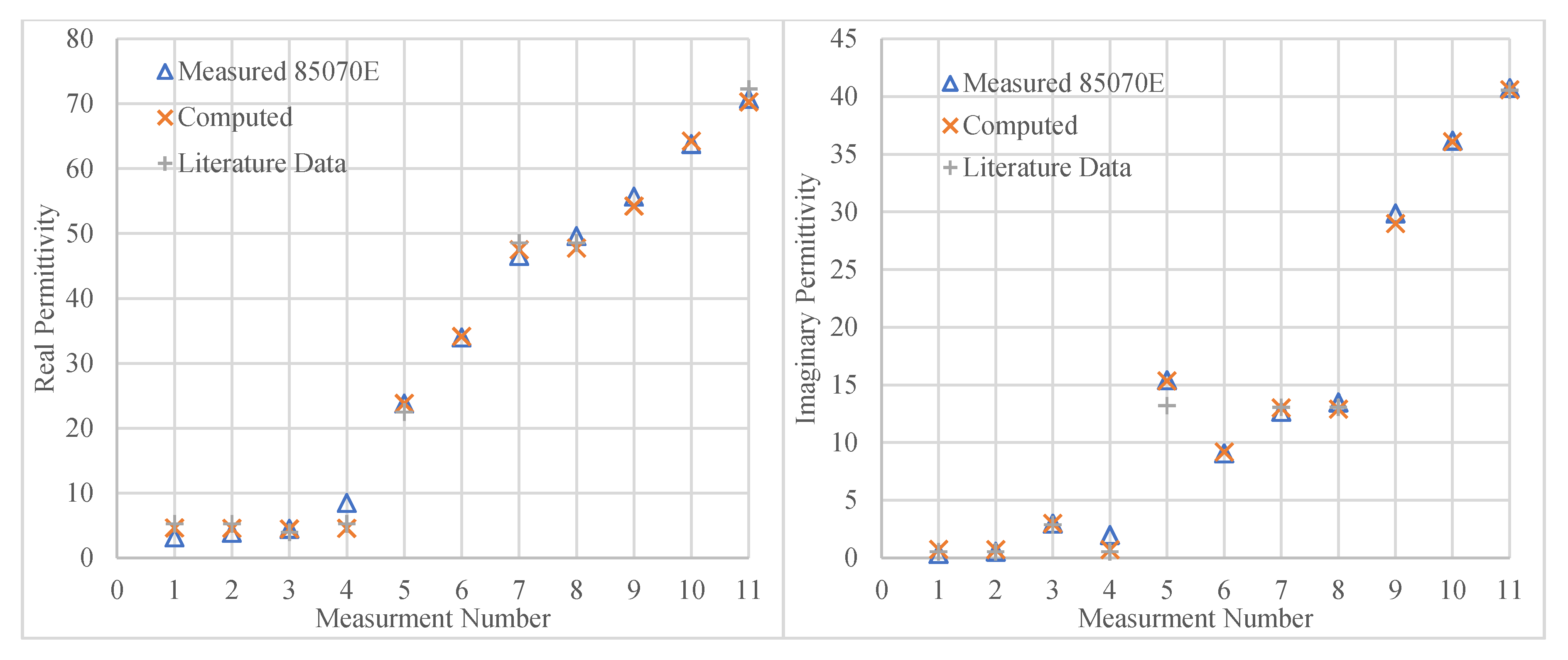
3.1. Calibration Performed at the Tip of the Probe—Reference Plane A
Analysis of Broadband Measurement and Predicted Results
3.2. Calibration Performed at VNA Test Port—Reference Plane B
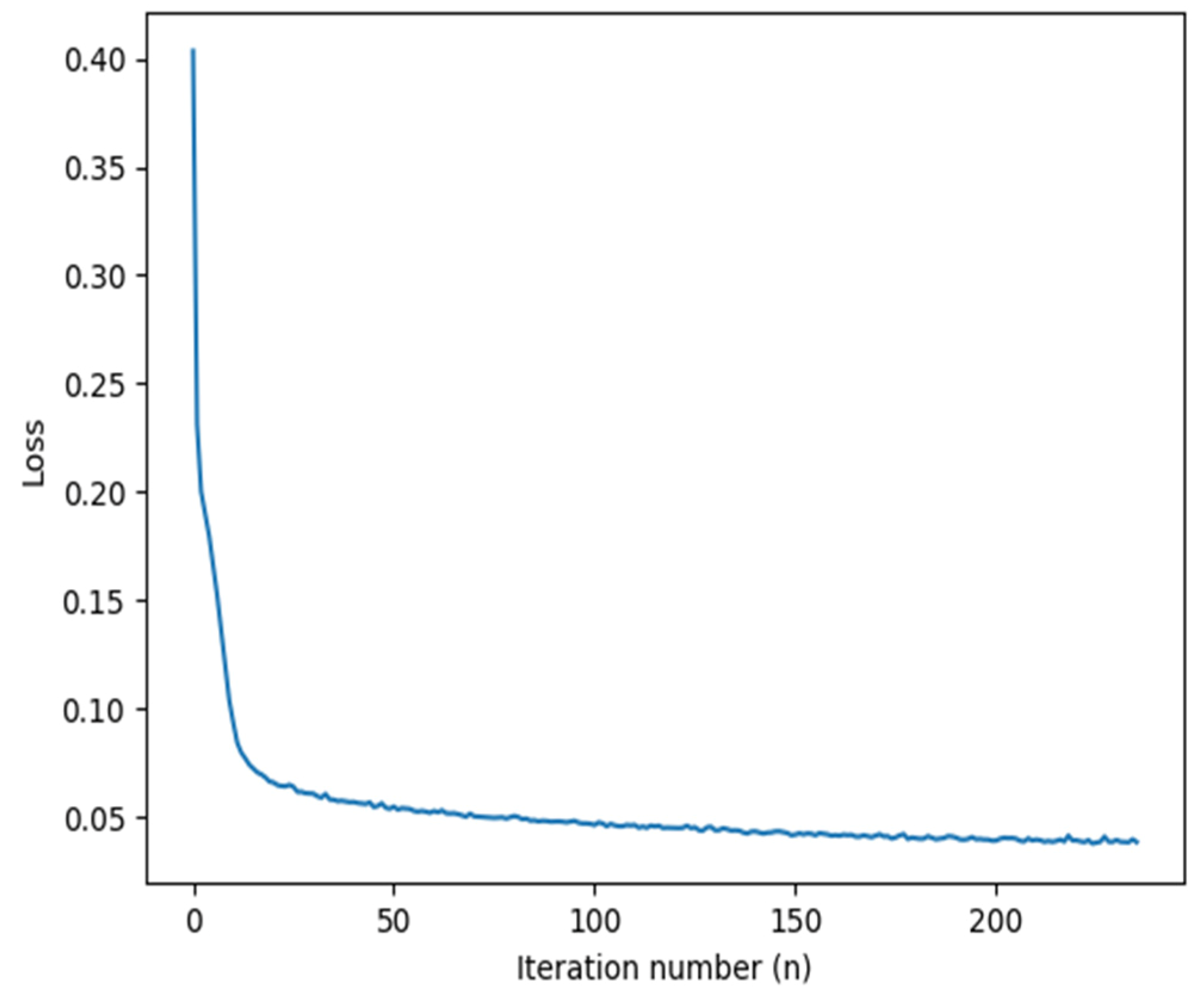
3.2.1. Training of the ANN Using S11 Measured at the VNA Test Port
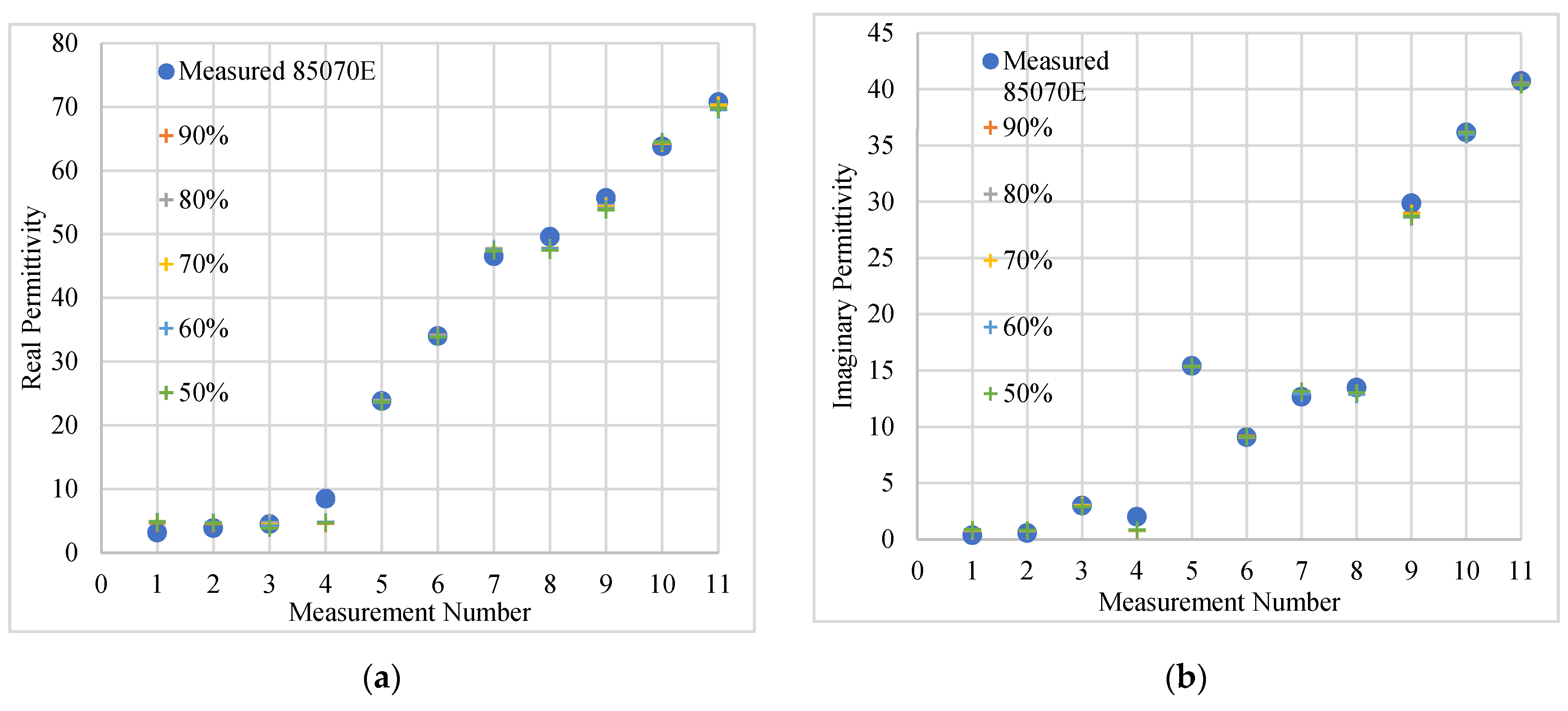
3.2.2. Influence of Training Data Size on ANN Performance
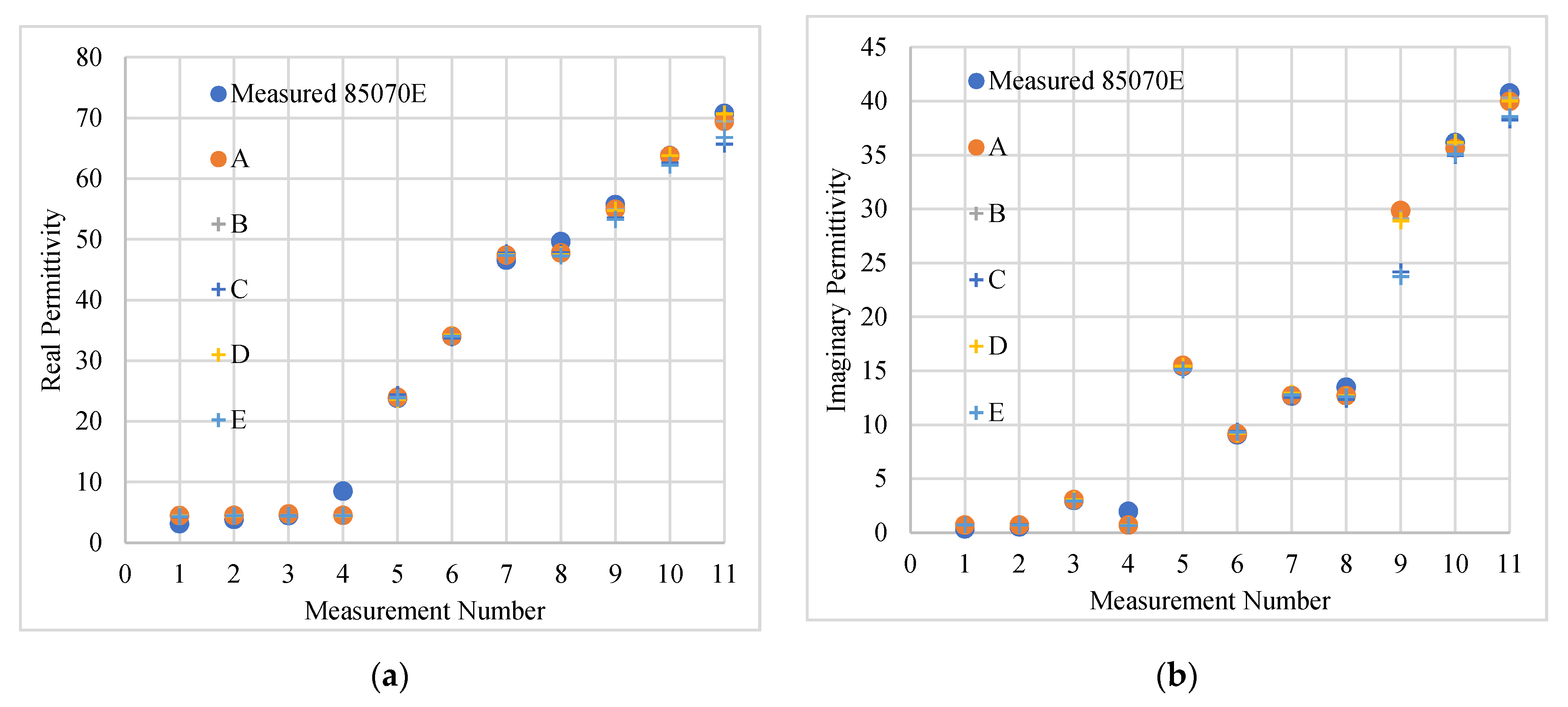
3.2.3. Testing Robustness of the ANN by Adding Noise to the Raw Input Data
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Giombini, A.; Giovannini, V.; Cesare, A.D.; Pacetti, P.; Ichinoseki-Sekine, N.; Shiraishi, M.; Naito, H.; Maffulli, N. Hyperthermia induced by microwave diathermy in the management of muscle and tendon injuries. Br. Med. Bull. 2007, 83, 379–396. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.T.; Tran, T.T.P.; Jin, S.G.; Yong, C.S.; Truong, D.H.; Tran, T.H.; Kim, J.O. Combined hyperthermia and chemotherapy as a synergistic anticancer treatment. J. Pharm. Investig. 2019, 49, 519–526. [Google Scholar] [CrossRef]
- Simo, K.A.; Tsirline, V.B.; Sindram, D.; McMillan, M.T.; Thompson, K.J.; Swan, R.Z.; McKillop, I.H.; Martinie, J.B.; Iannitti, D.A. Microwave ablation using 915-MHz and 2.45-GHz systems: What are the differences? Hpb 2013, 15, 991–996. [Google Scholar] [CrossRef] [PubMed]
- Hines-Peralta, A.U.; Pirani, N.; Clegg, P.; Cronin, N.; Ryan, T.P.; Liu, Z.; Goldberg, S.N. Microwave ablation: Results with a 2.45-GHz applicator in ex vivo bovine and in vivo porcine liver. Radiology 2006, 239, 94–102. [Google Scholar] [CrossRef] [PubMed]
- Brace, C.L.; Laeseke, P.F.; Sampson, L.A.; Frey, T.M.; van der Weide, D.W.; Lee, F.T., Jr. Microwave ablation with a single small-gauge triaxial antenna: In vivo porcine liver model. Radiology 2007, 242, 435–440. [Google Scholar] [CrossRef]
- Ireland, D.; Bialkowski, M.E. Microwave head imaging for stroke detection. Prog. Electromagn Res. 2011, 21, 163–175. [Google Scholar] [CrossRef]
- La Gioia, A.; Porter, E.; Merunka, I.; Shahzad, A.; Salahuddin, S.; Jones, M.; O’Halloran, M. Open-ended coaxial probe technique for dielectric measurement of biological tissues: Challenges and common practices. Diagnostics 2018, 8, 40. [Google Scholar] [CrossRef]
- Tereshchenko, O.V.; Buesink, F.J.K.; Leferink, F.B.J. An overview of the techniques for measuring the dielectric properties of materials. In Proceedings of the 2011 XXXth URSI General Assembly and Scientific Symposium, Istanbul, Turkey, 13–20 August 2011. [Google Scholar] [CrossRef]
- Brodie, G.; Jacob, M.; Farrell, P. Microwave and Radio-Frequency Technologies in Agriculture; De Gruyter Open: Berlin, Germany, 2016. [Google Scholar]
- Bonello, J.; Elahi, M.A.; Porter, E.; O’Hollaran, M.; Farrugia, L.; Sammut, C.V. An investigation of the variation of dielectric properties of ovine lung tissue with temperature. Biomed. Phys. Eng. Express 2019, 5, 045024. [Google Scholar] [CrossRef]
- Bonello, J.; Farrugia, L.; Schembri Wismayer, P.; Alborova, I.L.; Sammut, C.V. A study of the effects of preservative solutions on the dielectric properties of biological tissue. Int. J. RF Microw. Comput. Aided Eng. 2018, 28, e21214. [Google Scholar] [CrossRef]
- Farrugia, L.; Wismayer, P.S.; Mangion, L.Z.; Sammut, C.V. Accurate in vivo dielectric properties of liver from 500 MHz to 40 GHz and their correlation to ex vivo measurements. Electromagn. Biol. Med. 2016, 35, 365–373. [Google Scholar] [CrossRef]
- Di Meo, S.; Farhat, I.; Bonello, J.; Farrugia, L.; Pasian, M.; Sammut, C.V. Hydration as Classifier of Dielectric Measurement Data from 500 MHz to 50 GHz. In Proceedings of the 2019 PhotonIcs & Electromagnetics Research Symposium-Spring (PIERS-Spring), Rome, Italy, 17 June 2019; pp. 1416–1423. [Google Scholar] [CrossRef]
- Stuchly, M.A.; Stuchly, S.S. Dielectric properties of biological substances—Tabulated. J. Microw. Power 1980, 15, 19–25. [Google Scholar] [CrossRef]
- Rhode & Schwarz, Fundamentals of Vector Network Analysis. Available online: https://www.signalintegrityjournal.com/ext/resources/White-papers-App-notes/Vector-Network-Analyzer-Fundamentals-Primer.pdf (accessed on 27 April 2020).
- Misra, D. On the measurement of the complex permittivity of materials by an open-ended coaxial probe. IEEE Microw. Guided Wave Lett. 1995, 5, 161–163. [Google Scholar] [CrossRef]
- Misra, D.K. A quasi-static analysis of open-ended coaxial lines (short paper). IEEE Trans. Microw. Theory Tech. 1987, 35, 925–928. [Google Scholar] [CrossRef]
- Perez Cesaretti, M.D. General Effective Medium Model for the Complex Permittivity Extraction with an Open-Ended Coaxial Probe in Presence of a Multilayer Material under Test. Ph.D. Thesis, University of Bologna, Bologna, Italy, 2012. [Google Scholar]
- Keysight Technologies. Keysight E5063A ENA Series Network Analyzer; Keysight Technologies: Santa Clara, CA, USA, 2015; Available online: https://www.keysight.com/ie/en/assets/7018-03896/brochures/5991-2171.pdf (accessed on 27 April 2020).
- Grant, J.P.; Clarke, R.N.; Symm, G.T.; Spyrou, N.M. A critical study of the open-ended coaxial line sensor technique for RF and microwave complex permittivity measurements. J. Phys. E Sci. Instrum. 1989, 22, 757–770. [Google Scholar] [CrossRef]
- Chen, L.F.; Ong, C.K.; Neo, C.P.; Varadan, V.V.; Varadan, V.K. Microwave Electronics: Measurement and Materials Characterization; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Athey, T.W.; Stuchly, M.A.; Stuchly, S.S. Measurement of radio frequency permittivity of biological tissues with an open-ended coaxial line: Part I. IEEE Trans. Microw. Theory Tech. 1982, 30, 82–86. [Google Scholar] [CrossRef]
- Stuchly, M.A.; Athey, T.W.; Samaras, G.M.; Taylor, G.E. Measurement of radio frequency permittivity of biological tissues with an open-ended coaxial line: Part II-Experimental results. IEEE Trans. Microw. Theory Tech. 1982, 30, 87–92. [Google Scholar] [CrossRef]
- Brandy, M.M.; Symons, S.A.; Stuchly, S.S. Dielectric behaviour of selected animal tissues in vitro at frequencies from 2 to 4 GHz. IEEE Trans. Biomed. Eng. 1981, BME-28, 305–307. [Google Scholar] [CrossRef]
- Ghannouchi, F.M.; Bosisio, R.G. Measurement of microwave permittivity using a six-port reflectometer with an open-ended coaxial line. IEEE Trans. Instrum. Meas. 1989, 38, 505–508. [Google Scholar] [CrossRef]
- Stuchly, S.S.; Sibbald, C.L.; Anderson, J.M. A new aperture admittance model for open-ended waveguides. IEEE Trans. Microw. Theory Tech. 1994, 42, 192–198. [Google Scholar] [CrossRef]
- Anderson, J.M.; Sibbald, C.L.; Stuchly, S.S. Dielectric measurements using a rational function model. IEEE Trans. Microw. Theory Tech. 1994, 42, 199–204. [Google Scholar] [CrossRef]
- Anderson, J.M.; Sibbald, C.L.; Stuchly, S.S.; Caputa, K. September. Advances in dielectric measurements using an open-ended coaxial line sensor. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Vancouver, BC, Canada, 14–17 September 1993; pp. 916–919. [Google Scholar] [CrossRef]
- Jenkins, S.; Preece, A.W.; Hodgetts, T.E.; Symm, G.T.; Warham, A.G.P.; Clarke, R.N. Comparison of three numerical treatments for the open-ended coaxial line sensor. Electron. Lett. 1990, 26, 234–236. [Google Scholar] [CrossRef]
- Monsefi, F.; Otterskog, M.; Silvestrov, S. Direct and Inverse Computational Methods for Electromagnetic Scattering in Biological Diagnostics. arXiv 2013, arXiv:1312.4379. [Google Scholar]
- Berube, D.; Ghannouchi, F.M.; Savard, P. A comparative study of four open-ended coaxial probe models for permittivity measurements of lossy dielectric/biological materials at microwave frequencies. IEEE Trans. Microw. Theory Tech. 1996, 44, 1928–1934. [Google Scholar] [CrossRef]
- Ištuk, N.; Kienberger, F.; Porter, E.; O’Halloran, M.; Santorelli, A.; Alic, I.; Ragulskis, M.; Moradpour, A.; Kasper, M. Fast Measurements of Dielectric Properties with Small Size Microwave Transceiver. In Proceedings of the 2020 14th European Conference on Antennas and Propagation (EuCAP), Copenhagen, Denmark, 15 March 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Peyman, A.; Gabriel, C.; Grant, E.H. Complex permittivity of sodium chloride solutions at microwave frequencies. Bioelectromagnetics 2007, 28, 264–274. [Google Scholar] [CrossRef] [PubMed]
- SC2040-Fairview Microwave|RF Short’. Available online: https://www.fairviewmicrowave.com/2.4mm-male-open-circuit-connector-cap-sc2040-p.aspx (accessed on 25 June 2020).
- SC2152-Fairview Microwave|RF Dust Cap’. Available online: https://www.fairviewmicrowave.com/2.4mm-male-short-circuit-connector-cap-50-ghz-sc2152-p.aspx (accessed on 25 June 2020).
- SC5038-Fairview Microwave|Termination’. Available online: https://www.fairviewmicrowave.com/rf-load-1-watts-50-ghz-precision-2.4mm-male-st5038-p.aspx (accessed on 25 June 2020).
- Gabriel, C.; Peyman, A. Dielectric measurement: Error analysis and assessment of uncertainty. Phys. Med. Biol. 2006, 51, 6033–6046. [Google Scholar] [CrossRef]
- Russell, S.J.; Norvig, P.; Canny, J. Artificial Intelligence: A Modern Approach, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Scikit-Learn Developers, 2020, Sklearn, Beyrak Network. MLPRegressor. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.neural_network.MLPRegressor.html (accessed on 11 August 2020).
- Acharya, D.; Rani, A.; Agarwal, S.; Singh, V. Application of adaptive Savitzky–Golay filter for EEG signal processing. Perspect. Sci. 2016, 8, 677–679. [Google Scholar] [CrossRef]
- Abdilla, L.; Sammut, C.; Mangion, L.Z. Dielectric properties of muscle and liver from 500 MHz–40 GHz. Electromagn. Biol. Med. 2013, 32, 244–252. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271. [Google Scholar] [CrossRef]
- Gregory, A.P.; Clarke, R.N. Tables of the Complex Permittivity of Dielectric Reference Liquids at Frequencies up to 5 GHz; Technical Report for National physical Laboratory: London, UK, 2 February 2018. [Google Scholar]
- Farrugia, L. Dielectric Properties of Biological Tissues in Medical Applications. Ph.D. Thesis, University of Malta, Msida, Malta, 2016. [Google Scholar]
- Keysight. N1501A Dielectric Probe Kit 10 MHz to 50 GHz: Technical Overview. 2015. Available online: http://www.Keysight.Com/En/Pd-2492144-Pn-N1501A/Dielectric-Probe-Kit (accessed on 30 June 2020).

| Test Material | Number of Samples |
|---|---|
| 30 mL of 0.5 M NaCl | 3 |
| 30 mL of 0.5 M NaCl + 2 mL TX-100 | 3 |
| 30 mL of 0.5 M NaCl + 4 mL TX-100 | 3 |
| 30 mL of 0.5 M NaCl + 6 mL TX-100 | 3 |
| 30 mL of 0.5 M NaCl + 8 mL TX-100 | 3 |
| 30 mL of 0.5 M NaCl + 11 mL TX-100 | 3 |
| 30 mL of 0.5 M NaCl + 4 mL TX-100 + 2 g glucose | 3 |
| 30 mL of 0.5 M NaCl + 11 mL TX-100 + 2 g glucose | 3 |
| 30 mL of 0.1 M NaCl + 20 g glucose | 3 |
| Acetone (107901Z-Brenntag) | 3 |
| Propan-2-ol (1376-Girelli Alcohol) | 3 |
| Methanol (20864. 320-VWR) | 3 |
| 30 mL TX (TR04441000 – Scharlau) | 6 |
| 15 mL TX + 15 mL DI water | 6 |
| 15 mL TX + 20 mL DI water | 6 |
| 15 mL Isopropyl alcohol + 15 mL DI water | 3 |
| 27.5 mL Isopropyl alcohol + 15 mL DI water | 3 |
| Porcine liver (freshly excised) | 21 |
| Porcine fat (freshly excised) | 21 |
| Total | 102 |
| Measurement Type | Δ ε′ [%] | Δ ε″ [%] | ||||
|---|---|---|---|---|---|---|
| Max | Min | Mean | Max | Min | Mean | |
| Broadband (0.5–5 GHz) | 5.60 (1) | 0.31 (3) | 1.40 | 9.80 (2) | 0.03 (4) | 1.77 |
| Single frequency (2.45 GHz) | 2.60 | 0.60 | 1.20 | 3.90 | 1.00 | 2.50 |
| Measurement Number | Material Tested |
|---|---|
| 1 | Fat [42] |
| 2 | Fat [42] |
| 3 | Propan-2-ol [43] |
| 4 | Fat [42] |
| 5 | Methanol [43] |
| 6 | 15 mL TX + 15 mL DI water |
| 7 | Liver [33] |
| 8 | Liver [33] |
| 9 | 30 mL of 0.5 M NaCl + 11 mL TX-100 + 2 g glucose |
| 10 | 30 mL of 0.5 M NaCl + 4 mL TX-100 |
| 11 | 30 mL of 0.5 M NaCl [44] |
| Data Fraction Used for Training [%] | Max Iteration Number | Final Loss Value |
|---|---|---|
| 90 | 2099 | 0.00059 |
| 80 | 1929 | 0.00069 |
| 70 | 3081 | 0.00070 |
| 60 | 3243 | 0.00079 |
| 50 | 3076 | 0.00094 |
| Δ Training [%] | Δ ε′ [%] | Δ ε″ [%] | ||||
|---|---|---|---|---|---|---|
| Max | Min | Mean | Max | Min | Mean | |
| 90 | 47.6 | 0.15 | 11.1 | 119 | 0.16 | 21.0 |
| 80 | 54.0 | 0.29 | 12.5 | 126 | 0.07 | 21.8 |
| 70 | 57.1 | 0.48 | 12.4 | 140 | 0.01 | 23.4 |
| 60 | 55.8 | 0.47 | 12.8 | 150 | 0.27 | 25.0 |
| 50 | 52.6 | 0.56 | 13.2 | 152 | 0.07 | 25.2 |
| ANN Results Compared to Slim Form Probe Measurements as Indicated | Δ ε′ [%] | Δ ε″ [%] | ||||
|---|---|---|---|---|---|---|
| Max | Min | Mean | Max | Min | Mean | |
| No added noise | 88.5 | 0.07 | 13.5 | 184 | 0.01 | 24.7 |
| Scenario 1 | 87.0 | 0.03 | 13.3 | 181 | 0.02 | 25.6 |
| Scenario 1, 2nd run | 92.8 | 0.78 | 13.2 | 202 | 0.15 | 29.7 |
| Scenario 2 | 91.7 | 0.02 | 14.2 | 182 | 0.01 | 25.9 |
| Scenario 2, 2nd run | 91.4 | 0.12 | 14.0 | 198 | 0.86 | 29.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonello, J.; Demarco, A.; Farhat, I.; Farrugia, L.; Sammut, C.V. Application of Artificial Neural Networks for Accurate Determination of the Complex Permittivity of Biological Tissue. Sensors 2020, 20, 4640. https://doi.org/10.3390/s20164640
Bonello J, Demarco A, Farhat I, Farrugia L, Sammut CV. Application of Artificial Neural Networks for Accurate Determination of the Complex Permittivity of Biological Tissue. Sensors. 2020; 20(16):4640. https://doi.org/10.3390/s20164640
Chicago/Turabian StyleBonello, Julian, Andrea Demarco, Iman Farhat, Lourdes Farrugia, and Charles V. Sammut. 2020. "Application of Artificial Neural Networks for Accurate Determination of the Complex Permittivity of Biological Tissue" Sensors 20, no. 16: 4640. https://doi.org/10.3390/s20164640
APA StyleBonello, J., Demarco, A., Farhat, I., Farrugia, L., & Sammut, C. V. (2020). Application of Artificial Neural Networks for Accurate Determination of the Complex Permittivity of Biological Tissue. Sensors, 20(16), 4640. https://doi.org/10.3390/s20164640








