Modeling of Stochastic Wind Based on Operational Flight Data Using Karhunen–Loève Expansion Method
Abstract
1. Introduction
2. Modeling of Stochastic Process
2.1. Karhunen–LoèVe Expansion
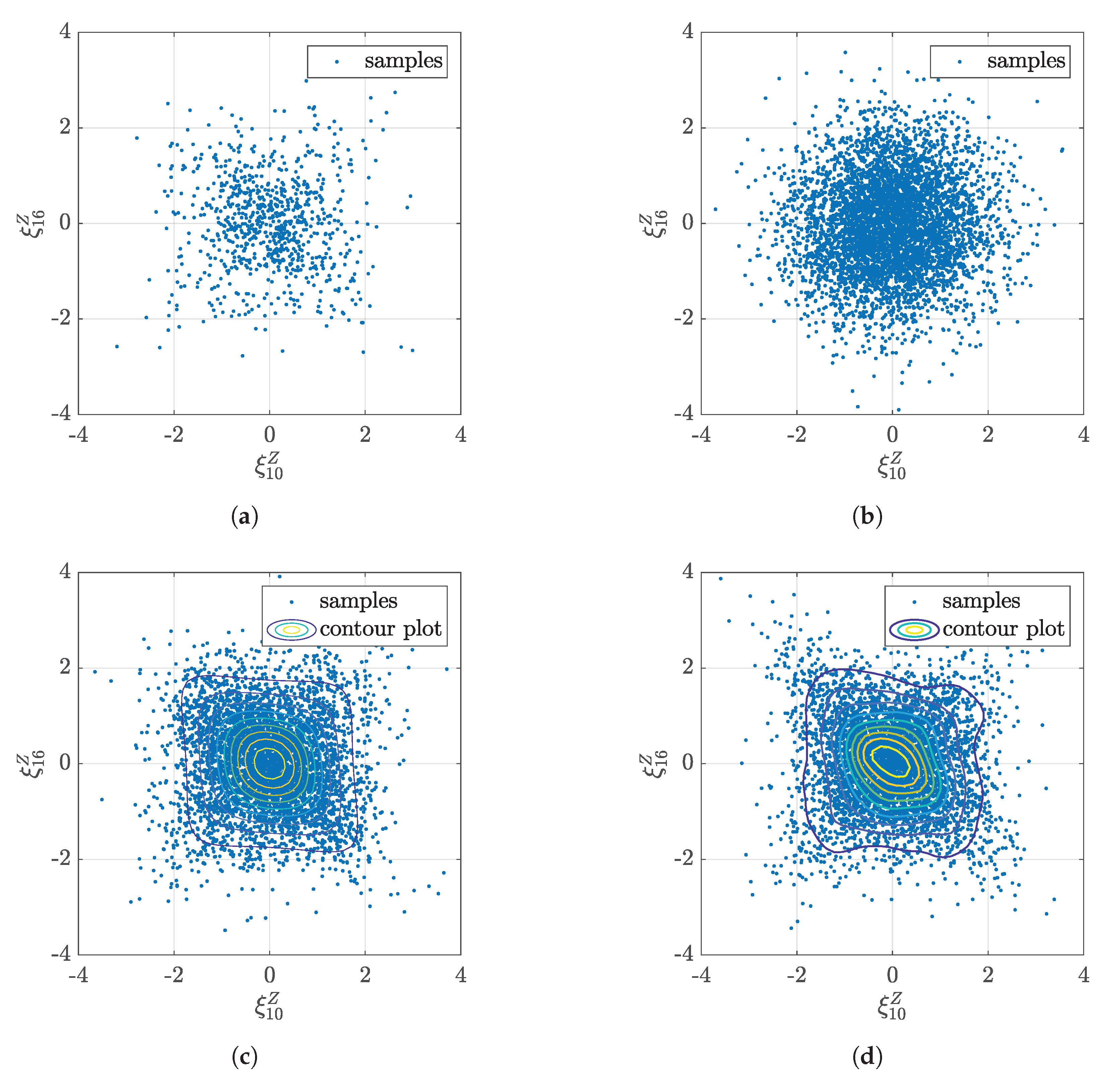
2.2. Vine Copula
| Algorithm 1 Procedure of the stochastic process reconstruction and regeneration |
|
2.3. Spectral Representation
3. Results and Discussion of Wind Process Modeling
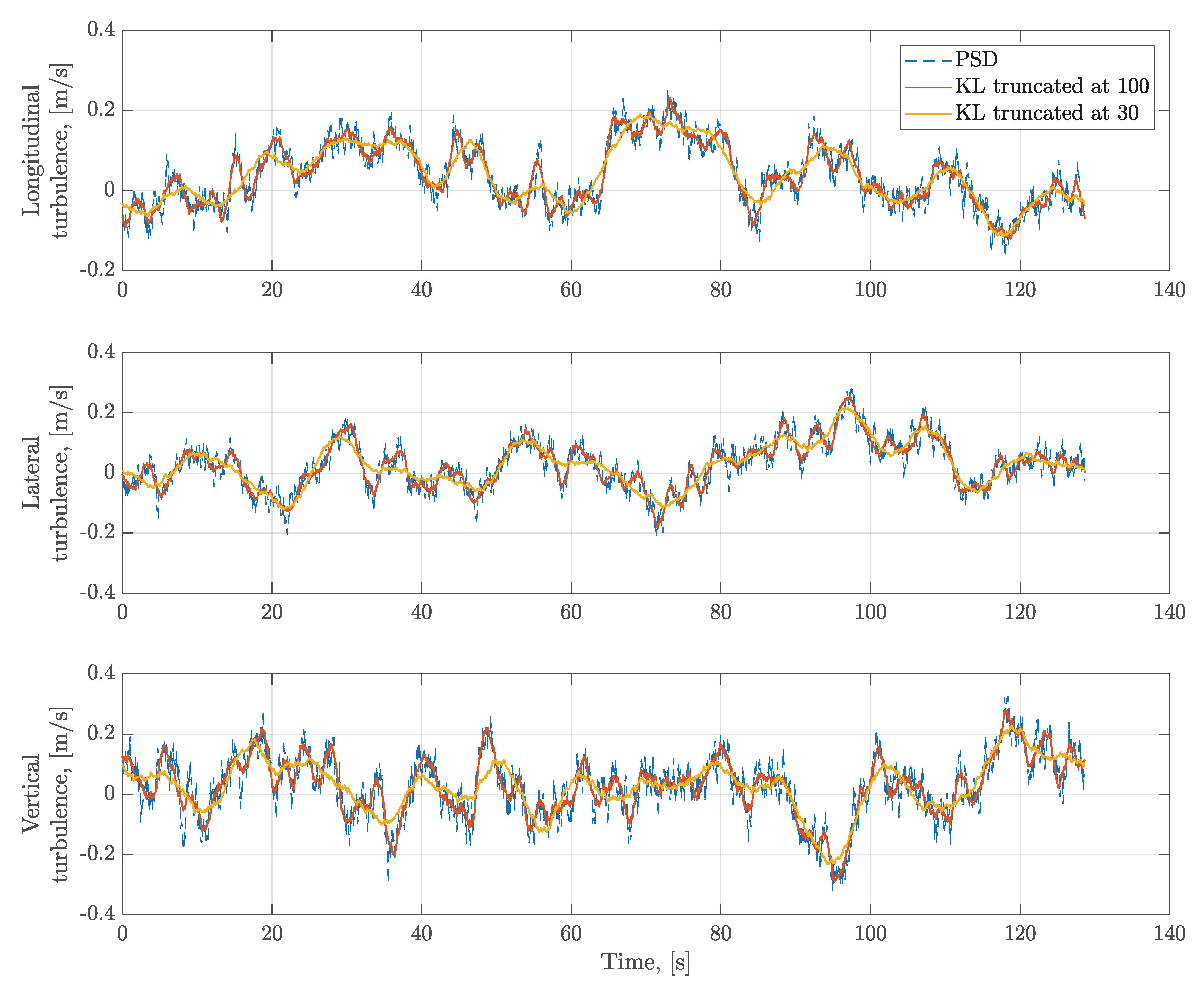
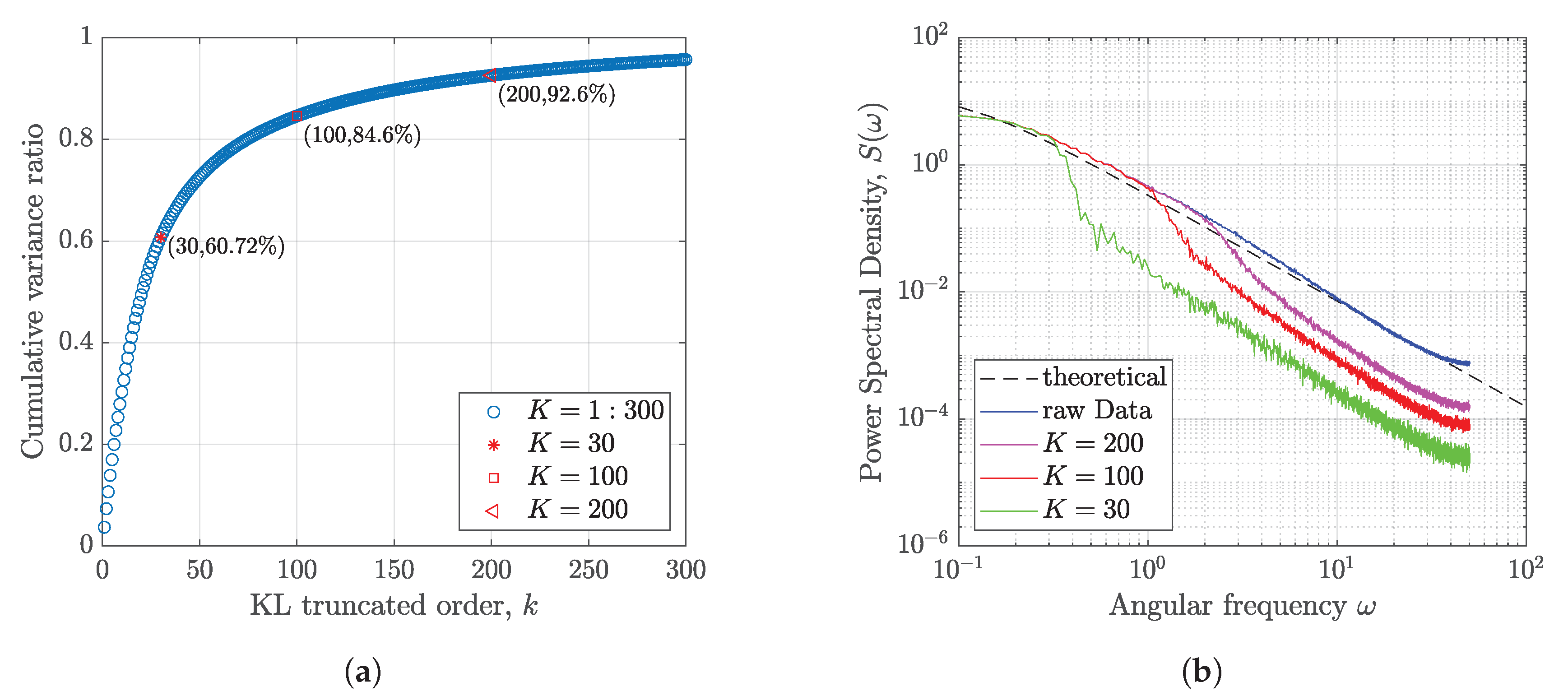
3.1. Turbulence
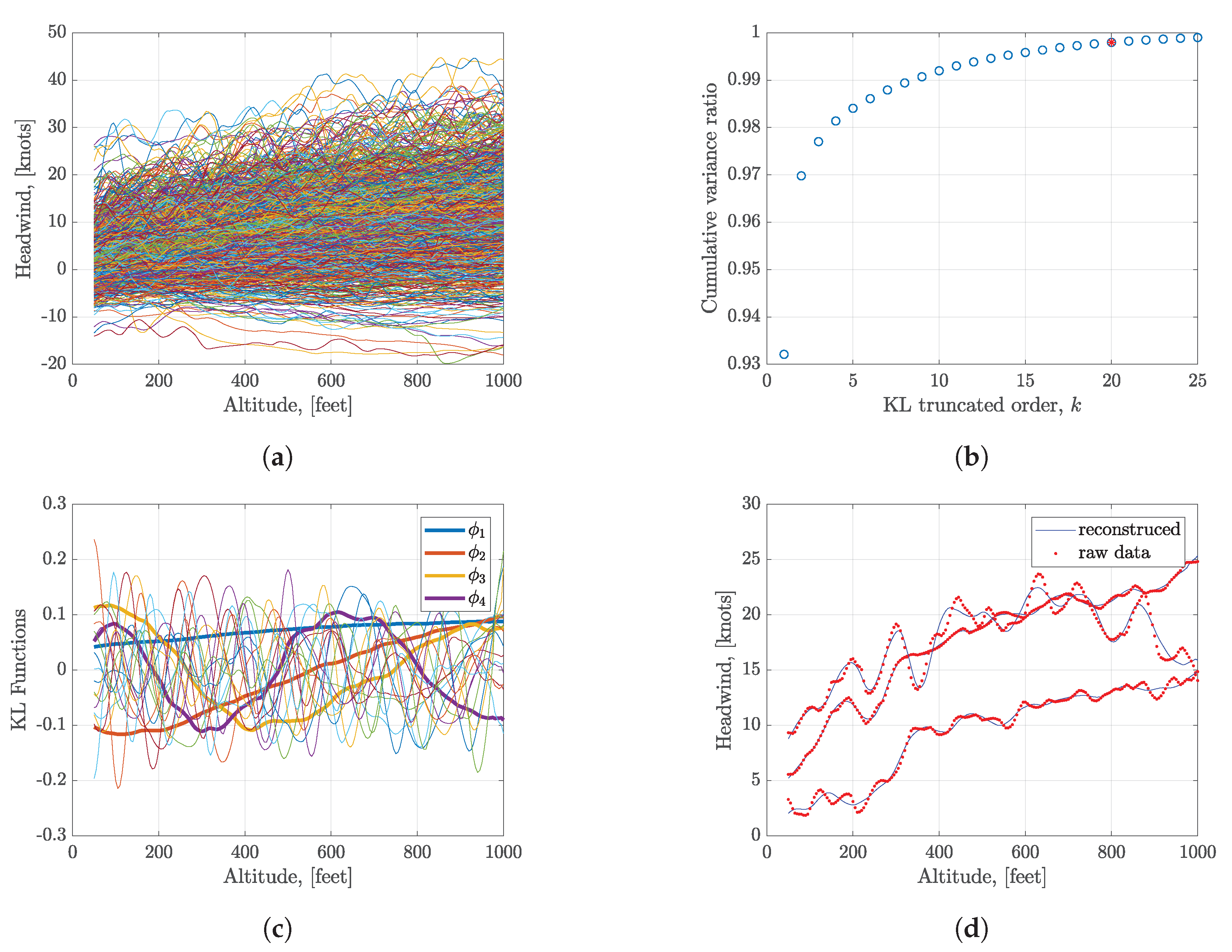
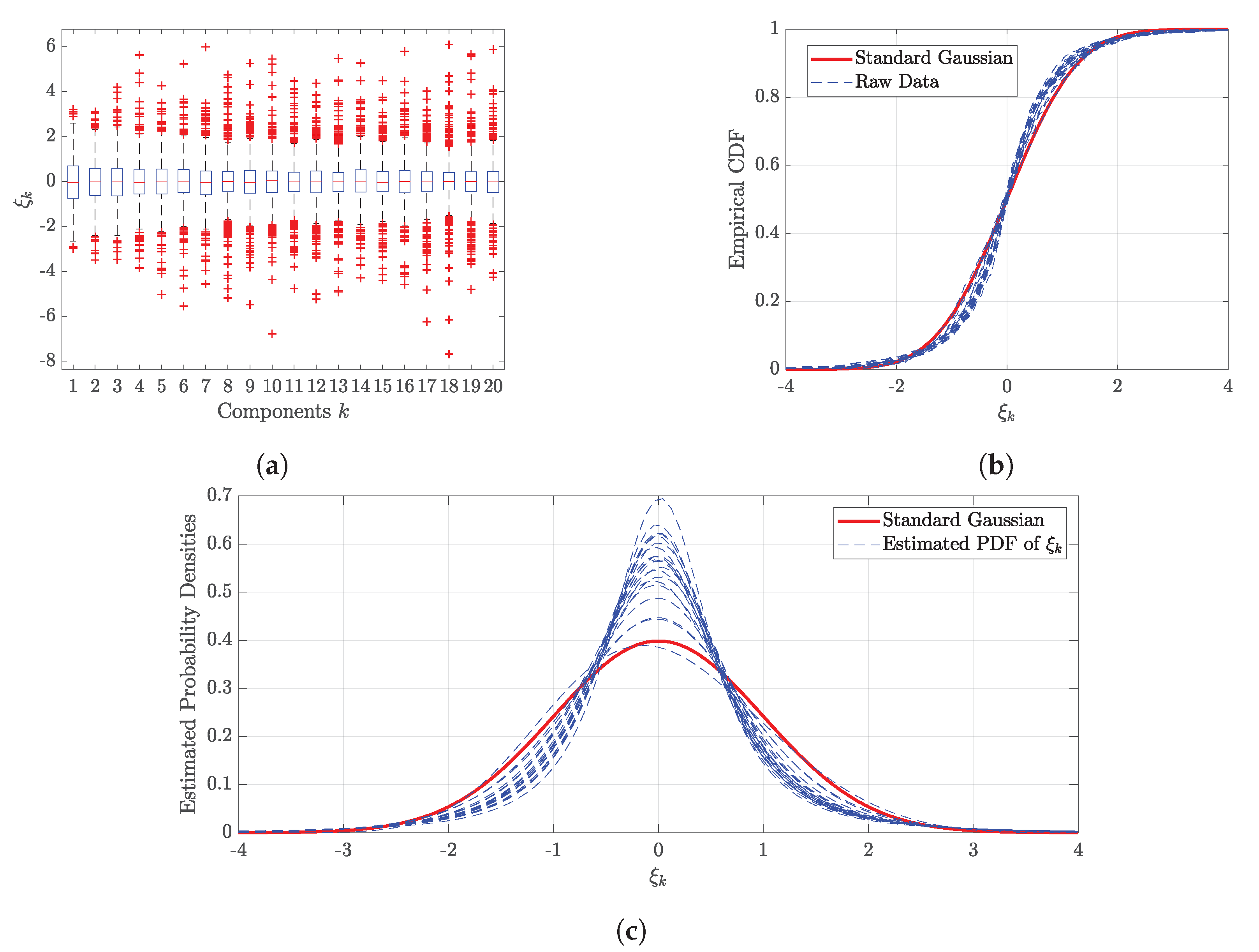
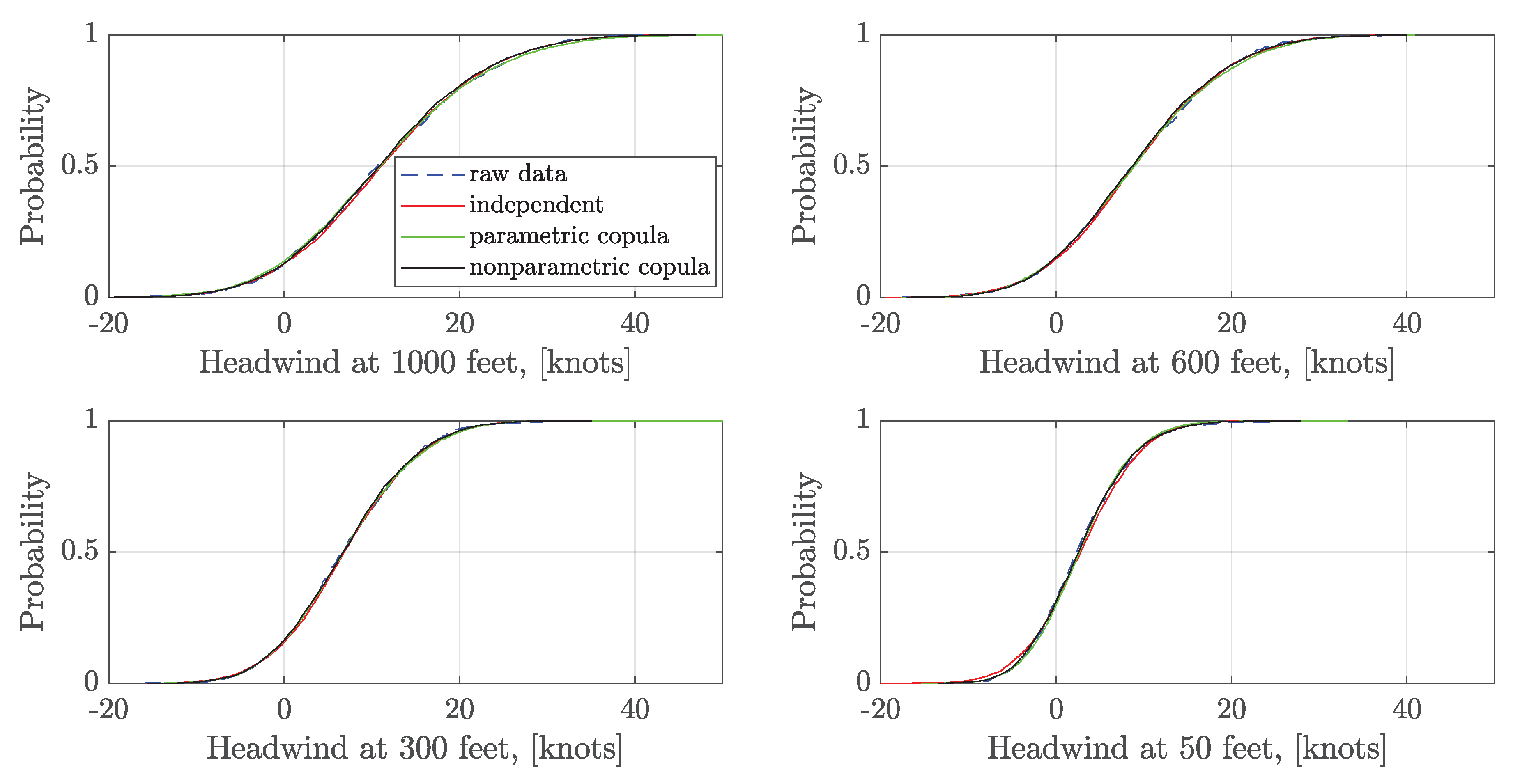
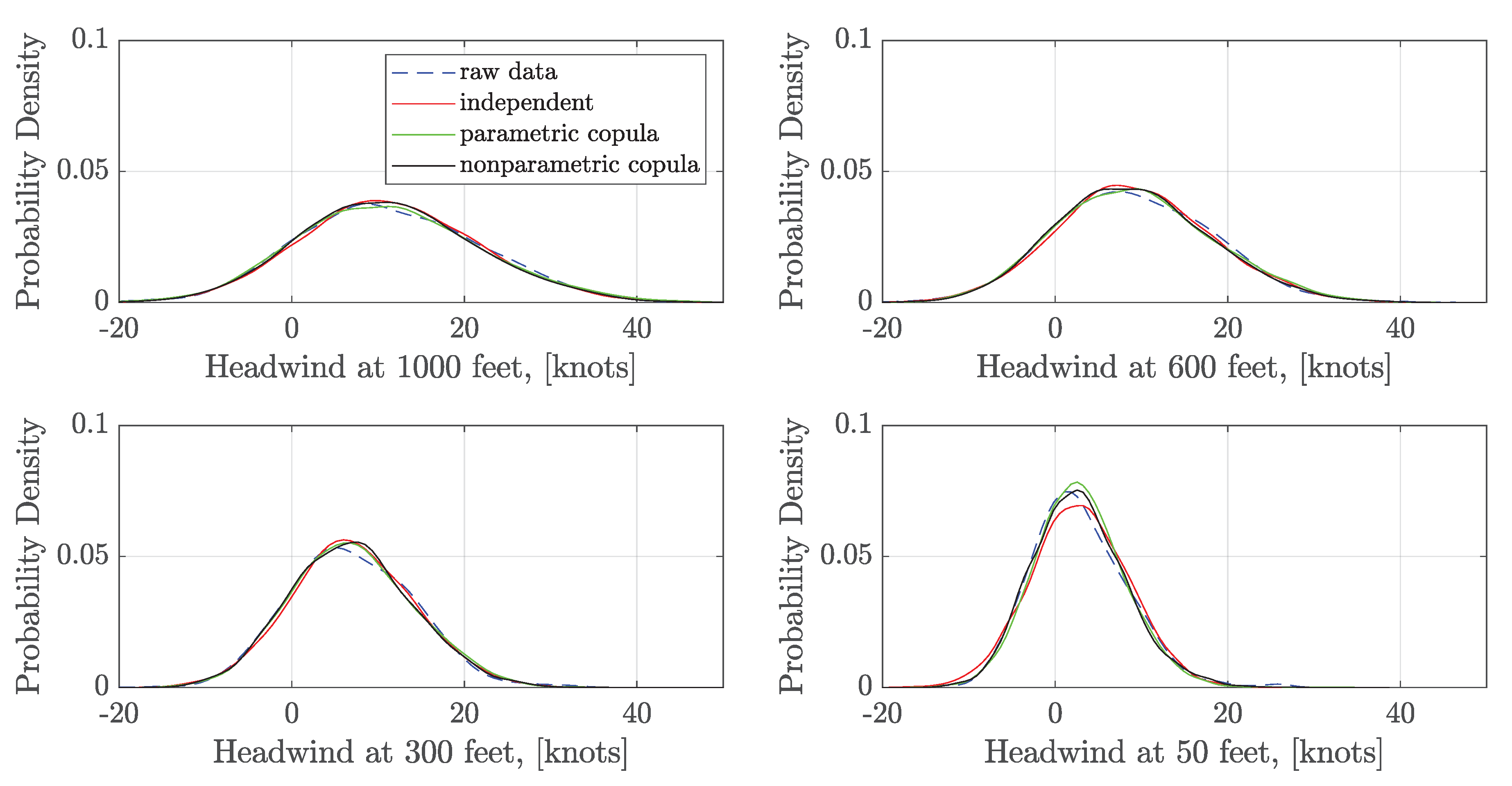
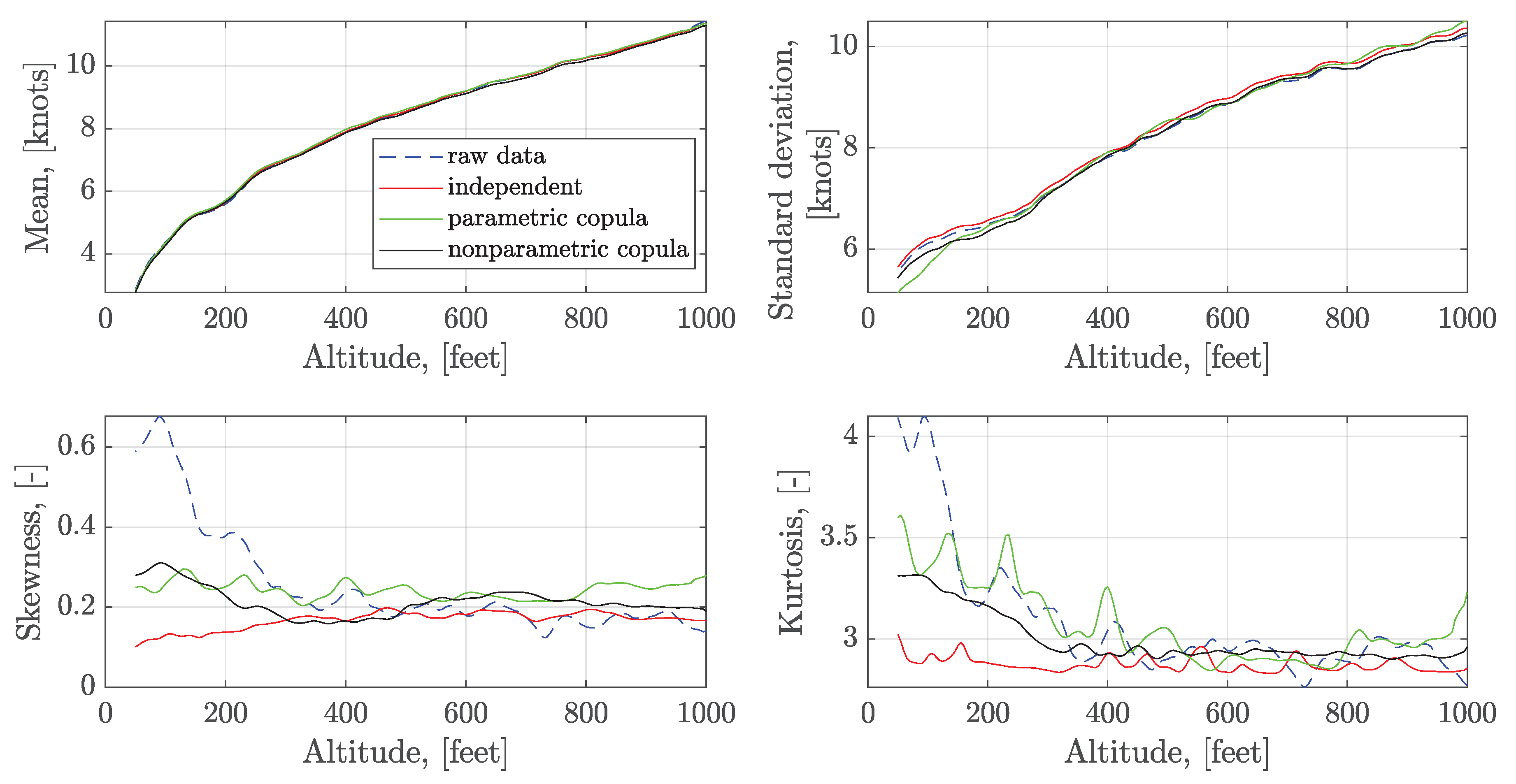
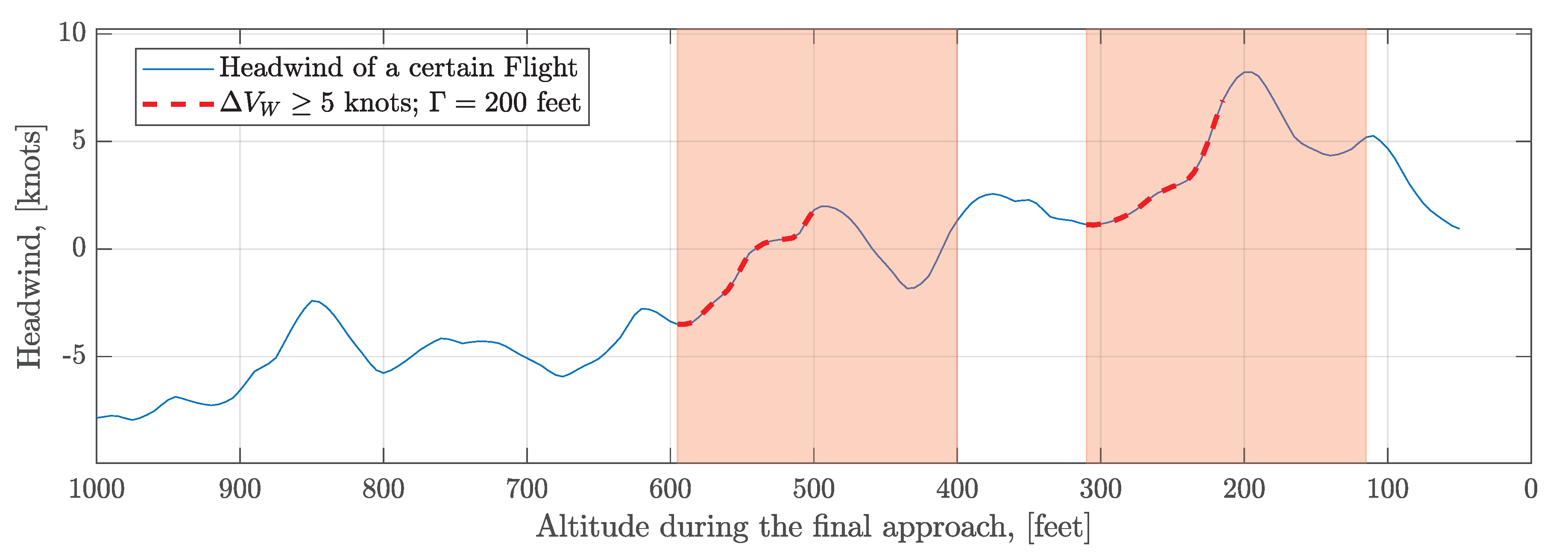
3.2. Headwind
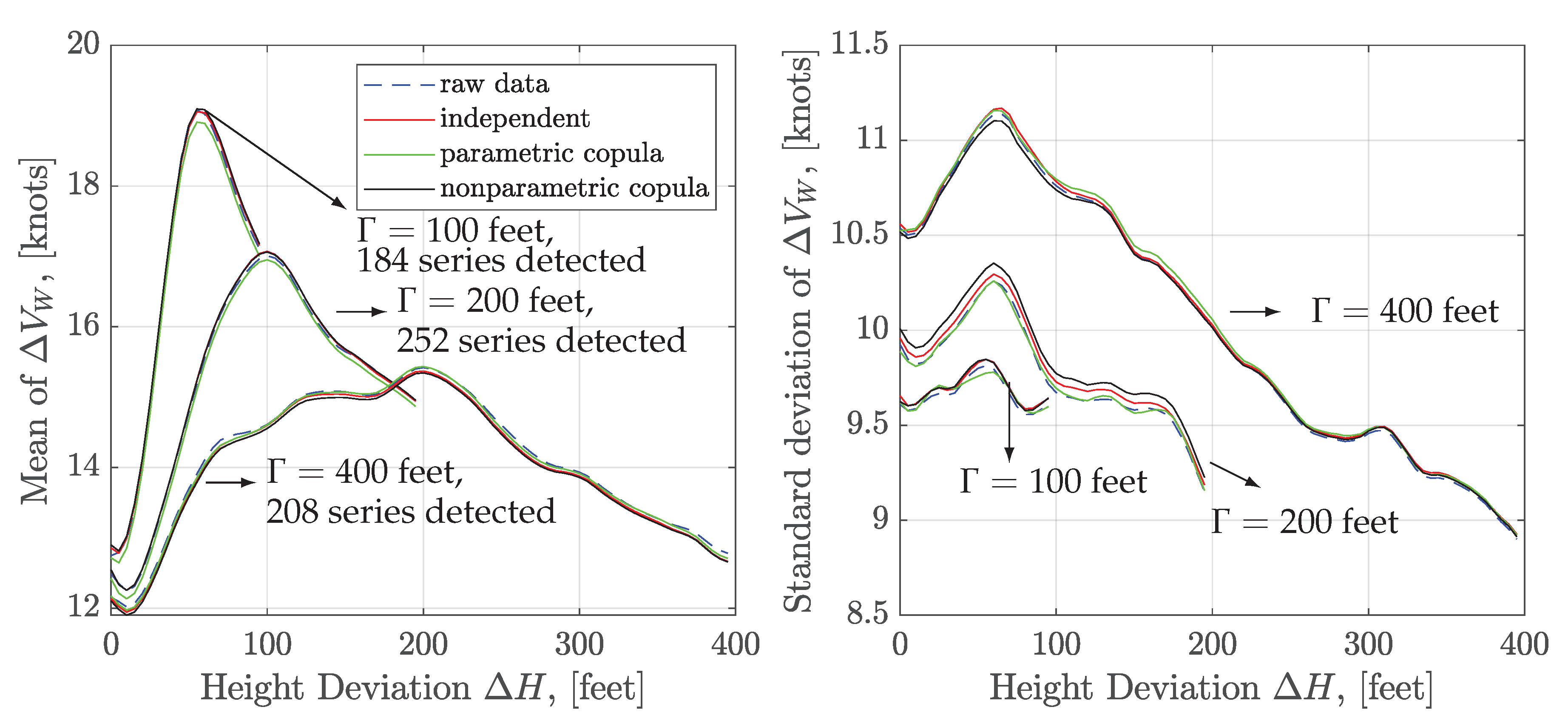
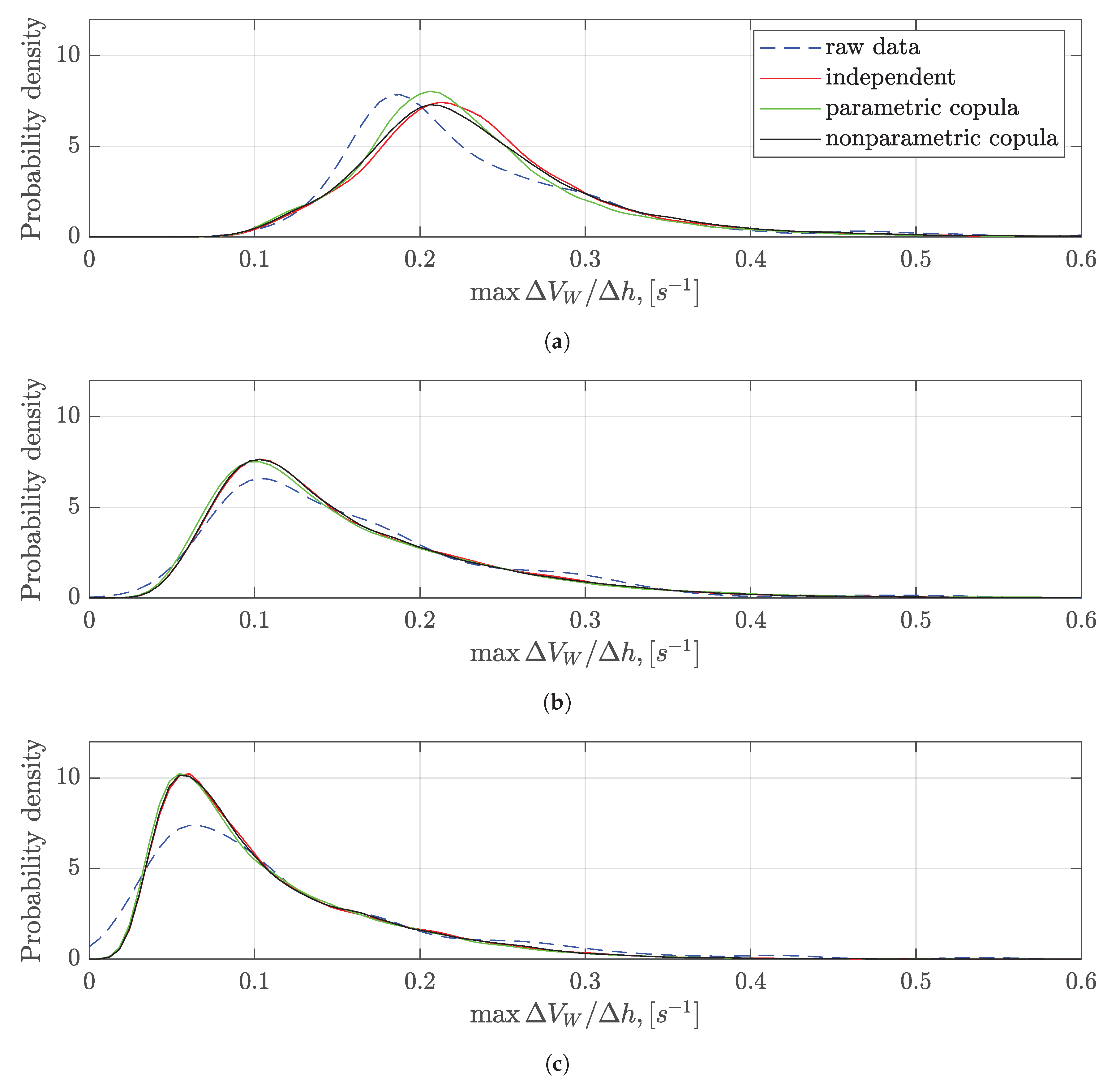
3.3. Windshear
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| KL | Karhunen–Loève |
| SR | Spectral representation |
| PSD | Power spectral density |
Appendix A. Three Dimensional Joint Probability Density Function Decomposition
Appendix B. Marginal Distributions of ξk in Headwind Modeling
| Distribution | Parameters | |
|---|---|---|
| Generalized Extreme Value | ||
| Logistic | ||
| t Location-Scale | ||
| t Location-Scale | ||
| t Location-Scale | ||
| t Location-Scale | ||
| t Location-Scale | ||
| t Location-Scale | ||
| t Location-Scale | ||
| t Location-Scale | ||
| t Location-Scale | ||
| t Location-Scale | ||
| t Location-Scale | ||
| t Location-Scale | ||
| t Location-Scale | ||
| t Location-Scale | ||
| t Location-Scale | ||
| t Location-Scale | ||
| t Location-Scale | ||
| t Location-Scale |
Appendix C. Dependence of ξk in Headwind Modeling


References
- International Civil Aviation Organization. Safety Management Manual (Doc 9859). 2013. Available online: https://www.skybrary.aero/bookshelf/books/644.pdf (accessed on 5 July 2020).
- Hoblit, F.M. Gust Loads on Aircraft: Concepts and Applications; AIAA Education Series; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1988. [Google Scholar] [CrossRef]
- Frost, W.; Camp, D.W.; Wang, S.T. Wind Shear Modeling for Aircraft Hazard Definition; National Aeronautics and Space Administration Marshall Space Flight Center: Huntsville, AL, USA, 1978.
- Tatom, F.B.; Smith, S.R.; Fichtl, G.H.; Campbell, C.W. Simulation of atmospheric turbulent gusts and gust gradients. J. Aircr. 1982, 19, 264–271. [Google Scholar] [CrossRef]
- European Aviation Safety Agency. Easy Access Rules for All Weather Operations (CS-AWO). 2018. Available online: https://www.easa.europa.eu/sites/default/files/dfu/Easy%20Access%20Rules%20for%20CS-AWO.pdf (accessed on 5 July 2020).
- Haverdings, H.; Chan, P.W. Quick access recorder data analysis software for windshear and turbulence studies. J. Aircr. 2010, 47, 1443–1447. [Google Scholar] [CrossRef]
- Sembiring, J.; Drees, L.; Holzapfel, F. Extracting Unmeasured Parameters Based on Quick Access Recorder Data Using Parameter-Estimation Method. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar] [CrossRef]
- Drees, L.; Holzapfel, F. Determining and quantifying hazard chains and their contribution to incident probabilities in flight operation. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Minneapolis, MN, USA, 13–16 August 2012. [Google Scholar] [CrossRef]
- Drees, L.; Sembiring, J.; Höhndorf, L.; Wang, C.; Holzapfel, F. IATA Safety Report 2013, Section 9: Predictive Analysis; International Air Transport Association: Montreal, Geneva, 2014. [Google Scholar]
- Moorhouse, D.; Woodcock, R. US Military Specification MIL-F-8785C; US Department of Defense: Arlington, VA, USA, 1980.
- Dehling, H.G.; Gottschalk, T.; Hoffmann, A.C. Stochastic Modelling in Process Technology; Elsevier: Amsterdam, The Netherlands, 2007; pp. 29–46. [Google Scholar]
- Poirion, F.; Zentner, I. Stochastic model construction of observed random phenomena. Probabilistic Eng. Mech. 2014, 36, 63–71. [Google Scholar] [CrossRef]
- Poirion, F.; Benoit, M. Stochastic Model Construction of Correlated Nonlinear Wave Fields. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St.John’s, NL, Canada, 31 May–5 June 2015. [Google Scholar] [CrossRef]
- Ramsay, J.O.; Silvermann, B.W. Functional Data Analysis, 2nd ed.; Springer: New York, NY, USA, 2005. [Google Scholar] [CrossRef]
- Grigoriu, M. Evaluation of Karhunen–Loève, spectral, and sampling representations for stochastic processes. J. Eng. Mech. 2006, 132, 179–189. [Google Scholar] [CrossRef]
- Chen, E.J.; Ding, L.; Liu, Y.; Ma, X.; Skibniewski, M.J. On spectral representation method and Karhunen–Loève expansion in modeling construction material properties. Arch. Civil Mech. Eng. 2018, 18, 768–783. [Google Scholar] [CrossRef]
- Czado, C. Analyzing Dependent Data with Vine Copulas; Springer International Publishing: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Le Maître, O.; Knio, O.M. Spectral Methods for Uncertainty Quantification: With Applications to Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2010; pp. 18–26. [Google Scholar] [CrossRef]
- Joe, H.; Kurowicka, D. Dependence Modeling: Vine Copula Handbook; World Scientific: Singapore, 2011. [Google Scholar] [CrossRef]
- Sklar, A.; SKLAR, A.; Sklar, C. Fonctions de reprtition an dimensions et leursmarges. Publ. Inst. Stat. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Rosenblatt, M. Remarks on a multivariate transformation. Ann. Math. Stat. 1952, 23, 470–472. [Google Scholar] [CrossRef]
- Dissmann, J.; Brechmann, E.C.; Czado, C.; Kurowicka, D. Selecting and estimating regular vine copulae and application to financial returns. Comput. Stat. Data Anal. 2013, 59, 52–69. [Google Scholar] [CrossRef]
- Ricker, D.W. Echo Signal Processing; Springer: New York, NY, USA, 2012; Volume 725. [Google Scholar] [CrossRef]
- Höhndorf, L.; Siegel, J.; Sembiring, J.; Koppitz, P.; Holzapfel, F. Reconstruction of Aircraft States During Landing Based on Quick Access Recorder Data. AIAA J. Guid. Control Dyn. 2017, 40, 1–6. [Google Scholar] [CrossRef]
- Thomas, N. Statistical Inference of Vine Copulas: Package ’ VineCopula’. 2019. Available online: https://cran.r-project.org/web/packages/VineCopula/VineCopula.pdf (accessed on 5 July 2020).
- Thomas, N. High Performance Algorithms for Vine Copula Modeling. 2019. Available online: https://cran.r-project.org/web/packages/rvinecopulib/rvinecopulib.pdf (accessed on 5 July 2020).

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Beller, L.; Czado, C.; Holzapfel, F. Modeling of Stochastic Wind Based on Operational Flight Data Using Karhunen–Loève Expansion Method. Sensors 2020, 20, 4634. https://doi.org/10.3390/s20164634
Wang X, Beller L, Czado C, Holzapfel F. Modeling of Stochastic Wind Based on Operational Flight Data Using Karhunen–Loève Expansion Method. Sensors. 2020; 20(16):4634. https://doi.org/10.3390/s20164634
Chicago/Turabian StyleWang, Xiaolong, Lukas Beller, Claudia Czado, and Florian Holzapfel. 2020. "Modeling of Stochastic Wind Based on Operational Flight Data Using Karhunen–Loève Expansion Method" Sensors 20, no. 16: 4634. https://doi.org/10.3390/s20164634
APA StyleWang, X., Beller, L., Czado, C., & Holzapfel, F. (2020). Modeling of Stochastic Wind Based on Operational Flight Data Using Karhunen–Loève Expansion Method. Sensors, 20(16), 4634. https://doi.org/10.3390/s20164634






