A Random Forest-Based Accuracy Prediction Model for Augmented Biofeedback in a Precision Shooting Training System
Abstract
1. Introduction
2. Methodology
2.1. Biofeedback System
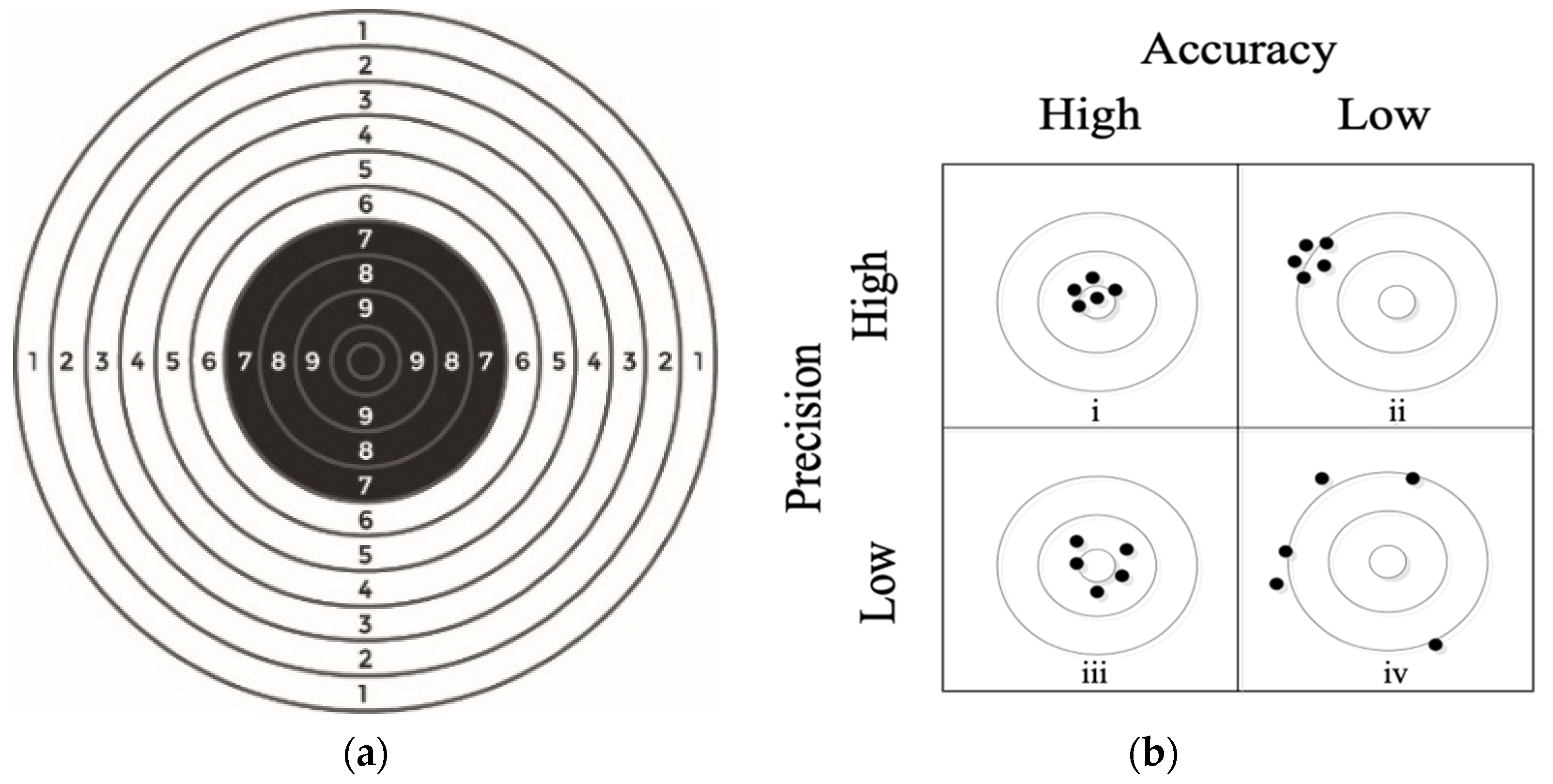
2.2. Measurement of Precise Shooting Performance
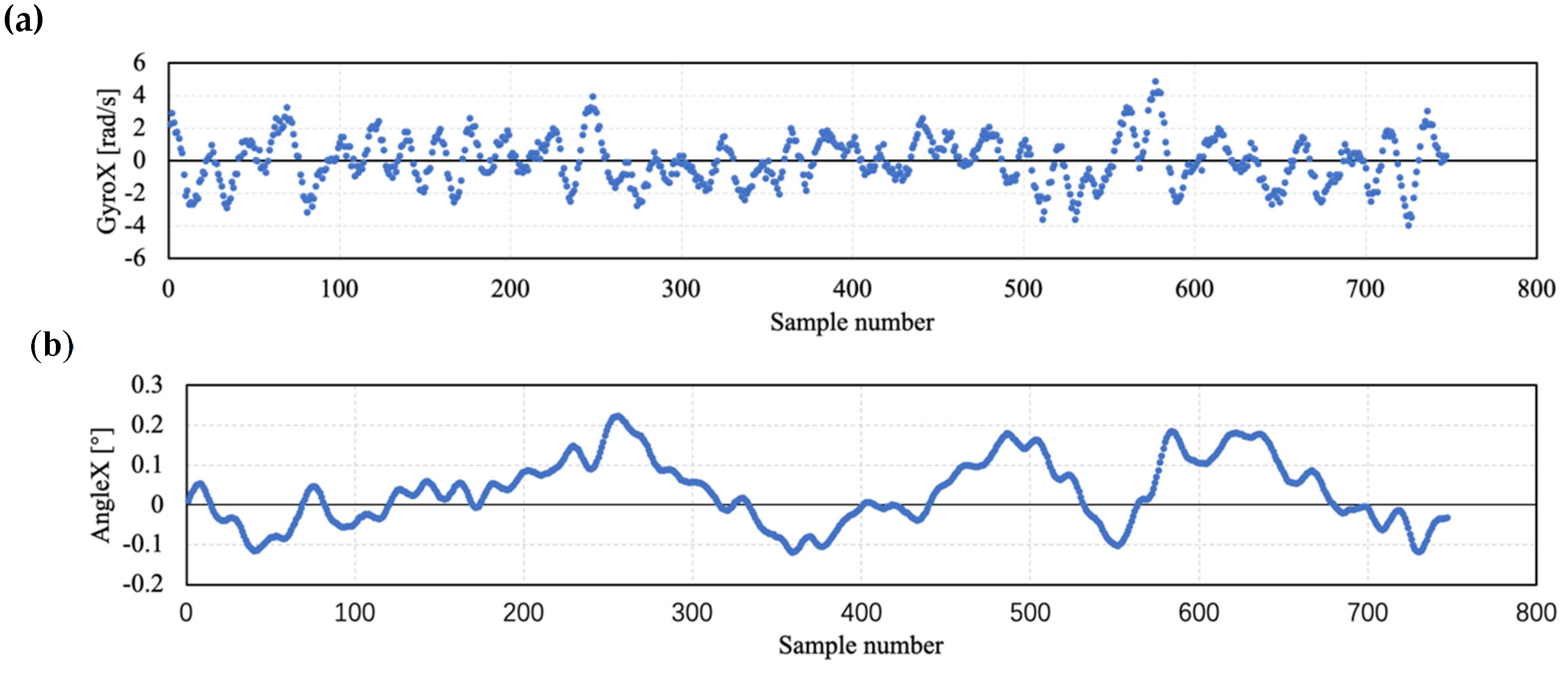
2.3. Data Acquisition and Preprocessing
2.4. Classification
- (a)
- Utilize bagging to randomly generate k diversified subsets () of the entire training set .
- (b)
- For each subset , grow an unpruned classification tree . During the splitting of each node, rather than choosing the best split among all predictors , randomly selects () of these predictors , and then choose the best split among those variables.
- (c)
- Predict new data by aggregating the predictions of the k trees following the majority decision rule.
2.5. Bayesian Hyper-Parameter Optimization
2.6. Biofeedback Application
- (a)
- The accuracy prediction model, gives the user concurrent feedback on hand movement error when working in a real-time scenario; if the result of the prediction is a bad shot, the application advises the user to suspend the shot, calm down and try again later;
- (b)
- After each shot, the application checks for possible triggering errors in post-processing mode and gives the terminal feedback to the user;
- (c)
- At the end of the shooting session, the application calculates the statistical values of precision and accuracy and provides terminal feedback about possible aiming errors.
3. Experiments and Results
3.1. Experimental Setup
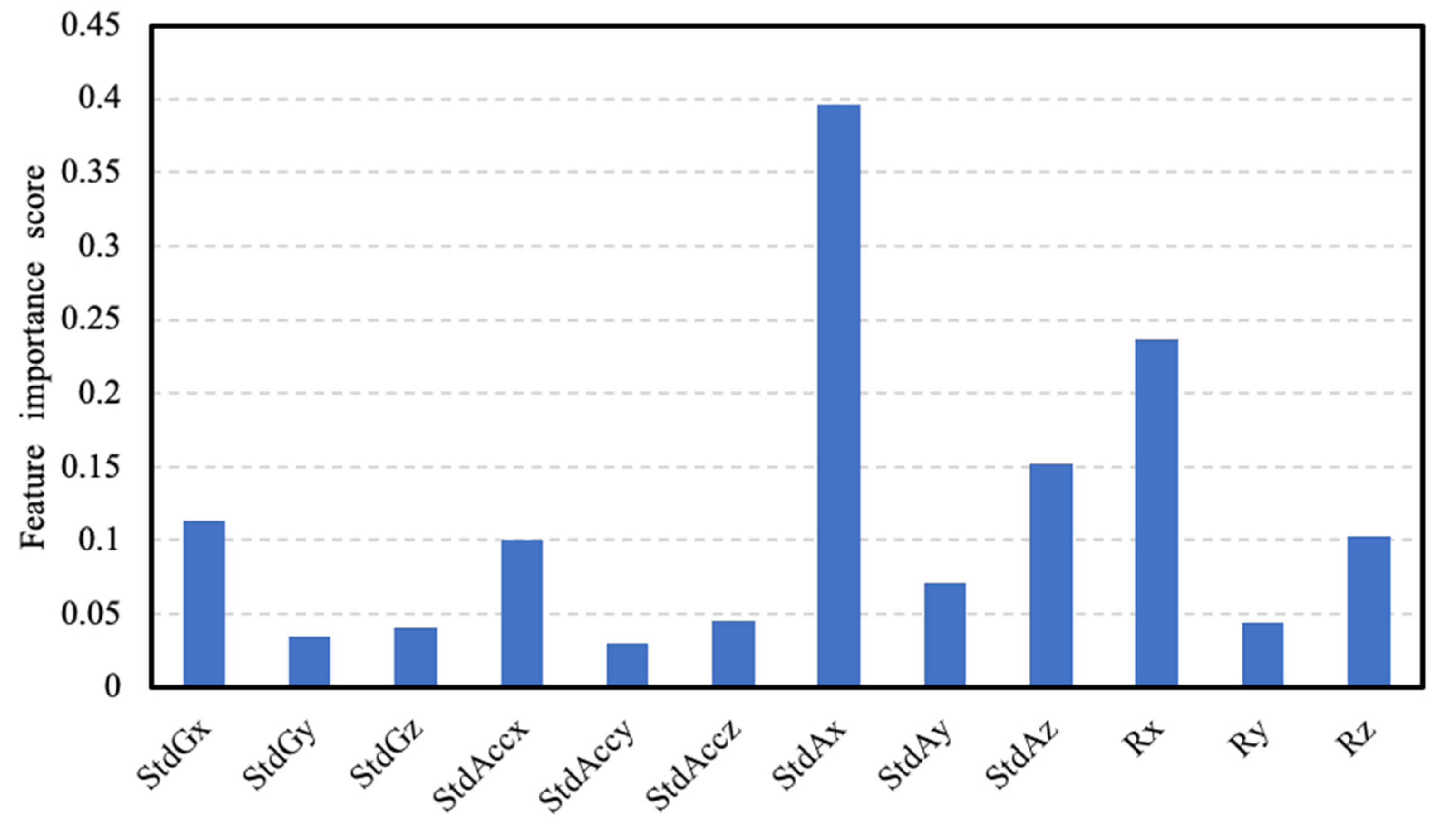
3.2. Feature Selection
3.3. Algorithm Testing and Selection
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vanrell, S.R.; Milone, D.H.; Rufiner, H.L. Assessment of homomorphic analysis for human activity recognition from acceleration signals. IEEE J. Biomed. Health 2017, 22, 1001–1010. [Google Scholar] [CrossRef]
- Duncan, M.J.; Roscoe, C.M.; Faghy, M.; Tallis, J.; Eyre, E.L. Estimating physical activity in children aged 8-11 years using accelerometry: Contributions from fundamental movement skills and different accelerometer placements. Front. Physiol. 2019, 10, 242. [Google Scholar] [CrossRef]
- Jiao, L.; Bie, R.; Wu, H.; Wei, Y.; Kos, A.; Umek, A. Golf Swing Data Classification with Deep Convolutional Neural Network. IPSI BGD Trans. Internet Res. 2018, 14, 29–34. [Google Scholar]
- Kidman, E.M.; D’Souza, M.J.A.; Singh, S.P.N. A wearable device with inertial motion tracking and vibro-tactile feedback for aesthetic sport athletes Diving Coach Monitor. In Proceedings of the 2016 10th International Conference on Signal Processing and Communication Systems (ICSPCS), Gold Coast, QLD, Australia, 19–21 December 2016; pp. 1–6. [Google Scholar]
- Wang, J.; Chen, Y.; Hao, S.; Peng, X.; Hu, L. Deep learning for sensor-based activity recognition: A survey. Pattern Recognit. Lett. 2019, 119, 3–11. [Google Scholar] [CrossRef]
- Aroganam, G.; Manivannan, N.; Harrison, D. Review on wearable technology sensors used in consumer sport applications. Sensors 2019, 19, 1983. [Google Scholar] [CrossRef] [PubMed]
- Loke, Y.L.; Gopalai, A.A.; Khoo, B.H.; Senanayake, S.M.N.A. Smart system for archery using ultrasound sensors. In Proceedings of the 2009 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Singapore, 14–17 July 2009; pp. 1160–1164. [Google Scholar]
- Ermes, M.; Pärkkä, J.; Mäntyjärvi, J.; Korhonen, I. Detection of daily activities and sports with wearable sensors in controlled and uncontrolled conditions. IEEE Trans. Inf. Technol. Biomed. 2008, 12, 20–26. [Google Scholar] [CrossRef] [PubMed]
- Rawashdeh, S.; Rafeldt, D.; Uhl, T. Wearable IMU for shoulder injury prevention in overhead sports. Sensors 2016, 16, 1847. [Google Scholar] [CrossRef] [PubMed]
- Kos, A.; Umek, A.; Marković, S.; Opsaj, M. Sensor System for Precision Precision shooting Evaluation and Real-time Biofeedback. Procedia Comput. Sci. 2019, 147, 319–323. [Google Scholar] [CrossRef]
- Yang, C.C.; Hsu, Y.L. A review of accelerometry-based wearable motion detectors for physical activity monitoring. Sensors 2010, 10, 7772–7788. [Google Scholar] [CrossRef]
- Johnson, R.F. Statistical Measures of Marksmanship; USARIEM Technical Note TN-01/2; U.S. Army Research Institute of Environmental Medicine: Fort Detrick, MD, USA, 2001.
- Dinu, D.; Fayolas, M.; Jacquet, M.; Leguy, E.; Slavinski, J.; Houel, N. Accuracy of postural human-motion tracking using miniature inertial sensors. Procedia Eng. 2016, 147, 655–658. [Google Scholar] [CrossRef]
- Osborn, J. Method and apparatus to provide precision aiming assistance to a shooter. U.S. Patent Application 10/365,022, 5 February 2004. [Google Scholar]
- Sattlecker, G.; Buchecker, M.; Müller, E.; Lindinger, S.J. Postural balance and rifle stability during standing precision shooting on an indoor gun range without physical stress in different groups of biathletes. Int. J. Sports Sci. Coaching 2014, 9, 171–184. [Google Scholar] [CrossRef]
- Deng, S.; Liu, D.M.; Hsieh, S.L. Applying machine learning methods to the precision shooting accuracy prediction: A case study of T-75 pistol precision shooting. Inf. Technol. J. 2011, 10, 1508–1517. [Google Scholar]
- Maier, T.; Meister, D.; Trösch, S.; Wehrlin, J.P. Predicting biathlon precision shooting performance using machine learning. J. Sports Sci. 2018, 36, 2333–2339. [Google Scholar] [CrossRef] [PubMed]
- Elola, A.; Aramendi, E.; Irusta, U.; Del, J.; Alonso, E.; Daya, M. ECG-based pulse detection during cardiac arrest using random forest classifier. Med. Biol. Eng. Comput. 2019, 57, 453–462. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Liu, C.; Li, Y.; Liu, N. A boosted decision tree approach using Bayesian hyper-parameter optimization for credit scoring. Expert Syst. Appl. 2017, 78, 225–241. [Google Scholar] [CrossRef]
- Kos, A.; Anton, U. Biomechanical Biofeedback Systems and Applications; Springer: Ljubljana, Slovenia, 2018; pp. 61–64. [Google Scholar]
- Matevž, H.; Anton, U.; Anton, K. Survey of recent development in real-time biofeedback systems in sport. Serbian J. Sports Sci. 2020, 11, 20–28. [Google Scholar]
- Zhang, Y.; Umek, A.; Obinikpo, A.A.; KOS, A. A Time-Dependent Multi-Class SVM Algorithm for Crowdsourced Mobility Prediction. Available online: http://ipsitransactions.org/journals/papers/tir/2018jan/p7.pdf (accessed on 16 January 2018).
- Dopsaj, M.; Markovic, S.; Umek, A.; Prebeg, G.; Kos, A. Mathematical model of short distance pistol shooting performance in experienced shooters of both gender. NBP Nauka Bezbednost Policija 2019, 24, 3–13. [Google Scholar] [CrossRef]
- Lawrence, I.; Lin, K. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar]
- Kosinski, R.J. A literature review on reaction time. Clemson Univ. 2008, 10, 1. [Google Scholar]
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. Wiley Interdiscip. Rev. 2019, 9, e1301. [Google Scholar] [CrossRef]
- Bergstra, J.S.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. In Proceedings of the Advances in Neural Information Processing Systems, Cambridge, MA, USA, 12 December 2011; pp. 2546–2554. [Google Scholar]
- Bardenet, R.; Brendel, M.; Kégl, B.; Sebag, M. Collaborative hyperparameter tuning. In Proceedings of the International conference on machine learning, Oxford, UK, 21 August 2013; pp. 199–207. [Google Scholar]
- Bergstra, J.; Komer, B.; Eliasmith, C.; Yamins, D.; Cox, D.D. Hyperopt: A python library for model selection and hyperparameter optimization. Comput. Sci. Discov. 2015, 8, 014008. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013; pp. 1–31. [Google Scholar]
- Choubin, B.; Moradi, E.; Golshan, M.; Adamowski, J.; Sajedi-Hosseini, F.; Mosavi, A. An ensemble prediction of flood susceptibility using multivariate discriminant analysis, classification and regression trees, and support vector machines. Sci. Total Environ. 2019, 651, 2087–2096. [Google Scholar] [CrossRef] [PubMed]
- Safavian, S.R.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE Trans. Syst. Man Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Schapire, R.E. Explaining Ada Boost; Springer: Berlin, Germany, 2013; pp. 37–52. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]






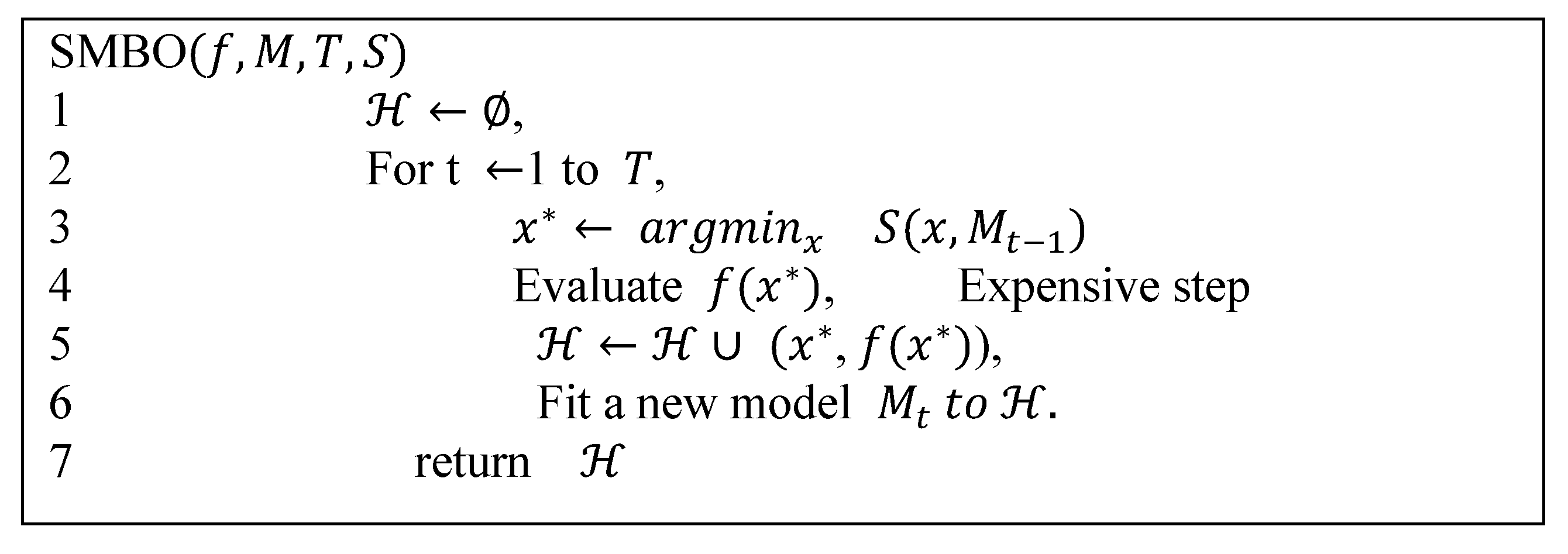




| Measurement Session | No. of Shots | Mean | StDev | CV | Max | Min |
|---|---|---|---|---|---|---|
| 1 | 200 | 1.39 | 1.38 | 1.00 | 7.16 | 0.02 |
| 2 | 170 | 1.23 | 1.15 | 0.94 | 7.39 | 0.02 |
| 3 | 180 | 1.22 | 1.37 | 1.13 | 7.40 | 0.04 |
| 4 | 210 | 1.48 | 1.48 | 1.00 | 7.39 | 0.03 |
| 5 | 205 | 1.26 | 1.20 | 0.95 | 7.33 | 0.01 |
| Skill Level | Mean | StDev | CV | Max | Min |
|---|---|---|---|---|---|
| Beginner | 1.65 | 1.45 | 0.88 | 7.40 | 0.03 |
| Intermediate | 1.01 | 0.73 | 0.72 | 4.19 | 0.02 |
| Experienced | 0.98 | 0.64 | 0.65 | 3.15 | 0.10 |
| Professional | 0.60 | 0.49 | 0.82 | 4.42 | 0.01 |
| Sportist | 0.21 | 0.11 | 0.53 | 0.38 | 0.01 |
| StdGx | StdGy | StdGz | StdAx | StdAy | StdAz | |
| Result | −0.46 | −0.41 | −0.40 | −0.54 | −0.54 | −0.30 |
| StdAccx | StdAccy | StdAccz | Rx | Ry | Rz | |
| Result | −0.52 | −0.30 | −0.05 | −0.51 | −0.31 | −0.04 |
| LR | SVM | DT | KNN | GBDT | AB | RF | |
|---|---|---|---|---|---|---|---|
| Recall | 0.90 | 0.97 | 0.83 | 0.86 | 0.88 | 0.87 | 0.90 |
| Precision | 0.82 | 0.77 | 0.83 | 0.79 | 0.93 | 0.89 | 0.96 |
| score | 0.86 | 0.86 | 0.83 | 0.82 | 0.90 | 0.88 | 0.93 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Yang, L.; Umek, A.; Bie, R.; Tomažič, S.; Kos, A. A Random Forest-Based Accuracy Prediction Model for Augmented Biofeedback in a Precision Shooting Training System. Sensors 2020, 20, 4512. https://doi.org/10.3390/s20164512
Guo J, Yang L, Umek A, Bie R, Tomažič S, Kos A. A Random Forest-Based Accuracy Prediction Model for Augmented Biofeedback in a Precision Shooting Training System. Sensors. 2020; 20(16):4512. https://doi.org/10.3390/s20164512
Chicago/Turabian StyleGuo, Junqi, Lan Yang, Anton Umek, Rongfang Bie, Sašo Tomažič, and Anton Kos. 2020. "A Random Forest-Based Accuracy Prediction Model for Augmented Biofeedback in a Precision Shooting Training System" Sensors 20, no. 16: 4512. https://doi.org/10.3390/s20164512
APA StyleGuo, J., Yang, L., Umek, A., Bie, R., Tomažič, S., & Kos, A. (2020). A Random Forest-Based Accuracy Prediction Model for Augmented Biofeedback in a Precision Shooting Training System. Sensors, 20(16), 4512. https://doi.org/10.3390/s20164512






