How Does the Location of Transfer Affect Travellers and Their Choice of Travel Mode?—A Smart Spatial Analysis Approach
Abstract
1. Introduction
2. Literature Review
3. Study Area and Data
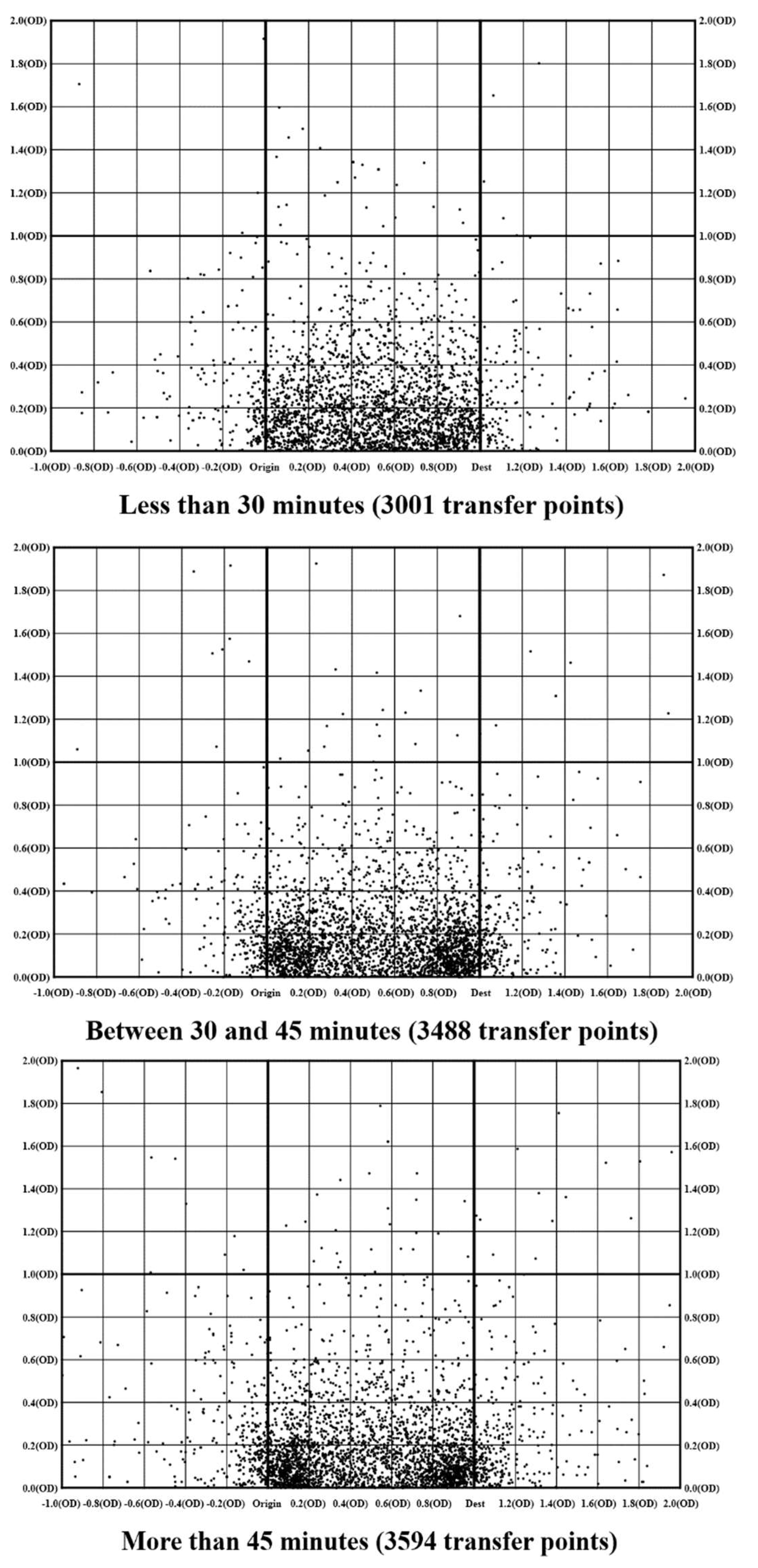
4. Transformation Mapping of Transfer Coordinate
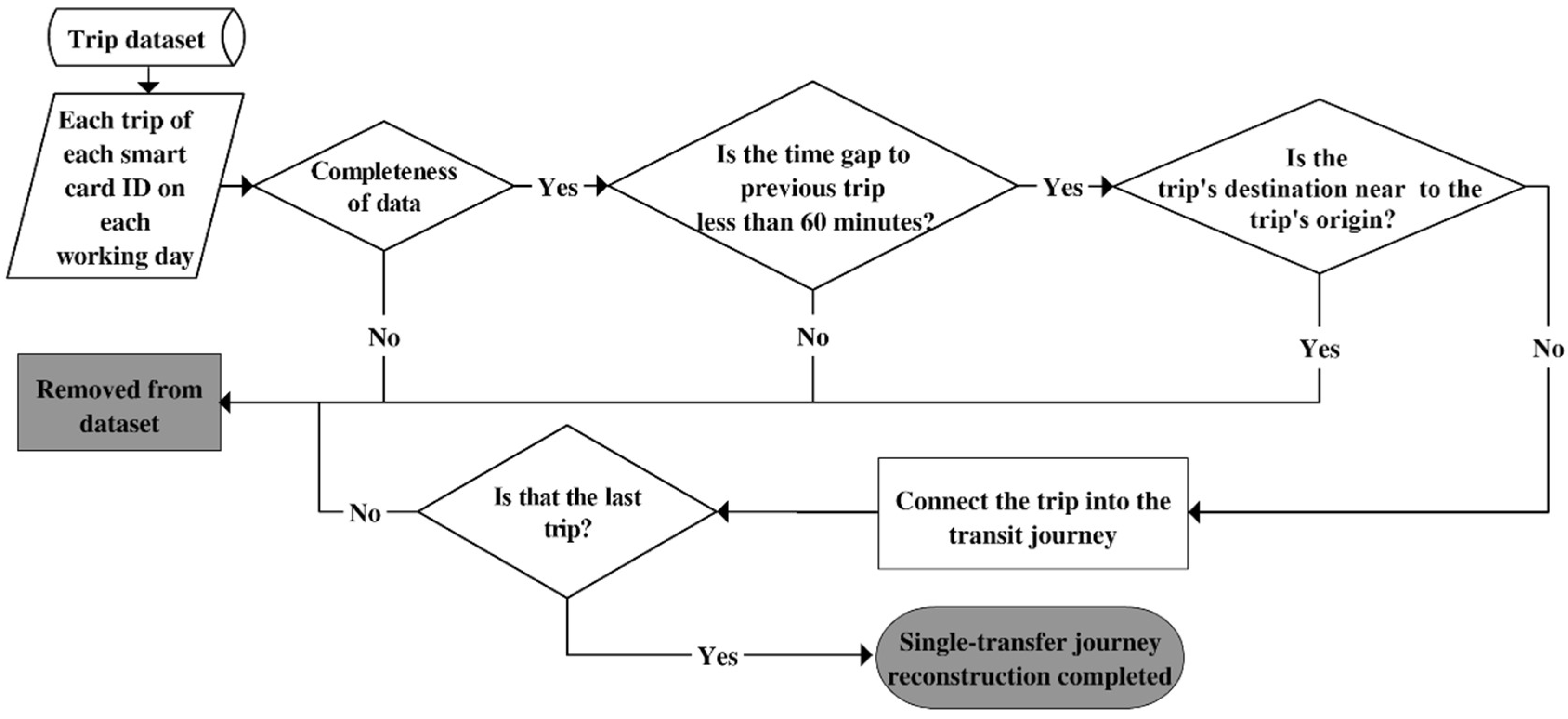
4.1. Processing for Single-Transfer Journey Itineraries
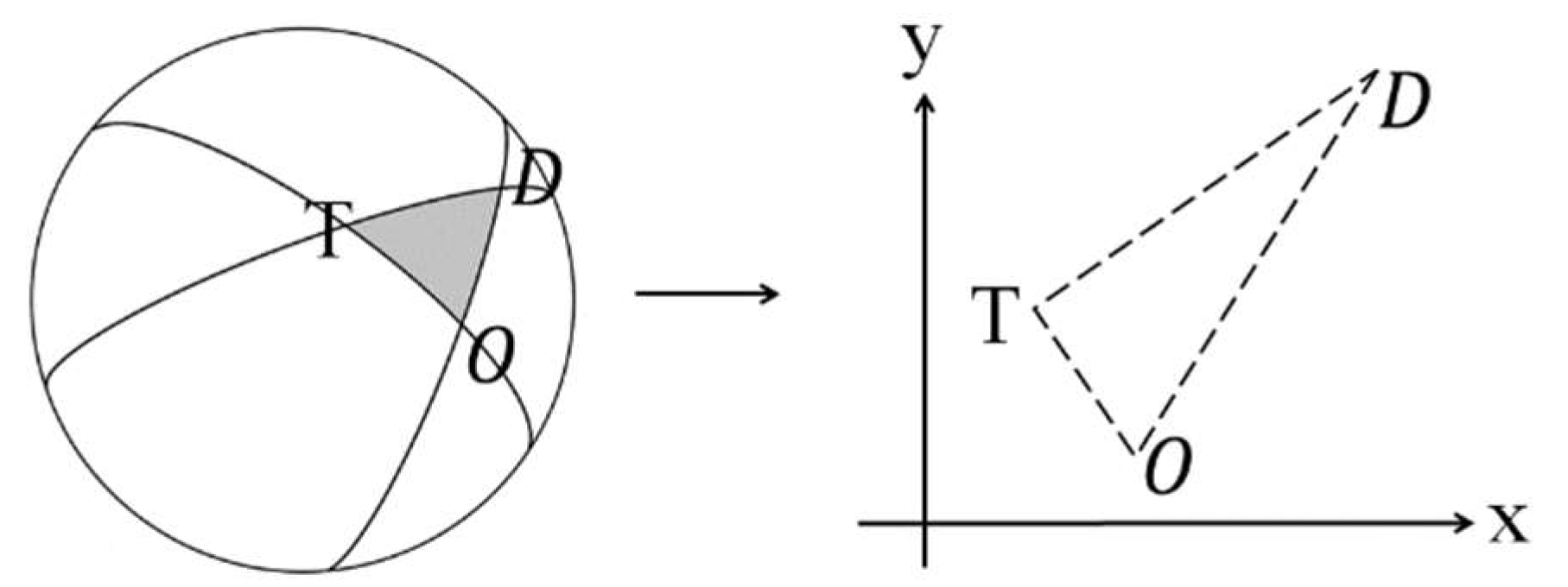
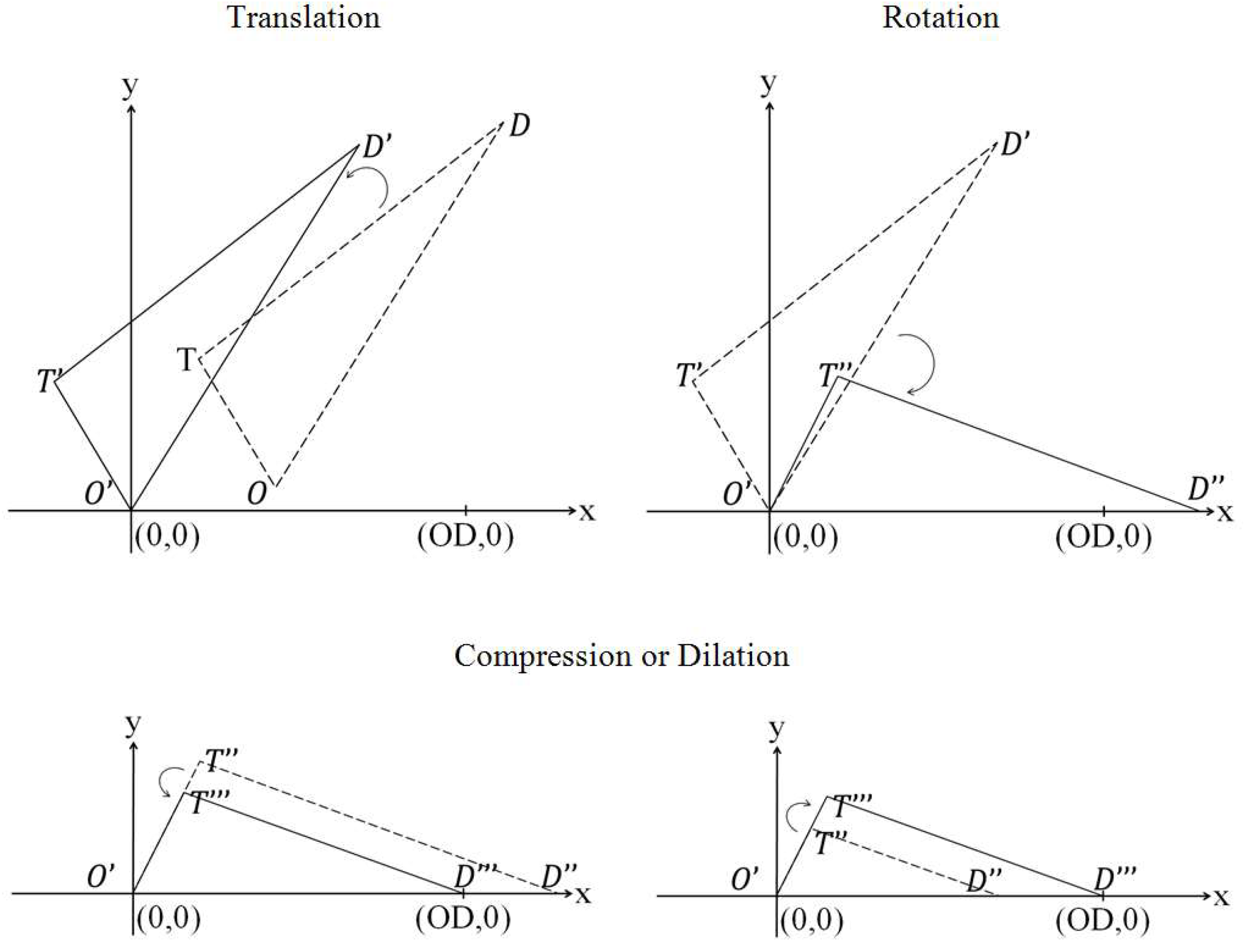
4.2. Transformation
- = Interest points of the journey triangle, OTD
- = Distance between origin point and destination point
- = Distance between origin point and transfer point
- = Distance between transfer point and destination point
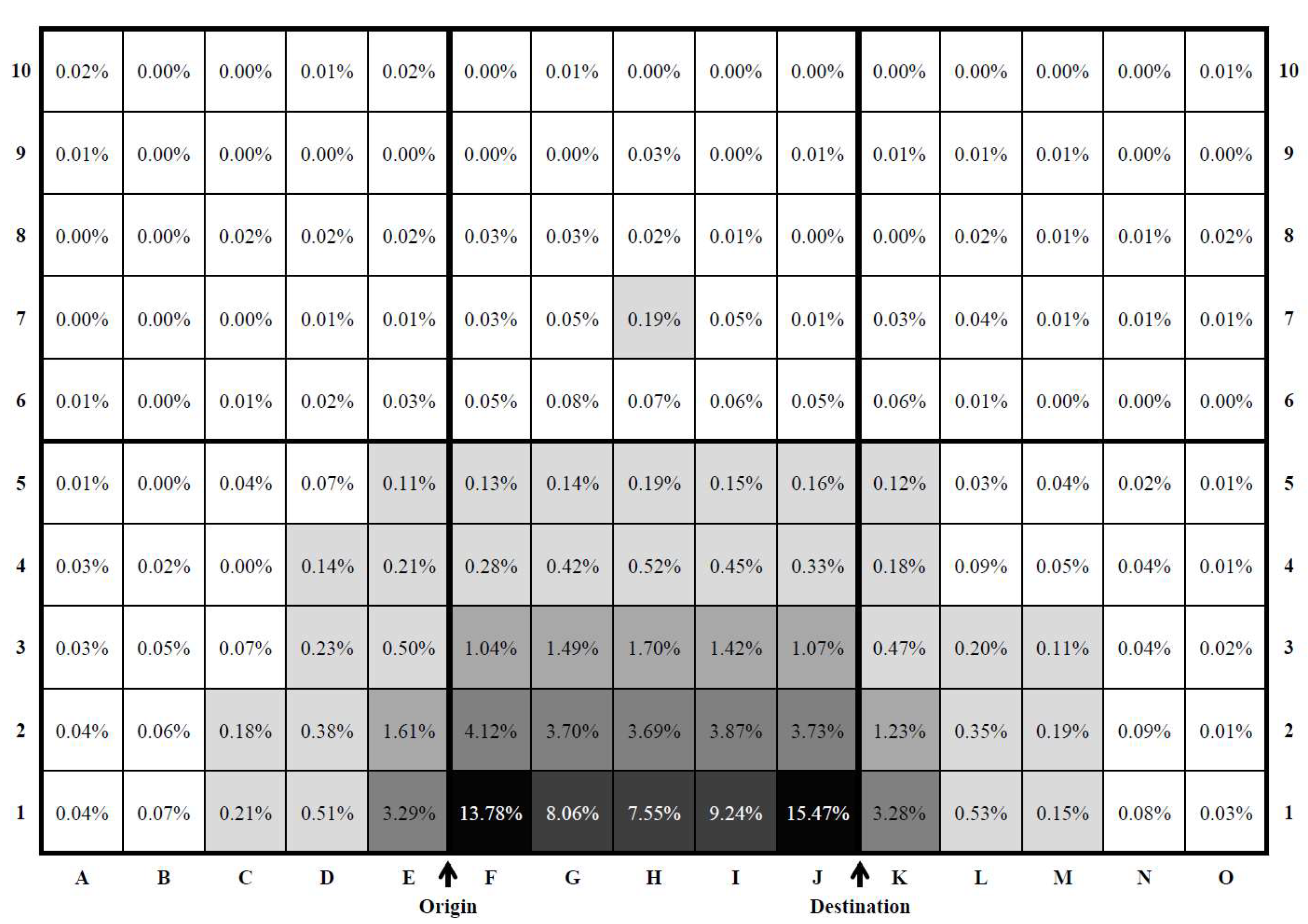
4.3. Transfer Location Map
4.4. Grid-Based Hierarchical Clustering
5. Mode Choice Analysis
Transfer Location and Transit Travel Time
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ceder, A.; Chowdhury, S.; Taghipouran, N.; Olsen, J. Modelling public-transport users’ behaviour at connection point. Transp. Policy 2013, 27, 112–122. [Google Scholar] [CrossRef]
- Currie, G.; Loader, C. Bus network planning for transfers and the network effect in Melbourne, Australia. J. Transp. Res. Board 2010, 2145, 8–17. [Google Scholar] [CrossRef]
- Guo, Z.; Ferreira, J. Pedestrian environments, transit path choice, and transfer penalties: Understanding land-use impacts on transit travel. Environ. Plan. B Plan. Des. 2008, 35, 461–479. [Google Scholar] [CrossRef]
- Hadas, Y.; Ceder, A. Public transit network connectivity. J. Transp. Res. Board 2012, 2143, 1–8. [Google Scholar] [CrossRef]
- Schakenbos, R.; Paix, L.L.; Nijenstein, S.; Geurs, K.T. Valuation of a transfer in a multimodal public transport trip. Transp. Policy 2016, 46, 72–81. [Google Scholar] [CrossRef]
- Sharaby, N.; Shiftan, Y. The impact of fare integration on travel behavior and transit ridership. Transp. Policy 2012, 21, 63–70. [Google Scholar] [CrossRef]
- Wardman, M.; Hine, J.; Stradling, S. Interchange and Travel Choice; Scottish Executive Central Research Unit: Edinburgh, UK, 2001. [Google Scholar]
- Liu, R.; Pendyala, R.; Polzin, S. Assessment of intermodal transfer penalties using stated preference data. J. Transp. Res. Board 1997, 1607, 74–80. [Google Scholar] [CrossRef]
- Givoni, M.; Banister, D. The need for integration in transport policy and practice. In Integrated Transport: From poLicy to Practice; Routledge: London, UK, 2010; p. 2. [Google Scholar]
- Luk, J.; Olszewski, P. Integrated public transport in Singapore and Hong Kong. Road Transp. Res. 2003, 12, 41–51. [Google Scholar]
- Guo, Z.; Wilson, N. Assessment of the transfer penalty for transit trips geographic information system-based disaggregate modeling approach. J. Transp. Res. Board 2004, 1872, 10–18. [Google Scholar] [CrossRef]
- Iseki, H.; Taylor, B.D. Not all transfers are created equal: Towards a framework relating transfer connectivity to travel behaviour. Transp. Rev. 2009, 29, 777–800. [Google Scholar] [CrossRef]
- Kittelson Associates Inc.; KFH Group Inc.; Parsons Brinckerhoff Quade Douglass, Inc.; Hunter-Zaworski, K. Transit Capacity and Quality of Service Manual; Texas Transport Institute and Transport Consulting Limited: Washington, DC, USA, 2013. [Google Scholar]
- Ceder, A.; Golany, B.; Tal, O. Creating bus timetables with maximal synchronization. Transp. Res. Part A Policy Pract. 2001, 35, 913–928. [Google Scholar] [CrossRef]
- Garcia-Martinez, A.; Cascajo, R.; Jara-Diaz, S.R.; Chowdhury, S.; Monzon, A. Transfer penalties in multimodal public transport networks. Transp. Res. Part A Policy Pract. 2018, 114, 52–66. [Google Scholar] [CrossRef]
- Vande Walle, S.; Steenberghen, T. Space and time related determinants of public transport use in trip chains. Transportation Research Part A Policy and Practice 2006, 40, 151–162. [Google Scholar] [CrossRef]
- Mishalani, R.G.; McCord, M.M.; Wirtz, J. Passenger wait time perceptions at bus stops: Empirical results and impact on evaluating real-time bus arrival information. J. Public Transp. 2006, 9, 89–106. [Google Scholar] [CrossRef]
- Iseki, H.; Taylor, B.D. Style versus service? An analysis of user perceptions of transit stops and stations. J. Public Transp. 2010, 13, 2. [Google Scholar] [CrossRef]
- Loukaitou-Sideris, A.; Liggett, R.; Iseki, H.; Thurlow, W. Measuring the effects of built environment on bus stop crime. Environ. Plan. B Plan. Des. 2001, 28, 255–280. [Google Scholar] [CrossRef]
- Guo, Z.; Wilson, N. Assessing the cost of transfer inconvenience in public transport systems: A case study of the London Underground. Transp. Res. Part A Policy Pract. 2011, 45, 91–104. [Google Scholar] [CrossRef]
- Chien, S.; Schonfeld, P. Joint optimization of a rail transit line and its feeder bus system. J. Adv. Transp. 1998, 32, 253–284. [Google Scholar] [CrossRef]
- Hall, R.W. Vehicle scheduling at a transportation terminal with random delay en route. Transp. Sci. 1985, 19, 308–320. [Google Scholar] [CrossRef]
- Lee, K.K.T.; Schonfeld, P. Optimal slack time for timed transfers at a transit terminal. J. Adv. Transp. 1991, 25, 281–308. [Google Scholar] [CrossRef]
- Shih, M.C.; Mahmassani, H.; Baaj, M. Planning and design model for transit route networks with coordinated operations. J. Transp. Res. Board 1998, 1623, 16–23. [Google Scholar] [CrossRef]
- Ting, C.J.; Schonfeld, P. Schedule coordination in a multiple hub transit network. J. Urban Plan. Dev. 2005, 131, 112–124. [Google Scholar] [CrossRef]
- Raveau, S.; Muñoz, J.C.; de Grange, L. A topological route choice model for metro. Transp. Res. Part A Policy Pract. 2011, 45, 138–147. [Google Scholar] [CrossRef]
- De Dios Ortúzar, J.; Willumsen, L.G.; Wiley, I. Modelling Transport, 4th ed.; Wiley-Blackwell: Oxford, UK, 2011. [Google Scholar]
- Queensland Government. Travel in South-East Queensland; Queensland Government: Brisbane, Australia, 2012.
- Queensland Government. TransLink Tracker January-March 2016 Q3; Department of Transport and Main Roads: Brisbane, Australia, 2016.
- Devney, J. Redesigning bus networks to be simpler, faster and more connected. In Proceedings of the Australian Institute of Traffic Planning and Management (AITPM) National Conference, Adelaide, Australia, 13 August 2014. [Google Scholar]
- Downs, R.M.; Stea, D. Maps in Minds: Reflections on Cognitive Mapping; HarperCollins Publishers: New York, NY, USA, 1977. [Google Scholar]
- Schönfelder, S.; Axhausen, K.W. Urban Rhythms and Travel Behaviour: Spatial and Temporal Phenomena of daily Travel; Ashgate: Burlington, NJ, USA, 2010. [Google Scholar]
- Bagchi, M.; White, P. What role for smart-card data from bus systems? Munic. Eng. 2004, 157, 39–46. [Google Scholar] [CrossRef]
- Hofmann, M.; O’Mahony, M. Transfer journey identification and analyses from electronic fare collection data. In Proceedings of the 2005 IEEE Intelligent Transportation Systems Conference, Vienna, Austria, 13–16 September 2005; pp. 34–39. [Google Scholar]
- Seaborn, C.; Attanucci, J.; Wilson, N.H.M. Analyzing multimodal public transport journeys in London with smart card fare payment data. Transp. Res. Rec. 2009, 2121, 55–62. [Google Scholar] [CrossRef]
- Chia, J.; Lee, J.; Kamruzzaman, M. Walking to public transit—Exploring variations by socio-economic status. Int. J. Sustain. Transp. 2016, 10, 805–814. [Google Scholar] [CrossRef]
- Horner, M.W.; Murray, A.T. Spatial representation and scale impacts in transit service assessment. Environ. Plan. B 2004, 31, 785–798. [Google Scholar] [CrossRef]
- O’Sullivan, S.; Morrall, J. Walking distances to and from light-rail transit stations. J. Transp. Res. Board 1996, 1538, 19–26. [Google Scholar] [CrossRef]
- Weinstein Agrawal, A.; Schlossberg, M.; Irvin, K. How far, by which route and why? A spatial analysis of pedestrian preference. J. Urban Des. 2008, 13, 81–98. [Google Scholar] [CrossRef]
- Sarstedt, M.; Mooi, E. Cluster Analysis. In A Concise Guide to Market Research: The Process, Data, and Methods Using IBM SPSS Statistics; Sarstedt, M., Mooi, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 273–324. [Google Scholar]
- Cheng, W.; Wang, W.; Batista, S. Grid-based clustering. In Data Clustering: Algorithms and Applications; Aggarwal, C.C., Reddy, C.K., Eds.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2013; Volume 31, pp. 127–148. [Google Scholar]
- Ward, J.H. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Cervero, R. Walk-and-ride: Factors influencing pedestrian access to transit. J. Public Transp. 2001, 3, 1. [Google Scholar] [CrossRef]
- Frank, L.; Bradley, M.; Kavage, S.; Chapman, J.; Lawton, T.K. Urban form, travel time, and cost relationships with tour complexity and mode choice. Transportation 2008, 35, 37–54. [Google Scholar] [CrossRef]
- Hadas, Y.; Ranjitkar, P. Modeling public-transit connectivity with spatial quality-of-transfer measurements. J. Transp. Geogr. 2012, 22, 137–147. [Google Scholar] [CrossRef]
- Louviere, J.J.; Hensher, D.A.; Swait, J.D. Stated Choice Methods: Analysis and Applications; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]



| Variable | Description |
|---|---|
| Socioeconomic Attributes | |
| Gender | Nominal variables: 0—male; 1—female |
| Age | Age of individuals |
| Individual weekly income | Individuals’ weekly income, given in different income bracket |
| Number of cars | Total number of cars per household |
| Household size | Number of persons in the household |
| Journey Attributes | |
| Car travel time (minutes) | Total time taken to travel from origins to destinations using private vehicle |
| Bus travel time (minutes) | Total time taken to travel from origins to destinations using bus |
| Initial wait time (minutes) | Total wait time for the next available bus service |
| First mile walk time (minutes) | Walk time taken to access bus station from origination |
| Last mile walk time (minutes) | Walk time taken from bus station to destination |
| Transfer Attributes | |
| Proportion of in-vehicle bus travel time | Proportion of a journey spent on two buses |
| Proportion of transfer walk time | Proportion of a journey spent on walking for a transfer |
| Proportion of transfer wait time | Proportion of a journey spent on waiting for a transfer |
| Type of transfer | Nominal variables: 0—non-walking transfer; 1—otherwise |
| Transfer location | Ordinal and nominal variables: The cluster developed using smart card data (i.e., Cluster A–F encoded to 0–5), of which individual transfer location falls into |
| Variables | Model I | Model II | ||||
|---|---|---|---|---|---|---|
| Base Model | Expanded Model | |||||
| Coefficient | Std. Err. | Exp. β | Coefficient | Std. Err. | Exp. β | |
| Constant | −0.85 | 1.27 | 0.43 | 0.35 | 1.39 | 1.42 |
| Socioeconomic Attributes | ||||||
| Individual weekly income | −0.00 *** | 0.00 | 1.00 | −0.00 *** | 0.00 | 1.00 |
| Household size | 0.43 *** | 0.14 | 1.54 | 0.40 *** | 0.14 | 1.49 |
| Number of cars | −1.22 *** | 0.24 | 0.29 | −1.31 *** | 0.25 | 0.27 |
| Journey Attributes | ||||||
| Car travel time (minutes) | 0.04 *** | 0.02 | 1.04 | 0.06 *** | 0.02 | 1.07 |
| Initial wait time (minutes) | −0.03 | 0.02 | 0.97 | −0.03 * | 0.02 | 0.97 |
| First mile walk time (minutes) | −0.08 * | 0.04 | 0.93 | −0.09 ** | 0.04 | 0.92 |
| Last mile walk time (minutes) | −0.07 * | 0.04 | 0.93 | −0.08 ** | 0.04 | 0.92 |
| Transfer Attributes | ||||||
| Proportion of in-vehicle bus travel time | 3.90 ** | 1.54 | 49.45 | 4.24 ** | 1.59 | 69.27 |
| Transfer location | Not included | −0.28 ** | 0.13 | 0.75 | ||
| Number of observation | 393 | 393 | ||||
| Log-likelihood function value: Constant only model | −172.99 | −172.99 | ||||
| Log-likelihood function value: Parameterised model | −122.40 | −119.88 | ||||
| Goodness of fit (McFadden rho squared) | 0.29 | 0.31 | ||||
| Model Improvement Test: −2 *(log-likelihood of basic model—log-likelihood of expanded model) | 5.04 | |||||
| Chi-critical based on 1 degree of freedom | 3.84 | |||||
| Variables | Model I | Model II | ||||
|---|---|---|---|---|---|---|
| Base Model | Expanded Model | |||||
| Coefficient | Std. Err. | Exp. β | Coefficient | Std. Err. | Exp. β | |
| Constant | 0.16 | 1.37 | 1.18 | −0.98 | 1.53 | 0.38 |
| Socioeconomic Attributes | ||||||
| Age | −0.03 ** | 0.01 | 0.97 | −0.03 *** | 0.01 | 0.97 |
| Individual weekly income | −0.00 *** | 0.00 | 1.00 | −0.00 *** | 0.00 | 1.00 |
| Household size | 0.34 ** | 0.14 | 1.41 | 0.32 ** | 0.15 | 1.37 |
| Number of cars | −1.32 *** | 0.24 | 0.27 | −1.48 *** | 0.26 | 0.23 |
| Journey Attributes | ||||||
| Car travel time (minutes) | −0.05 *** | 0.02 | 0.95 | −0.07 *** | 0.02 | 0.94 |
| Initial wait time (minutes) | −0.02 * | 0.01 | 0.98 | −0.02 ** | 0.01 | 0.98 |
| Last mile walk time (minutes) | −0.07 * | 0.04 | 0.93 | −0.08 ** | 0.04 | 0.92 |
| Transfer Attributes | ||||||
| Proportion of in-vehicle bus travel time | 4.00 *** | 1.51 | 54.52 | 4.52 *** | 1.59 | 91.84 |
| Transfer Location The reference category: Cluster F | ||||||
| Cluster A | Not included | 1.79 * | 1.05 | 5.99 | ||
| Cluster B | 2.34 ** | 0.98 | 10.40 | |||
| Cluster C | 2.31 ** | 0.96 | 10.04 | |||
| Cluster D | 1.99 ** | 1.01 | 7.30 | |||
| Cluster E | 1.21 | 0.95 | 3.36 | |||
| Number of observation | 393 | 393 | ||||
| Log-likelihood function value: Constant only model | −172.99 | −172.99 | ||||
| Log-likelihood function value: Parameterised model | −121.58 | −116.20 | ||||
| Goodness of fit (Nagelkerke R Square) | 0.39 | 0.43 | ||||
| Goodness of fit (McFadden R Square) | 0.30 | 0.33 | ||||
| Model improvement test (Chi-squared test, χ2): −2 *(log-likelihood of basic model—log-likelihood of expanded model) | 10.76 | |||||
| The critical chi-squared value with 5 degrees of freedom at the 0.10 α-level | 9.24 | |||||
| The critical chi-squared value with 5 degrees of freedom at the 0.05 α-level | 11.07 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chia, J.; Lee, J.; Han, H. How Does the Location of Transfer Affect Travellers and Their Choice of Travel Mode?—A Smart Spatial Analysis Approach. Sensors 2020, 20, 4418. https://doi.org/10.3390/s20164418
Chia J, Lee J, Han H. How Does the Location of Transfer Affect Travellers and Their Choice of Travel Mode?—A Smart Spatial Analysis Approach. Sensors. 2020; 20(16):4418. https://doi.org/10.3390/s20164418
Chicago/Turabian StyleChia, Jason, Jinwoo (Brian) Lee, and Hoon Han. 2020. "How Does the Location of Transfer Affect Travellers and Their Choice of Travel Mode?—A Smart Spatial Analysis Approach" Sensors 20, no. 16: 4418. https://doi.org/10.3390/s20164418
APA StyleChia, J., Lee, J., & Han, H. (2020). How Does the Location of Transfer Affect Travellers and Their Choice of Travel Mode?—A Smart Spatial Analysis Approach. Sensors, 20(16), 4418. https://doi.org/10.3390/s20164418



_Lee.png)



