Earthquake Probability Assessment for the Indian Subcontinent Using Deep Learning
Abstract
1. Introduction
1.1. Global Earthquake Probability Assessment
1.2. Probabilistic Earthquake Hazard Assessment in India
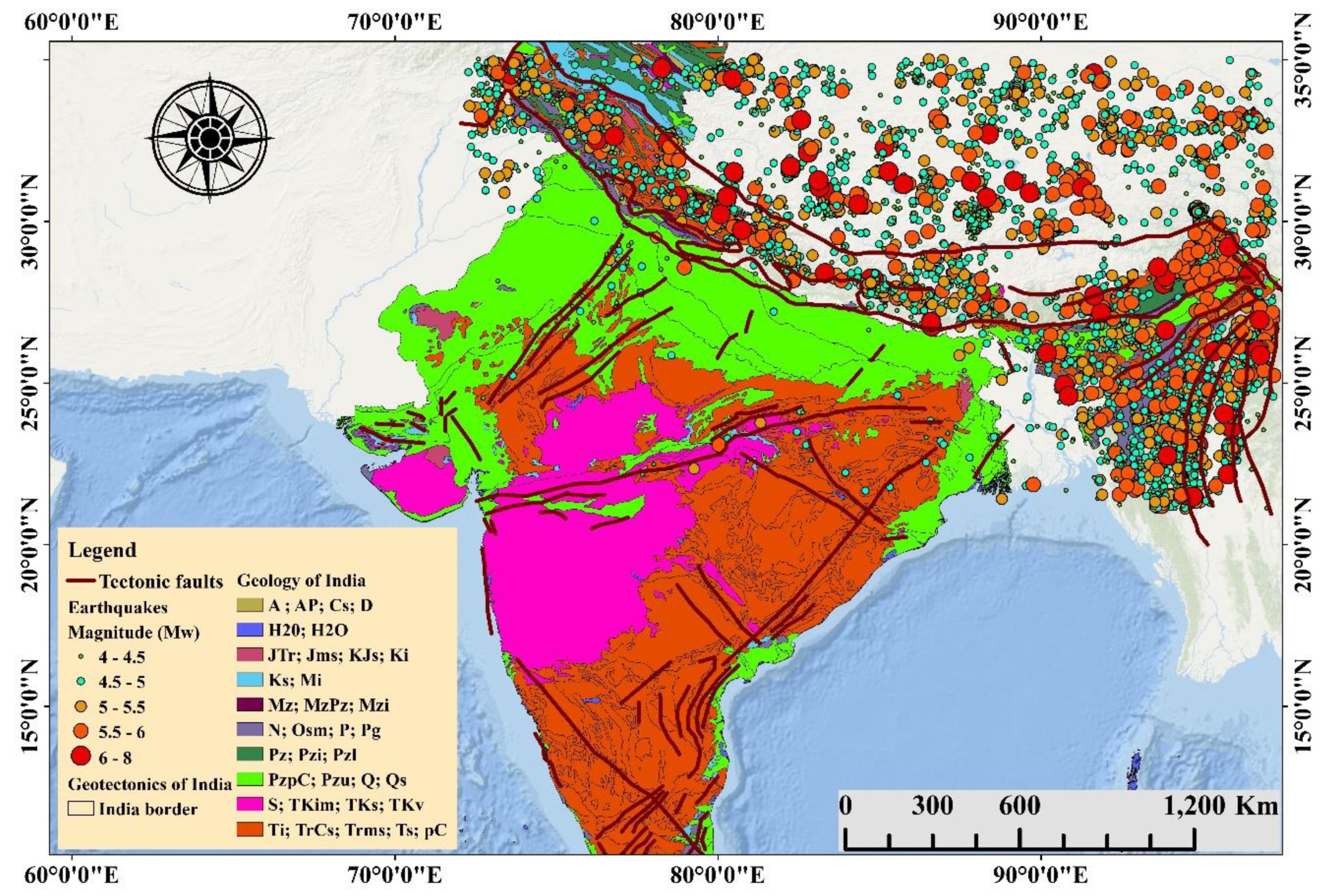
2. Seismic Tectonics of the Study Area
Study Region
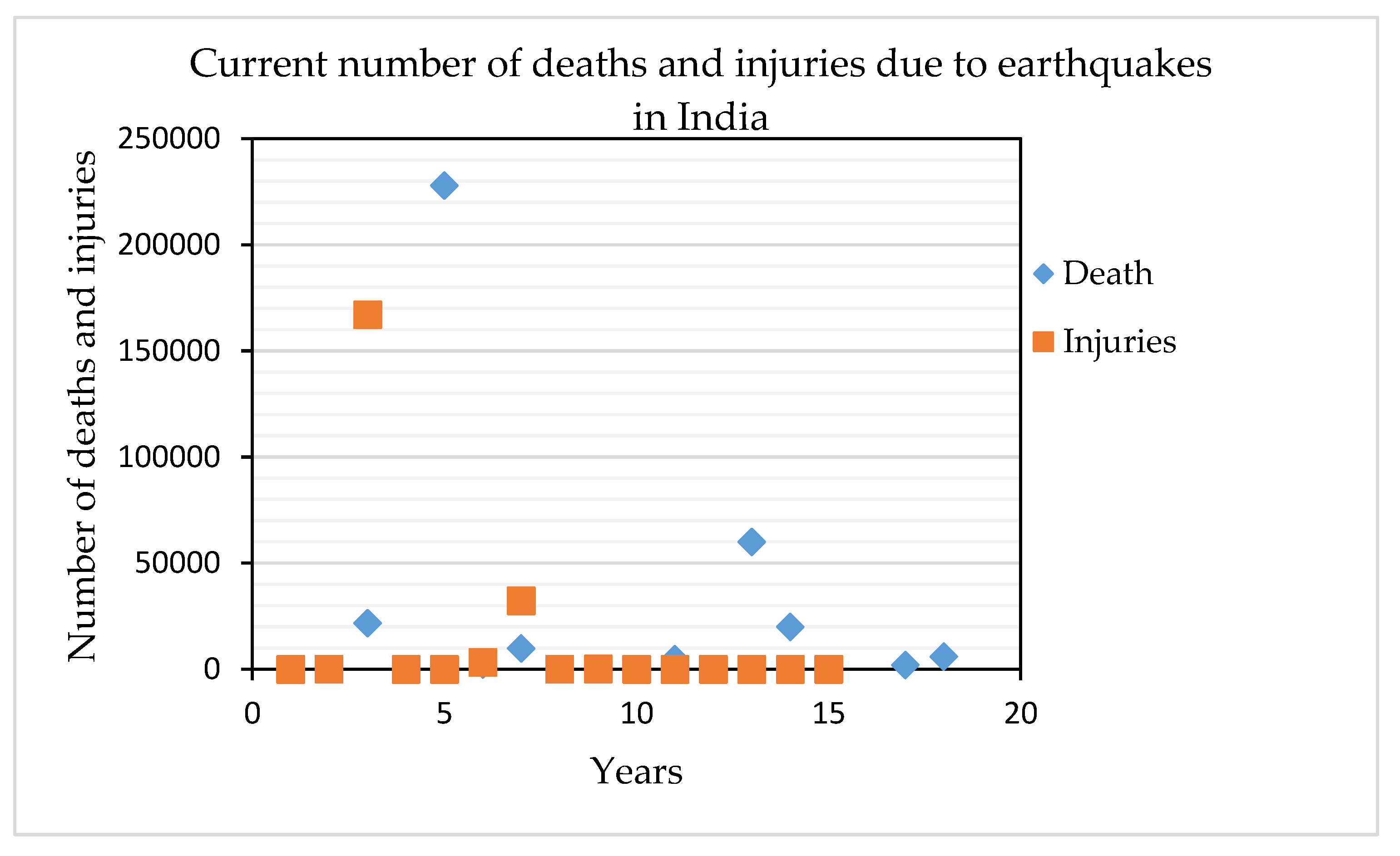
3. Geopotential Data Acquisition and Analysis
3.1. Catalog
3.2. Local Sources
3.3. Thematic Layers
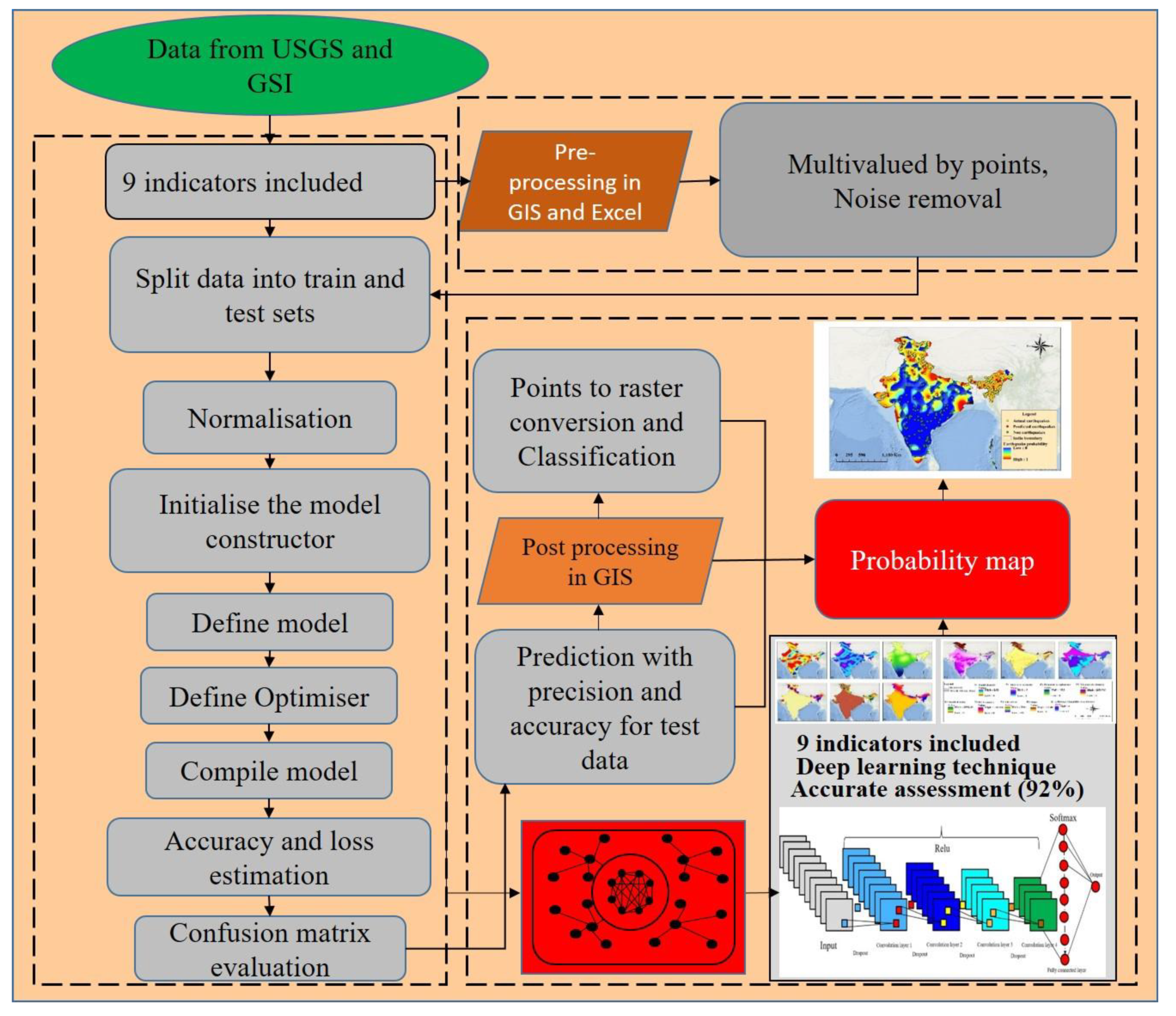
4. Methodology
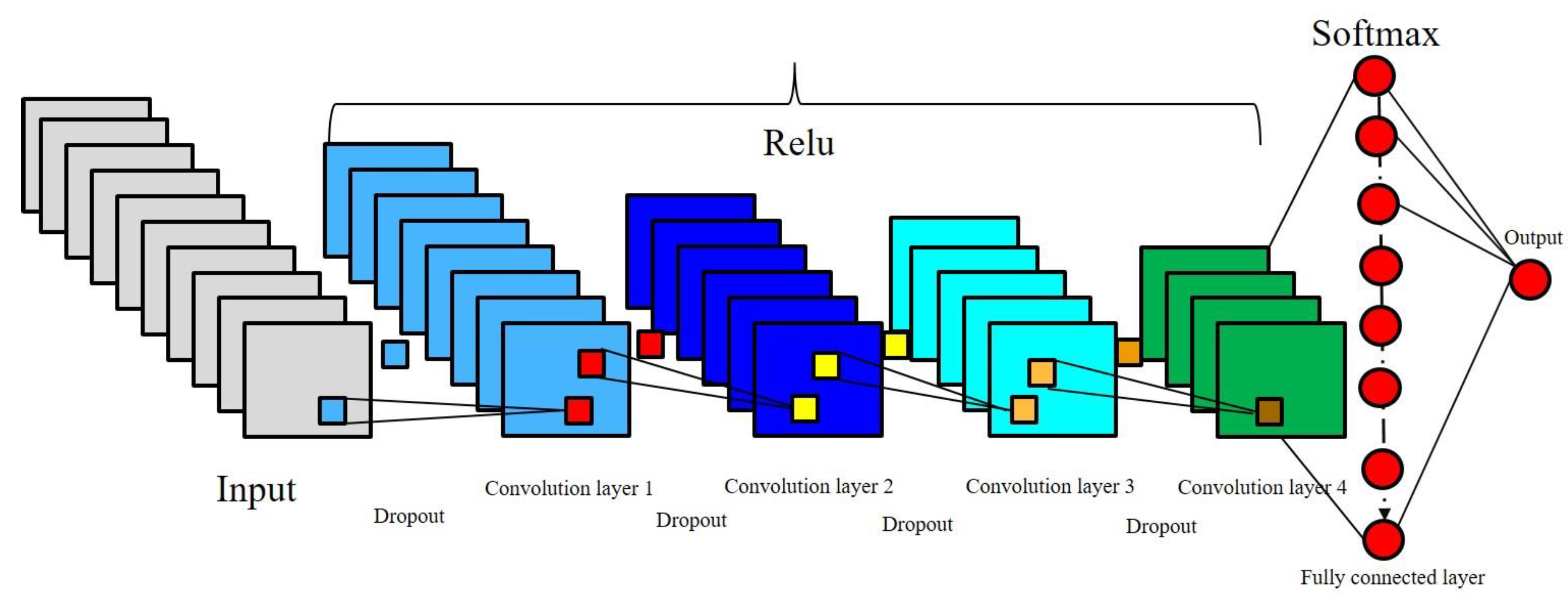
4.1. CNN Architecture
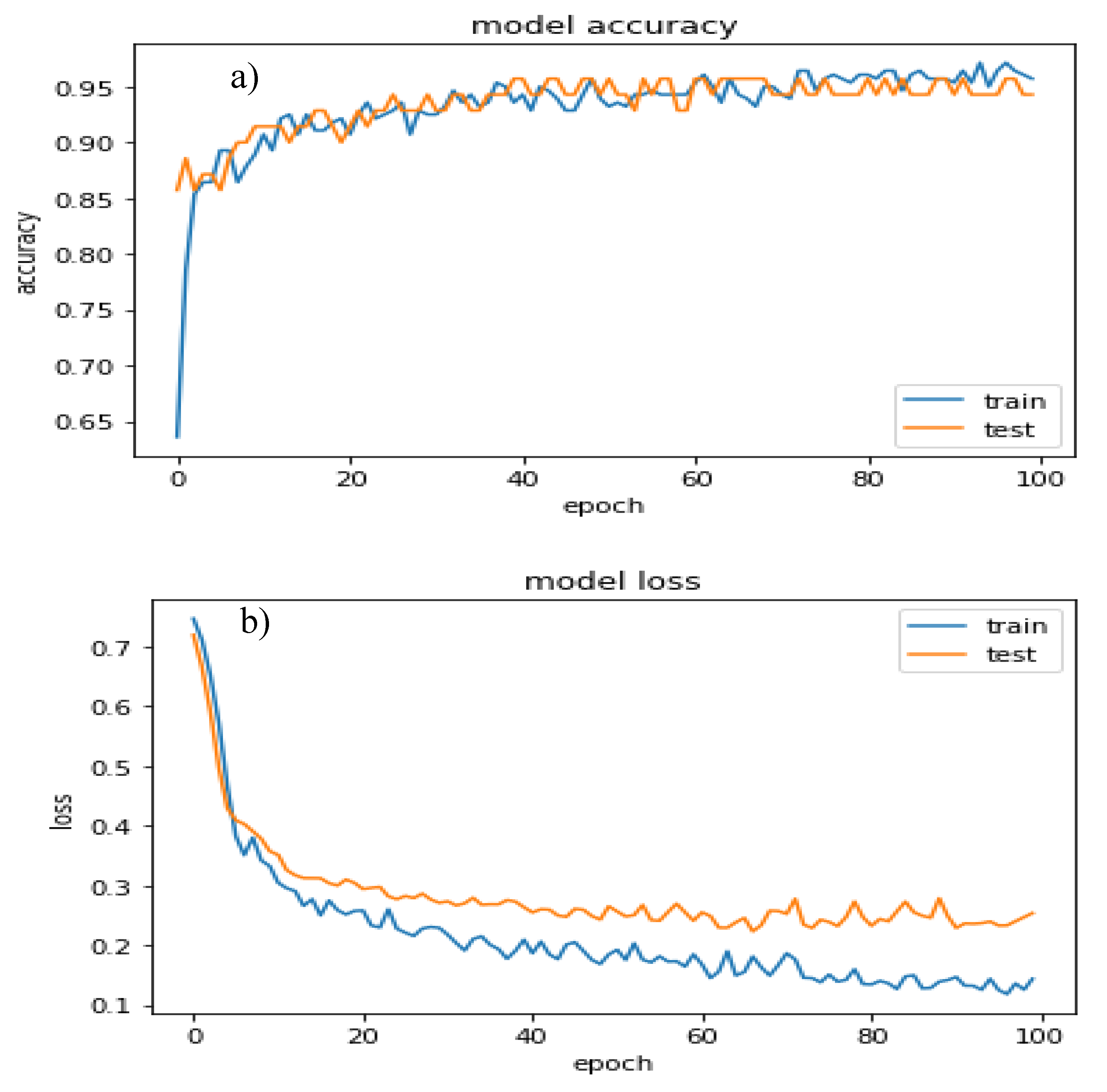
4.2. Learning the Model Parameters and Performance
4.3. PGA, Source to Site Distance and Intensity Calculation
5. CNN Model Implementation for Prediction and Probability Mapping
6. Results
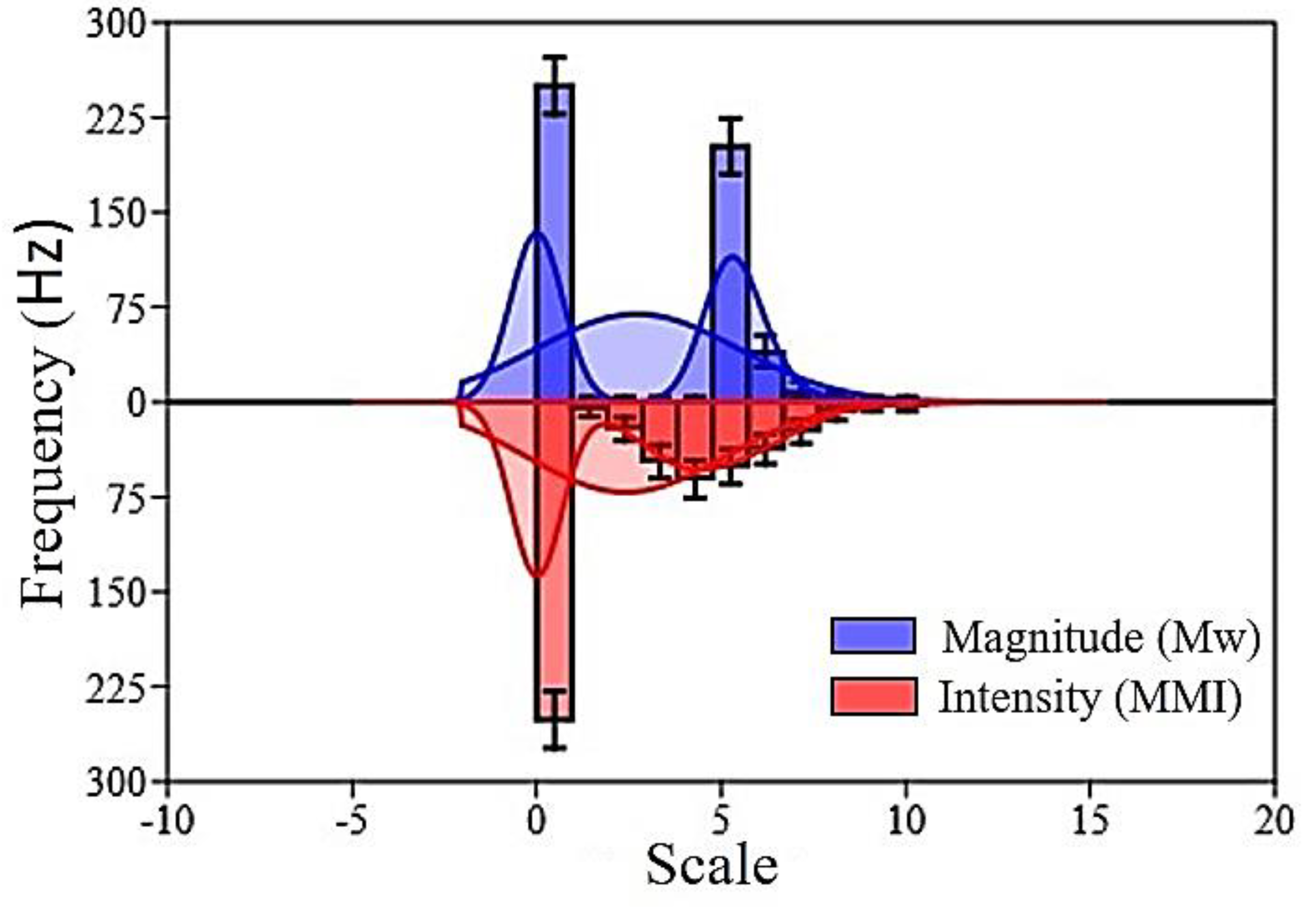
6.1. CNN Classification and Bi-histogram Results
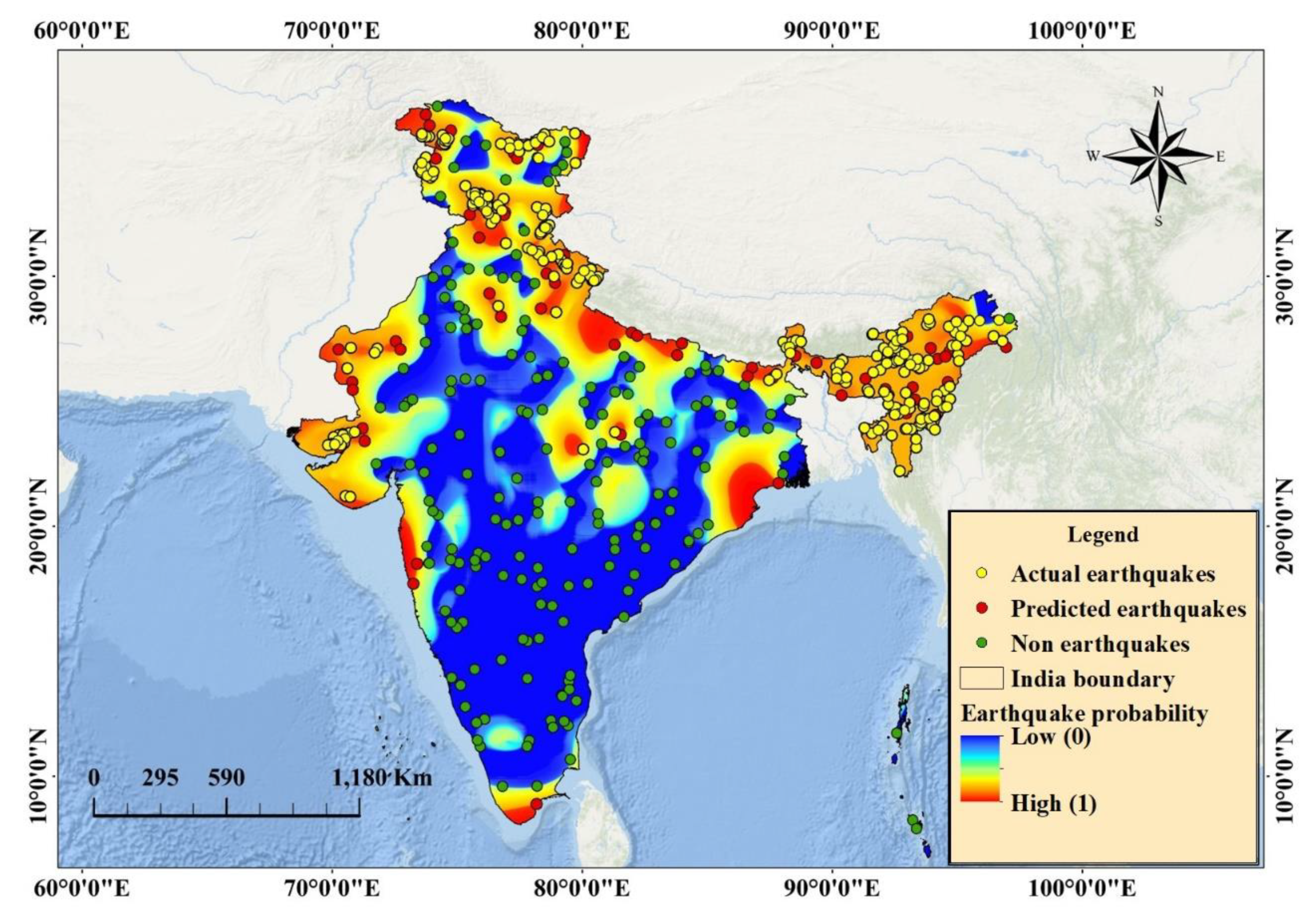
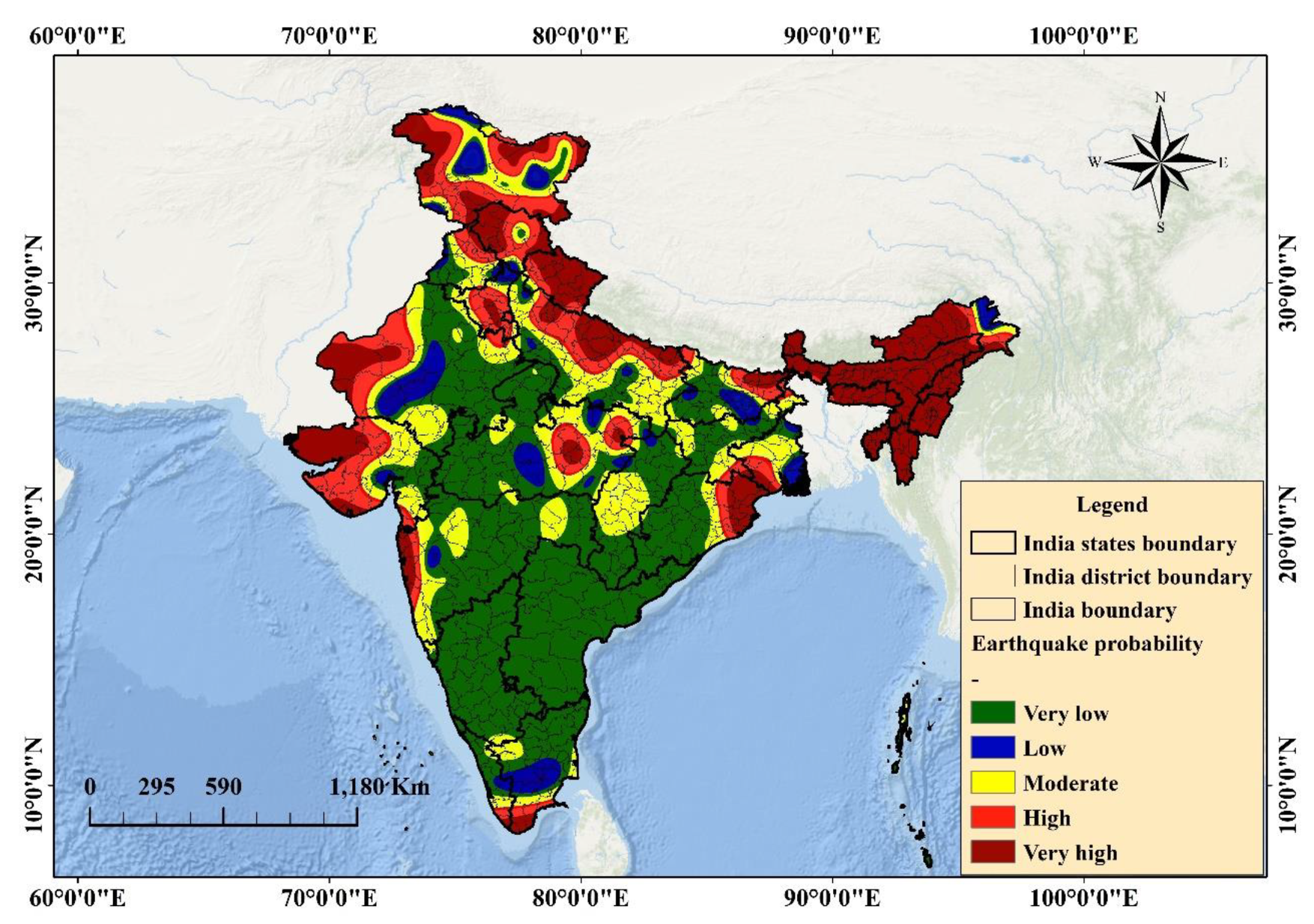
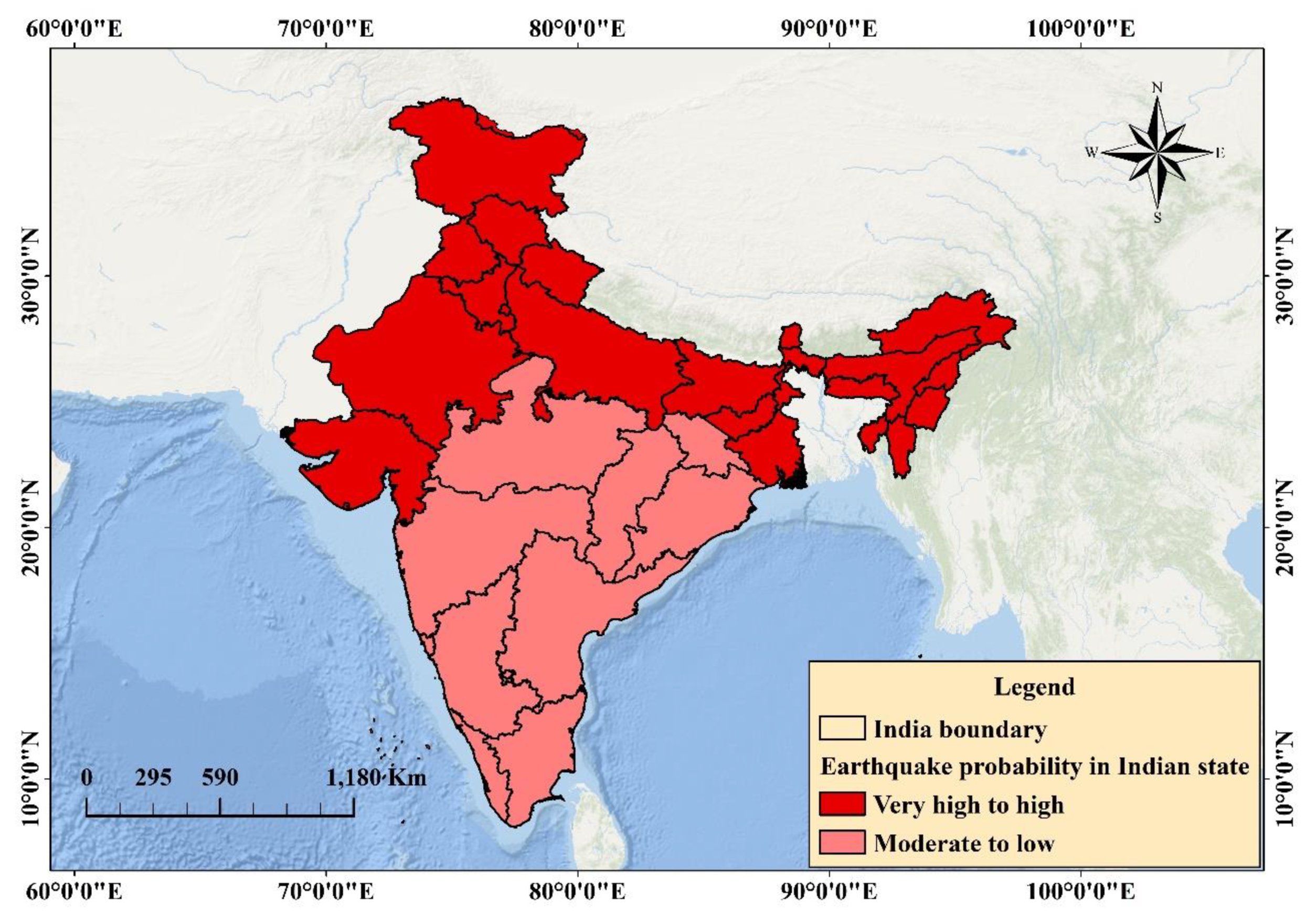
6.2. Probability Mapping
6.3. Result Validation
7. Discussion
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Allen, R. Automatic phase pickers: Their present use and future prospects. Bull. Seismol. Soc. Am. 1982, 72, S225–S242. [Google Scholar]
- Withers, M.; Aster, R.; Young, C.; Beiriger, J.; Harris, M.; Moore, S.; Trujillo, J. A comparison of select trigger algorithms for automated global seismic phase and event detection. Bull. Seismol. Soc. Am. 1998, 88, 95–106. [Google Scholar]
- Gibbons, S.J.; Ringdal, F. The detection of low magnitude seismic events using array-based waveform correlation. Geophys. J. Int. 2006, 165, 149–166. [Google Scholar] [CrossRef]
- Perol, T.; Gharbi, M.; Denolle, M. Convolutional neural network for earthquake detection and location. Sci. Adv. 2018, 4, e1700578. [Google Scholar] [CrossRef]
- Park, S.K.; Johnston, M.J.S.; Madden, T.R.; Morgan, F.D.; Morrison, H.F. Electromagnetic precursors to earthquakes in the Ulf band: A review of observations and mechanisms. Rev. Geophys. 1993, 31, 117–132. [Google Scholar] [CrossRef]
- Bilham, R. Earthquakes in India and the Himalaya: Tectonics, geodesy and history. Ann. Geophys. 2004, 47, 839–858. [Google Scholar]
- Matsagar, V. Special Issue: Earthquake Engineering and Structural Dynamics. J. Inst. Eng. (India): Ser. A 2016, 97, 355–357. [Google Scholar] [CrossRef][Green Version]
- Krinitzsky, E.L. Earthquake probability in engineering—Part 2: Earthquake recurrence and limitations of Gutenberg-Richter b-values for the engineering of critical structures. Eng. Geol. 1993, 36, 1–52. [Google Scholar] [CrossRef]
- Hardebeck, J.L. Stress triggering and earthquake probability estimates. J. Geophys. Res. Space Phys. 2004, 109, 4. [Google Scholar] [CrossRef]
- Parsons, T. Significance of stress transfer in time-dependent earthquake probability calculations. J. Geophys. Res. Space Phys. 2005, 110, 5. [Google Scholar] [CrossRef]
- Shapiro, S.; Dinske, C.; Kummerow, J. Probability of a given-magnitude earthquake induced by a fluid injection. Geophys. Res. Lett. 2007, 34, 22. [Google Scholar] [CrossRef]
- Hagiwara, Y. Probability of earthquake occurrence as obtained from a Weibull distribution analysis of crustal strain. Tectonophysics 1974, 23, 313–318. [Google Scholar] [CrossRef]
- Shcherbakov, R.; Zhuang, J.; Zöller, G.; Ogata, Y. Forecasting the magnitude of the largest expected earthquake. Nat. Commun. 2019, 10, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Brinkman, B.A.W.; Leblanc, M.; Ben-Zion, Y.; Uhl, J.T.; Dahmen, K.A. Probing failure susceptibilities of earthquake faults using small-quake tidal correlations. Nat. Commun. 2015, 6, 6157. [Google Scholar] [CrossRef]
- Wyss, M.; Pouysségur, J. Change in the Probability for Earthquakes in Southern California Due to the Landers Magnitude 7.3 Earthquake. Science 2000, 290, 1334–1338. [Google Scholar] [CrossRef]
- Jena, R.; Pradhan, B.; Beydoun, G.; Nizamuddin; Ardiansyah; Sofyan, H.; Affan, M. Integrated model for earthquake risk assessment using neural network and analytic hierarchy process: Aceh province, Indonesia. Geosci. Front. 2020, 11, 613–634. [Google Scholar] [CrossRef]
- Parvez, I.A.; Ram, A. Probabilistic Assessment of Earthquake Hazards in the North-East Indian Peninsula and Hindukush Regions. Pure Appl. Geophys. PAGEOPH 1997, 149, 731–746. [Google Scholar] [CrossRef]
- Tripathi, J.N. Probabilistic assessment of earthquake recurrence in the January 26, 2001 earthquake region of Gujrat, India. J. Seism. 2006, 10, 119–130. [Google Scholar] [CrossRef]
- Yadav, R.B.S.; Tripathi, J.N.; Rastogi, B.K.; Das, M.C.; Chopra, S. Probabilistic Assessment of Earthquake Recurrence in Northeast India and Adjoining Regions. Pure Appl. Geophys. PAGEOPH 2010, 167, 1331–1342. [Google Scholar] [CrossRef]
- Thaker, T.P.; Rathod, G.W.; Rao, K.S.; Gupta, K.K. Use of Seismotectonic Information for the Seismic Hazard Analysis for Surat City, Gujarat, India: Deterministic and Probabilistic Approach. Pure Appl. Geophys. PAGEOPH 2011, 169, 37–54. [Google Scholar] [CrossRef]
- Gupta, H.; Singh, H. Earthquake swarms precursory to moderate to great earthquakes in the northeast India region. Tectonophysics 1989, 167, 285–298. [Google Scholar] [CrossRef]
- Evison, F.F. Fluctuations of seismicity before major earthquakes. Nature 1977, 266, 710–712. [Google Scholar] [CrossRef]
- Kayal, J.R.; Banerjee, B. Anomalous behaviour of precursor resistivity in Shillong area, NE India. Geophys. J. Int. 1988, 94, 97–103. [Google Scholar] [CrossRef]
- Kayal, J.R. Earthquake prediction in northeast India?A review. Pure Appl. Geophys. PAGEOPH 1991, 136, 297–313. [Google Scholar] [CrossRef]
- Sitharam, T.; Vipin, K.S. Evaluation of spatial variation of peak horizontal acceleration and spectral acceleration for south India: A probabilistic approach. Nat. Hazards 2011, 59, 639–653. [Google Scholar] [CrossRef]
- Sitharam, T.; Kolathayar, S.; James, N. Probabilistic assessment of surface level seismic hazard in India using topographic gradient as a proxy for site condition. Geosci. Front. 2015, 6, 847–859. [Google Scholar] [CrossRef]
- Chandramouli, C.; General, R. Census of India 2011. Available online: https://censusindia.gov.in/2011-prov-results/data_files/india/paper_contentsetc.pdf (accessed on 28 February 2020).
- Kolathayar, S.; Sitharam, T.G.; Vipin, K.S. Deterministic seismic hazard macrozonation of India. J. Earth Syst. Sci. 2012, 121, 1351–1364. [Google Scholar] [CrossRef]
- India, G.S.o.; Dasgupta, S.; Narula, P.; Acharyya, S.; Banerjee, J. Seismotectonic Atlas of India and its Environs; Geological Survey of India: Kolkata, India, 2000. [Google Scholar]
- Iyengar, R.; Ghosh, S. Microzonation of earthquake hazard in greater Delhi area. Curr. Sci. 2004, 87, 1193–1202. [Google Scholar]
- Nath, S.K.; Thingbaijam, K.K.S.; Raj, A. Earthquake hazard in Northeast India — A seismic microzonation approach with typical case studies from Sikkim Himalaya and Guwahati city. J. Earth Syst. Sci. 2008, 117, 809–831. [Google Scholar] [CrossRef]
- Boominathan, A.; Dodagoudar, G.R.; Suganthi, A.; Maheswari, R.U. Seismic hazard assessment of Chennai city considering local site effects. J. Earth Syst. Sci. 2008, 117, 853–863. [Google Scholar] [CrossRef]
- Kanth, S.R.; Iyengar, R. Seismic hazard estimation for Mumbai city. Curr. Sci. 2006, 91, 1486–1494. [Google Scholar]
- Anbazhagan, P.; Vinod, J.S.; Sitharam, T. Probabilistic seismic hazard analysis for Bangalore. Nat. Hazards 2008, 48, 145–166. [Google Scholar] [CrossRef]
- Vipin, K.S.; Anbazhagan, P.; Sitharam, T. Estimation of peak ground acceleration and spectral acceleration for South India with local site effects: Probabilistic approach. Nat. Hazards Earth Syst. Sci. 2009, 9, 865–878. [Google Scholar] [CrossRef]
- Mitchell, T.M. Machine Learning; McGraw-hill: New York, NY, USA, 1997. [Google Scholar]
- Severyn, A.; Moschitti, A. Unitn: Training deep convolutional neural network for twitter sentiment classification. In Proceedings of the 9th international workshop on semantic evaluation (SemEval 2015), Denver, CO, USA, 4–5 June 2015; pp. 464–469. [Google Scholar]
- Jena, R.; Pradhan, B.; Beydoun, G. Earthquake vulnerability assessment in Northern Sumatra province by using a multi-criteria decision-making model. Int. J. Disaster Risk Reduct. 2020, 46, 101518. [Google Scholar] [CrossRef]
- Joyner, W.; Boore, D.M.; Porcella, R. Peak horizontal acceleration and velocity from strong motion records including records from the 1979 Imperial Valley, California, earthquake. Open-File Rep. 1981, 71, 2011–2038. [Google Scholar] [CrossRef]
- Boore, D.M.; Joyner, W.B. The empirical prediction of ground motion. Bull. Seismol. Soc. Am. 1982, 72, S43–S60. [Google Scholar]
- Campbell, G.S. Soil Physics with BASIC: Transport Models for Soil-Plant Systems; Elsevier: Pullman, WA, USA, 1985. [Google Scholar]
- Fukushima, Y.; Tanaka, T. A new attenuation relation for peak horizontal acceleration of strong earthquake ground motion in Japan. Bull. Seismol. Soc. Am. 1990, 80, 757–783. [Google Scholar]
- Jena, R.; Pradhan, B. Integrated ANN-cross-validation and AHP-TOPSIS model to improve earthquake risk assessment. Int. J. Disaster Risk Reduct. 2020, 50, 101723. [Google Scholar] [CrossRef]
- Alizadeh, M.; Ngah, I.; Hashim, M.; Pradhan, B.; Pour, A.B. A Hybrid Analytic Network Process and Artificial Neural Network (ANP-ANN) Model for Urban Earthquake Vulnerability Assessment. Remote Sens. 2018, 10, 975. [Google Scholar] [CrossRef]
- Bathrellos, G.; Skilodimou, D.; Chousianitis, K.; Youssef, A.; Pradhan, B. Suitability estimation for urban development using multi-hazard assessment map. Sci. Total Environ. 2017, 575, 119–134. [Google Scholar] [CrossRef]
- Soe, M.; Ryutaro, T.; Ishiyama, D.; Takashima, I.; Charusiri, K.W.-I.P. Remote sensing and GIS based approach for earthquake probability map: A case study of the northern Sagaing fault area, Myanmar. J. Geol. Soc. Thail. 2009, 1, 29–46. [Google Scholar]
- Yoon, C.E.; O’Reilly, O.; Bergen, K.J.; Beroza, G.C. Earthquake detection through computationally efficient similarity search. Sci. Adv. 2015, 1, e1501057. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Teng, T.-L. Artificial neural network-based seismic detector. Bull. Seismol. Soc. Am. 1995, 85, 308–319. [Google Scholar]
- Khattri, K.; Rogers, A.; Perkins, D.; Algermissen, S. A seismic hazard map of India and adjacent areas. Tectonophysics 1984, 108, 93–134. [Google Scholar] [CrossRef]
- Bhatia, S.C.; Kumar, M.R.; Gupta, H.K. A probabilistic seismic hazard map of India and adjoining regions. Annali di Geofisica. 1999, 42, 1153–1164. [Google Scholar]
- Joyner, W.B.; Boore, D.M. Measurement, Characterization, and Prediction of Strong Ground Motion. Available online: http://ww.daveboore.com/pubs_online/joyner_boore_park_city_1988.pdf (accessed on 26 February 2020).
- Aman, A.; Singh, U.K.; Singh, R.P. A new empirical relation for strong seismic ground motion for the Himalayan region. Curr. Sci. 1995, 69, 772–777. [Google Scholar]
- Singh, R.P.; Aman, A.; Prasad, Y.J.J. Attenuation relations for strong seismic ground motion in the Himalayan region. Pure Appl. Geophys. PAGEOPH 1996, 147, 161–180. [Google Scholar] [CrossRef]
- Lyubushin, A.; Parvez, I. Map of seismic hazard of India using Bayesian approach. Nat. Hazards 2010, 55, 543–556. [Google Scholar] [CrossRef]
- Jena, R.; Pradhan, B. A model for visual assessment of fault plane solutions and active tectonics analysis using the global centroid moment tensor catalog. Earth Syst. Environ. 2019, 4, 197–211. [Google Scholar] [CrossRef]
- Fanos, A.M.; Pradhan, B. A novel hybrid machine learning-based model for rockfall source identification in presence of other landslide types using LiDAR and GIS. Earth Syst. Environ. 2019, 3, 491–506. [Google Scholar] [CrossRef]
- Fanos, A.M.; Pradhan, B. Laser scanning systems and techniques in rockfall source identification and risk assessment: A critical review. Earth Syst. Environ. 2018, 2, 163–182. [Google Scholar] [CrossRef]
| Parameters | Data Source | Resolution | Scale | Description |
|---|---|---|---|---|
| Slope Elevation | DEM (USGS) https://earthexplorer.usgs.gov/ | 30 m | 1:250000 | Derived from raster DEM |
| Fault density Distance from fault | Geological map of India, GSI | Derived from image digitization in ArcGIS | ||
| Magnitude density Epicenter density Distance from epicenter | USGS earthquake catalog (https://earthquake.usgs.gov) | Derived using Joyner and Boore (1981), Campbell (1981) | ||
| PGA density | USGS earthquake catalog | PGA can be derived using | ||
| Lithology and amplification factor | Geological map of India, GSI (www.gsi.gov.in), (bhuvan.nrsc.gov.in), (USGS World Geologic Map) | Derived from image digitization in ArcGIS 1. Unknown:1 2. Hard rock:0.55 3. Soft rock:0.70 4. Medium soil:1 5. Soft soil:1.30 |
| Layer (Type) | Output | Shape Parameter |
|---|---|---|
| dense_1 (Dense) | (None, 200) | 2000 |
| dropout_1 | (None, 200) | 0 |
| dense_2 (Dense) | (None, 200) | 40,200 |
| dropout_2 | (None, 200) | 0 |
| dense_3 (Dense) | (None, 200) | 40,200 |
| dropout_3 | (None, 200) | 0 |
| dense_4 (Dense) | (None, 200) | 40,200 |
| dropout_4 | (None, 200) | 0 |
| dense_4 (Dense) | (None, 2) | 402 |
| Input number of units = 9 | ||
| Output = 2 | ||
| Hidden units = 200 | ||
| Kernel regularizer = l2(0.0001) | ||
| Activation = ‘relu’ | ||
| Activation = ‘softmax’ | ||
| Total params: 123,002 | ||
| Trainable params: 123,002 | ||
| Non-trainable params: 0 | ||
| Predicted | |||
| Positive | Negative | ||
| Actual | Positive | 60 | 11 |
| Negative | 1 | 79 | |
| Classification Report | Precision | Recall | F1 Score | Support |
|---|---|---|---|---|
| 0 | 0.98 | 0.85 | 0.91 | 71 |
| 1 | 0.88 | 0.99 | 0.93 | 80 |
| Micro average | 0.92 | 0.92 | 0.92 | 151 |
| Micro average | 0.93 | 0.92 | 0.92 | 151 |
| Weighted average | 0.93 | 0.92 | 0.92 | 151 |
| Prediction accuracy: 0.920530 | ||||
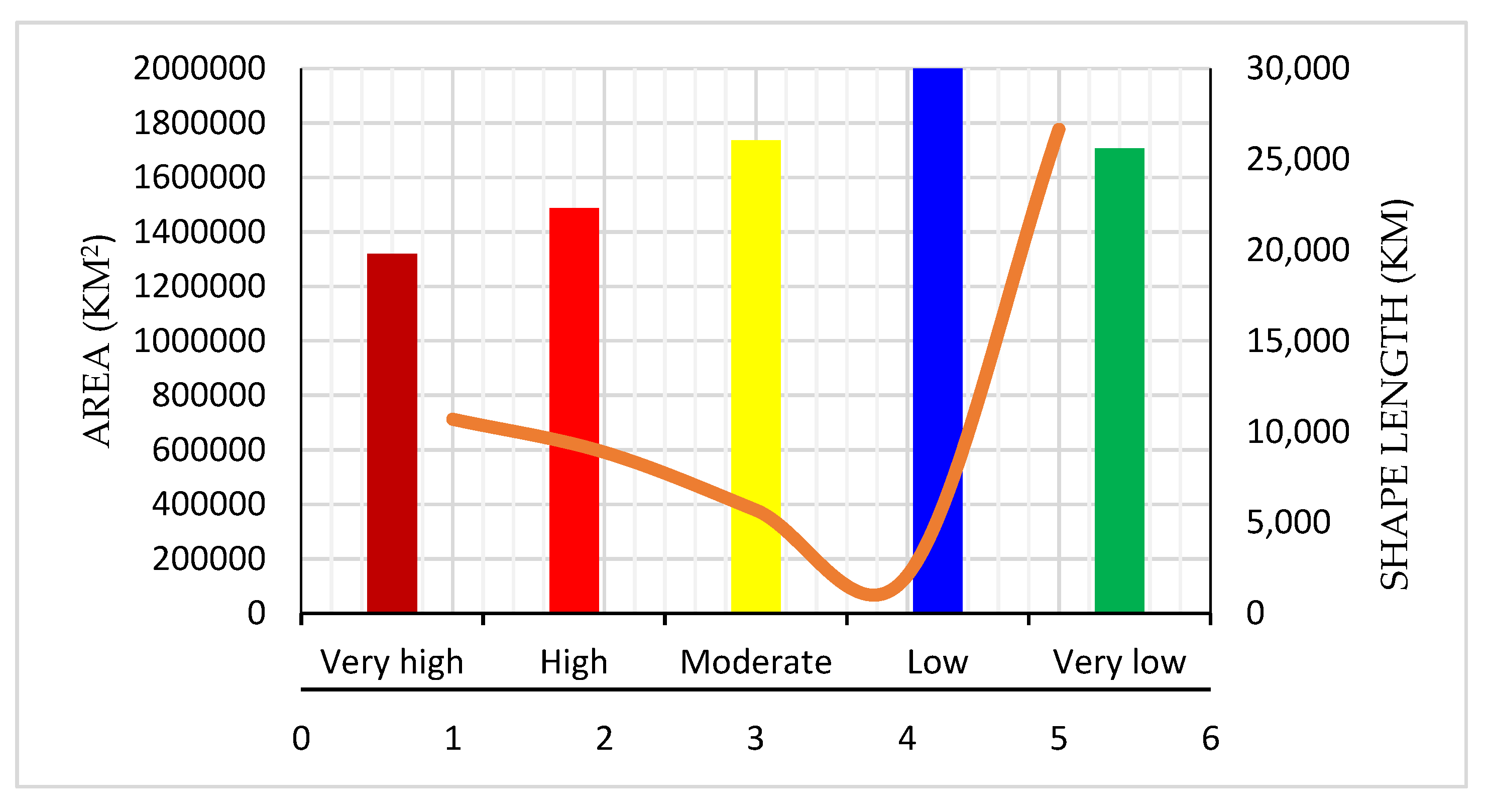
| Class No. | Probability Classes | Shape Length (km) | Area (km2) | Area (%) |
|---|---|---|---|---|
| 1 | Very-high | 19,788.24 | 712,375 | 19.8 |
| 2 | High | 22,309.64 | 591,240.5 | 16.43 |
| 3 | Moderate | 26,041.08 | 37,8887.6 | 10.53 |
| 4 | Low | 30,004.07 | 139,123.1 | 3.87 |
| 5 | Very-low | 25,599.15 | 1,776,265 | 49.37 |
| Total | 3,597,891 | 100 |
| Category | No. of Experts | Profession | Specialization | Recruitment Process | Validation Criteria | Feedback |
|---|---|---|---|---|---|---|
| Researchers | 5 | Seismologist, geologist, hydrologist, GIS analyst, soil physicist, geotechnical researcher | Researcher on natural hazards using GIS and remote sensing, monitoring, mapping, GIS, artificial intelligence |
|
|
|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jena, R.; Pradhan, B.; Al-Amri, A.; Lee, C.W.; Park, H.-j. Earthquake Probability Assessment for the Indian Subcontinent Using Deep Learning. Sensors 2020, 20, 4369. https://doi.org/10.3390/s20164369
Jena R, Pradhan B, Al-Amri A, Lee CW, Park H-j. Earthquake Probability Assessment for the Indian Subcontinent Using Deep Learning. Sensors. 2020; 20(16):4369. https://doi.org/10.3390/s20164369
Chicago/Turabian StyleJena, Ratiranjan, Biswajeet Pradhan, Abdullah Al-Amri, Chang Wook Lee, and Hyuck-jin Park. 2020. "Earthquake Probability Assessment for the Indian Subcontinent Using Deep Learning" Sensors 20, no. 16: 4369. https://doi.org/10.3390/s20164369
APA StyleJena, R., Pradhan, B., Al-Amri, A., Lee, C. W., & Park, H.-j. (2020). Earthquake Probability Assessment for the Indian Subcontinent Using Deep Learning. Sensors, 20(16), 4369. https://doi.org/10.3390/s20164369








