Depth-of-Field-Extended Plenoptic Camera Based on Tunable Multi-Focus Liquid-Crystal Microlens Array
Abstract
1. Introduction
2. Materials and Methods
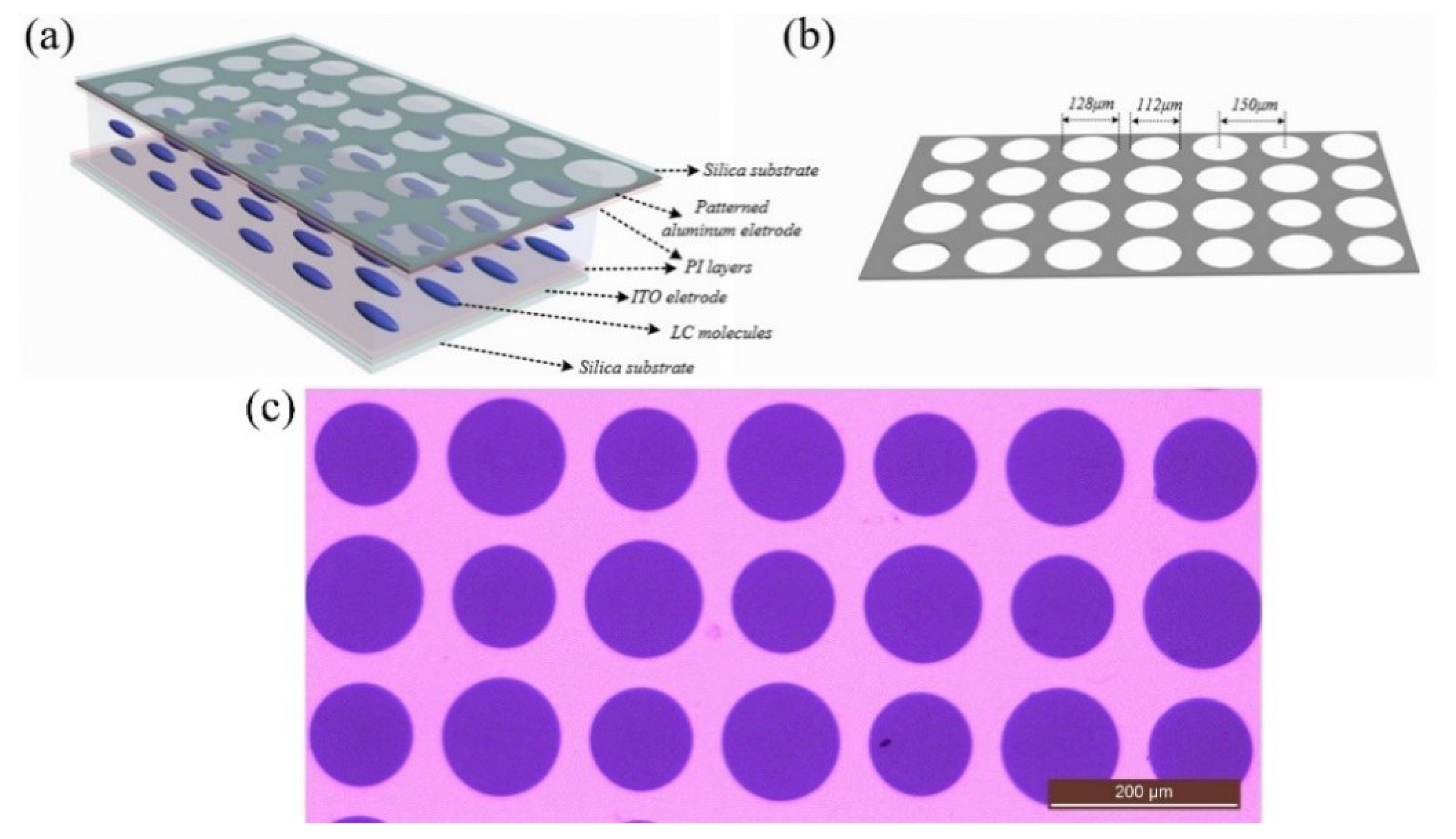
2.1. Structure of TMF-LCMLA
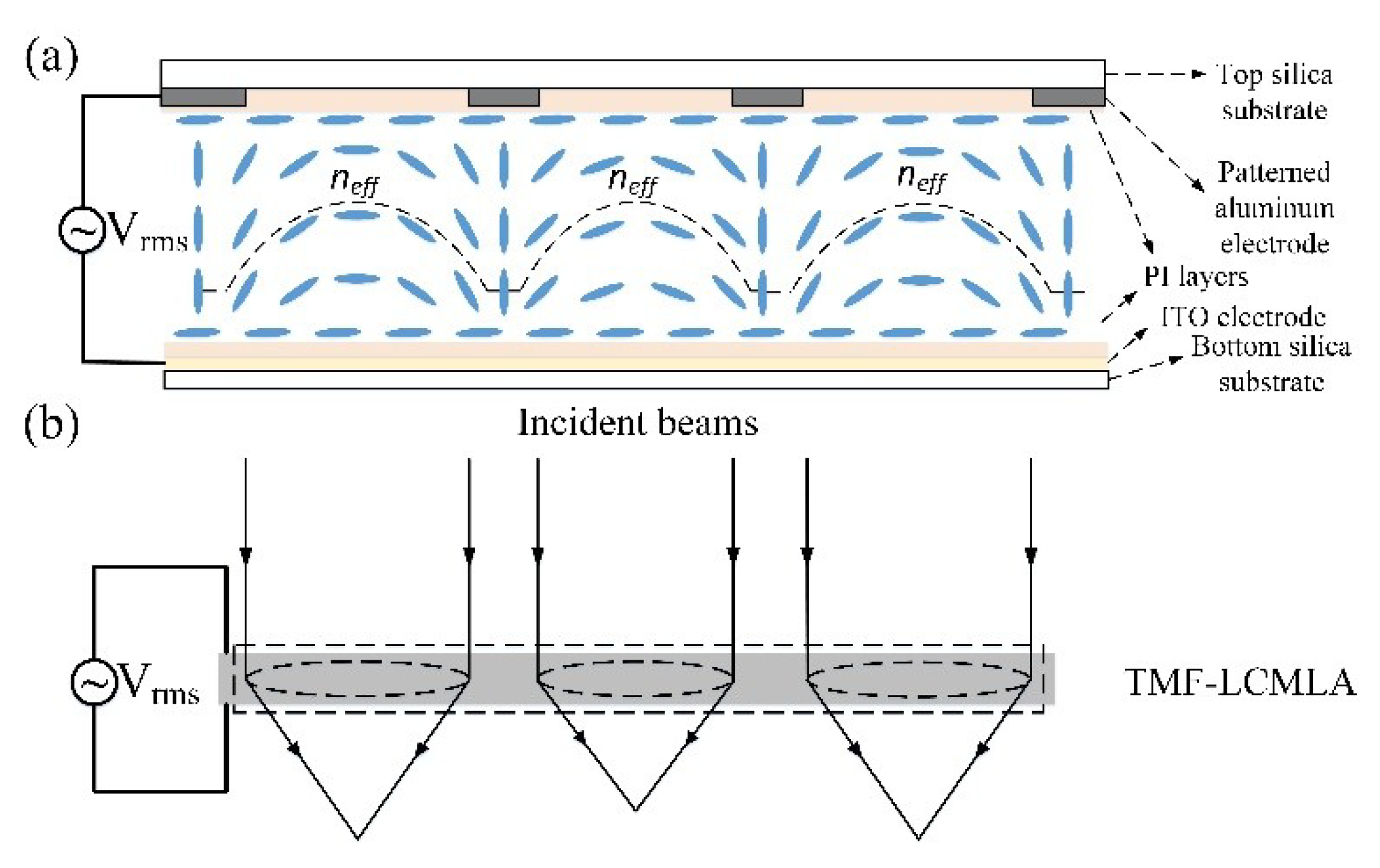
2.2. Principle of TMF-LCMLA
2.3. Principle of Plenoptic Camera Based on TMF-LCMLA
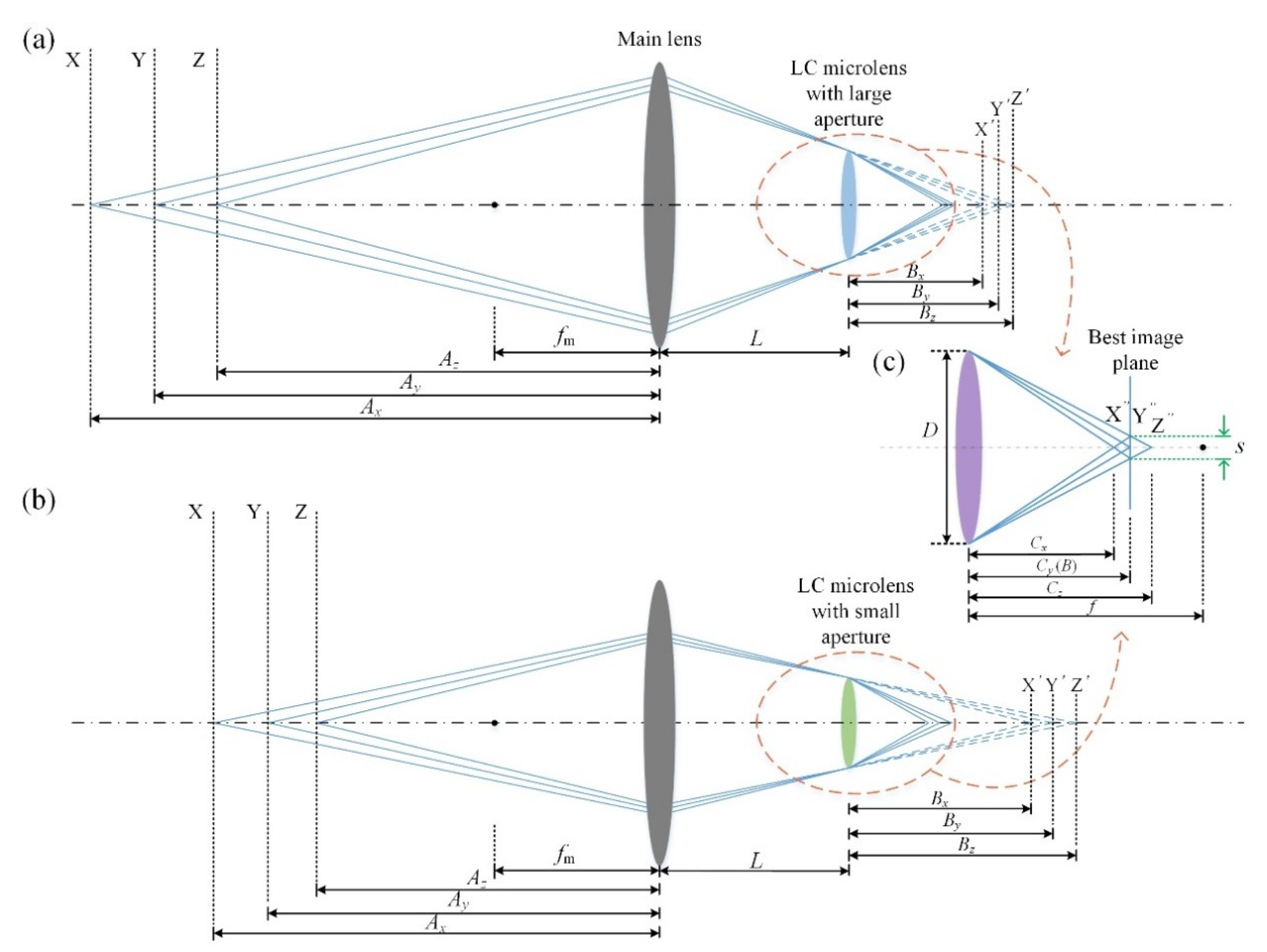
2.4. Digital Refocusing Range
3. Results
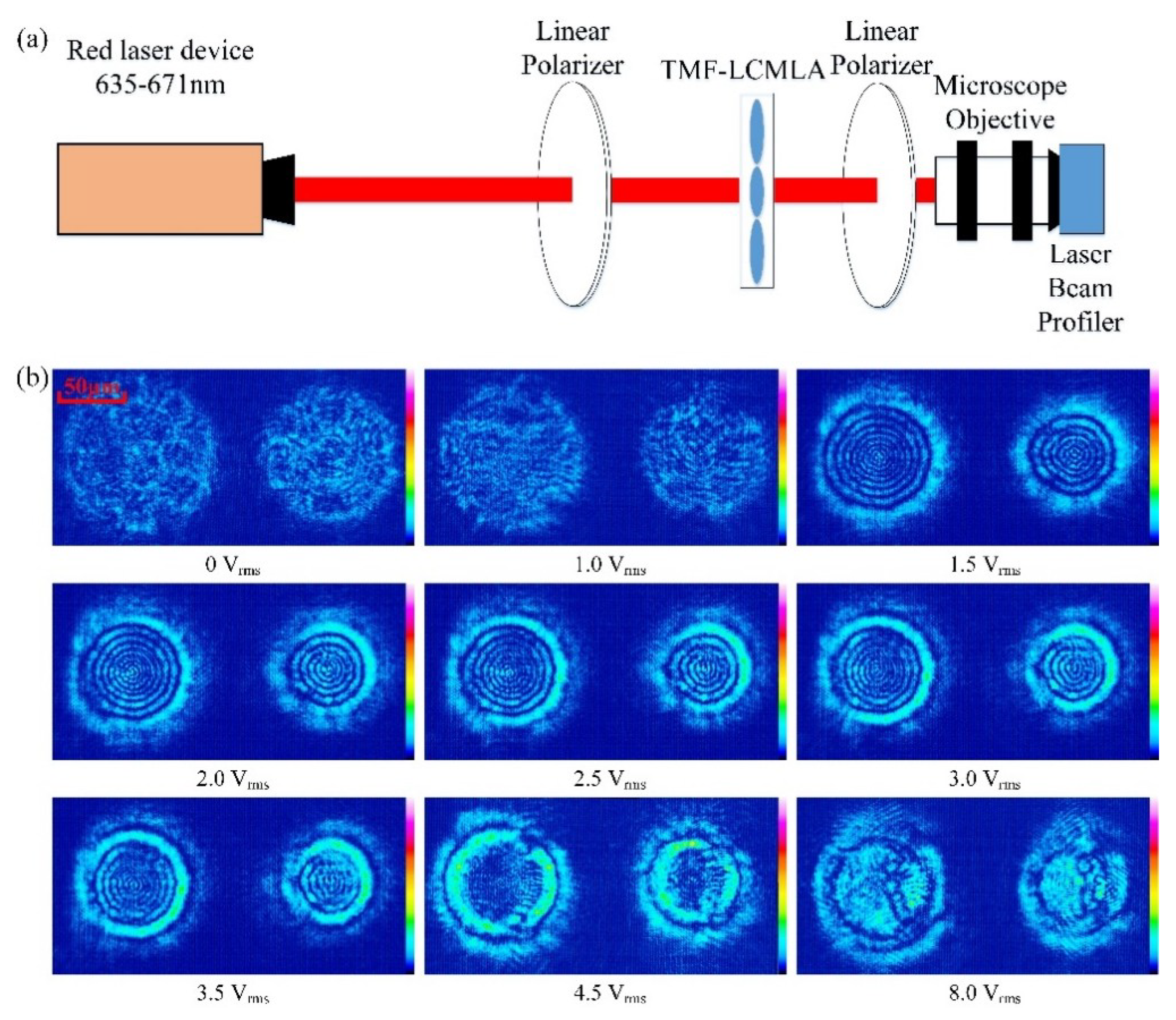
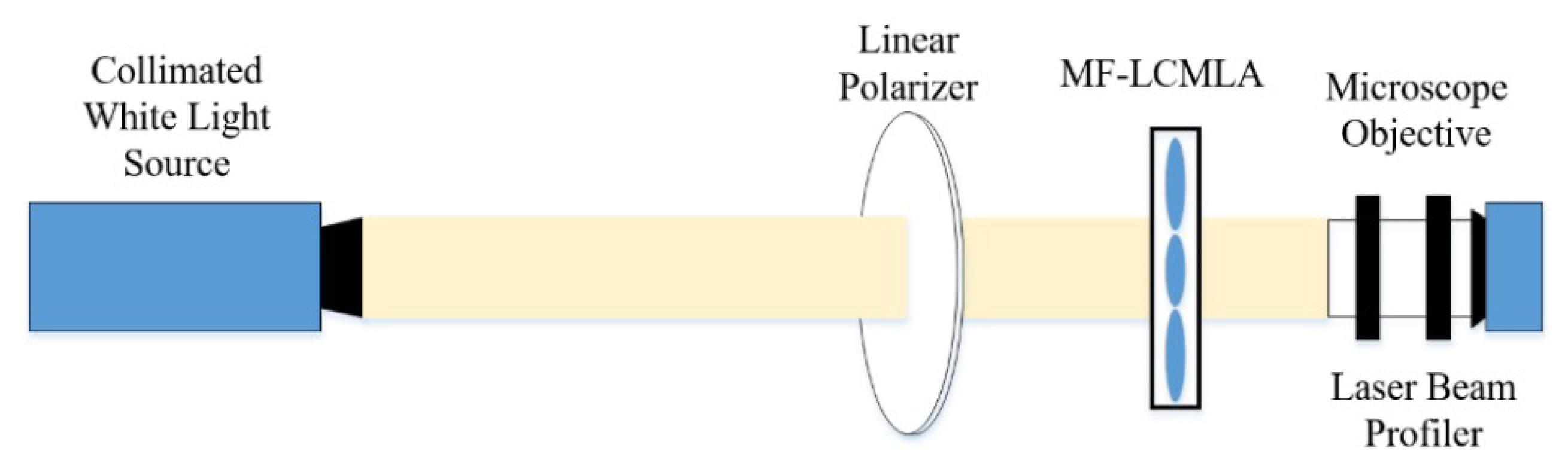
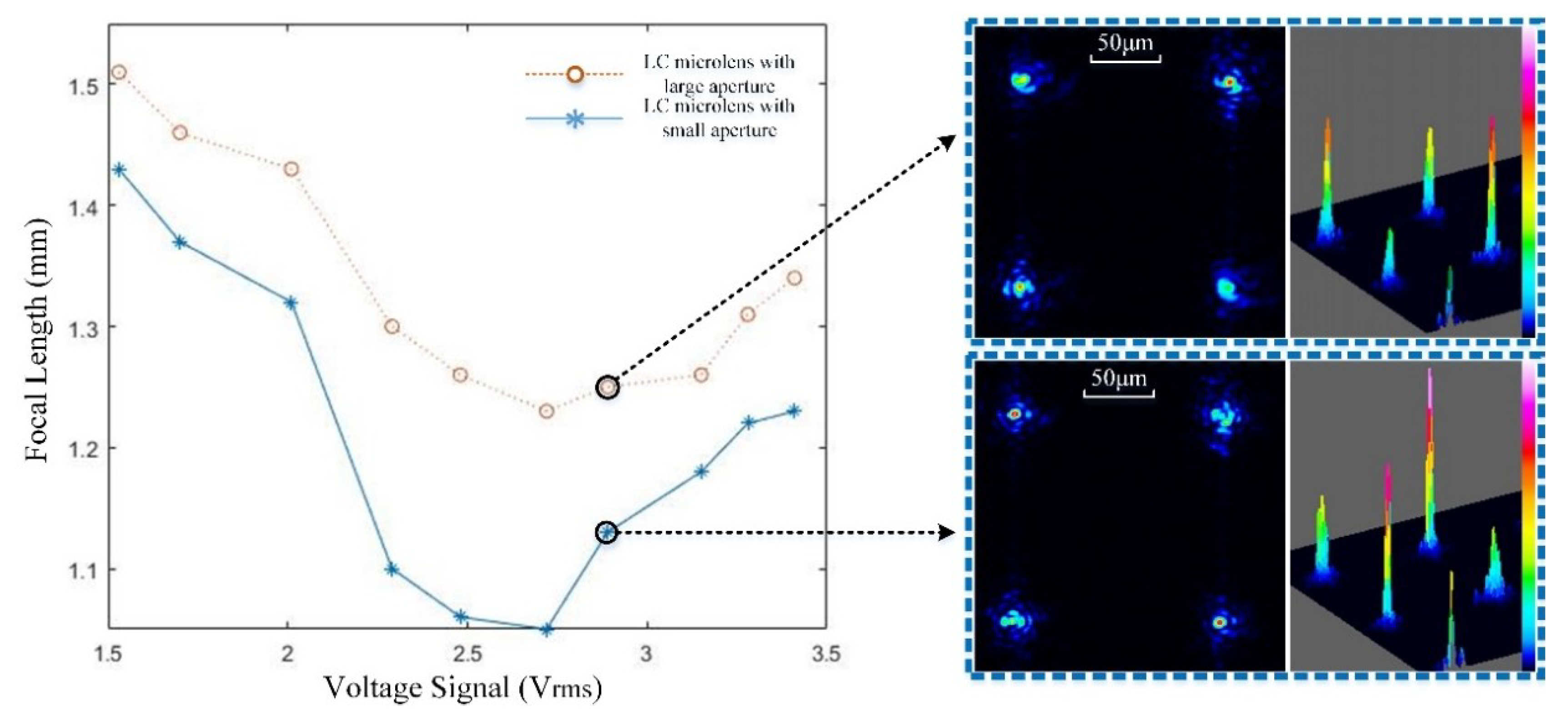
3.1. Optical Features of TMF-LCMLA
3.2. Imaging Application of Plenoptic Camera Based on TMF-LCMLA
3.3. 2D/3D Switchable Function
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ng, R.; Levoy, M.; Brédif, M.; Duval, G.; Horowitz, M.; Hanrahan, P. Light field photography with a hand-held plenoptic camera. Stanf. Tech. Rep. CTSR 2005, 2, 1–11. [Google Scholar]
- Lumsdaine, A.; Georgiev, T. Focused plenoptic camera and rendering. J. Electron. Imaging 2010, 19, 021106. [Google Scholar] [CrossRef]
- Levoy, M.; Zhang, Z.; McDowall, I. Recording and controlling the 4D light field in a microscope using microlens arrays. J. Microsc. 2009, 235, 144–162. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.M.; Kim, M.S.; Lee, G.J.; Yoo, Y.J.; Song, Y.M. Large area fabrication of engineered microlens array with low sag height for light-field imaging. Opt. Express 2019, 27, 4435–4444. [Google Scholar] [CrossRef] [PubMed]
- Palmieri, L.; Scrofani, G.; Incardona, N.; Saavedra, G.; Martínez-Corral, M.; Koch, R. Robust Depth Estimation for Light Field Microscopy. Sensors 2019, 19, 500. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Zhou, W.; Qian, T.; Cai, X. A depth estimation algorithm of plenoptic camera for the measurement of particles. In Proceedings of the IEEE International Conference on Imaging Systems and Techniques, Beijing, China, 18–20 October 2017; pp. 1–5. [Google Scholar]
- Kim, J.; Jung, J.-H.; Jeong, Y.; Hong, K.; Lee, B. Real-time integral imaging system for light field microscopy. Opt. Express 2014, 22, 10210–10220. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, X.; Peng, X.; Yin, Y.; Li, A.; Wu, J.; Gao, B.Z. Structured light field 3D imaging. Opt. Express 2016, 24, 20324–20334. [Google Scholar] [CrossRef]
- Galdi, C.; Chiesa, V.; Busch, C.; Correia, P.L.; Dugelay, J.-L.; Guillemot, C. Light Fields for Face Analysis. Sensors 2019, 19, 2687. [Google Scholar] [CrossRef]
- Adelson, E.; Wang, J. Single lens stereo with a plenoptic camera. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 99–106. [Google Scholar] [CrossRef]
- Li, S.; Zhu, Y.; Zhang, C.; Yuan, Y.; Tan, H. Rectification of Images Distorted by Microlens Array Errors in Plenoptic Cameras. Sensors 2018, 18, 2019. [Google Scholar] [CrossRef]
- Li, S.; Yuan, Y.; Gao, Z.; Tan, H. High-Accuracy Correction of a Microlens Array for Plenoptic Imaging Sensors. Sensors 2019, 19, 3922. [Google Scholar] [CrossRef] [PubMed]
- Seo, M.; Seo, J.-M.; Cho, D.-I.D.; Koo, K.-I. Insect-Mimetic Imaging System Based on a Microlens Array Fabricated by a Patterned-Layer Integrating Soft Lithography Process. Sensors 2018, 18, 2011. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Wu, J.; Dai, Q. Camera array based light field microscopy. Biomed. Opt. Express 2015, 6, 3179–3189. [Google Scholar] [CrossRef] [PubMed]
- Lanman, D. Mask-based Light Field Capture and Display. Ph.D. Thesis, Brown University, Providence, RI, USA, 2010. [Google Scholar]
- Kwon, H.; Kizu, Y.; Kizaki, Y.; Ito, M.; Kobayashi, M.; Ueno, R.; Suzuki, K.; Funaki, H. A Gradient Index Liquid Crystal Microlens Array for Light-Field Camera Applications. IEEE Photonics Technol. Lett. 2015, 27, 836–839. [Google Scholar] [CrossRef]
- Algorri, J.F.; Urruchi, V.; Bennis, N.; Morawiak, P.; Oton, J.M.; Oton, J.M. Integral Imaging Capture System With Tunable Field of View Based on Liquid Crystal Microlenses. IEEE Photon Technol. Lett. 2016, 28, 1854–1857. [Google Scholar] [CrossRef]
- Lei, Y.; Tong, Q.; Zhang, X.; Sang, H.; Ji, A.; Xie, C. An electrically tunable plenoptic camera using a liquid crystal microlens array. Rev. Sci. Instrum. 2015, 86, 053101. [Google Scholar] [CrossRef]
- Xin, Z.; Wei, D.; Xie, X.; Chen, M.; Zhang, X.; Liao, J.; Wang, H.; Xie, C. Dual-polarized light-field imaging micro-system via a liquid-crystal microlens array for direct three-dimensional observation. Opt. Express 2018, 26, 4035–4049. [Google Scholar] [CrossRef]
- Tong, Q.; Lei, Y.; Xin, Z.; Zhang, X.; Sang, H.; Xie, C. Dual-mode photosensitive arrays based on the integration of liquid crystal microlenses and CMOS sensors for obtaining the intensity images and wavefronts of objects. Opt. Express 2016, 24, 1903–1923. [Google Scholar] [CrossRef]
- Tong, Q.; Chen, M.; Xin, Z.; Wei, D.; Zhang, X.; Liao, J.; Wang, H.; Xie, C. Depth of field extension and objective space depth measurement based on wavefront imaging. Opt. Express 2018, 26, 18368–18385. [Google Scholar] [CrossRef]
- Algorri, J.F.; Urruchi, V.; Bennis, N.; Morawiak, P.; Sanchez-Pena, J.M.; Otón, J.M.; Oton, J.M. Liquid crystal spherical microlens array with high fill factor and optical power. Opt. Express 2017, 25, 605. [Google Scholar] [CrossRef]
- Algorri, J.F.; Urruchi, V.; Bennis, N.; Oton, J.M.; Oton, J.M. Cylindrical Liquid Crystal Microlens Array With Rotary Optical Power and Tunable Focal Length. IEEE Electron Device Lett. 2015, 36, 582–584. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Wang, Y.-J.; Reshetnyak, V. Liquid crystal lenses with tunable focal length. Liq. Cryst. Rev. 2017, 5, 111–143. [Google Scholar] [CrossRef]
- Shen, X.; Wang, Y.-J.; Chen, H.-S.; Xiao, X.; Lin, Y.-H.; Javidi, B. Extended depth-of-focus 3D micro integral imaging display using a bifocal liquid crystal lens. Opt. Lett. 2015, 40, 538–541. [Google Scholar] [CrossRef] [PubMed]
- Algorri, J.F.; Urruchi, V.; Bennis, N.; Oton, J.M.; Otón, J.M. Tunable liquid crystal cylindrical micro-optical array for aberration compensation. Opt. Express 2015, 23, 13899–13915. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Wu, S.-T. Tunable-focus liquid microlens array using dielectrophoretic effect. Opt. Express 2008, 16, 2646–2652. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wu, S.-T. Polarization independent adaptive microlens with a blue-phase liquid crystal. Opt. Express 2011, 19, 8045–8050. [Google Scholar] [CrossRef]
- Hassanfiroozi, A.; Huang, Y.-P.; Javidi, B.; Shieh, H.-P.D. Hexagonal liquid crystal lens array for 3D endoscopy. Opt. Express 2015, 23, 971–981. [Google Scholar] [CrossRef]
- Wang, Y.-J.; Shen, X.; Lin, Y.-H.; Javidi, B. Extended depth-of-field 3D endoscopy with synthetic aperture integral imaging using an electrically tunable focal-length liquid-crystal lens. Opt. Lett. 2015, 40, 3564–3567. [Google Scholar] [CrossRef]
- Ren, H.; Fox, D.W.; Wu, B.; Wu, S.-T. Liquid crystal lens with large focal length tunability and low operating voltage. Opt. Express 2007, 15, 11328–11335. [Google Scholar] [CrossRef]
- Algorri, J.F.; Bennis, N.; Herman, J.; Kula, P.; Urruchi, V.; Sanchez-Pena, J.M. Low aberration and fast switching microlenses based on a novel liquid crystal mixture. Opt. Express 2017, 25, 14795. [Google Scholar] [CrossRef]
- Shen, Z.; Zhou, S.; Ge, S.; Duan, W.; Ma, L.; Lu, Y.; Hu, W. Liquid crystal tunable terahertz lens with spin-selected focusing property. Opt. Express 2019, 27, 8800–8807. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Tam, A.M.W.; Gan, X.T.; Shi, L.Y.; Srivastava, A.K.; Chigrinov, V.G.; Kwok, H.S.; Zhao, J. Fast switching ferroelectric liquid crystal Pancharatnam-Berry lens. Opt. Express 2019, 27, 10079–10086. [Google Scholar] [CrossRef] [PubMed]
- Xiong, J.; Chen, R.; Wu, S.-T. Device simulation of liquid crystal polarization gratings. Opt. Express 2019, 27, 18102–18112. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.-L.; Deng, H.; Li, J.-J.; He, M.-Y.; Li, D.; Wang, J. Integral imaging-based 2D/3D convertible display system by using holographic optical element and polymer dispersed liquid crystal. Opt. Lett. 2019, 44, 387–390. [Google Scholar] [CrossRef] [PubMed]
- Dou, H.; Chu, F.; Guo, Y.; Tian, L.-L.; Wang, Q.-H.; Sun, Y. Large aperture liquid crystal lens array using a composited alignment layer. Opt. Express 2018, 26, 9254–9262. [Google Scholar] [CrossRef] [PubMed]
- Georgiev, T.; Lumsdaine, A. The multifocus plenoptic camera. In Proceedings of the Digital Photography VIII, Burlingame, CA, USA, 22–26 January 2016. [Google Scholar]
- Perwass, C.; Wietzke, L. Single-lens 3D camera with extended depth-of-field. In Proceedings of the Human Vision and Electronic Imaging XVII, Burlingame, CA, USA, 22–26 January 2012. [Google Scholar]
- Algorri, J.F.; Bennis, N.; Urruchi, V.; Morawiak, P.; Sánchez-Pena, J.M.; Jaroszewicz, L.R. Tunable liquid crystal multifocal microlens array. Sci. Rep. 2017, 7, 17318. [Google Scholar] [CrossRef]
- Hassanfiroozi, A.; Huang, Y.-P.; Javidi, B.; Shieh, H.-P.D. Dual layer electrode liquid crystal lens for 2D/3D tunable endoscopy imaging system. Opt. Express 2016, 24, 8527–8538. [Google Scholar] [CrossRef]
- Georgiev, T.; Lunmsdaine, A. Depth of field in plenoptic cameras. In Proceedings of the Eurographics, Munich, Germany, 30 March–3 April 2009. [Google Scholar]
- Wu, S.-T.; Efron, U.; Hess, L.D. Birefringence measurements of liquid crystals. Appl. Opt. 1984, 23, 3911–3915. [Google Scholar] [CrossRef]
- Chou, P.-Y.; Wu, J.-Y.; Huang, S.-H.; Wang, C.-P.; Qin, Z.; Huang, C.-T.; Hsieh, P.-Y.; Lee, H.-H.; Lin, T.-H.; Huang, Y.-P. Hybrid light field head-mounted display using time-multiplexed liquid crystal lens array for resolution enhancement. Opt. Express 2019, 27, 1164–1177. [Google Scholar] [CrossRef]
- Fraval, N.; de Bougrenet de la Tocnaye, J.L. Low aberrations symmetrical adaptive modal liquid crystal lens with short focal lengths. Appl. Opt. 2010, 49, 2778–2783. [Google Scholar] [CrossRef]
- Wu, S.-T. Birefringence dispersions of liquid crystals. Phys. Rev. A 1986, 33, 1270–1274. [Google Scholar] [CrossRef] [PubMed]
- Gvozden, G.; Grgic, S.; Grgic, M. Blind image sharpness assessment based on local contrast map statistics. J. Vis. Commun. Image Represent. 2018, 50, 145–158. [Google Scholar] [CrossRef]








© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; He, W.; Wei, D.; Hu, C.; Shi, J.; Zhang, X.; Wang, H.; Xie, C. Depth-of-Field-Extended Plenoptic Camera Based on Tunable Multi-Focus Liquid-Crystal Microlens Array. Sensors 2020, 20, 4142. https://doi.org/10.3390/s20154142
Chen M, He W, Wei D, Hu C, Shi J, Zhang X, Wang H, Xie C. Depth-of-Field-Extended Plenoptic Camera Based on Tunable Multi-Focus Liquid-Crystal Microlens Array. Sensors. 2020; 20(15):4142. https://doi.org/10.3390/s20154142
Chicago/Turabian StyleChen, Mingce, Wenda He, Dong Wei, Chai Hu, Jiashuo Shi, Xinyu Zhang, Haiwei Wang, and Changsheng Xie. 2020. "Depth-of-Field-Extended Plenoptic Camera Based on Tunable Multi-Focus Liquid-Crystal Microlens Array" Sensors 20, no. 15: 4142. https://doi.org/10.3390/s20154142
APA StyleChen, M., He, W., Wei, D., Hu, C., Shi, J., Zhang, X., Wang, H., & Xie, C. (2020). Depth-of-Field-Extended Plenoptic Camera Based on Tunable Multi-Focus Liquid-Crystal Microlens Array. Sensors, 20(15), 4142. https://doi.org/10.3390/s20154142




