Microwave Photon Detectors Based on Semiconducting Double Quantum Dots
Abstract
1. Introduction
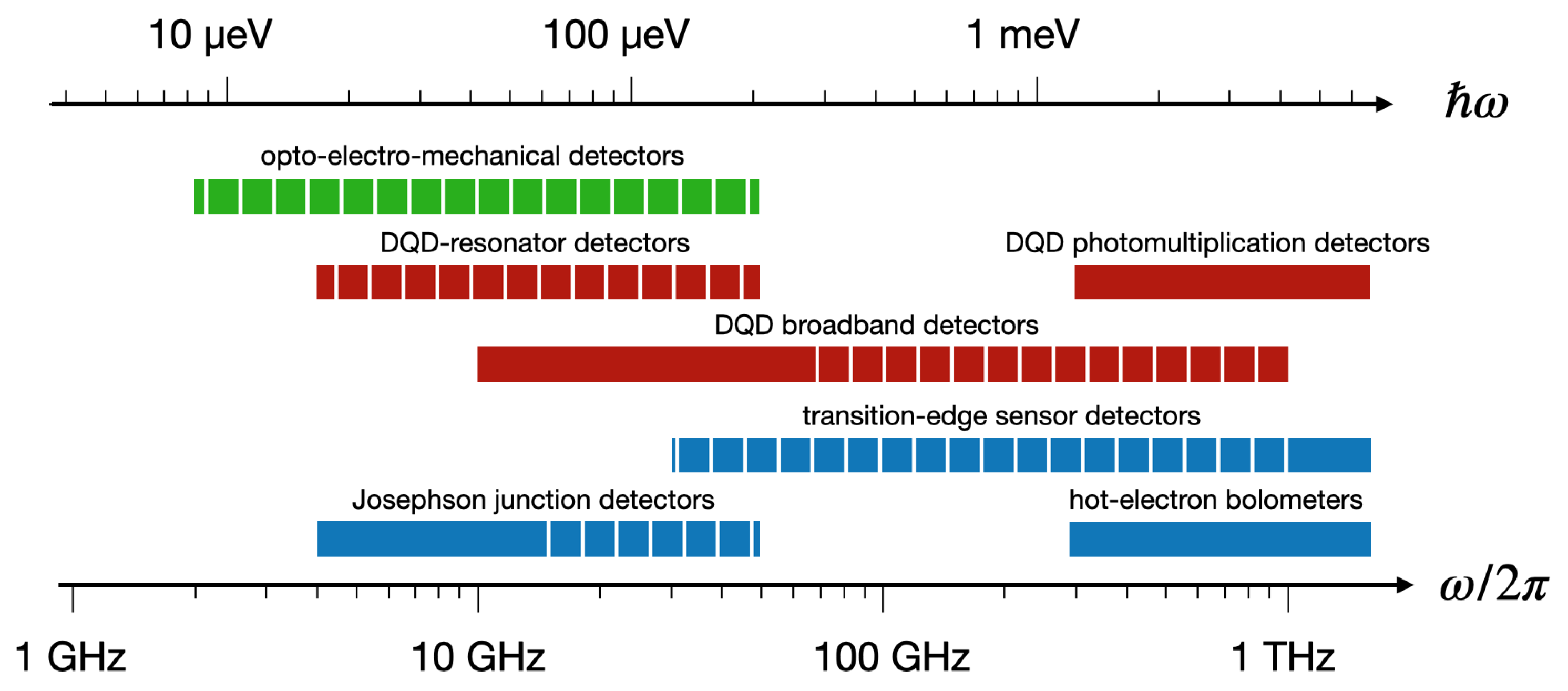
2. State of the Art
3. Detection of Sub-Millimeter Wave Photons by DQDs
4. DQD Broadband Microwave Photon Detectors
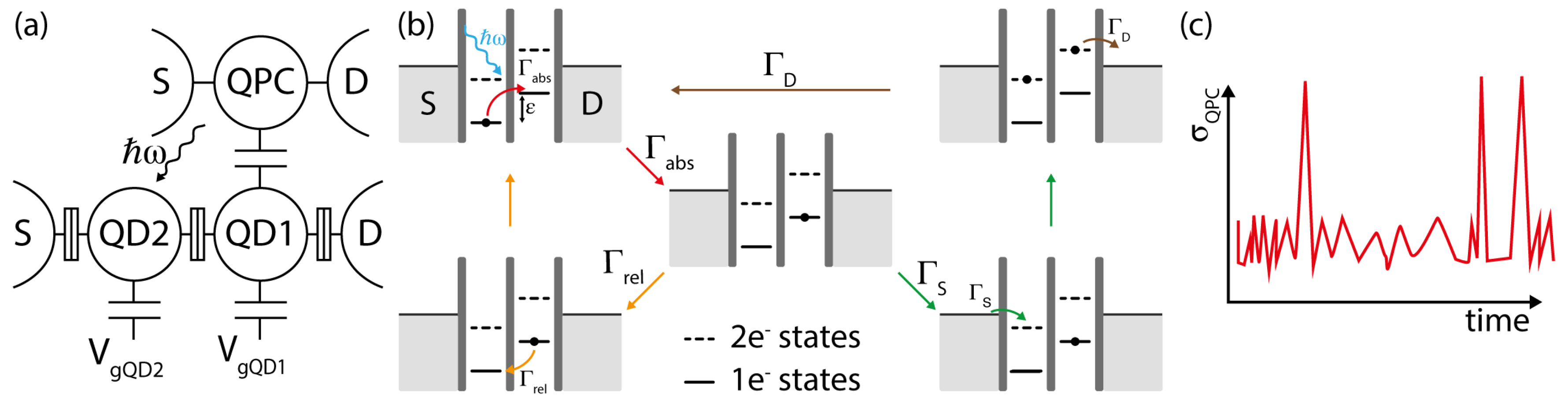
4.1. DQD Noise Detectors
4.2. Charge Sensing of DQDs
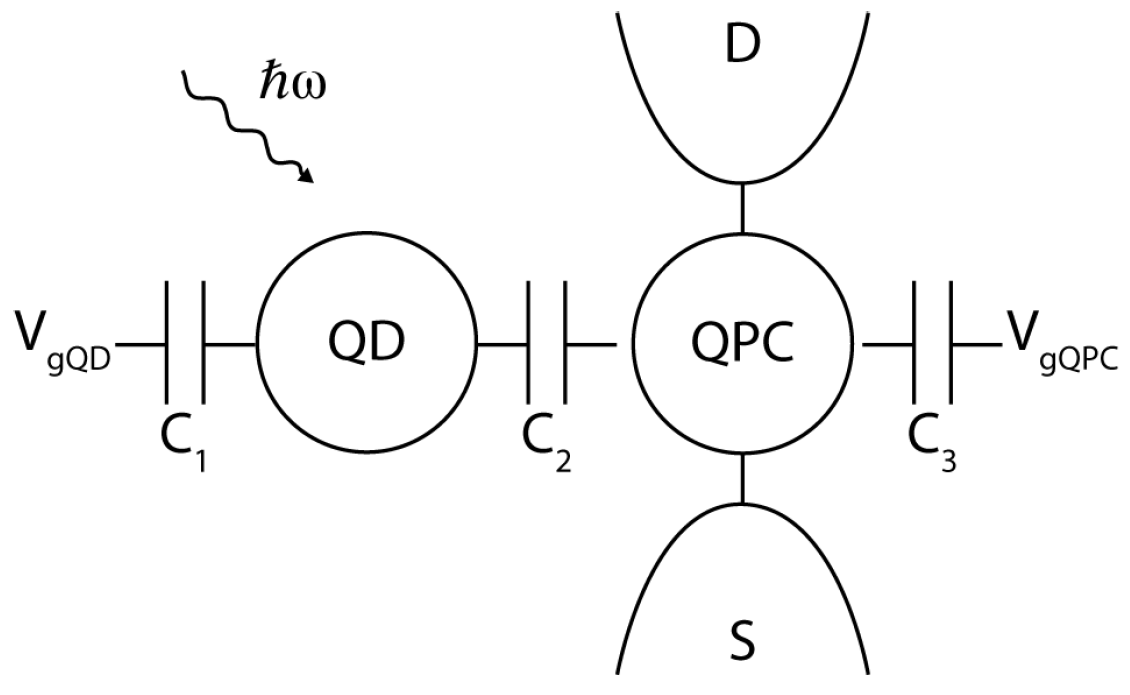
4.3. Detection of Microwave Photons by Conductivity Measurements
5. Photon Detectors Based on DQDs Coupled to a Microwave Cavity
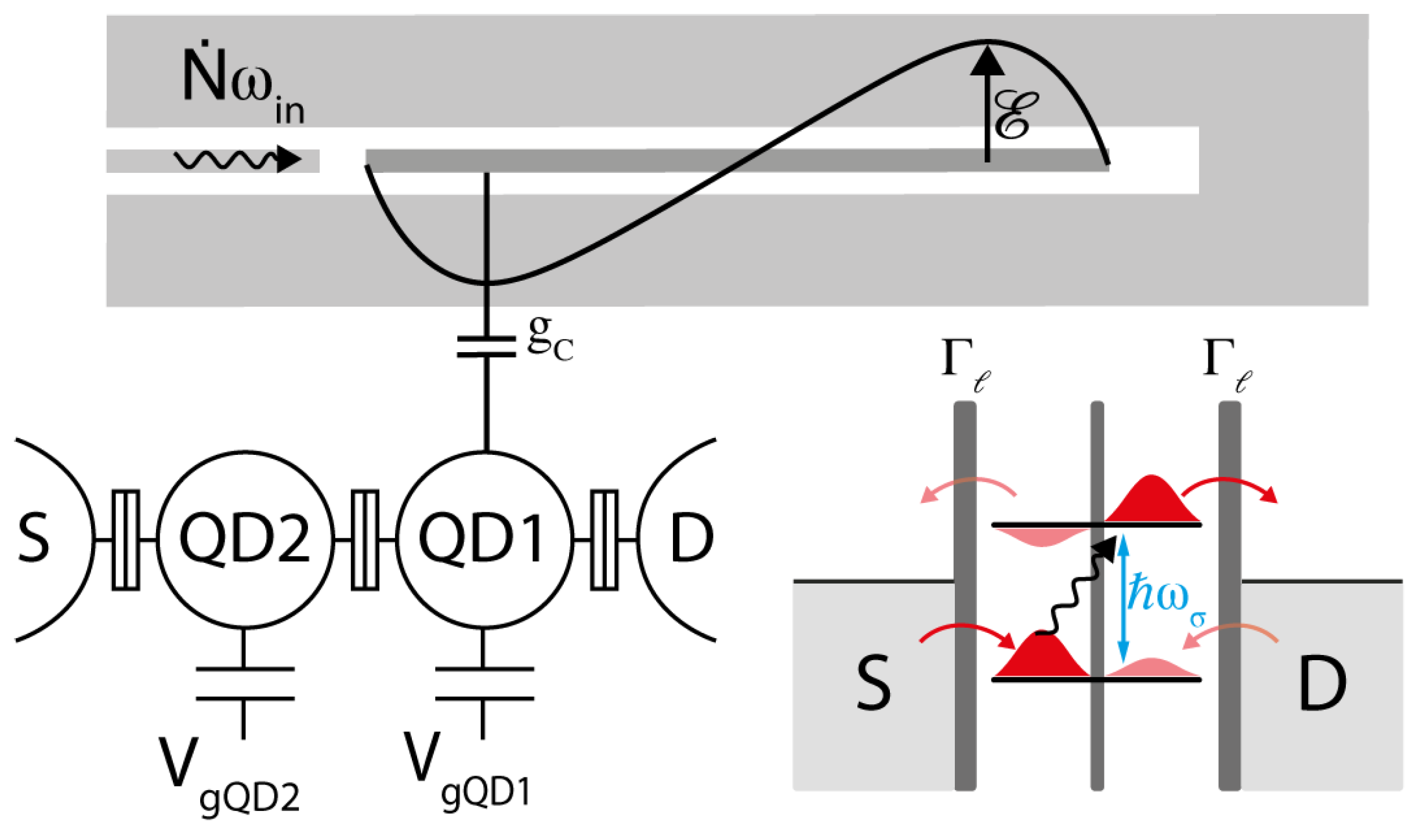
5.1. Coupling of DQD to a Single Mode Resonator
5.2. Photon Detection by DQD Coupled to a Microwave Resonator
5.3. Experimental Realization of DQD-Resonator Microwave Photon Detectors
6. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MW | Microwave |
| QD | Quantum dot |
| DQD | Double quantum dot |
| QPC | Quantum point contact |
| SET | Single electron transistor |
| cQED | Circuit quantum electrodynamics |
| dc | Direct current |
| rf | Radio frequency |
| NW | Nanowire |
| CNT | Carbon nanotube |
| Res | Resonator |
References
- Gu, X.; Kockum, A.F.; Miranowicz, A.; Liu, Y.X.; Nori, F. Microwave photonics with superconducting quantum circuits. Phys. Rep. 2017, 718–719, 1–102. [Google Scholar] [CrossRef]
- Lamoreaux, S.K.; van Bibber, K.A.; Lehnert, K.W.; Carosi, G. Analysis of single-photon and linear amplifier detectors for microwave cavity dark matter axion searches. Phys. Rev. D 2013, 88, 035020. [Google Scholar] [CrossRef]
- Brubaker, B.M.; Zhong, L.; Gurevich, Y.V.; Cahn, S.B.; Lamoreaux, S.K.; Simanovskaia, M.; Root, J.R.; Lewis, S.M.; Al Kenany, S.; Backes, K.M.; et al. First Results from a Microwave Cavity Axion Search at 24 μeV. Phys. Rev. Lett. 2017, 118, 061302. [Google Scholar] [CrossRef]
- Du, N.; Force, N.; Khatiwada, R.; Lentz, E.; Ottens, R.; Rosenberg, L.J.; Rybka, G.; Carosi, G.; Woollett, N.; Bowring, D.; et al. Search for Invisible Axion Dark Matter with the Axion Dark Matter Experiment. Phys. Rev. Lett. 2018, 120, 151301. [Google Scholar] [CrossRef] [PubMed]
- Zhong, L.; Al Kenany, S.; Backes, K.M.; Brubaker, B.M.; Cahn, S.B.; Carosi, G.; Gurevich, Y.V.; Kindel, W.F.; Lamoreaux, S.K.; Lehnert, K.W.; et al. Results from phase 1 of the HAYSTAC microwave cavity axion experiment. Phys. Rev. D 2018, 97, 092001. [Google Scholar] [CrossRef]
- Eisaman, M.D.; Fan, J.; Migdall, A.; Polyakov, S.V. Invited Review Article: Single-photon sources and detectors. Rev. Sci. Instrum. 2011, 82, 071101. [Google Scholar] [CrossRef]
- Schuster, D.I.; Houck, A.A.; Schreier, J.A.; Wallraff, A.; Gambetta, J.M.; Blais, A.; Frunzio, L.; Majer, J.; Johnson, B.; Devoret, M.H.; et al. Resolving photon number states in a superconducting circuit. Nature 2007, 445, 515–518. [Google Scholar] [CrossRef] [PubMed]
- Johnson, B.R.; Reed, M.D.; Houck, A.A.; Schuster, D.I.; Bishop, L.S.; Ginossar, E.; Gambetta, J.M.; DiCarlo, L.; Frunzio, L.; Girvin, S.M.; et al. Quantum non-demolition detection of single microwave photons in a circuit. Nat. Phys. 2010, 6, 663–667. [Google Scholar] [CrossRef]
- Chen, Y.F.; Hover, D.; Sendelbach, S.; Maurer, L.; Merkel, S.T.; Pritchett, E.J.; Wilhelm, F.K.; McDermott, R. Microwave Photon Counter Based on Josephson Junctions. Phys. Rev. Lett. 2011, 107, 217401. [Google Scholar] [CrossRef]
- Eichler, C.; Lang, C.; Fink, J.M.; Govenius, J.; Filipp, S.; Wallraff, A. Observation of Entanglement between Itinerant Microwave Photons and a Superconducting Qubit. Phys. Rev. Lett. 2012, 109, 240501. [Google Scholar] [CrossRef]
- Inomata, K.; Lin, Z.; Koshino, K.; Oliver, W.D.; Tsai, J.S.; Yamamoto, T.; Nakamura, Y. Single microwave-photon detector using an artificial Λ-type three-level system. Nat. Commun. 2016, 7, 12303. [Google Scholar] [CrossRef]
- Narla, A.; Shankar, S.; Hatridge, M.; Leghtas, Z.; Sliwa, K.M.; Zalys-Geller, E.; Mundhada, S.O.; Pfaff, W.; Frunzio, L.; Schoelkopf, R.J.; et al. Robust Concurrent Remote Entanglement Between Two Superconducting Qubits. Phys. Rev. X 2016, 6, 031036. [Google Scholar] [CrossRef]
- Kono, S.; Koshino, K.; Tabuchi, Y.; Noguchi, A.; Nakamura, Y. Quantum non-demolition detection of an itinerant microwave photon. Nat. Phys. 2018, 14, 546–549. [Google Scholar] [CrossRef]
- Besse, J.C.; Gasparinetti, S.; Collodo, M.C.; Walter, T.; Kurpiers, P.; Pechal, M.; Eichler, C.; Wallraff, A. Single-Shot Quantum Nondemolition Detection of Individual Itinerant Microwave Photons. Phys. Rev. X 2018, 8, 021003. [Google Scholar] [CrossRef]
- Romero, G.; García-Ripoll, J.J.; Solano, E. Microwave Photon Detector in Circuit QED. Phys. Rev. Lett. 2009, 102, 173602. [Google Scholar] [CrossRef] [PubMed]
- Peropadre, B.; Romero, G.; Johansson, G.; Wilson, C.M.; Solano, E.; García-Ripoll, J.J. Approaching perfect microwave photodetection in circuit QED. Phys. Rev. A 2011, 84, 063834. [Google Scholar] [CrossRef]
- Poudel, A.; McDermott, R.; Vavilov, M.G. Quantum efficiency of a microwave photon detector based on a current-biased Josephson junction. Phys. Rev. B 2012, 86, 174506. [Google Scholar] [CrossRef]
- Eichler, C.; Bozyigit, D.; Wallraff, A. Characterizing quantum microwave radiation and its entanglement with superconducting qubits using linear detectors. Phys. Rev. A 2012, 86, 032106. [Google Scholar] [CrossRef]
- Koshino, K.; Inomata, K.; Yamamoto, T.; Nakamura, Y. Implementation of an Impedance-Matched Λ System by Dressed-State Engineering. Phys. Rev. Lett. 2013, 111, 153601. [Google Scholar] [CrossRef]
- Sathyamoorthy, S.R.; Tornberg, L.; Kockum, A.F.; Baragiola, B.Q.; Combes, J.; Wilson, C.M.; Stace, T.M.; Johansson, G. Quantum Nondemolition Detection of a Propagating Microwave Photon. Phys. Rev. Lett. 2014, 112, 093601. [Google Scholar] [CrossRef]
- Koshino, K.; Inomata, K.; Lin, Z.; Nakamura, Y.; Yamamoto, T. Theory of microwave single-photon detection using an impedance-matched Λ system. Phys. Rev. A 2015, 91, 043805. [Google Scholar] [CrossRef]
- Sathyamoorthy, S.R.; Stace, T.M.; Johansson, G. Detecting itinerant single microwave photons. Quantum microwaves/Micro-ondes quantiques. C. R. Phys. 2016, 17, 756–765. [Google Scholar] [CrossRef]
- Kyriienko, O.; Sørensen, A.S. Continuous-Wave Single-Photon Transistor Based on a Superconducting Circuit. Phys. Rev. Lett. 2016, 117, 140503. [Google Scholar] [CrossRef] [PubMed]
- Grimsmo, A.L.; Royer, B.; Kreikebaum, J.M.; Ye, Y.; O’Brien, K.; Siddiqi, I.; Blais, A. Quantum metamaterial for nondestructive microwave photon counting. arXiv 2020, arXiv:quant-ph/2005.06483. [Google Scholar]
- Devoret, M.H.; Martinis, J.M. Course 12—Superconducting Qubits. In Quantum Entanglement and Information Processing; Estève, D., Raimond, J.M., Dalibard, J., Eds.; Elsevier: Les Houches, France, 2004; Volume 79, pp. 443–485. [Google Scholar] [CrossRef]
- Alesini, D.; Babusci, D.; Barone, C.; Buonomo, B.; Beretta, M.M.; Bianchini, L.; Castellano, G.; Chiarello, F.; Di Gioacchino, D.; Falferi, P.; et al. Status of the SIMP Project: Toward the Single Microwave Photon Detection. J. Low Temp. Phys. 2020, 199, 348–354. [Google Scholar] [CrossRef]
- Gleyzes, S.; Kuhr, S.; Guerlin, C.; Bernu, J.; Deléglise, S.; Busk Hoff, U.; Brune, M.; Raimond, J.M.; Haroche, S. Quantum jumps of light recording the birth and death of a photon in a cavity. Nature 2007, 446, 297–300. [Google Scholar] [CrossRef] [PubMed]
- Pepe, G.P.; Cristiano, R.; Gatti, F. Superconducting Hot Electron Bolometers and Transition Edge Sensors. In Digital Encyclopedia of Applied Physics; American Cancer Society: Atlanta, GA, USA, 2016; pp. 1–21. [Google Scholar]
- Barzanjeh, S.; De Oliveira, M.C.; Pirandola, S. Microwave Photodetection with Electro-Opto-Mechanical Systems. arXiv 2014, arXiv:1410.4024. [Google Scholar]
- Barzanjeh, S.; Guha, S.; Weedbrook, C.; Vitali, D.; Shapiro, J.H.; Pirandola, S. Microwave Quantum Illumination. Phys. Rev. Lett. 2015, 114, 080503. [Google Scholar] [CrossRef]
- Zhang, K.; Bariani, F.; Dong, Y.; Zhang, W.; Meystre, P. Proposal for an Optomechanical Microwave Sensor at the Subphoton Level. Phys. Rev. Lett. 2015, 114, 113601. [Google Scholar] [CrossRef]
- Komiyama, S. Single-Photon Detectors in the Terahertz Range. IEEE J. Sel. Top. Quantum Electron. 2011, 17, 54–66. [Google Scholar] [CrossRef]
- Komiyama, S.; Astafiev, O.; Antonov, V.; Kutsuwa, T.; Hirai, H. A single-photon detector in the far-infrared range. Nature 2000, 403, 405–407. [Google Scholar] [CrossRef] [PubMed]
- Astafiev, O.; Komiyama, S.; Kutsuwa, T.; Antonov, V.; Kawaguchi, Y.; Hirakawa, K. Single-photon detector in the microwave range. Appl. Phys. Lett. 2002, 80, 4250–4252. [Google Scholar] [CrossRef]
- Kouwenhoven, L.P.; Jauhar, S.; Orenstein, J.; McEuen, P.L.; Nagamune, Y.; Motohisa, J.; Sakaki, H. Observation of Photon-Assisted Tunneling through a Quantum Dot. Phys. Rev. Lett. 1994, 73, 3443–3446. [Google Scholar] [CrossRef] [PubMed]
- Blick, R.H.; Haug, R.J.; van der Weide, D.W.; von Klitzing, K.; Eberl, K. Photon-assisted tunneling through a quantum dot at high microwave frequencies. Appl. Phys. Lett. 1995, 67, 3924–3926. [Google Scholar] [CrossRef]
- van der Wiel, W.G.; De Franceschi, S.; Elzerman, J.M.; Fujisawa, T.; Tarucha, S.; Kouwenhoven, L.P. Electron transport through double quantum dots. Rev. Mod. Phys. 2002, 75, 1–22. [Google Scholar] [CrossRef]
- Elzerman, J.M.; Hanson, R.; Greidanus, J.S.; Willems van Beveren, L.H.; De Franceschi, S.; Vandersypen, L.M.K.; Tarucha, S.; Kouwenhoven, L.P. Few-electron quantum dot circuit with integrated charge read out. Phys. Rev. B 2003, 67, 161308. [Google Scholar] [CrossRef]
- Aguado, R.; Kouwenhoven, L.P. Double Quantum Dots as Detectors of High-Frequency Quantum Noise in Mesoscopic Conductors. Phys. Rev. Lett. 2000, 84, 1986–1989. [Google Scholar] [CrossRef]
- Onac, E.; Balestro, F.; van Beveren, L.H.W.; Hartmann, U.; Nazarov, Y.V.; Kouwenhoven, L.P. Using a Quantum Dot as a High-Frequency Shot Noise Detector. Phys. Rev. Lett. 2006, 96, 176601. [Google Scholar] [CrossRef]
- Fujisawa, T.; Hayashi, T.; Tomita, R.; Hirayama, Y. Bidirectional Counting of Single Electrons. Science 2006, 312, 1634–1636. [Google Scholar] [CrossRef]
- Gustavsson, S.; Studer, M.; Leturcq, R.; Ihn, T.; Ensslin, K.; Driscoll, D.C.; Gossard, A.C. Frequency-Selective Single-Photon Detection Using a Double Quantum Dot. Phys. Rev. Lett. 2007, 99, 206804. [Google Scholar] [CrossRef]
- Leturcq, R.; Gustavsson, S.; Studer, M.; Ihn, T.; Ensslin, K.; Driscoll, D.; Gossard, A. Frequency-selective single-photon detection with a double quantum dot. Phys. E Low Dimens. Syst. Nanostruct. 2008, 40, 1844–1847. [Google Scholar] [CrossRef]
- Field, M.; Smith, C.G.; Pepper, M.; Ritchie, D.A.; Frost, J.E.F.; Jones, G.A.C.; Hasko, D.G. Measurements of Coulomb blockade with a noninvasive voltage probe. Phys. Rev. Lett. 1993, 70, 1311–1314. [Google Scholar] [CrossRef] [PubMed]
- Wallin, D.; Fuhrer, A.; Fröberg, L.E.; Samuelson, L.; Xu, H.Q.; Hofling, S.; Forchel, A. Detection of charge states in nanowire quantum dots using a quantum point contact. Appl. Phys. Lett. 2007, 90, 172112. [Google Scholar] [CrossRef]
- Higginbotham, A.P.; Larsen, T.W.; Yao, J.; Yan, H.; Lieber, C.M.; Marcus, C.M.; Kuemmeth, F. Hole Spin Coherence in a Ge/Si Heterostructure Nanowire. Nano Lett. 2014, 14, 3582–3586. [Google Scholar] [CrossRef][Green Version]
- Schoelkopf, R.J.; Wahlgren, P.; Kozhevnikov, A.A.; Delsing, P.; Prober, D.E. The Radio-Frequency Single-Electron Transistor (RF-SET): A Fast and Ultrasensitive Electrometer. Science 1998, 280, 1238–1242. [Google Scholar] [CrossRef]
- Lu, W.; Ji, Z.; Pfeiffer, L.; West, K.W.; Rimberg, A.J. Real-time detection of electron tunnelling in a quantum dot. Nature 2003, 423, 422–425. [Google Scholar] [CrossRef]
- Cassidy, M.C.; Dzurak, A.S.; Clark, R.G.; Petersson, K.D.; Farrer, I.; Ritchie, D.A.; Smith, C.G. Single shot charge detection using a radio-frequency quantum point contact. Appl. Phys. Lett. 2007, 91, 222104. [Google Scholar] [CrossRef]
- Reilly, D.J.; Marcus, C.M.; Hanson, M.P.; Gossard, A.C. Fast single-charge sensing with a rf quantum point contact. Appl. Phys. Lett. 2007, 91, 162101. [Google Scholar] [CrossRef]
- Müller, T.; Küng, B.; Hellmüller, S.; Studerus, P.; Ensslin, K.; Ihn, T.; Reinwald, M.; Wegscheider, W. An in situ tunable radio-frequency quantum point contact. Appl. Phys. Lett. 2010, 97, 202104. [Google Scholar] [CrossRef]
- Ibberson, D.J.; Ibberson, L.A.; Smithson, G.; Haigh, J.A.; Barraud, S.; Gonzalez-Zalba, M.F. Low-temperature tunable radio-frequency resonator for sensitive dispersive readout of nanoelectronic devices. Appl. Phys. Lett. 2019, 114, 123501. [Google Scholar] [CrossRef]
- Barthel, C.; Kjærgaard, M.; Medford, J.; Stopa, M.; Marcus, C.M.; Hanson, M.P.; Gossard, A.C. Fast sensing of double-dot charge arrangement and spin state with a radio-frequency sensor quantum dot. Phys. Rev. B 2010, 81, 161308. [Google Scholar] [CrossRef]
- Jung, M.; Schroer, M.D.; Petersson, K.D.; Petta, J.R. Radio frequency charge sensing in InAs nanowire double quantum dots. Appl. Phys. Lett. 2012, 100, 253508. [Google Scholar] [CrossRef]
- Schroer, M.D.; Jung, M.; Petersson, K.D.; Petta, J.R. Radio Frequency Charge Parity Meter. Phys. Rev. Lett. 2012, 109, 166804. [Google Scholar] [CrossRef] [PubMed]
- Sabonis, D.; O’Farrell, E.C.T.; Razmadze, D.; van Zanten, D.M.T.; Suter, J.; Krogstrup, P.; Marcus, C.M. Dispersive sensing in hybrid InAs/Al nanowires. Appl. Phys. Lett. 2019, 115, 102601. [Google Scholar] [CrossRef]
- Ares, N.; Schupp, F.J.; Mavalankar, A.; Rogers, G.; Griffiths, J.; Jones, G.A.C.; Farrer, I.; Ritchie, D.A.; Smith, C.G.; Cottet, A.; et al. Sensitive Radio-Frequency Measurements of a Quantum Dot by Tuning to Perfect Impedance Matching. Phys. Rev. Appl. 2016, 5, 034011. [Google Scholar] [CrossRef]
- Noiri, A.; Takeda, K.; Yoneda, J.; Nakajima, T.; Kodera, T.; Tarucha, S. Radio-Frequency-Detected Fast Charge Sensing in Undoped Silicon Quantum Dots. Nano Lett. 2020, 20, 947–952. [Google Scholar] [CrossRef]
- Duty, T.; Johansson, G.; Bladh, K.; Gunnarsson, D.; Wilson, C.; Delsing, P. Observation of Quantum Capacitance in the Cooper-Pair Transistor. Phys. Rev. Lett. 2005, 95, 206807. [Google Scholar] [CrossRef]
- Ranjan, V.; Puebla-Hellmann, G.; Jung, M.; Hasler, T.; Nunnenkamp, A.; Muoth, M.; Hierold, C.; Wallraff, A.; Schönenberger, C. Clean carbon nanotubes coupled to superconducting impedance-matching circuits. Nat. Commun. 2015, 6, 7165. [Google Scholar] [CrossRef]
- Ahmed, I.; Haigh, J.A.; Schaal, S.; Barraud, S.; Zhu, Y.; Lee, C.M.; Amado, M.; Robinson, J.W.A.; Rossi, A.; Morton, J.J.L.; et al. Radio-Frequency Capacitive Gate-Based Sensing. Phys. Rev. Appl. 2018, 10, 014018. [Google Scholar] [CrossRef]
- de Jong, D.; van Veen, J.; Binci, L.; Singh, A.; Krogstrup, P.; Kouwenhoven, L.P.; Pfaff, W.; Watson, J.D. Rapid Detection of Coherent Tunneling in an InAs Nanowire Quantum Dot through Dispersive Gate Sensing. Phys. Rev. Appl. 2019, 11, 044061. [Google Scholar] [CrossRef]
- Mizuta, R.; Otxoa, R.M.; Betz, A.C.; Gonzalez-Zalba, M.F. Quantum and tunneling capacitance in charge and spin qubits. Phys. Rev. B 2017, 95. [Google Scholar] [CrossRef]
- West, A.; Hensen, B.; Jouan, A.; Tanttu, T.; Yang, C.H.; Rossi, A.; Gonzalez-Zalba, M.F.; Hudson, F.; Morello, A.; Reilly, D.J.; et al. Gate-based single-shot readout of spins in silicon. Nat. Nanotechnol. 2019, 14, 437–441. [Google Scholar] [CrossRef] [PubMed]
- Petersson, K.D.; McFaul, L.W.; Schroer, M.D.; Jung, M.; Taylor, J.M.; Houck, A.A.; Petta, J.R. Circuit quantum electrodynamics with a spin qubit. Nature 2012, 490, 380–383. [Google Scholar] [CrossRef] [PubMed]
- Frey, T.; Leek, P.J.; Beck, M.; Blais, A.; Ihn, T.; Ensslin, K.; Wallraff, A. Dipole Coupling of a Double Quantum Dot to a Microwave Resonator. Phys. Rev. Lett. 2012, 108, 046807. [Google Scholar] [CrossRef] [PubMed]
- Scarlino, P.; van Woerkom, D.J.; Stockklauser, A.; Koski, J.V.; Collodo, M.C.; Gasparinetti, S.; Reichl, C.; Wegscheider, W.; Ihn, T.; Ensslin, K.; et al. All-Microwave Control and Dispersive Readout of Gate-Defined Quantum Dot Qubits in Circuit Quantum Electrodynamics. Phys. Rev. Lett. 2019, 122, 206802. [Google Scholar] [CrossRef] [PubMed]
- Mi, X.; Benito, M.; Putz, S.; Zajac, D.M.; Taylor, J.M.; Burkard, G.; Petta, J.R. A coherent spin-photon interface in silicon. Nature 2018, 555, 599. [Google Scholar] [CrossRef]
- Landig, A.J.; Koski, J.V.; Scarlino, P.; Mendes, U.C.; Blais, A.; Reichl, C.; Wegscheider, W.; Wallraff, A.; Ensslin, K.; Ihn, T. Coherent spin-photon coupling using a resonant exchange qubit. Nature 2018, 560, 179–184. [Google Scholar] [CrossRef]
- Pfund, A.; Shorubalko, I.; Leturcq, R.; Ensslin, K. Top-gate defined double quantum dots in InAs nanowires. Appl. Phys. Lett. 2006, 89, 252106. [Google Scholar] [CrossRef]
- Rossella, F.; Bertoni, A.; Ercolani, D.; Rontani, M.; Sorba, L.; Beltram, F.; Roddaro, S. Nanoscale spin rectifiers controlled by the Stark effect. Nat. Nanotechnol. 2014, 9, 997–1001. [Google Scholar] [CrossRef]
- Nilsson, M.; Chen, I.J.; Lehmann, S.; Maulerova, V.; Dick, K.A.; Thelander, C. Parallel-Coupled Quantum Dots in InAs Nanowires. Nano Lett. 2017, 17, 7847–7852. [Google Scholar] [CrossRef]
- Cornia, S.; Rossella, F.; Demontis, V.; Zannier, V.; Beltram, F.; Sorba, L.; Affronte, M.; Ghirri, A. Microwave-Assisted Tunneling in Hard-Wall InAs/InP Nanowire Quantum Dots. Sci. Rep. 2019, 9, 19523. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Payette, C.; Dovzhenko, Y.; Deelman, P.W.; Petta, J.R. Charge Relaxation in a Single-Electron Si/SiGe Double Quantum Dot. Phys. Rev. Lett. 2013, 111, 046801. [Google Scholar] [CrossRef] [PubMed]
- Fujisawa, T.; Oosterkamp, T.H.; van der Wiel, W.G.; Broer, B.W.; Aguado, R.; Tarucha, S.; Kouwenhoven, L.P. Spontaneous Emission Spectrum in Double Quantum Dot Devices. Science 1998, 282, 932–935. [Google Scholar] [CrossRef] [PubMed]
- Weber, C.; Fuhrer, A.; Fasth, C.; Lindwall, G.; Samuelson, L.; Wacker, A. Probing Confined Phonon Modes by Transport through a Nanowire Double Quantum Dot. Phys. Rev. Lett. 2010, 104, 036801. [Google Scholar] [CrossRef]
- Roulleau, P.; Baer, S.; Choi, T.; Molitor, F.; Güttinger, J.; Müller, T.; Dröscher, S.; Ensslin, K.; Ihn, T. Coherent electron-phonon coupling in tailored quantum systems. Nat. Commun. 2011, 2, 239. [Google Scholar] [CrossRef][Green Version]
- Burkard, G.; Gullans, M.J.; Mi, X.; Petta, J.R. Superconductor—Semiconductor hybrid-circuit quantum electrodynamics. Nat. Rev. Phys. 2020, 2, 129–140. [Google Scholar] [CrossRef]
- Wallraff, A.; Schuster, D.I.; Blais, A.; Frunzio, L.; Huang, R.S.; Majer, J.; Kumar, S.; Girvin, S.M.; Schoelkopf, R.J. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 2004, 431, 162–167. [Google Scholar] [CrossRef]
- Megrant, A.; Neill, C.; Barends, R.; Chiaro, B.; Chen, Y.; Feigl, L.; Kelly, J.; Lucero, E.; Mariantoni, M.; O’Malley, P.J.J.; et al. Planar superconducting resonators with internal quality factors above one million. Appl. Phys. Lett. 2012, 100, 113510. [Google Scholar] [CrossRef]
- Quintana, C.M.; Megrant, A.; Chen, Z.; Dunsworth, A.; Chiaro, B.; Barends, R.; Campbell, B.; Chen, Y.; Hoi, I.C.; Jeffrey, E.; et al. Characterization and reduction of microfabrication-induced decoherence in superconducting quantum circuits. Appl. Phys. Lett. 2014, 105, 062601. [Google Scholar] [CrossRef]
- Göppl, M.; Fragner, A.; Baur, M.; Bianchetti, R.; Filipp, S.; Fink, J.M.; Leek, P.J.; Puebla, G.; Steffen, L.; Wallraff, A. Coplanar waveguide resonators for circuit quantum electrodynamics. J. Appl. Phys. 2008, 104, 113904. [Google Scholar] [CrossRef]
- Childress, L.; Sørensen, A.S.; Lukin, M.D. Mesoscopic cavity quantum electrodynamics with quantum dots. Phys. Rev. A 2004, 69, 042302. [Google Scholar] [CrossRef]
- Mi, X.; Cady, J.V.; Zajac, D.M.; Stehlik, J.; Edge, L.F.; Petta, J.R. Circuit quantum electrodynamics architecture for gate-defined quantum dots in silicon. Appl. Phys. Lett. 2017, 110, 043502. [Google Scholar] [CrossRef]
- Stockklauser, A.; Scarlino, P.; Koski, J.V.; Gasparinetti, S.; Andersen, C.K.; Reichl, C.; Wegscheider, W.; Ihn, T.; Ensslin, K.; Wallraff, A. Strong Coupling Cavity QED with Gate-Defined Double Quantum Dots Enabled by a High Impedance Resonator. Phys. Rev. X 2017, 7, 011030. [Google Scholar] [CrossRef]
- Samkharadze, N.; Zheng, G.; Kalhor, N.; Brousse, D.; Sammak, A.; Mendes, U.C.; Blais, A.; Scappucci, G.; Vandersypen, L.M.K. Strong spin-photon coupling in silicon. Science 2018, 359, 1123–1127. [Google Scholar] [CrossRef] [PubMed]
- Samkharadze, N.; Bruno, A.; Scarlino, P.; Zheng, G.; DiVincenzo, D.P.; DiCarlo, L.; Vandersypen, L.M.K. High-Kinetic-Inductance Superconducting Nanowire Resonators for Circuit QED in a Magnetic Field. Phys. Rev. Appl. 2016, 5, 044004. [Google Scholar] [CrossRef]
- Trif, M.; Golovach, V.N.; Loss, D. Spin dynamics in InAs nanowire quantum dots coupled to a transmission line. Phys. Rev. B 2008, 77, 045434. [Google Scholar] [CrossRef]
- Nadj-Perge, S.; Frolov, S.M.; Bakkers, E.P.A.M.; Kouwenhoven, L.P. Spin-orbit qubit in a semiconductor nanowire. Nature 2010, 468, 1084. [Google Scholar] [CrossRef]
- Tokura, Y.; van der Wiel, W.G.; Obata, T.; Tarucha, S. Coherent Single Electron Spin Control in a Slanting Zeeman Field. Phys. Rev. Lett. 2006, 96, 047202. [Google Scholar] [CrossRef]
- Viennot, J.J.; Dartiailh, M.C.; Cottet, A.; Kontos, T. Coherent coupling of a single spin to microwave cavity photons. Science 2015, 349, 408–411. [Google Scholar] [CrossRef]
- Mi, X.; Cady, J.V.; Zajac, D.M.; Deelman, P.W.; Petta, J.R. Strong coupling of a single electron in silicon to a microwave photon. Science 2017, 355, 156–158. [Google Scholar] [CrossRef]
- Viennot, J.J.; Delbecq, M.R.; Dartiailh, M.C.; Cottet, A.; Kontos, T. Out-of-equilibrium charge dynamics in a hybrid circuit quantum electrodynamics architecture. Phys. Rev. B 2014, 89, 165404. [Google Scholar] [CrossRef]
- Deng, G.W.; Wei, D.; Johansson, J.R.; Zhang, M.L.; Li, S.X.; Li, H.O.; Cao, G.; Xiao, M.; Tu, T.; Guo, G.C.; et al. Charge Number Dependence of the Dephasing Rates of a Graphene Double Quantum Dot in a Circuit QED Architecture. Phys. Rev. Lett. 2015, 115, 126804. [Google Scholar] [CrossRef]
- Stockklauser, A.; Maisi, V.F.; Basset, J.; Cujia, K.; Reichl, C.; Wegscheider, W.; Ihn, T.; Wallraff, A.; Ensslin, K. Microwave Emission from Hybridized States in a Semiconductor Charge Qubit. Phys. Rev. Lett. 2015, 115, 046802. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Deacon, R.S.; Car, D.; Bakkers, E.P.A.M.; Ishibashi, K. InSb nanowire double quantum dots coupled to a superconducting microwave cavity. Appl. Phys. Lett. 2016, 108, 203502. [Google Scholar] [CrossRef]
- Hanson, R.; Kouwenhoven, L.P.; Petta, J.R.; Tarucha, S.; Vandersypen, L.M.K. Spins in few-electron quantum dots. Rev. Mod. Phys. 2007, 79, 1217–1265. [Google Scholar] [CrossRef]
- Hayashi, T.; Fujisawa, T.; Cheong, H.D.; Jeong, Y.H.; Hirayama, Y. Coherent Manipulation of Electronic States in a Double Quantum Dot. Phys. Rev. Lett. 2003, 91, 226804. [Google Scholar] [CrossRef] [PubMed]
- Petersson, K.D.; Petta, J.R.; Lu, H.; Gossard, A.C. Quantum Coherence in a One-Electron Semiconductor Charge Qubit. Phys. Rev. Lett. 2010, 105, 246804. [Google Scholar] [CrossRef]
- Paladino, E.; Galperin, Y.M.; Falci, G.; Altshuler, B.L. 1/f noise: Implications for solid-state quantum information. Rev. Mod. Phys. 2014, 86, 361–418. [Google Scholar] [CrossRef]
- You, J.Q.; Hu, X.; Nori, F. Correlation-induced suppression of decoherence in capacitively coupled Cooper-pair boxes. Phys. Rev. B 2005, 72, 144529. [Google Scholar] [CrossRef]
- Wong, C.H.; Vavilov, M.G. Quantum efficiency of a single microwave photon detector based on a semiconductor double quantum dot. Phys. Rev. A 2017, 95, 012325. [Google Scholar] [CrossRef]
- Schöndorf, M.; Govia, L.C.G.; Vavilov, M.G.; McDermott, R.; Wilhelm, F.K. Optimizing microwave photodetection: Input–output theory. Quantum Sci. Technol. 2018, 3, 024009. [Google Scholar] [CrossRef]
- Rausch, D.S.; Thiemann, M.; Dressel, M.; Bothner, D.; Koelle, D.; Kleiner, R.; Scheffler, M. Superconducting coplanar microwave resonators with operating frequencies up to 50 GHz. J. Phys. Appl. Phys. 2018, 51, 465301. [Google Scholar] [CrossRef]
- Wolff, I. Coplanar Waveguide Discontinuities. In Coplanar Microwave Integrated Circuits; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006; Chapter 3; pp. 145–248. [Google Scholar] [CrossRef]
- Hettak, K.; Dib, N.; Sheta, A.; Toutain, S. A class of novel uniplanar series resonators and their implementation in original applications. IEEE Trans. Microw. Theory Tech. 1998, 46, 1270–1276. [Google Scholar] [CrossRef]
- Wei, Y.M.; Guo, X.G.; Chen, L.; Zhu, Y.M. A novel coplanar waveguide resonator on flexible substrate. Optik 2016, 127, 9937–9941. [Google Scholar] [CrossRef]
- Paik, H.; Schuster, D.I.; Bishop, L.S.; Kirchmair, G.; Catelani, G.; Sears, A.P.; Johnson, B.R.; Reagor, M.J.; Frunzio, L.; Glazman, L.I.; et al. Observation of High Coherence in Josephson Junction Qubits Measured in a Three-Dimensional Circuit QED Architecture. Phys. Rev. Lett. 2011, 107, 240501. [Google Scholar] [CrossRef] [PubMed]
- Reagor, M.; Paik, H.; Catelani, G.; Sun, L.; Axline, C.; Holland, E.; Pop, I.M.; Masluk, N.A.; Brecht, T.; Frunzio, L.; et al. Reaching 10 ms single photon lifetimes for superconducting aluminum cavities. Appl. Phys. Lett. 2013, 102, 192604. [Google Scholar] [CrossRef]
- Romanenko, A.; Pilipenko, R.; Zorzetti, S.; Frolov, D.; Awida, M.; Belomestnykh, S.; Posen, S.; Grassellino, A. Three-Dimensional Superconducting Resonators at T < 20 mK with Photon Lifetimes up to τ = 2 s. Phys. Rev. Appl. 2020, 13, 034032. [Google Scholar]
- Kudra, M.; Biznárová, J.; Roudsari, F.; Burnett, J.J.; Niepce, D.; Gasparinetti, S.; Wickman, B.; Delsing, P. High Quality 3-Dimensional Aluminum Microwave Cavities. arXiv 2020, arXiv:physics.app-ph/2006.02213. [Google Scholar]
- Suleymanzade, A.; Anferov, A.; Stone, M.; Naik, R.K.; Oriani, A.; Simon, J.; Schuster, D. A tunable high-Q millimeter wave cavity for hybrid circuit and cavity QED experiments. Appl. Phys. Lett. 2020, 116, 104001. [Google Scholar] [CrossRef]
- Kong, W.C.; Deng, G.W.; Li, S.X.; Li, H.O.; Cao, G.; Xiao, M.; Guo, G.P. Introduction of DC line structures into a superconducting microwave 3D cavity. Rev. Sci. Instrum. 2015, 86, 023108. [Google Scholar] [CrossRef]
- Cohen, M.A.; Yuan, M.; de Jong, B.W.A.; Beukers, E.; Bosman, S.J.; Steele, G.A. A split-cavity design for the incorporation of a DC bias in a 3D microwave cavity. Appl. Phys. Lett. 2017, 110, 172601. [Google Scholar] [CrossRef]
- Stammeier, M.; Garcia, S.; Wallraff, A. Applying electric and magnetic field bias in a 3D superconducting waveguide cavity with high quality factor. Quantum Sci. Technol. 2018, 3, 045007. [Google Scholar] [CrossRef]

| DQD | Res. | (GHz) | (GHz) | (MHz) | (MHz) | (MHz) | (MHz) | Ref. | |
|---|---|---|---|---|---|---|---|---|---|
| GaAs | Al | 6.755 | 2630 | 9 | 50 | 900 | - | - | [66] |
| InAs NW | Nb | 6.2 | 2000 | 1.8–7 | 30 | 5100 | - | - | [65] |
| CNT | Al | 6.72 | 3500 | 5.5 | 3.3 | 550 | - | - | [93] |
| Graphene | Al | 6.23896 | 3100 | 6.4 | 6 | 400 | - | - | [94] |
| CNT | Nb | 6.75 | 9650 | - | - | - | 1.3 | 2.5 | [91] |
| GaAs | Al | 6.852 | 2058 | 7.4 | 11 | 250 | - | - | [95] |
| InSb NW | Nb | 6.0749 | 8000 | 7 | 14 | 1000–4000 | - | - | [96] |
| Si | Nb | 7.684 | 7460 | 7.68 | 6.7 | 2.6 | - | - | [92] |
| GaAs | SQUID | 5.03 | 401 | 4.13 | 119 | 20 | - | - | [85] |
| Si | Nb | 5.846 | 4700 | 4.9, 7.4 | 40 | 35 | 5.3 | 2.4 | [68] |
| Si | NbTiN | 6.051 | 1120 | 12.6 | 200 | 52 | 13 | 2.5 | [86] |
| GaAs | SQUID | 5.07 | 169 | 3.3 | 57 | 3.3 | - | - | [67] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghirri, A.; Cornia, S.; Affronte, M. Microwave Photon Detectors Based on Semiconducting Double Quantum Dots. Sensors 2020, 20, 4010. https://doi.org/10.3390/s20144010
Ghirri A, Cornia S, Affronte M. Microwave Photon Detectors Based on Semiconducting Double Quantum Dots. Sensors. 2020; 20(14):4010. https://doi.org/10.3390/s20144010
Chicago/Turabian StyleGhirri, Alberto, Samuele Cornia, and Marco Affronte. 2020. "Microwave Photon Detectors Based on Semiconducting Double Quantum Dots" Sensors 20, no. 14: 4010. https://doi.org/10.3390/s20144010
APA StyleGhirri, A., Cornia, S., & Affronte, M. (2020). Microwave Photon Detectors Based on Semiconducting Double Quantum Dots. Sensors, 20(14), 4010. https://doi.org/10.3390/s20144010





