Validation of a Wireless Bluetooth Photoplethysmography Sensor Used on the Earlobe for Monitoring Heart Rate Variability Features during a Stress-Inducing Mental Task in Healthy Individuals
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Software and Scripts Development
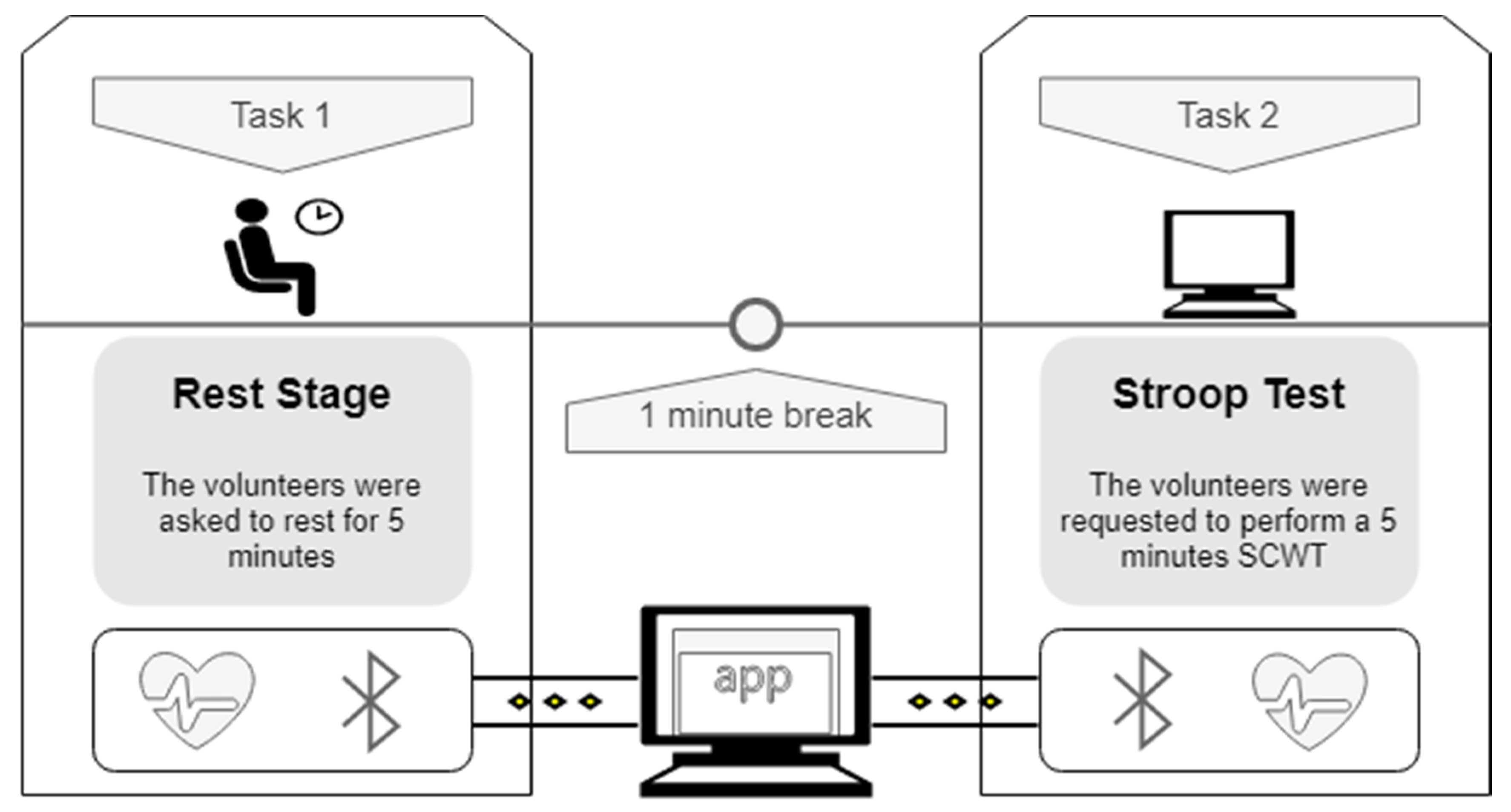
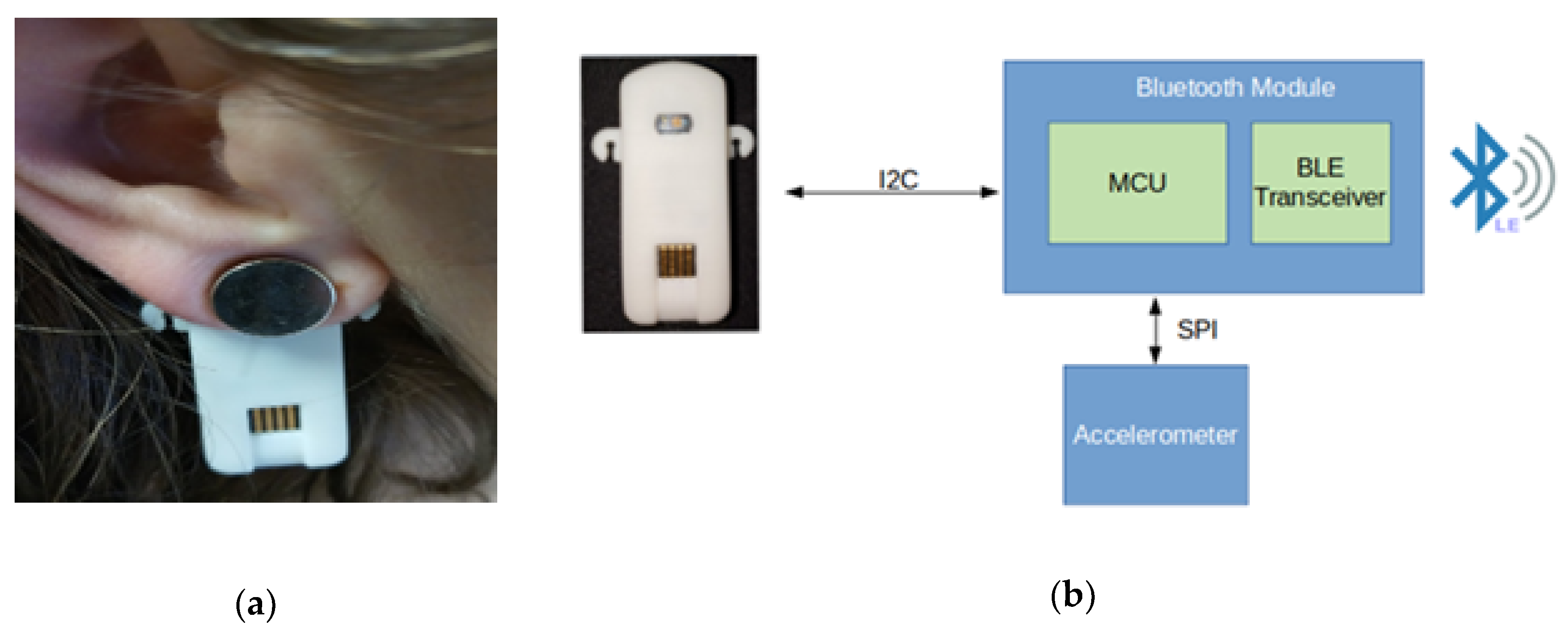
2.3. Experimental Setup and Data Acquisition
2.4. Data Processing
2.4.1. Intervals Synchronization
2.4.2. Artifacts Correction
2.4.3. HRV Features Calculations
2.5. Data and Statistical Analysis
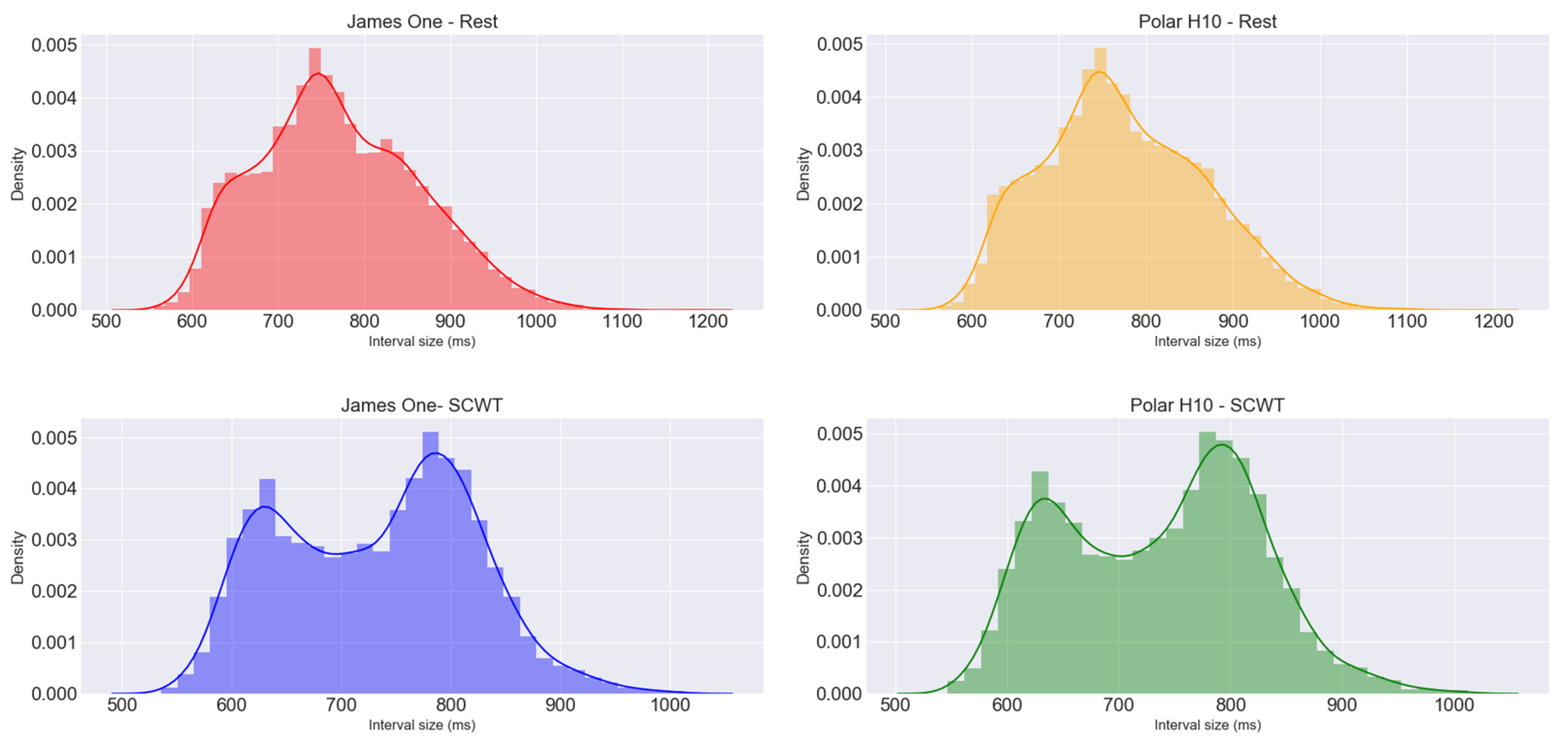
2.5.1. Interbeat Intervals Description
2.5.2. Determination of the Agreement between HRV Features
2.5.3. Comparison of HRV Metrics during Rest and SCWT
3. Results
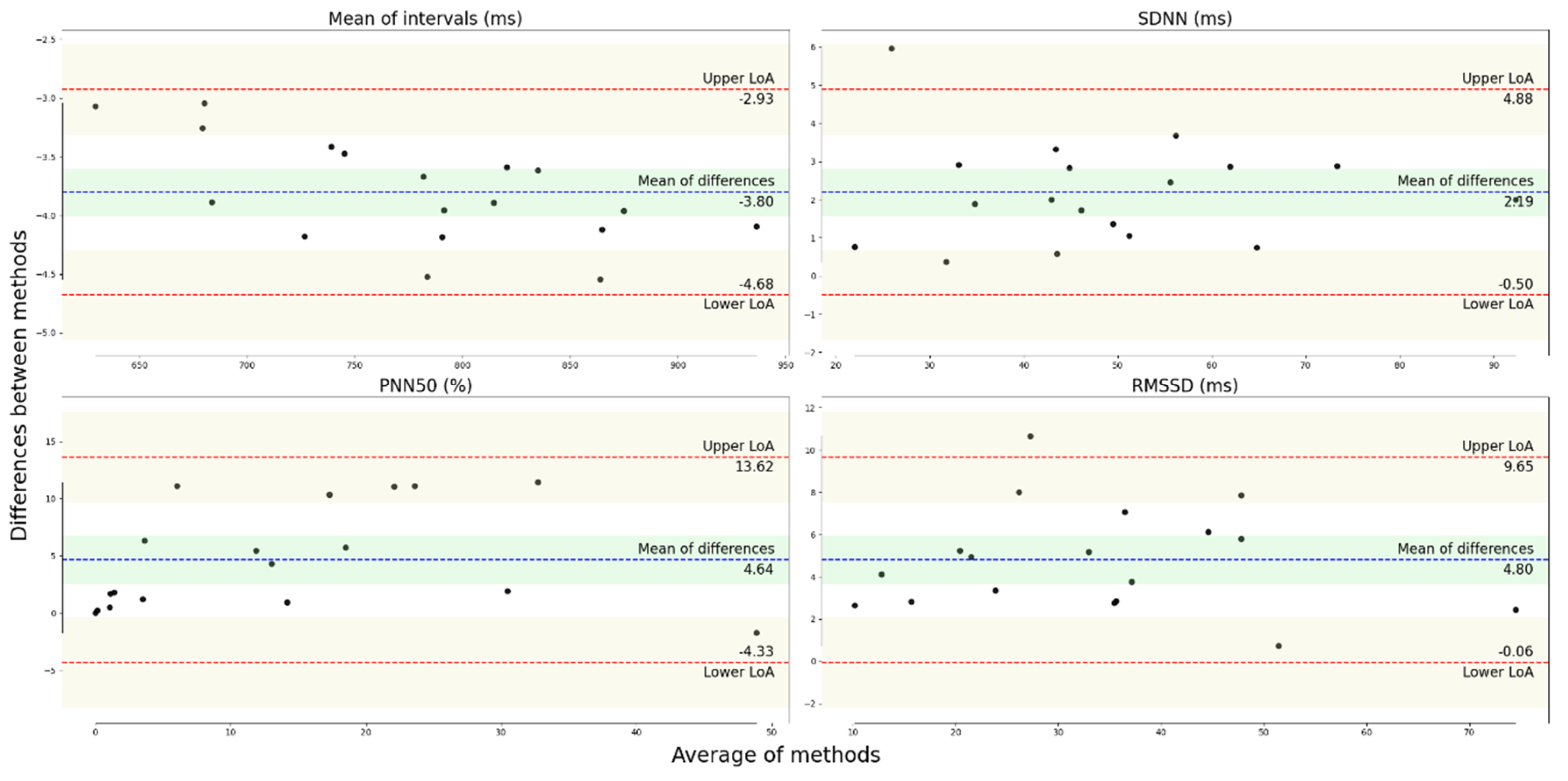
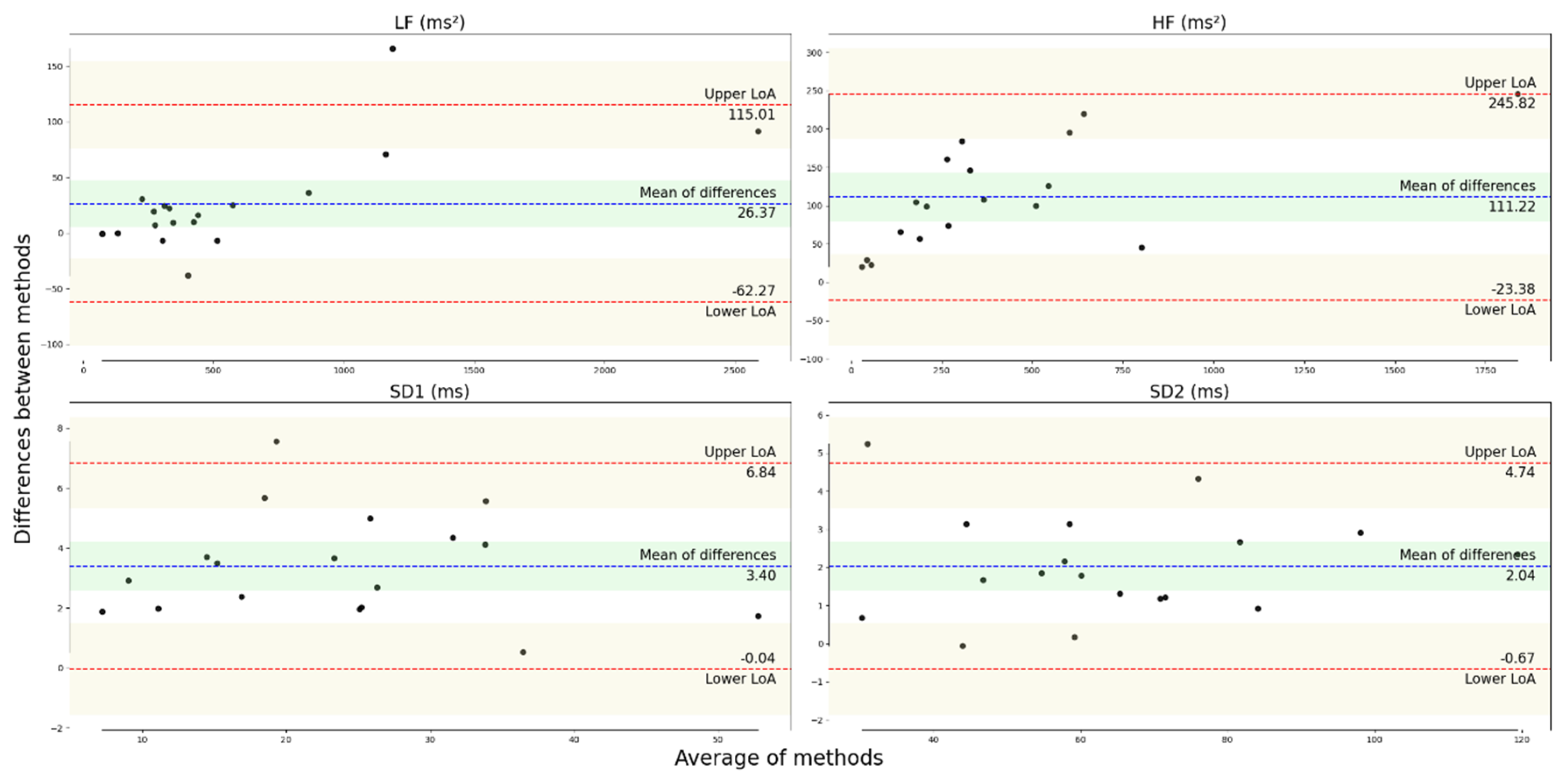
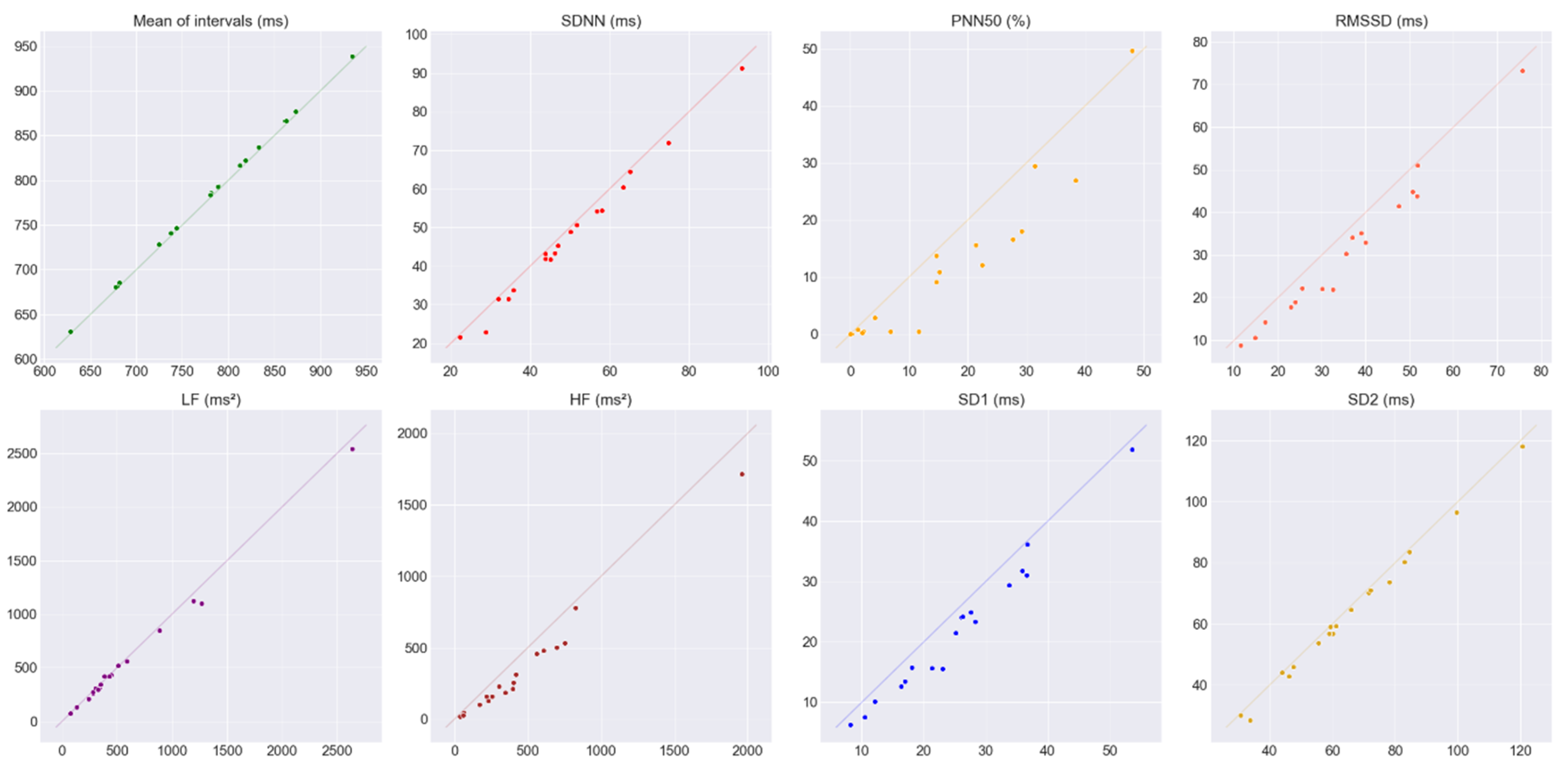
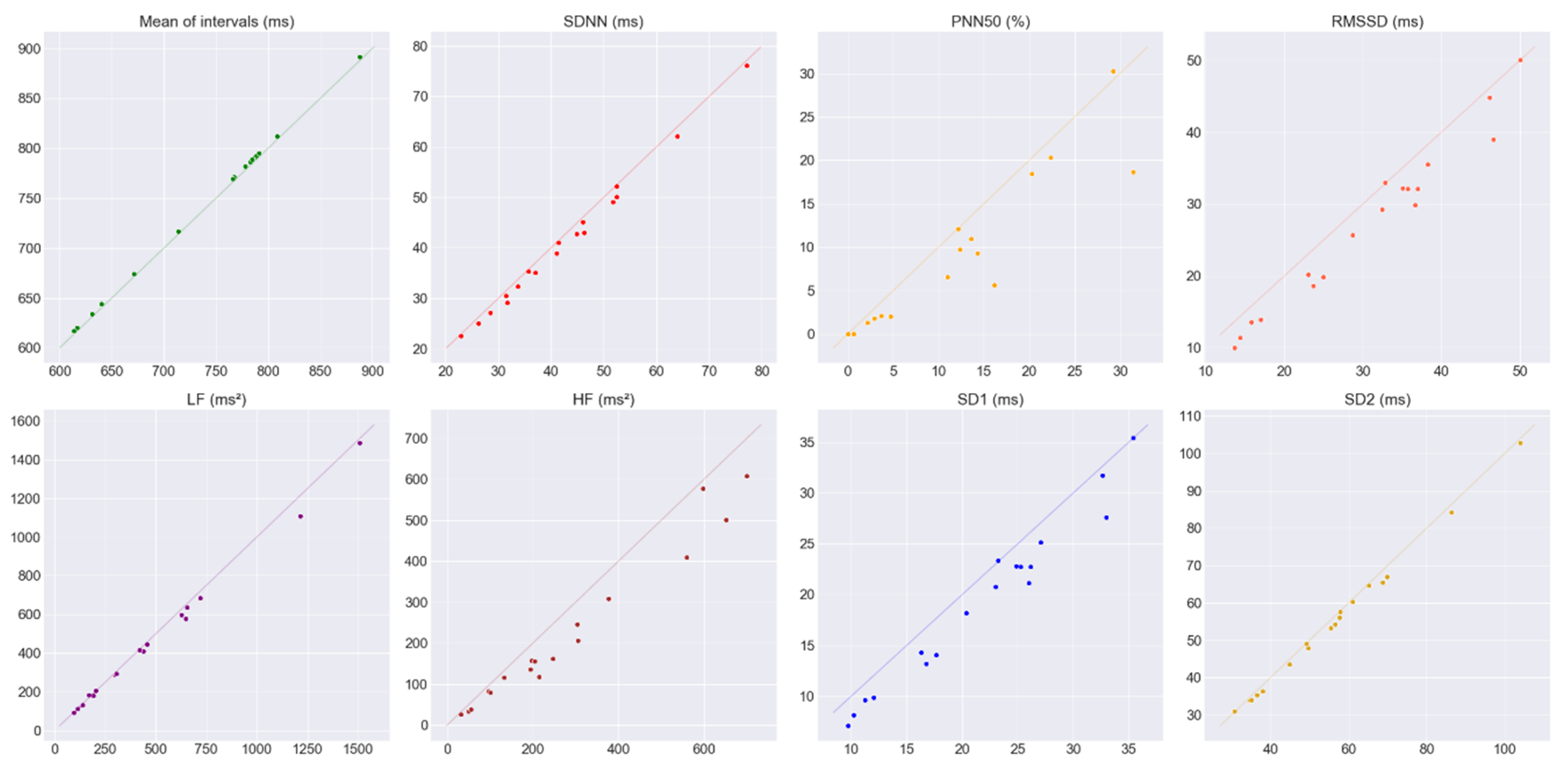
3.1. Agreement of the HRV Metrics at rest
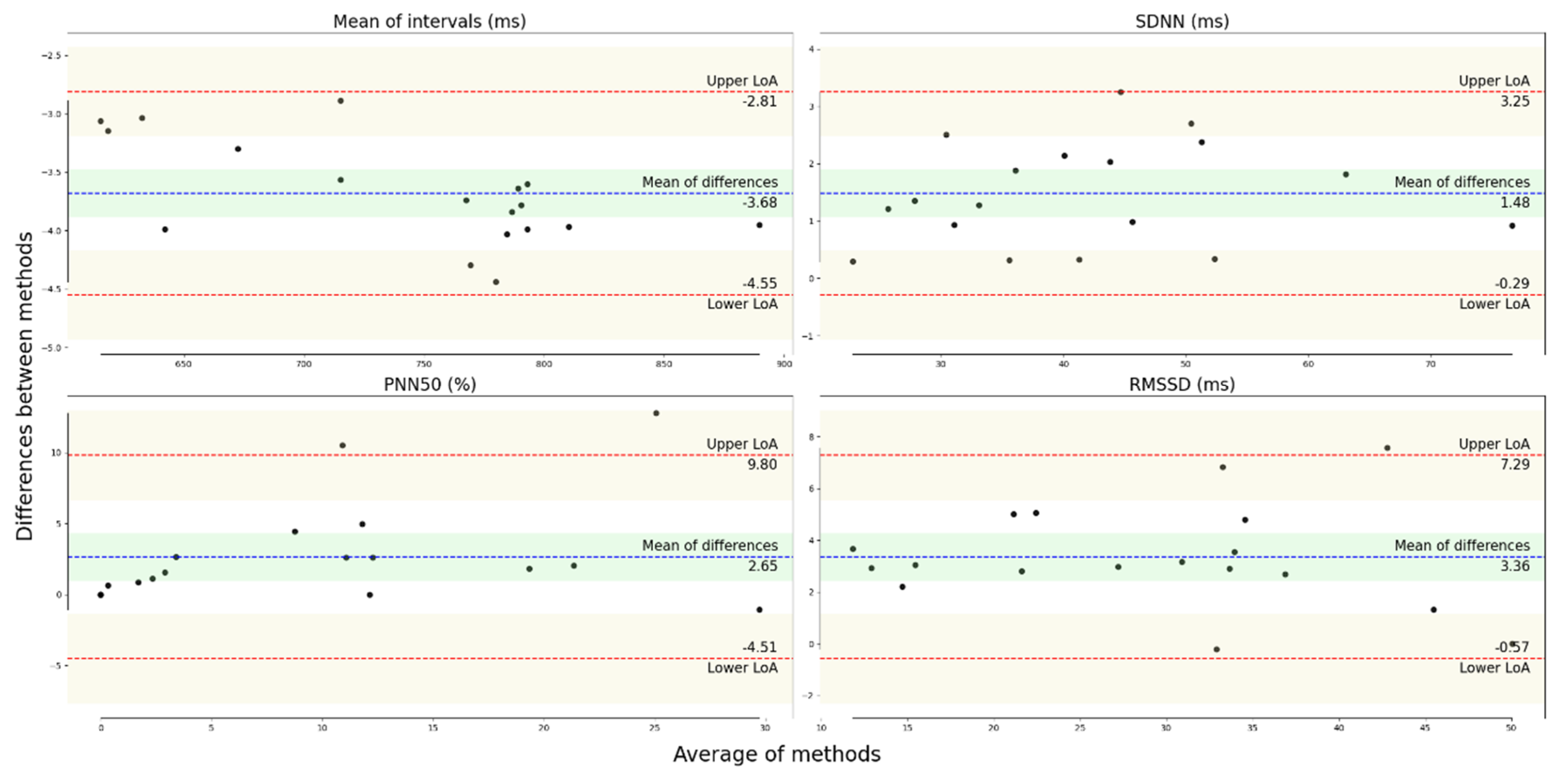
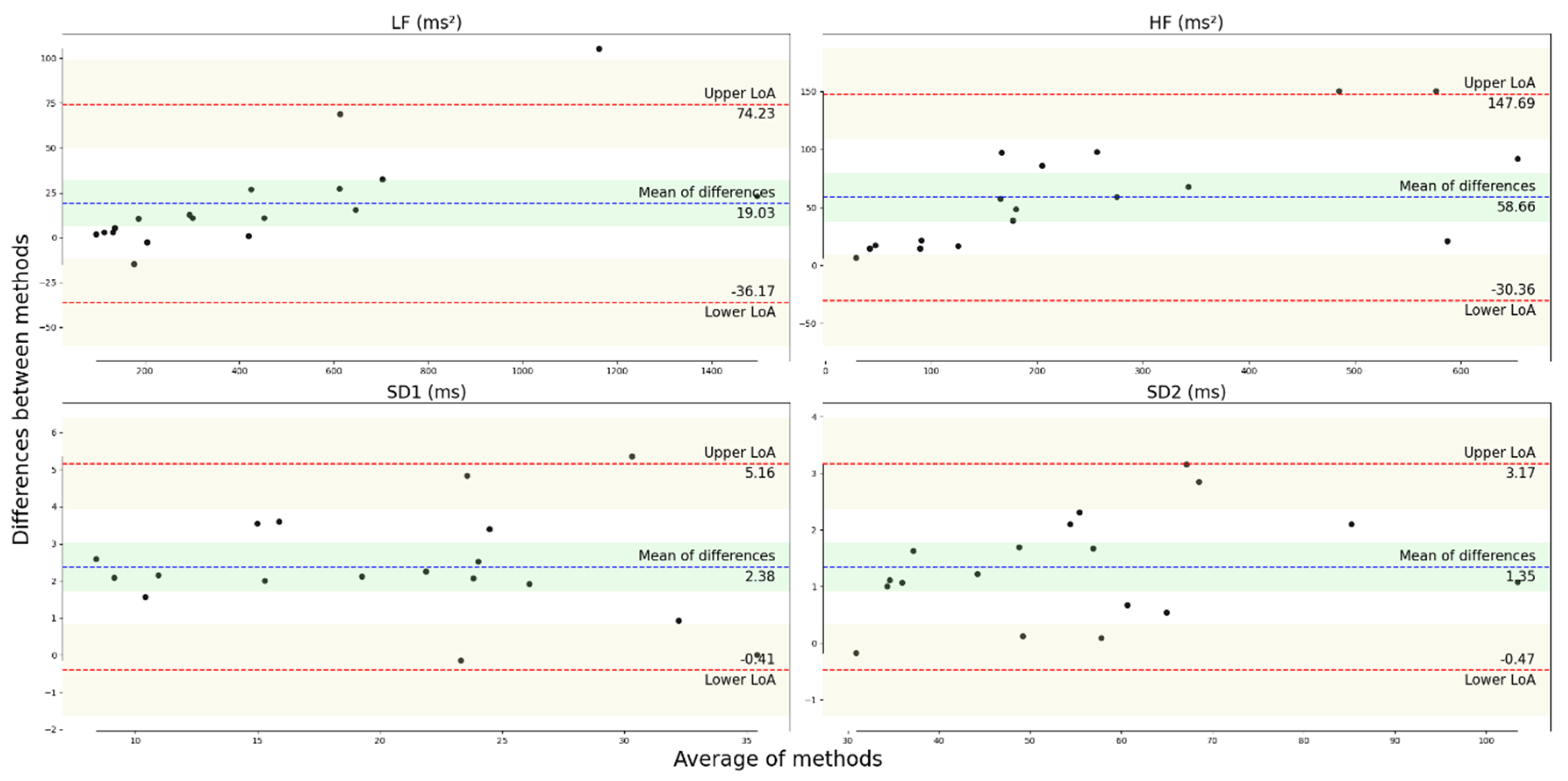
3.2. Agreement of the HRV Metrics during the SCWT
3.3. Comparison between HRV Metrics at Rest and SCWT
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Ethical Statements
Appendix A
References
- Caminal, P.; Sola, F.; Gomis, P.; Guasch, E.; Perera, A.; Soriano, N.; Mont, L. Validity of the Polar V800 monitor for measuring heart rate variability in mountain running route conditions. Eur. J. Appl. Physiol. 2018, 118, 669–677. [Google Scholar] [CrossRef] [PubMed]
- Malik, M.; Bigger, J.T.; Camm, A.J.; Kleiger, R.E.; Malliani, A.; Moss, A.J.; Schwartz, P.J. Heart rate variability: Standards of measurement, physiological interpretation, and clinical use. Eur. Heart J. 1996, 17, 354–381. [Google Scholar] [CrossRef]
- Hernando, D.; Roca, S.; Sancho, J.; Alesanco, Á.; Bailón, R. Validation of the apple watch for heart rate variability measurements during relax and mental stress in healthy subjects. Sensors 2018, 18, 2619. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, A.; Vagedes, J. How accurate is pulse rate variability as an estimate of heart rate variability? A review on studies comparing photoplethysmographic technology with an electrocardiogram. Int. J. Cardiol. 2013, 166, 15–29. [Google Scholar] [CrossRef] [PubMed]
- Billman, G.E.; Huikuri, H.V.; Sacha, J.; Trimmel, K. An introduction to heart rate variability: Methodological considerations and clinical applications. Front. Physiol. 2015, 6, 2013–2015. [Google Scholar] [CrossRef] [PubMed]
- Plews, D.J.; Scott, B.; Altini, M.; Wood, M.; Kilding, A.E.; Laursen, P.B. Comparison of heart-rate-variability recording with smartphone photoplethysmography, polar H7 chest strap, and electrocardiography. Int. J. Sports Physiol. Perform. 2017, 12, 1324–1328. [Google Scholar] [CrossRef]
- Alberdi, A.; Aztiria, A.; Basarab, A. Towards an automatic early stress recognition system for office environments based on multimodal measurements: A review. J. Biomed. Inform. 2016, 59, 49–75. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.-G.; Cheon, E.-J.; Bai, D.-S.; Lee, Y.H.; Koo, B.-H. Stress and Heart Rate Variability: A Meta-Analysis and Review of the Literature. Psychiatry Investig. 2018, 15, 235–245. [Google Scholar] [CrossRef]
- Ledowski, T.; Tiong, W.S.; Lee, C.; Wong, B.; Fiori, T.; Parker, N. Analgesia nociception index: Evaluation as a new parameter for acute postoperative pain. Br. J. Anaesth. 2013, 111, 627–629. [Google Scholar] [CrossRef]
- Dobbs, W.C.; Fedewa, M.V.; MacDonald, H.V.; Holmes, C.J.; Cicone, Z.S.; Plews, D.J.; Esco, M.R. The Accuracy of Acquiring Heart Rate Variability from Portable Devices: A Systematic Review and Meta-Analysis. Sports Med. 2019, 49, 417–435. [Google Scholar] [CrossRef]
- Gilgen-Ammann, R.; Schweizer, T.; Wyss, T. RR interval signal quality of a heart rate monitor and an ECG Holter at rest and during exercise. Eur. J. Appl. Physiol. 2019. [Google Scholar] [CrossRef] [PubMed]
- Pernice, R.; Javorka, M.; Krohova, J.; Czippelova, B.; Turianikova, Z.; Busacca, A.; Faes, L. Reliability of Short-Term Heart Rate Variability Indexes Assessed through Photoplethysmography. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; Volume 2018, p. 5610-5513. [Google Scholar] [CrossRef]
- Shaffer, F.; Ginsberg, J.P. An Overview of Heart Rate Variability Metrics and Norms. Front. Public Health 2017, 5, 1–17. [Google Scholar] [CrossRef]
- Sun, Y.; Thakor, N. Photoplethysmography Revisited: From Contact to Noncontact, from Point to Imaging. IEEE Trans. Biomed. Eng. 2016, 63, 463–477. [Google Scholar] [CrossRef] [PubMed]
- Allen, J. Photoplethysmography and its application in clinical physiological measurement. Physiol. Meas. 2007, 28, R1–R39. [Google Scholar] [CrossRef] [PubMed]
- Mejía-Mejía, E.; May, J.M.; Torres, R.; Kyriacou, P.A. Pulse rate variability in cardiovascular health: A review on its applications and relationship with heart rate variability. Physiol. Meas. 2020. [Google Scholar] [CrossRef] [PubMed]
- Peralta, E.; Lazaro, J.; Bailon, R.; Marozas, V.; Gil, E. Optimal fiducial points for pulse rate variability analysis from forehead and finger photoplethysmographic signals. Physiol. Meas. 2019, 40, 025007. [Google Scholar] [CrossRef]
- Yuda, E.; Yamamoto, K.; Yoshida, Y.; Hayano, J. Differences in pulse rate variability with measurement site. J. Physiol. Anthropol. 2020, 39, 4. [Google Scholar] [CrossRef]
- Castaneda, D.; Esparza, A.; Ghamari, M.; Soltanpur, C.; & Nazeran, H. A review on wearable photoplethysmography sensors and their potential future applications in health care. Int. J. Biosens. Bioelectron. 2018, 4, 195–202. [Google Scholar] [CrossRef]
- Khan, M.; Pretty, C.G.; Amies, A.C.; Elliott, R.; Shaw, G.M.; Chase, J.G. Investigating the Effects of Temperature on Photoplethysmography. IFAC-PapersOnLine 2015, 48, 360–365. [Google Scholar] [CrossRef]
- Wong, J.-S.; Lu, W.-A.; Wu, K.-T.; Liu, M.; Chen, G.-Y.; Kuo, C.-D. A comparative study of pulse rate variability and heart rate variability in healthy subjects. J. Clin. Monit. Comput. 2012, 26, 107–114. [Google Scholar] [CrossRef]
- Giles, D.; Draper, N.; Neil, W. Validity of the Polar V800 heart rate monitor to measure RR intervals at rest. Eur. J. Appl. Physiol. 2016, 116, 563–571. [Google Scholar] [CrossRef] [PubMed]
- Van Rossum, G.; Drake, F.L., Jr. Python Tutorial. Centrum voor Wiskunde en Informatica; CWI: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- van der Walt, S.; Colbert, S.C.; Varoquaux, G. The NumPy Array: A Structure for Efficient Numerical Computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef]
- Pandas-Dev/Pandas: Pandas 1.0.0. 2020. Available online: https://zenodo.org/record/3630805#.Xw0FmiMzaUk (accessed on 13 July 2020).
- Tulen, J.H.; Moleman, P.; van Steenis, H.G.; Boomsma, F. Characterization of stress reactions to the Stroop Color Word Test. Pharmacol. Biochem. Behav. 1989, 32, 9–15. [Google Scholar] [CrossRef]
- Karthikeyan, P.; Murugappan, M.; Yaacob, S. Analysis of Stroop Color Word Test-Based Human Stress Detection using Electrocardiography and Heart Rate Variability Signals. Arab. J. Sci. Eng. 2014, 39, 1835–1847. [Google Scholar] [CrossRef]
- Delaney, J.P.A.; Brodie, D.A. Effects of short-term psychological stress on the time and frequency domains of heart-rate variability. Percept. Mot. Skills 2000, 91, 515. [Google Scholar] [CrossRef]
- Karlsson, M.; Hörnsten, R.; Rydberg, A.; Wiklund, U. Automatic filtering of outliers in RR intervals before analysis of heart rate variability in Holter recordings: A comparison with carefully edited data. Biomed. Eng. Online 2012, 11, 2. [Google Scholar] [CrossRef]
- Peltola, M.A. Role of editing of R–R intervals in the analysis of heart rate variability. Front. Physiol. 2012, 3, 1–10. [Google Scholar] [CrossRef]
- Choi, A.; Shin, H. Quantitative Analysis of the Effect of an Ectopic Beat on the Heart Rate Variability in the Resting Condition. Front. Physiol. 2018, 9. [Google Scholar] [CrossRef]
- Weinschenk, S.W.; Beise, R.D.; Lorenz, J. Heart rate variability (HRV) in deep breathing tests and 5-min short-term recordings: Agreement of ear photoplethysmography with ECG measurements, in 343 subjects. Eur. J. Appl. Physiol. 2016, 116, 1527–1535. [Google Scholar] [CrossRef]
- Ang, S.-S.; Wieczorkowski-Rettinger, K.; Hernandez-Silveira, M. Real-time activity energy expenditure estimation for embedded ambulatory systems using SensiumTM technologies. In Handbook of Bioelectronics; Carrara, S., Iniewski, K., Eds.; Cambridge University Press: Cambridge, UK, 2015; pp. 513–542. [Google Scholar] [CrossRef]
- Stein, P.K.; Reddy, A. Non-linear heart rate variability and risk stratification in cardiovascular disease. Indian Pacing Electrophysiol. J. 2005, 5, 210–220. [Google Scholar] [PubMed]
- Ciccone, A.B.; Siedlik, J.A.; Wecht, J.M.; Deckert, J.A.; Nguyen, N.D.; Weir, J.P. Reminder: RMSSD and SD1 are identical heart rate variability metrics. Muscle Nerve 2017, 56, 674–678. [Google Scholar] [CrossRef]
- Turner, I.; Herbert, M.; Bernard, R.M. Calculating and Synthesizing Effect Sizes. Contemp. Issues Commun. Sci. Disord. 2006, 33, 42–55. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Routledge: New York, NY, USA, 1988. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An Analysis of Variance Test for Normality (Complete Samples). Biometrika 1965, 52, 591. [Google Scholar] [CrossRef]
- Lin, L.I. A Concordance Correlation Coefficient to Evaluate Reproducibility. Biometrics 1989, 45, 255. [Google Scholar] [CrossRef] [PubMed]
- McBride, G.B. A Proposal for Strength-of-Agreement Criteria for Lin’s Concordance Correlation Coefficient; NIWA Client Report: HAM2005-062; National Institute of Water and Atmospheric Research: Hamilton, New Zeeland, 2005; Available online: http://www.medcalc.org/download/pdf/McBride2005.pdf (accessed on 27 July 2019).
- Giavarina, D. Understanding Bland Altman analysis. Biochem. Med. 2015, 25, 141–151. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D. Statistical Methods for Assessing Agreement Between Two Methods of Clinical Measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef] [PubMed]
- O’Brien, E.; Petrie, J.; Littler, W.; de Swiet, M.; Padfield, P.L.; Altman, D.; Bland, M.; Coats, A.; Atkins, N. The British Hypertension Society protocol for the evaluation of blood pressure measuring devices. J. Hypertens. 1993, 11, 43–62. Available online: http://www.eoinobrien.org/wp-content/uploads/2008/08/x.BHS-Protocol.Revision.J-Hypertens-1993.df_.pdf (accessed on 6 June 2019).
- Radespiel-Tröger, M.; Rauh, R.; Mahlke, C.; Gottschalk, T.; Mück-Weymann, M. Agreement of two different methods for measurement of heart rate variability. Clin. Auton. Res. 2003, 13, 99–102. [Google Scholar] [CrossRef] [PubMed]
- Burr, R.L. Interpretation of Normalized Spectral Heart Rate Variability Indices in Sleep Research: A Critical Review. Sleep 2007, 30, 913–919. [Google Scholar] [CrossRef] [PubMed]
- McGraw, K.O.; Wong, S.P. A common language effect size statistic. Psychol. Bull. 1992, 111, 361–365. [Google Scholar] [CrossRef]
- Nogueira, P.; Urbano, J.; Reis, L.P.; Cardoso, H.L.; Silva, D.C.; Rocha, A.P.; Gonçalves, J.; Faria, B.M. A Review of Commercial and Medical-Grade Physiological Monitoring Devices for Biofeedback-Assisted Quality of Life Improvement Studies. J. Med. Syst. 2018, 42, 101. [Google Scholar] [CrossRef]
- Yetisen, A.K.; Martinez-Hurtado, J.L.; Ünal, B.; Khademhosseini, A.; Butt, H. Wearables in Medicine. Adv. Mater. 2018, 30, 1706910. [Google Scholar] [CrossRef]
- Haghi, M.; Thurow, K.; Stoll, R. Wearable Devices in Medical Internet of Things: Scientific Research and Commercially Available Devices. Healthc. Inform. Res. 2017, 23, 4. [Google Scholar] [CrossRef]
- Chen, X.; Huang, Y.-Y.; Yun, F.; Chen, T.-J.; Li, J. Effect of changes in sympathovagal balance on the accuracy of heart rate variability obtained from photoplethysmography. Exp. Ther. Med. 2015, 10, 2311–2318. [Google Scholar] [CrossRef]
- Hjortskov, N.; Rissén, D.; Blangsted, A.K.; Fallentin, N.; Lundberg, U.; Søgaard, K. The effect of mental stress on heart rate variability and blood pressure during computer work. Eur. J. Appl. Physiol. 2004, 92, 84–89. [Google Scholar] [CrossRef]
- Melillo, P.; Formisano, C.; Bracale, U.; Pecchia, L. Classification Tree for Real-Life Stress Detection Using Linear Heart Rate Variability Analysis. Case Study: Students under Stress Due to University Examination. In Proceedings of the World Congress on Medical Physics and Biomedical Engineering, Beijing, China, 26–31 May 2012; pp. 477–480. [Google Scholar] [CrossRef]


| Number of Intervals | Errors in the Intervals (%) | ||
|---|---|---|---|
| James One | Polar H10 | ||
| Rest | 6976 | 12 (0.17) | 7 (0.10) |
| SCWT | 7320 | 9 (0.12) | 2 (0.03) |
| Total | 14,296 | 21 (0.15) | 9 (0.06) |
| Nº. of Intervals | Min. (ms) | Max. (ms) | Mean (ms) | SD (ms) | Skewness | Kurtosis | CV (%) | |
|---|---|---|---|---|---|---|---|---|
| James One—Rest | 6976 | 555 | 1180 | 770 | 94 | 0.34 | −0.33 | 12.2 |
| Polar H10—Rest | 6976 | 563 | 1180 | 774 | 93 | 0.34 | −0.31 | 12.0 |
| James One—SCWT | 7320 | 536 | 1012 | 732 | 88 | 0.042 | −0.81 | 12.1 |
| Polar H10—SCWT | 7320 | 547 | 1013 | 736 | 88 | 0.039 | −0.82 | 11.9 |
| Mean ± SD James One | Mean ± SD Polar H10 | CVJ – CVP (%) | Hg | LCCC | Bias ± SD | LoA Upper; Lower | BA Ratio | |
|---|---|---|---|---|---|---|---|---|
| Mean int. (ms) | 778 ± 80.8 | 782 ± 81.1 | 0.015 | −0.046 | 0.998 | −3.80 ± 0.45 | −2.93; −4.68 | 0.005 |
| SDNN (ms) | 49.6 ± 17.3 | 47.4 ± 17.4 | −1.70 | 0.123 | 0.989 | 2.19 ± 1.38 | 4.88; −0.50 | 0.055 |
| pNN50 (%) | 16.2 ± 14.3 | 11.5 ± 13.4 | −27.0 | 0.327 | - | 4.64 ± 4.58 | 13.6; −4.33 | 0.648 |
| RMSSD (ms) | 35.8 ± 15.9 | 31.0 ± 16.2 | −7.34 | 0.292 | 0.944 | 4.80 ± 2.48 | 9.65; −0.060 | 0.145 |
| LF (ms2) | 593 ± 606 | 566 ± 575 | 0.64 | 0.0436 | - | 26.4 ± 45.2 | 115; −62.3 | 0.153 |
| HF (ms2) | 462 ± 443 | 350 ± 398 | −17.1 | 0.2581 | - | 111 ± 68.7 | 246; −23.4 | 0.331 |
| SD1 (ms) | 25.4 ± 11.3 | 21.9 ± 11.4 | −7.34 | 0.292 | 0.944 | 3.40 ± 1.75 | 6.84; −0.04 | 0.145 |
| SD2 (ms) | 65.1 ± 22.7 | 63.1 ± 23 | −1.00 | 0.088 | 0.994 | 2.04 ± 1.38 | 4.74; −0.67 | 0.042 |
| Mean ± SD James One | Mean ± SD Polar H10 | CVJ – CVP (%) | Hg | LCCC | Bias ± SD | LoA Upper; Lower | BA Ratio | |
|---|---|---|---|---|---|---|---|---|
| Mean int. (ms) | 741 ± 77.5 | 744 ± 77.8 | 0.013 | −0.046 | - | −3.68 ± 0.44 | −2.81; −4.55 | 0.005 |
| SDNN (ms) | 42.5 ± 13.7 | 41.0 ± 13.6 | −0.85 | 0.106 | 0.992 | 1.48 ± 0.90 | 3.25; −0.29 | 0.042 |
| pNN50 (%) | 10.9 ± 10.1 | 8.3 ± 8.8 | −13.8 | 0.274 | - | 2.65 ± 3.65 | 9.80; −4.51 | 0.744 |
| RMSSD (ms) | 30.7 ± 11.3 | 27.3 ± 11.5 | −5.16 | 0.289 | 0.941 | 3.36 ± 2.01 | 7.29; −0.57 | 0.136 |
| LF (ms2) | 463 ± 389 | 444 ± 370 | 0.51 | 0.049 | - | 19.0 ± 28.2 | 74.2; −36.2 | 0.121 |
| HF (ms2) | 279 ± 214 | 220 ± 186 | −7.14 | 0.286 | - | 58.7 ± 45.4 | 148; −30.4 | 0.357 |
| SD1 (ms) | 21.7 ± 7.97 | 19.3 ± 8.1 | −5.16 | 0.289 | 0.941 | 2.38 ± 1.42 | 5.16; −0.405 | 0.136 |
| SD2 (ms) | 55.6 ± 18.9 | 54.3 ± 18.7 | −0.31 | 0.070 | 0.996 | 1.35 ± 0.93 | 3.17; −0.47 | 0.033 |
| Mean int. | SDNN | pNN50 | RMSSD | LF | HF | LF/HF | SD2 | |
|---|---|---|---|---|---|---|---|---|
| James One Rest → SCWT | ↓; p = 0.002 CLES = 0.633 | ↓; p = 0.005 CLES = 0.623 | ↓; p = 0.008 CLES = 0.602 | ↓; p = 0.017 CLES = 0.611 | ↓; p = 0.082 CLES = 0.556 | ↓; p = 0.003 CLES = 0.651 | ↑; p = 0.408 CLES = 0.602 | ↓; p = 0.009 CLES = 0.633 |
| Polar H10 Rest → SCWT | ↓; p = 0.002 CLES = 0.636 | ↓; p = 0.015 CLES = 0.623 | ↓; p = 0.171 CLES = 0.528 | ↓; p = 0.055 CLES = 0.571 | ↓; p = 0.117 CLES = 0.571 | ↓; p = 0.008 CLES = 0.605 | ↓; p = 0.931 CLES = 0.556 | ↓; p = 0.017 CLES = 0.620 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Correia, B.; Dias, N.; Costa, P.; Pêgo, J.M. Validation of a Wireless Bluetooth Photoplethysmography Sensor Used on the Earlobe for Monitoring Heart Rate Variability Features during a Stress-Inducing Mental Task in Healthy Individuals. Sensors 2020, 20, 3905. https://doi.org/10.3390/s20143905
Correia B, Dias N, Costa P, Pêgo JM. Validation of a Wireless Bluetooth Photoplethysmography Sensor Used on the Earlobe for Monitoring Heart Rate Variability Features during a Stress-Inducing Mental Task in Healthy Individuals. Sensors. 2020; 20(14):3905. https://doi.org/10.3390/s20143905
Chicago/Turabian StyleCorreia, Bruno, Nuno Dias, Patrício Costa, and José Miguel Pêgo. 2020. "Validation of a Wireless Bluetooth Photoplethysmography Sensor Used on the Earlobe for Monitoring Heart Rate Variability Features during a Stress-Inducing Mental Task in Healthy Individuals" Sensors 20, no. 14: 3905. https://doi.org/10.3390/s20143905
APA StyleCorreia, B., Dias, N., Costa, P., & Pêgo, J. M. (2020). Validation of a Wireless Bluetooth Photoplethysmography Sensor Used on the Earlobe for Monitoring Heart Rate Variability Features during a Stress-Inducing Mental Task in Healthy Individuals. Sensors, 20(14), 3905. https://doi.org/10.3390/s20143905





