Underwater Localization via Wideband Direction-of-Arrival Estimation Using Acoustic Arrays of Arbitrary Shape †
Abstract
1. Introduction
2. Related Work
3. Wideband DoA Estimation Algorithm
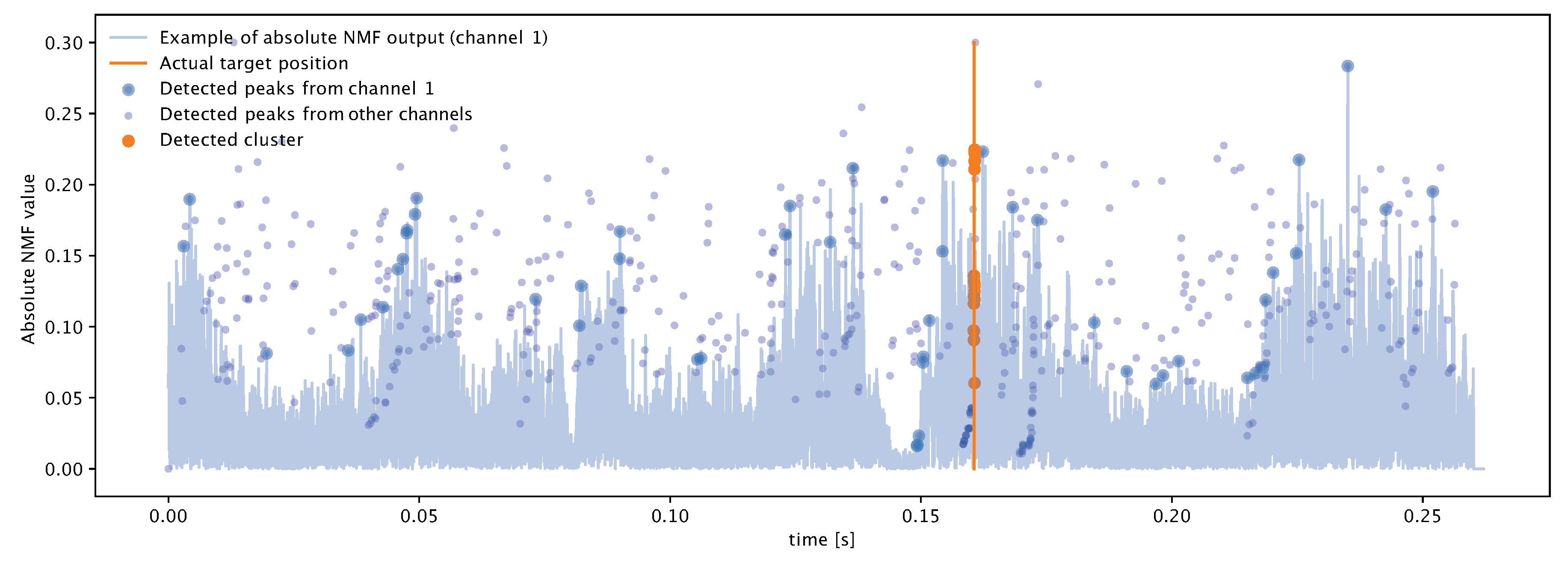
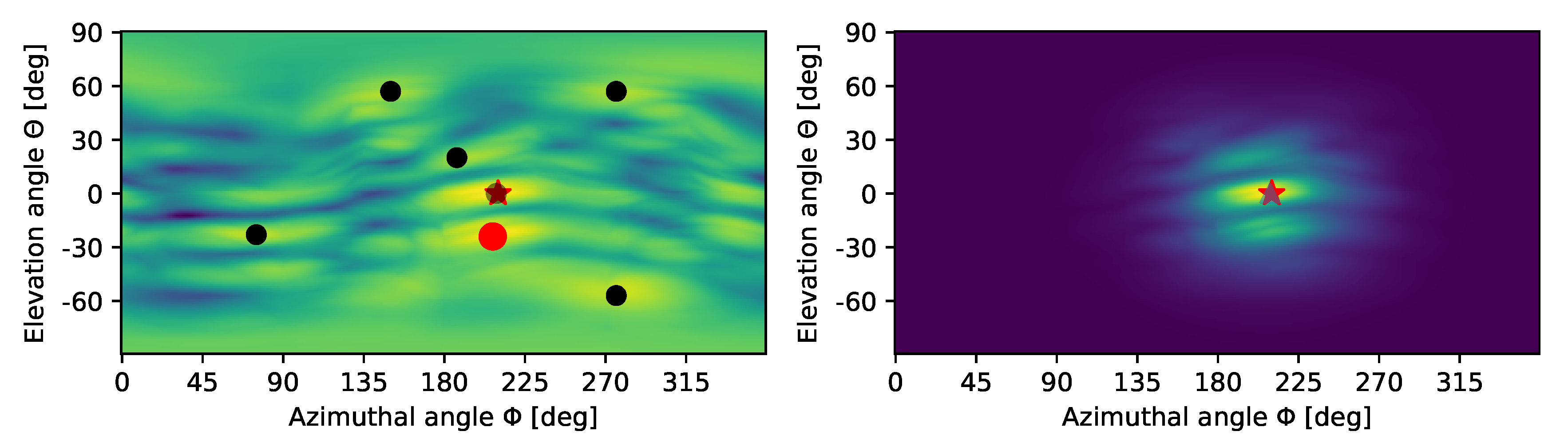
3.1. Key Idea
3.2. Algorithm Description
4. Materials and Methods
4.1. Common Setup and Parameter Configurations
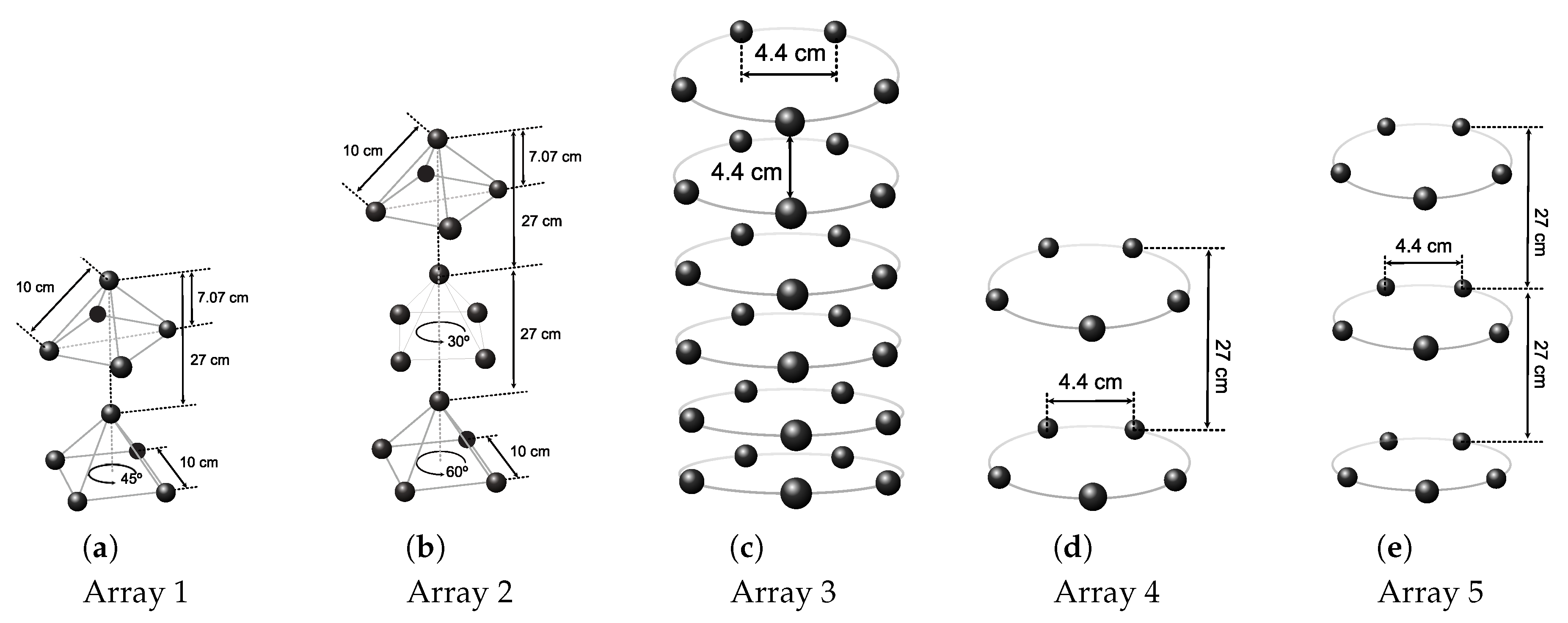
4.2. Emulation
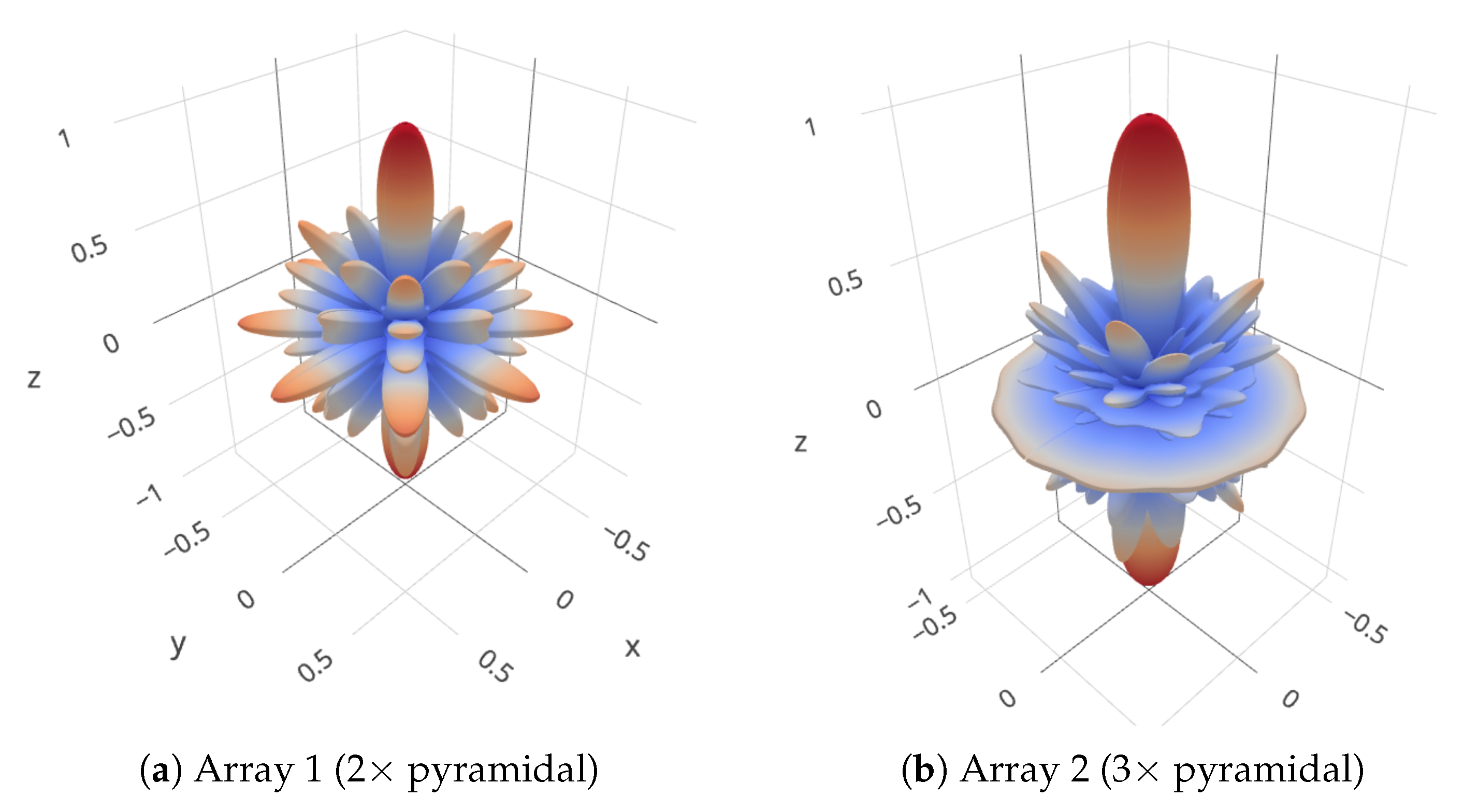
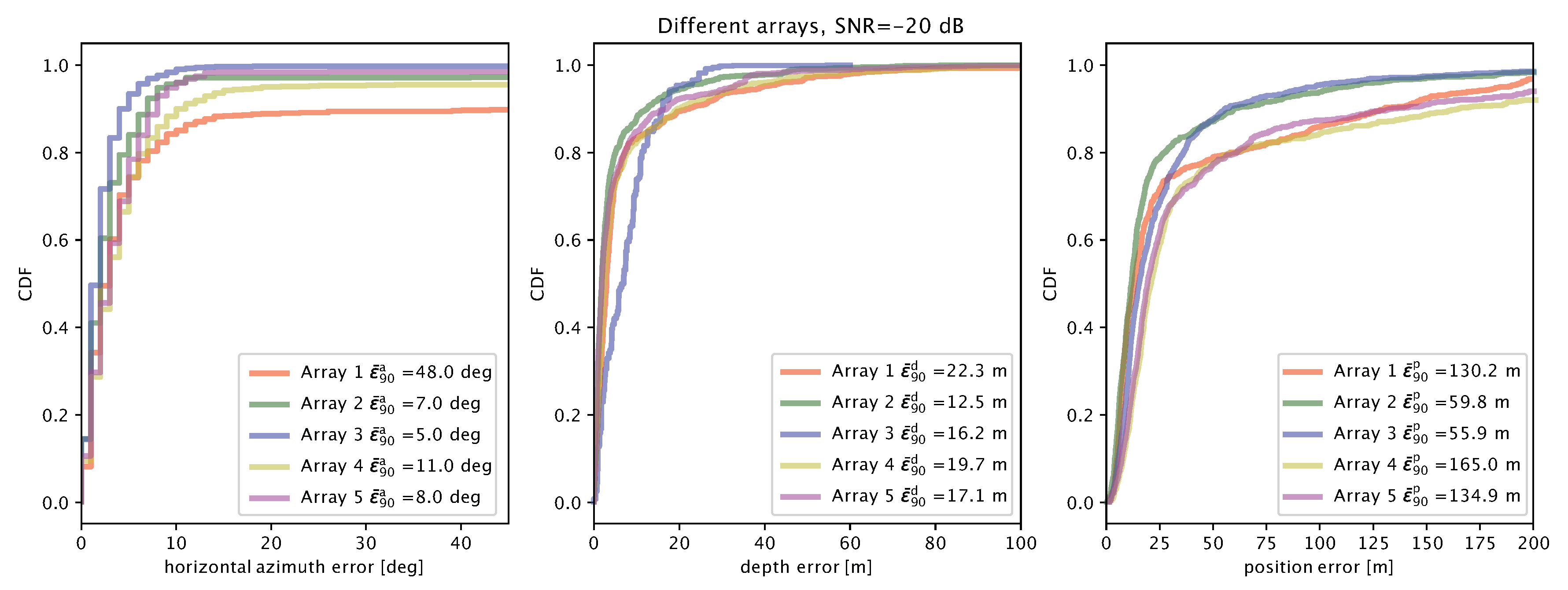
- Array 1 is composed of two 5-element pyramidal arrays having a base side length of 10 cm and an height of 7.07 cm. The sub-arrays are stacked at a distance of 27 cm, and the bottom one is rotated by 45. This is typical in the case in which each 5-element pyramidal array actually comes as a separate unit, whose connector mounting and cable bending constraints prevents placing the units closer than a given maximum distance;
- Array 2 is similar to array 1 but is composed of three pyramidal arrays stacked at a distance of 27 cm. In this case, the second array is rotated by 30 and the third by 60;
- Array 3 is a cylindrical array composed of 6 circular sub-arrays of 5 elements each (the same number of elements as in the pyramidal arrays of Array 1 and Array 2). The distance between closest elements along the same ring and across different rings is 4.4 cm;
- Array 4 is composed of two circular sub-arrays of radius 3.5 cm, placed at a distance of 27 cm from each other. Each sub-array embeds 5 elements. The elements are equally spaced along the ring and closest elements are 4.4 cm apart;
- Array 5 is similar to array 4 but is composed of three rather than two rings.
4.3. Lake Experiment
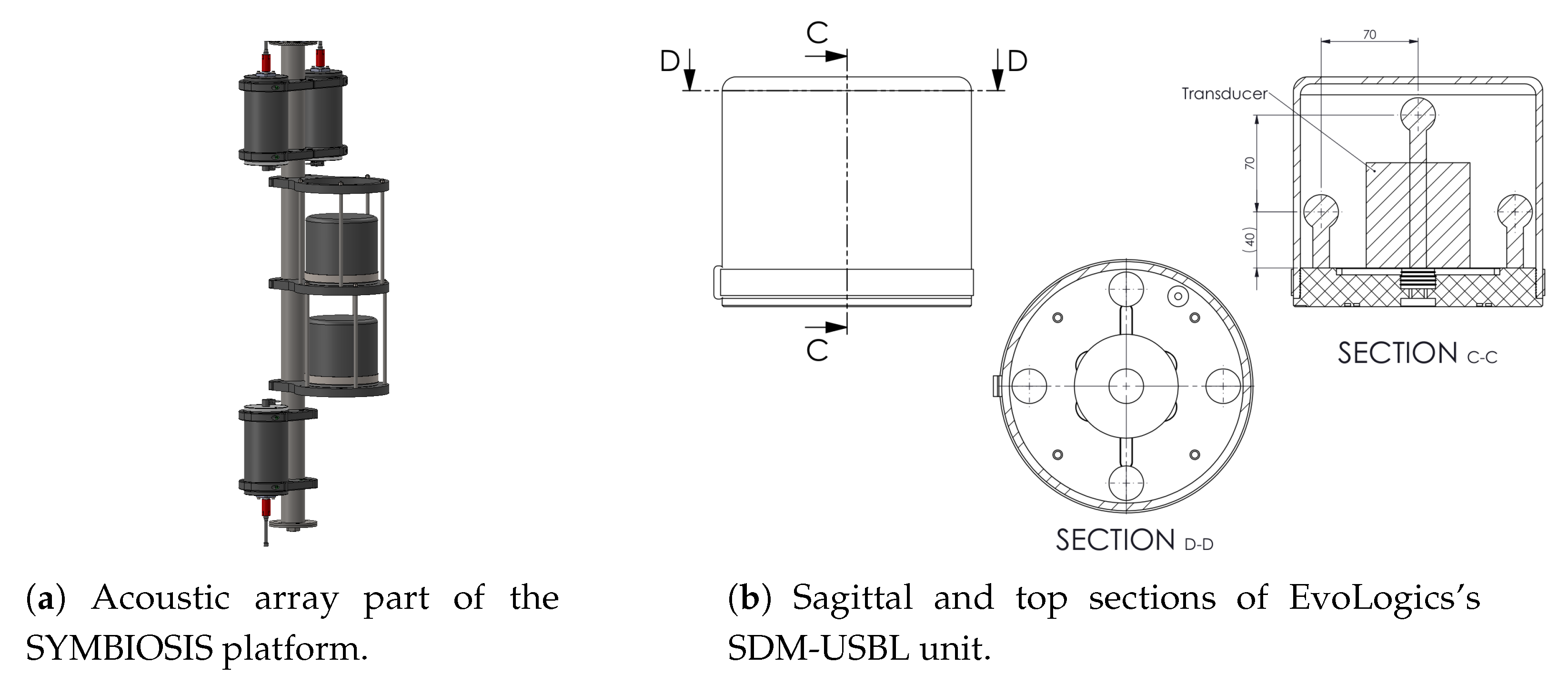
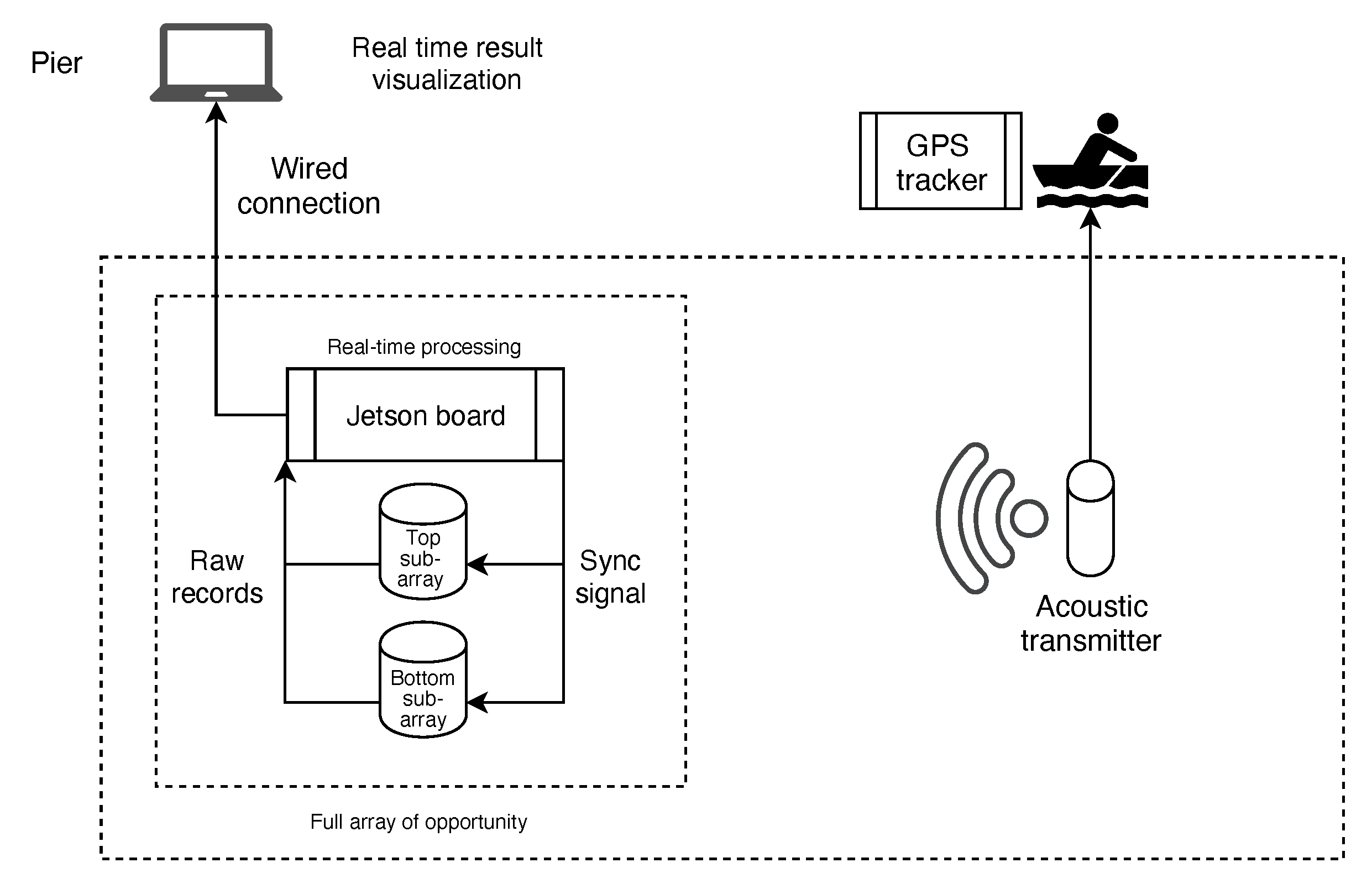
4.3.1. Equipment and Software
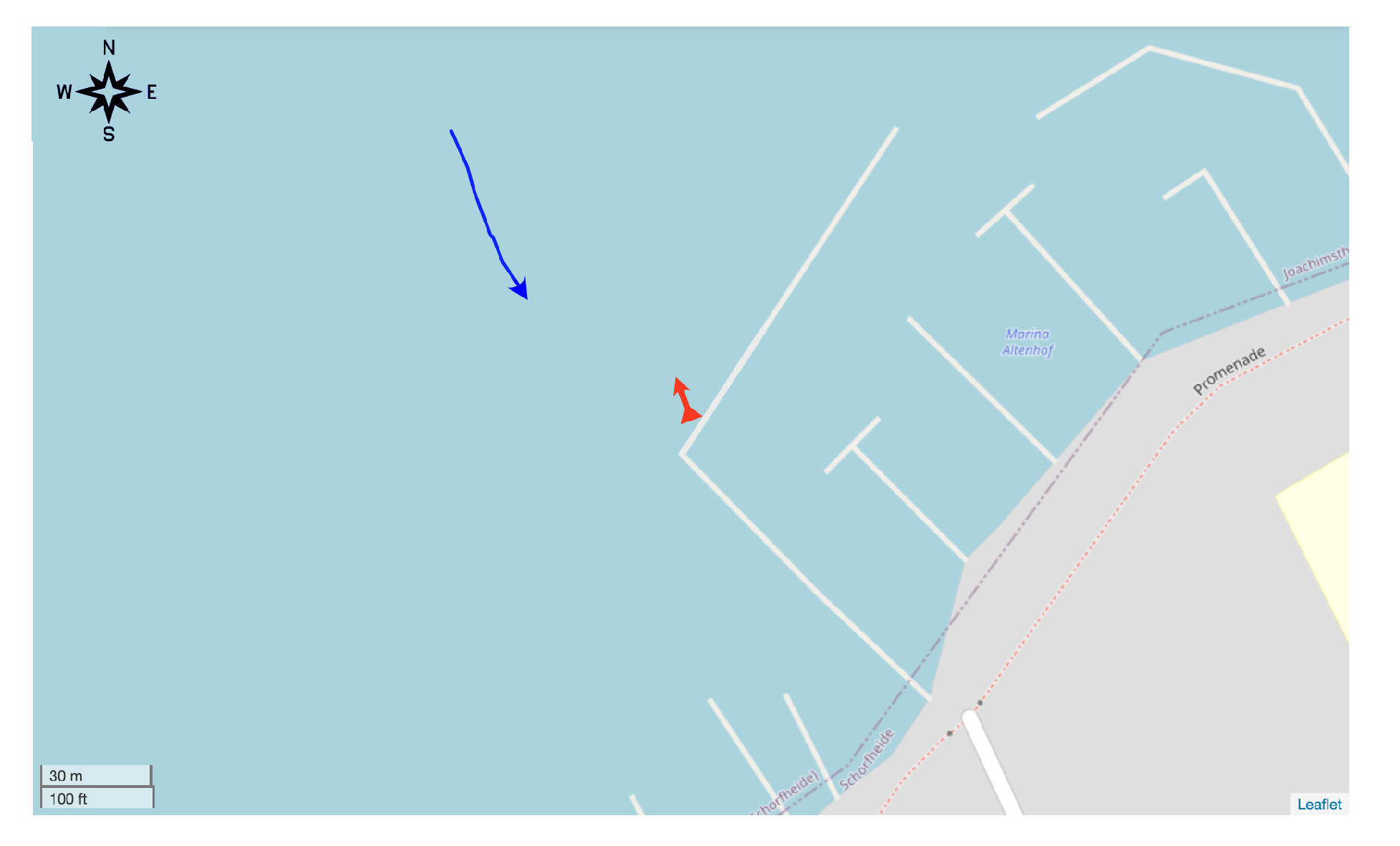
4.3.2. Experiment Setup
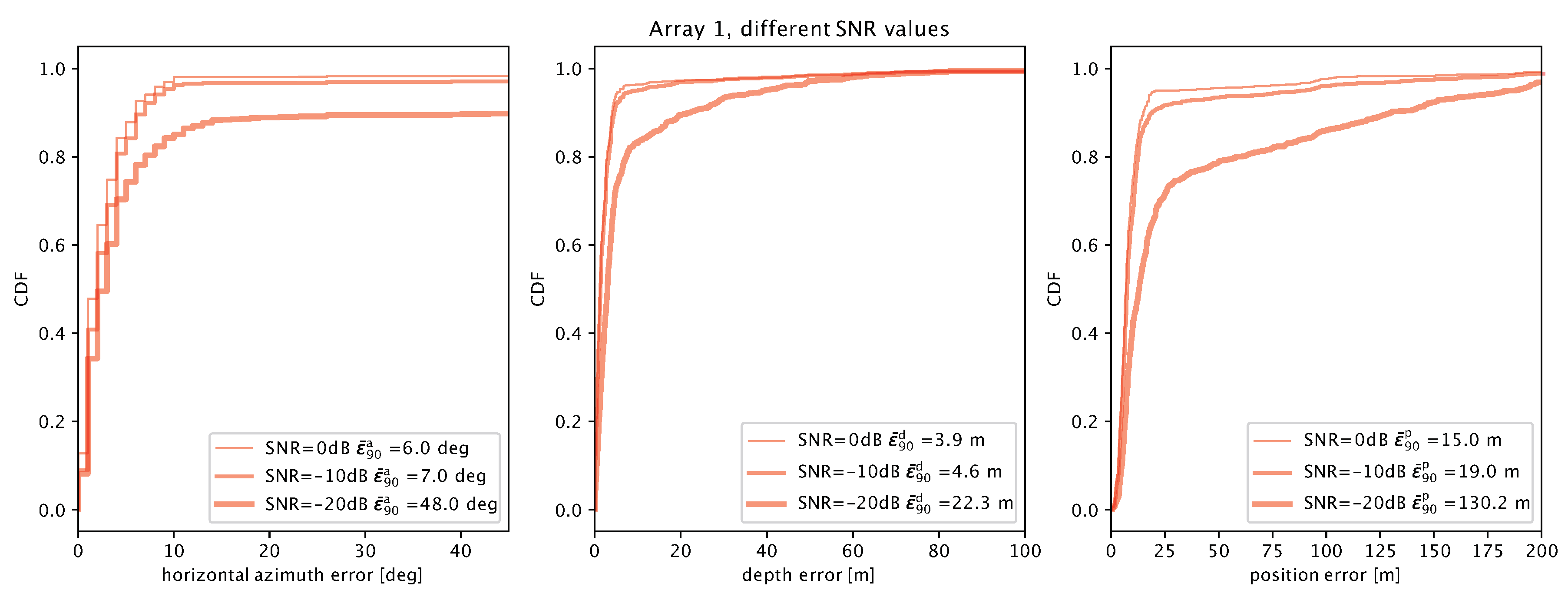
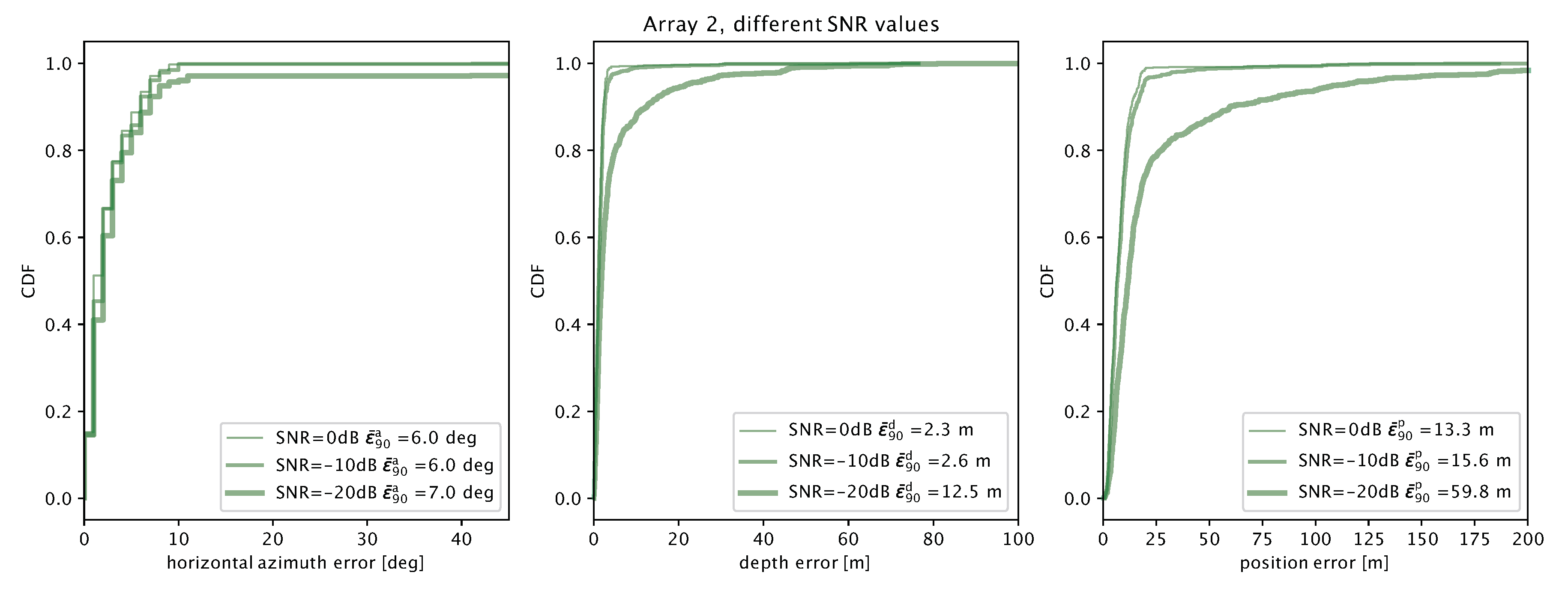
5. Emulation-Based Performance Evaluation
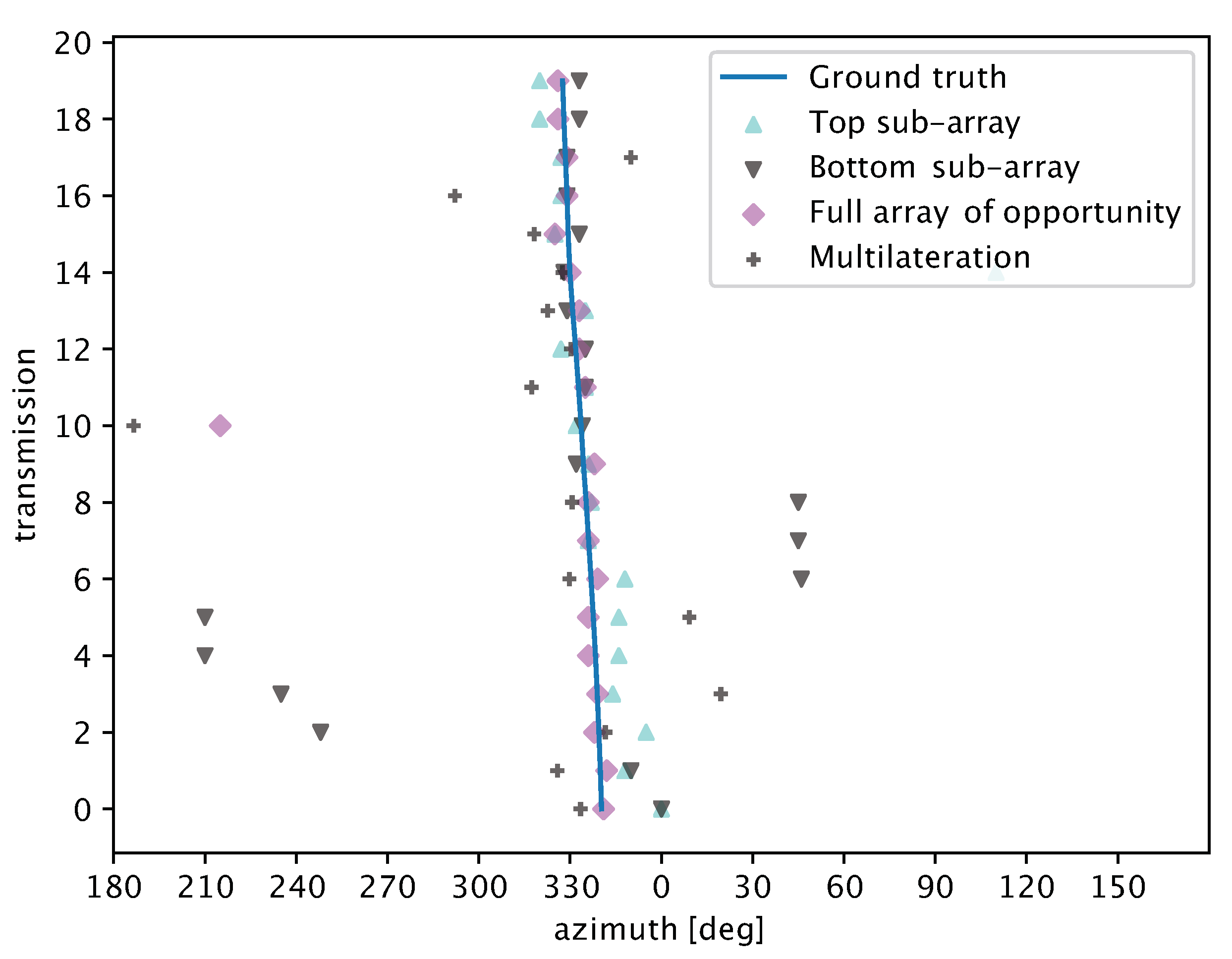
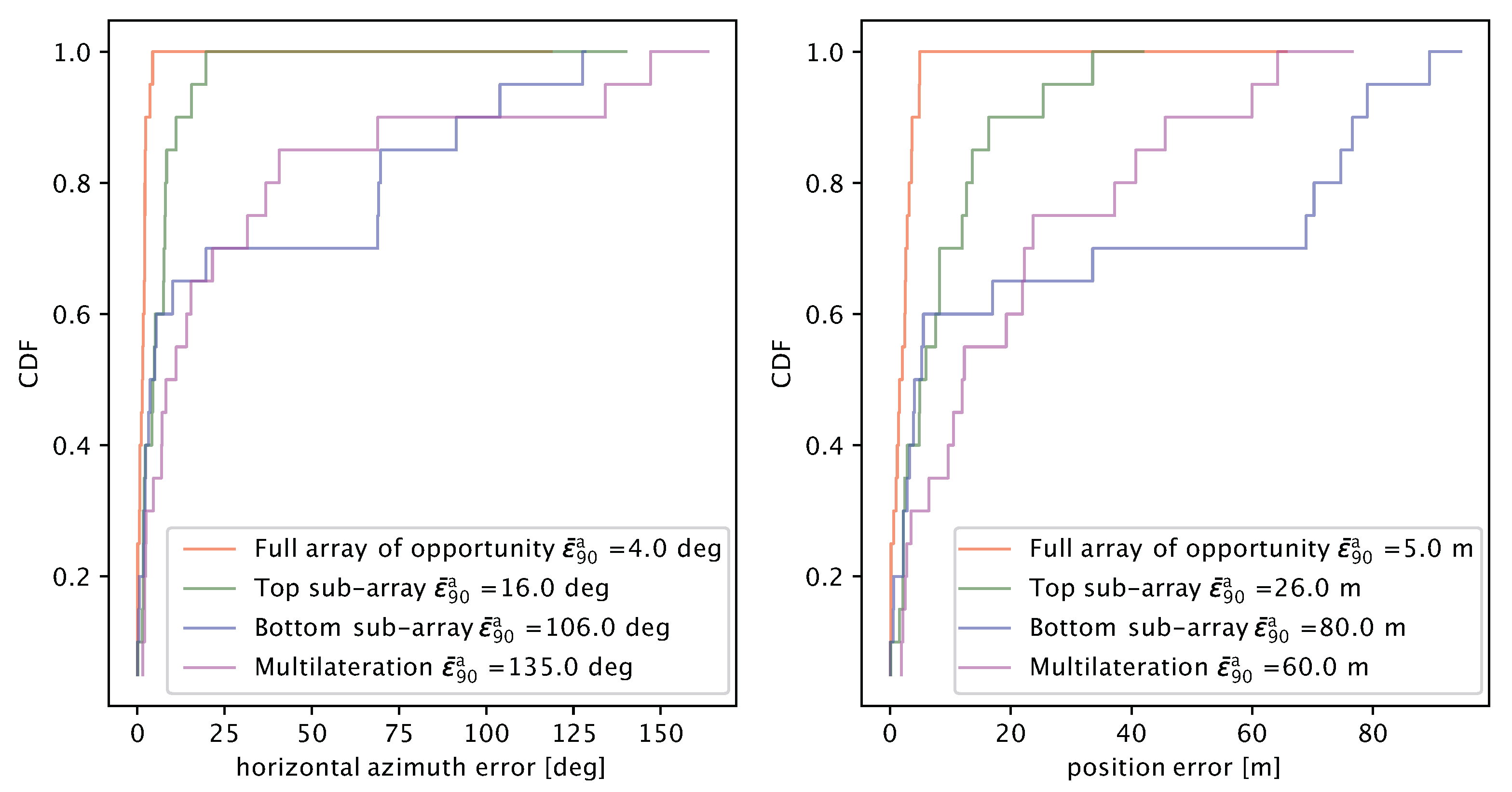
6. Lake Experiment Results
7. Summary of Results and Discussion
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Levy, D.; Belfer, Y.; Osherov, E.; Bigal, E.; Scheinin, A.P.; Nativ, H.; Tchernov, D.; Treibitz, T. Automated Analysis of Marine Video With Limited Data. In Proceedings of the IEEE/CVF CVPRW, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Dubrovinskaya, E.; Dalgleish, F.; Ouyang, B.; Casari, P. Underwater LiDAR Signal Processing for Enhanced Detection and Localization of Marine Life. In Proceedings of the MTS/IEEE OCEANS, Kobe, Japan, 28–31 May 2018. [Google Scholar]
- Paull, L.; Saeedi, S.; Seto, M.; Li, H. AUV navigation and localization: A review. IEEE J. Ocean. Eng. 2014, 39, 131–149. [Google Scholar] [CrossRef]
- Zerr, B.; Mailfert, G.; Bertholom, A.; Ayreault, H. Sidescan sonar image processing for AUV navigation. In Proceedings of the MTS/IEEE Oceans, Brest, France, 20–23 June 2005; Volume 1, pp. 124–130. [Google Scholar]
- Gallimore, E.; Terrill, E.; Hess, R.; Nager, A.; Bachelor, H.; Pietruszka, A. Integration and Evaluation of a Next, Generation Chirp-Style Sidescan Sonar on the REMUS 100. In Proceedings of the IEEE/OES AUV Workshop, Porto, Portugal, 6–9 November 2018; pp. 1–6. [Google Scholar]
- Tang, Z.; Blacquiere, G.; Leus, G. Aliasing-Free Wideband Beamforming Using Sparse Signal Representation. IEEE Trans. Signal Process. 2011, 59, 3464–3469. [Google Scholar] [CrossRef]
- Arkhipov, M. An approach to using basic three-element arrays in tetrahedral-based USBL systems. In Proceedings of the MTS/IEEE OCEANS, San Diego, CA, USA, 23–27 September 2013; pp. 1–8. [Google Scholar]
- Tesei, A.; Fioravanti, S.; Grandi, V.; Guerrini, P.; Maguer, A. Localization of small surface vessels through acoustic data fusion of two tetrahedralarrays of hydrophones. IProc. Mtgs. Acoust. 2012, 17, 070050. [Google Scholar]
- Devi, M.R.; Kumar, N.S.; Joseph, J. Sparse reconstruction based direction of arrival estimation of underwater targets. In Proceedings of the SYMPOL, Kochi, India, 18–20 November 2015; pp. 1–6. [Google Scholar]
- Liu, W.; Weiss, S. Wideband Beamforming: Concepts and Techniques; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Stergiopoulos, S. Advanced Signal Processing Handbook: Theory and Implementation for Radar, Sonar, and Medical Imaging Real Time Systems; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Andersson, F.; Carlsson, M.; Tourneret, J.Y.; Wendt, H. A method for 3D direction of arrival estimation for general arrays using multiple frequencies. In Proceedings of the CAMSAP, Cancun, Mexico, 13–16 December 2015. [Google Scholar]
- Wong, K.T.; Zoltowski, M.D. Closed-form underwater acoustic direction-finding with arbitrarily spaced vector hydrophones at unknown locations. IEEE J. Ocean. Eng. 1997, 22, 566–575. [Google Scholar] [CrossRef]
- Chandrika, U.K.; Hari, V.N. A vector sensing scheme for underwater acoustics based on particle velocity measurements. In Proceedings of the MTS/IEEE OCEANS 2015, Washington, DC, USA, 19–22 October 2015; pp. 1–7. [Google Scholar]
- Bereketli, A.; Guldogan, M.B.; Kolcak, T.; Gudu, T.; Avsar, A.L. Experimental Results for Direction of Arrival Estimation with a Single Acoustic Vector Sensor in Shallow Water. Hindawi J. Sens. 2015, 2015, 401353. [Google Scholar] [CrossRef]
- EvoLogics GmbH, S2C R 7/17 USBL Communication and Positioning Device. Available online: https://evologics.de/acoustic-modem/7-17/usbl-serie (accessed on 1 July 2020).
- Dubrovinskaya, E.; Casari, P. Underwater Direction of Arrival Estimation using Wideband Arrays of Opportunity. In Proceedings of the MTS/IEEE OCEANS, Marseille, France, 17–20 June 2019. [Google Scholar]
- Vaccaro, R.J. The past, present, and the future of underwater acoustic signal processing. IEEE Signal Process. Mag. 1998, 15, 21–51. [Google Scholar] [CrossRef]
- Zhong, X.; Premkumar, A.B.; Wang, W. Direction of arrival tracking of an underwater acoustic source using particle filtering: Real data experiments. In Proceedings of the IEEE Tencon-Spring, Sydney, NSW, Australia, 17–19 April 2013; pp. 420–424. [Google Scholar]
- Chen, W.; Luo, T.; Chen, F.; Ji, F.; Yu, H. Directions of arrival and channel parameters estimation in multipath underwater environment. In Proceedings of the MTS/IEEE OCEANS, Shanghai, China, 10–13 April 2016; pp. 1–4. [Google Scholar]
- Amindavar, H.; Reza, A.M. A new simultaneous estimation of directions of arrival and channel parameters in a multipath environment. IEEE Trans. Signal Process. 2005, 53, 471–483. [Google Scholar] [CrossRef]
- Van Kleunen, W.A.P.; Blom, K.C.H.; Meratnia, N.; Kokkeler, A.B.J.; Havinga, P.J.M.; Smit, G.J.M. Underwater localization by combining Time-of-Flight and Direction-of-Arrival. In Proceedings of the MTS/IEEE OCEANS, Taipei, Taiwan, 7–10 April 2014; pp. 1–6. [Google Scholar]
- Guo, X.; Yang, K.; Yan, X.; Ma, Y. Theory of passive localization for underwater sources based on multipath arrival structures. In Proceedings of the MTS/IEEE OCEANS, Anchorage, AK, USA, 18–21 September 2017. [Google Scholar]
- Song, H.; Qin, J.; Yang, C.; Diao, M. Compressive Beamforming for Underwater Acoustic Source Direction-of-Arrival Estimation. In Proceedings of the IEEE ICCE-TW, Taichung, Taiwan, 19–21 May 2018. [Google Scholar]
- Lin, J.; Ma, X.; Hao, C.; Jiang, L. Direction of arrival estimation of sparse rectangular array via two-dimensional continuous compressive sensing. In Proceedings of the ICIST, Dalian, China, 6–8 May 2016; pp. 539–543. [Google Scholar]
- Li, J.; Lin, Q.h.; Kang, C.Y.; Wang, K.; Yang, X.T. DOA Estimation for Underwater Wideband Weak Targets Based on Coherent Signal Subspace and Compressed Sensing. Sensors 2018, 18, 902. [Google Scholar] [CrossRef] [PubMed]
- Abdi, A.; Guo, H.; Sutthiwan, P. A New Vector Sensor Receiver for Underwater Acoustic Communication. In Proceedings of the MTS/IEEE OCEANS, Vancouver, BC, Canada, 29 September–4 October 2007; pp. 1–10. [Google Scholar]
- Zhao, T.; Chen, H.; Zhang, H.; Li, Z.; Tong, L. Design of underwater particle velocity pickup sensor. In Proceedings of the IEEE/OES COA, Harbin, China, 9–11 January 2016; pp. 1–6. [Google Scholar]
- Cao, J.; Liu, J.; Wang, J.; Lai, X. Acoustic vector sensor: Reviews and future perspectives. IET Signal Process. 2017, 11, 1–9. [Google Scholar] [CrossRef]
- Sun, G.; Hui, J.; Chen, Y. Fast direction of arrival algorithm based on vector-sensor arrays using wideband sources. Springer J. Mar. Sci. Appl. 2008, 7, 195–199. [Google Scholar] [CrossRef]
- Gentner, P.K.; Gartner, W.; Hilton, G.; Beach, M.E.; Mecklenbräuker, C.F. Towards a hardware implementation of ultra-wideband beamforming. In Proceedings of the ITG WSA, Bremen, Germany, 23–24 February 2010; pp. 408–413. [Google Scholar]
- Wang, L.; Heng, C.; Lian, Y. CMOS UWB beamforming radar system. In Proceedings of the IEEE ICECS, Marseille, France, 7–10 December 2014; pp. 810–813. [Google Scholar]
- Wang, B.; Gao, H.; Matters-Kammerer, M.K.; Baltus, P.G.M. Interpolation based wideband beamforming architecture. In Proceedings of the IEEE ISCAS, Baltimore, MD, USA, 28–31 May 2017; pp. 1–4. [Google Scholar]
- Stojanovic, M.; Catipovic, J.A.; Proakis, J.G. Reduced-complexity spatial and temporal processing of underwater acoustic communication signals. J. Acoust. Soc. Am. 1995, 98, 961–972. [Google Scholar] [CrossRef]
- Nieman, K.F.; Perrine, K.A.; Henderson, T.L.; Lent, K.H.; Brudner, T.J.; Evans, B.L. Wideband monopulse spatial filtering for large receiver arrays for reverberant underwater communication channels. In Proceedings of the MTS/IEEE OCEANS, Seattle, WA, USA, 20–23 September 2010; pp. 1–8. [Google Scholar]
- Li, X.; Jia, H.; Yang, M. Underwater target detection based on fourth-order cumulant beamforming. ASA Proc. Meet. Acoust. 2017, 31, 1–9. [Google Scholar]
- Diamant, R. Closed Form Analysis of the Normalized Matched Filter With a Test Case for Detection of Underwater Acoustic Signals. IEEE Access 2016, 4, 8225–8235. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. Proc. AAAI KDD 1996, 96, 226–231. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Scikit-learn—Clustering. Available online: https://scikit-learn.org/stable/modules/clustering.html#clustering (accessed on 1 July 2020).
- Diamant, R.; Voronin, V.; Kebkal, K.G. Design Structure of SYMBIOSIS: An Opto-Acoustic System for Monitoring Pelagic Fish. In Proceedings of the MTS/IEEE OCEANS, Marseille, France, 17–20 June 2019; pp. 1–6. [Google Scholar]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A Fresh Approach to Numerical Computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dubrovinskaya, E.; Kebkal, V.; Kebkal, O.; Kebkal, K.; Casari, P. Underwater Localization via Wideband Direction-of-Arrival Estimation Using Acoustic Arrays of Arbitrary Shape. Sensors 2020, 20, 3862. https://doi.org/10.3390/s20143862
Dubrovinskaya E, Kebkal V, Kebkal O, Kebkal K, Casari P. Underwater Localization via Wideband Direction-of-Arrival Estimation Using Acoustic Arrays of Arbitrary Shape. Sensors. 2020; 20(14):3862. https://doi.org/10.3390/s20143862
Chicago/Turabian StyleDubrovinskaya, Elizaveta, Veronika Kebkal, Oleksiy Kebkal, Konstantin Kebkal, and Paolo Casari. 2020. "Underwater Localization via Wideband Direction-of-Arrival Estimation Using Acoustic Arrays of Arbitrary Shape" Sensors 20, no. 14: 3862. https://doi.org/10.3390/s20143862
APA StyleDubrovinskaya, E., Kebkal, V., Kebkal, O., Kebkal, K., & Casari, P. (2020). Underwater Localization via Wideband Direction-of-Arrival Estimation Using Acoustic Arrays of Arbitrary Shape. Sensors, 20(14), 3862. https://doi.org/10.3390/s20143862





