Development and Application of Infrared Thermography Non-Destructive Testing Techniques
Abstract
1. Introduction
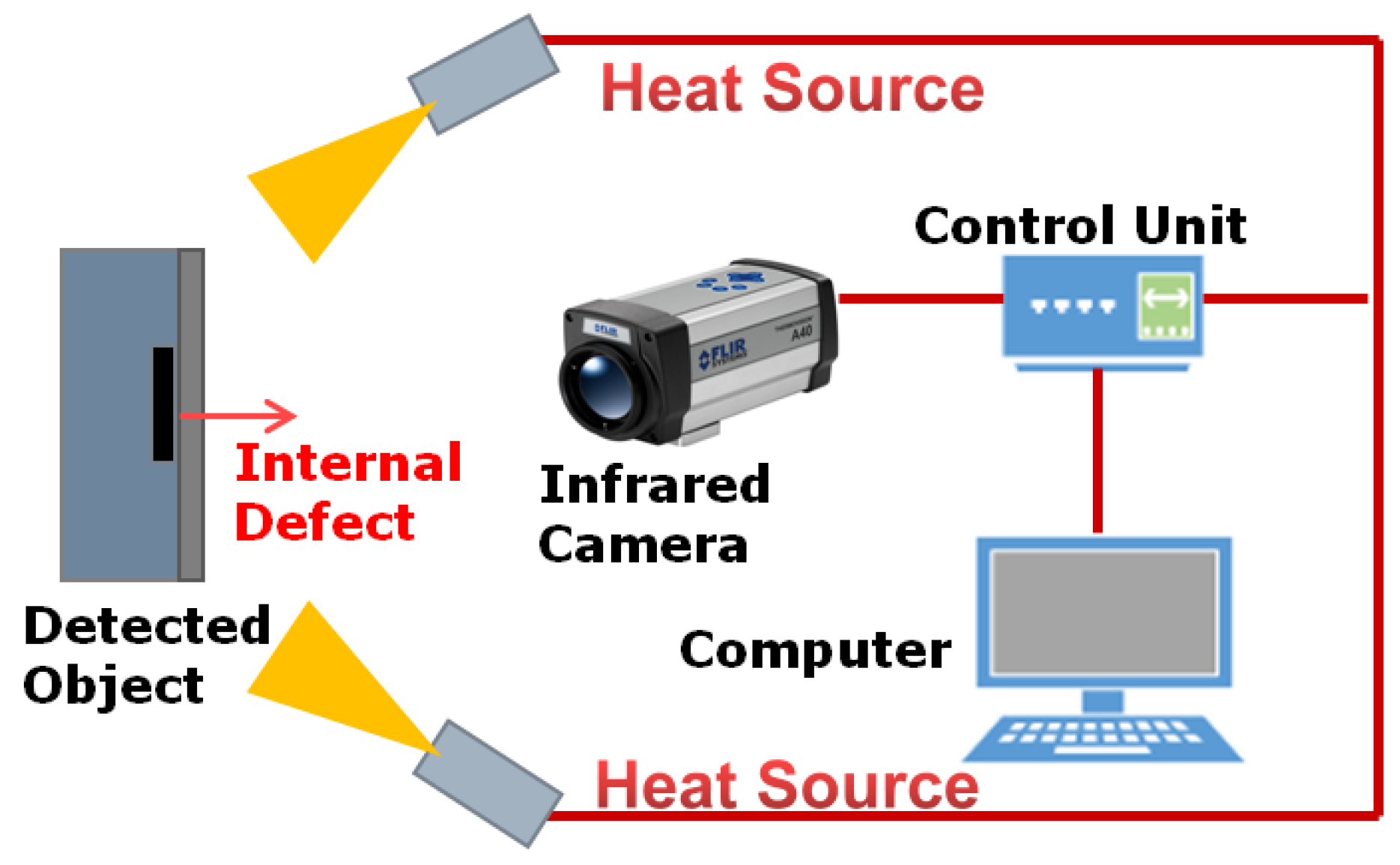
2. Principle and Classification
2.1. Theoretical Basis
2.2. Classification of Infrared Thermal Wave Testing
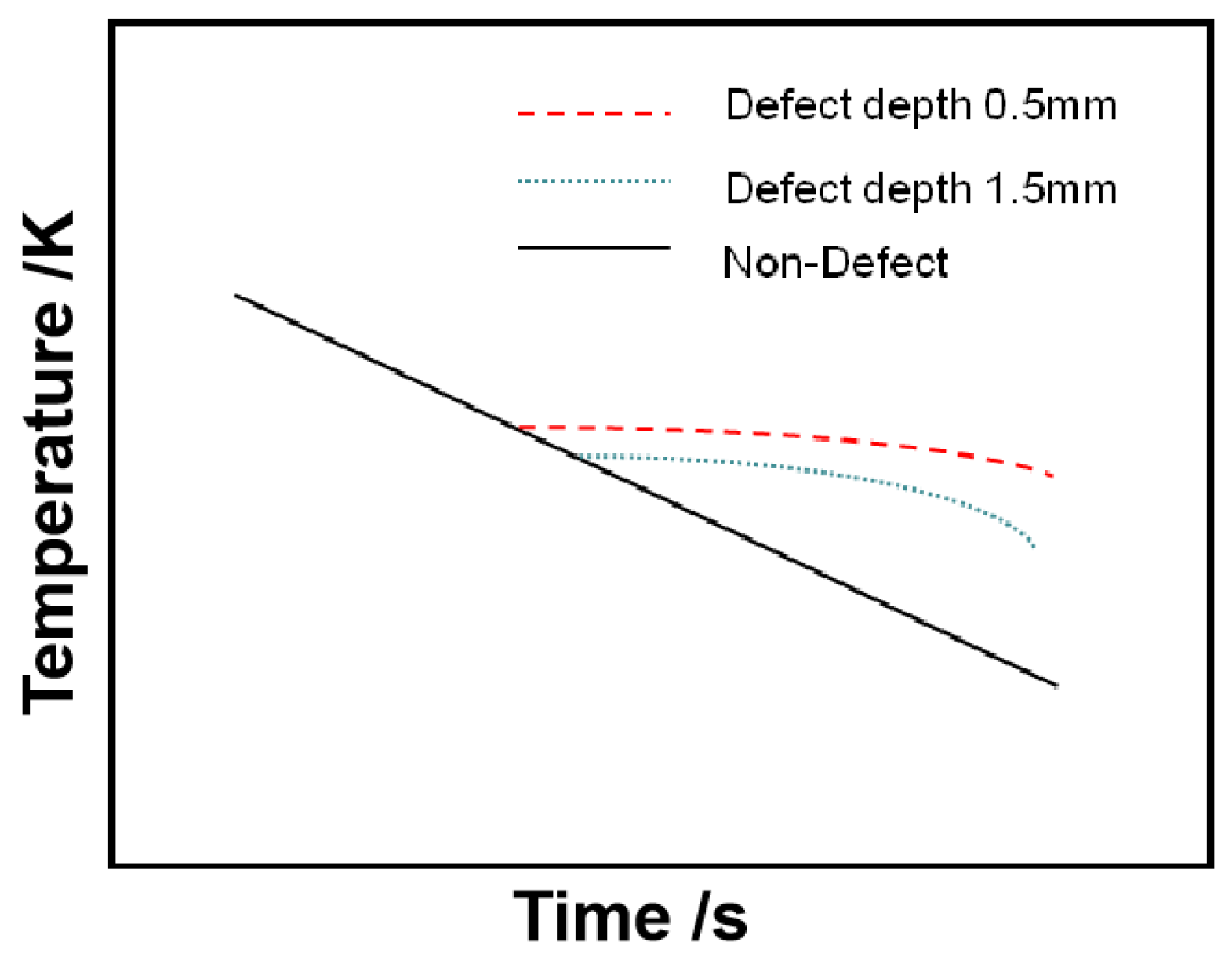
2.2.1. Infrared Pulsed Thermography Testing
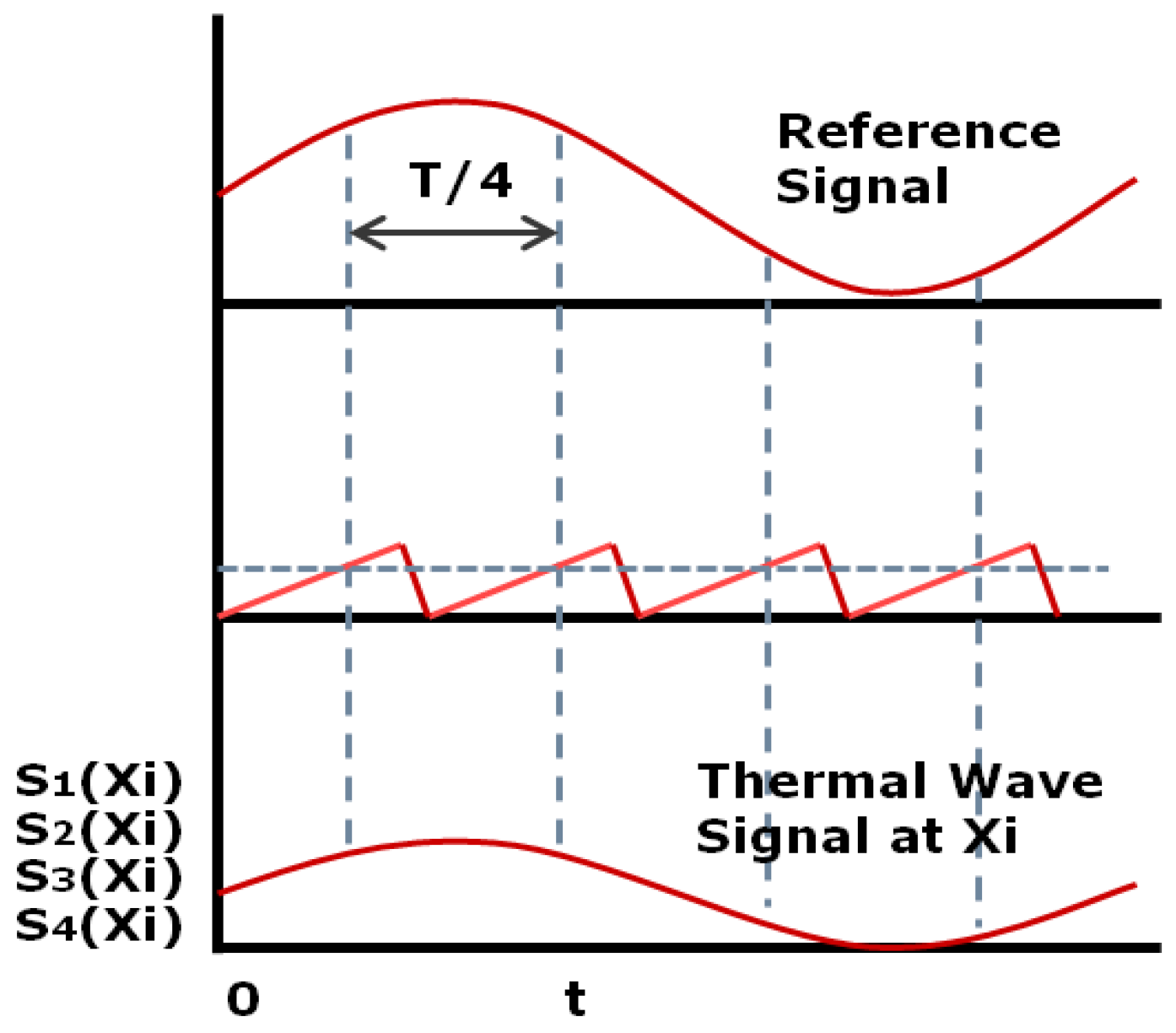
2.2.2. Infrared Lock-in Thermography Testing
2.2.3. Infrared Ultrasonic Thermography Testing
- (1)
- Ultrasonic wave propagation in sheet metal.The displacement partial differential control equation (Navier governing equation) iswhere ui and fi are the position and volume force tensors, respectively, μ is the trimming modulus λ is the lame constant, and ρ is the component density.
- (2)
- Ultrasonic vibration heat generation at defect contact interface.The heat flux Q(t) is calculated by the equationwhere v(t) and are the relative and tangential velocity of the interface contact point respectively, and μs and μd are the static and dynamic friction coefficients at the defect, respectively. FN(t) is the contact force, and c is the velocity coefficient for converting static friction into dynamic friction.
- (3)
- Conduction of heat flow at the defect.The propagation of the heat flux Q caused by ultrasonic stimulation at the defect satisfies the heat conduction differential equationwhere k and c are the thermal conductivity, density, and specific heat of object, respectively.
2.2.4. Infrared Laser Scanning Thermography Testing
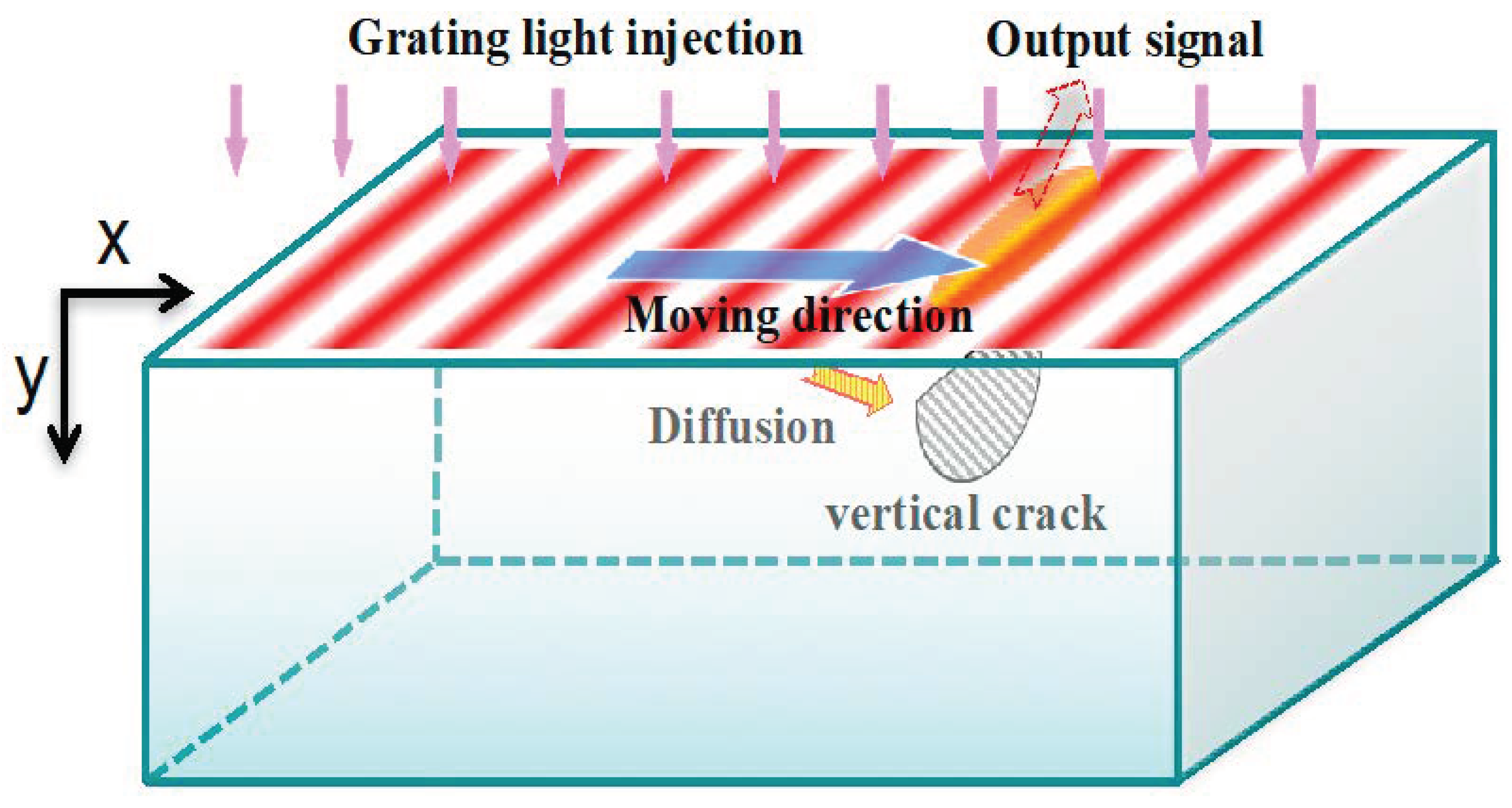
2.2.5. Grating Infrared Thermal Wave Scanning Testing
3. Infrared Image-Processing Technology
3.1. Analysis of Infrared Thermography Testing Factors
3.2. Thermal Wave Image-Processing Method
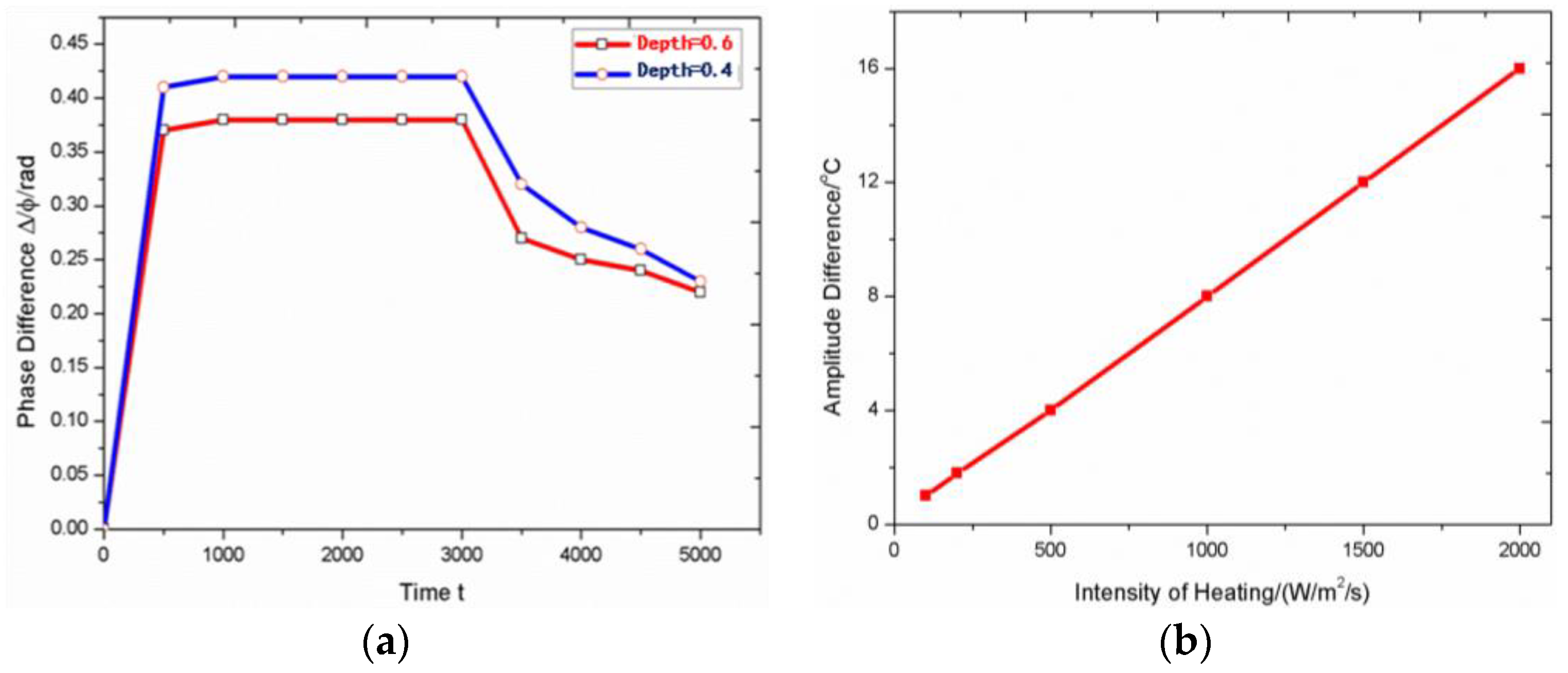
4. Quantitative Detection of Defects
5. Application of Infrared Thermography Testing
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vavilov, V.P.; Shirvaev, V.V.; Rinato, E.G. Detection of hidden corrison in metals by using transient infrared thermography. Insight 1998, 40, 408–410. [Google Scholar]
- Milne, J.M.; Reynolds, W.N. The nondestructive evaluation of composite and other materials by thermal pulse video thermography. SPIE 1984, 520, 112–119. [Google Scholar]
- Itoh, Y.; Saitoh, M. Evaluation of delamination crack for thermal barrier coating using infrared thermography analysis. J. Hig. Temp. Soc. JPN. 1995, 21, 240–247. [Google Scholar]
- Busse, G.; Wu, D.; Karpen, W. Thermal wave imaging with phase sensitive modulated thermography. J. Appl. Phys. 1992, 71, 3962. [Google Scholar] [CrossRef]
- Wu, D.; Salerno, A.; Busse, G. Lock-in thermography for non-destructive evaluation of aerospace structures [A]. In Proceedings of the 7th European Conference on Non-Destructive Testing, Copenhagen, Denmark, 26–29 May 1998. [Google Scholar]
- Dillenz, A.; Busse, G.; Wu, D. Ultrasound Lock-in thermography: Feasibilities and limitation [A]. In Proceedings of the Diagnostic Imaging Technologies and Industrial Applications, Munich, Germany, 14–15 June 1999; Volume 3827, pp. 10–15. [Google Scholar]
- Wu, D.; Busse, G. Lock-in thermography for nondestructive evaluation of materials. Rev. Gen. Therm. 1998, 37, 693–703. [Google Scholar] [CrossRef]
- Lau, S.K.; Almond, D.P.; Milne, J.M. A quantitative analysis of pulsed video thermography. NDT E Int. 1991, 24, 195–202. [Google Scholar] [CrossRef]
- Almond, D.P.; Patel, P.M. Photo Thermal Science and Techniques; Chapman-Hall: London, UK, 1996; Volume 2, pp. 313–326. [Google Scholar]
- Ball, R.J.; Almond, D.P. The Detection and measurement of impact damage in thick carbon fiber reinforced laminates by transient thermography. NDT E Int. 1998, 31, 165–175. [Google Scholar] [CrossRef]
- Almond, D.P.; Peng, W. Thermal imaging of composites. J. Microsc. 2001, 201, 163–170. [Google Scholar] [CrossRef]
- Avdelidis, N.P.; Almond, D.P.; Dobbinson, A. Aircraft composites assessment by means of transient thermal NDT. Prog. Aerosp. Sci. 2004, 40, 143–162. [Google Scholar] [CrossRef]
- Barden, T.J.; Almond, D.P.; Morbidini, M. Advances in thermosonics for detecting impact damage in CFRP composites. Insight-Non-Destr. Test. Cond. Monit. 2006, 48, 90–93. [Google Scholar] [CrossRef]
- Pickering, S.G.; Almond, D.P. An evaluation of the performance of an uncooled micro bolometer array infrared camera for transient thermography NDE. Nondestr. Test. Eval. 2007, 22, 63–70. [Google Scholar] [CrossRef]
- Jiang, H.J.; Chen, L. Research status and development trend of pulsed infrared nondestructive testing technology. Infrared Technol. 2007, 40, 946–951. [Google Scholar]
- Ptaszek, G.; Cawley, P.; Almond, D. Artificial disbonds for calibration of transient thermography inspection of thermal barrier coating systems. NDT E Int. 2012, 45, 71–78. [Google Scholar] [CrossRef]
- Almond, D.P.; Pickering, S.G. An analytical study of the pulsed thermograpy defectdetection limit. J. Appl. Phys. 2012, 093510, 1. [Google Scholar]
- Maldague, X.V.; Marinetti, S. Pulse phase infrared thermography. Appl. Phys. 1996, 79, 2694–2698. [Google Scholar] [CrossRef]
- Vallerand, S.; Maldague, X. Defect Characterization in pulsed thermography:a statistical method compared with Kohonen and perceptron neural networks. NDT E Int. 2000, 33, 307–315. [Google Scholar] [CrossRef]
- Maldague, X.V.; Galmiche, F.; Ziadi, A. Advances in pulsed phase thermography. Infrared Phys. Technol. 2002, 43, 175–181. [Google Scholar] [CrossRef]
- Maldague, X.V. Introduction to NDT by active Infrared thermography. Mater. Eval. 2002, 60, 1060–1073. [Google Scholar]
- Maldague, X.V.; Ziadi, A.; Klein, M. Double pulse infrared thermography. NDT E Int. 2004, 37, 559–564. [Google Scholar] [CrossRef]
- Tuli, S.; Mulaveesala, R. Defect detection by pulse compression in frequency modulated thermal wave imaging. Quant. Infrared Thermogr. 2005, 2, 41. [Google Scholar] [CrossRef]
- Tuli, S.; Mulaveesala, R. Theory of frequency modulated thermal wave imaging for nondestructive subsurface defect detection. Appl. Phys. Lett. 2006, 89, 191–913. [Google Scholar]
- Ibrra-Castanedo, C.; Marc, G.; Maldague, X.V. Inspection of aerospace materials by pulsed thermography, 1ock-in thermography and vibrothermography: A Comparative Study. In Proceedings of the Thermosence XXIX, Defense and Security Symposium SPIE, Orlando, FL, USA, 9–12 April 2007; Volume 6541, pp. 1–9. [Google Scholar]
- Vavilov, V.P.; Klimov, A.G.; Shiryaev, V.V. Active thermal detection of water in cellular aircraft structures. Russ. J. Nondestruct+. 2002, 38, 927–936. [Google Scholar] [CrossRef]
- Schroeder, J.A.; Ahmed, T.; Chaudhry, B. Non-destructive testing of structural composites and adhesively bonded composite joints: Pulsed thermography. Compos. Part A Appl. Sci. Manuf. 2002, 33, 1511–1517. [Google Scholar] [CrossRef]
- Shepard, S.M.; Lhota, J.R.; Rubadeux, B.A. Reconstructionand enhancement of active thermographic images equences. SPIE Opt. Eng. 2003, 42, 1337–1342. [Google Scholar] [CrossRef]
- Mulaveesala, R.; Tuli, S. Phase sensitive digitized thermal wave imagingand pulse compression for NDE applications. In Proceedings of the SPIE 2006, Orlando, FL, USA, 18 April 2006; Volume 620, pp. 5–15. [Google Scholar]
- Favro, L.D.; Kuo, P.K.; Thomas, R.L. Thermal wave imaging for aging aircraft inspection. Mater. Eval. 1993, 53, 1386–1389. [Google Scholar]
- Gonzalez, D.A.; Ibarra-Castanedo, C.; Madruga, F.J. Differentiated absolute phasecontrast algorithm for the analysis of pulsed thermographic sequences. Infrared Phys. Tech. 2006, 48, 16–21. [Google Scholar] [CrossRef]
- Krishnapillai, M.; Jones, R.; Marshall, I.H. NDTE using pulse thermography: Numerical modeling of composite subsurface defects. Compos. Struct. 2006, 75, 241–249. [Google Scholar] [CrossRef]
- Sun, J.G. Analysis of pulsed thermography methods for detect depth prediction. J. Heat Trans. 2006, 28, 329–338. [Google Scholar] [CrossRef]
- Pan, M.C.; He, Y.Z.; Tian, G.Y. Defect characterisation using pulsed eddy current thermography under transmission mode and NDT applications. NDT E Int. 2012, 52, 28–36. [Google Scholar] [CrossRef]
- Han, X.Y.; Favro, L.D.; Kuo, P.K. Early-time pulse-echo thermal wave imaging. In Proceedings of the Twenty-Second Symposium on Quantitative Nondestructive Evaluation. Seattle: CSA, Seattle, WA, USA, 3–8 August 1986; pp. 519–524. [Google Scholar]
- Newaz, G.; Chen, X. Progressive damage assessment in thermal barrier coatings using thermal wave imaging technique. Surf. Coat. Tech. 2005, 190, 7–14. [Google Scholar] [CrossRef]
- Carlomagno, G.M.; Meola, C. Comparison between thermographic techniques for frescoes NDT. NDT E Int. 2006, 35, 559–565. [Google Scholar] [CrossRef]
- Angelidis, N.; Irving, P.E. Detection of impact damage in CFRPlaminates by means of electrical potential techniques. Compos. Sci. Tecnol. 2007, 67, 594–604. [Google Scholar] [CrossRef]
- Chambers, A.R.; Mowlem, M.C.; Dokos, L. Evaluating impact damage in CFRP using fiber optic sensors. Compos. Sci. Tecnol. 2007, 67, 1235–1242. [Google Scholar] [CrossRef]
- Thomas, R.L.; Han, X.Y.; Favro, L.D. Thermal wave imaging of aircraft for evaluation of disbonding and corrosion. In Proceedings of the 7th European Conference on Non-Destructive Testing Copenhagen: NDT, Copenhagen, Denmark, 26–29 May 1998; pp. 126–130. [Google Scholar]
- Favro, L.D.; Ahmed, T.; Han, X.Y. Thermal Wave Imaging of Disbonding and Corrosion on Aircraft. Rev. Prog. Quant. Nondestruct. Evaluation. 1995, 15, 1747–1753. [Google Scholar]
- Han, X.Y.; Favro, L.D.; Thomas, R.L. Thermal wave NDI of Disbonds and corrosion in aircraft. In Proceedings of the Second Joint NASA/FAA/DOD Conference on Aging Aircraft America: NASA, Ogden, UT, USA, 8–10 July 1999; pp. 265–274. [Google Scholar]
- Bisle, W. NDT toolbox for honeycomb sandwich structures-a comprehensive approach for maintenance inspections. In Proceedings of the ATA NDT Forum America: ATA NDT Forum, Albuquerque, NM, USA, 20–23 September 2010; pp. 1–8. [Google Scholar]
- Giguere, J. Damage mechanisms and non-destructive testing in case of water ingress in CF-18 flight control surfaces. In Proceedings of the Canada: Canada Defence and Civil Institute of Environmental Medicine, Downsview Ontario, ON, USA, August 2000; pp. 1–36. Available online: https://apps.dtic.mil/sti/citations/ADA388125 (accessed on 10 July 2020).
- Genest, M.; Ibarra-Castanedo, C.; Piau, J.M. Comparison of thermography techniques for inspection of F/A-18 honeycomb structures. In Proceedings of the ASNT Spring Conference America: ASNT Spring Conference, St. Louis, MO, USA, 16–20 March 2009; pp. 1–14. [Google Scholar]
- Ibrra-Castanedo, C.; Brault, L.; Marcotte, F. Water ingress detection in honeycomb sandwich panels by passive infrared thermography using a high-esolution thermal imaging camera. In Proceedings of the Thermosense, Thermal Infrared Applications XXXIV, Orlando, FL, USA, 25 April 2012; Volume 8354, pp. 1–8. [Google Scholar]
- Minh, P.H. Fatigue limit evaluation of metals using a infrared thermographic techniques. Mech Mater. 1998, 28, 155–163. [Google Scholar]
- Manohar, A.; di Lanza, S.F. Determination of Defect Depth and Size Using Virtual Heat Sources in Pulsed Infrared Thermography. Infrared Phys. Tech. 2012, 53, 661–671. [Google Scholar] [CrossRef]
- Dillenz, A.; Zweschper, T.; Busse, G. Burst phase angle thermographywith elstic waves. Proc. SPIE 2002, 4710, 572–577. [Google Scholar]
- Han, X.Y.; Favro, L.D.; Li, L. Quantitative thermal wave carrion measurements on a DC-9 Belly skin in the presence of irregular paint thickness variations. Rev. Prog. Quant. Nondestruct. Eval. 2001, 20, 483–486. [Google Scholar]
- Ludwig, N.; Teruzzi, P. Heat losses and 3D diffusion phenomena for defect sizingprocedures in video pulse Thermography. Infrared Phys. Tech. 2002, 43, 297–301. [Google Scholar] [CrossRef]
- Han, X.Y.; Favro, L.D.; Thomas, R.L. Quantitative Defect Depth Measurements for NDE of Composites [A]. In Proceedings of the American Society for Composites, Dayton, OH, USA, 7–9 October 1986; Technomic Publishing: Lancaster, PA, USA, 1998; pp. 1077–1081. [Google Scholar]
- Gleiter, A.; Riegert, G.; Zweachper, T. Ultrasound lock –in thermography for advanced depth resolved defect selective imaging. Insight Non-Destr. Test. Cond. Monit. 2007, 5, 272–274. [Google Scholar] [CrossRef]
- Wallbrink, C.; Wade, S.A.; Jones, R. The effect of size on the quantitative estimation of defect depth in steel structures using lock-in thermography. J. Appl. Phys. 2007, 101, 104907. [Google Scholar] [CrossRef]
- Liu, J.Y.; Dai, J.M.; Wang, Y. Theory and experiment of IR lock-in thermography with image sequence processing. Infrared Laser Eng. 2009, 38, 346–351. (In Chinese) [Google Scholar]
- Bai, W.; Wong, B.S. Evaluation of defects in composite plates under convective environments using lock-in thermography. Meas. Sci. Technol. 2001, 12, 142–150. [Google Scholar] [CrossRef]
- Montanini, R. Quantitative determination of subsurface defects in a reference specimenmade of Plexiglas by means of lock-in and pulse phase infrared thermography. Infrared Phys. Tech. 2010, 53, 363–371. [Google Scholar] [CrossRef]
- Feng, L.; Tao, N.; Xu, C. Lock-in thermography and its application in nondestructive evaluation. Infrared Laser Eng. 2010, 39, 1121–1123. [Google Scholar]
- Denis, A.; Vasyl, R. A digital lock-in technique for small signal detection with square wave reference over a wide frequency range. In Proceedings of the 14th International Conference on Advanced Trends in Radioelecrtronics, Telecommunications and Computer Engineering, Lvivska Oblast, Ukraine, 20–24 February 2018. [Google Scholar]
- Li, G.; Zhang, S.; Zhou, M.; Li, Y.; Lin, L. A method to remove odd harmonic interferences in square wave reference digital lock-in amplifier. Rev. Sci. Instrum. 2013, 84, 025115. [Google Scholar] [CrossRef]
- Zweschper, T.; Gleiter, A.; Riegert, G. Ultrasound excited thermography using frequency modulated elastic waves. Insight Non-Destr. Test. Cond. Monit. 2003, 45, 178–182. [Google Scholar] [CrossRef]
- Chen, D.P.; Zeng, Z.; Tao, N. Air-coupled ultrasonic thermography for inspecting impact damages in CFRP composite. Chin. Opt. Lett. 2012, 10, S10401. [Google Scholar] [CrossRef]
- Krapez, J.C.; Taillade, F.; Balageas, D. Untrasound-Lock-in-Thermography NDE Ofcomposite Plates with Low Power Actuators. Experimrntal Investigation of the Influence of the Lamb Wave Frequency. Quant. InfraRed Thermogr. J. 2005, 2, 191–206. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C.; Piau, J.M.; Guilbert, S. Comparative study of active thermography techniques for the nondestructive evaluation of honeycomb structures. Res. Nondestruct. Eval. 2009, 20, 1–31. [Google Scholar] [CrossRef]
- Qu, Z.; Zhang, W.X.; Lv, Z.C. A New Grating Thermography for Nondestructive Detection of Cracks in Coatings: Fundamental Principle. Coatings 2019, 9, 411. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C.; Maldague, X. Pulsed Phase Thermography Inversion Procedureusing Normalized Parameters to Account for Defect Size Variations. In Thermosense XXVII International Society for Optics and Photonics; SPIE: Bellingham, WA, USA, 2006; Volume 5782, pp. 334–341. [Google Scholar]
- Chen, D.P.; Wu, N.M.; Zhang, Z. Defect recognition in thermosonic imaging. Chin. J. Aeronaut. 2012, 25, 657–662. [Google Scholar] [CrossRef]
- Am, Y.K.; Kim, J.M.; Sohn, H. Laser lock-in thermography for fatigue crack detection in an uncoated metallic strncture. SPIE 2013, 8692, 1–11. [Google Scholar]
- Liu, J.Y.; Dai, J.M.; Wang, Y. Thermal wave detection and defect depth measurement based on lock-in thermography. Opt. Precis. Eng. 2010, 18, 37–44. [Google Scholar]
- Jiang, H.Y.; Chen, L. Application of Laser Scanning Infrared Thermography for Measuring Film Thickness. Infrared Technol. 2017, 39, 1144–1148. [Google Scholar]
- Burrows, S.E.; Dixon, S.; Pickering, S.G. Thermographic detection of surface breaking defects using ascanning laser source. NDT E Int. 2011, 44, 589–596. [Google Scholar] [CrossRef]
- Palumbo, D.; Galietti, U. Damage investigation in composite materials by means of new thermal data processing procedures. Strain 2016, 52, 276–285. [Google Scholar] [CrossRef]
- Chen, J.; Tong, W.; Cao, Y.; Feng, J.; Zhang, X. Effect of atmosphere on phase transformation in plasma-sprayed hydroxyapatite coatings during heat treatment. J. Biomed. Mater. Res. 1997, 34, 15–20. [Google Scholar] [CrossRef]
- Pitarresi, G. Lock-In Signal Post-Processing Techniques in Infra-Red Thermography for Materials Structural Evaluation. Exp. Mech. 2016, 55, 667–680. [Google Scholar] [CrossRef]
- Toubal, L.; Karama, M.; Lorrain, B. Damage evolution and infrared thermography in woven composite laminates under fatigue loading. Int. J. Fatigu. 2006, 28, 1867–1872. [Google Scholar] [CrossRef]
- Dolinkoa, A.E.; Kaufmann, G.H. Enhancement in flaw detectability by means of lock-in temporal speckle pattern interferometry and thermal Waves. Opt. Laser Eng. 2007, 45, 690–694. [Google Scholar] [CrossRef]
- Breitenstein, O.; Warta, W.; Langenkamp, M. Lock-in Thermography Basics and Use for Evaluating Electronic Devices and Materials; Springer Series in Advanced Microelectronies; Springer: Berlin/Heidelberg, Germany, 2010; pp. 149–224. [Google Scholar]
- Zenzinger, G.; Bamberg, J.; Satzger, W. Thermographic crack detection by eddy current excitation. Nondestruct. T. Eva. 2007, 22, 101–111. [Google Scholar] [CrossRef]
- Li, T.; Almond, D.P.; Rees, D.A.S. Crack Imaging by Scanning Laser-Line. Meas. Sci. Technol. 2011, 22, 407–414. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Xinmin, Z.; Xiao, H.; Hu, X.; Sun, J. Sinewave fit algorithm based on total least-squares method with application to ADC effective bits measurement. Instrumentation and Measurement. IEEE Trans. 1997, 46, 1026–1030. [Google Scholar]
- Forsyth, D.S.; Genest, M.; Shaver, J. Nondestructive testing methods for the detection. Int. J. Fatigue. 2007, 29, 810–821. [Google Scholar] [CrossRef]
- Shepard, S.M.; Lhota, J.R.; Ahmed, T. Measurement Limits in FlashThermography. In Thermosense XXXI, International Society for Optics and Photonics; SPIE: Bellingham, WA, USA, 2009; Volume 7299, pp. 1–7. [Google Scholar]
- Qu, Z.; Li, L.X.; Zhang, W.X. Research on finite element analysis of the infrared grating lock-in thermal imaging method. Int. J. Comput. Phys. 2018, 1, 204–215. [Google Scholar] [CrossRef]
- Marinetti, S.; Grinzato, E.; Bison, P.G. Statistical analysis of IRthermographic sequences by PCA. Infrared Phys. Technol. 2004, 46, 85–91. [Google Scholar] [CrossRef]
- Mandelis, A.; Paoloni, S.; Nicolaides, L. Lock-in common-mode rejection demodulation: Measurement technique and applications to thermal-wave detection: Theoretical. Rev. Sci. Instrum. 2000, 71, 2440–2449. [Google Scholar] [CrossRef][Green Version]
- Ptaszek, G.; Cawley, P.; Almond, D. Transient thermography testing of unpainted thermal barrier coating (TBC) systems. NDT E Int. 2013, 59, 48–56. [Google Scholar] [CrossRef]
- Tse, P.W.; Zhang, J.Y.; Wang, X.J. Blind source separation and blind equalization algorithms for mechanical signal separation and identification. J. Vib. Control 2016, 12, 395–423. [Google Scholar] [CrossRef]
- Castanedo, I.C.; Gonzalez, D.; Klein, M. Infrared image processing and data analysis. Elsevier 2004, 46, 75–83. [Google Scholar]
- Tang, Q.J.; Liu, J.Y.; Wang, Y. Experimental study of inspection on SiC coated high—Temperature alloy plates with defects using pulsed thermographic technique. Infrared Phys. Technol. 2013, 57, 21–27. [Google Scholar] [CrossRef]
- Rajic, N. Principal component thermography for flaw contrast enhancement and flaw depth characterisation in composite structures. Compos. Struct. 2002, 58, 521–528. [Google Scholar] [CrossRef]
- Yang, L.; Zhou, Y.C.; Lu, C. Damage evolution and rupture time prediction in thermal barrier coatings subjected to cyclic heating and cooling: An acoustic emission method. Elsevier 2011, 59, 6519–6529. [Google Scholar] [CrossRef]
- Omar, M.A.; Parvataneni, R.; Zhou, Y. A combined approach of self-referencing and Principle Component Thermography for transient, steady, and selective heating scenarios. Infrared Phys. Technol. 2010, 53, 358–362. [Google Scholar] [CrossRef]
- Rami, H.A.; Bo-Siou, W.; Shane, J. Thermoelastic and infrared-thermography methods for surface strains in cracked orthotropic composite materials. Eng. Fract. Mech. 2008, 75, 58–75. [Google Scholar]
- Sun, J.G.; Deemer, C.M.; Ellingson, W.A. NDT technologies for ceramic matrix composites: Oxide andnonoxide. Mater. Eval. 2006, 64, 52–60. [Google Scholar]
- Yao, W.B.; Dai, C.Y.; Mao, W.G. Acoustic emission analysis on tensile failure of air plasma-sprayed thermal barrier coatings. Surf. Coat. 2012, 206, 3803–3807. [Google Scholar] [CrossRef]
- Marinetitis, F.; Marsilloe, E. Matrix factorization methods: Application to thermal. NDT E Int. 2006, 39, 611–616. [Google Scholar] [CrossRef]
- Pickering, S.G.; Almond, D.P. Matched excitation energy comparison of the pulse and lock-in thermography NDE techniques. NDT E Int. 2008, 41, 501–509. [Google Scholar] [CrossRef]
- Maldague, X.; Moor, P.O. Infrared and Thermal Testing: Nondestructive Testing Handbook; The American Society for Nondestructive Testing: Columbus, OH, USA, 2001; pp. 48–93. [Google Scholar]
- Shepard, S.M.; Lhota, J.R.; Hou, Y.L. Blind Characterization of Materials Using Single-Sided Thermography. In Proceedings of the SPIE Defense and Security, Orlando, FL, USA, 12–16 April 2004; Volume 5405, pp. 442–446. [Google Scholar]
- Bision, P.G.; Marinetti, S.; Grinzato, E. Inspecting thermal barrier coatings by IR thermography. In Proceedings of the Aerosense 2003, Orlando, FL, USA, 21–25 April 2003; pp. 318–327. [Google Scholar]
- Shi, W.X.; Huang, X.F.; Liu, Z.W. Transmission-lattice based geometric phase analysis for evaluating the dynamic deformation of a liquid surface. Opt. Express 2014, 22, 10559. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.M.; Miya, K.; Kurokawa, M. Enhancement of ECT Technique by Probe Optimization and Reconstruction of Cracks. NDT E Int. 1999, 32, 54–56. [Google Scholar]
- Golosnoy, I.O.; Tsipas, S.A.; Clyne, T.W. An Analytical Model for Simulation of Heat Flow in Plasma-Sprayed Thermal Barrier Coatings. J. Therm. Spray Technol. 2005, 14, 205–214. [Google Scholar] [CrossRef]
- Chaki, S.; Marical, P.; Panier, S. Interfacial defects detection in plasma-sprayed ceramic coating components using two stimulated infrared thermography techniques. NDT E Int. 2011, 44, 519–522. [Google Scholar] [CrossRef]
- Chen, D.P.; Zhang, X.L.; Zhang, G. Infrared thermography and its applications in aircraft Non-destructive testing. In Proceedings of the 2016 International Conference on Identification, Information and Knowledge in the Internet of Things (IIKI), Beijing, China, 20–21 October 2016; pp. 374–379. [Google Scholar]
- Swiderski, W. Loci-in Thermography to rapid evaluation of destruction areain composite materials used in military application. SPIE 2002, 5132, 506–517. [Google Scholar]
- Steven, M.S.; James, R.L. Flash Duration and Timing ffects in Thermographic NDT. SPIE 2005, 5782, 352–358. [Google Scholar]
- Bento, A.C.; Brown, S.R.; Almond, D.P. Thermal wave nondestructive thickness measurement of hydroxyapatite coating applied to prosthetic hip stems. J. Mater. Sci. Mater. Med. 1995, 6, 335–339. [Google Scholar] [CrossRef]
- Sargent, J.P.; Almond, D.P.; Gathercole, N. Thermal wave measurement of wet paint film thickness. J. Mater. Sci. 2006, 41, 333–339. [Google Scholar] [CrossRef]
- Franke, B.; Sohn, Y.H.; Chen, X. Monitoring damage evolution in thermal brrier coating with thermal wave imaging. Surf. Coat. Technol. 2005, 200, 1292–1297. [Google Scholar] [CrossRef]
- Marinetti, S.; Robba, D.; Cermuschi, F. Thermographic inspection of TBC coated gas turbine blades discrimination beween coating over thickness and adhesion defeats. Infared Phys. Technol. 2007, 49, 281–285. [Google Scholar] [CrossRef]
- Ivan, G.; Susana, L.; Pedro, A. Infrared Thermography’s Application to Infrastructure Inspections. Infrastructures 2018, 3, 339–346. [Google Scholar]
- Fokaides, P.A.; Kalogirou, S.A. Application of infrared thermography for the determination of the overall heat transfer coefficient (U-Value) in building envelopes. Appl. Energy 2011, 88, 4358–4365. [Google Scholar] [CrossRef]
- Meola, C.; Carlomagno, G.M.; Squillace, A.; Giorleo, G. Non-destructive control of industrial materials by means of lock-in thermography. Meas. Sci. Technol. 2002, 13, 1583–1590. [Google Scholar] [CrossRef]
- Orlande, H.R.B. Inverse problems in heat transfer: New trends on solution methodologies and applications. J. Heat Transf. 2012, 134, 112–117. [Google Scholar] [CrossRef]
- Peng, D.; Jones, R. Modelling of the lock-in thermography rocess through finite element method for estimating the rail squat defects. Eng. Fail. Anal. 2013, 28, 275–288. [Google Scholar] [CrossRef]
- Chatterjeea, K.; Tuli, S.; Pickering, S.G.; Almond, D.P. An objective comparison of pulsed, lock-in, and frequency modulated thermal wave imaging. In Proceedings of the AIP Conference Proceedings, Burlington, VT, USA, 16–21 July 2011; pp. 1812–1815. [Google Scholar]
- Sakagami, T.; Izumi, Y.; Mori, N. Development of self-reference lock-in thermography and its application to remote nondestructive inspection of fatigue cracks in steel bridges. In Proceedings of the 10th international conference on quantitative infrared thermography, Québec, ON, Canada, 24–29 June 2010. [Google Scholar]
- Shrestha, R.; Choi, M.; Kim, W. Quantification of defects depth in glass fiber reinforced plastic plate by infrared lock-in thermography. J. Mech. Sci. Technol. 2016, 30, 1111–1118. [Google Scholar]
- Shi, W.X.; Liu, Z.W.; Xie, H.M. Multi-mode scanning laser thermography method and its application in surface crack detection of thermal barrier coatings. In Proceedings of the SEM Fall Conference, Beijing, China, 19–22 October 2014. [Google Scholar]
- Siddiqui, J.A.; Arora, V.; Mulaveesala, R. Infrared Thermal Wave Imaging for Nondestructive Testing of Fibre Reinforced Polymers. Exp. Mech. 2015, 55, 1239–1245. [Google Scholar] [CrossRef]
- An, Y.K.; Kim, J.M.; Sohn, H. Laser lock-in thermography for detection of surface-breaking fatigue cracks on uncoated steel structures. NDT E Int. 2014, 65, 54–63. [Google Scholar] [CrossRef]
- Meola, C. A new approach for estimation of defects detection with infrared thermography. Mater. Lett. 2007, 61, 747–750. [Google Scholar] [CrossRef]
- Mouritz, A.P.; Townsend, C.; Shah Khan, M.Z. Non-destructive detection of fatigue damage in thick composite by pulse-echo ultrasonics. Compos. Sci. Technol. 2000, 60, 23–32. [Google Scholar] [CrossRef]
- Chen, L.; Ahmed, T.H.J.; Wang, J.X. Thermal Wave Lockin Imaging of Cracks in Cu Microbridges Embedded in Polyimide. Rev. Prog. Quant.Nondestr. Eval. 1992, 11, 1933–1941. [Google Scholar]
- Zalameda, J.N.; Rajie, N.; Winfree, W.P. A Comparison of Image Processing Algorithms for Thermalnondestructive Evaluation. In Thermosense XXV, Proceedings of the SPIE; SPIE: Bellingham, WA, USA, 2014; Volume 5073, pp. 374–385. [Google Scholar]
- Roth, D.J.; Bodis, J.R. Thermographic Imaging for High-Temperature Composite Materials-A Defect Detection Study. Res. Nondestruct. Eval. 1997, 9, 147–169. [Google Scholar]
- Omar, M.A.; Gharaibeh, B.; Salaza, A.J. Infrared thermography (IRT) and ultraviolet fluorescence (UVF) for the nondestructive evaluation of ballast tanks coated surfaces. NDT E Int. 2007, 40, 62–71. [Google Scholar] [CrossRef]
- Christiane, M.; Mathias, R.; Rainer, K.; Myrach, P. Comparison of quantitative defect characterization using pulse-phase and lock-in thermography. Appl. Opt. 2016, 55, D76–D86. [Google Scholar]

| Technology | Test Object | Scope of Application | Advantage | Disadvantage |
|---|---|---|---|---|
| X-Ray testing | Internal defects | Casting, weldments, non-metallic products and composite materials, etc. | Not limited by material and geometry, and can keep permanent records. most sensitive to volumetric defects such as porosity, slag inclusion and incomplete penetration | not easy to find the crack perpendicular to the ray; not convenient to give the depth of the defect; strict requirements on installation and safety and is not suitable for on-site online detection; the detection cycle is long; the cost is high |
| Ultrasonic testing | Surface and internal defects | Forgings, weldments, glued joints and non-metallic materials | Sensitive to defects, quick results and convenient defect location | Difficult to detect small, thin and complex parts; coupling agent is needed; complex structure is difficult to detect; speed is slow; detection period is long |
| Magnetic particle testing | Surface and subsurface defects | Ferromagnetic material | higher sensitivity than ultrasonic or radiographic examination when testing surface defects of ferromagnetic materials; the operation is simple and the results are intuitive | Limited to ferromagnetic materials; difficult to measure the defect depth quantitatively |
| Penetrant testing | Surface opening defect | Various non loose materials | the equipment is simple, the operation is simple and the sensitivity is high. Display defects intuitively. especially suitable for the inspection of large work pieces and irregular parts as well as the maintenance and inspection of on-site parts | The process is complex; the test solution is volatile; only surface opening defects can be detected; surface porous materials cannot be detected |
| Eddy current testing | Surface and subsurface defects | Conductive material | The equipment is highly automated; not necessary to clean the surface of the test piece; time saving; no couplant required | Sensitive to the edge effect caused by part geometry and sudden change; easy to give false display |
| Infrared thermal wave imaging testing | measure the damage depth, material thickness and the thickness of various coatings and interlayer, as well as the identification of material and structural characteristics under the surface | Metallic and non-metallic materials | Fast; large detection area; the test results are intuitive. No contamination or contact of the test piece | More effective mathematical calculation model is needed to determine the depth of defects for structural parts with complex shape; the detection depth is not deep enough |
| Method | Advantage | Disadvantage | Application |
|---|---|---|---|
| Flash | High power, high efficiency and high detection accuracy | Cumbersome volume, depth of detection | Metals, nonmetals and composites |
| Laser | High energy density, very uniform light intensity and high detection accuracy | Large volume, complex system and image time correction | Metals, nonmetals, composites and crackle |
| IR-Lamp | Wide wavelength range, stable power and portable | The depth of detection is low | Metals, nonmetals and composites |
| Hot air | Small size, easy to carry, cheap | The depth of detection is low and the energy is low | Less material for light absorption coefficient |
| Method | Advantage | Disadvantage |
|---|---|---|
| Infrared Pulsed Thermography Testing | The heating mode is simple, fast detection speed and high efficiency | Not suitable for the detection of complex structural components, only for the detection of flat components. In addition, the uniformity of the heat source is very high and the detection depth is limited |
| Infrared Lock-in Thermography Testing | Large area for one-time detection; provide certain depth information; continuous thermal excitation modulation requires only a small amount of thermal load. Strong ability to suppress noise | For a specific defect depth, a specific frequency is required for detection, with low efficiency; the phenomenon of blind frequency, which is easy to be missed |
| Infrared Ultrasonic Thermography Testing | Strong penetration and high detection depth; high detection sensitivity and safe operation | Not easy to check the workpiece with complex shape, and the surface finish of the tested object is required to be high; couplant should be filled in the test piece |
| Infrared Laser Thermography Testing | High power density; high detection accuracy | The method of laser point heat source is limited by the small area of single detection and the longtime of detection process; the laser line scanning method requires higher signal sensitivity; the high-power laser may cause surface damage |
| Grating Infrared Thermal Wave Scanning Testing | Simultaneous detection of horizontal and vertical cracks; localizable detection; low requirement for sampling frequency of thermal imager | Lack of experimental verification; the existing heat sources are not satisfactory |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, Z.; Jiang, P.; Zhang, W. Development and Application of Infrared Thermography Non-Destructive Testing Techniques. Sensors 2020, 20, 3851. https://doi.org/10.3390/s20143851
Qu Z, Jiang P, Zhang W. Development and Application of Infrared Thermography Non-Destructive Testing Techniques. Sensors. 2020; 20(14):3851. https://doi.org/10.3390/s20143851
Chicago/Turabian StyleQu, Zhi, Peng Jiang, and Weixu Zhang. 2020. "Development and Application of Infrared Thermography Non-Destructive Testing Techniques" Sensors 20, no. 14: 3851. https://doi.org/10.3390/s20143851
APA StyleQu, Z., Jiang, P., & Zhang, W. (2020). Development and Application of Infrared Thermography Non-Destructive Testing Techniques. Sensors, 20(14), 3851. https://doi.org/10.3390/s20143851





