A Novel Just-in-Time Learning Strategy for Soft Sensing with Improved Similarity Measure Based on Mutual Information and PLS
Abstract
1. Introduction
2. Preliminaries
2.1. Mutual Information
2.2. Locally Weighted PLS
- 1: Set the number of latent variables R and the tuning parameter h;
- 2: Calculate Ω;
- 3: Calculate X0, Y0, and xq,0;
- 4: Initialize: Xr = X0, Yr = Y0, xq,r = xq,0, ;
- 5: For r = 1: R;
- 6: Calculate the weight loading Wr;Derive the rth latent variables.
- 7: Derive X-loading vector pr and Y-regression coefficient qr;
- 8: Update ;
- 9: Update Xr+1, Yr+1, and xq,r+1;
- 10: End for;
- 11: Output .
3. The Proposed Method
3.1. PLS-Based Similarity Measure
3.2. The Proposed MI-PLS-LWPLS Method
3.2.1. Training Stage
3.2.2. Prediction Phase
4. Case Studies
4.1. Numerical Experiment on Friedman Dataset
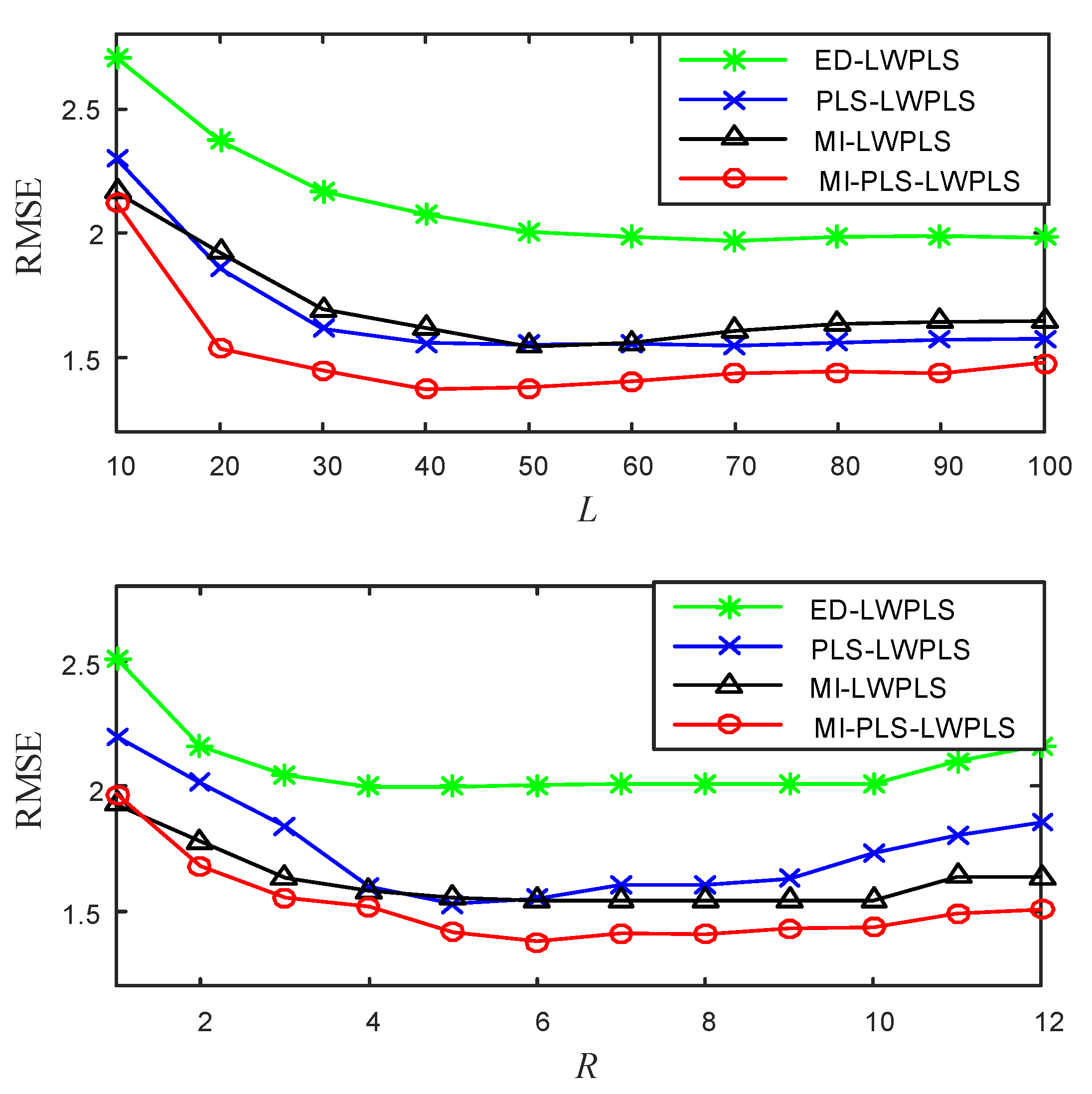
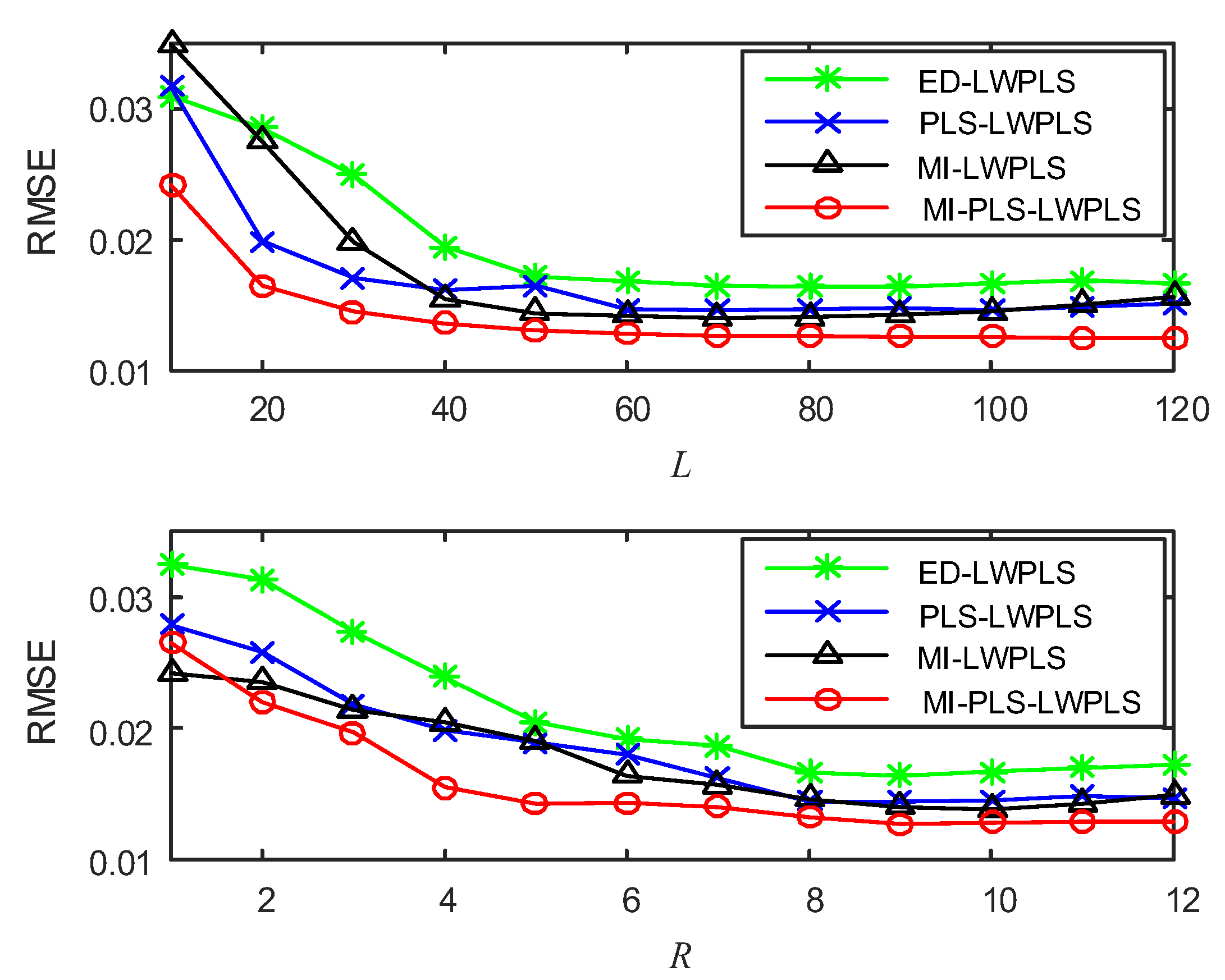
4.1.1. Experimental Design
- L: Number of neighbor samples used for local modeling in LWPLS;
- R: Number of latent variables in LWPLS;
- h: Tuning parameter in sample weight calculation;
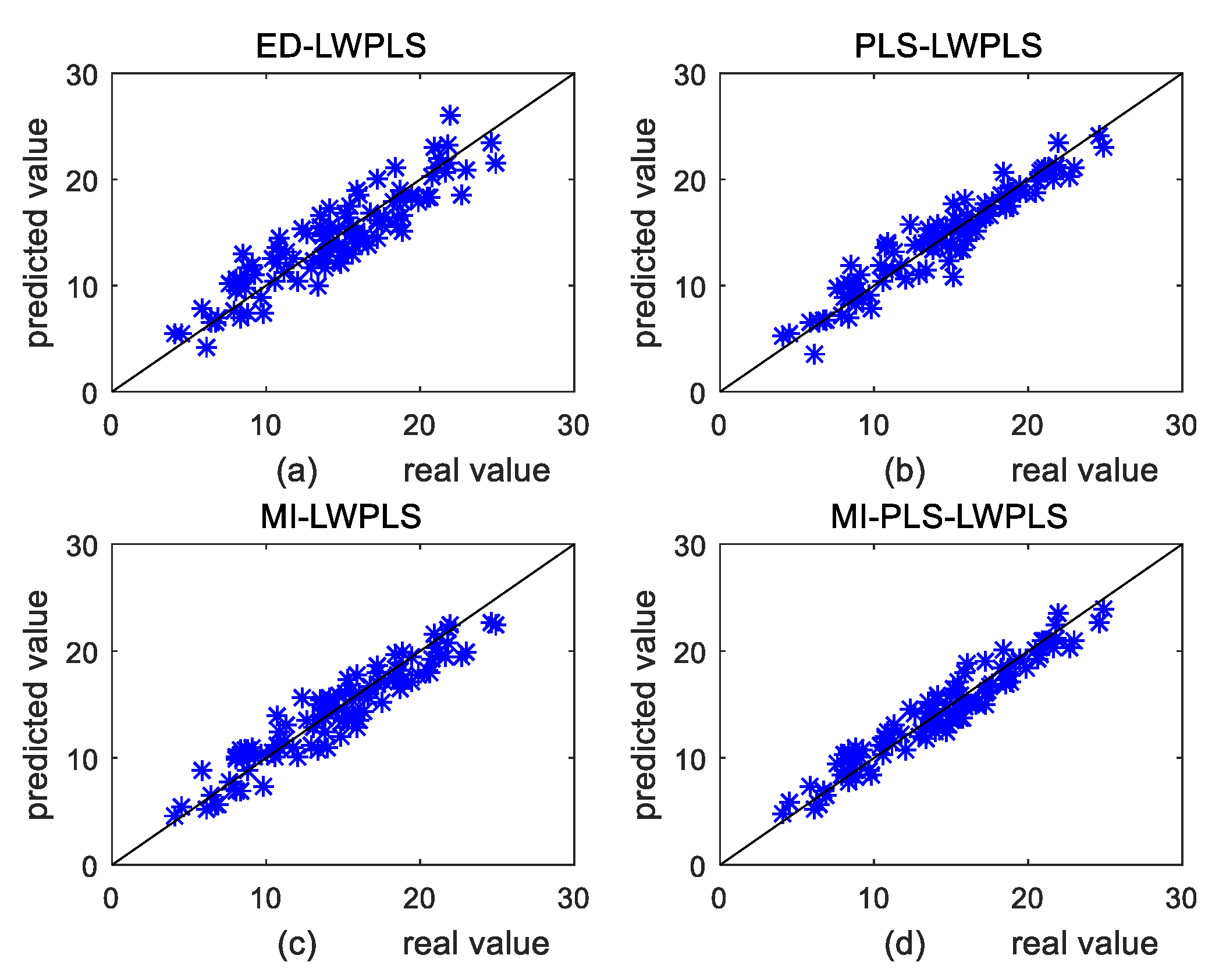
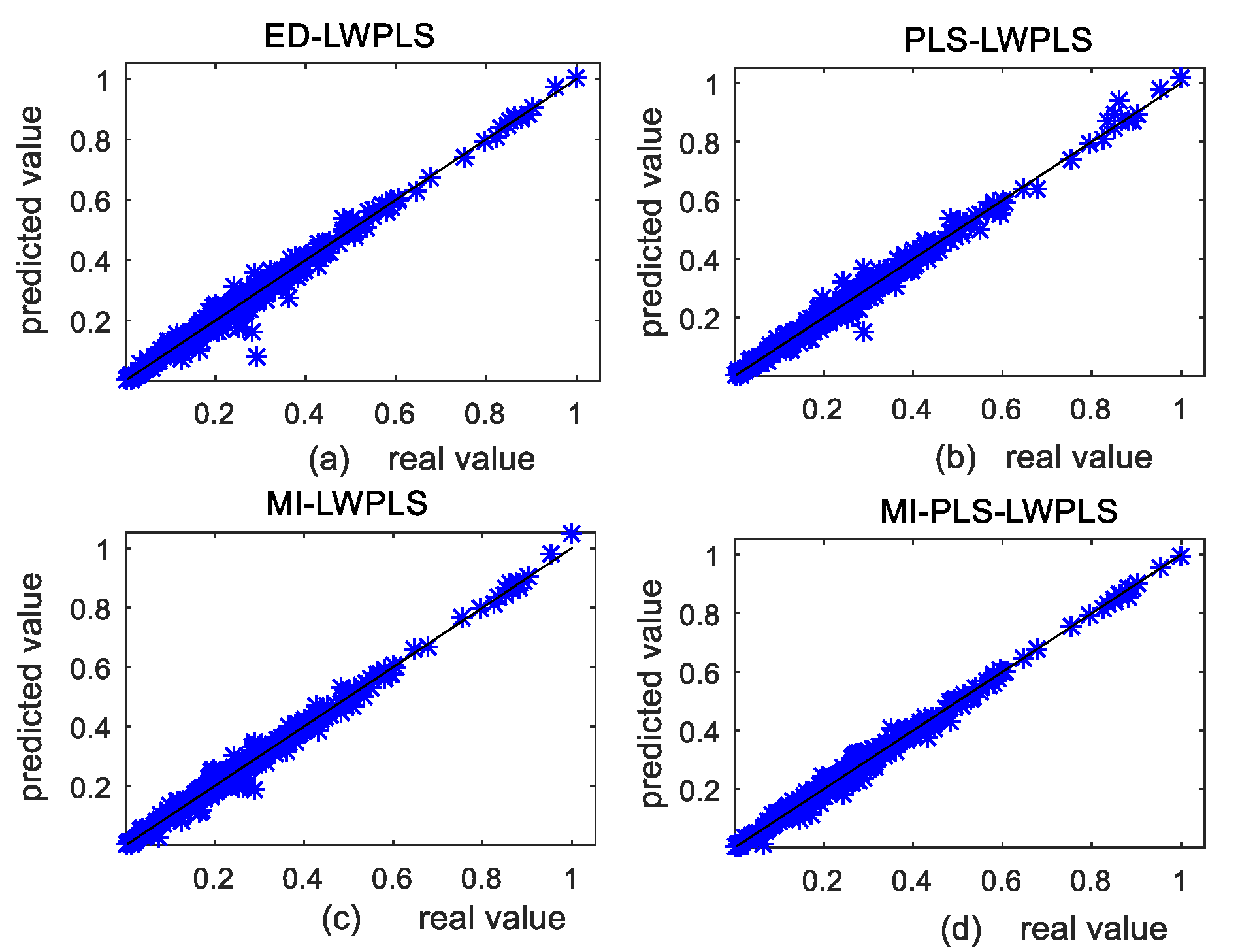
4.1.2. Results and Discussion
4.2. Industrial Case
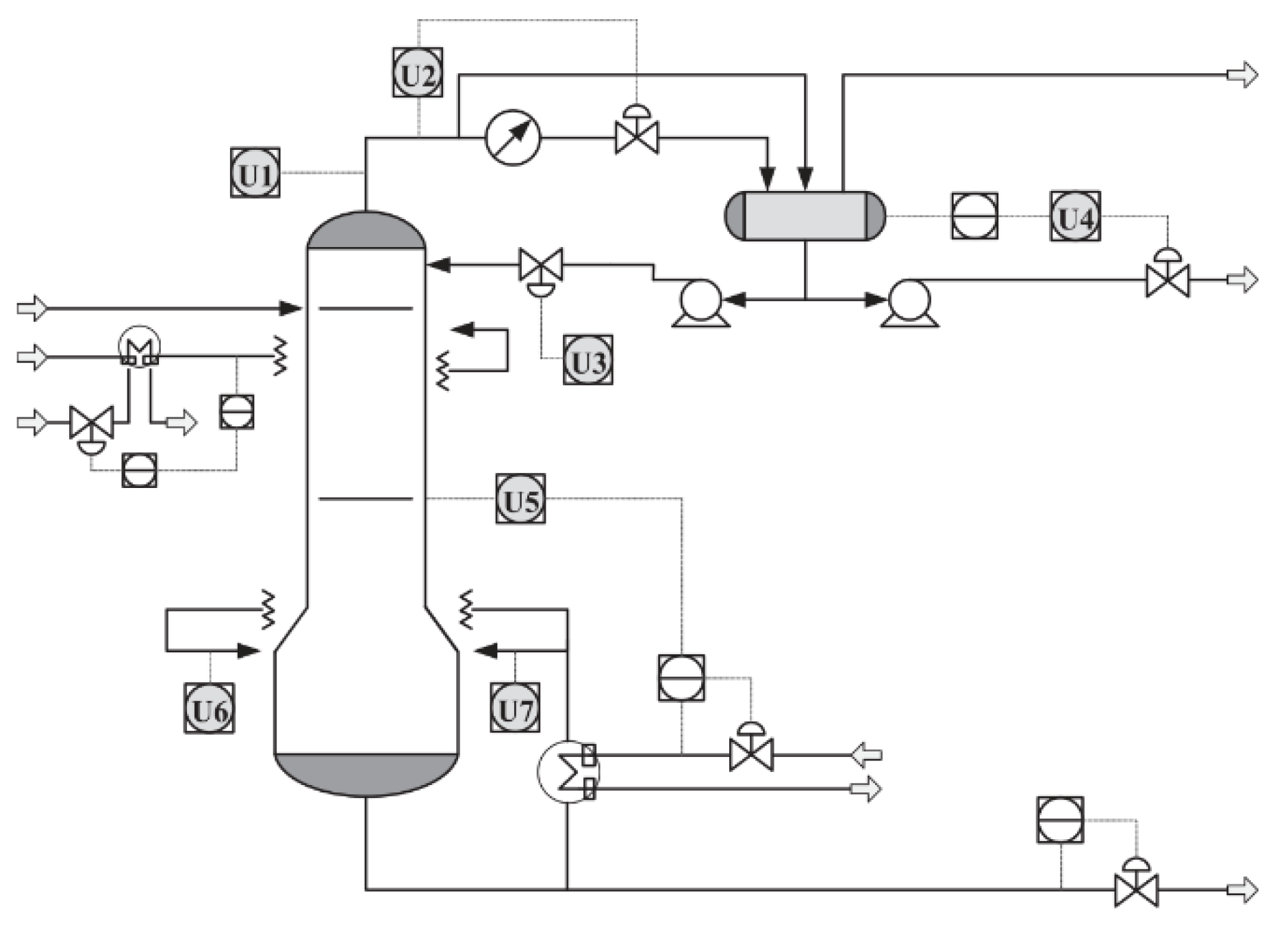
4.2.1. Debutanizer Column Process
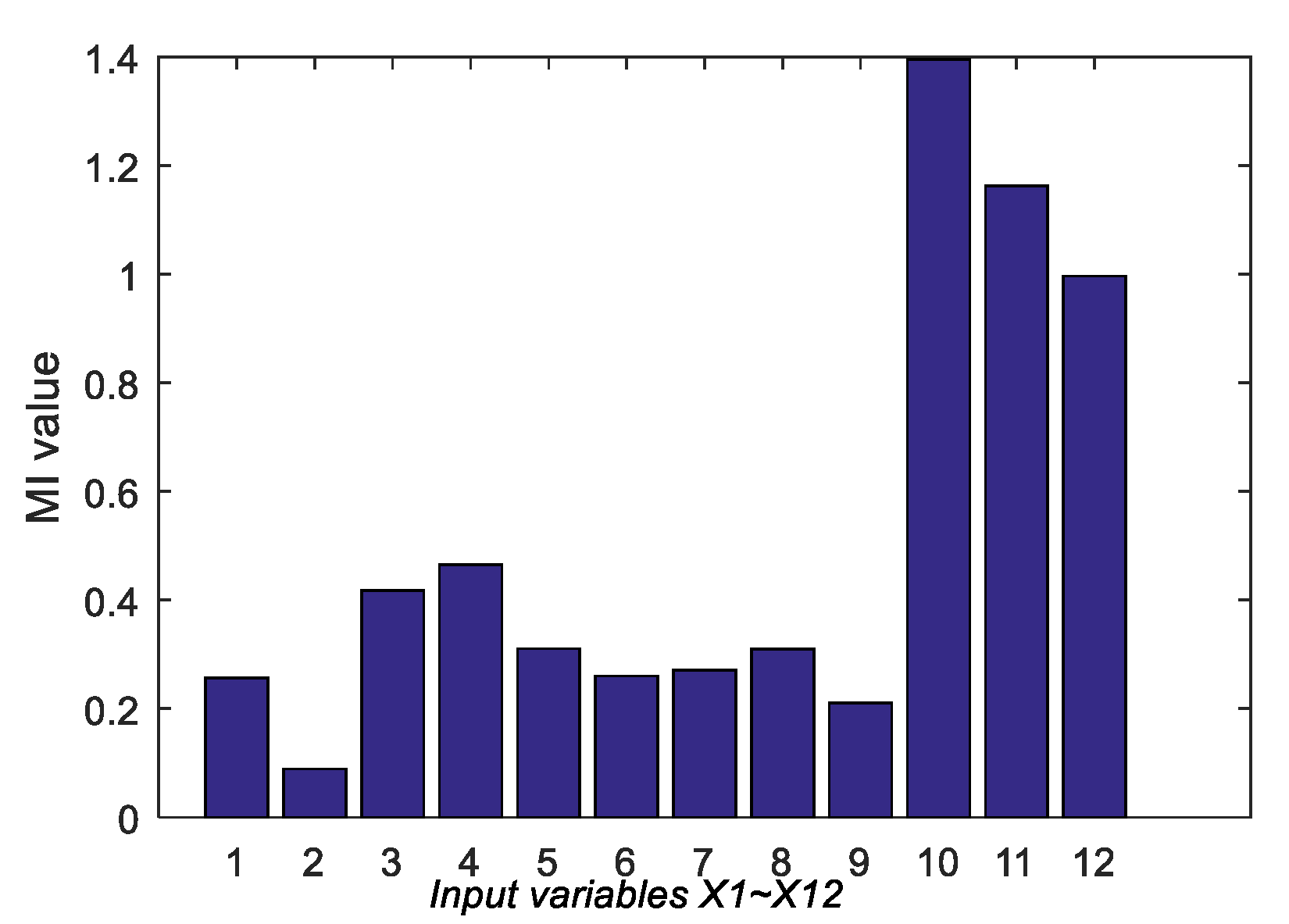
4.2.2. DCP Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fortuna, L.; Graziani, S.; Rizzo, A.; Xibilia, M.G. Soft Sensors for Monitoring and Control of Industrial Processes; Springer: London, UK, 2007. [Google Scholar]
- Kadlec, P.; Gabrys, B.; Strandt, S. Data-driven Soft Sensors in the process industry. Comput. Chem. Eng. 2009, 33, 795–814. [Google Scholar] [CrossRef]
- Zhang, S.; Chu, F.; Deng, G.; Wang, F. Soft Sensor Model Development for Cobalt Oxalate Synthesis Process Based on Adaptive Gaussian Mixture Regression. IEEE Access 2019, 7, 118749–118763. [Google Scholar] [CrossRef]
- Grbic, R.; Sliskovic, D.; Kadlec, P. Adaptive soft sensor for online prediction and process monitoring based on a mixture of Gaussian process models. Comput. Chem. Eng. 2013, 58, 84–97. [Google Scholar] [CrossRef]
- He, Y.; Zhu, B.; Liu, C.; Zeng, J. Quality-Related Locally Weighted Non-Gaussian Regression Based Soft Sensing for Multimode Processes. Ind. Eng. Chem. Res. 2018, 57, 17452–17461. [Google Scholar] [CrossRef]
- Facco, P.; Doplicher, F.; Bezzo, F.; Barolo, M. Moving average PLS soft sensor for online product quality estimation in an industrial batch polymerization process. J. Process Control 2009, 19, 520–529. [Google Scholar] [CrossRef]
- Camacho, J.; Pico, J.; Ferrer, A. Bilinear modelling of batch processes. Part II: A comparison of PLS soft-sensors. J. Chemom. 2008, 22, 533–547. [Google Scholar] [CrossRef]
- Jiang, H.; Yan, Z.; Liu, X. Melt index prediction using optimized least squares support vector machines based on hybrid particle swarm optimization algorithm. Neurocomputing 2013, 119, 469–477. [Google Scholar] [CrossRef]
- Chang, Y.; Wang, F.; Wang, X.; Lv, Z. Soft sensor modeling based on support vector machines and its applications to fermentation process. Chin J. Sci. Instrum. 2006, 27, 241–244, 271. [Google Scholar]
- Yan, X. Hybrid artificial neural network based on BP-PLSR and its application in development of soft sensors. Chemom. Intell. Lab. Syst. 2010, 103, 152–159. [Google Scholar] [CrossRef]
- Pisa, I.; Santin, I.; Lopez Vicario, J.; Morell, A.; Vilanova, R. ANN-Based Soft Sensor to Predict Effluent Violations in Wastewater Treatment Plants. Sensors 2019, 19, 1280. [Google Scholar] [CrossRef]
- Liu, J.; Chen, D.-S.; Shen, J.-F. Development of Self-Validating Soft Sensors Using Fast Moving Window Partial Least Squares. Ind. Eng. Chem. Res. 2010, 49, 11530–11546. [Google Scholar] [CrossRef]
- Yao, L.; Ge, Z. Online Updating Soft Sensor Modeling and Industrial Application Based on Selectively Integrated Moving Window Approach. IEEE Trans. Instrum. Meas. 2017, 66, 1985–1993. [Google Scholar] [CrossRef]
- Wang, X.; Kruger, U.; Irwin, G.W. Process monitoring approach using fast moving window PCA. Ind. Eng. Chem. Res. 2005, 44, 5691–5702. [Google Scholar] [CrossRef]
- Kaneko, H.; Funatsu, K. Development of Soft Sensor Models Based on Time Difference of Process Variables with Accounting for Nonlinear Relationship. Ind. Eng. Chem. Res. 2011, 50, 10643–10651. [Google Scholar] [CrossRef]
- Kaneko, H.; Funatsu, K. Discussion on Time Difference Models and Intervals of Time Difference for Application of Soft Sensors. Ind. Eng. Chem. Res. 2013, 52, 1322–1334. [Google Scholar] [CrossRef]
- Ahmed, F.; Nazir, S.; Yeo, Y.K. A recursive PLS-based soft sensor for prediction of the melt index during grade change operations in HDPE plant. Korean J. Chem. Eng. 2009, 26, 14–20. [Google Scholar] [CrossRef]
- Yuan, X.; Ge, Z.; Huang, B.; Song, Z.; Wang, Y. Semisupervised JITL Framework for Nonlinear Industrial Soft Sensing Based on Locally Semisupervised Weighted PCR. IEEE Trans. Ind. Informat. 2017, 13, 532–541. [Google Scholar] [CrossRef]
- Yuan, X.; Huang, B.; Ge, Z.; Song, Z. Double locally weighted principal component regression for soft sensor with sample selection under supervised latent structure. Chemom. Intell. Lab. Syst. 2016, 153, 116–125. [Google Scholar] [CrossRef]
- Cheng, C.; Chiu, M.S. A new data-based methodology for nonlinear process modeling. Chem. Eng. Sci. 2004, 59, 2801–2810. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Kano, M. Quality Prediction in Complex Batch Processes with Just-in-Time Learning Model Based on Non-Gaussian Dissimilarity Measure. Ind. Eng. Chem. Res. 2015, 54, 7694–7705. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z. A comparative study of just-in-time-learning based methods for online soft sensor modeling. Chemom. Intell. Lab. Syst. 2010, 104, 306–317. [Google Scholar] [CrossRef]
- Hazama, K.; Kano, M. Covariance-based locally weighted partial least squares for high-performance adaptive modeling. Chemom. Intell. Lab. Syst. 2015, 146, 55–62. [Google Scholar] [CrossRef]
- Kim, S.; Okajima, R.; Kano, M.; Hasebe, S. Development of soft-sensor using locally weighted PLS with adaptive similarity measure. Chemom. Intell. Lab. Syst. 2013, 124, 43–49. [Google Scholar] [CrossRef]
- Shigemori, H.; Kano, M.; Hasebe, S. Optimum quality design system for steel products through locally weighted regression model. J. Process Control 2011, 21, 293–301. [Google Scholar] [CrossRef]
- Fujiwara, K.; Kano, M.; Hasebe, S. Development of Correlation-Based Pattern Recognition and Its Application to Adaptive Soft-Sensor Design. In Proceedings of the ICCAS-SICE 2009, Fukuoka, Japan, 18–21 August 2009; pp. 1990–1995. [Google Scholar]
- Fujiwara, K.; Kano, M.; Hasebe, S.; Takinami, A. Soft-Sensor Development Using Correlation-Based Just-in-Time Modeling. Aiche J. 2009, 55, 1754–1765. [Google Scholar] [CrossRef]
- Chang, S.Y.; Ernie, H.B.; Bruce, C.M. Implementation of Locally Weighted Regression to Maintain Calibrations on FT-NIR Analyzers for Industrial Processes. Appl. Spectrosc. 2001, 55, 1199–1206. [Google Scholar] [CrossRef]
- Wang, Z.; Isaksson, T.; BR, K. New approach for distance measurement in locally weighted regression. Anal. Chem. 1994, 66, 249–260. [Google Scholar] [CrossRef]
- Zhao, D.; Pan, T.H.; Sheng, B.Q. Just-in-time Learning Algorithm Using the Improved Similarity Index. In Proceedings of the 35th Chinese Control Conference 2016, Chengdu, China, 27–29 July 2016; pp. 9065–9068. [Google Scholar]
- Jin, H.; Chen, X.; Yang, J.; Wang, L.; Wu, L. Online local learning based adaptive soft sensor and its application to an industrial fed-batch chlortetracycline fermentation process. Chemom. Intell. Lab. Syst. 2015, 143, 58–78. [Google Scholar] [CrossRef]
- Khan, S.; Bandyopadhyay, S.; Ganguly, A.R.; Saigal, S.; Erickson, D.J., 3rd; Protopopescu, V.; Ostrouchov, G. Relative performance of mutual information estimation methods for quantifying the dependence among short and noisy data. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007, 76, 026209. [Google Scholar] [CrossRef]
- Kraskov, A.; Stogbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004, 69, 066138. [Google Scholar] [CrossRef]
- Gao, W.; Oh, S.; Viswanath, P. Demystifying Fixed k-Nearest Neighbor Information Estimators. IEEE Trans. Inf. Theory 2018, 64, 5629–5661. [Google Scholar] [CrossRef]
- Kano, M.; Kim, S.; Okajima, R.; Hasebe, S. Industrial Applications of Locally Weighted PLS to Realize Maintenance-Free High-Performance Virtual Sensing. In Proceedings of the 2012 12th International Conference on Control, Automation and Systems, Jeju Island, Korea, 17–21 October 2012; pp. 545–548. [Google Scholar]
- Kim, S.; Kano, M.; Hasebe, S.; Takinami, A.; Seki, T. Long-Term Industrial Applications of Inferential Control Based on Just-In-Time Soft-Sensors: Economical Impact and Challenges. Ind. Eng. Chem. Res. 2013, 52, 12346–12356. [Google Scholar] [CrossRef]
- Ren, M.; Song, Y.; Chu, W. An Improved Locally Weighted PLS Based on Particle Swarm Optimization for Industrial Soft Sensor Modeling. Sensors 2019, 19, 4099. [Google Scholar] [CrossRef] [PubMed]
- Kamata, K.; Fujiwara, K.; Kinoshita, T.; Kano, M. Missing RRI Interpolation Algorithm based on Locally Weighted Partial Least Squares for Precise Heart Rate Variability Analysis. Sensors 2018, 18, 3870. [Google Scholar] [CrossRef]
- Chen, C.; Yan, X. Selection and transformation of input variables for RVM based on MIPCAMI and 4-CBA concentration model. Asia-Pac. J. Chem. Eng. 2013, 8, 69–76. [Google Scholar] [CrossRef]
- Jerome, H.F. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar]
- Han, M.; Ren, W.J. Global mutual information-based feature selection approach using single-objective and multi-objective optimization. Neurocomputing 2015, 168, 47–54. [Google Scholar] [CrossRef]
- Kadlec, P.; Grbić, R.; Gabrys, B. Review of adaptation mechanisms for data-driven soft sensors. Comput. Chem. Eng. 2011, 35, 1–24. [Google Scholar] [CrossRef]
- Shao, W.; Tian, X. Semi-supervised selective ensemble learning based on distance to model for nonlinear soft sensor development. Neurocomputing 2017, 222, 91–104. [Google Scholar] [CrossRef]
- Yao, L.; Ge, Z. Locally Weighted Prediction Methods for Latent Factor Analysis with Supervised and Semisupervised Process Data. IEEE Trans. Autom. Sci. Eng. 2017, 14, 126–138. [Google Scholar] [CrossRef]
- Shao, W.; Tian, X.; Wang, P. Local Partial Least Squares Based Online Soft Sensing Method for Multi-output Processes with Adaptive Process States Division. Chin. J. Chem. Eng. 2014, 22, 828–836. [Google Scholar] [CrossRef]

| Method | Case 1 | Case 2 | ||
|---|---|---|---|---|
| RMSE | MARE (%) | RMSE | MARE (%) | |
| ED-LWPLS | 1.98 | 13.28 | 2.01 | 13.58 |
| PLS-LWPLS | 1.61 | 11.13 | 1.55 | 10.15 |
| MI-LWPLS | 1.50 | 9.99 | 1.54 | 10.11 |
| MI-PLS-LWPLS | 1.42 | 9.70 | 1.38 | 9.47 |
| Case 1 | Case 2 |
|---|---|
| U1 | Top temperature |
| U2 | Top pressure |
| U3 | Reflux flow |
| U4 | Flow to next process |
| U5 | 6th tray temperature |
| U6 | Bottom temperature |
| U7 | Bottom pressure |
| Input Variables | X1 | X2 | X3 | X4 | X5 | X6 |
| VIF | 1.6 | 1.2 | 1.5 | 1.3 | 38.6 | 118.7 |
| Input Variables | X7 | X8 | X9 | X10 | X11 | X12 |
| VIF | 119.3 | 36.4 | 3.4 | 1078.5 | 3972.6 | 1020.7 |
| Method | Validation Dataset | Test Dataset | ||
|---|---|---|---|---|
| RMSE | MARE (%) | RMSE | MARE (%) | |
| ED-LWPLS | 0.0164 | 5.81 | 0.0188 | 6.20 |
| PLS-LWPLS | 0.0146 | 5.27 | 0.0155 | 5.47 |
| MI-LWPLS | 0.0140 | 5.16 | 0.0153 | 5.42 |
| MI-PLS-LWPLS | 0.0129 | 4.10 | 0.0135 | 4.73 |
| Method | Prediction Time (s) |
|---|---|
| ED-LWPLS | 6.41 |
| PLS-LWPLS | 6.22 |
| MI-LWPLS | 7.19 |
| MI-PLS-LWPLS | 7.32 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Ren, M. A Novel Just-in-Time Learning Strategy for Soft Sensing with Improved Similarity Measure Based on Mutual Information and PLS. Sensors 2020, 20, 3804. https://doi.org/10.3390/s20133804
Song Y, Ren M. A Novel Just-in-Time Learning Strategy for Soft Sensing with Improved Similarity Measure Based on Mutual Information and PLS. Sensors. 2020; 20(13):3804. https://doi.org/10.3390/s20133804
Chicago/Turabian StyleSong, Yueli, and Minglun Ren. 2020. "A Novel Just-in-Time Learning Strategy for Soft Sensing with Improved Similarity Measure Based on Mutual Information and PLS" Sensors 20, no. 13: 3804. https://doi.org/10.3390/s20133804
APA StyleSong, Y., & Ren, M. (2020). A Novel Just-in-Time Learning Strategy for Soft Sensing with Improved Similarity Measure Based on Mutual Information and PLS. Sensors, 20(13), 3804. https://doi.org/10.3390/s20133804





