Three Dimensional Upper Limb Joint Kinetics of a Golf Swing with Measured Internal Grip Force
Abstract
1. Introduction
2. Methods
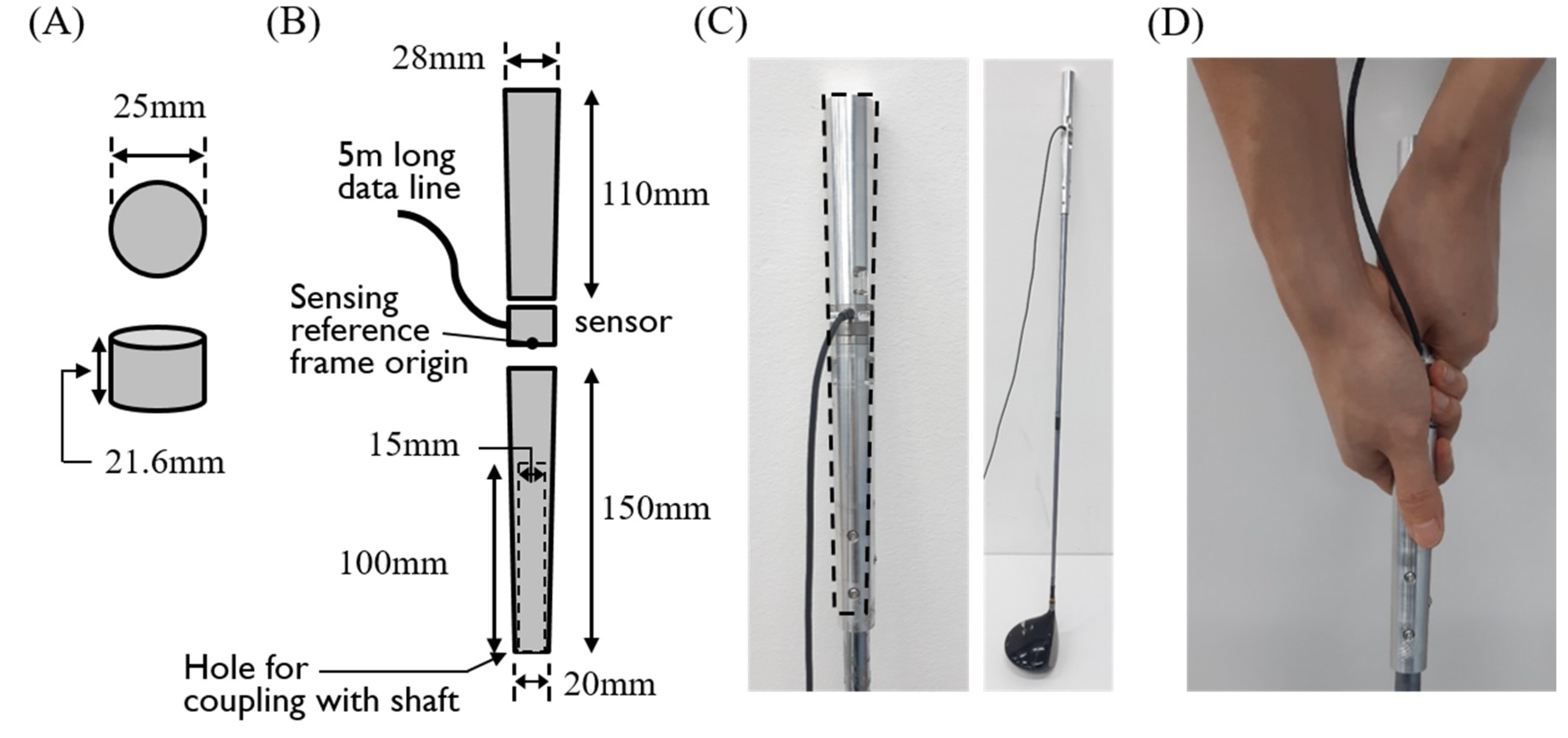
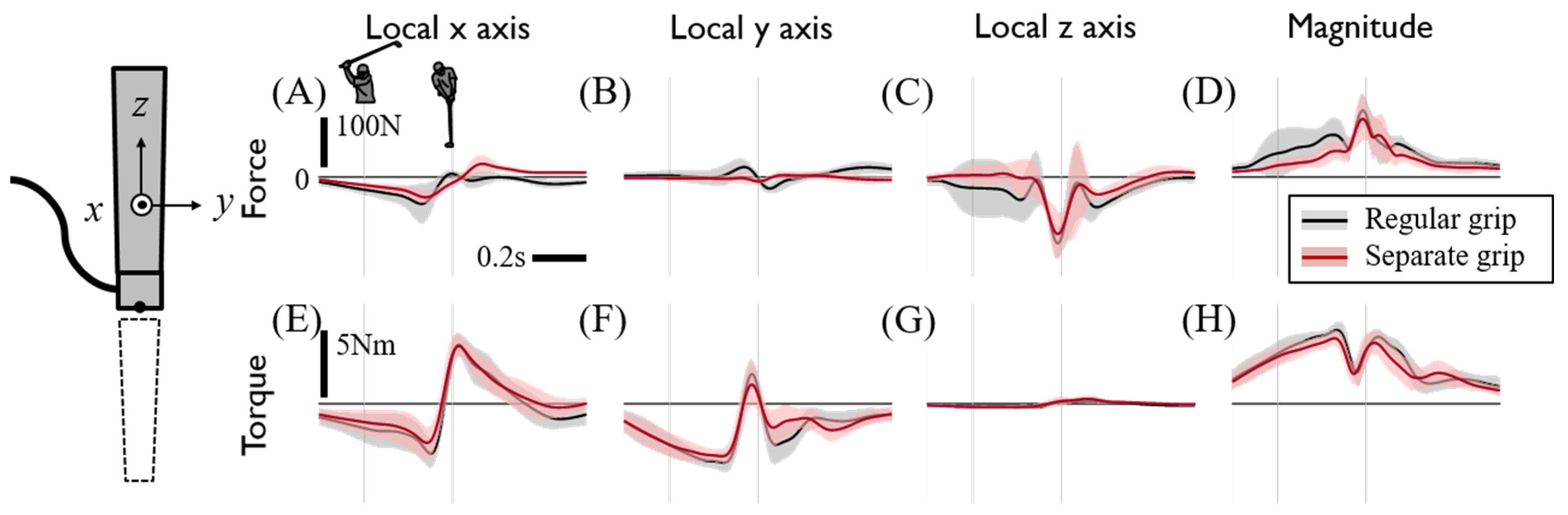
2.1. Design of the Six-Axis Internal Grip Force Measurement System
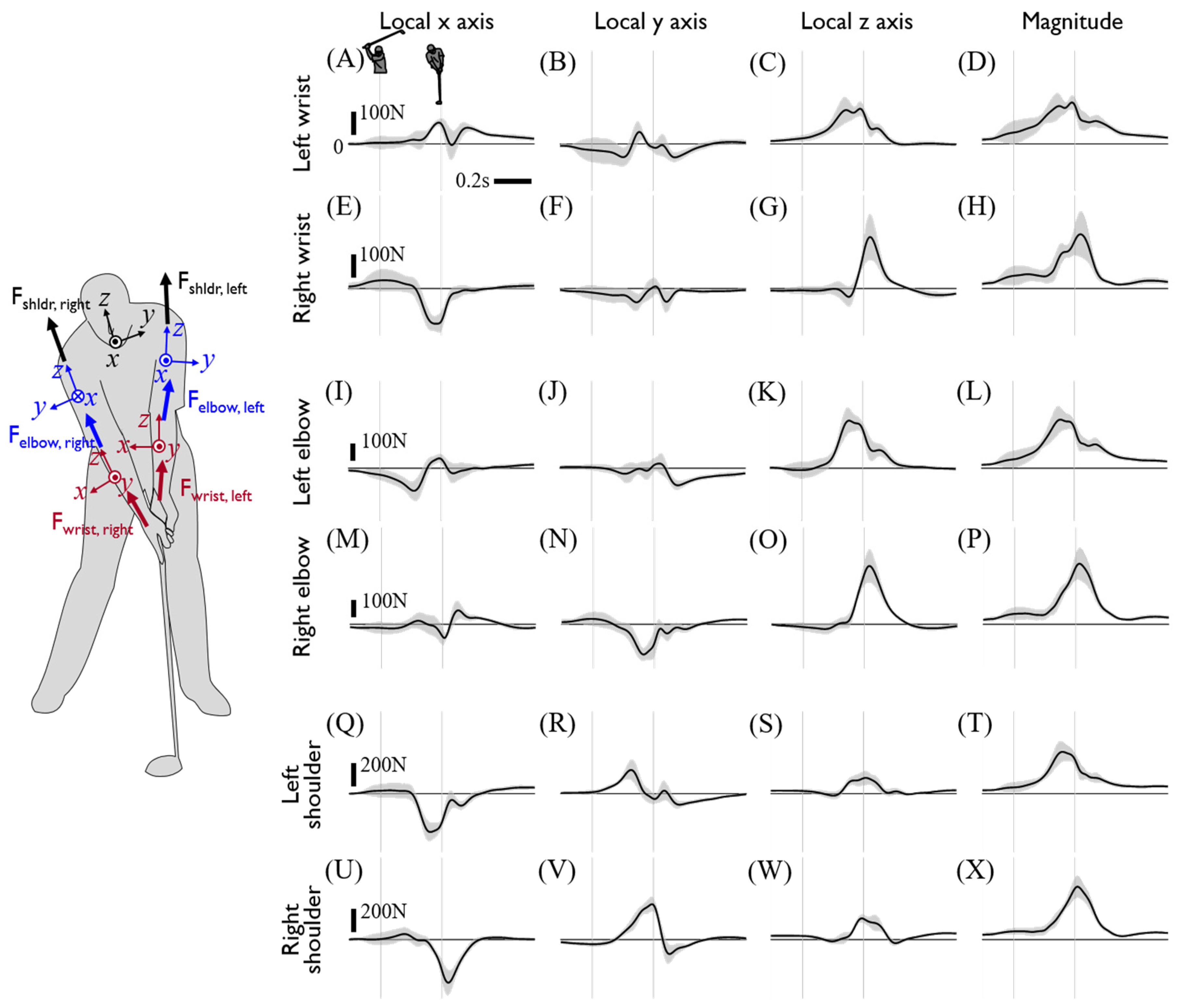
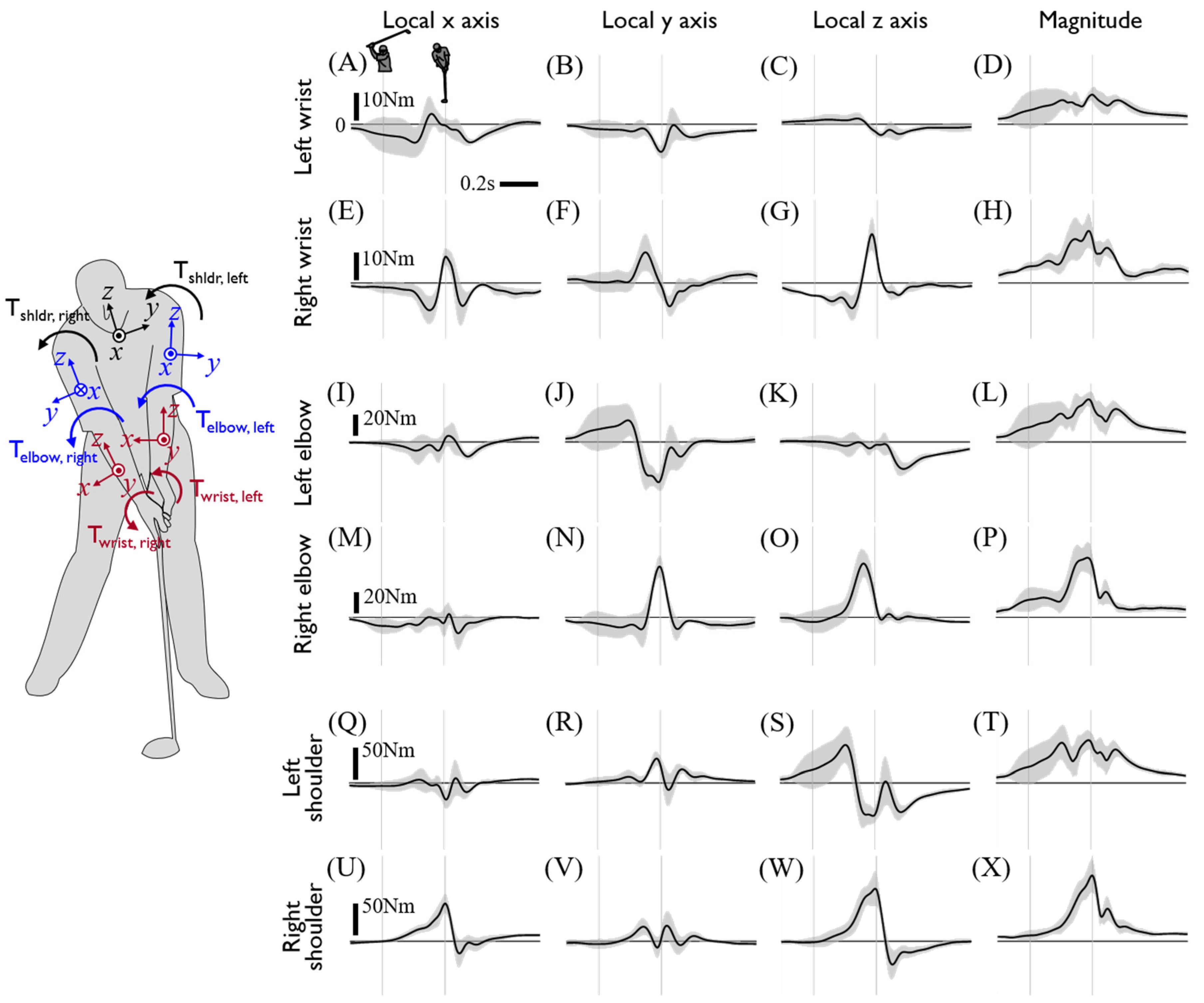
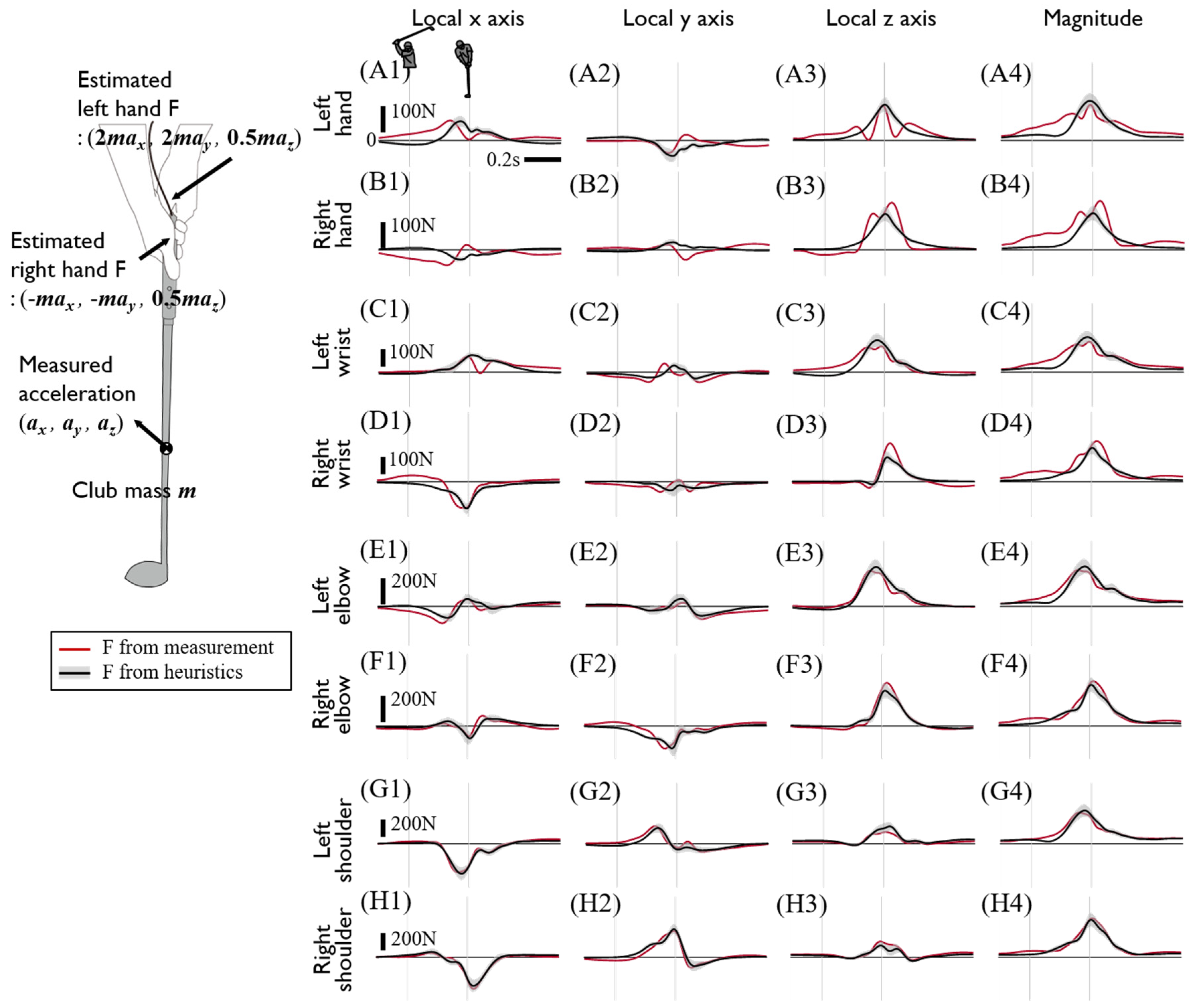
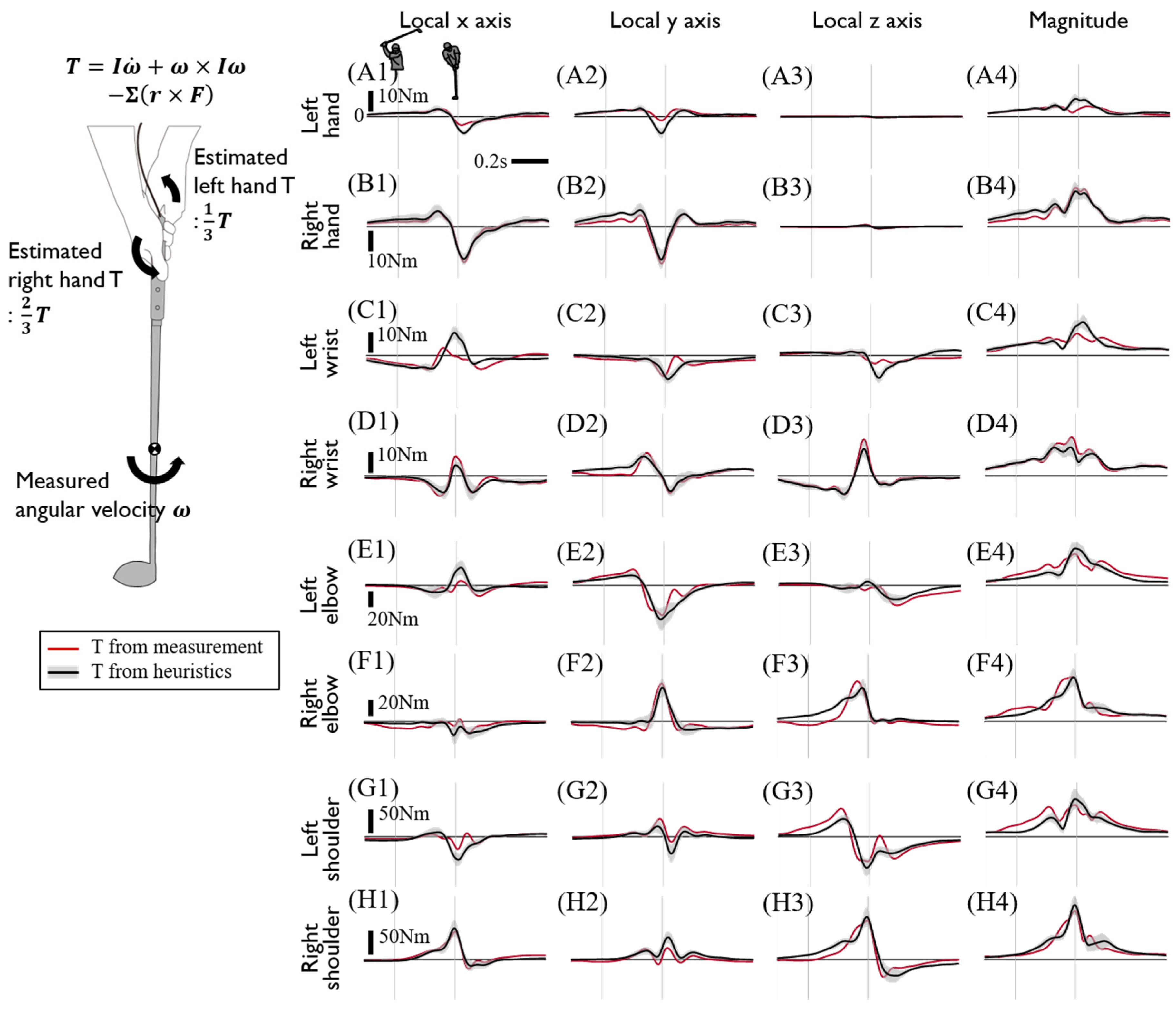
2.2. Inverse Dynamics Model
2.3. Experiment
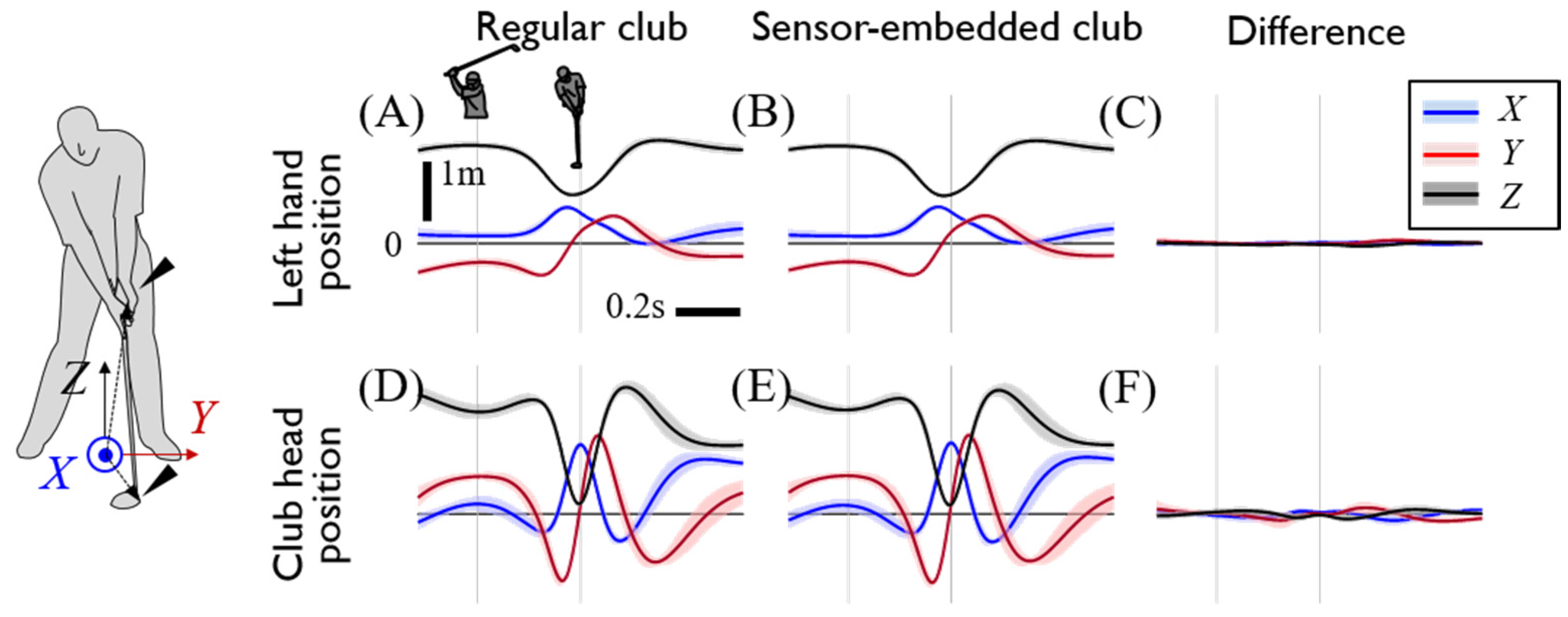
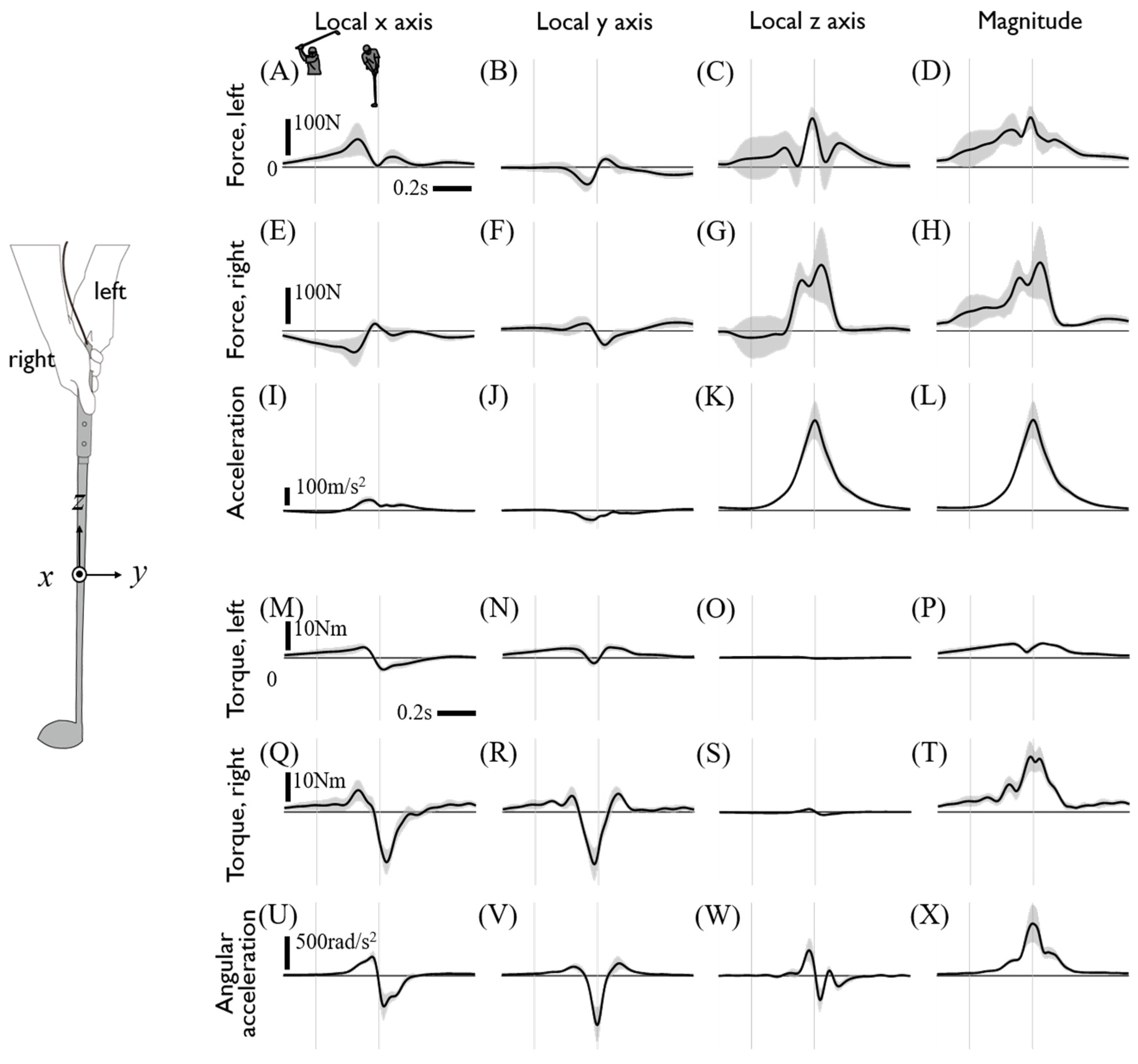
2.4. Data Processing
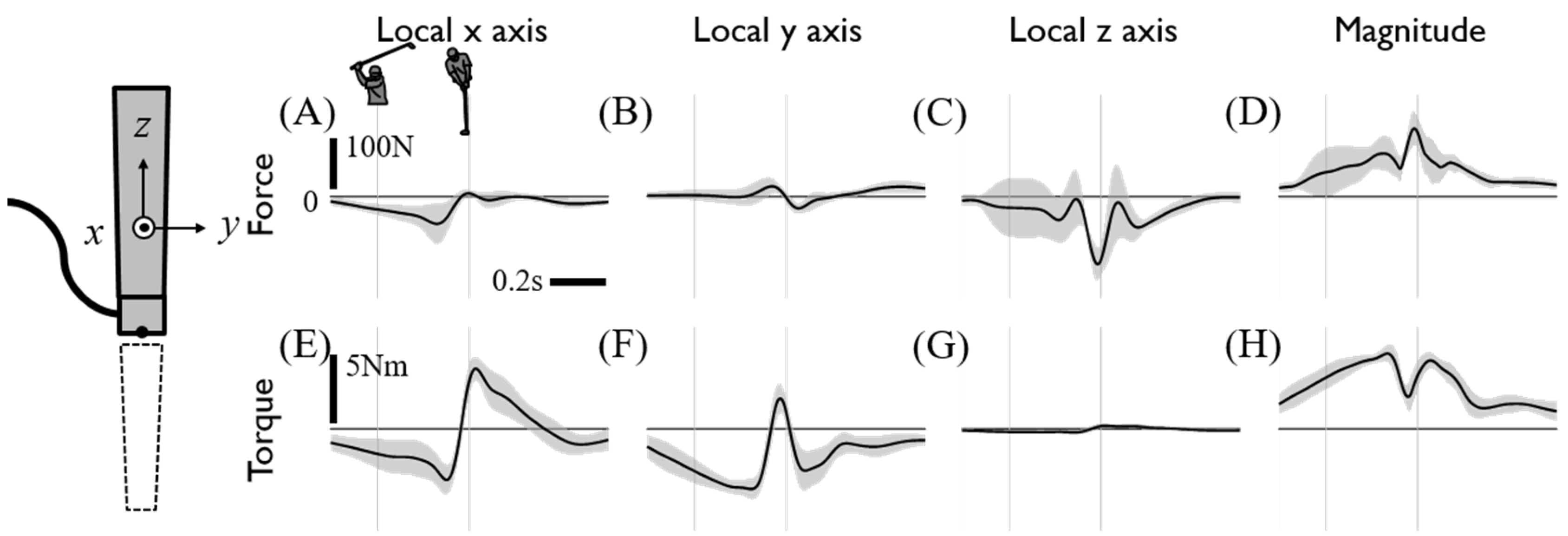
3. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gatt, C.J.; Pavol, M.J.; Parker, R.D.; Grabiner, M.D. Three-dimensional knee joint kinetics during a golf swing. Am. J. Sports Med. 1998, 26, 285–294. [Google Scholar] [CrossRef]
- Hellström, J. Competitive elite golf. Sports Med. 2009, 39, 723–741. [Google Scholar] [CrossRef] [PubMed]
- Hume, P.A.; Keogh, J.; Reid, D. The role of biomechanics in maximising distance and accuracy of golf shots. Sports Med. 2005, 35, 429–449. [Google Scholar] [CrossRef] [PubMed]
- Takagi, T.; Murata, M.; Yokozawa, T. Kinetic mechanisms of the pelvis rotation about its longitudinal axis during the golf swing. ISBS Proc. Arch. 2017, 35, 235. [Google Scholar]
- Chu, Y.; Sell, T.C.; Lephart, S.M. The relationship between biomechanical variables and driving performance during the golf swing. J. Sports Sci. 2010, 28, 1251–1259. [Google Scholar] [CrossRef] [PubMed]
- Lai, D.T.; Hetchl, M.; Wei, X.; Ball, K.; Mclaughlin, P. On the difference in swing arm kinematics between low handicap golfers and non-golfers using wireless inertial sensors. Procedia Eng. 2011, 13, 219–225. [Google Scholar] [CrossRef]
- Meister, D.W.; Ladd, A.L.; Butler, E.E.; Zhao, B.; Rogers, A.P.; Ray, C.J.; Rose, J. Rotational biomechanics of the elite golf swing: Benchmarks for amateurs. J. Appl. Biomech. 2011, 27, 242–251. [Google Scholar] [CrossRef]
- Zheng, N.; Barrentine, S.; Fleisig, G.; Andrews, J. Kinematic analysis of swing in pro and amateur golfers. Int. J. Sports Med. 2008, 29, 487–493. [Google Scholar] [CrossRef]
- Crews, D.; Lutz, R. Comparison of kinematic sequence parameters between amateur and professional golfers. Sci. Golf 2007, 5, 30–36. [Google Scholar]
- Neal, R.; Lumsden, R.; Holland, M.; Mason, B. Body segment sequencing and timing in golf. Int. J. Sports Sci. Coach. 2007, 2, 25–36. [Google Scholar] [CrossRef]
- Foxworth, J.L.; Millar, A.L.; Long, B.L.; Way, M.; Vellucci, M.W.; Vogler, J.D. Hip joint torques during the golf swing of young and senior healthy males. J. Orthop. Sports Phys. Ther. 2013, 43, 660–665. [Google Scholar] [CrossRef] [PubMed]
- McNally, M.; Yontz, N.; Chaudhari, A. Lower extremity work is associated with club head velocity during the golf swing in experienced golfers. Int. J. Sports Med. 2014, 35, 785–788. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Koike, S. Force and moment exerted by each hand on an instrumented golf club. In Proceedings of the ISBS-Conference Proceedings Archive, Tsukuba, Japan, 18–22 July 2016; pp. 1218–1221. [Google Scholar]
- Vaughan, C.L.; Hay, J.G.; Andrews, J.G. Closed loop problems in biomechanics. Part I—A classification system. J. Biomech. 1982, 15, 197–200. [Google Scholar] [CrossRef]
- Vaughan, C.L.; Hay, J.G.; Andrews, J.G. Closed loop problems in biomechanics. Part II—An optimization approach. J. Biomech. 1982, 15, 201–210. [Google Scholar] [CrossRef]
- Balzerson, D.; Banerjee, J.; McPhee, J. A three-dimensional forward dynamic model of the golf swing optimized for ball carry distance. Sports Eng. 2016, 19, 237–250. [Google Scholar] [CrossRef]
- MacKenzie, S.J.; Sprigings, E.J. A three-dimensional forward dynamics model of the golf swing. Sports Eng. 2009, 11, 165–175. [Google Scholar] [CrossRef]
- Nesbit, S. Development of a full-body biomechanical model of the golf swing. Int. J. Model. Simul. 2007, 27, 392–404. [Google Scholar] [CrossRef]
- Koike, S.; Shiraki, H.; Fujii, N.; Ae, M. S9 Joint torques of the upper limbs in golf swing. In Proceedings of the Joint Symposium: Symposium on Sports Engineering, Symposium on Human Dynamics; Japan Society of Mechanical Engineers: Tokyo, Japan, 2005; pp. 39–44. [Google Scholar] [CrossRef]
- Hanavan, E.P., Jr. A Mathematical Model of the Human Body; Air Force Aerospace Medical Research Lab: Wright-Patterson AFB, OH, USA, 1964. [Google Scholar]
- Dempster, W.T. Space Requirements of the Seated Operator, Geometrical, Kinematic, and Mechanical Aspects of the Body with Special Reference to the Limbs; Michigan State Univ.: East Lansing, MI, USA, 1955. [Google Scholar]
- Wu, G.; Van der Helm, F.C.; Veeger, H.D.; Makhsous, M.; Van Roy, P.; Anglin, C.; Nagels, J.; Karduna, A.R.; McQuade, K.; Wang, X. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion—Part II: Shoulder, elbow, wrist and hand. J. Biomech. 2005, 38, 981–992. [Google Scholar] [CrossRef] [PubMed]
- Kwon, Y.-H.; Como, C.S.; Singhal, K.; Lee, S.; Han, K.H. Assessment of planarity of the golf swing based on the functional swing plane of the clubhead and motion planes of the body points. Sports Biomech. 2012, 11, 127–148. [Google Scholar] [CrossRef]
- Okuda, I.; Gribble, P.; Armstrong, C. Trunk rotation and weight transfer patterns between skilled and low skilled golfers. J. Sports Sci. Med. 2010, 9, 127. [Google Scholar]
- Teu, K.K.; Kim, W.; Fuss, F.K.; Tan, J. The analysis of golf swing as a kinematic chain using dual Euler angle algorithm. J. Biomech. 2006, 39, 1227–1238. [Google Scholar] [CrossRef] [PubMed]
- Fornberg, B. Generation of finite difference formulas on arbitrarily spaced grids. Math. Comput. 1988, 51, 699–706. [Google Scholar] [CrossRef]
- McHardy, A.; Pollard, H. Muscle activity during the golf swing. Br. J. Sports Med. 2005, 39, 799–804. [Google Scholar] [CrossRef]
- Huang, Y.-C.; Chen, T.-L.; Chiu, B.-C.; Yi, C.-W.; Lin, C.-W.; Yeh, Y.-J.; Kuo, L.-C. Calculate golf swing trajectories from imu sensing data. In Proceedings of the 2012 41st International Conference on Parallel Processing Workshops, Pittsburgh, PA, USA, 10–13 September 2012; pp. 505–513. [Google Scholar]
- Kim, Y.J.; Kim, K.D.; Kim, S.H.; Lee, S.; Lee, H.S. Golf swing analysis system with a dual band and motion analysis algorithm. IEEE Trans. Consum. Electron. 2017, 63, 309–317. [Google Scholar] [CrossRef]
- King, K.; Yoon, S.W.; Perkins, N.; Najafi, K. Wireless MEMS inertial sensor system for golf swing dynamics. Sens. Actuators A Phys. 2008, 141, 619–630. [Google Scholar] [CrossRef]
- Stančin, S.; Tomažič, S. Early improper motion detection in golf swings using wearable motion sensors: The first approach. Sensors 2013, 13, 7505–7521. [Google Scholar] [CrossRef]
- Umek, A.; Zhang, Y.; Tomažič, S.; Kos, A. Suitability of strain gage sensors for integration into smart sport equipment: A golf club example. Sensors 2017, 17, 916. [Google Scholar] [CrossRef]
- Han, K.H.; Como, C.; Kim, J.; Lee, S.; Kim, J.; Kim, D.K.; Kwon, Y.-H. Effects of the golfer–ground interaction on clubhead speed in skilled male golfers. Sports Biomech. 2019, 18, 115–134. [Google Scholar] [CrossRef]
- Horan, S.A.; Evans, K.; Morris, N.R.; Kavanagh, J.J. Thorax and pelvis kinematics during the downswing of male and female skilled golfers. J. Biomech. 2010, 43, 1456–1462. [Google Scholar] [CrossRef]
- Zhang, X.; Shan, G. Where do golf driver swings go wrong? Factors influencing driver swing consistency. Scand. J. Med. Sci. Sports 2014, 24, 749–757. [Google Scholar] [CrossRef]
- Arakawa, K.; Mada, T.; Komatsu, H.; Shimizu, T.; Satou, M.; Takehara, K.; Etoh, G. Dynamic deformation behavior of a golf ball during normal impact. Exp. Mech. 2009, 49, 471–477. [Google Scholar] [CrossRef]
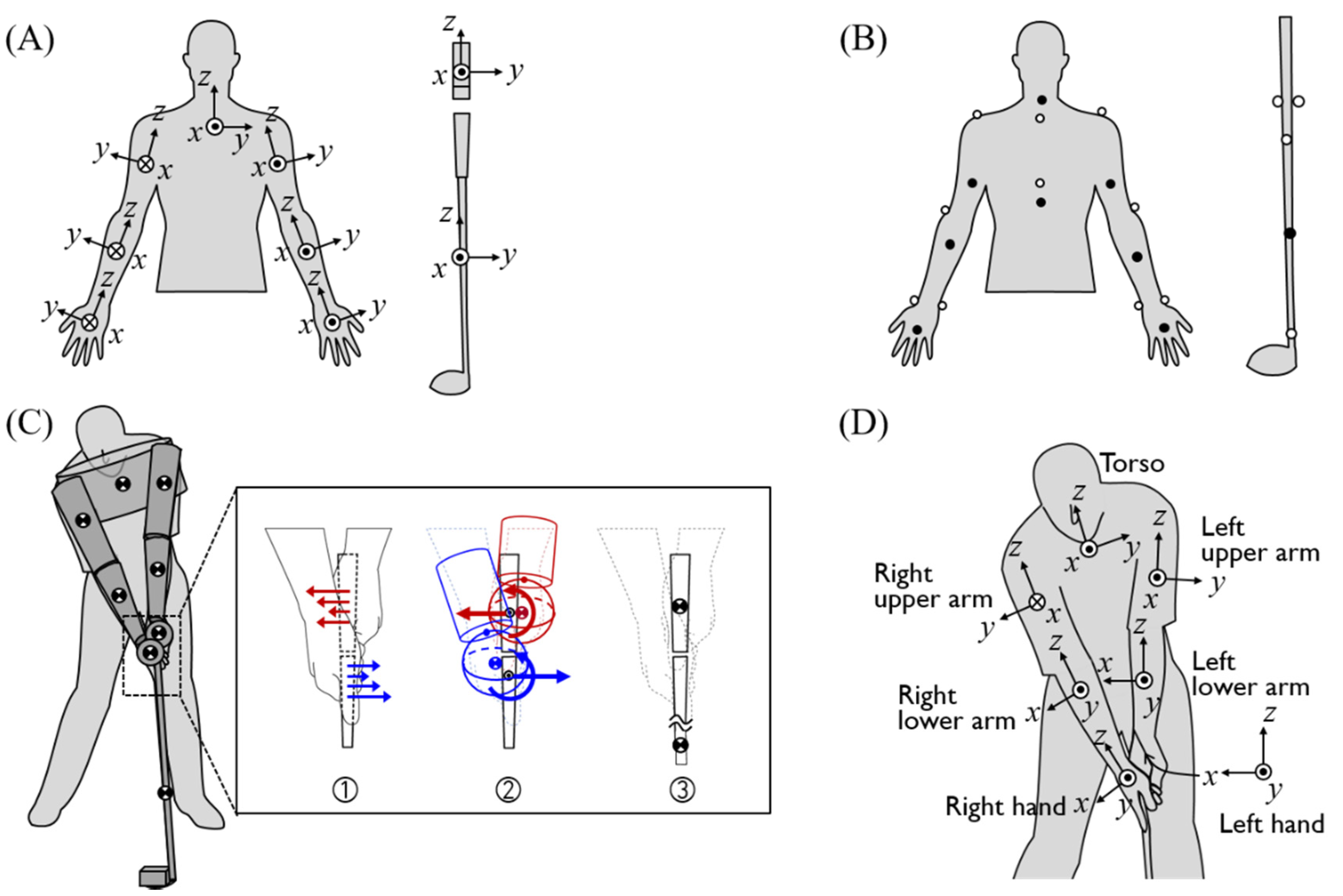
| Segment | Local x-Axis | Local y-Axis | Local z-Axis |
|---|---|---|---|
| Both club segment | Cross product of the local y- and z-axis | The direction of the clubface | Grip direction of the longitudinal axis |
| Hand | Perpendicular –direction to the palm (left) and back of hand (right) | Cross product of local z- and x-axis | The Proximal direction of longitudinal axis |
| Lower arm | Cross product of the local y- and z-axis | Lateral direction of wrist flexion axis | `` |
| Upper arm | `` | Lateral direction of elbow flexion axis | `` |
| Torso | `` | Right shoulder to left shoulder direction | Upper direction of longitudinal axis |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, H.; Park, S. Three Dimensional Upper Limb Joint Kinetics of a Golf Swing with Measured Internal Grip Force. Sensors 2020, 20, 3672. https://doi.org/10.3390/s20133672
Choi H, Park S. Three Dimensional Upper Limb Joint Kinetics of a Golf Swing with Measured Internal Grip Force. Sensors. 2020; 20(13):3672. https://doi.org/10.3390/s20133672
Chicago/Turabian StyleChoi, Hyeob, and Sukyung Park. 2020. "Three Dimensional Upper Limb Joint Kinetics of a Golf Swing with Measured Internal Grip Force" Sensors 20, no. 13: 3672. https://doi.org/10.3390/s20133672
APA StyleChoi, H., & Park, S. (2020). Three Dimensional Upper Limb Joint Kinetics of a Golf Swing with Measured Internal Grip Force. Sensors, 20(13), 3672. https://doi.org/10.3390/s20133672





