Effectiveness of Multidimensional Controllers Designated to Steering of the Motions of Ship at Low Speed
Abstract
1. Introduction
- 1.
- For exploitation speed i.e., ‘Full ahead’ or a similar one used on open sea:
- 2.
- For low speed i.e., ‘Slow or Very Slow ahead’ and ‘Slow or Very Slow Astern’ used mainly in constrained areas:
- 3.
- For speed close to zero:
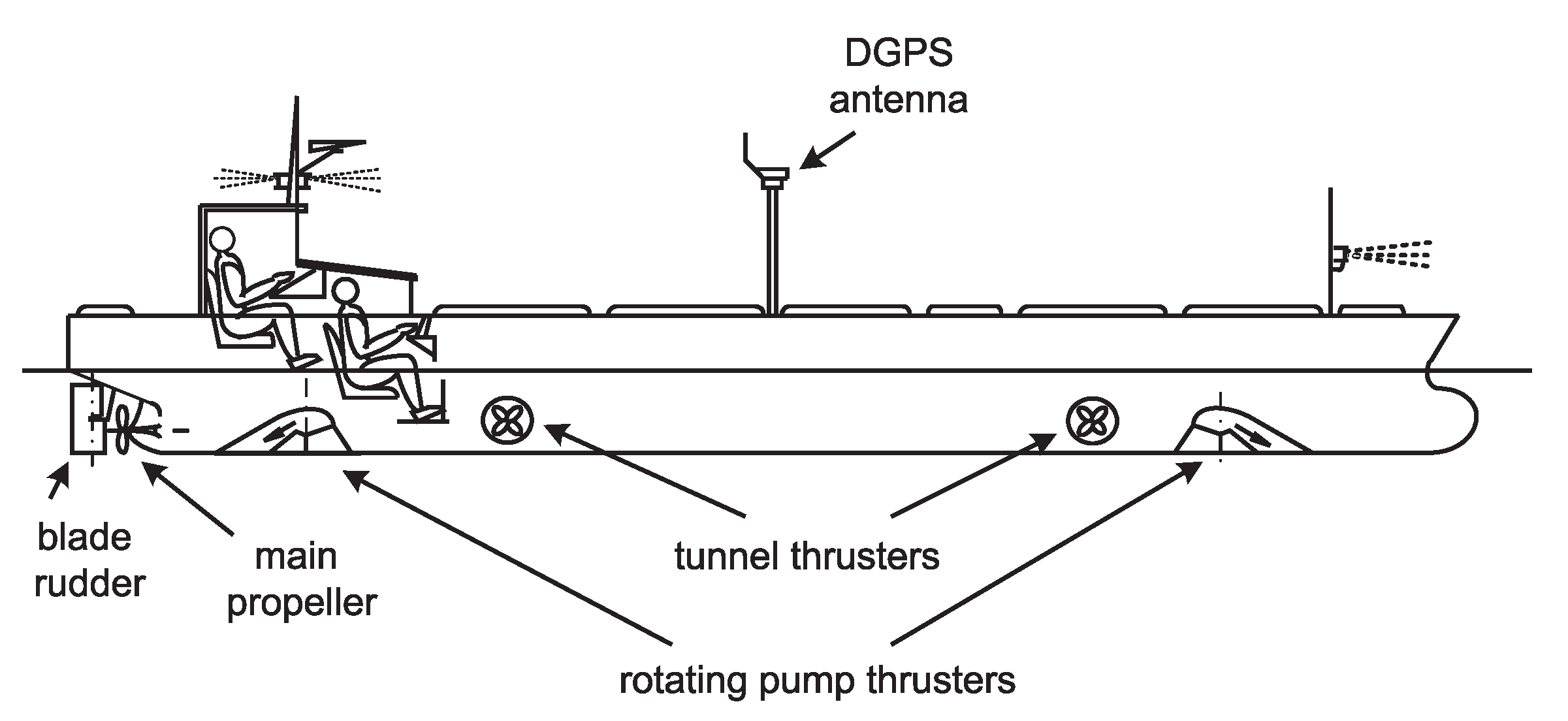
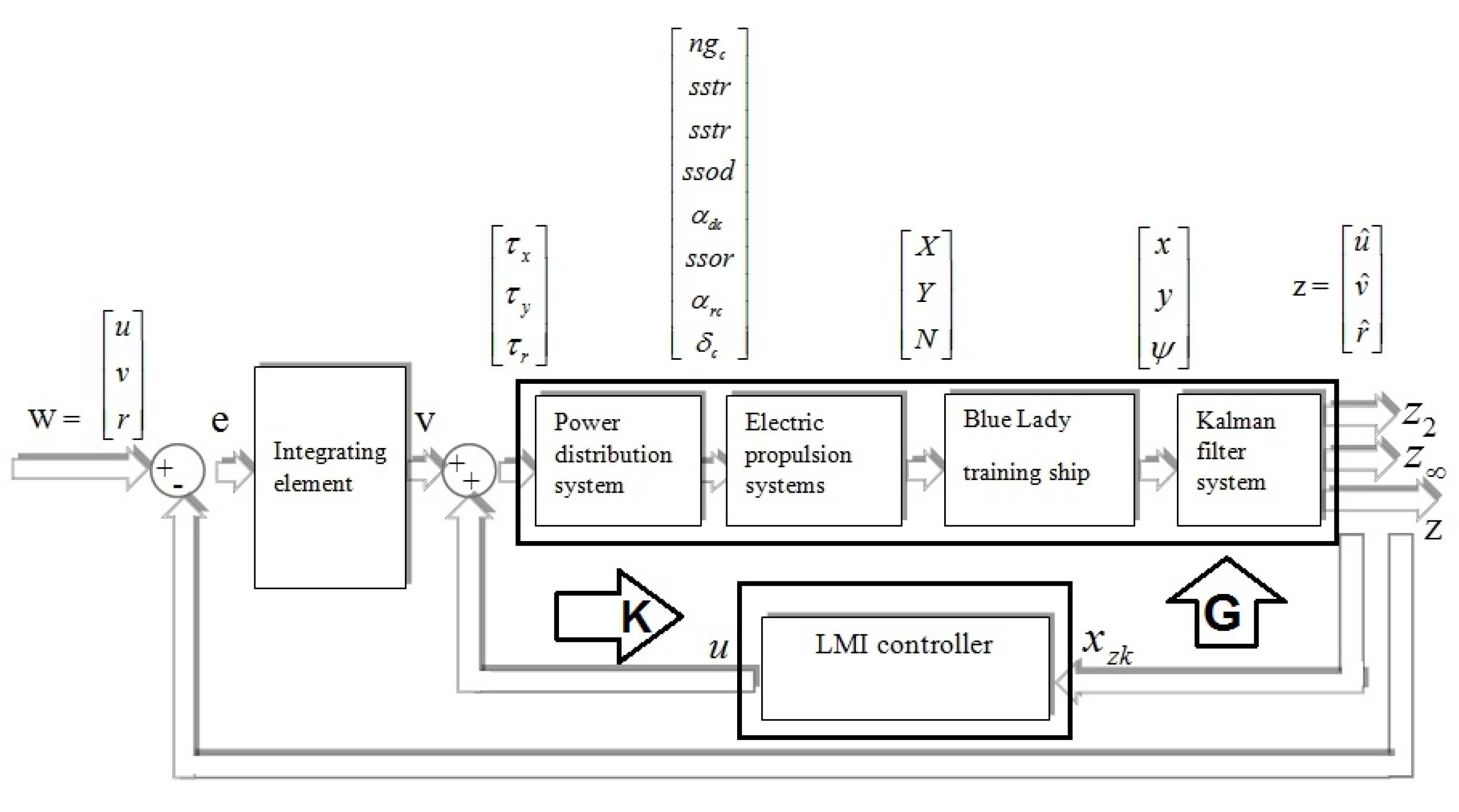
2. Controlled Object
- -
- Anschütz Standard 20 gyrocompass,
- -
- GILL WindObserver II ultrasonic anemometer,
- -
- LEICA DGPS System 500 receiver working in HPN (High Precision Network) mode.
- -
- propulsion operation,
- -
- ship hull construction,
- -
- stationary Kalman filter system (this system is used for velocities recreation) (‘Blue Lady’ ship model was not equipped with equipment for measuring linear velocities thus the need for Kalman filter system),
- -
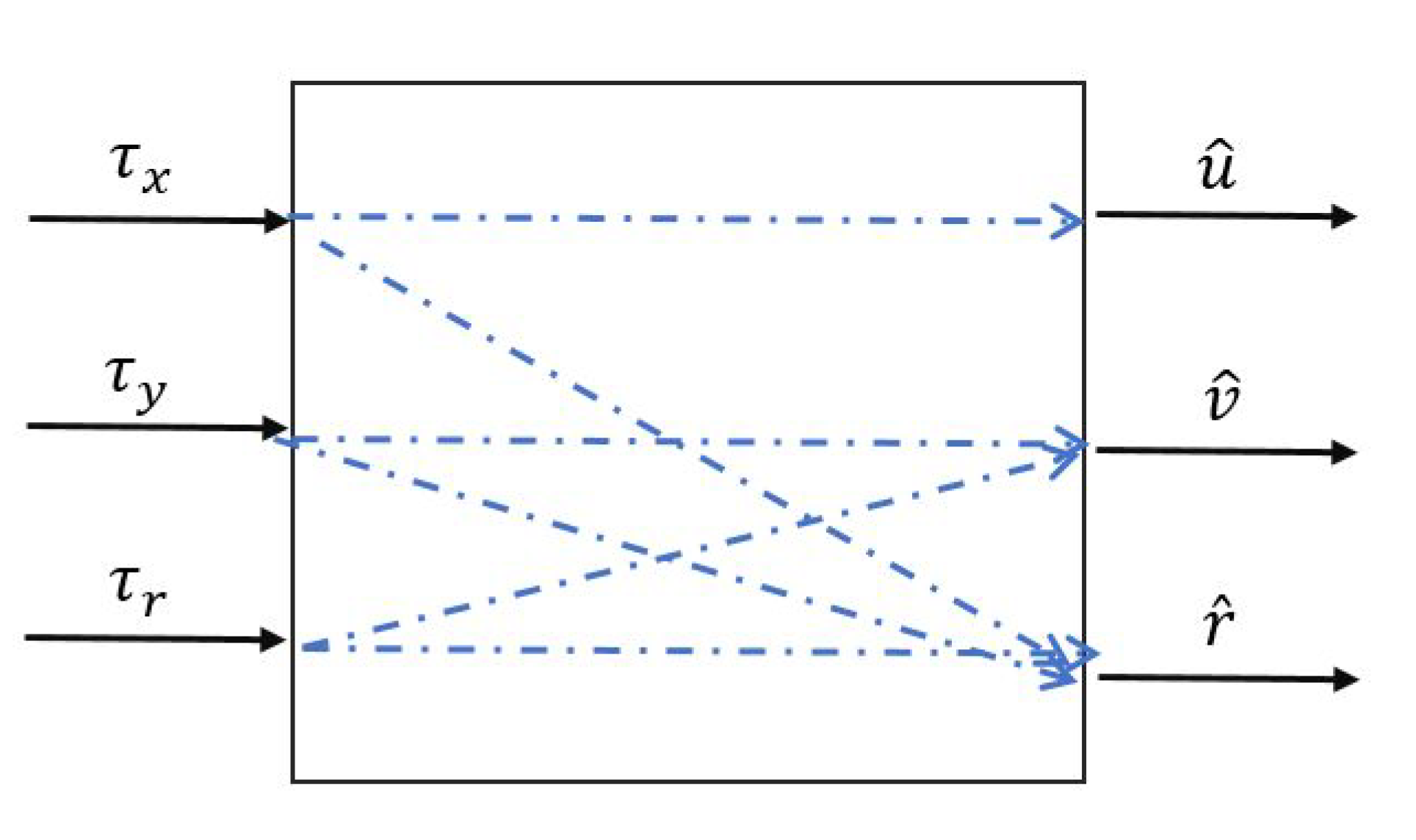
- power distribution system used for calculating three components of vector:to vector T with seven components of propulsion systems control signals (, , , , , , , . The details, symbols and ranges of these signals are presented in Table 1. Allocation is not directly the topic of this paper and as such is desribed in detail in [37]
3. Robust Controller
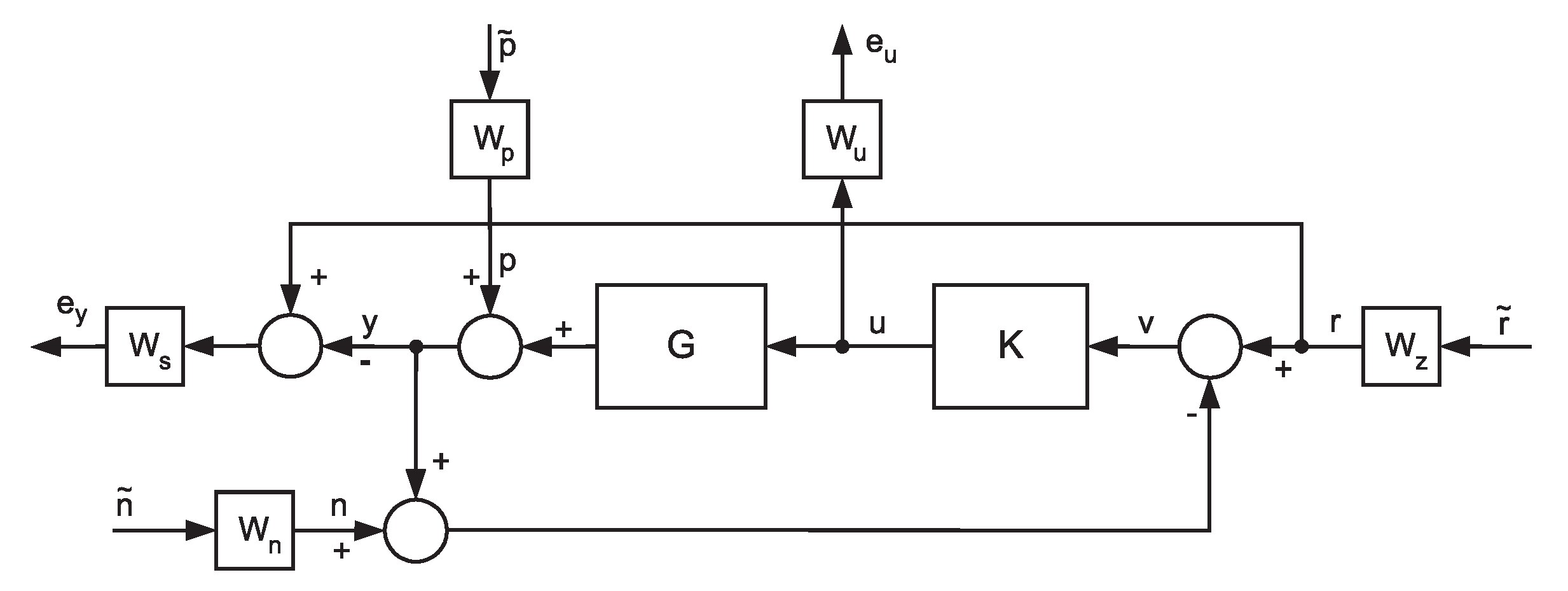
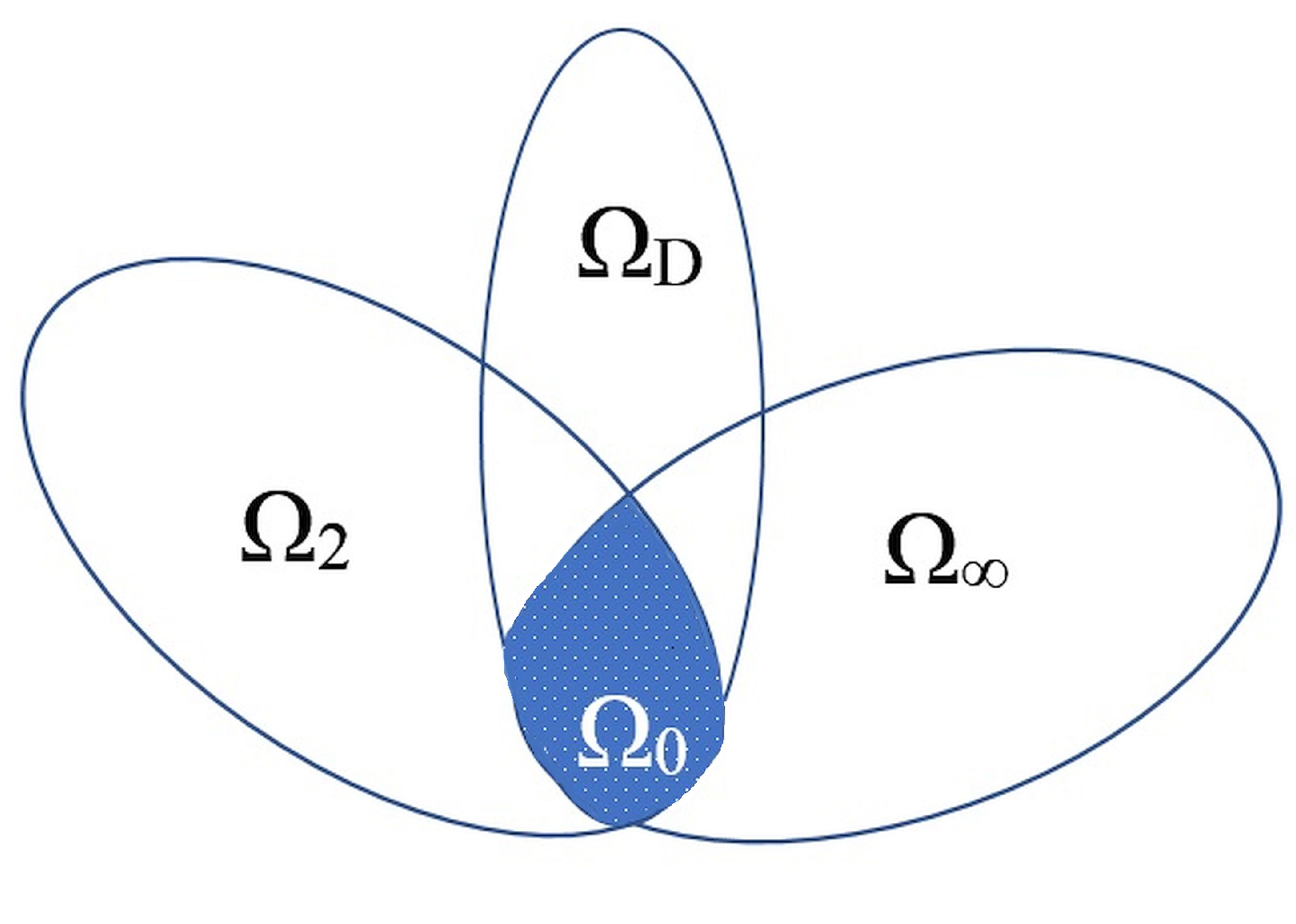
3.1. The Augmented Plant
- -
- such quantities can be used for different purposes e.g., establishing the requirements for control quality, description of disturbances, introduction of the influence of non-modelling dynamics of the plant etc.,
- -
- the signals scaling operation is easy to perform by means of weighting functions,
- -
- one can distinguish between more and less important components of the signals vectors (e.g., in errors vector) by proper gain coefficients,
- -
- designer requirements related to the particular signals can be formulated for specified frequency ranges in a natural way.
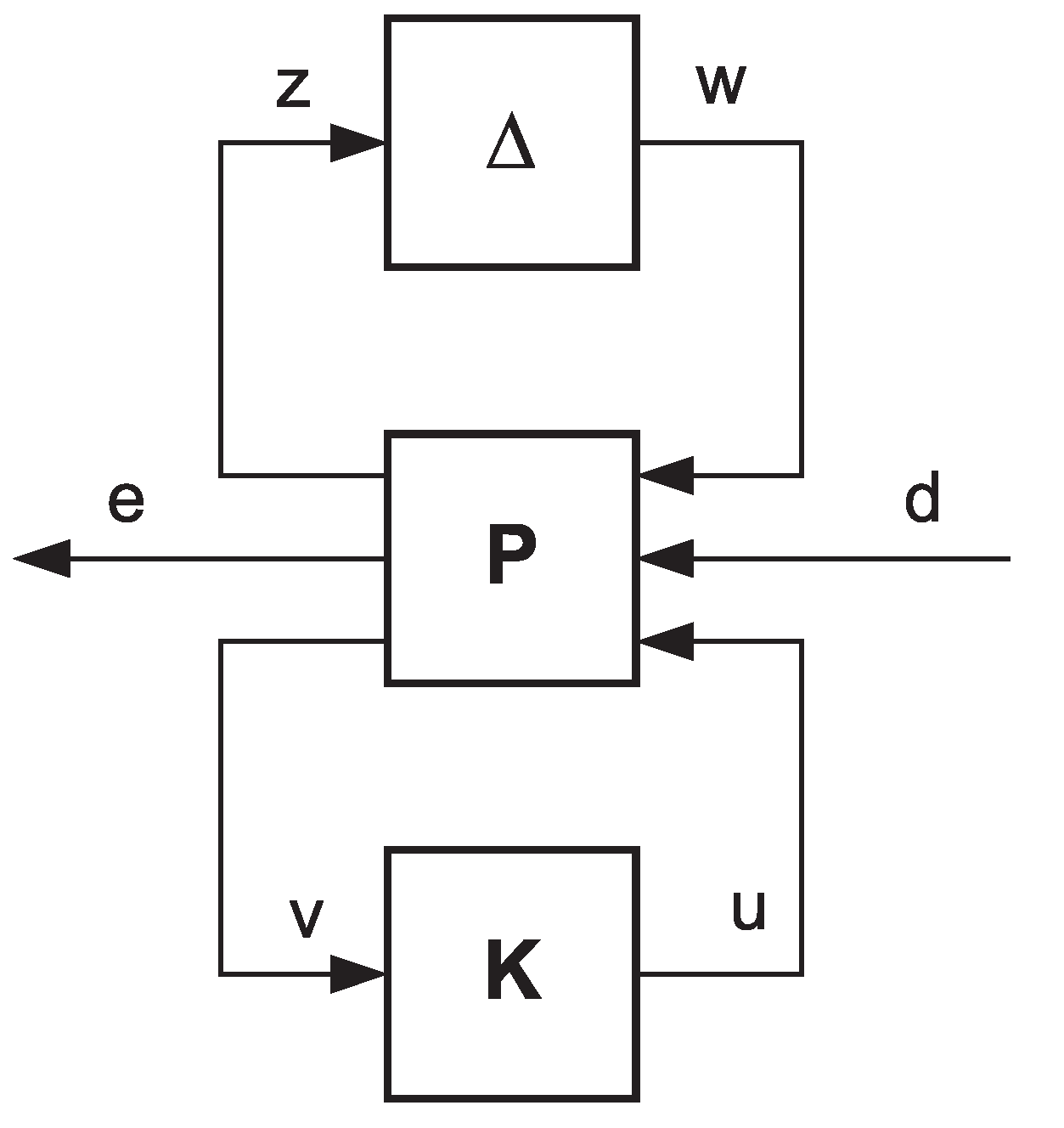
- -
- the first one is the “pure” uncertainty , bounded in the norm sense, i.e.,
- -
- the second one it is the weighting function modeling the magnitude and shape of the uncertainty in the frequency domain.
3.2. The Controller Synthesis
4. LMI Controller
4.1. The LMI Concept and the Formulation of the Plant
- -
- decision variable vector (unknown) x = ,
- -
- matrices marked as are real and symmetrical,
- -
- the term “” means that the matrix is positively defined.
- -
- —controlled object state space matrix, represents system dynamics;
- -
- —control matrix of control ‘u’ signal ;
- -
- —control matrix of input ‘w’ signal ;
- -
- —output matrix of output signal ‘z’;
- -
- —output matrix of ‘’ signal;
- -
- —output matrix of ‘’ signal;
- -
- —transition matrix of ‘z’ and ‘u’ signals;
- -
- —transition matrix of ‘z’ and ‘w’ signals;
- -
- —transition matrix of ‘’ and ‘u’ signals;
- -
- —transition matrix of ‘’ and ‘w’ signals;
- -
- —transition matrix of ‘’ and ‘u’ signals;
- -
- —transition matrix of ‘’ and ‘w’ signals;
- -
- ‘’ and ‘’—additional output signals necessary for calculations of and norms.
4.2. Stability Restriction—Poles in the Left Half-Plane of Complex Variable Plane s
- -
- —in this specific case instead of matrix we have to use the form , has to be used,
- -
- —the unknown, symmetrical positively defined Lyapunov matrix ,
- -
- —specific, user defined matrices.
4.3. Minimization of Matrix Norm
- -
- = ;
- -
- = ;
- -
- = ;
- -
- = .
4.4. Minimization of Matrix Norm
- -
- = ;
- -
- = ;
- -
- = ;
- -
- = .
4.5. Last Assumption and Final Controller
5. Experiments
5.1. The Steering Quality Validation
- -
- —maximum output signal value received from the system,
- -
- —minimum output signal value received from the system.
5.2. Exemplary Results of Three Exercises
- -
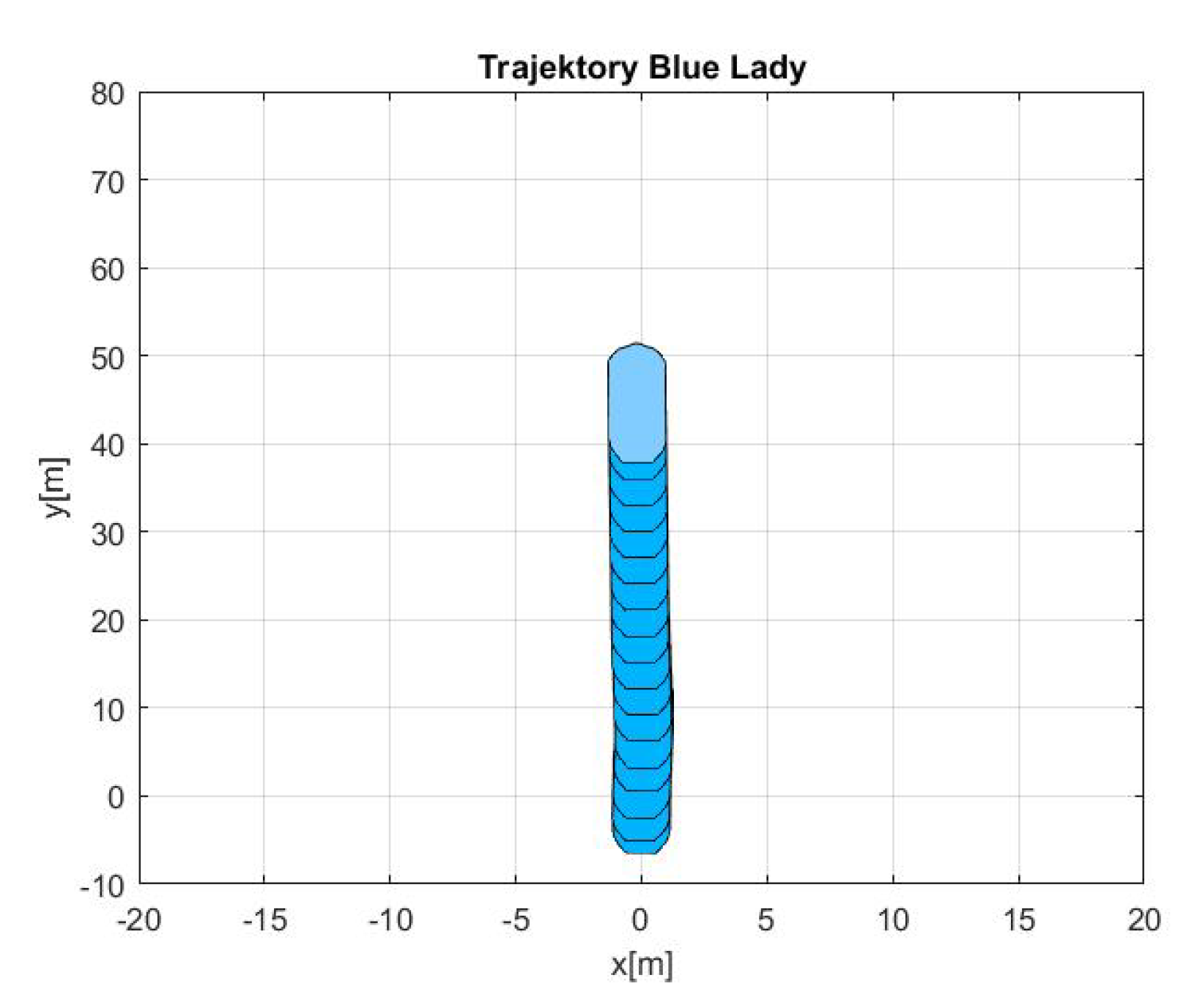
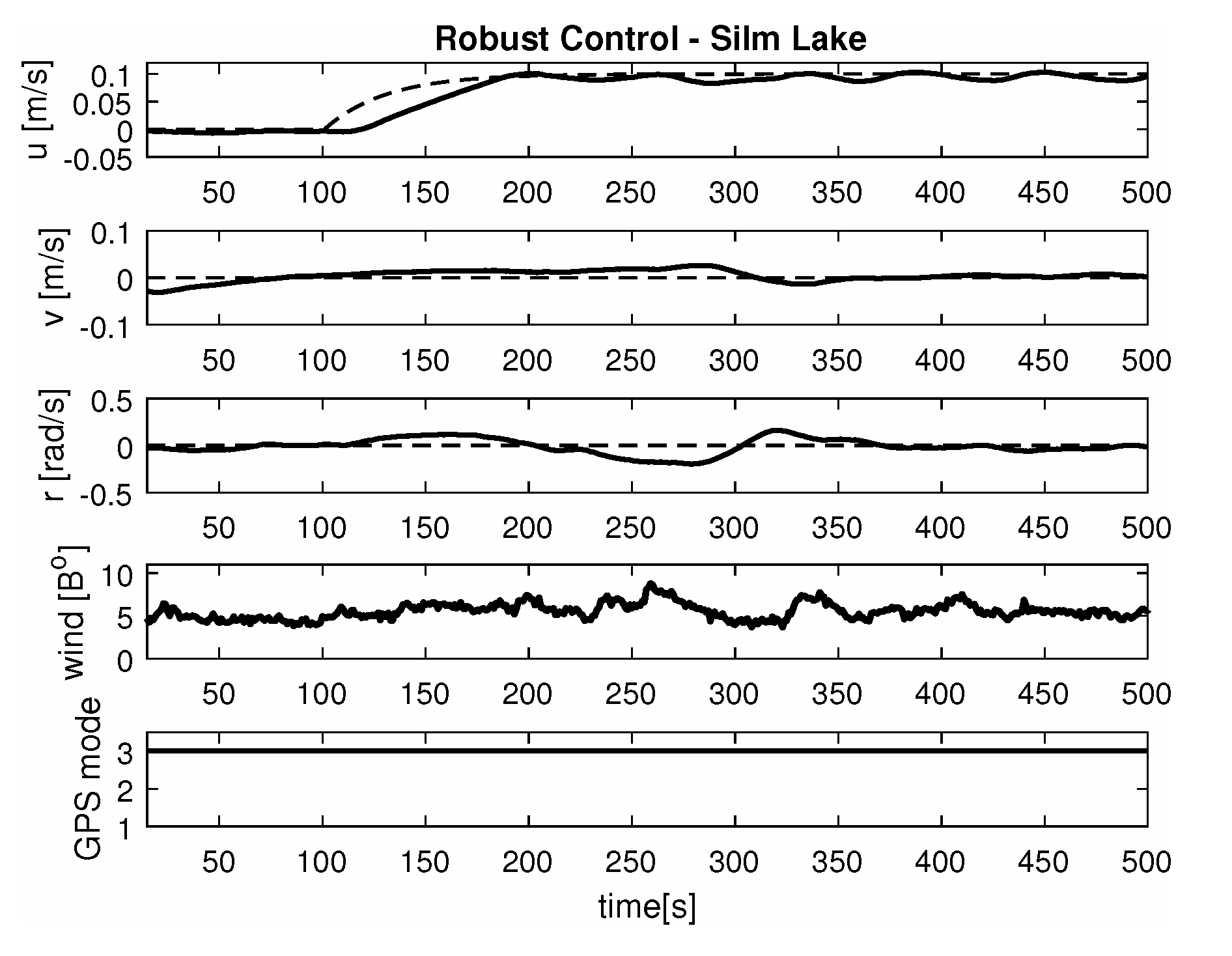
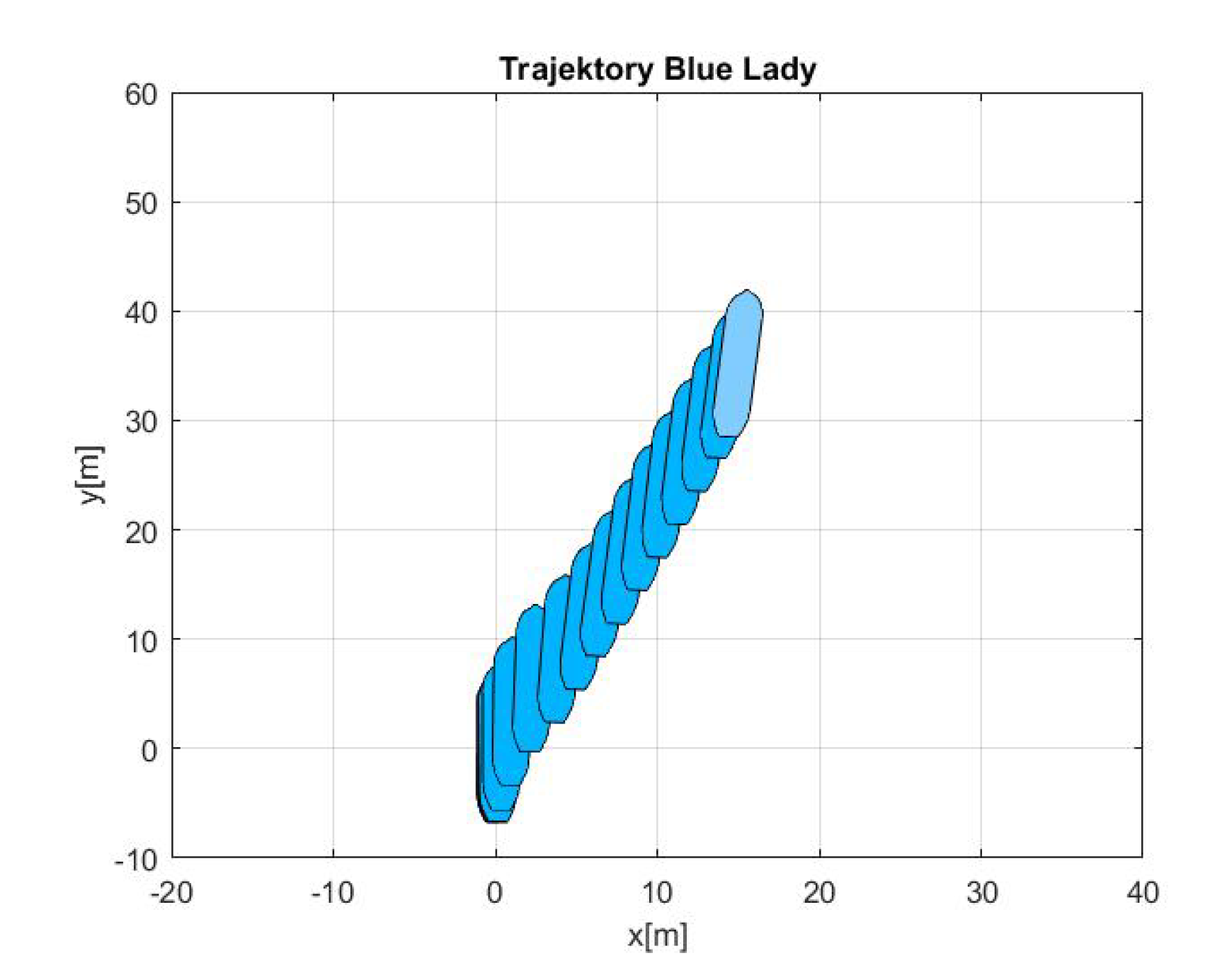
- Maneuver no. 1Ahead movement with a given longitudinal velocity u = 0.1 [m/s], with maneuver of the duration of 700 [s]. Values of lateral and rotational velocities were set to v = 0 [m/s], r = 0 [deq/s]. This type of ship maneuver, at low velocities, is very common when navigating narrow passages like channels, rivers or entering harbors. Trajectory ship are shown on Figure 8. Results of the Robust controller are shown on Figure 9, and for the LMI controller on Figure 10.
- -
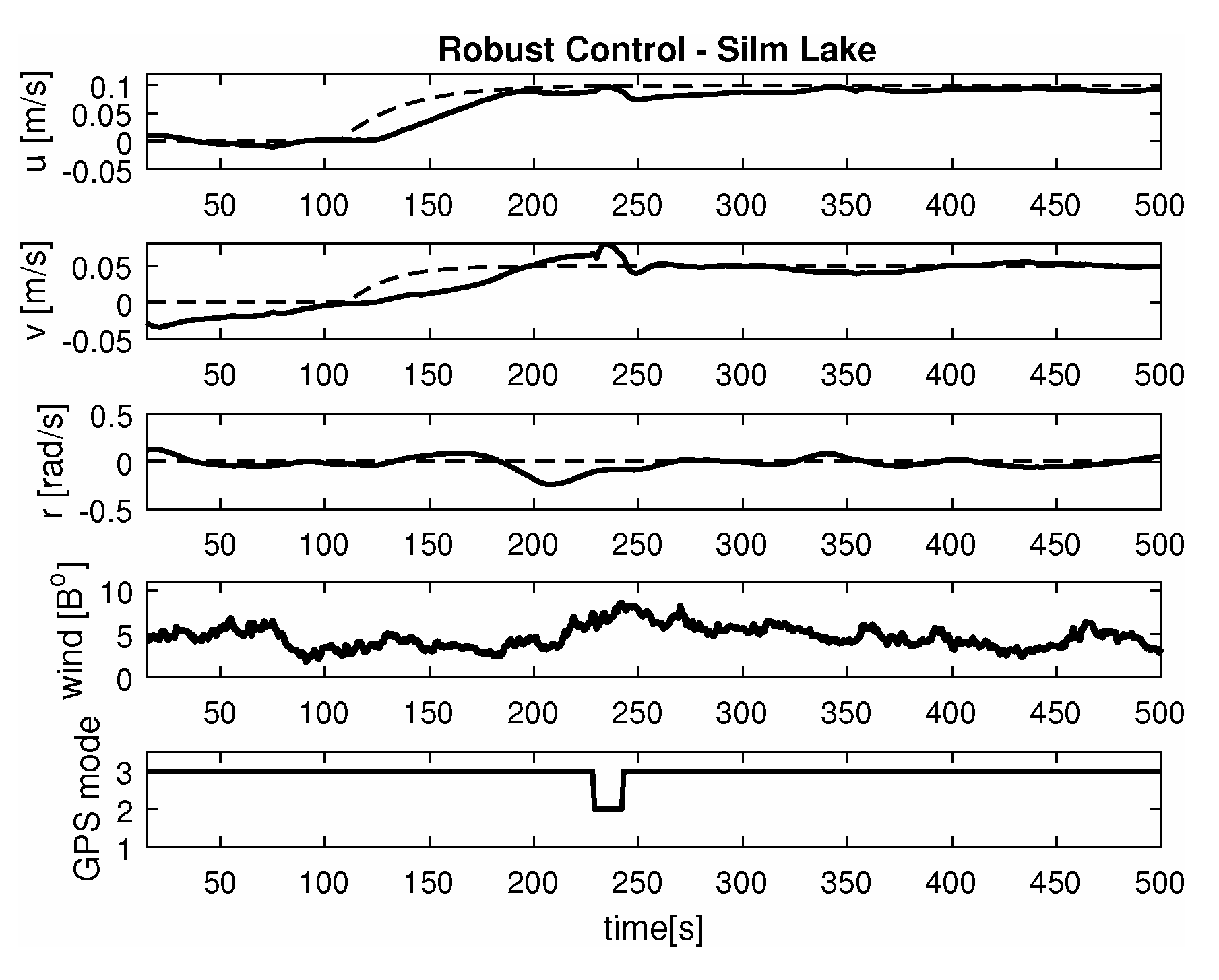
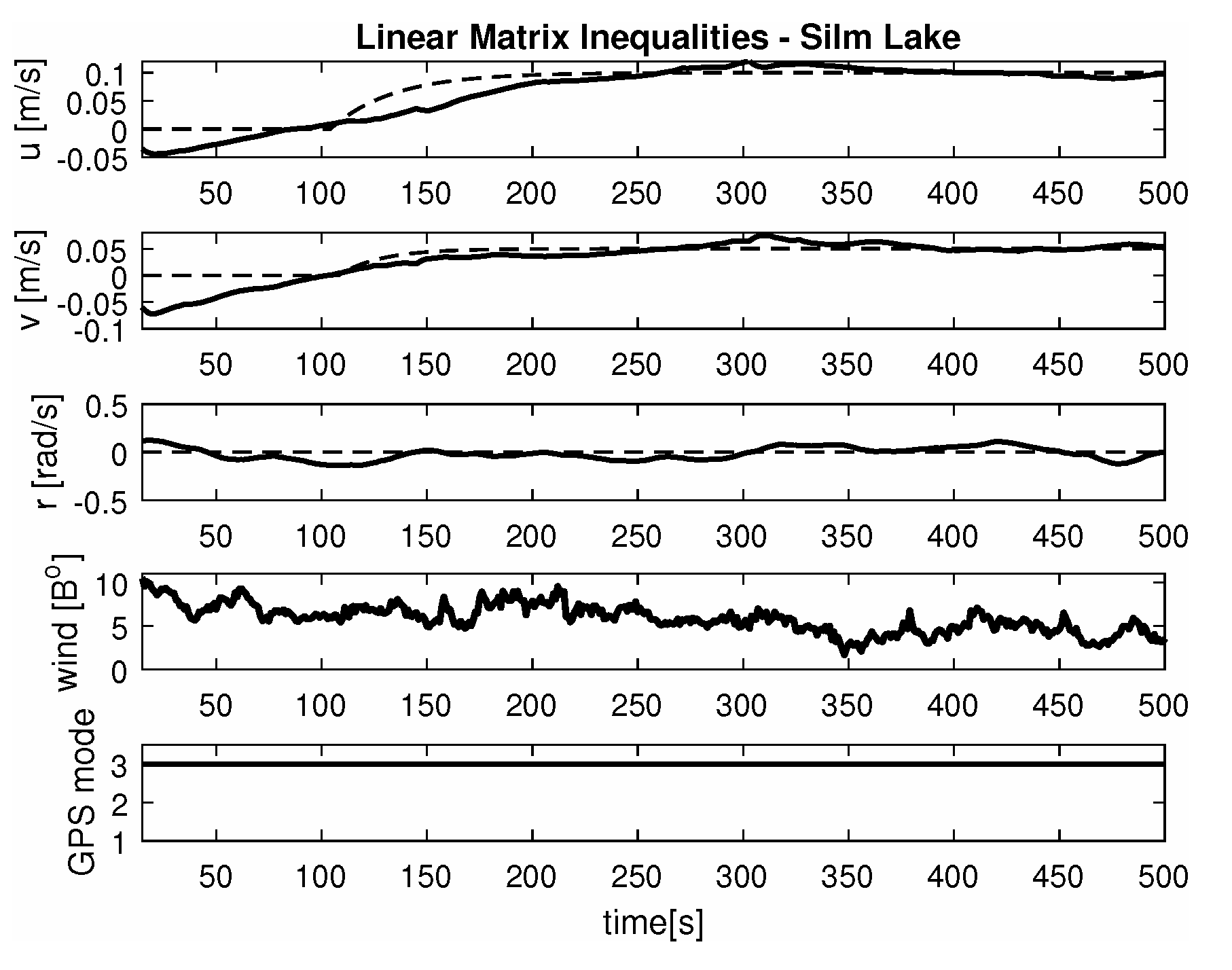
- Maneuver no. 2Ahead and sideways movement with given longitudinal velocity u = 0.1 [m/s] and lateral one v = 0.05 [m/s] with no rotational velocity r = 0 [rad/s] and with maneuver duration of 500 [s]. This type of ship maneuver, at low velocities, is a typical approach to berth which is located parallel to ships. Trajectory ship are shown on Figure 11. Results of the Robust controller are shown on Figure 12 position, and for the LMI controller respectively on Figure 13.
- -
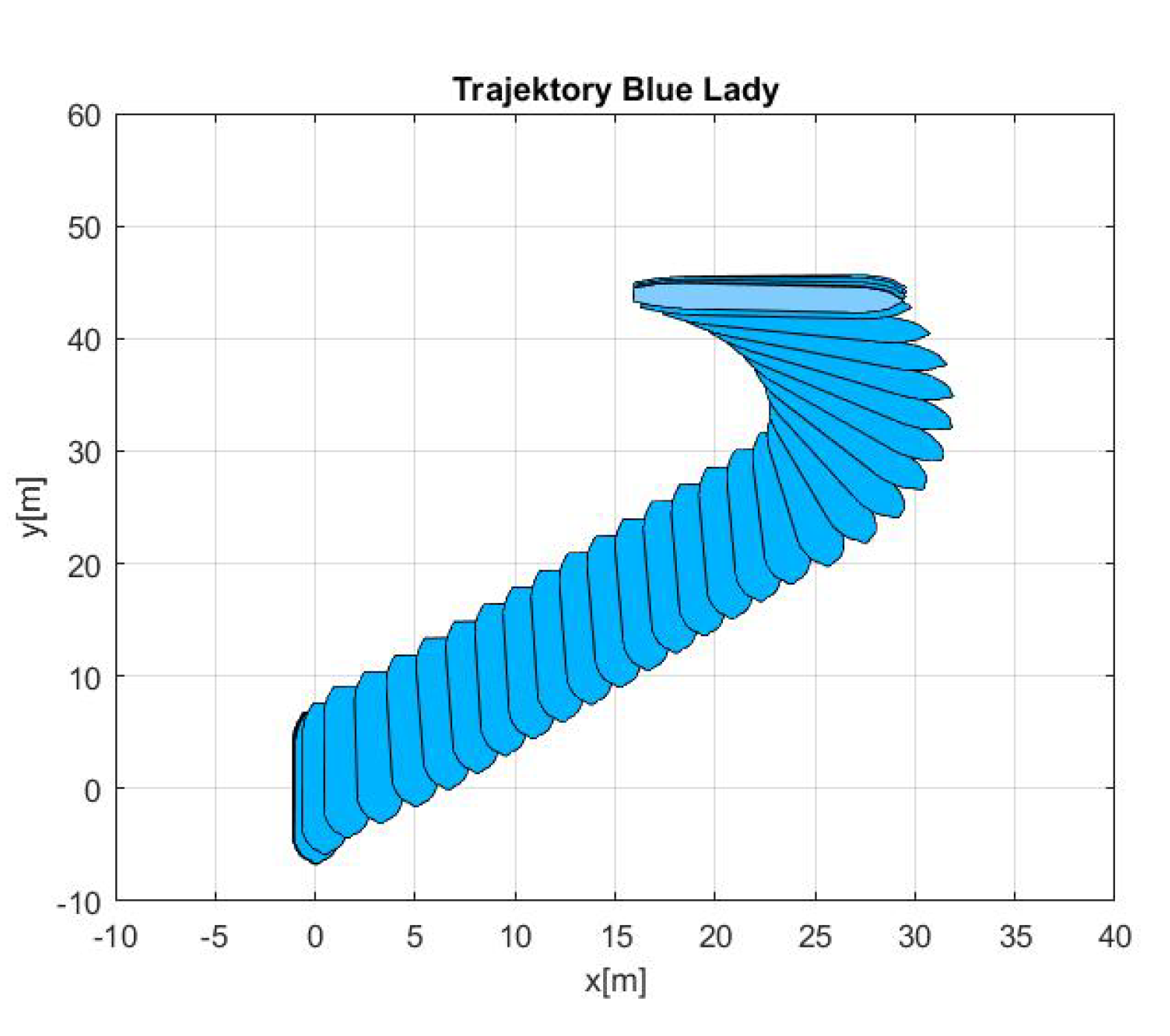
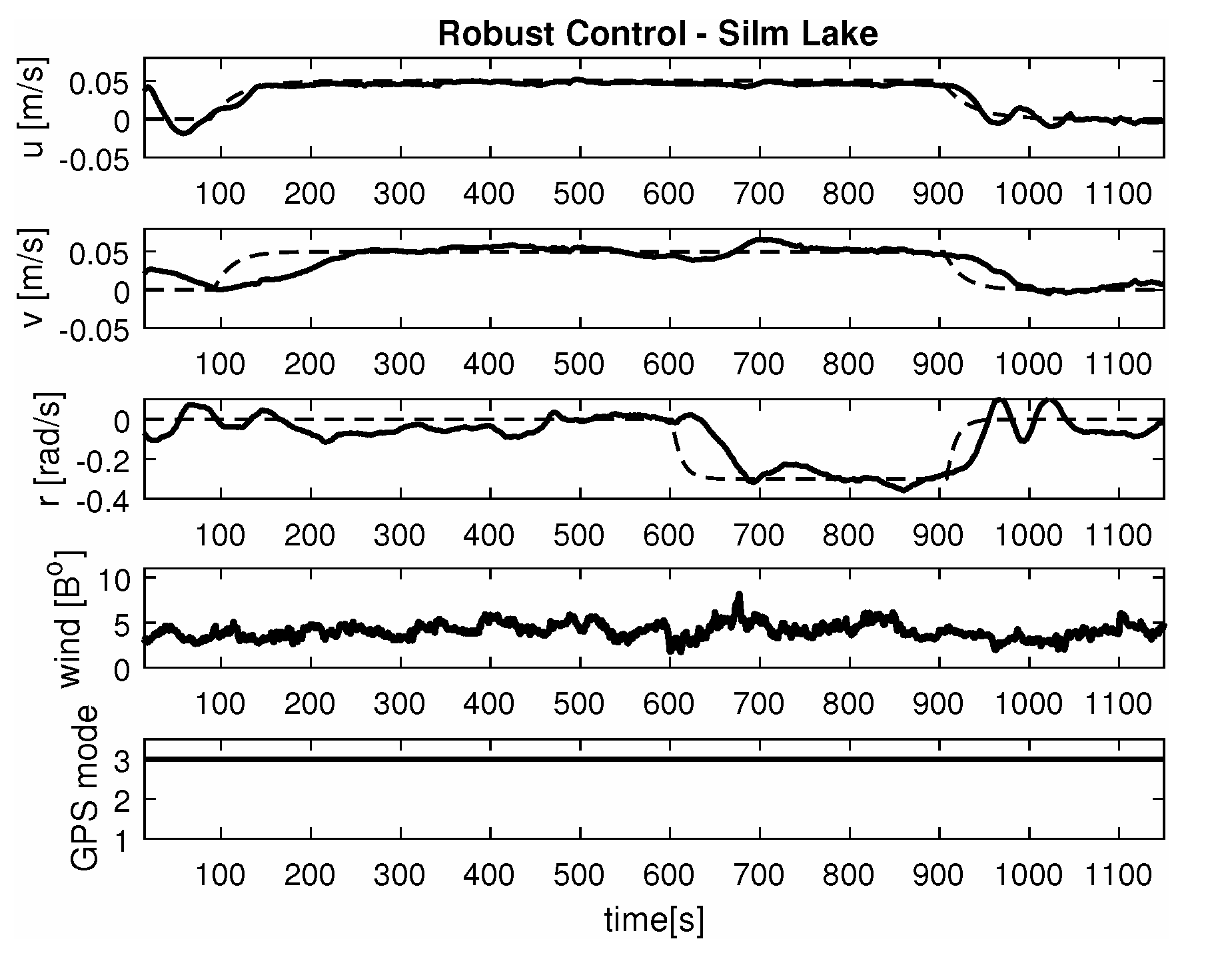
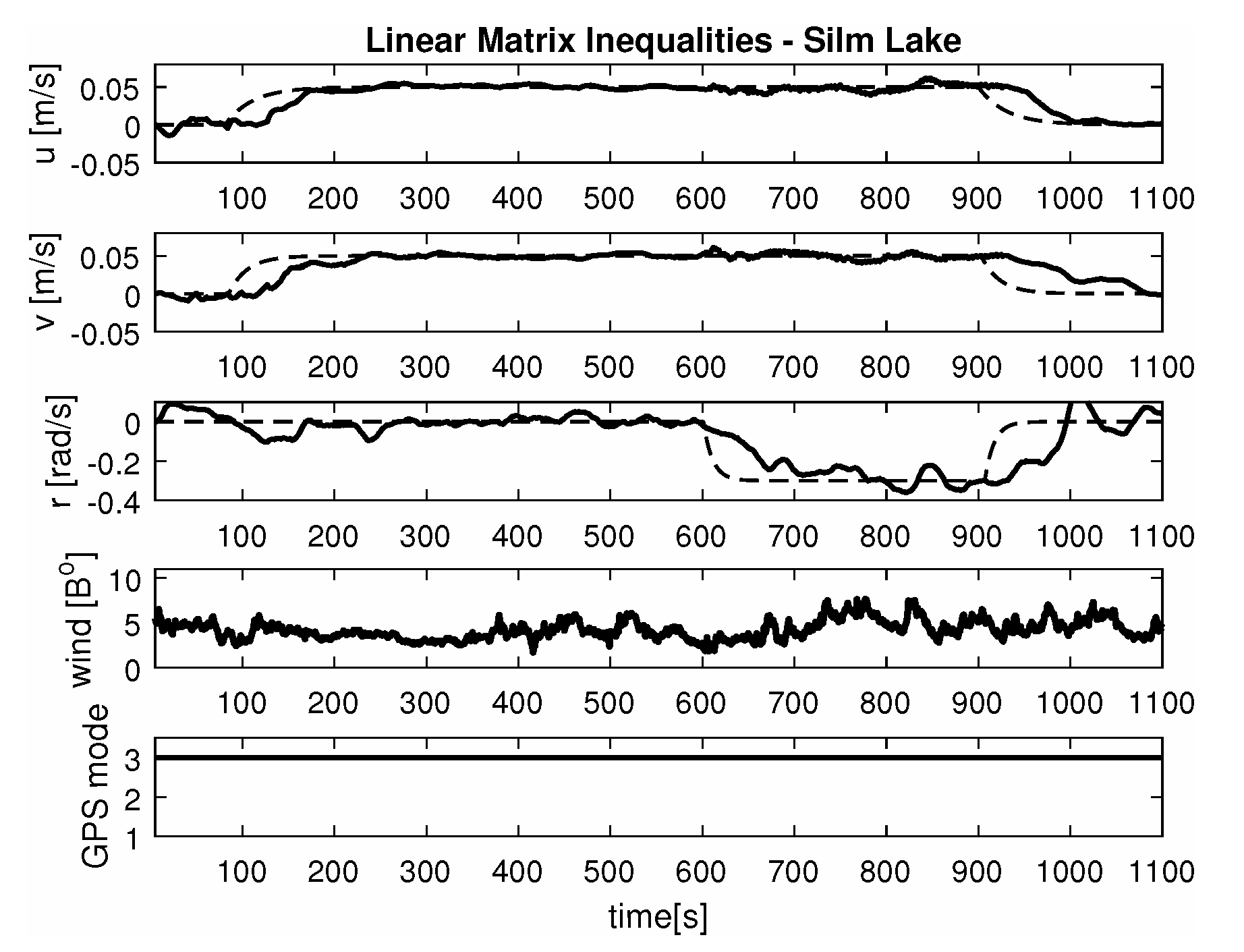
- Maneuver no. 3Ahead and sideways movement with rotation when performance velocities were set as follows. Duration of the maneuver was 1100 [s]. This type of ship maneuver, at low velocities, is a typical approach to berth which is located perpendicular to ships course. Trajectory ship are shown on Figure 14. Results of the Robust controller are shown on Figure 15, and for the LMI controller on Figure 16.
5.3. Comparison and Comments
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fossen, T.I. Guidance and Control of Ocean Vehicles; Wiley and Sons: Chichester, UK, 1994. [Google Scholar]
- Fossen, T.I.; Perez, T. Kalman filtering for positioning and heading control of ships and offshore rigs. IEEE Control Syst. Mag. 2009, 29, 32–46. [Google Scholar]
- Tomera, M. A multivariable low speed controller for a ship autopilot with experimental results. In Proceedings of the 20th International Conference on Methods and Models in Automation and Robotics (MMAR), Międzyzdroje, Poland, 24–27 August 2015; pp. 17–22. [Google Scholar]
- Tomera, M. Swarm intelligence applied to identification of nonlinear ship steering model. In 2015 IEEE 2nd International Conference on Cybernetics (CYBCONF); IEEE: Piscataway, NJ, USA, 2015; pp. 133–139. [Google Scholar]
- Zhang, X.; Yang, G.; Zhang, Q.; Zhang, G.; Zhang, Y. Improved Concise Backstepping Control of Course Keeping for Ships Using Nonlinear Feedback Technique. J. Navig. 2017, 70, 1401–1414. [Google Scholar] [CrossRef]
- Kula, K.S. Model-based controller for ship track-keeping using neural network. In Proceedings of the IEEE 2nd International Conference on Cybernetics (CYBCONF), Gdynia, Poland, 24–26 June 2015; pp. 178–183. [Google Scholar]
- Hu, Z.; Peng, X. Integral nested sliding mode control for ship turning. In Proceedings of the 3rd IEEE International Conference on Communication Software and Networks (ICCSN), Xi’an, China, 27–29 May 2011. [Google Scholar]
- Perez, T. Ship Motion Control: Course Keeping and Roll Stabilisation Using Rudder and Fins; Springer: Berlin, Germany, 2015. [Google Scholar]
- Perez, T.; Blanke, M. Ship roll damping control. Ann. Rev. Control 2012, 36, 129–147. [Google Scholar] [CrossRef]
- Lisowski, J.; Mohamed-Seghir, M. Comparison of Computational Intelligence Methods Based on Fuzzy Sets and Game Theory in the Synthesis of Safe Ship Control Based on Information from a Radar ARPA System. Remote Sens. 2019, 11, 82. [Google Scholar] [CrossRef]
- Gierusz, W.; Vinh, N.C.; Rak, A. Maneuvering control and trajectory tracking of very large crude carrier. Ocean Eng. 2007, 34, 932–945. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley and Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Zhang, G.; Zhang, X.; Pang, H. Multi-innovation auto-constructed least squares identification for 4 DOF ship manoeuvring mode modeling with full-scale trial data. ISA Trans. 2015, 58, 186–195. [Google Scholar] [CrossRef]
- Ramire, W.; Leong, Z.; Nguyen, H.; Jayasinghe, S.G. Non-parametric dynamic system identification of ships using multi-output Gaussian Processes. Ocean Eng. 2018, 166, 26–36. [Google Scholar] [CrossRef]
- Zhu, M.; Hahn, A.; Wen, Y. Identification-based controller design using cloud model for course-keeping of ships in waves. Eng. Appl. Artif. Intell. 2018, 75, 22–35. [Google Scholar] [CrossRef]
- Park, J.; Sung, H.; Ahmad, F.; So, S.H.; Syngellakis, S.; Jung, K.H.; Jang, T.S. A Numerical Identification of Excitation Force and Nonlinear Restoring Characteristics of Ship Roll Motion. J. Mar. Sci. Technol. Taiwan 2017, 25, 475–481. [Google Scholar]
- Zhang, Z.; Zhang, X.; Zhang, G. ANFIS-based course-keeping control for ships using nonlinear feedback technique. J. Mar. Sci. Technol. 2019, 24, 1326–1333. [Google Scholar] [CrossRef]
- Alfi, A.; Shokrzadeh, A.; Asadi, M. Reliability analysis of H∞ control for a container ship in way-point tracking. Appl. Ocean Res. 2015, 52, 309–316. [Google Scholar] [CrossRef]
- Veremey, E.I.; Korovkin, M.V.; Sotnikova, M.V. Ships’ Steering in Accurate Regime Using Autopilot with Special Structure of Control Law. IFAC-PapersOnLine 2015, 48, 7–12. [Google Scholar] [CrossRef]
- Boyd, S.; El-Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar]
- El Ghaoui, L.; Niculescu, S.L. Advances in Linear Matrix Inequality Methods in Control; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000. [Google Scholar]
- Lam, H.K.; Leung, F.H.F. Stability Analysis of Fuzzy-Model-Based Control Systems; Springer: Berlin, Germany, 2011; Volume 264, pp. 191–215. [Google Scholar]
- Ostertag, E. Mono- and Multivariable Control and Estimation: Linear, Quadratic and LMI Methods; Springer Science and Business Media: Berlin, Germany, 2011; Volume 2. [Google Scholar]
- Patel, H.R.; Shah, V.A. Stable Fault Tolerant Controller Design for Takagi–Sugeno Fuzzy Model-Based Control Systems via Linear Matrix Inequalities: Three Conical Tank Case Study. Energies 2019, 12, 2221. [Google Scholar] [CrossRef]
- Duan, G.R.; Yu, H.H. LMIs in Control Systems: Analysis, Design and Applications; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Gao, X.; Teo, K.L.; Duan, G.R.; Wang, N. Robust reliable H∞ control for uncertain systems with pole constraints. Int. J. Innov. Comput. Inf. Control 2012, 8, 3071–3079. [Google Scholar]
- Zhang, X.K.; Han, X.; Guan, W.; Zhang, G.Q. Improvement of integrator backstepping control for ships with concise robust control and nonlinear decoration. Ocean Eng. 2019, 189, 106349. [Google Scholar] [CrossRef]
- Zhang, Q.; Sijun, Y.; Yan, L.; Xinmin, W. An enhanced LMI approach for mixed H∞/H2 flight tracking control. Chin. J. Aeronaut. 2011, 24, 324–328. [Google Scholar] [CrossRef]
- Balandin, D.V.; Kogan, M.M. Pareto optimal generalized H2-control and optimal protection from vibration. IFAC-PapersOnLine 2017, 50, 4442–4447. [Google Scholar] [CrossRef]
- Joelianto, E.; Gani, G.; Putri, N.K. Robust control with linear matrix inequality approach for ship steering problem. In Proceedings of the Instrumentation, Control and Automation (ICA), 2016 International Conference, Bandung, Indonesia, 29–31 August 2016; pp. 126–131. [Google Scholar]
- Rolls-Royce. The Next Steps of Remote and Autonomous Ships’. Rolls-Royce Holdings plc. 2018. Available online: https://www.rolls-royce.com//media/Files/R/Rolls-Royce/documents/customers/marine/ship-intel/aawa-whitepaper210616.pdf (accessed on 30 March 2020).
- Konsberg. Autonomous Ship Project, Key Facts about YARA Birkeland. (OpenDocument). 2019. Available online: https://www.km.kongsberg.com/ks/web/nokbg0240.nsf/AllWeb/4B8113B707A50A4FC125811D00407045 (accessed on 13 January 2020).
- Doyle, J.C.; Glover, K.; Khargonekar, P.P.; Francis, B.A. State-space Solutions to Standard H2 and H∞ Control Problems. IEEE Trans. Autom. Control 1989, 34, 831–847. [Google Scholar] [CrossRef]
- Gierusz, W. Simulation model of the shiphandling training boat “Blue Lady”. In IFAC Proceedings Volumes; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Pomirski, J.; Rak, A.; Gierusz, W. Control system for trials on material ship model. Pol. Marit. Res. 2012, 19, 25–30. [Google Scholar] [CrossRef]
- Rybczak, M. Improvement of control precision for ship movement using a multidimensional controller. Automatika 2018, 59, 63–70. [Google Scholar] [CrossRef]
- Miller, A.; Rybczak, M. Thrust allocation system for Blue Lady training ship taking into account efficient work of main propeller. Sci. J. Maritime Univ. Szczecin 2013, 36, 123–130. [Google Scholar]
- Redheffer, R.M. On a Certain Linear Fractional Transformation. J. Math. Phys. 1960, 39, 269–286. [Google Scholar] [CrossRef]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control–Analysis and Design; John Wiley and Sons: Chichester, UK, 2003. [Google Scholar]
- Gierusz, W. The steernig of the ship motion: A μ synthesis approach. Arch. Control Sci. 2006, 16, 87–109. [Google Scholar]
- Da Ponte Caun, R.; Assunção, E.; Minhoto Teixeira, M.C.; da Ponte Caun, A. LQR-LMI control applied to convex-bounded domains. Cogit. Eng. 2018, 5, 1–27. [Google Scholar] [CrossRef]
- Miller, A. Identification of a multivariable incremental model of the vessel. In Proceedings of the 21st International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 29 August–1 September 2016; pp. 218–224. [Google Scholar]
- Miller, A.; Rybczak, M. Methods of controller synthesis using linear matrix inequalities and model predictive control. Sci. J. Maritime Univ. Szczecin 2015, 43, 22–28. [Google Scholar]
- Nodozi, I.; Rahmani, M. LMI-based model predictive control for switched nonlinear systems. J. Proc. Control Xi’an 2017, 59, 49–58. [Google Scholar] [CrossRef]
- Xue, A.; Zou, H. Pole placement with LMI constraint of fuzzy descriptor system. J. Franklin Inst. 2015, 352, 2665–2678. [Google Scholar]
- Chiu, W.Y. Multiobjective controller design by solving a multiobjective matrix inequality problem. IET Control Theory Appl. 2014, 8, 1656–1665. [Google Scholar] [CrossRef]
- Molina-Cristóbal, A.; Griffin, I.A.; Fleming, P.J.; Owens, D.H. Linear matrix inequalities and evolutionary optimization in multiobjective control. Int. J Syst. Sci. 2006, 37, 513–522. [Google Scholar] [CrossRef]
- Łebkowski, A.; Smierzchalski, R. Hybrid System of Safe Ship Steering at Sea. In Proceedings of the 9th IEEE International Conference on Methods and Models in Automation and Robotics, Międzyzdroje, Poland, 25–28 August 2003; pp. 263–268. [Google Scholar]
- Łebkowski, A. Design of an Autonomous Transport System for Coastal Areas, TRANSNAV. Int. J. Mar. Navig. Saf. Sea Trans. 2018, 12, 117–124. [Google Scholar]
- Łebkowski, A. Analysis of the Use of Electric Drive Systems for Crew Transfer Vessels Servicing Offshore Wind Farms. Energies 2020, 13, 1466. [Google Scholar] [CrossRef]


| No | Signal | Symbol | Range | Unit |
|---|---|---|---|---|
| 1 | revolutions of the main propeller | ngc | [−200–480] | [rpm] |
| 2 | conventional rudder angle | [−35–35] | [deg] | |
| 3 | relative thrust of the bow tunnel thr. | sstdc | [−1–1] | [-] |
| 4 | relative thrust of the stern tunnel thr. | sstrc | [−1–1] | [-] |
| 5 | relative thrust of the bow pump thr. | ssodc | [0–1] | [-] |
| 6 | turn angle of the bow pump thr. | [−120–120] | [deg] | |
| 7 | relative thrust of the stern pump thr. | ssorc | [0–1] | [-] |
| 8 | turn angle of the stern pump thr | [60–300] | [deg] |
| Coeff. | Value Min. | Value Max. | Mean Value |
|---|---|---|---|
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - |
| Manouvre | Signal | Robust Control Sim Lake | Linear Matrix Inequalities Sim Lake |
|---|---|---|---|
| 1 | 0.0280 | 0.0167 | |
| 2 | 0.0385 | 0.0282 | |
| 0.0249 | 0.0306 | ||
| 3 | 0.0086 | 0.0088 | |
| 0.0137 | 0.0079 | ||
| 0.0627 | 0.0760 |
| Manouvre | Signal | Robust Control Sim Lake | Linear Matrix Inequalities Sim Lake |
|---|---|---|---|
| 1 | 2.0897 | 3.6033 | |
| 2 | 2.3078 | 3.8103 | |
| 4.0525 | 3.9736 | ||
| 3 | 1.0119 | 2.2886 | |
| 2.7124 | 2.0503 | ||
| 8.6222 | 8.8481 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gierusz, W.; Rybczak, M. Effectiveness of Multidimensional Controllers Designated to Steering of the Motions of Ship at Low Speed. Sensors 2020, 20, 3533. https://doi.org/10.3390/s20123533
Gierusz W, Rybczak M. Effectiveness of Multidimensional Controllers Designated to Steering of the Motions of Ship at Low Speed. Sensors. 2020; 20(12):3533. https://doi.org/10.3390/s20123533
Chicago/Turabian StyleGierusz, Witold, and Monika Rybczak. 2020. "Effectiveness of Multidimensional Controllers Designated to Steering of the Motions of Ship at Low Speed" Sensors 20, no. 12: 3533. https://doi.org/10.3390/s20123533
APA StyleGierusz, W., & Rybczak, M. (2020). Effectiveness of Multidimensional Controllers Designated to Steering of the Motions of Ship at Low Speed. Sensors, 20(12), 3533. https://doi.org/10.3390/s20123533






