RETRACTED: W-GPCR Routing Method for Vehicular Ad Hoc Networks
Abstract
1. Introduction
- Routing protocols based on greedy algorithms, such as Geographic Perimeter Stateless Routing (GPSR) [9] and Greedy Perimeter Coordinator Routing (GPCR) [10] protocols. When the source node knows the location of its target node, this type of routing protocol greedily chooses to forward the data packet to the neighbor node closer to the target node until the data packet is successfully sent to the target node. When a node forwards data, it does not need to know the status information of nodes other than the target node and neighbor nodes. This reduces the cost of routine maintenance. When forwarding data, there is only one next-hop node selected, and there is no need to flood forward data.
- Routing protocols based on mobile prediction, such as DGRP (Directional Greedy Routing Protocol) [11], PDGR (Predictive Directional Greedy Routing) [12], PGRP (Predictive Geographic Routing Protocol) [13], and MPBRP (Mobility Prediction Based Routing Protocol) [14]. In this type of routing protocol, the location of the node is predicted. In the selection of nodes, the reference indexes of the movement direction and position of the nodes are weighed. This can reduce the number of routing hops and end-to-end delay. However, this kind of routing needs to predict the position of the current node and all of its neighboring nodes, which increases the calculation task of the system and increases the network overhead.
- Routing protocols based on delay tolerance, such as GeoDTN+Nav (Geographic Delay Tolerant Network Routing With Navigator) [15]. This type of routing protocol mitigates the impact of network partitions and intermittent connections through a delay-tolerant store-and-forward scheme, thereby improving the reachability of routes. However, this kind of routing protocol has a poor real-time performance. When the data packet is cached to a certain node, and there is no suitable opportunity to forward it, the information will be lost due to the excessive accumulation of data packets.
- Routing protocols based on a combination of topology and location, such as GPCR-D(A Topology and Position Based Routing Protocol in VANET) [16] and HybTGR (Hybrid Routing Protocol Based on Topological and Geographical) [17]. In this type of routing protocol, each network node is assigned a weight based on parameters including the node’s moving speed, the life of the routing link, the number of vehicles near the node, and the distance to the target node. According to the weight, the topology or location routing protocol is used. Its implementation is more complicated, and there is the problem of frequent switching of routing protocols, which will increase the overhead of the system network and result in poor real-time performance.
- Routing protocols based on bionic algorithms, such as EGSR (Enhanced Geographical Source Routing) [18], GSO (Glowworm Swarm Optimization) [19], and ASGR (Artificial Spider-Web-Based Geographic Routing) [20]. This type of routing protocol uses a bionic algorithm to select the optimal path to deliver data packets, which can reduce network overhead and end-to-end delay. However, this type of routing protocol is not suitable for high-speed dynamic scenarios.
- The greedy forwarding strategy has a locally optimal solution when selecting a node. The choice of the next-hop node simply depends on the distance between the judgment node and the target node. There is no global consideration.
- The right-hand rule used when the greedy forwarding strategy fails has drawbacks.
- It does not work well in a sparse network, and can easily fall into a routing hole, resulting in routing death.
- The node’s movement direction and density are also taken into consideration, and the optimal next-hop node is selected through weight calculation.
- Through the weight calculation, the direction of data packet delivery will always converge towards the target node, which solves the drawbacks of the right-hand rule.
- Using a restricted forwarding strategy, weight selection can prevent data packets from being delivered again in the direction of routing holes, and find other hidden paths to deliver data packets to target nodes.
2. Materials and Methods
2.1. Greedy Forwarding Strategy Based on Weight Selection
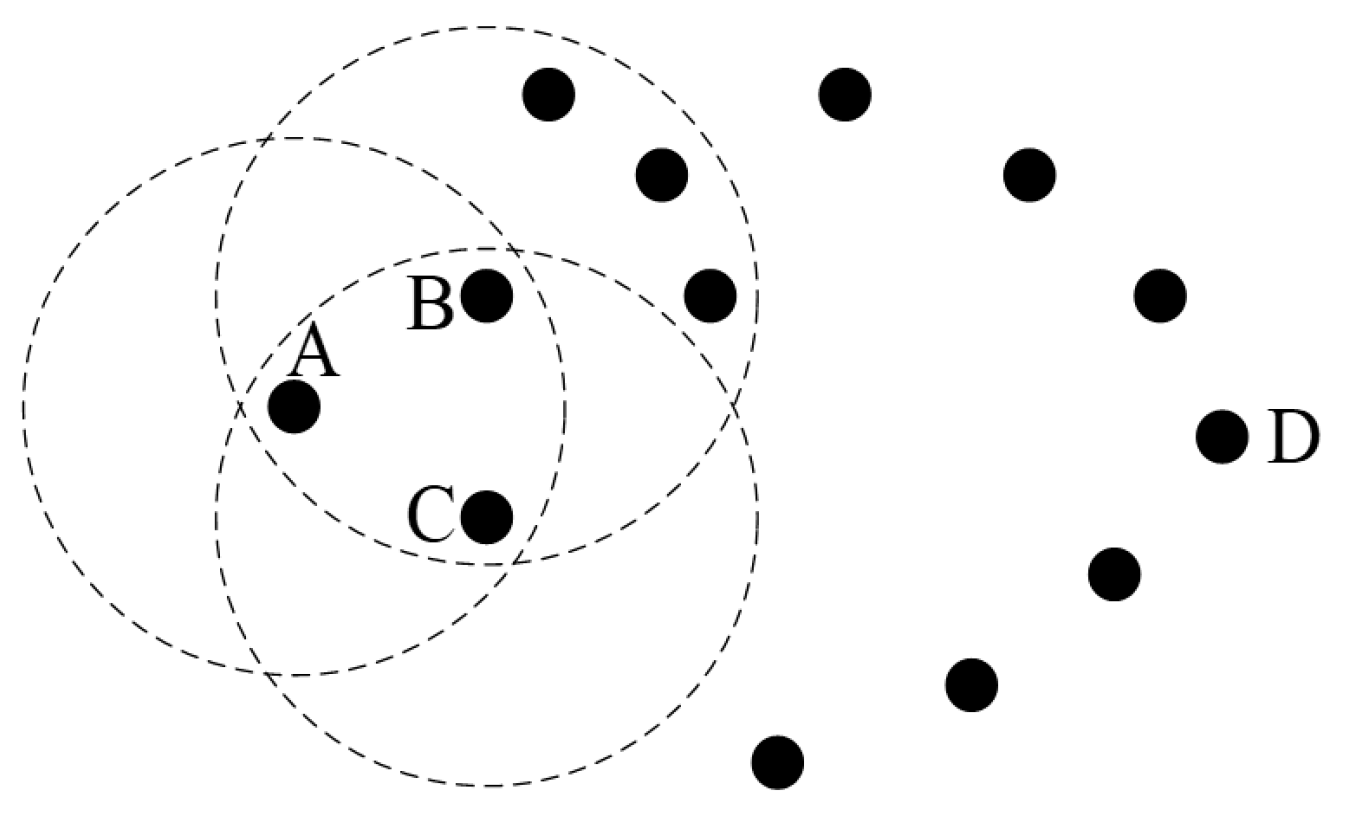
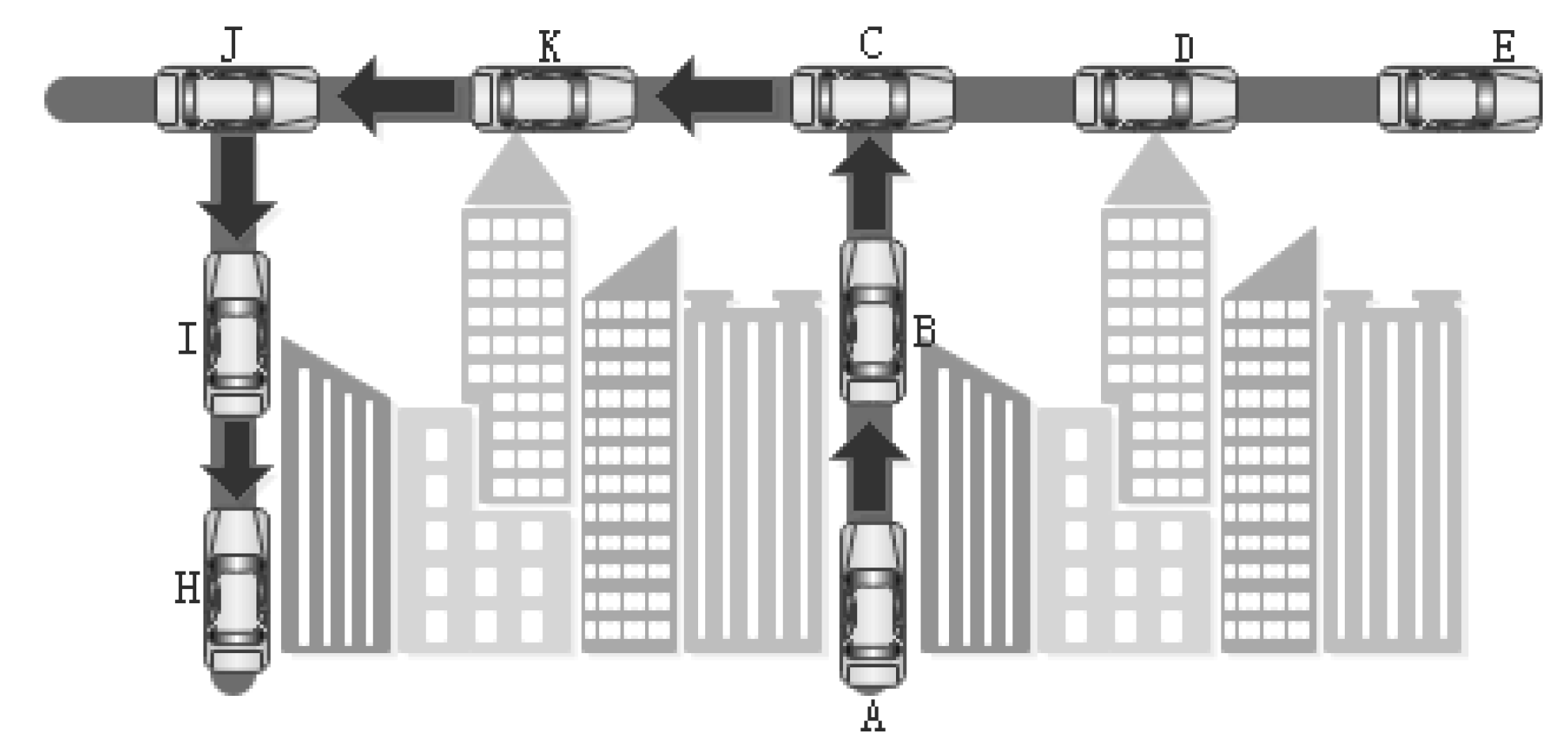
2.1.1. Influence of Node Movement Direction on Routing Performance
2.1.2. Impact of Node Density on Routing Performance
2.1.3. Weight Calculation of Greedy Forwarding Strategy
| Algorithm 1 Pseudo code for W-GPCR |
|
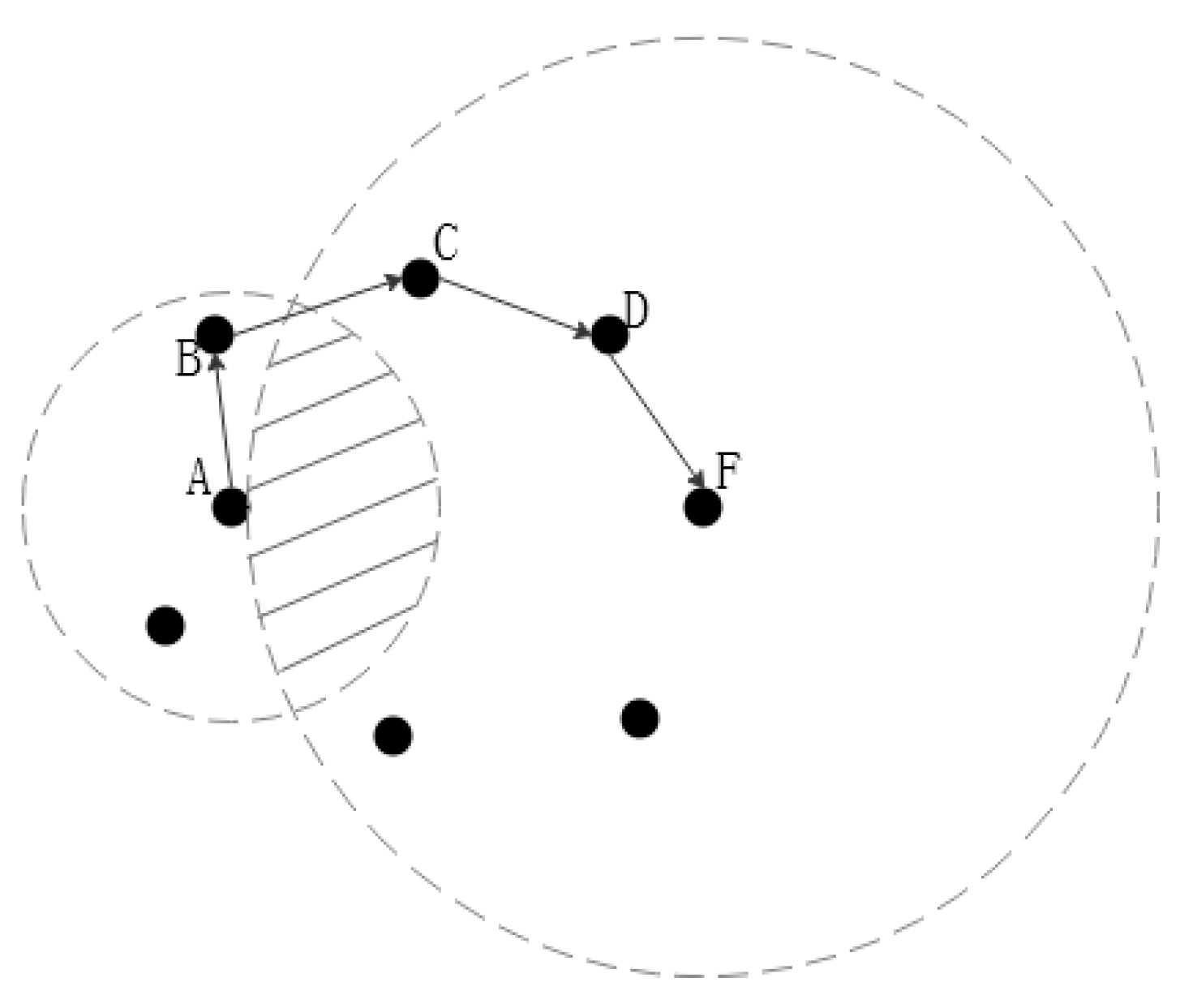
2.2. Weight Selection Repair Strategy
2.3. Restricted Forwarding Strategy
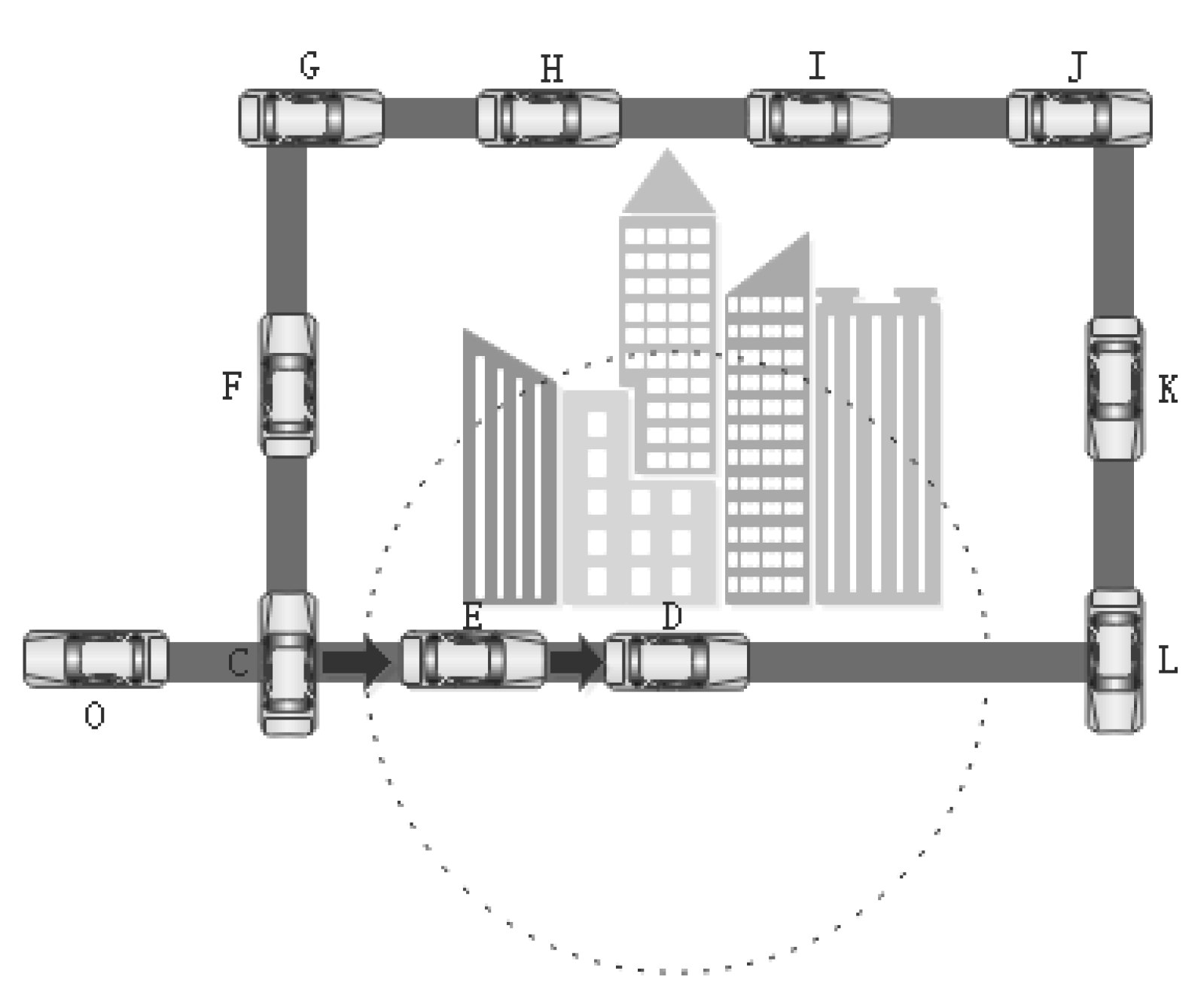
2.4. Simulation Model
3. Results
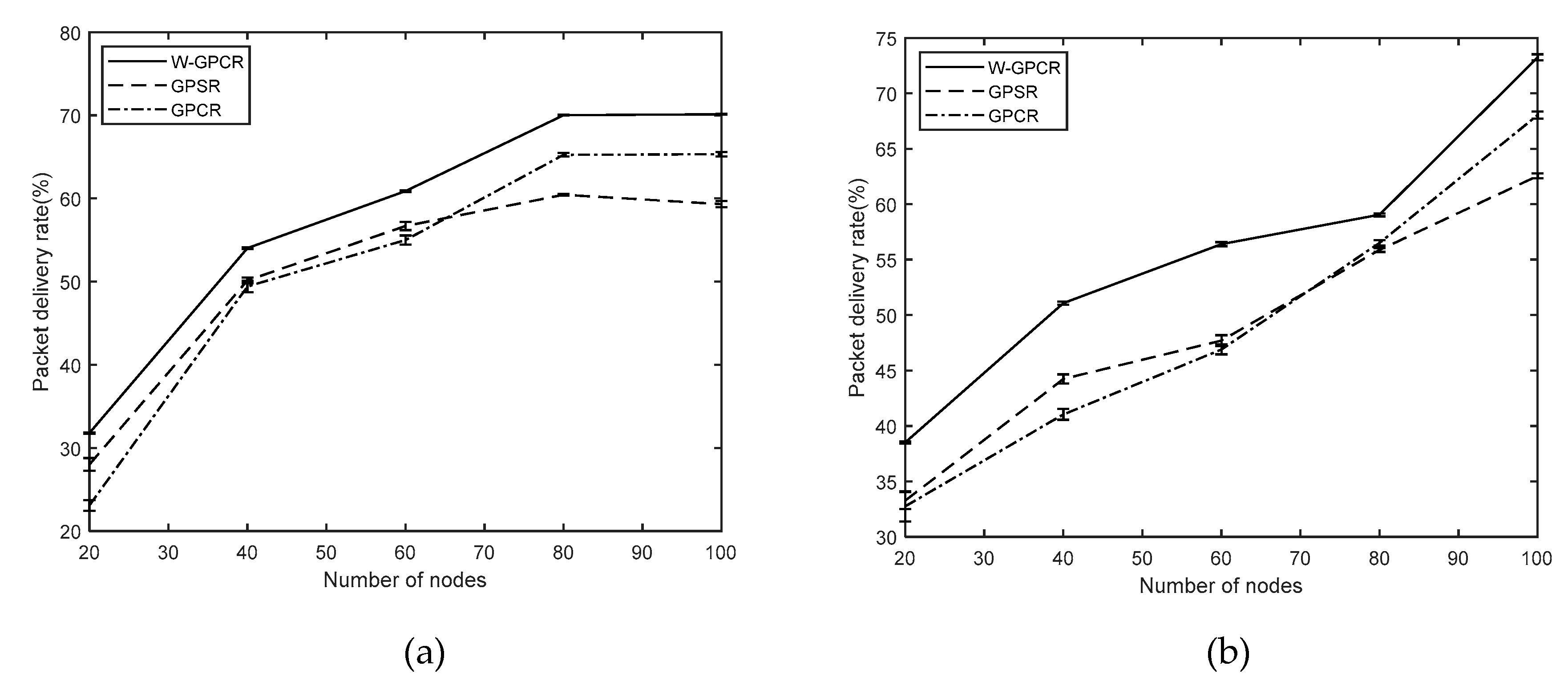
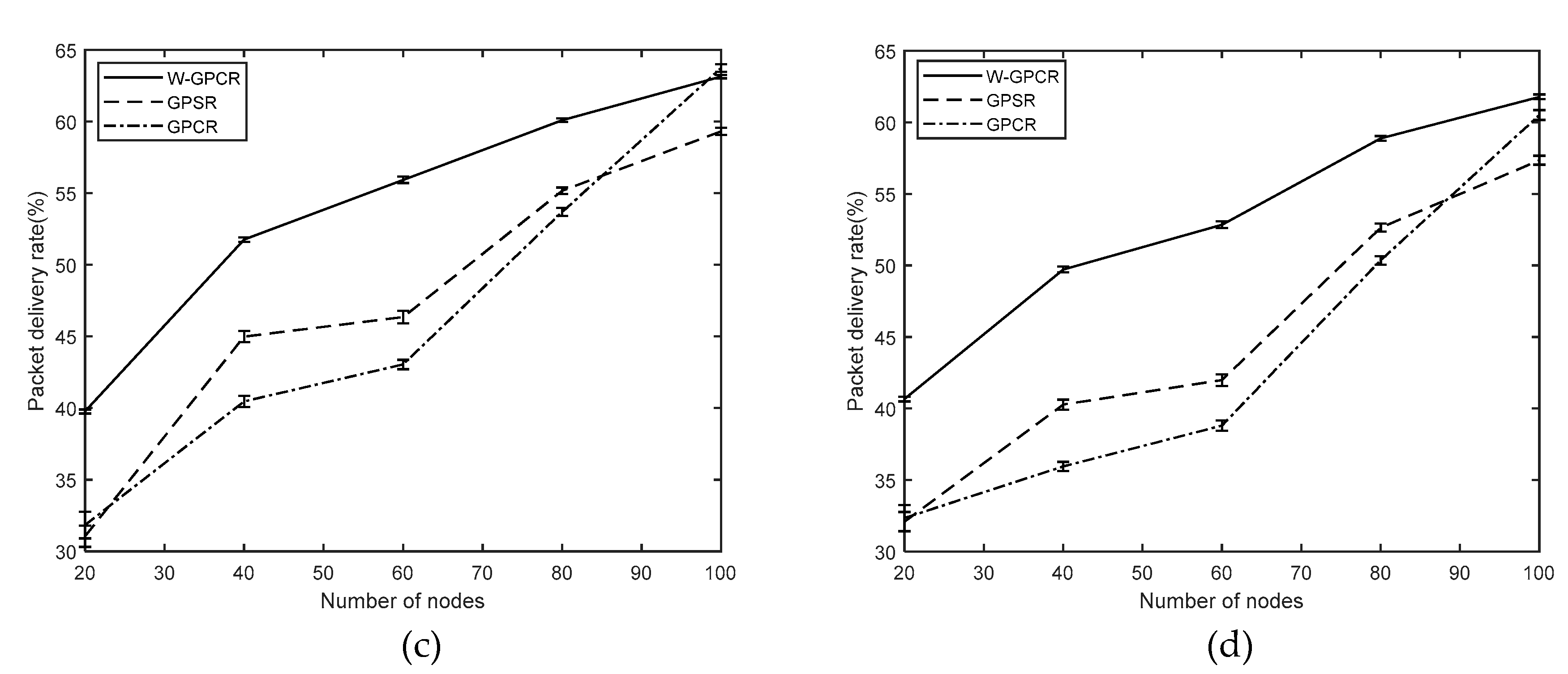
- Packet delivery rate: the ratio of the total number of packets received by the target node to the total number of packets sent by the source node.
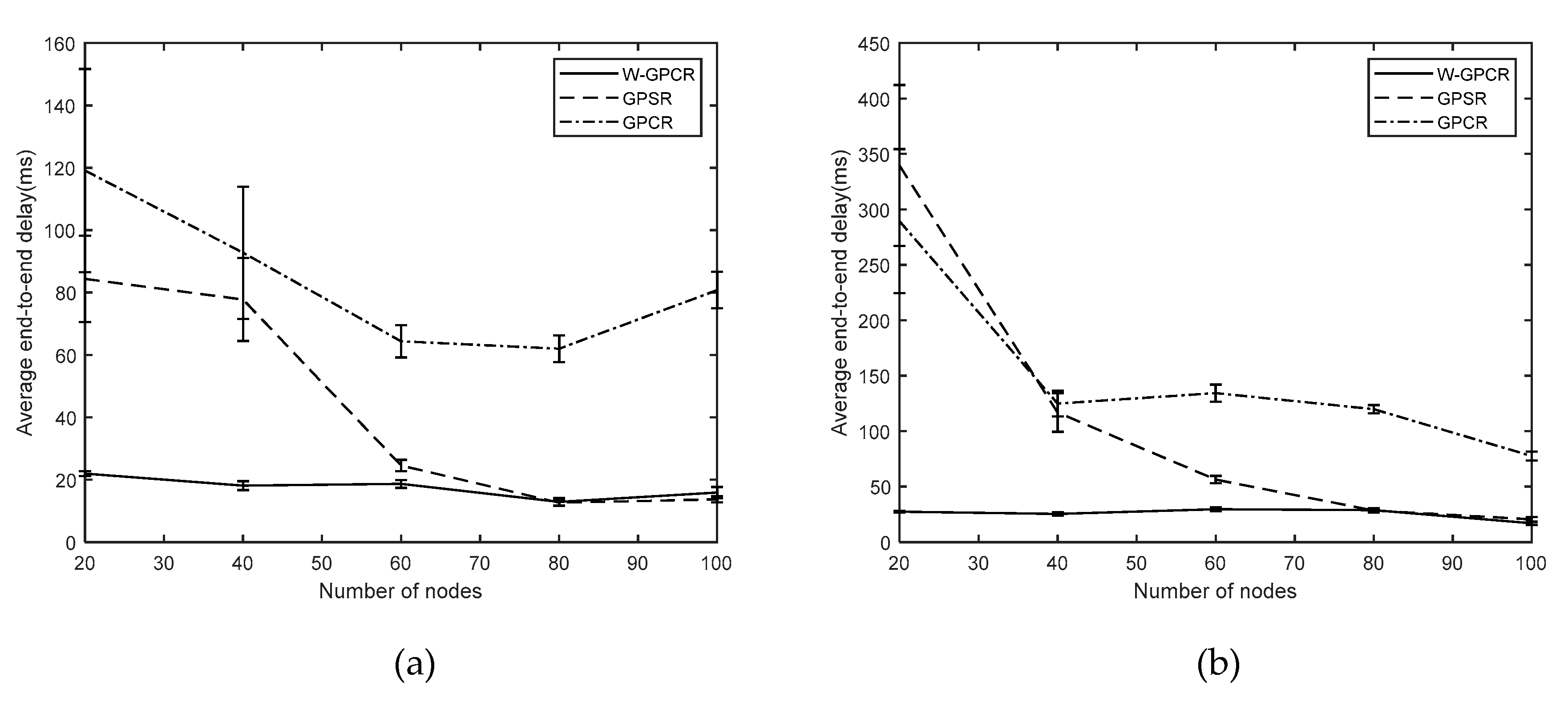
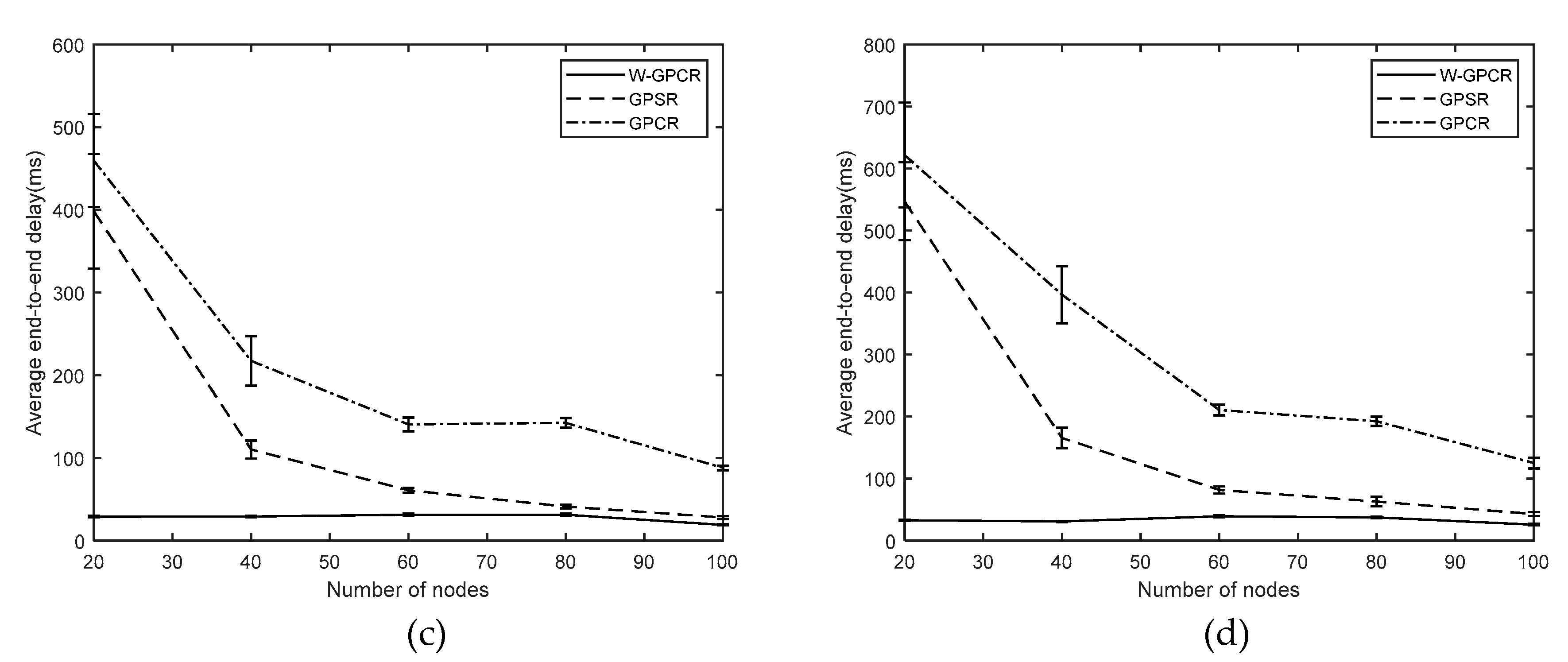
- Average end-to-end delay: The average delay of all successfully received packets.
- Average hop: the average number of hops of all nodes in the network.
3.1. Packet Delivery Rate
3.2. Average End-To-End Delay
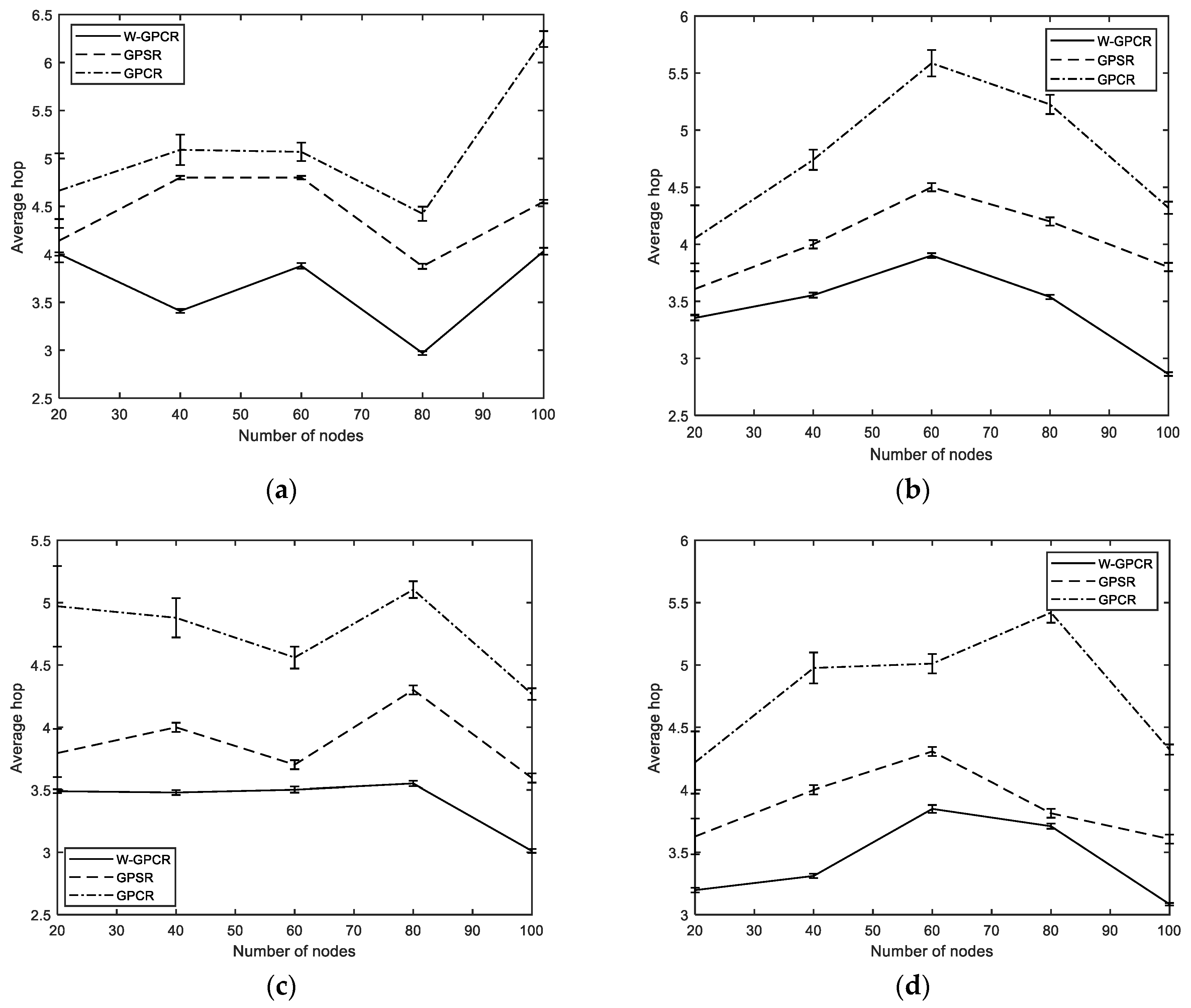
3.3. Average Hop
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wu, C.; Yoshinaga, T.; Ji, Y.S.; Zhang, Y. Computational Intelligence Inspired Data Delivery for Vehicle-to-Roadside Communications. IEEE Trans. Veh. Technol. 2018, 67, 12038–12048. [Google Scholar] [CrossRef]
- Djahel, S.; Jabeur, N.; Naitabdesselam, F.; Wolstencroft, T. A WAVE Based and Collaboration Driven Framework for Reduced Traffic Congestion in Smart Cities. IEEE Intell. Transp. Syst. Mag. 2020, 20, 1–11. [Google Scholar] [CrossRef]
- Djahel, S.; Sommer, C.; Marconi, A. Guest Editorial: Introduction to the Special Issue on Advances in Smart and Green Transportation for Smart Cities. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2152–2155. [Google Scholar] [CrossRef]
- Manvi, S.S.; Kakkasageri, M.S.; Mahapurush, C.V. Performance Analysis of AODV, DSR, and Swarm Intelligence Routing Protocols in Vehicular Ad Hoc Network Environment. In Proceedings of the 2009 International Conference on Future Computer and Communication, Washington, DC, USA, 3–5 April 2009; pp. 21–25. [Google Scholar] [CrossRef]
- Feng, J.Y.; Liu, Z.; Wu, C.; Ji, Y.S. Mobile Edge Computing for the Internet of Vehicles: Offloading Framework and Job Scheduling. IEEE Veh. Technol. Mag. 2019, 14, 28–36. [Google Scholar] [CrossRef]
- Guleng, S.; Wu, C.; Yoshinaga, T.; Ji, Y.S. Traffic big data assisted broadcast in vehicular networks. In Proceedings of the Conference on Research in Adaptive and Convergent Systems, Chongqing, China, 24–27 September 2019; pp. 236–240. [Google Scholar] [CrossRef]
- Wex, P.; Breuer, J.; Held, A.; Leinmuller, T.; Delgrossi, L. Trust Issues for Vehicular Ad Hoc Networks. In Proceedings of the 67th IEEE Vehicular Technology Conference, Singapore, 11–14 May 2008; pp. 2800–2804. [Google Scholar] [CrossRef]
- Ranjan, P.; Ahirwar, K.K. Comparative Study of VANET and MANET Routing Protocols. In Proceedings of the International Conference on Advanced Computing and Communication Technologies, Haryana, India, 7–8 January 2011; pp. 517–523. [Google Scholar]
- Karp, B.; Kung, H.T. GPSR: Greedy perimeter stateless routing for wireless networks. In Proceedings of the 6th annual international conference on Mobile computing and networking, Boston, MA, USA, 6–11 August 2000; pp. 243–254. [Google Scholar] [CrossRef]
- Lochert, C.; Mauve, M.; Fusler, H.; Hartenstein, H. Geographic routing in city scenarios. Mob. Comput. Commun. Rev. 2005, 9, 69–72. [Google Scholar] [CrossRef]
- Kumar, R.; Rao, S.V. Directional Greedy Routing Protocol in Mobile Ad Hoc Networks. In Proceedings of the 2008 International Conference on Information Technology, Bhubaneswar, India, 17–20 December 2008; pp. 183–188. [Google Scholar] [CrossRef]
- Gong, J.Y.; Xu, C.Z.; Holle, J. Predictive Directional Greedy Routing in Vehicular Ad Hoc Networks. In Proceedings of the 27th International Conference on Distributed Computing Systems Workshops, Toronto, ON, Canada, 22–29 June 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Karimi, R.; Shokrollahi, S. Predictive geographic routing protocol for VANETs. Comput. Netw. 2018, 141, 67–81. [Google Scholar] [CrossRef]
- Ye, M.; Guan, L.; Quddus, M.A. Mobility Prediction Based Routing Protocol in VANETs. In Proceedings of the International Conference on Advanced Communication Technologies and Networking, Rabat, Morocco, 12–14 April 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Cheng, P.C.; Lee, K.; Gerla, M.; Harri, J. GeoDTN+Nav: Geographic DTN routing with navigator prediction for urban vehicular environments. Mob. Netw. Appl. 2010, 15, 61–82. [Google Scholar] [CrossRef]
- Yang, X.L.; Liao, D.; Sun, G.; Lu, C.; Yu, H.F. GPCR-D: A Topology and Position Based Routing Protocol in VANET. Adv. Mater. Res. 2013, 846, 858–863. [Google Scholar] [CrossRef]
- Arianmehr, S.; Jamali, M.A. A Hybrid Routing Protocol Based on Topological and Geographical Information in Vehicular Ad Hoc Networks. J. Ambient Intell. Humaniz. Comput. 2019, 11, 1–13. [Google Scholar] [CrossRef]
- Goudarzi, F.; Asgari, H.; Alraweshidy, H.S. Traffic-Aware VANET Routing for City Environments—A Protocol Based on Ant Colony Optimization. IEEE Syst. J. 2019, 13, 571–581. [Google Scholar] [CrossRef]
- Yarinezhad, R.; Sarabi, A. A New Routing Algorithm for Vehicular Ad Hoc Networks based on Glowworm Swarm Optimization Algorithm. J. AI Data Min. 2019, 7, 69–76. [Google Scholar] [CrossRef]
- Chen, C.; Liu, L.; Qiu, T.; Yang, K.; Gong, F.K.; Song, H.B. ASGR: An Artificial Spider-Web-Based Geographic Routing in Heterogeneous Vehicular Networks. IEEE Trans. Intell. Transp. Syst. 2019, 20, 1604–1620. [Google Scholar] [CrossRef]
- Krajzewicz, D.; Erdmann, J.; Behrisch, M.; Bieker, L. Recent development and applications of SUMO— Simulation of urban mobility. Int. J. Adv. Syst. Meas. 2012, 5, 128–138. [Google Scholar]
- Zhang, X.M.; Chen, K.H.; Cao, X.L.; Sung, D.K. A Street-Centric Routing Protocol Based on Microtopology in Vehicular Ad Hoc Networks. IEEE Trans. Veh. Technol. 2016, 65, 5680–5694. [Google Scholar] [CrossRef]
- Zhang, X.M.; Cao, X.L.; Yan, L.; Sung, D.K. A Street-Centric Opportunistic Routing Protocol Based on Link Correlation for Urban VANETs. IEEE. Trans. Mob. Comput. 2016, 15, 1586–1599. [Google Scholar] [CrossRef]
- Li, N.; Martinezortega, J.; Diaz, V.H.; Fernandez, J.A. Probability Prediction-Based Reliable and Efficient Opportunistic Routing Algorithm for VANETs. IEEE-ACM Trans. Netw. 2018, 26, 1933–1947. [Google Scholar] [CrossRef]


| Notation | Description |
|---|---|
| the current node | |
| next-hop node | |
| target node | |
| the position coordinates of node x | |
| the velocity vector of node x | |
| the vector where node x points to the target node | |
| the number of neighbors of node x | |
| the i-th neighbor node | |
| the communication radius of the node | |
| to get the position coordinates of the node | |
| to get the speed vector of the node | |
| to get the number of neighbor nodes |
| Parameter | Value |
|---|---|
| Packet size | 512 bytes |
| Simulation time | 200 s |
| Simulation area | 1000 × 1000 m |
| Bit rate | 5, 10, 15, 20 |
| Maximum rate | 15 m/s |
| Number of nodes | 20, 40, 60, 80, 100 |
| Hello packet interval | 1 s |
| Transfer Protocol | UDP |
| Packet interval | 0.2 s |
| MAC layer protocol | 802.11p |
| Channel transmission rate | 3 Mbps |
| Communication distance | 250 m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Gu, Z.; Long, Y.; Shu, X.; Rong, Q.; Ma, Z.; Shao, X. RETRACTED: W-GPCR Routing Method for Vehicular Ad Hoc Networks. Sensors 2020, 20, 3406. https://doi.org/10.3390/s20123406
Li M, Gu Z, Long Y, Shu X, Rong Q, Ma Z, Shao X. RETRACTED: W-GPCR Routing Method for Vehicular Ad Hoc Networks. Sensors. 2020; 20(12):3406. https://doi.org/10.3390/s20123406
Chicago/Turabian StyleLi, Min, Zhiru Gu, Yonghong Long, Xiaohua Shu, Qing Rong, Ziji Ma, and Xun Shao. 2020. "RETRACTED: W-GPCR Routing Method for Vehicular Ad Hoc Networks" Sensors 20, no. 12: 3406. https://doi.org/10.3390/s20123406
APA StyleLi, M., Gu, Z., Long, Y., Shu, X., Rong, Q., Ma, Z., & Shao, X. (2020). RETRACTED: W-GPCR Routing Method for Vehicular Ad Hoc Networks. Sensors, 20(12), 3406. https://doi.org/10.3390/s20123406





