Design and Development of a Fully Printed Accelerometer with a Carbon Paste-Based Strain Gauge
Abstract
1. Introduction
2. Materials and Methods
2.1. Sensor Design and Analysis
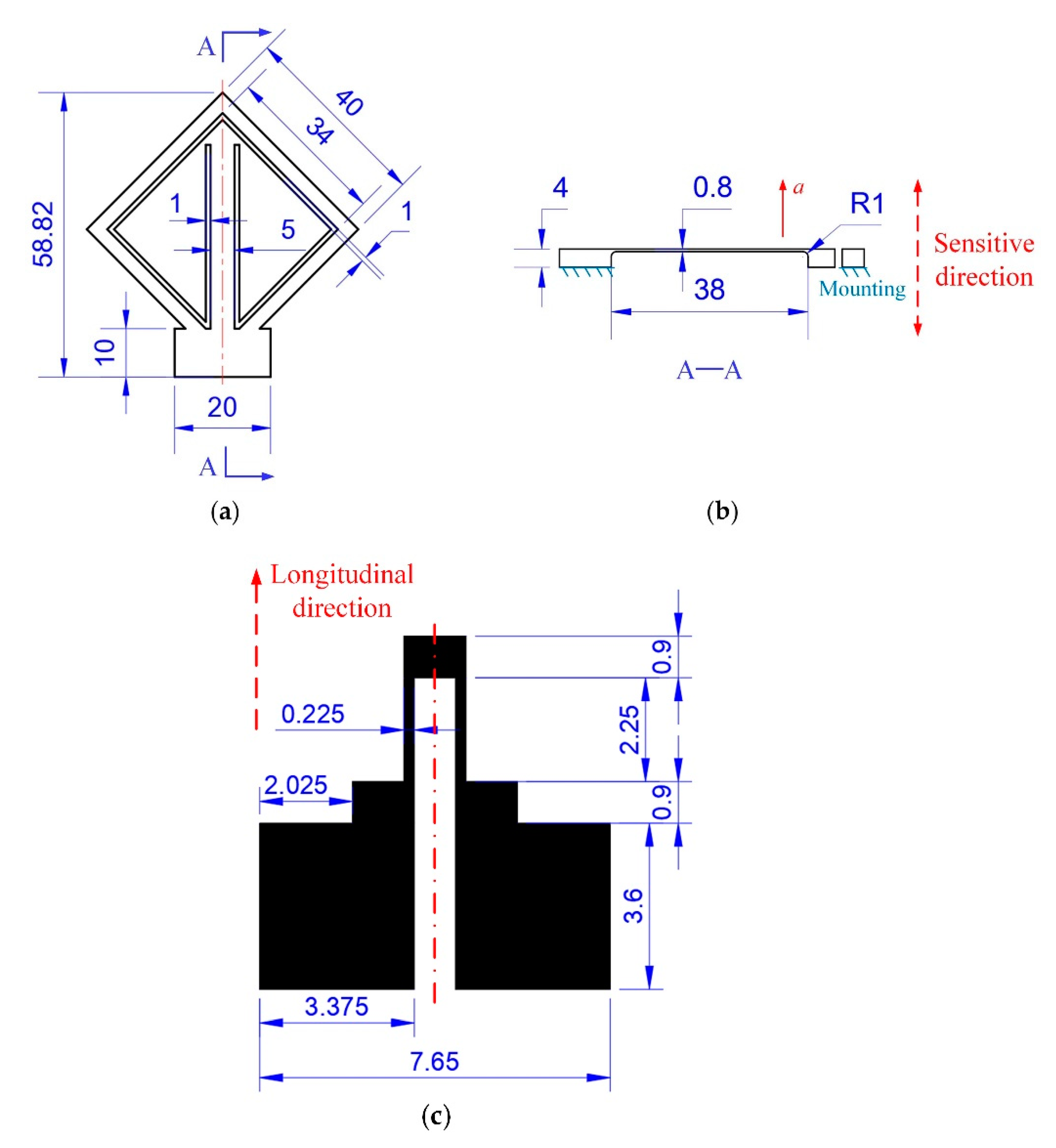
2.1.1. Structure Design and Theoretical Analysis of the Accelerometer
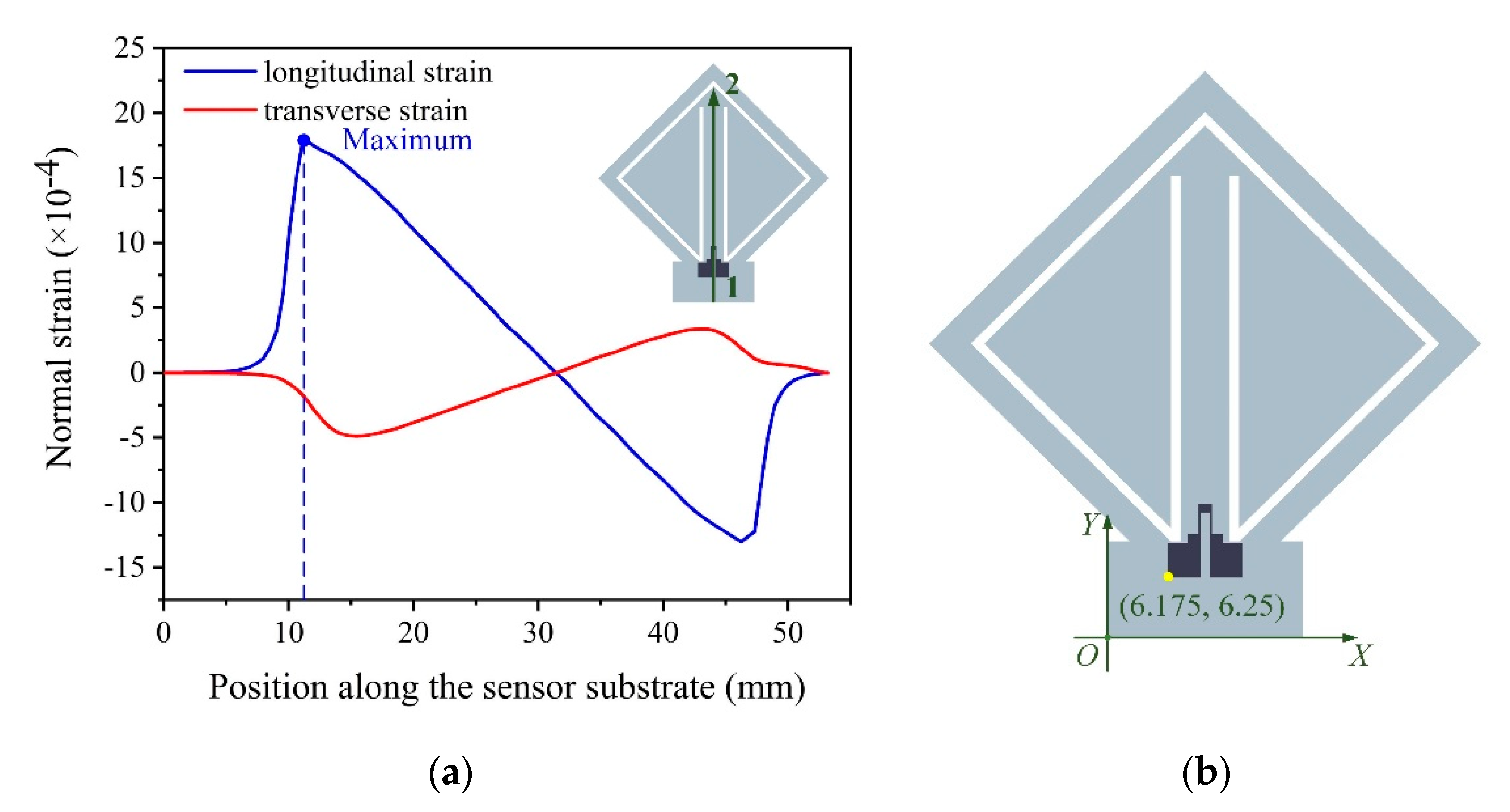
2.1.2. Simulation Analysis of the Accelerometer
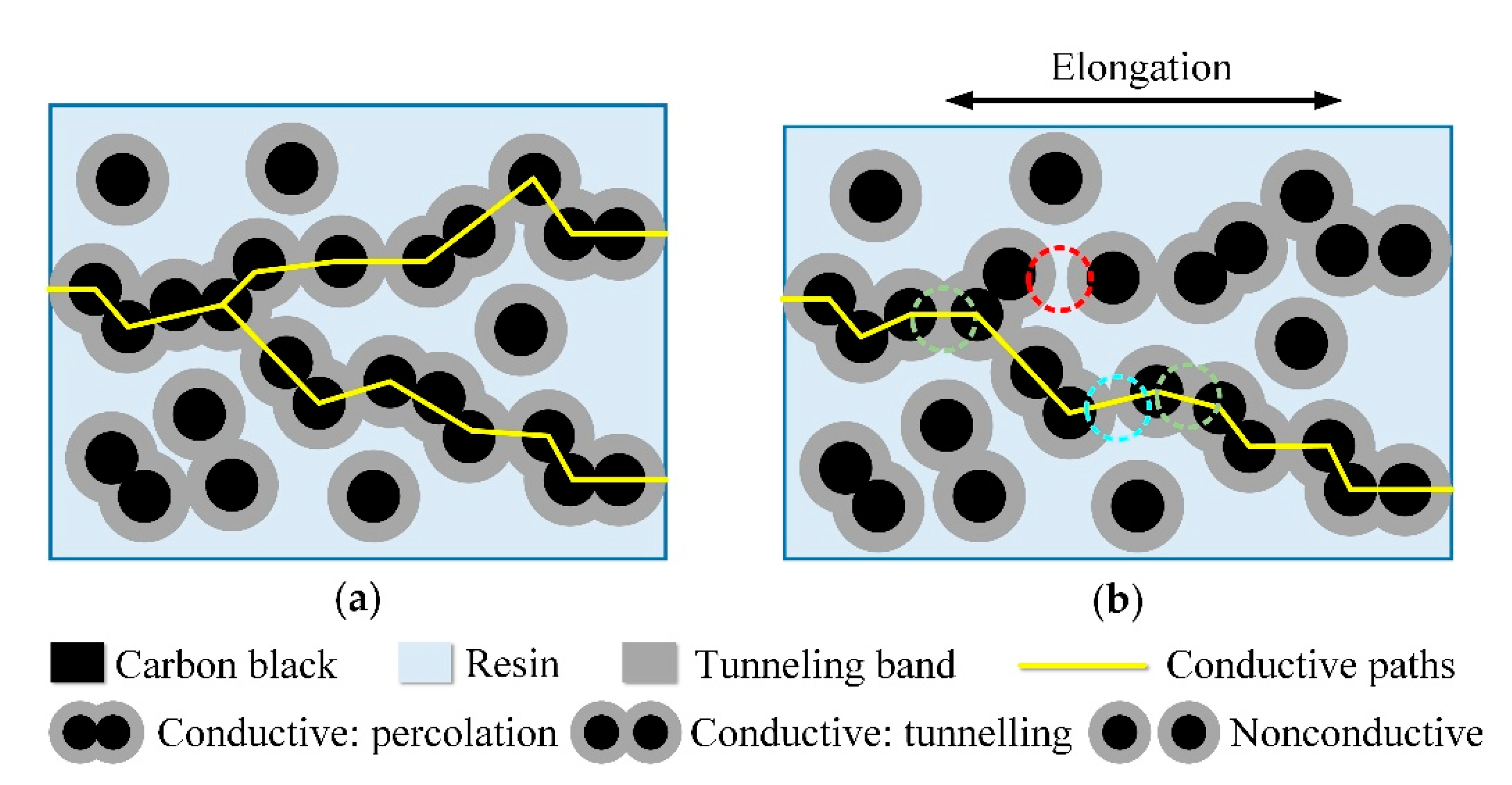
2.1.3. Conductive Mechanism and Piezoresistive Mechanism of the Carbon Paste-Based Strain Gauge
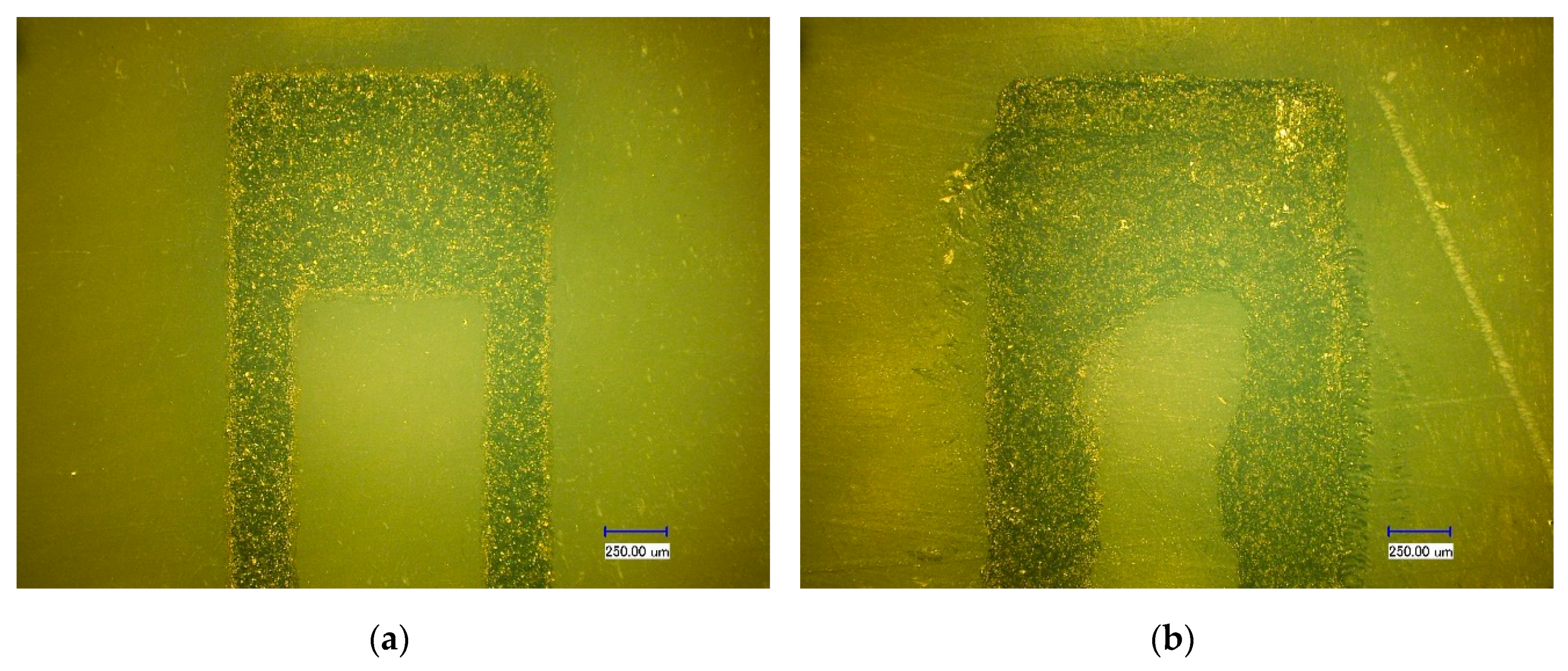
2.2. Sensor Fabrication
3. Results and Discussion
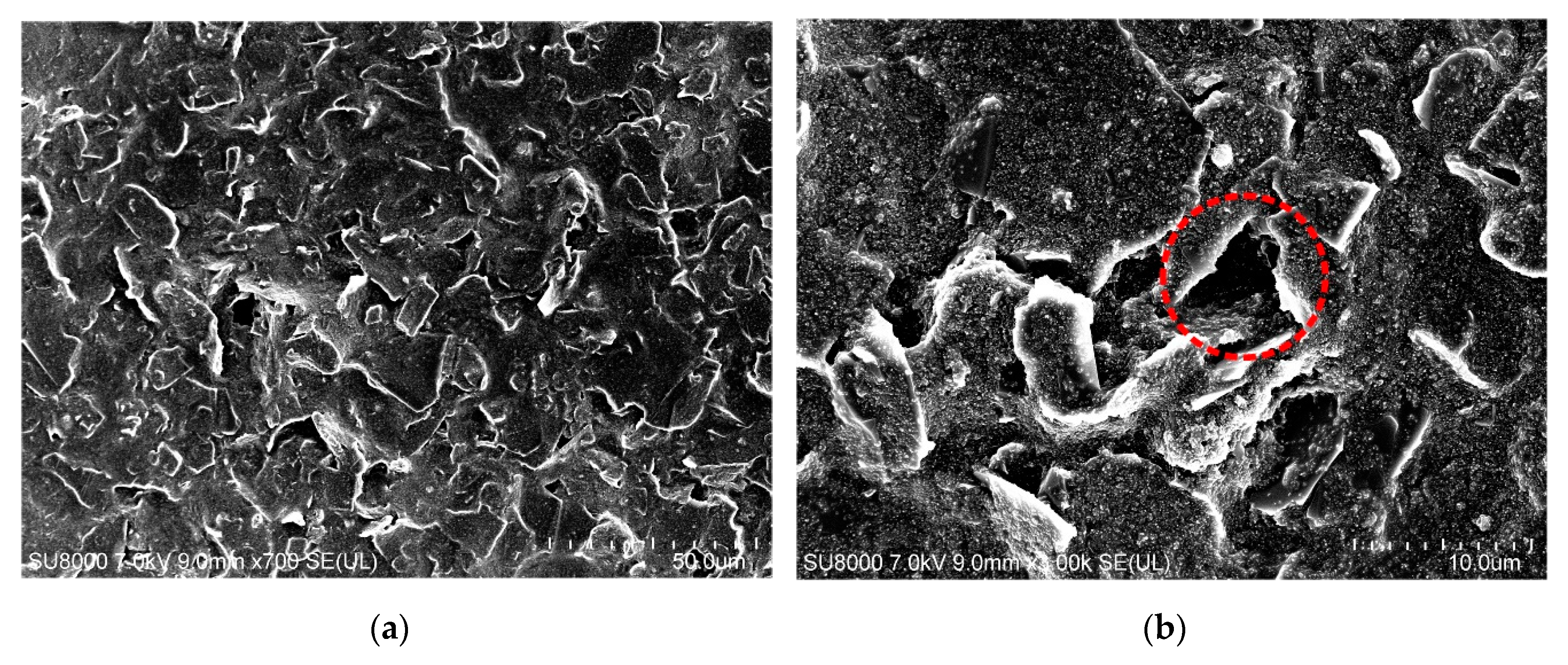
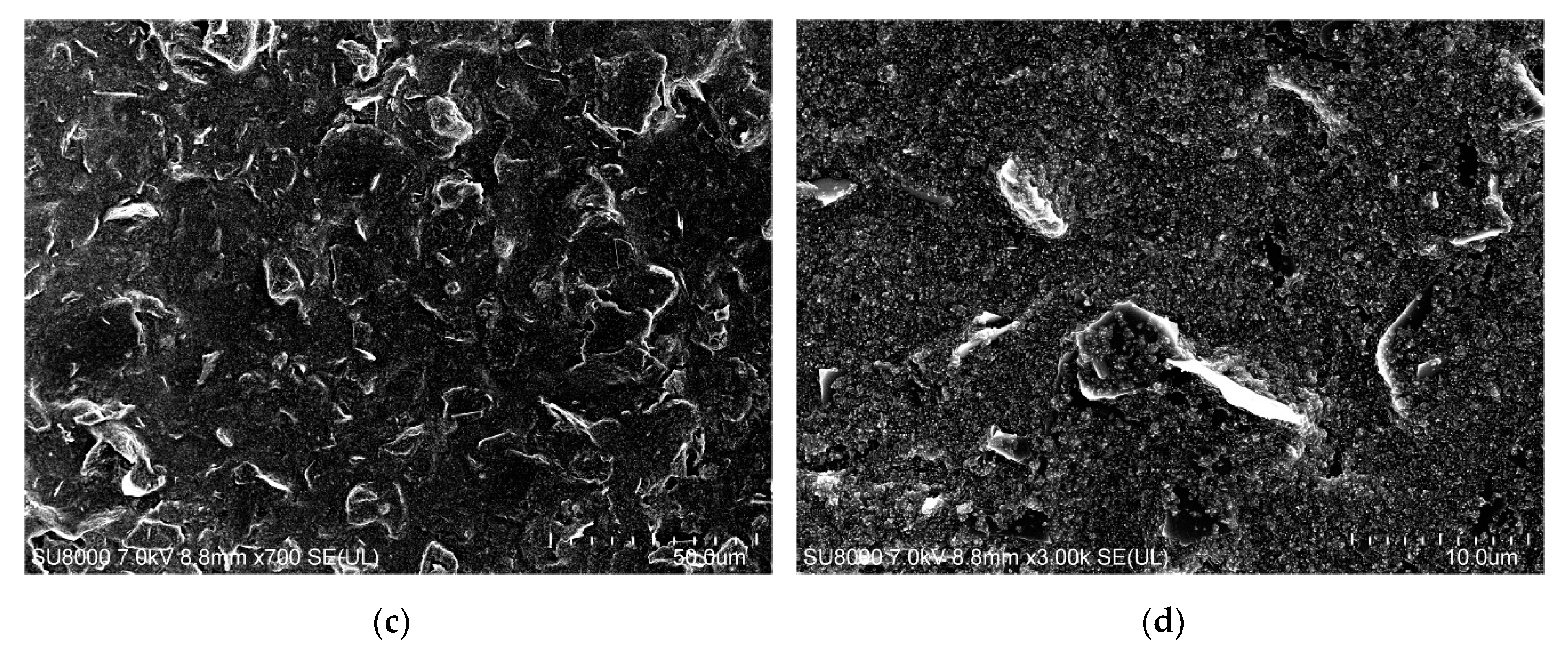
3.1. Characterization of the Carbon Paste-Based Strain Gauge
3.2. Investigation of the Piezoresistive Properties of the Carbon Paste-Based Strain Gauge
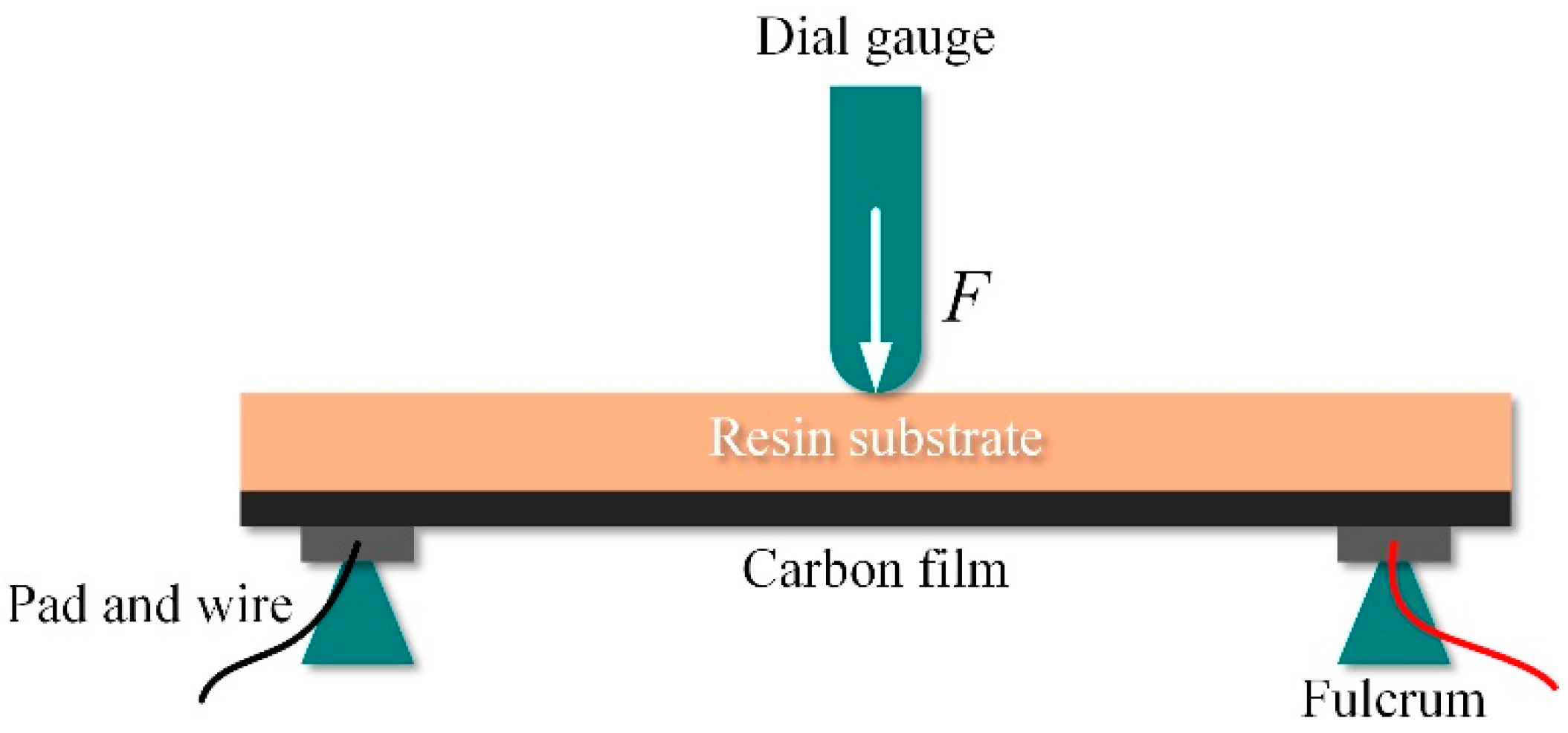
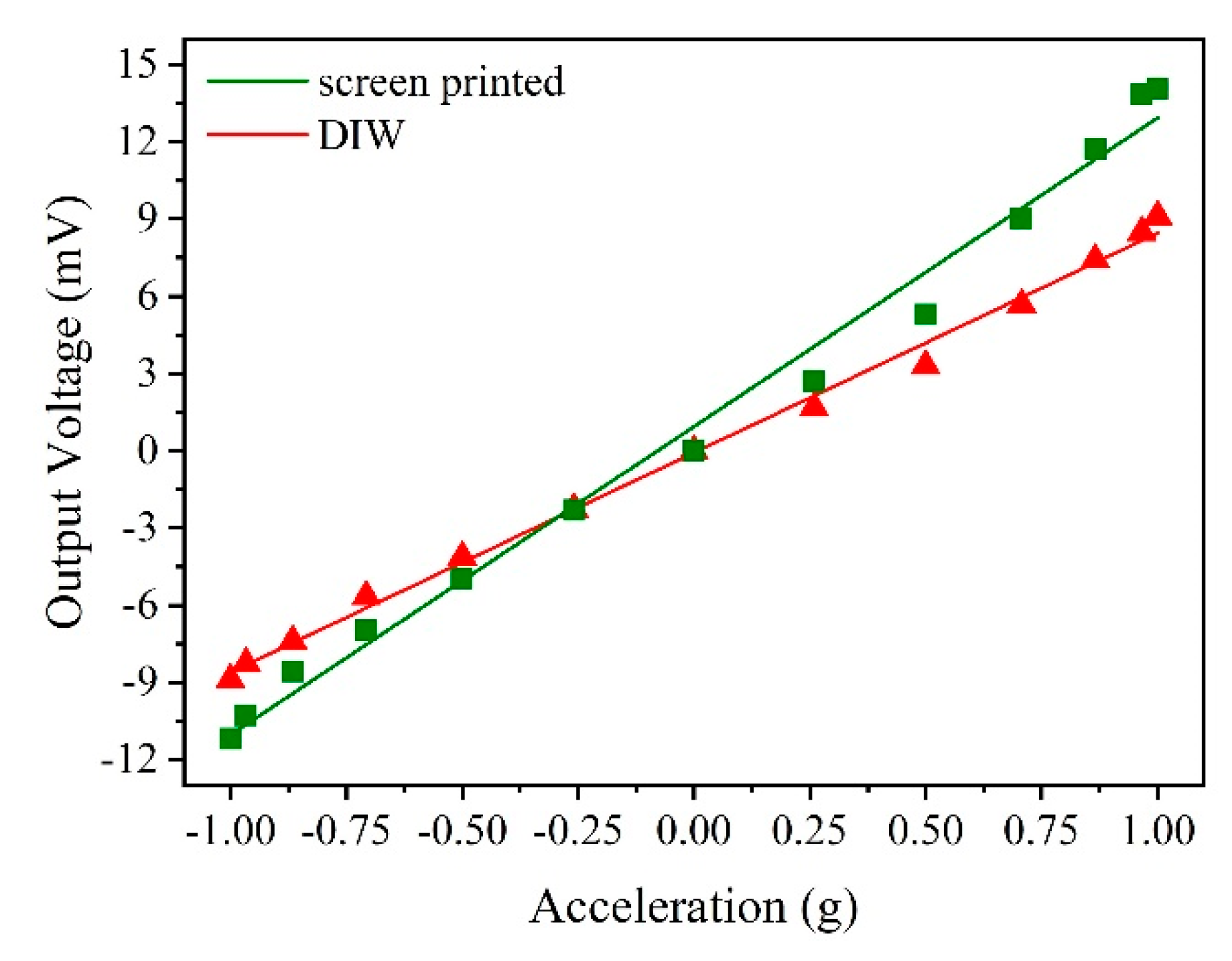
3.3. Characterization of the Accelerometer
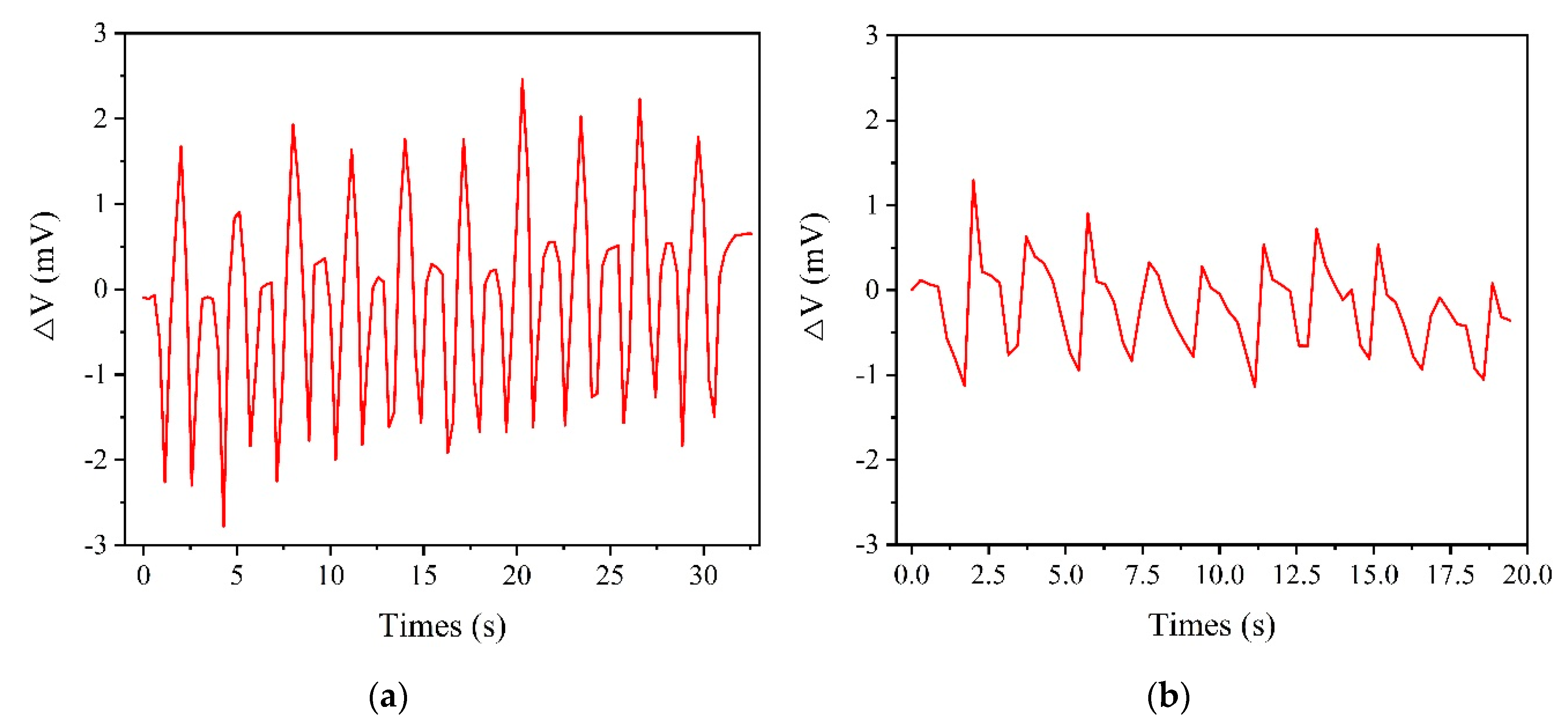
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chua, C.K.; Yeong, W.Y.; An, J. 3D Printing and Bioprinting in MEMS Technology. Micromachines 2017, 8, 229. [Google Scholar] [CrossRef] [PubMed]
- Lind, J.U.; Busbee, T.A.; Valentine, A.D.; Pasqualini, F.S.; Yuan, H.; Yadid, M.; Park, S.J.; Kotikian, A.; Nesmith, A.P.; Campbell, P.H.; et al. Instrumented Cardiac Microphysiological Devices via Multimaterial Three-Dimensional Printing. Nat. Mater. 2017, 16, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Leal-Junior, A.; Casas, J.; Marques, C.; Pontes, M.J.; Frizera, A. Application of Additive Layer Manufacturing Technique on the Development of High Sensitive Fiber Bragg Grating Temperature Sensors. Sensors 2018, 18, 4120. [Google Scholar] [CrossRef] [PubMed]
- Sharafeldin, M.; Jones, A.; Rusling, J.F. 3D-Printed Biosensor Arrays for Medical Diagnostics. Micromachines 2018, 9, 394. [Google Scholar] [CrossRef] [PubMed]
- Lan, H.B.; Li, D.C.; Lu, B.H. Micro and Nano 3D Printing. Sci. Sin. Tech. 2015, 45, 919–940. [Google Scholar]
- Hull, C. Apparatus for Production of Three-Dimensional Objects by Stereolithography. U.S. Patent No 4575330, 11 March 1986. [Google Scholar]
- Chockalingam, K.; Jawahar, N.; Chandrasekar, U.; Ramanathan, K.N. Establishment of Process Model for Part Strength in Stereolithography. J. Mater. Process. Tech. 2008, 208, 348–365. [Google Scholar] [CrossRef]
- Bertana, V.; De Pasquale, G.; Ferrero, S.; Scaltrito, L.; Catania, F.; Nicosia, C.; Marasso, S.L.; Cocuzza, M.; Perrucci, F. 3D Printing with the Commercial UV-Curable Standard Blend Resin: Optimized Process Parameters towards the Fabrication of Tiny Functional Parts. Polymers 2019, 11, 292. [Google Scholar] [CrossRef]
- Emon, M.O.F.; Choi, J.-W. Flexible Piezoresistive Sensors Embedded in 3D Printed Tires. Sensors 2017, 17, 656. [Google Scholar] [CrossRef]
- Kim, H.; Torres, F.; Wu, Y.Y.; Villagran, D.; Lin, Y.R.; Tseng, T.L. Integrated 3D Printing and Corona Poling Process of PVDF Piezoelectric Films for Pressure Sensor Application. Smart Mater. Struct. 2017, 26, 085027. [Google Scholar] [CrossRef]
- Tuna, A.; Erden, O.K.; Gokdel, Y.D.; Sarioglu, B. 3D Printed Capacitive Pressure Sensor with Corrugated Surface. In Proceedings of the 13th Conference on Ph.D. Research in Microelectronics and Electronics (PRIME)/14th International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Application to Circuit Design (SMACD), Taormina, Italy, 12–15 June 2017. [Google Scholar]
- Seo, M.; Hwang, S.; Hwang, T.; Yeo, J. Fabrication of Soft Sensor Using Laser Processing Techniques: For the Alternative 3D Printing Process. Materials 2019, 12, 2955. [Google Scholar] [CrossRef]
- Muth, J.T.; Vogt, D.M.; Truby, R.L.; Menguc, Y.; Kolesky, D.B.; Wood, R.J.; Lewis, J.A. Embedded 3D Printing of Strain Sensors within Highly Stretchable Elastomers. Adv. Mater. 2014, 26, 6307–6312. [Google Scholar] [CrossRef] [PubMed]
- Al-Rubaiai, M.; Tsuruta, R.; Gandhi, U.; Wang, C.; Tan, X.B. A 3D-Printed Stretchable Strain Sensor for Wind Sensing. Smart Mater. Struct. 2019, 28, 084001. [Google Scholar] [CrossRef]
- Kisic, M.; Blaz, N.; Zivanov, L.; Damnjanovic, M. Elastomer Based Force Sensor Fabricated by 3D Additive Manufacturing. AIP Adv. 2020, 10, 015017. [Google Scholar] [CrossRef]
- Kisic, M.; Blaz, N.; Zivanov, L.; Damnjanovic, M. Capacitive Force Sensor Fabricated in Additive Technology. In Proceedings of the 42nd International Spring Seminar on Electronics Technology (ISSE), Wroclaw, Poland, 15–19 May 2019. [Google Scholar]
- Adamski, K.; Kawa, B.; Walczak, R. Inkjet 3D Printed Micropot with Integrated Cantilever-Like Force Sensor for Growing Plant Biological Potential Measurement. Proceedings 2018, 2, 720. [Google Scholar] [CrossRef]
- Delamare, J.; Sanders, R.; Krijnen, G. 3D Printed Biomimetic Whisker-based Sensor with Co-Planar Capacitive Sensing. In Proceedings of the 15th IEEE Sensors Conference, Orlando, FL, USA, 30 October–3 November 2016. [Google Scholar]
- Qu, J.T.; Wu, Q.Y.; Clancy, T.; Liu, X.Y. Design and Calibration of 3D-Printed Micro Force Sensors. In Proceedings of the 1st International Conference on Manipulation, Automation and Robotics at Small Scales, Paris, France, 18–21 July 2016. [Google Scholar]
- Zhao, Z.; Liu, H.G.; Xiong, K. Research on Preparation and Performance of a Waist-Shaped Micro Pressure Sensor based on 3D printing Technology. J. Changzhou Univ. 2017, 29, 68–73. [Google Scholar]
- Lucklum, F.; Dumstorff, G. 3D Printed Pressure Sensor with Screen-Printed Resistive Read-Out. In Proceedings of the 15th IEEE Sensors Conference, Orlando, FL, USA, 30 October–3 November 2016. [Google Scholar]
- Joo, H.; Cho, S. Comparative Studies on Polyurethane Composites Filled with Polyaniline and Graphene for DLP-Type 3D Printing. Polymers 2020, 12, 67. [Google Scholar] [CrossRef]
- Han, H.; Cho, S. Fabrication of Conducting Polyacrylate Resin Solution with Polyaniline Nanofiber and Graphene for Conductive 3D Printing Application. Polymers 2018, 10, 1003. [Google Scholar] [CrossRef]
- BMF nanoArch M160. Available online: http://www.bmftec.cn/zh/print/details/5 (accessed on 10 March 2020).
- Faller, L.M.; Granig, W.; Krivec, M.; Abram, A.; Zangl, H. Rapid Prototyping of Force/Pressure Sensors Using 3D- and Inkjet-Printing. J. Micromech. Microeng. 2018, 28, 104002. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Q.; Shao, Y.; Liu, C.; Zhao, Y. Research of a Novel 3D Printed Strain Gauge Type Force Sensor. Micromachines 2019, 10, 20. [Google Scholar] [CrossRef]
- Al-Chami, H. Inkjet Printing of Transducers. Master of Applied Science Thesis; The University of British Columbia: Vancouver, BC, Canada, 2010. [Google Scholar]
- Li, K.J. New Sourcebook of Sensor Technology; National Defense Industry Press: Beijing, China, 2002; pp. 427–430. ISBN 7-118-02505-4. [Google Scholar]
- Dawoud, M.; Taha, I.; Ebeid, S.J. Strain Sensing Behaviour of 3D Printed Carbon Black Filled ABS. J. Manuf. Process. 2018, 35, 337–342. [Google Scholar] [CrossRef]
- Zhang, B. Research on Piezoresistive Performance of Nanocarbons/Silicon Rubber Composites based on Conductive Structure Construction. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2017. [Google Scholar]
- High Temp Resin for Heat Resistance, Material Data Sheet. Available online: https://formlabs-media.formlabs.com/datasheets/High_Temp_Technical.pdf (accessed on 10 March 2020).
- Wang, Y.; Liu, Z.; Yi, J.; Xue, Z. Study on the Piezoresistive Effect of the Multiwalled Carbon Nanotube Films. Acta Phys. Sin. 2011, 61, 057302. [Google Scholar]
- He, Y.; Wu, X.; Lin, H.; Yu, M. The Structure and Piezo-Resistance Effect of Hydrogenated Nano-Si Films. Chinses J. Mater. Res. 1996, 10, 33–38. [Google Scholar]
- Ma, Q.; Xu, H.; Lei, C.; Zhang, Z.; Zhang, P.; Wu, S.; Li, H. Effect of Curing Conditions on Curing Rate and Mechanical Strength of Unsaturated Polyester Resin. Guangzhou Archit. 2018, 46, 7–10. [Google Scholar]
- Grimaldi, C.; Ryser, P.; Strassler, S. Gauge Factor Enhancement Driven by Heterogeneity in Thick-Film Resistors. J. Appl. Phys. 2001, 90, 322–327. [Google Scholar] [CrossRef][Green Version]
- Li, B.; Zhao, Y.; Li, C.; Cheng, R.; Sun, D.; Wang, S. A Differential Resonant Accelerometer with Low Cross-Interference and Temperature Drift. Sensors 2017, 17, 178. [Google Scholar] [CrossRef]








| Properties | Green 1 | Post-Cured 2 | Method |
|---|---|---|---|
| Ultimate tensile strength | 20.9 MPa | 58.3 MPa | ASTM D 638-14 |
| Elongation at break | 14% | 3.3% | ASTM D 638-14 |
| Tensile modulus | 0.75 GPa | 2.75 GPa | ASTM D 638-14 |
| Flexural strength at break | 24.1 MPa | 94.5 MPa | ASTM D 790-15 |
| Flexural modulus | 0.69 GPa | 2.62 GPa | ASTM D 790-15 |
| Thermal expansion (0–150 °C) | 118.1 (μm/m/°C) | 79.6 (μm/m/°C) | ASTM E 831-13 |
| Strain Gauge (#) | Resistance (kΩ) |
|---|---|
| 1 | 5.11396 |
| 2 | 5.89182 |
| 3 | 5.44968 |
| 4 | 23.2046 |
| 5 | 14.3772 |
| 6 | 18.6191 |
| Test Sample (#) | Gauge Factor |
|---|---|
| 1 | 16.78 |
| 2 | 16.51 |
| 3 | 14.14 |
| 4 | 22.80 |
| 5 | 27.20 |
| 6 | 27.62 |
| Angle θ 1 (°) | Acceleration (g) | ΔV (mV) | |
|---|---|---|---|
| Screen Printed | DIW | ||
| −90 | −1 | −11.2048 | −8.8877 |
| −75 | −0.966 | −10.2810 | −8.2614 |
| −60 | −0.866 | −8.5833 | −7.4040 |
| −45 | −0.707 | −7.0026 | −5.6695 |
| −30 | −0.5 | −4.9683 | −4.1343 |
| −15 | −0.259 | −2.3217 | −2.2670 |
| 0 | 0 | 0 | 0 |
| 15 | 0.259 | 2.6855 | 1.6702 |
| 30 | 0.5 | 5.2875 | 3.3052 |
| 45 | 0.707 | 9.0066 | 5.6687 |
| 60 | 0.866 | 11.7177 | 7.4244 |
| 75 | 0.966 | 13.8422 | 8.4762 |
| 90 | 1 | 14.0693 | 9.0919 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Zhang, Q.; Zhao, Y.; Shao, Y.; Zhang, D. Design and Development of a Fully Printed Accelerometer with a Carbon Paste-Based Strain Gauge. Sensors 2020, 20, 3395. https://doi.org/10.3390/s20123395
Liu M, Zhang Q, Zhao Y, Shao Y, Zhang D. Design and Development of a Fully Printed Accelerometer with a Carbon Paste-Based Strain Gauge. Sensors. 2020; 20(12):3395. https://doi.org/10.3390/s20123395
Chicago/Turabian StyleLiu, Mingjie, Qi Zhang, Yulong Zhao, Yiwei Shao, and Dongliang Zhang. 2020. "Design and Development of a Fully Printed Accelerometer with a Carbon Paste-Based Strain Gauge" Sensors 20, no. 12: 3395. https://doi.org/10.3390/s20123395
APA StyleLiu, M., Zhang, Q., Zhao, Y., Shao, Y., & Zhang, D. (2020). Design and Development of a Fully Printed Accelerometer with a Carbon Paste-Based Strain Gauge. Sensors, 20(12), 3395. https://doi.org/10.3390/s20123395







