An Open-Source 7-DOF Wireless Human Arm Motion-Tracking System for Use in Robotics Research
Abstract
1. Introduction
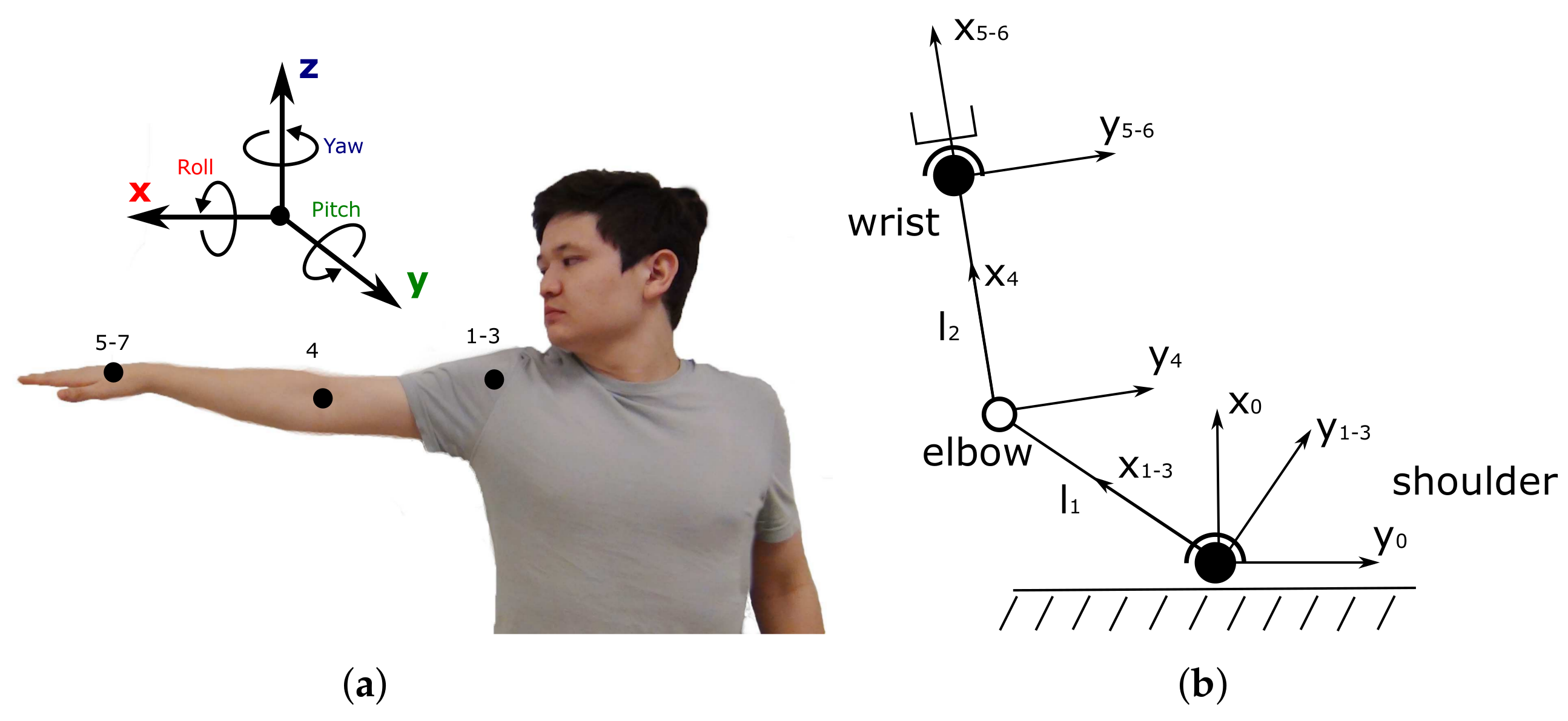
2. Kinematic Modeling of a Human Arm
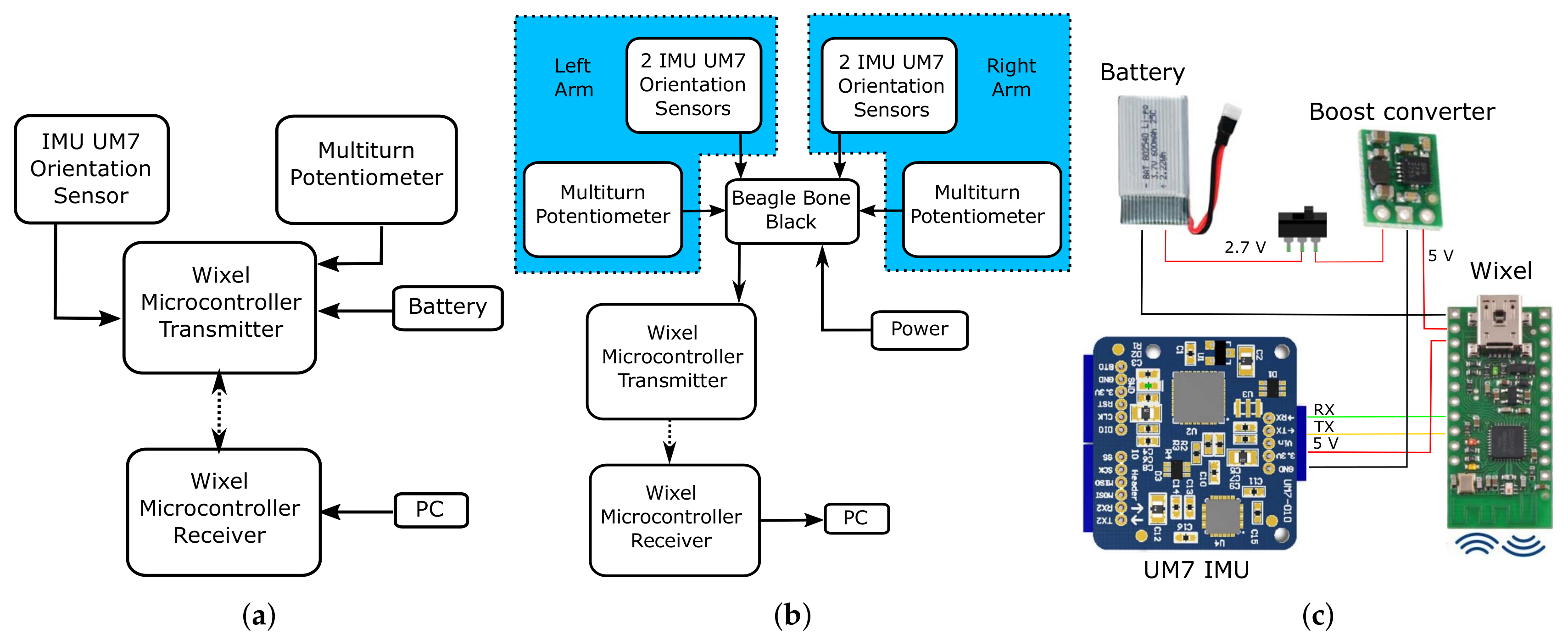
3. Design of a 7-DOF Arm Motion-Tracking System
3.1. Phase 1
3.2. Phase 2
3.3. Phase 3
4. Experimental Results
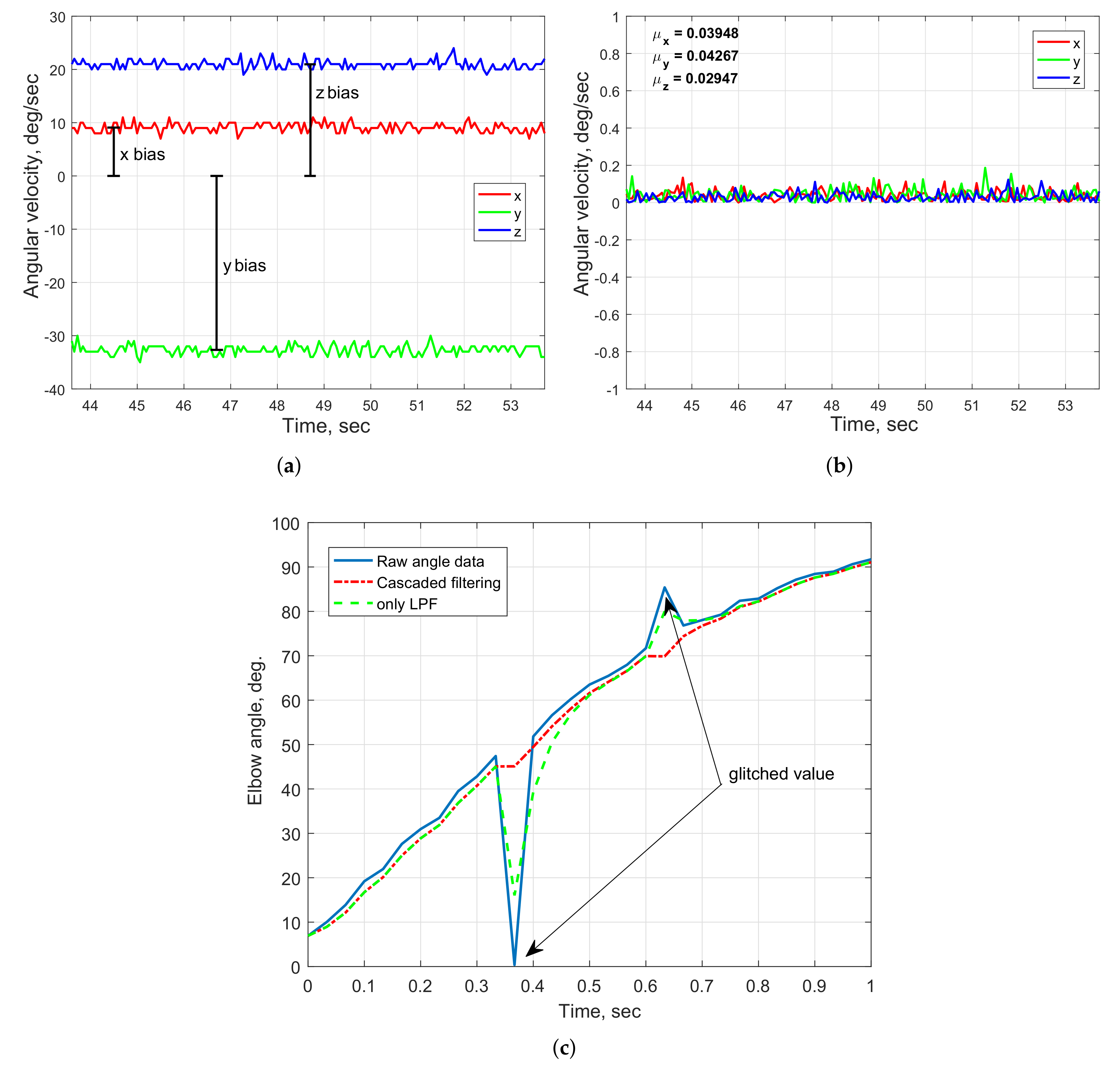
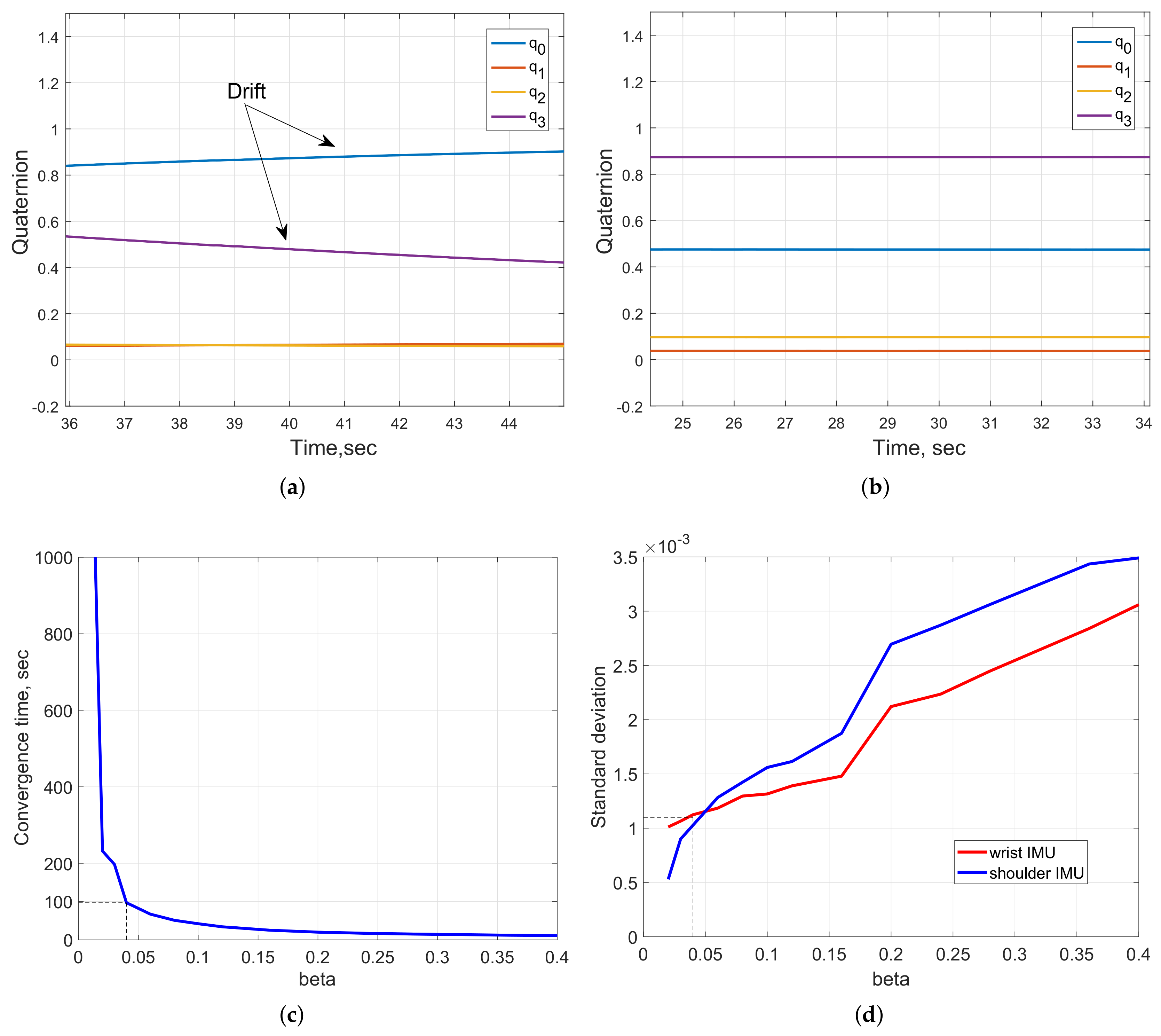
4.1. System Sensor Calibration
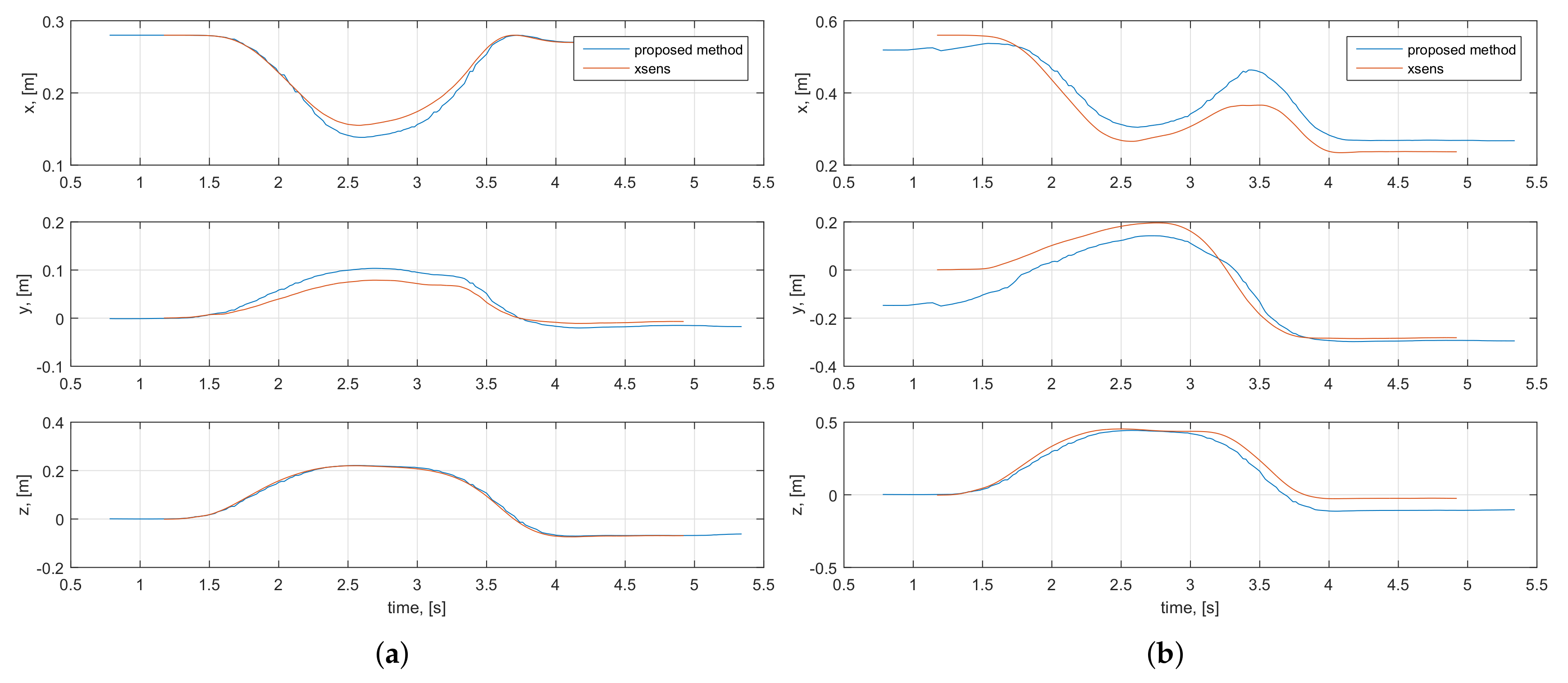
4.2. System Tracking Accuracy Evaluation
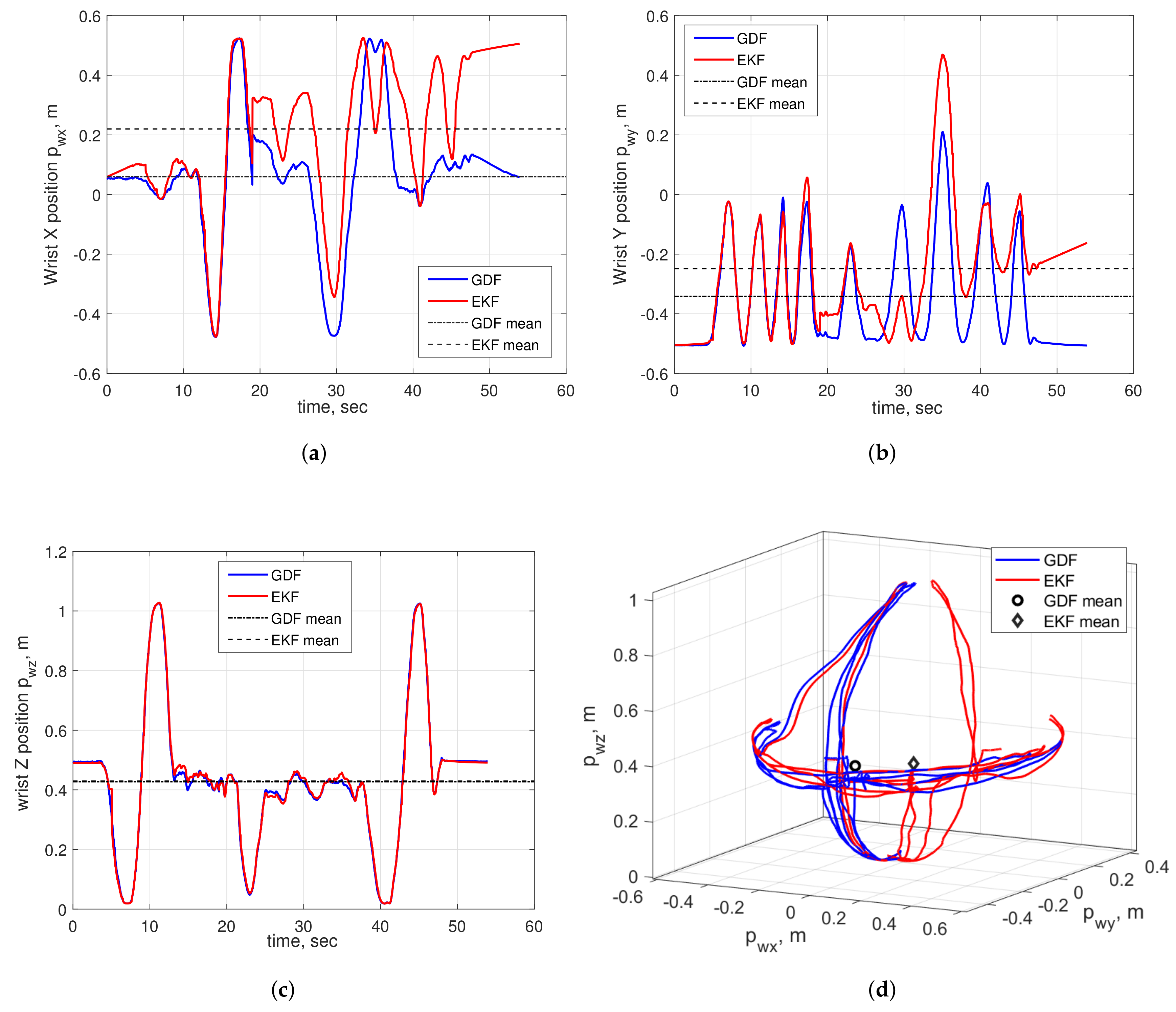
4.3. Selection of the Data Processing Algorithm
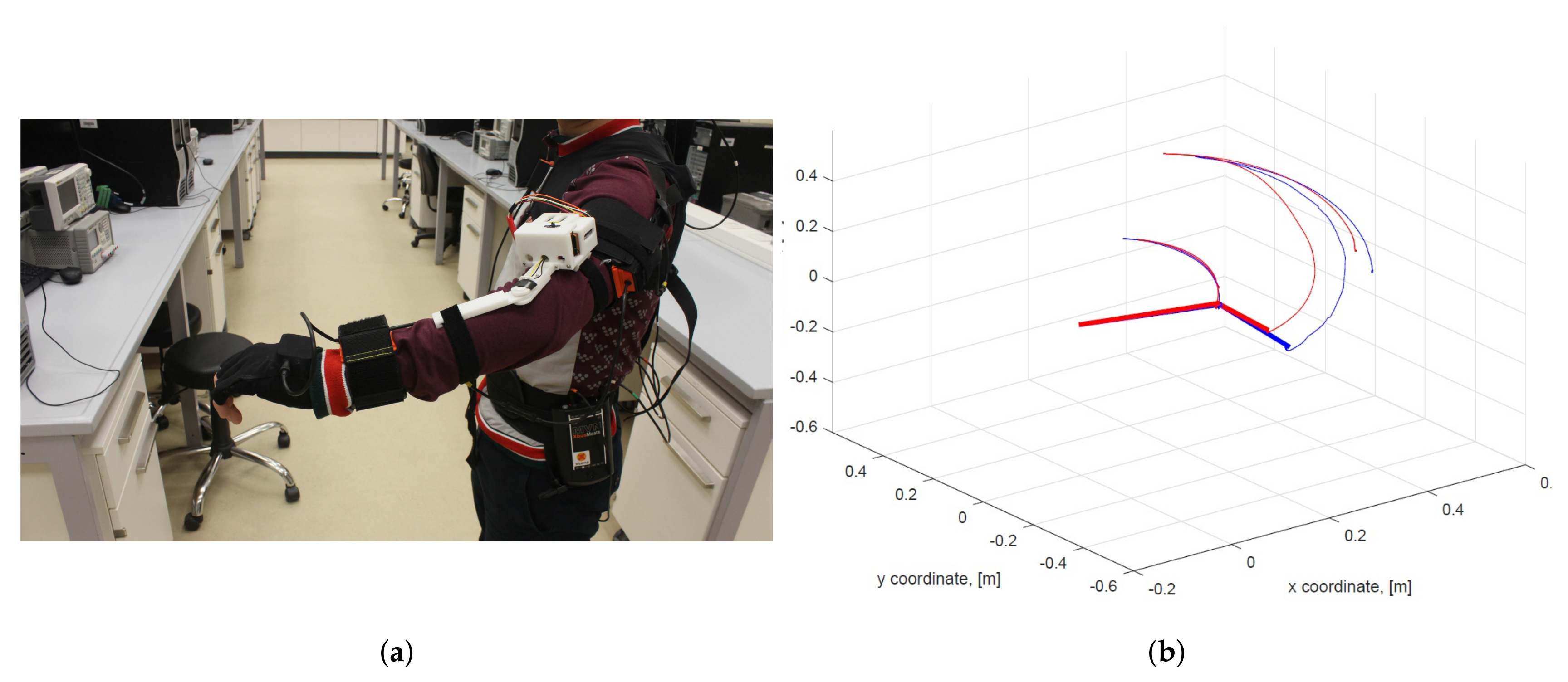
4.4. Pick-and-Place Motion Analyses
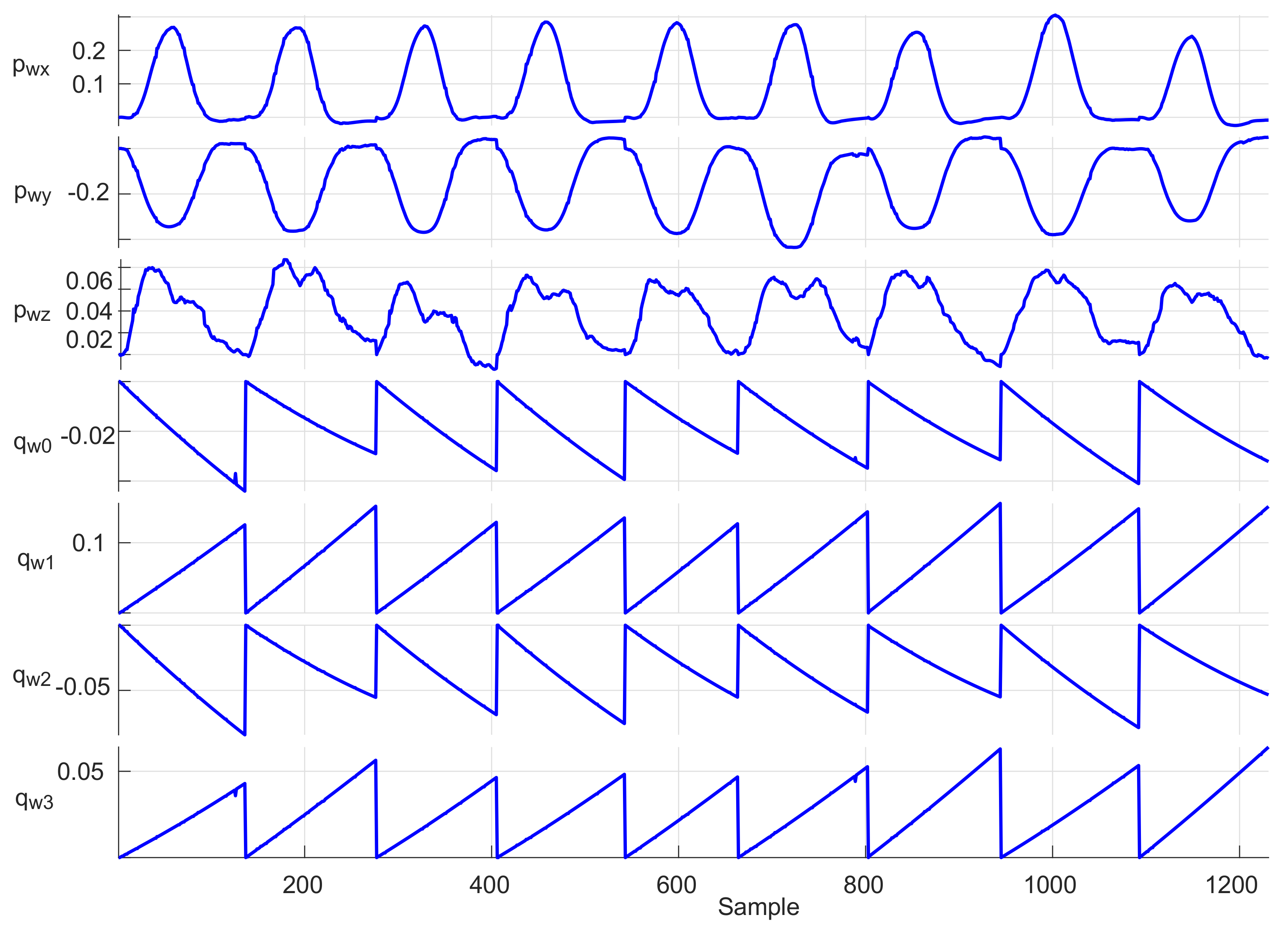
4.4.1. Repeatability Testing
4.4.2. Reliability Analysis
4.5. System Application in Robotics Research
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhou, H.; Hu, H. Human motion tracking for rehabilitation—A survey. Biomed. Signal Process. Control 2008, 3, 1–18. [Google Scholar]
- Ligorio, G.; Sabatini, A.M. A Novel Kalman Filter for Human Motion Tracking With an Inertial-Based Dynamic Inclinometer. IEEE Trans. Biomed. Eng. 2015, 62, 2033–2043. [Google Scholar] [CrossRef] [PubMed]
- El-Gohary, M.; McNames, J. Shoulder and Elbow Joint Angle Tracking with Inertial Sensors. IEEE Trans. Biomed. Eng. 2012, 59, 2635–2641. [Google Scholar] [CrossRef] [PubMed]
- Wong, C.; Zhang, Z.Q.; Lo, B.; Yang, G.Z. Wearable Sensing for Solid Biomechanics: A Review. IEEE Sens. J. 2015, 15, 2747–2760. [Google Scholar]
- Yang, Y.; Yan, H.; Dehghan, M.; Ang, M.H. Real-time human-robot interaction in complex environment using Kinect v2 image recognition. In Proceedings of the 2015 IEEE 7th International Conference on Cybernetics and Intelligent Systems (CIS) and IEEE Conference on Robotics, Automation and Mechatronics (RAM), Angkor Wat, Cambodia, 15–17 July 2015; pp. 112–117. [Google Scholar]
- Rodriguez-Angeles, A.; Morales-Diaz, A.; Bernabé, J.C.; Arechavaleta, G. An online inertial sensor-guided motion control for tracking human arm movements by robots. In Proceedings of the 3rd IEEE RAS and EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob 2010), Tokyo, Japan, 26–29 September 2010; pp. 319–324. [Google Scholar]
- Roetenberg, D.; Luinge, H.; Slycke, P. Xsens MVN: Full 6-DOF Human Motion Tracking Using Miniature Inertial Sensors; Technical Report; Xsens Motion Technologies BV: Enschede, The Netherlands, 2009. [Google Scholar]
- Luinge, H.J.; Veltink, P.H. Measuring orientation of human body segments using miniature gyroscopes and accelerometers. Med. Biol. Eng. Comput. 2005, 43, 273–282. [Google Scholar] [CrossRef]
- Baldi, T.L.; Scheggi, S.; Meli, L.; Mohammadi, M.; Prattichizzo, D. GESTO: A Glove for Enhanced Sensing and Touching Based on Inertial and Magnetic Sensors for Hand Tracking and Cutaneous Feedback. IEEE Trans. Hum.-Mach. Syst. 2017. [Google Scholar] [CrossRef]
- Sabatini, A.M.; Mannini, A. Ambulatory Assessment of Instantaneous Velocity during Walking Using Inertial Sensor Measurements. Sensors 2016, 16, 2206. [Google Scholar] [CrossRef]
- Sabatini, A.M. Estimating Three-Dimensional Orientation of Human Body Parts by Inertial/Magnetic Sensing. Sensors 2011, 11, 1489–1525. [Google Scholar] [CrossRef]
- Filippeschi, A.; Schmitz, N.; Miezal, M.; Bleser, G.; Ruffaldi, E.; Stricker, D. Survey of Motion Tracking Methods Based on Inertial Sensors: A Focus on Upper Limb Human Motion. Sensors 2017, 17, 1257. [Google Scholar] [CrossRef]
- Lambrecht, J.M.; Kirsch, R.F. Miniature Low-Power Inertial Sensors: Promising Technology for Implantable Motion Capture Systems. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 1138–1147. [Google Scholar]
- Yun, X.; Bachmann, E.R. Design, Implementation, and Experimental Results of a Quaternion-Based Kalman Filter for Human Body Motion Tracking. IEEE Trans. Robot. 2006, 22, 1216–1227. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Wu, J.K. A Novel Hierarchical Information Fusion Method for Three-Dinemsional Upper Limb Motion Estimation. IEEE Trans. Instrum. Meas. 2011, 60, 3709–3719. [Google Scholar]
- Zhang, Z.Q.; Ji, L.Y.; Huang, Z.; Wu, J.K. Adaptive information fusion for human upper limb movement estimation. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2012, 42, 1100–1108. [Google Scholar]
- Zhu, R.; Zhou, Z. A real-time articulated human motion tracking using tri-axis inertial/magnetic sensors package. IEEE Trans. Neural Syst. Rehabil. Eng. 2004, 12, 295–302. [Google Scholar]
- Yun, X.; Bachmann, E.R.; McGhee, R.B. A simplified quaternion-based algorithm for orientation estimation from earth gravity and magnetic field measurements. IEEE Trans. Instrum. Meas. 2008, 57, 638–650. [Google Scholar]
- Madgwick, S.O.H.; Harrison, A.J.L.; Vaidyanathan, R. Estimation of IMU and MARG orientation using a gradient descent algorithm. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011; pp. 1–7. [Google Scholar]
- Adamowicz, L.; Gurchiek, R.; Ferri, J.; Ursiny, A.; Fiorentino, N.; McGinnis, R. Validation of Novel Relative Orientation and Inertial Sensor-to-Segment Alignment Algorithms for Estimating 3D Hip Joint Angles. Sensors 2019, 19, 5143. [Google Scholar]
- Zanchettin, A.M.; Rocco, P.; Bascetta, L.; Symeonidis, I.; Peldschus, S. Kinematic analysis and synthesis of the human arm motion during a manipulation task. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 2692–2697. [Google Scholar]
- Taunyazov, T.; Omarali, B.; Shintemirov, A. A novel low-cost 4-DOF wireless human arm motion tracker. In Proceedings of the 2016 6th IEEE International Conference on Biomedical Robotics and Biomechatronics (BioRob), Singapore, 26–29 June 2016; pp. 157–162. [Google Scholar]
- Prayudi, I.; Kim, D. Design and implementation of IMU-based human arm motion capture system. In Proceedings of the 2012 International Conference on Mechatronics and Automation (ICMA), Chengdu, China, 5–8 August 2012; pp. 670–675. [Google Scholar]
- Bai, L.; Pepper, M.G.; Yan, Y.; Phillips, M.; Sakel, M. Low Cost Inertial Sensors for the Motion Tracking and Orientation Estimation of Human Upper Limbs in Neurological Rehabilitation. IEEE Access 2020, 8, 54254–54268. [Google Scholar] [CrossRef]
- Perry, J.C.; Rosen, J. Design of a 7 degree-of-freedom upper-limb powered exoskeleton. In Proceedings of the First IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Pisa, Italy, 20–22 February 2006; pp. 805–810. [Google Scholar]
- BoneSpine, Degrees of Freedom of Upper Limb. Available online: http://boneandspine.com/degrees-of-freedom-of-upper-limb/ (accessed on 20 November 2019).
- Kuipers, J.B. Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace and Virtual Reality; Princeton University Press: Princeton, NJ, USA, 2002. [Google Scholar]
- Madden, K.E.; Deshpande, A. On Integration of Additive Manufacturing During the Design and Development of a Rehabilitation Robot: A Case Study. J. Mech. Des. 2015, 137, 111471. [Google Scholar] [CrossRef]
- Telegenov, K.; Tlegenov, Y.; Shintemirov, A. A Low-Cost Open-Source 3-D-Printed Three-Finger Gripper Platform for Research and Educational Purposes. IEEE Access 2015, 3, 638–647. [Google Scholar] [CrossRef]
- Omarali, B.; Taunyazov, T.; Bukeyev, A.; Shintemirov, A. Real-Time Predictive Control of an UR5 Robotic Arm Through Human Upper Limb Motion Tracking. In Proceedings of the Companion of the 2017 ACM/IEEE International Conference on Human-Robot Interaction, Vienna, Austria, 6–9 March 2017; pp. 237–238. [Google Scholar]
- Rubagotti, M.; Taunyazov, T.; Omarali, B.; Shintemirov, A. Semi-Autonomous Robot Teleoperation with Obstacle Avoidance via Model Predictive Control. IEEE Robot. Autom. Lett. 2019, 4, 2746–2753. [Google Scholar]
- Rosario, M.B.D.; Khamis, H.; Ngo, P.; Lovell, N.H.; Redmond, S.J. Computationally Efficient Adaptive Error-State Kalman Filter for Attitude Estimation. IEEE Sens. J. 2018, 18, 9332–9342. [Google Scholar] [CrossRef]
- Valenti, R.G.; Dryanovski, I.; Xiao, J. Keeping a Good Attitude: A Quaternion-Based Orientation Filter for IMUs and MARGs. Sensors 2015, 15, 19302–19330. [Google Scholar] [CrossRef] [PubMed]
- Fan, B.; Li, Q.; Liu, T. How Magnetic Disturbance Influences the Attitude and Heading in Magnetic and Inertial Sensor-Based Orientation Estimation. Sensors 2018, 18, 76. [Google Scholar] [CrossRef]
- Ojeda, L.; Borenstein, J. Non-GPS Navigation for Security Personnel and First Responders. J. Navig. 2007, 60, 391–407. [Google Scholar] [CrossRef]
- Muller, P.; Steel, T.; Schauer, T. Experimental evaluation of a novel inertial sensor based realtime gait phase detection algorithm. In Proceedings of the 5th European Conference on Technically Assisted Rehabilitation, Athens, Greece, 11–13 November 2015. [Google Scholar]
- Nguyen, K.D.; Chen, I.M.; Luo, Z.; Yeo, S.H.; Duh, H.B.L. A wearable sensing system for tracking and monitoring of functional arm movement. IEEE/ASME Trans. Mechatron. 2010, 16, 213–220. [Google Scholar] [CrossRef]
- Koo, T.K.; Li, M.Y. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, J.; Wu, X.; Pottie, G.; Kaiser, W. A simple calibration for upper limb motion tracking and reconstruction. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; pp. 5868–5871. [Google Scholar]
- Mazomenos, E.B.; Biswas, D.; Cranny, A.; Rajan, A.; Maharatna, K.; Achner, J.; Klemke, J.; Jöbges, M.; Ortmann, S.; Langendörfer, P. Detecting Elementary Arm Movements by Tracking Upper Limb Joint Angles With MARG Sensors. IEEE J. Biomed. Health Inform. 2016, 20, 1088–1099. [Google Scholar] [CrossRef]






| Sensor Module | IMU | Potentiometer |
|---|---|---|
| Battery capacity | 600 mAh | 600 mAh |
| Supply voltage | 5 V | 5 V |
| Time duration of one charge | ∼2 h | ∼2.5 h |
| Wireless transmission frequency | up to 100 Hz | up to 100 Hz |
| Programming interface | mini-USB | mini-USB |
| Dimensions | mm | mm |
| Parameter | Starting Point, m | Mean (m) | SD (m) | Mean Difference, % (‖GDF-EKF‖/Initial Point) | ||
|---|---|---|---|---|---|---|
| GDF | EKF | GDF | EKF | |||
| 0.05 | 0.062 | 0.220 | 0.215 | 0.239 | 316 | |
| −0.5 | −0.342 | −0.249 | 0.178 | 0.200 | 18 | |
| 0.49 | 0.427 | 0.429 | 0.228 | 0.228 | 0.4 | |
| 0.942 | 0.912 | 0.814 | 0.854 | 0.89 | 0.837 | 0.852 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shintemirov, A.; Taunyazov, T.; Omarali, B.; Nurbayeva, A.; Kim, A.; Bukeyev, A.; Rubagotti, M. An Open-Source 7-DOF Wireless Human Arm Motion-Tracking System for Use in Robotics Research. Sensors 2020, 20, 3082. https://doi.org/10.3390/s20113082
Shintemirov A, Taunyazov T, Omarali B, Nurbayeva A, Kim A, Bukeyev A, Rubagotti M. An Open-Source 7-DOF Wireless Human Arm Motion-Tracking System for Use in Robotics Research. Sensors. 2020; 20(11):3082. https://doi.org/10.3390/s20113082
Chicago/Turabian StyleShintemirov, Almas, Tasbolat Taunyazov, Bukeikhan Omarali, Aigerim Nurbayeva, Anton Kim, Askhat Bukeyev, and Matteo Rubagotti. 2020. "An Open-Source 7-DOF Wireless Human Arm Motion-Tracking System for Use in Robotics Research" Sensors 20, no. 11: 3082. https://doi.org/10.3390/s20113082
APA StyleShintemirov, A., Taunyazov, T., Omarali, B., Nurbayeva, A., Kim, A., Bukeyev, A., & Rubagotti, M. (2020). An Open-Source 7-DOF Wireless Human Arm Motion-Tracking System for Use in Robotics Research. Sensors, 20(11), 3082. https://doi.org/10.3390/s20113082





