Sparsity-Aware Noise Subspace Fitting for DOA Estimation
Abstract
1. Introduction
2. Signal Model
2.1. Array Processing Model
2.2. OWNSF and Its Sparse Representation
3. The Proposed SANSF Algorithm for DOA Estimation
3.1. Sparsity-Aware Noise Subspace Fitting
3.2. About the Initialization
3.3. The Effect of Sparsity Enhancement
4. Numerical and Experimental Results
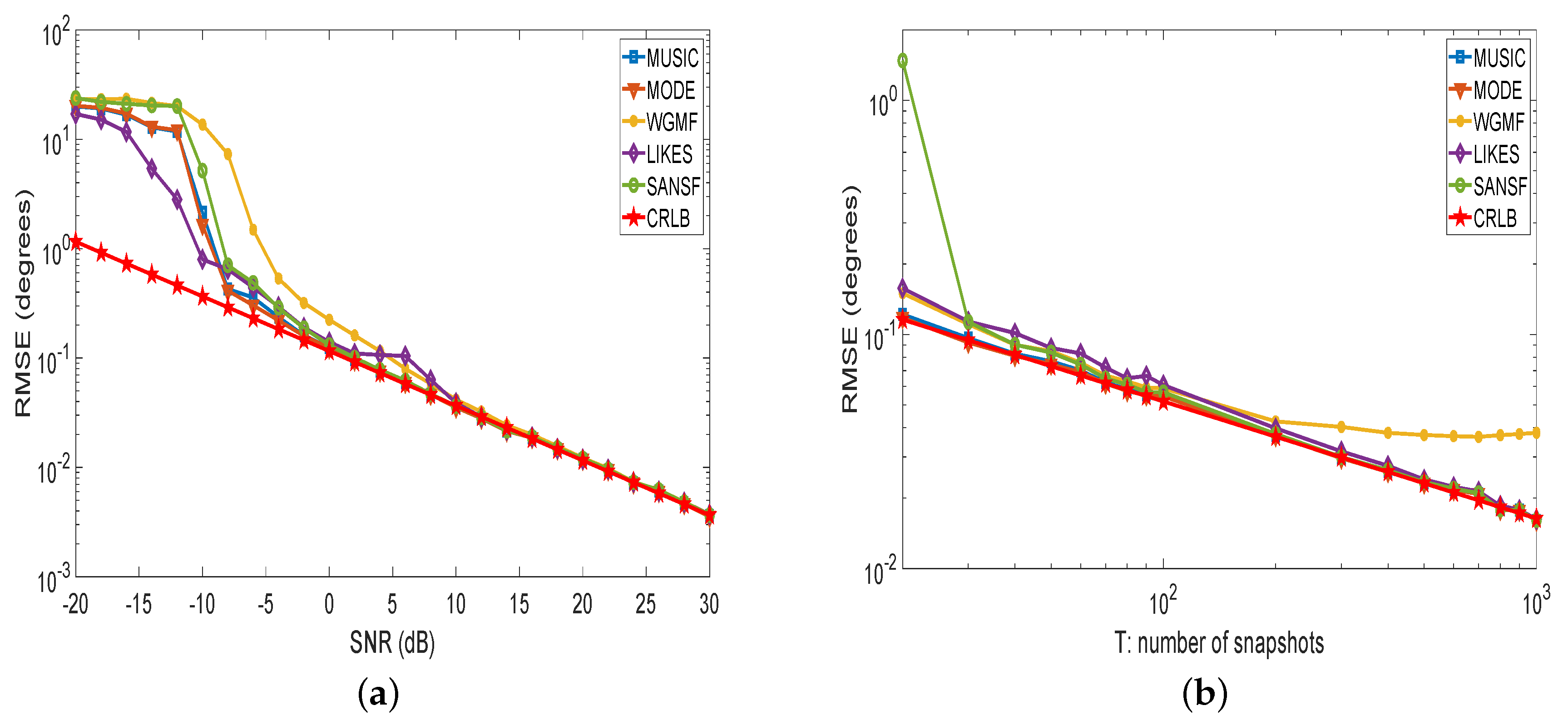
4.1. Root-Mean-Squared-Errors (RMSEs)
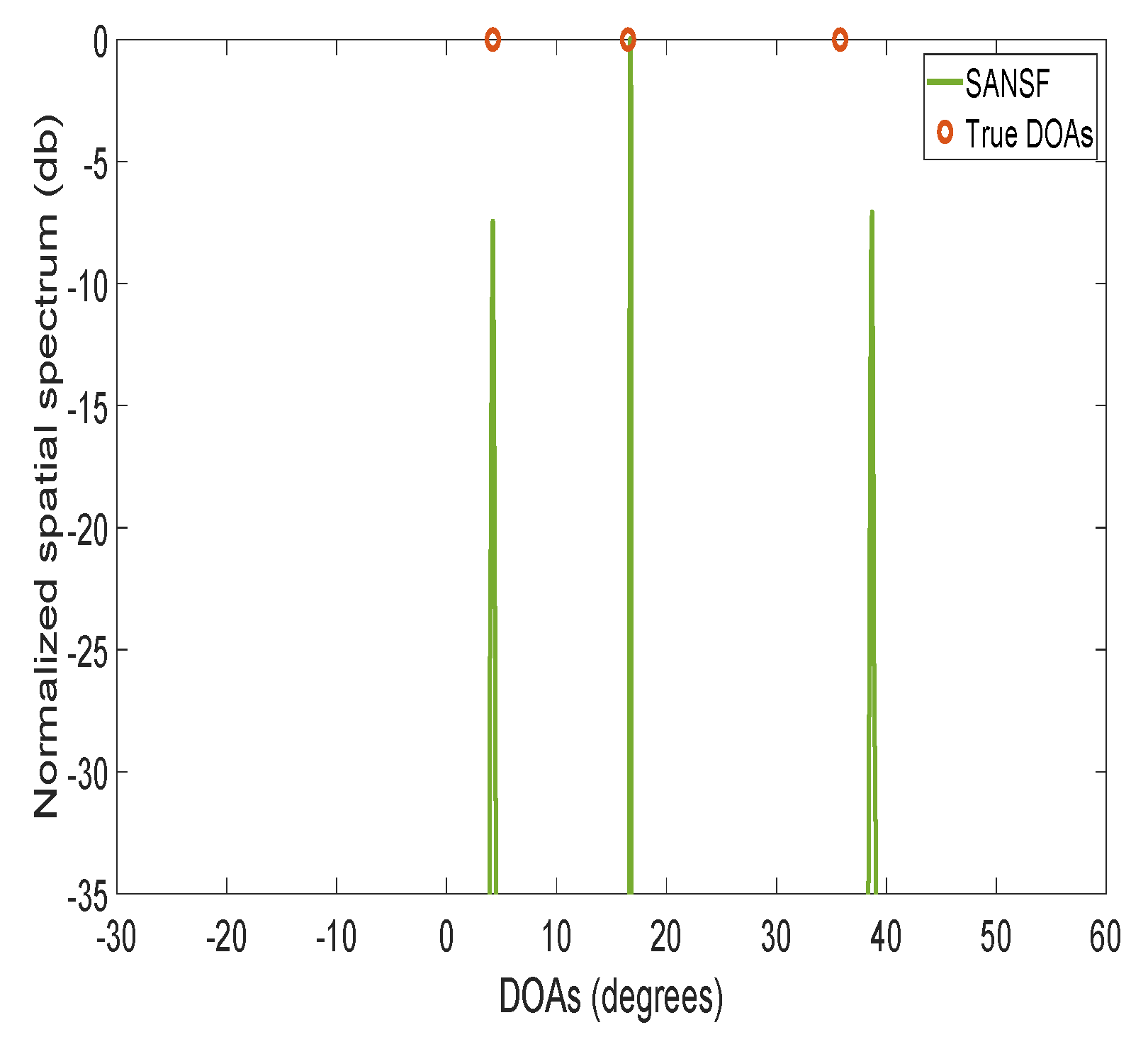
4.2. Resolution
4.2.1. Probability of Resolution
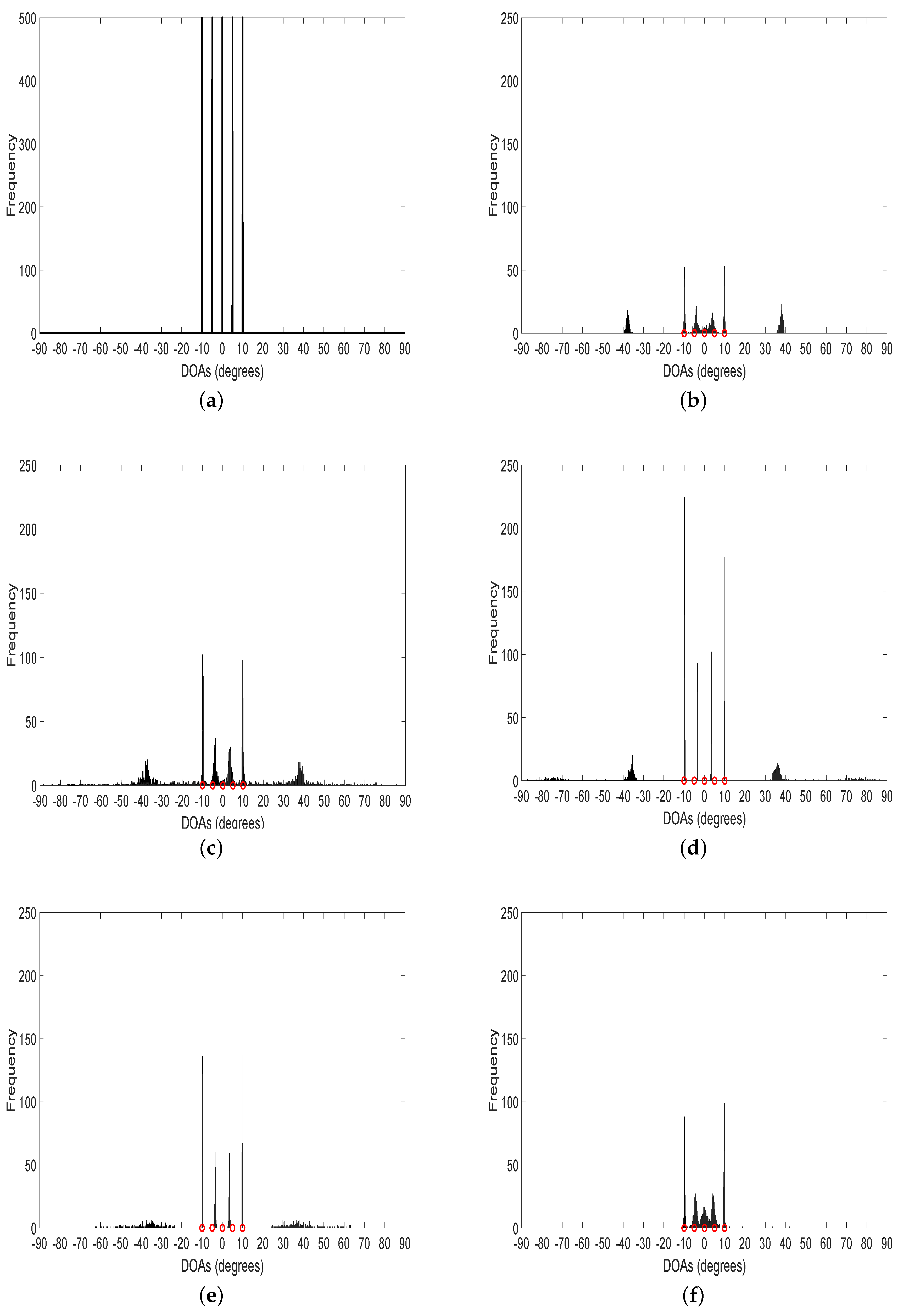
4.2.2. Histogram for 1D Closely Spaced Sources
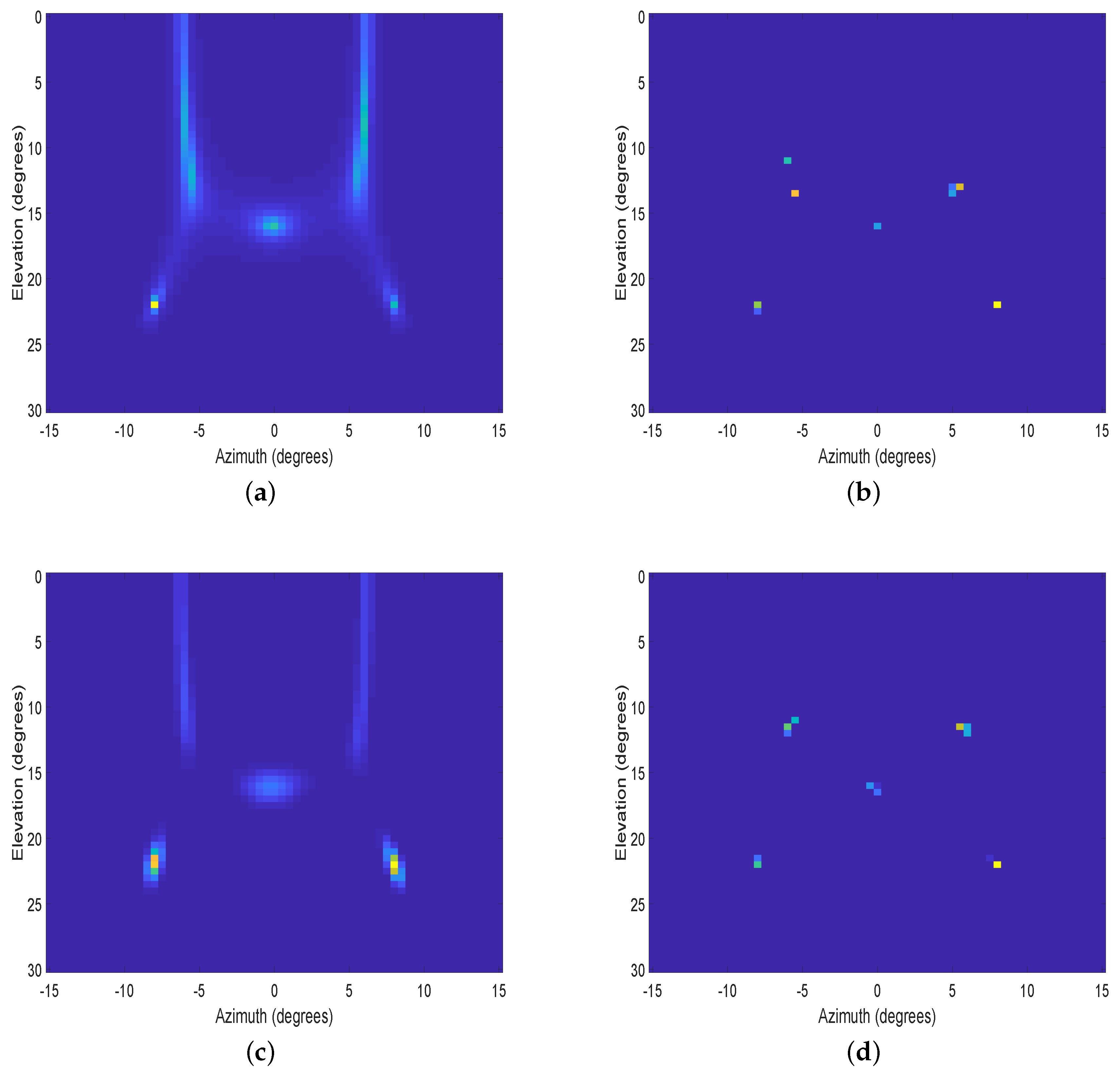
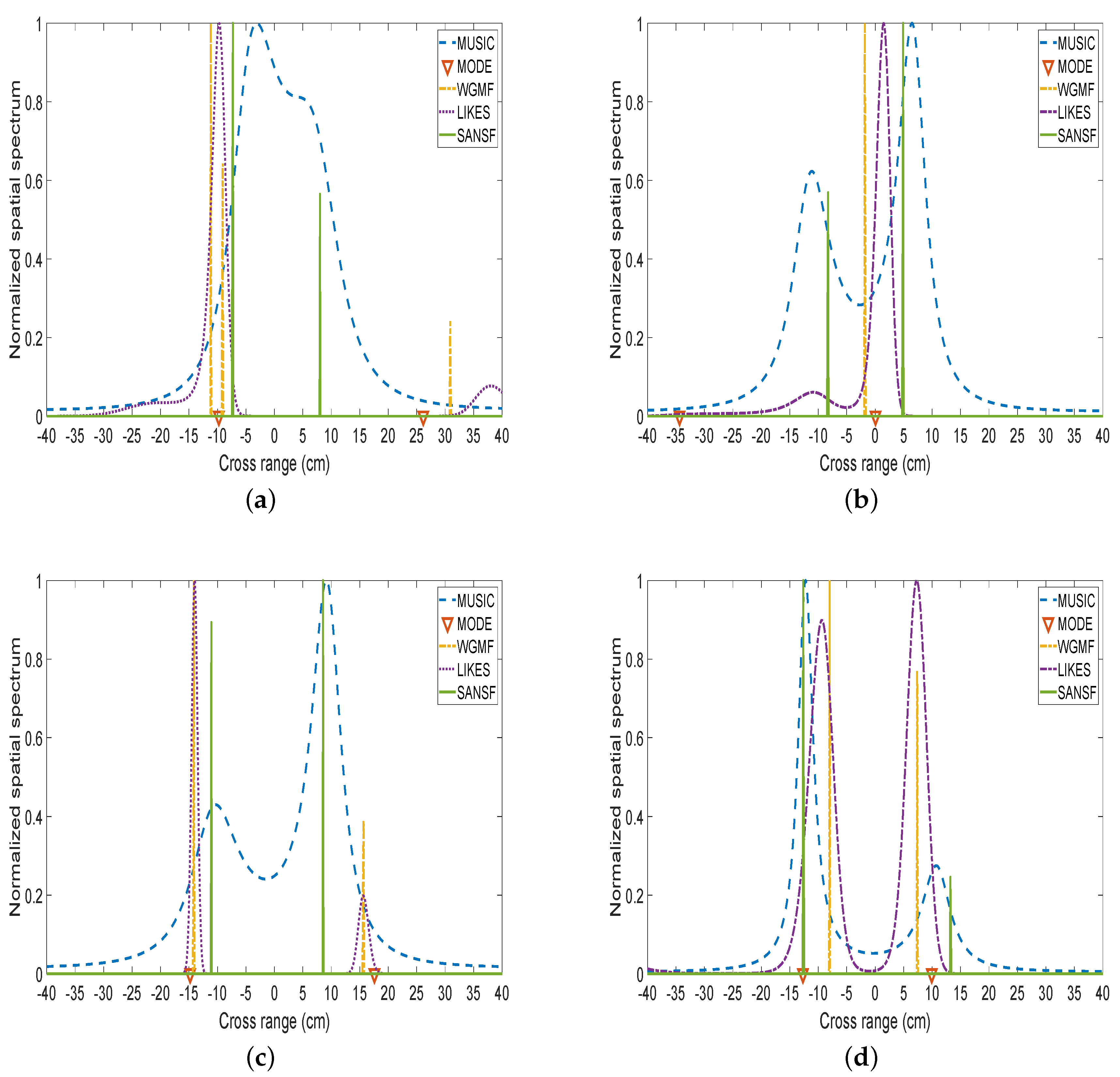
4.2.3. Spatial Spectrum for 2D Closely Spaced Sources
4.3. Robustness to the Assumption of Uncorrelated Sources
4.4. Computational Complexity
4.5. DOA Tracking Results with Real Measured Ultrasonic Data
4.6. DOA Eestimation Results with Real Radar Data
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Athanassios, M. Beamforming: Sensor Signal Processing for Defence Applications; Imperial College Press: London, UK, 2015. [Google Scholar]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Stoica, P.; Sharman, K.C. Maximum likelihood methods for direction-of-arrival estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1132–1143. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Cotter, S.; Rao, B.; Engan, K.; Kreutz-Delgado, K. Sparse solutions to linear inverse problems with multiple measurement vectors. IEEE Trans. Signal Process. 2005, 53, 2477–2488. [Google Scholar] [CrossRef]
- Malioutov, D.; Cetin, M.; Willsky, A. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef]
- Stoica, P.; Babu, P.; Li, J. SPICE: A sparse covariance-based estimation method for array processing. IEEE Trans. Signal Process. 2011, 59, 629–638. [Google Scholar] [CrossRef]
- Yin, J.; Chen, T. Direction-of-arrival estimation using a sparse representation of array covariance vectors. IEEE Trans. Signal Process. 2011, 59, 4489–4493. [Google Scholar] [CrossRef]
- Xu, X.; Wei, X.; Ye, Z. DOA Estimation Based on Sparse Signal Recovery Utilizing Weighted ℓ1 norm penalty. IEEE Signal Process. Lett. 2012, 19, 155–158. [Google Scholar] [CrossRef]
- Dai, J.; Bao, X.; Xu, W.; Chang, C. Root sparse Bayesian learning for off-grid DOA estimation. IEEE Process. Lett. 2016, 24, 46–50. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, J.; Du, R.; Lv, G. Sparse method for direction of arrival estimation using denoised fourth-order cumulants vector. Sensors 2018, 18, 1815. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Yang, J.; Huang, H.; Song, Y.; Gui, G. Deep learning for super-resolution channel estimation and DOA estimation based massive MIMO system. IEEE Trans. Veh. Technol. 2018, 67, 8549–8560. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. Performance study of conditional and unconditional direction-of-arrival estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1783–1795. [Google Scholar] [CrossRef]
- Ottersten, B.; Viberg, M.; Stoica, P.; Nehorai, A. Exact and Large Sample Maximum Likelihood Techniques for Parameter Estimation and Detection in Array Processing. In Radar Array Processing; Springer Series in Information Sciences; Springer: Berlin/Heidelberg, Germany, 1993; Volume 25. [Google Scholar]
- Stoica, P.; Ottersten, B.; Viberg, M.; Moses, R.L. Maximum likelihood array processing for stochastic coherent sources. IEEE Trans. Signal Process. 1996, 44, 96–105. [Google Scholar] [CrossRef]
- Swindlehurst, A.L.; Stoica, P. Maximum likelihood methods in radar array signal processing. Proc. IEEE 1998, 86, 421–441. [Google Scholar] [CrossRef]
- Takahashi, R.; Inaba, T.; Takahashi, T.; Tasaki, H. Digital monopulse beamforming for achieving the CRLB for angle accuracy. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 315–323. [Google Scholar] [CrossRef]
- Ziskind, I.; Wax, M. Maximum likelihood localization of multiple sources by alternating projection. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 1553–1560. [Google Scholar] [CrossRef]
- Stoica, P.; Sharman, K. Novel eigenanalysis method for direction estimation. IEE Proc. F (Radar Signal Process.) 1990, 137, 19–26. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P.; Liu, Z.S. Comparative study of IQML and MODE direction-of-arrival estimators. IEEE Trans. Signal Process. 1998, 46, 149–160. [Google Scholar]
- Zheng, C.; Li, G.; Zhang, H.; Wang, X. An approach of DOA estimation using noise subspace weighted ℓ1 minimization. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 2856–2859. [Google Scholar]
- Yang, Z.; Xie, L.; Zhang, C. Off-grid direction of arrival estimation using sparse Bayesian inference. IEEE Trans. Signal Process. 2012, 61, 38–43. [Google Scholar] [CrossRef]
- Hu, N.; Ye, Z.; Xu, X.; Bao, M. DOA Estimation for Sparse Array via Sparse Signal Reconstruction. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 760–773. [Google Scholar] [CrossRef]
- Si, W.; Zeng, F.; Hou, C.; Peng, Z. A sparse-based off-grid DOA estimation method for coprime arrays. Sensors 2018, 18, 3025. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, J.J. On the application of the global matched filter to DOA estimation with uniform circular arrays. IEEE Trans. Signal Process. 2001, 49, 702–709. [Google Scholar] [CrossRef]
- Fuchs, J.J. DOA estimation in the presence of modeling errors, the global matched filter approach. In Proceedings of the 17th European Signal Processing Conference (EUSIPCO), Glasgow, UK, 24–28 August 2009; pp. 1963–1967. [Google Scholar]
- Nesterov, Y.; Nemirovskii, A.; Ye, Y. Interior-Point Polynomial Algorithms in Convex Programming; SIAM: Philadelphia, PA, USA, 1994; Volume 13. [Google Scholar]
- Stoica, P.; Babu, P. SPICE and LIKES: Two hyperparameter-free methods for sparse-parameter estimation. Signal Process. 2012, 92, 1580–1590. [Google Scholar] [CrossRef]
- Babu, P.; Stoica, P. Sparse spectral-line estimation for nonuniformly sampled multivariate time series: SPICE, LIKES and MSBL. In Proceedings of the 20th European Signal Processing Conference (EUSIPCO), Bucharest, Romania, 27–31 August 2012; pp. 445–449. [Google Scholar]
- Yang, Z.; Xie, L. On gridless sparse methods for multi-snapshot DOA estimation. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 3236–3240. [Google Scholar]
- Yang, Z.; Xie, L. On gridless sparse methods for multi-snapshot direction of arrival estimation. Circuits Syst. Signal Process. 2017, 36, 3370–3384. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, T.; Li, Y.; Zakharov, Y. A novel block sparse reconstruction method for DOA estimation with unknown mutual coupling. IEEE Commun. Lett. 2019, 23, 1845–1848. [Google Scholar] [CrossRef]
- Ferreau, H.J.; Kirches, C.; Potschka, A.; Bock, H.G.; Diehl, M. qpOASES: A parametric active-set algorithm for quadratic programming. Math. Program. Comput. 2014, 6, 327–363. [Google Scholar] [CrossRef]
- Pougkakiotis, S.; Gondzio, J. An Interior Point-Proximal Method of Multipliers for Convex Quadratic Programming. arXiv 2019, arXiv:1904.10369v2. [Google Scholar]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]
- Santo, H.; Samejima, M.; Matsushita, Y. Numerical shape-from-shading revisited. IPSJ Trans. Comput. Vis. Appl. 2018, 10, 1–12. [Google Scholar] [CrossRef][Green Version]
- Rissanen, J. A universal prior for integers and estimation by minimum description length. Ann. Stat. 1983, 11, 416–431. [Google Scholar] [CrossRef]
- DI Serafino, D.; Toraldo, G.; Viola, M.; Barlow, J. A two-phase gradient method for quadratic programming problems with a single linear constraint and bounds on the variables. SIAM J. Optim. 2018, 28, 2809–2838. [Google Scholar] [CrossRef]
- Liu, W.; Wang, N.; Jin, M.; Xu, H. Denoising detection for the generalized spatial modulation system using sparse property. IEEE Commun. Lett. 2014, 18, 22–25. [Google Scholar] [CrossRef]
- Swindlehurst, A. Alternative algorithm for maximum likelihood DOA estimation and detection. IEE Proc. Radar Sonar Navig. 1994, 141, 293–299. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: New York, NY, UAS, 1990. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Topics in Matrix Analysis; Cambridge University Press: New York, NY, USA, 1991. [Google Scholar]
- Li, F.; Liu, H.; Vaccaro, R.J. Performance analysis for DOA estimation algorithms: Unification, simplification, and observations. IEEE Trans. Aerosp. Electron. Syst. 1993, 29, 1170–1184. [Google Scholar] [CrossRef]
- Candes, E.; Wakin, M.; Boyd, S. Enhancing sparsity by reweighted ℓ1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Xu, W.; Khajehnejad, M.; Avestimehr, A.; Hassibi, B. Breaking through the thresholds: An analysis for iterative reweighted ℓ1 minimization via the Grassmann angle framework. In Proceedings of the 2010 IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP ), Dallas, TX, USA, 14–19 March 2010; pp. 5498–5501. [Google Scholar]
- Zheng, C.; Li, G.; Liu, Y.; Wang, X. Subspace weighted ℓ2,1, minimization for sparse signal recovery. EURASIP Eurasip J. Adv. Signal Process. 2012, 2012, 98. [Google Scholar] [CrossRef]
- Wipf, D.; Nagarajan, S. Iterative reweighted ℓ1 and ℓ2 methods for finding sparse solutions. IEEE J. Sel. Top. Signal Process. 2010, 4, 317–329. [Google Scholar] [CrossRef]
- Gu, Y.; Goodman, N.A.; Hong, S.; Li, Y. Robust adaptive beamforming based on interference covariance matrix sparse reconstruction. Signal Process. 2014, 96, 375–381. [Google Scholar] [CrossRef]
- Slawski, M.; Hein, M. Non-negative least squares for high-dimensional linear models: Consistency and sparse recovery without regularization. Electron. J. Stat. 2013, 7, 3004–3056. [Google Scholar] [CrossRef]
- Eftekhari, A.; Tanner, J.; Thompson, A.; Toader, B.; Tyagi, H. Sparse non-negative super-resolution—simplified and stabilised. Appl. Comput. Harmon. Anal. 2019. [Google Scholar] [CrossRef]
- Kou, J.; Li, M.; Jiang, C. A Robust DOA Estimator Based on Compressive Sensing for Coprime Array in the Presence of Miscalibrated Sensors. Sensors 2019, 19, 3538. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.L.; Buckley, K.M. Bias analysis of the MUSIC location estimator. IEEE Trans. Signal Process. 1992, 40, 2559–2569. [Google Scholar] [CrossRef]
- Richmond, C. Capon algorithm mean-squared error threshold SNR prediction and probability of resolution. IEEE Trans. Signal Process. 2005, 53, 2748–2764. [Google Scholar] [CrossRef]
- Johnson, D.; Dudgeon, D. Array Signal Processing: Concepts and Techniques; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Das, A.; Zachariah, D.; Stoica, P. Comparison of Two Hyperparameter-Free Sparse Signal Processing Methods for Direction-of-Arrival Tracking in the HF97 Ocean Acoustic Experiment. IEEE J. Ocean. Eng. 2018, 43, 725–734. [Google Scholar] [CrossRef]
- Zhang, Q.T. Probability of resolution of the MUSIC algorithm. IEEE Trans. Signal Process. 1995, 43, 978–987. [Google Scholar] [CrossRef]
- Stoica, P.; Moses, R. Spectral Analysis of Signals; Pearson/Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Pierre, J.W.; Scott, E.D.; Hays, M.P. A sensor array testbed for source tracking algorithms. In Proceedings of the 1997 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Munich, Germany, 21–24 April 1997; pp. 3769–3772. [Google Scholar]
- Gershman, A.B.; Bohme, J.F. A pseudo-noise approach to direction finding. Signal Process. 1998, 71, 1–13. [Google Scholar] [CrossRef]
- Gershman, A.B.; Stoica, P. On Unitary and Forward-Backward MODE. Digit. Signal Process. 1999, 9, 67–75. [Google Scholar] [CrossRef]
- Browne, K.E.; Burkholder, R.J.; Volakis, J.L. Through-wall opportunistic sensing system utilizing a low-cost flat-panel array. IEEE Trans. Antennas Propag. 2011, 59, 859–868. [Google Scholar] [CrossRef]




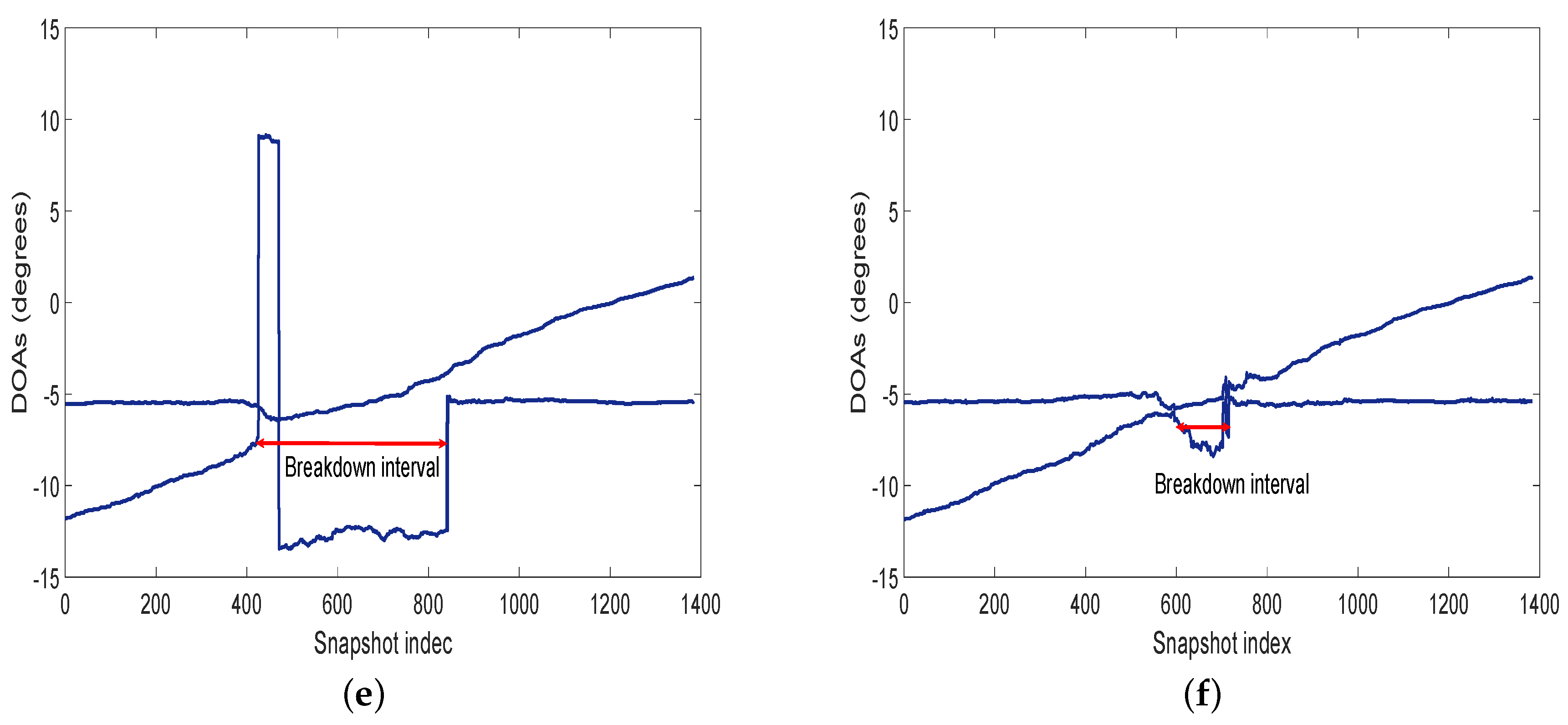

| Algorithms | MUSIC | MODE-ULA | WGMF | LIKES | SANSF |
|---|---|---|---|---|---|
| Start | 488 | 314 | 560 | 426 | 601 |
| End | 789 | 809 | 680 | 847 | 715 |
| Parameters | Tx Channel | Rx Channel | Start Frequency | Frequency Slope | ADC Samples | Sample Rate |
|---|---|---|---|---|---|---|
| Value | Tx1 | Rx1,2,3,4 | 77 GHz | 66.626 MHz/s | 256 | 5000 ksps |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, C.; Chen, H.; Wang, A. Sparsity-Aware Noise Subspace Fitting for DOA Estimation. Sensors 2020, 20, 81. https://doi.org/10.3390/s20010081
Zheng C, Chen H, Wang A. Sparsity-Aware Noise Subspace Fitting for DOA Estimation. Sensors. 2020; 20(1):81. https://doi.org/10.3390/s20010081
Chicago/Turabian StyleZheng, Chundi, Huihui Chen, and Aiguo Wang. 2020. "Sparsity-Aware Noise Subspace Fitting for DOA Estimation" Sensors 20, no. 1: 81. https://doi.org/10.3390/s20010081
APA StyleZheng, C., Chen, H., & Wang, A. (2020). Sparsity-Aware Noise Subspace Fitting for DOA Estimation. Sensors, 20(1), 81. https://doi.org/10.3390/s20010081




