Research on Mechanical Fault Prediction Method Based on Multifeature Fusion of Vibration Sensing Data
Abstract
1. Introduction
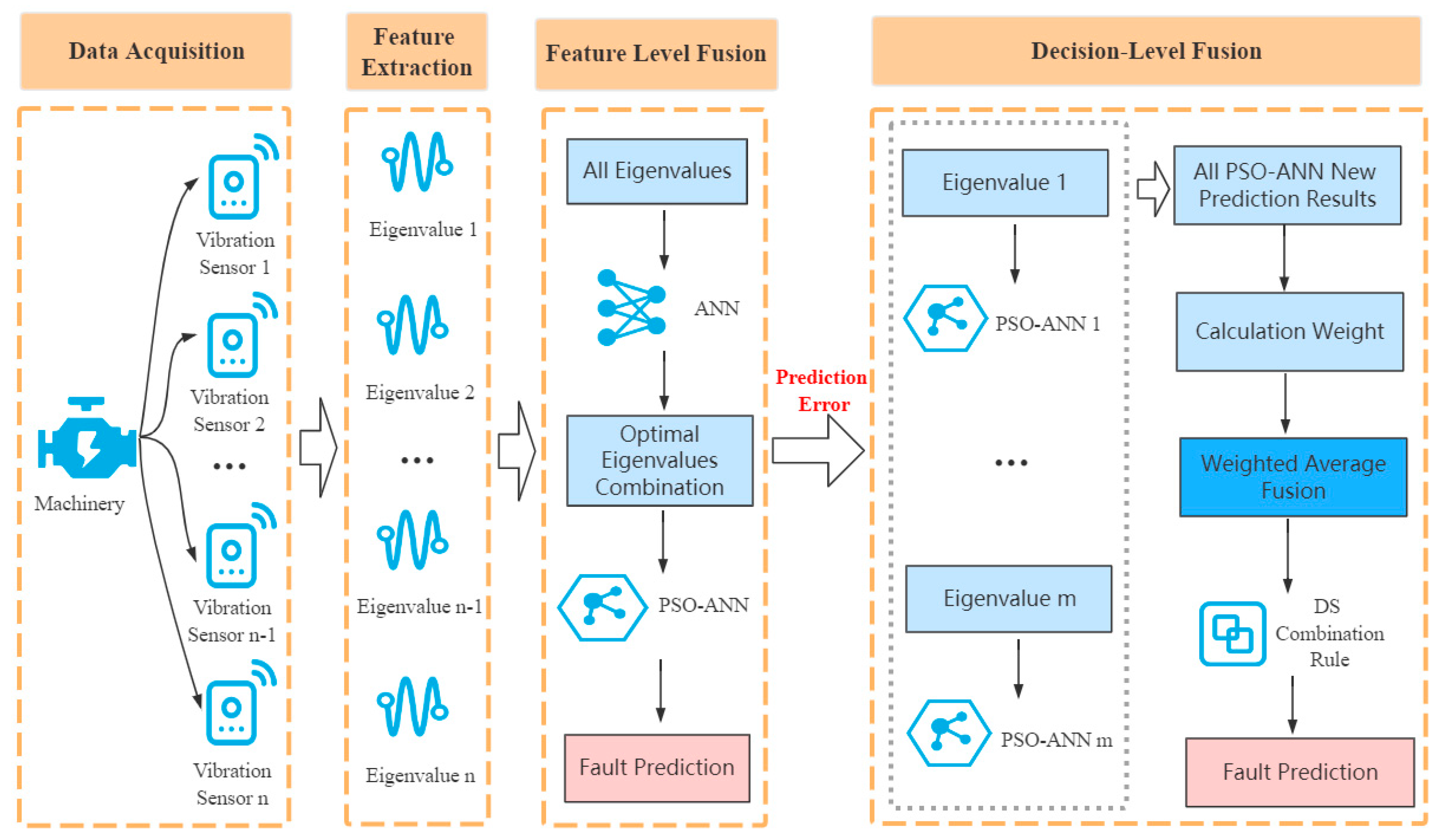
2. Multifeature Fusion Model Based on Vibration Sensing Data
3. Feature Extraction Method Based on Vibration Sensing Data
4. Feature-Level Fusion Based on the Use of a PSO-ANN
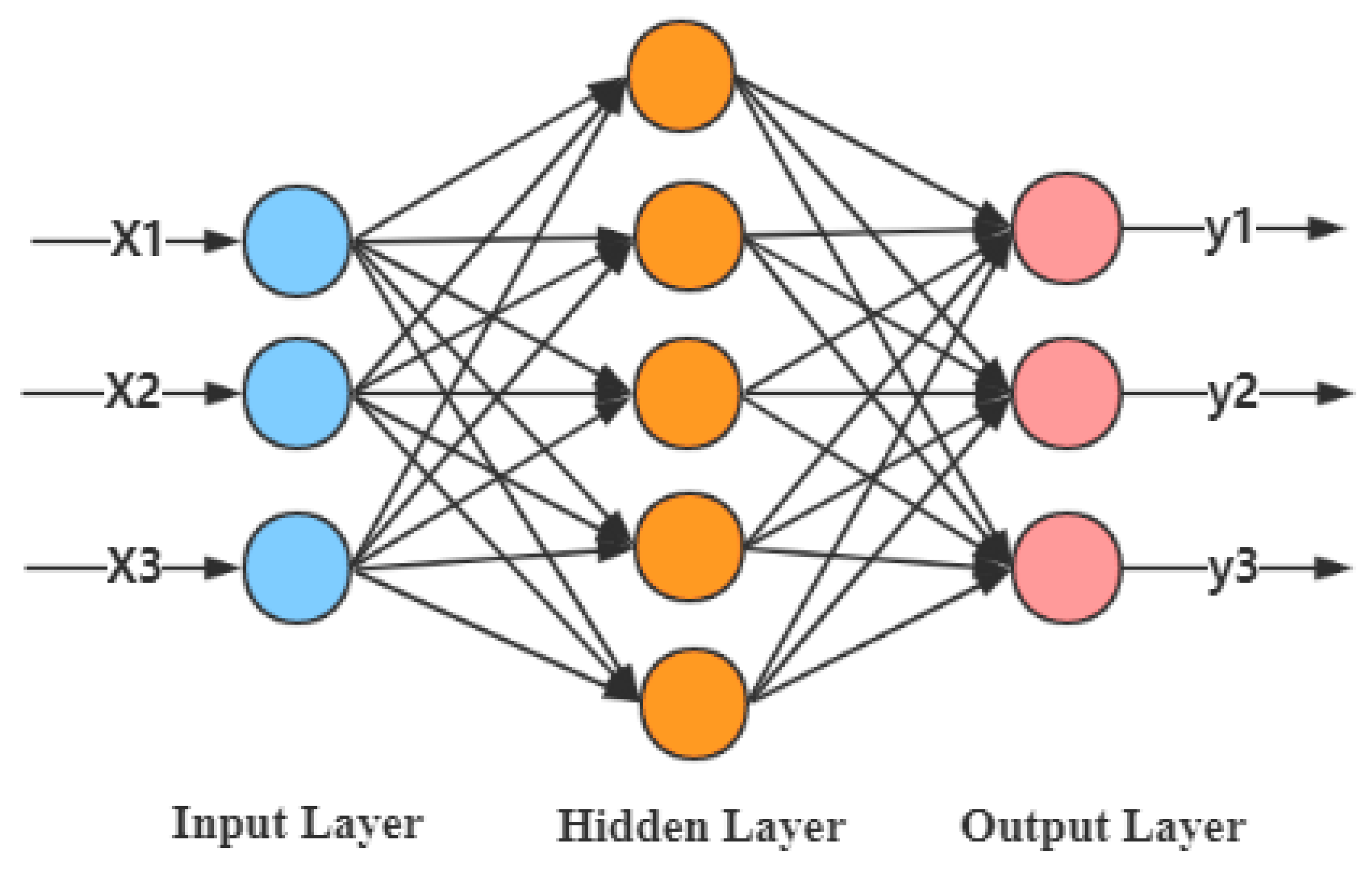
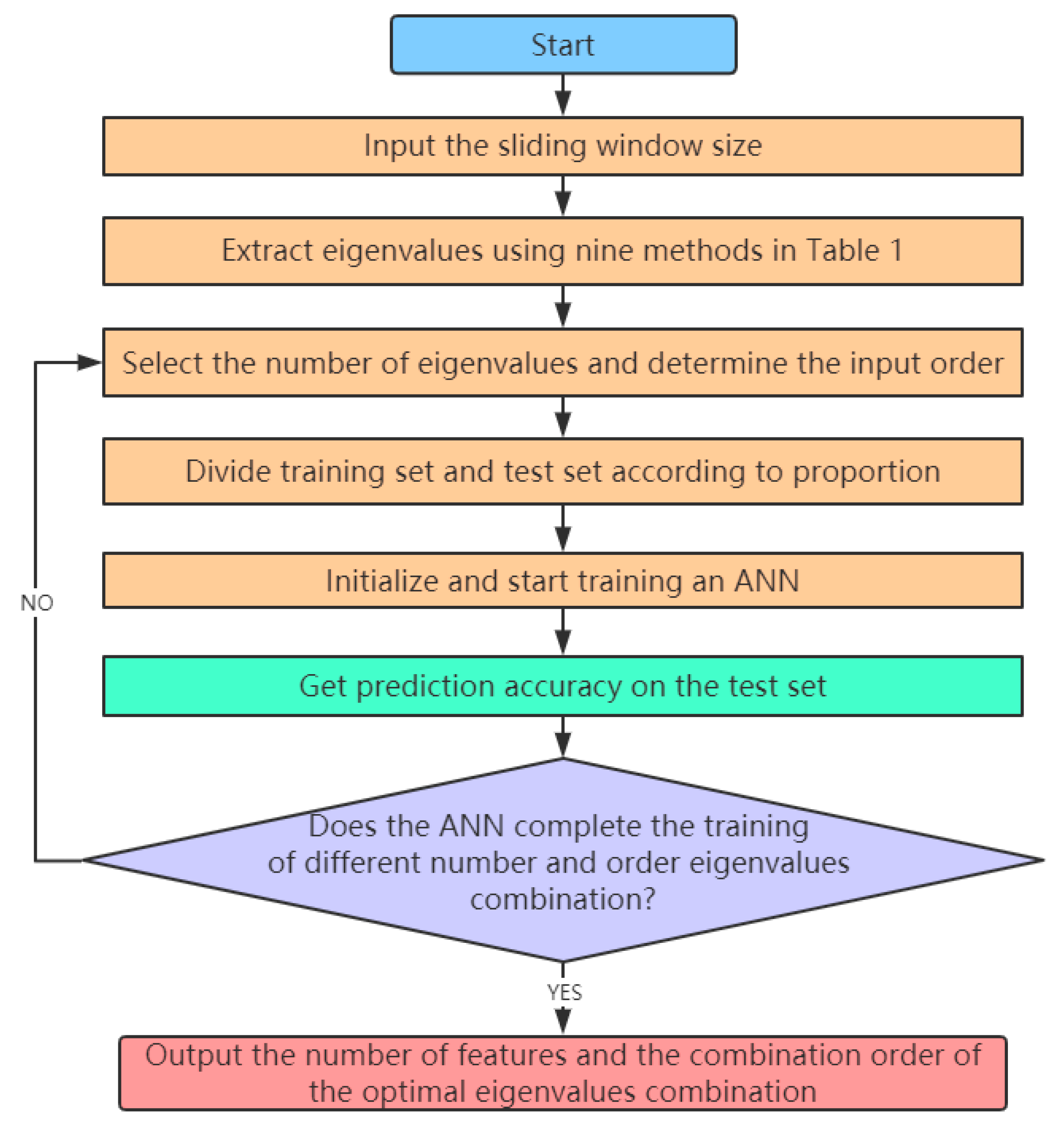
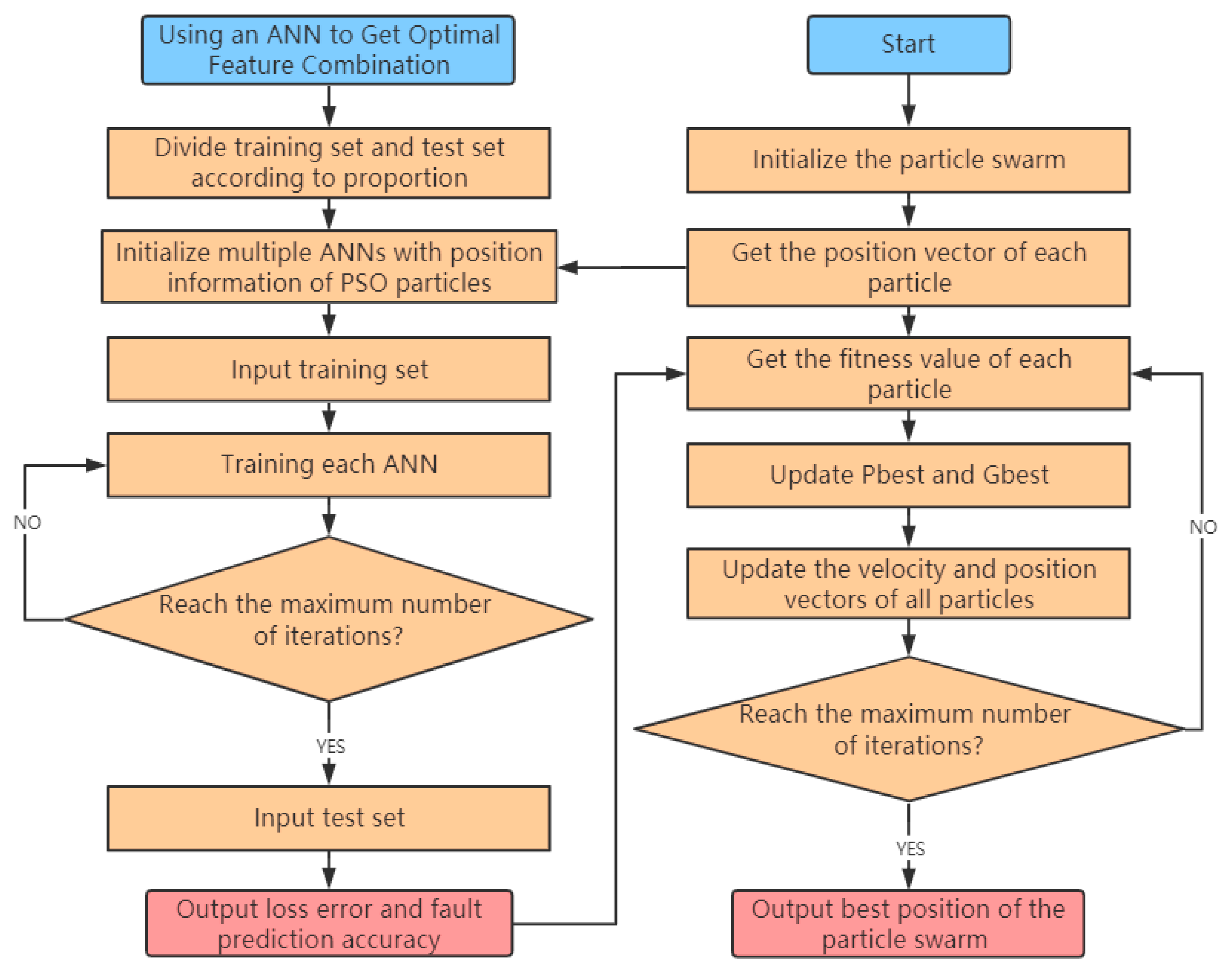
4.1. Artificial Neural Network and the Strategy to Obtain the Optimal Eigenvalues Combination
4.2. Optimization Principle Using the Particle Swarm Optimization Algorithm
4.3. Algorithm Principle of Feature-Level Fusion Using a PSO-ANN
| Algorithm 1: PSO-ANN algorithm. |
| Input: All the eigenvalues of the optimal feature combination. |
| Output: The best position of the particle swarm Gbest, and the best prediction accuracy. |
| 01: Set the parameters {n,, , , , } 02: for i = 1 to n do /* n is the number of particles */ 03: Initialize = (), = (), 04: end for 05: Acquire training set , and test set , 06: Set the particle with best to be 07: for k = 1 do 08: Update with Equation (3) 09: Update , with Equation (4) 10: for i = 1 to n do 11: ann_model(learning_rate = , hidden_layer_ neurons = , 12: momentum_parameter = , rmsprop_parameter = ) 13: .fit(, ) /* Training ANN model */ 14: = .loss_value 15: = .score(, ) 16: if ( > fitness().loss_value and 17: < fitness().prediction_accuracy) then 18: 19: end if 20: if ( > fitness().loss_value and 21: < fitness().prediction_accuracy) then 22: 23: end if 24: for j = 1 to 4 do 25: 26: 27: end for 28: end for 29: end for |
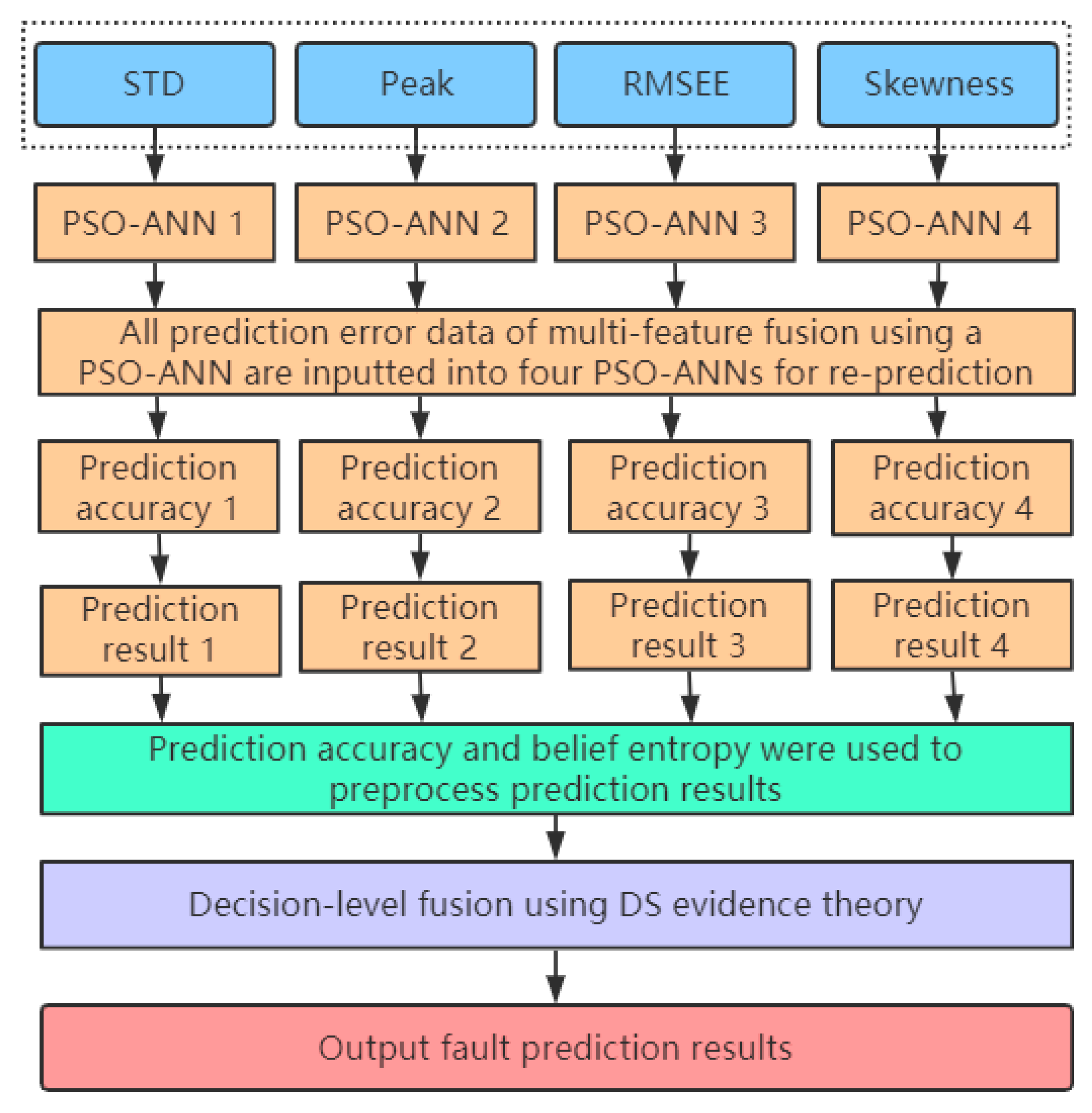
5. Decision-Level Fusion Based on Multiple PSO-ANN Models and Dempster-Shafer Evidence Theory
5.1. Running Process of a PSO-ANN-DS
5.2. Algorithm Principle of Decision-Level Fusion Using a PSO-ANN-DS
| Algorithm 2: PSO-ANN-DS algorithm. |
| Input: Four single eigenvalues, and fault data with high levels of uncertainty. |
| Output: Decision-level fusion result Fus(m). |
| 01: /* Step 1 */ 02: Train_data = {STD, Peak, RMSEE, Skewness} /* Four single eigenvalues */ 03: for i = 1 to 4 do 04: = PSO-ANN_algorithm(Input = Train_data [i]) 05: PRE[i] = (test_data = fault data with high 06: uncertainty). prediction_accuracy 07: end for 08: /* Step 2 */ 09: for i = 1 to 4 do 10: CRD[i] = PRE[i] / sum(PRE) 11: end for 12: /* Step 3 */ 13: for i = 1 to 4 do 14: MUN[i] = Calculate the value with Equation (8) and (9) 15: end for 16: /* Step 4 */ 17: for i = 1 to 4 do 18: MCRD[i] = CRD[i] * MUN[i] 19: end for 20: /* Step 5 */ 21: for i = 1 to 4 do 22: NMCRD[i] = MCRD[i] / sum(MCRD) 23: end for 24: /* Step 6 */ 25: for j = 1 to J do /* J is the number of fault types */ 26: WAE[j] = 0 27: for i = 1 to 4 do 28: WAE[j] = WAE[j] + NMCRD[i] * .prediction_result(fault_type = j) 29: end for 30: end for 31: /* Step 7 */ 32: Fus(m) = WAE 33: for i = 1 to 3 do /* There are 4 single features, which need to be merged 3 times. */ 34: Fus(m) = Fus(m) WAE /* refers to the DS fusion rule */ 35: end for |
6. Bearing Fault Prediction Experiment Based on Vibration Sensing Data
6.1. Introduction to Data Set and Experimental Environment
6.2. Using an ANN to Get Optimal Feature Combination
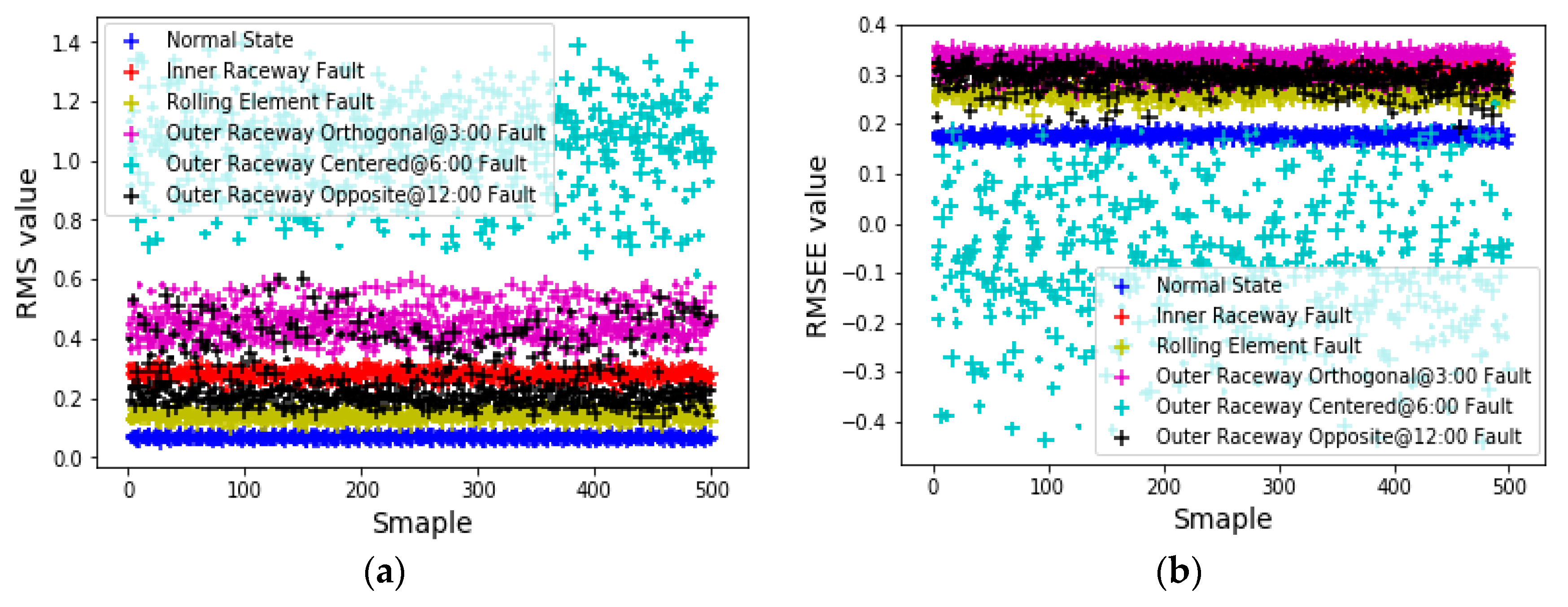
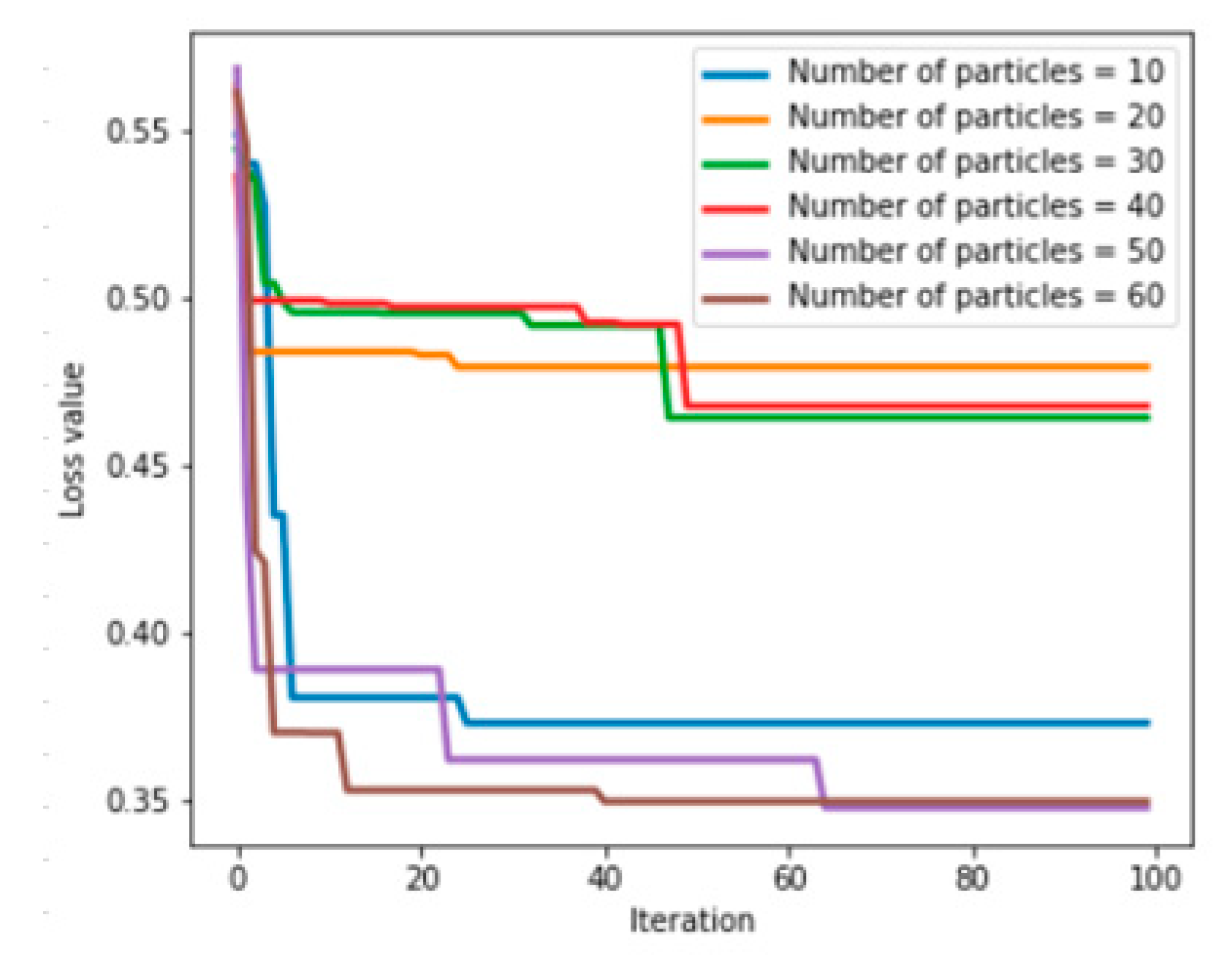
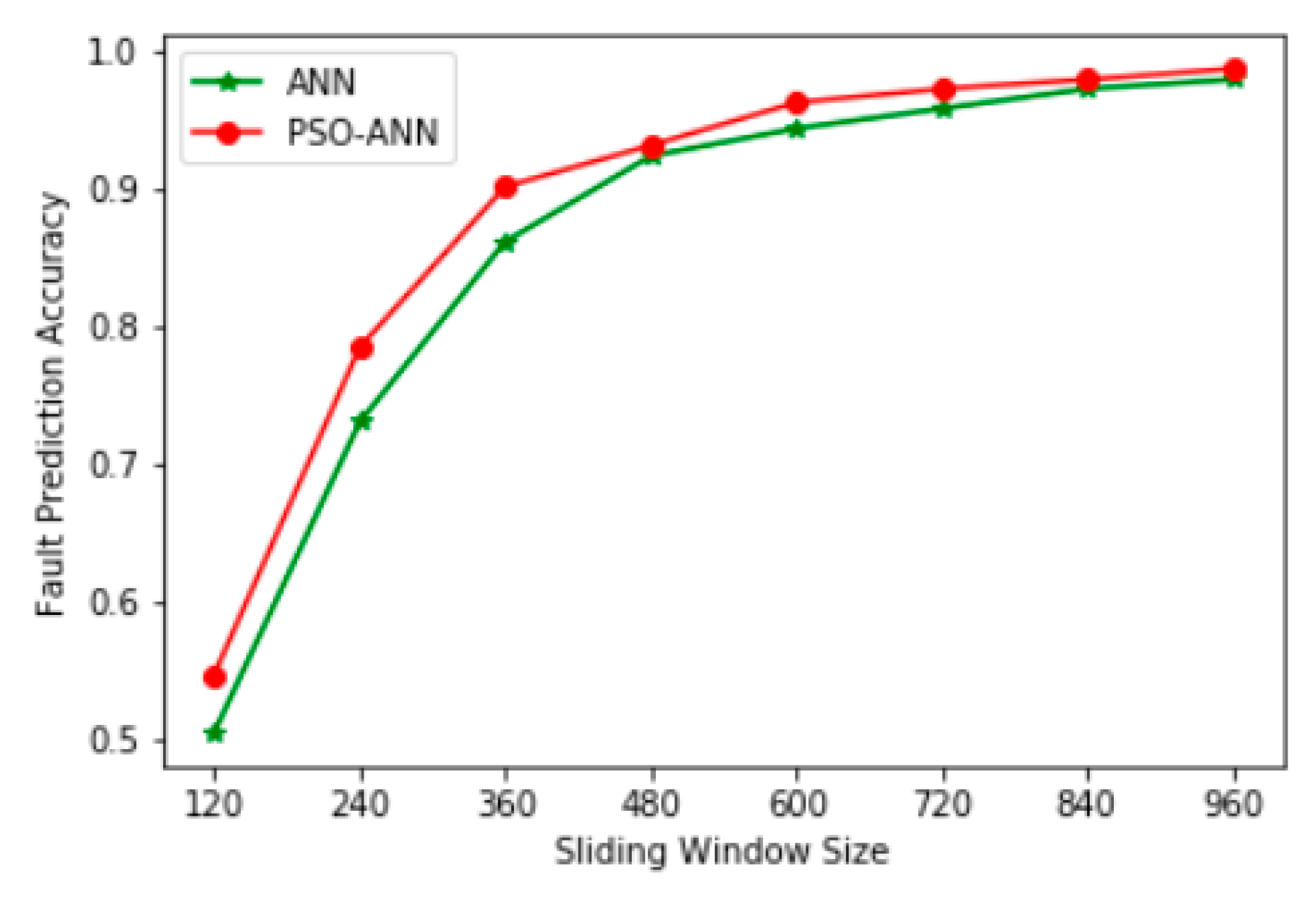
6.3. Feature-Level Fusion Fault Prediction Experiment Based on a PSO-ANN
6.4. Decision-Level Fusion Fault Prediction Experiment Based on PSO-ANN-DS
6.5. Comparison and Analysis of Fault Prediction Accuracy of Various Models
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Glowacz, A.; Glowacz, W. Vibration-Based Fault Diagnosis of Commutator Motor. Shock Vib. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Wang, H.; Li, S.; Song, L.; Cui, L. A novel convolutional neural network based fault recognition method via image fusion of multi-vibration-signals. Comput. Ind. 2019, 105, 182–190. [Google Scholar] [CrossRef]
- Huang, M.; Liu, Z.; Tao, Y. Mechanical fault diagnosis and prediction in IoT based on multi-source sensing data fusion. Simul. Model. Pract. Theory. [CrossRef]
- Yu, Y.; Li, W.; Sheng, D.; Chen, J. A novel sensor fault diagnosis method based on Modified Ensemble Empirical Mode Decomposition and Probabilistic Neural Network. Measurement 2015, 68, 328–336. [Google Scholar] [CrossRef]
- Wu, L.; Yao, B.; Peng, Z.; Guan, Y. Fault Diagnosis of Roller Bearings Based on a Wavelet Neural Network and Manifold Learning. Appl. Sci. 2017, 7, 158. [Google Scholar] [CrossRef]
- Zhao, Z.; Xu, Q.; Jia, M. Improved shuffled frog leaping algorithm-based BP neural network and its application in bearing early fault diagnosis. Neural Comput. Appl. 2016, 27, 375–385. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, W.; Tang, Z.; Chen, Y. Multi-Sensor Data Fusion Using a Relevance Vector Machine Based on an Ant Colony for Gearbox Fault Detection. Sensors 2015, 15, 21857–21875. [Google Scholar] [CrossRef]
- Qi, G.; Zhu, Z.; Erqinhu, K.; Chen, Y.; Chai, Y.; Sun, J. Fault-diagnosis for reciprocating compressors using big data and machine learning. Simul. Model. Pract. Theory 2018, 80, 104–127. [Google Scholar] [CrossRef]
- Guo, S.; Yang, T.; Gao, W.; Zhang, C.; Zhang, Y. An Intelligent Fault Diagnosis Method for Bearings with Variable Rotating Speed Based on Pythagorean Spatial Pyramid Pooling CNN. Sensors 2018, 18, 3857. [Google Scholar] [CrossRef]
- Xie, J.; Du, G.; Shen, C.; Chen, N.; Chen, L.; Zhu, Z. An End-to-End Model Based on Improved Adaptive Deep Belief Network and Its Application to Bearing Fault Diagnosis. IEEE Access 2018, 6, 63584–63596. [Google Scholar] [CrossRef]
- Lei, J.; Liu, C.; Jiang, D. Fault diagnosis of wind turbine based on Long Short-term memory networks. Renew. Energy 2019, 133, 422–432. [Google Scholar] [CrossRef]
- Ben Ali, J.; Fnaiech, N.; Saidi, L.; Chebel-Morello, B.; Fnaiech, F. Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals. Appl. Acoust. 2015, 89, 16–27. [Google Scholar] [CrossRef]
- Jiang, L.; Yin, H.; Li, X.; Tang, S. Fault Diagnosis of Rotating Machinery Based on Multisensor Information Fusion Using SVM and Time-Domain Features. Shock Vib. 2014, 2014, 1–8. [Google Scholar] [CrossRef]
- Su, L.; Ma, L.; Qin, N.; Huang, D.; Kemp, A.H. Fault Diagnosis of High-Speed Train Bogie by Residual-Squeeze Net. IEEE Trans. Ind. Inform. 2019, 15, 3856–3863. [Google Scholar] [CrossRef]
- Yang, J.; Guo, Y.; Zhao, W. Long short-term memory neural network based fault detection and isolation for electro-mechanical actuators. Neurocomputing 2019, 360, 85–96. [Google Scholar] [CrossRef]
- Dai, J.; Song, H.; Sheng, G.; Jiang, X. Dissolved gas analysis of insulating oil for power transformer fault diagnosis with deep belief network. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 2828–2835. [Google Scholar] [CrossRef]
- Jiang, G.; He, H.; Xie, P.; Tang, Y. Stacked Multilevel-Denoising Autoencoders: A New Representation Learning Approach for Wind Turbine Gearbox Fault Diagnosis. IEEE Trans. Instrum. Meas. 2017, 66, 2391–2402. [Google Scholar] [CrossRef]
- Illias, H.A.; Chai, X.R.; Abu Bakar, A.H. Hybrid modified evolutionary particle swarm optimisation-time varying acceleration coefficient-artificial neural network for power transformer fault diagnosis. Measurement 2016, 90, 94–102. [Google Scholar] [CrossRef]
- Alnaqi, A.A.; Moayedi, H.; Shahsavar, A.; Nguyen, T.K. Prediction of energetic performance of a building integrated photovoltaic/thermal system thorough artificial neural network and hybrid particle swarm optimization models. Energy Convers. Manag. 2019, 183, 137–148. [Google Scholar] [CrossRef]
- Liao, Y.; Zhang, L.; Li, W. Regrouping particle swarm optimization based variable neural network for gearbox fault diagnosis. J. Intell. Fuzzy Syst. 2018, 34, 3671–3680. [Google Scholar] [CrossRef]
- Chatterjee, S.; Sarkar, S.; Hore, S.; Dey, N.; Ashour, A.S.; Balas, V.E. Particle swarm optimization trained neural network for structural failure prediction of multistoried RC buildings. Neural Comput. Appl. 2017, 28, 2005–2016. [Google Scholar] [CrossRef]
- Yang, L.; Chen, H. Fault diagnosis of gearbox based on RBF-PF and particle swarm optimization wavelet neural network. Neural Comput. Appl. 2019, 31, 4463–4478. [Google Scholar] [CrossRef]
- Li, S.; Liu, G.; Tang, X.; Lu, J.; Hu, J. An Ensemble Deep Convolutional Neural Network Model with Improved D-S Evidence Fusion for Bearing Fault Diagnosis. Sensors 2017, 17, 1729. [Google Scholar] [CrossRef] [PubMed]
- Hui, K.H.; Ooi, C.S.; Lim, M.H.; Leong, M.S. A hybrid artificial neural network with Dempster-Shafer theory for automated bearing fault diagnosis. J. VibroEng. 2016, 18, 4409–4418. [Google Scholar] [CrossRef]
- Deng, Y. Deng entropy. Chaos Solitons Fractals 2016, 91, 549–553. [Google Scholar] [CrossRef]
- Jiroušek, R.; Shenoy, P.P. A new definition of entropy of belief functions in the Dempster–Shafer theory. Int. J. Approx. Reason. 2018, 92, 49–65. [Google Scholar] [CrossRef]
- Pan, L.; Deng, Y. A new belief entropy to measure uncertainty of basic probability assignments based on belief function and plausibility function. Entropy 2018, 20, 842. [Google Scholar] [CrossRef]
- Cui, H.; Liu, Q.; Zhang, J.; Kang, B. An improved deng entropy and its application in pattern recognition. IEEE Access 2019, 7, 18284–18292. [Google Scholar] [CrossRef]
- Jiang, W.; Wei, B.; Xie, C.; Zhou, D. An evidential sensor fusion method in fault diagnosis. Adv. Mech. Eng. 2016, 8, 1687814016641820. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, D.; Xu, S.; He, Z. A weighted belief entropy-based uncertainty measure for multi-sensor data fusion. Sensors 2017, 17, 928. [Google Scholar] [CrossRef]
- Wang, Z.; Xiao, F. An improved multisensor data fusion method and its application in fault diagnosis. IEEE Access 2019, 7, 3928–3937. [Google Scholar] [CrossRef]
- Xiao, F.; Qin, B. A weighted combination method for conflicting evidence in multi-sensor data fusion. Sensors 2018, 18, 1487. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Han, T.; Tan, A.C.C.; Lin, T.R. Fault Diagnosis System of Induction Motors Based on Multiscale Entropy and Support Vector Machine with Mutual Information Algorithm. Shock Vib. 2016, 2016, 1–12. [Google Scholar] [CrossRef]
- Ai, Y.-T.; Guan, J.-Y.; Fei, C.-W.; Tian, J.; Zhang, F.-L. Fusion information entropy method of rolling bearing fault diagnosis based on n-dimensional characteristic parameter distance. Mech. Syst. Signal Process. 2017, 88, 123–136. [Google Scholar] [CrossRef]
- Zhu, K.; Song, X.; Xue, D. A roller bearing fault diagnosis method based on hierarchical entropy and support vector machine with particle swarm optimization algorithm. Measurement 2014, 47, 669–675. [Google Scholar] [CrossRef]
- Boudiaf, A.; Moussaoui, A.; Dahane, A.; Atoui, I. A Comparative Study of Various Methods of Bearing Faults Diagnosis Using the Case Western Reserve University Data. J. Fail. Anal. Prev. 2016, 16, 271–284. [Google Scholar] [CrossRef]
- Feng, Z.; Qin, S.; Liang, M. Time–frequency analysis based on Vold-Kalman filter and higher order energy separation for fault diagnosis of wind turbine planetary gearbox under nonstationary conditions. Renew. Energy 2016, 85, 45–56. [Google Scholar] [CrossRef]
- Gai, J.; Hu, Y.; Shen, J. A Bearing Performance Degradation Modeling Method Based on EMD-SVD and Fuzzy Neural Network. Shock Vib. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Bin, G.F.; Gao, J.J.; Li, X.J.; Dhillon, B.S. Early fault diagnosis of rotating machinery based on wavelet packets—Empirical mode decomposition feature extraction and neural network. Mech. Syst. Signal Process. 2012, 27, 696–711. [Google Scholar] [CrossRef]
- Lv, Y.; Yuan, R.; Song, G. Multivariate empirical mode decomposition and its application to fault diagnosis of rolling bearing. Mech. Syst. Signal Process. 2016, 81, 219–234. [Google Scholar] [CrossRef]
- Zhang, Q.; Gao, J.; Dong, H.; Mao, Y. WPD and DE/BBO-RBFNN for solution of rolling bearing fault diagnosis. Neurocomputing 2018, 312, 27–33. [Google Scholar] [CrossRef]
- Zhao, L.-Y.; Wang, L.; Yan, R.-Q. Rolling bearing fault diagnosis based on wavelet packet decomposition and multi-scale permutation entropy. Entropy 2015, 17, 6447–6461. [Google Scholar] [CrossRef]
- Mahamad, A.K.; Saon, S.; Hiyama, T. Predicting remaining useful life of rotating machinery based artificial neural network. Comput. Math. Appl. 2010, 60, 1078–1087. [Google Scholar] [CrossRef]
- Ben Ali, J.; Chebel-Morello, B.; Saidi, L.; Malinowski, S.; Fnaiech, F. Accurate bearing remaining useful life prediction based on Weibull distribution and artificial neural network. Mech. Syst. Signal Process. 2015, 56, 150–172. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, S.; Li, W. Bearing performance degradation assessment using long short-term memory recurrent network. Comput. Ind. 2019, 106, 14–29. [Google Scholar] [CrossRef]
- Bottou, L. Stochastic Gradient Descent Tricks. In Neural Networks: Tricks of the Trade, 2nd ed.; Montavon, G., Orr, G.B., Müller, K.-R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; pp. 421–436. ISBN 978-3-642-35289-8. [Google Scholar]
- Rehman, M.Z.; Nawi, N.M. The Effect of Adaptive Momentum in Improving the Accuracy of Gradient Descent Back Propagation Algorithm on Classification Problems. In Proceedings of the Software Engineering and Computer Systems; Springer: Berlin/Heidelberg, Germany, 2011; pp. 380–390. [Google Scholar]
- Dozat, T. Incorporating Nesterov Momentum into Adam. In Proceedings of the International Conference on Learning Representations, San Juan, Philippines, 2–4 May 2016; pp. 1–6. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science (MHS’95), Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Huang, H.; Qin, H.; Hao, Z.; Lim, A. Example-based learning particle swarm optimization for continuous optimization. Inf. Sci. 2012, 182, 125–138. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A Modified Particle Swarm Optimizer; IEEE: Anchorage, AK, USA, 1998; pp. 69–73. [Google Scholar]
- Deng, W.; Yao, R.; Zhao, H.; Yang, X.; Li, G. A novel intelligent diagnosis method using optimal LS-SVM with improved PSO algorithm. Soft Comput. 2019, 23, 2445–2462. [Google Scholar] [CrossRef]
- Janocha, K.; Czarnecki, W.M. On loss functions for deep neural networks in classification. arXiv 2017, arXiv:1702.05659. [Google Scholar] [CrossRef]
- Dempster, A.P. Upper and Lower Probabilities Induced by a Multivalued Mapping. In Classic Works of the Dempster-Shafer Theory of Belief Functions; Yager, R.R., Liu, L., Eds.; Studies in Fuzziness and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2008; pp. 57–72. ISBN 978-3-540-44792-4. [Google Scholar]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976; ISBN 978-0-691-10042-5. [Google Scholar]
- Murphy, C.K. Combining belief functions when evidence conflicts. Decis. Support Syst. 2000, 29, 1–9. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center Website. Available online: https://csegroups.case.edu/bearingdatacenter/pages/welcome-case-western-reserve-university-bearing-data-center-website (accessed on 30 July 2019).

| Serial Number | Feature Name | Formula |
|---|---|---|
| 1 | Root mean square (RMS) | |
| 2 | Standard deviation (STD) | |
| 3 | Peak | |
| 4 | Root mean square entropy estimator (RMSEE) | |
| 5 | Waveform entropy (WFE) | |
| 6 | Kurtosis | |
| 7 | Skewness | |
| 8 | Crest factor (CRF) | |
| 9 | Impulse factor (IMF) |
| Noise Location | Reason | Explanation |
|---|---|---|
| Mechanical equipment | Eddy noise | Increased external air velocity causes eddies around machinery. |
| Rotating noise | The vibration force of rotating machinery deviates easily from the normal value when encountering strong air flow. | |
| Energy shortage | Energy issues (for example, oil level below average) cause large levels of noise pollution. | |
| Impact noise | Large levels of noise pollution caused by impacts. | |
| Other reasons | Suddenly increasing the operating power of mechanical equipment, manual operation of mechanical equipment. | |
| Vibration sensor | Temperature factor | In general, the higher the temperature, the greater the measurement error. |
| Resonant frequency | The closer the vibration frequency of the machine is to the value of the resonance frequency, the greater the measurement error. | |
| Placement deviation | Vibration sensors generally get acceleration sensing data in three directions. The larger the deviation in the placement direction, the greater the measurement error. | |
| Original error | Different types of vibration sensors have different original errors. | |
| Other environmental factors | Under the condition of a strong electrostatic field, alternating magnetic field, or nuclear radiation, the measurement error may become larger. |
| Fault Type | File Name |
|---|---|
| Normal Baseline Data | 98.mat |
| 48K Drive End Bearing Fault Data (Inner Race) | 110.mat |
| 48K Drive End Bearing Fault Data (Ball) | 123.mat |
| 48K Drive End Bearing Fault Data (Outer Race Orthogonal@3:00) | 149.mat |
| 48K Drive End Bearing Fault Data (Outer Race Centered@6:00) | 136.mat |
| 48K Drive End Bearing Fault Data (Outer Race Opposite@12:00) | 162.mat |
| Eigenvalue | Sliding Window Size | |||||||
|---|---|---|---|---|---|---|---|---|
| 120 | 240 | 360 | 480 | 600 | 720 | 840 | 960 | |
| RMS | 31.67% | 52.11% | 77.22% | 86.11% | 88.67% | 88.11% | 91.33% | 91.89% |
| STD | 30.11% | 52.11% | 76.78% | 85.89% | 88.44% | 88.00% | 91.22% | 91.78% |
| Peak | 30.67% | 41.89% | 63.67% | 73.22% | 76.89% | 79.00% | 81.56% | 80.44% |
| RMSEE | 23.89% | 41.78% | 46.22% | 52.33% | 53.78% | 55.44% | 56.78% | 52.78% |
| WFE | 1.11% | 7.22% | 7.22% | 20.22% | 24.11% | 27.22% | 39.78% | 46.44% |
| Kurtosis | 2.67% | 9.67% | 20.78% | 23.44% | 12.33% | 12.11% | 29.56% | 31.00% |
| Skewness | 1.78% | 6.56% | 15.11% | 20.11% | 23.11% | 22.89% | 22.11% | 23.78% |
| CRF | 0.44% | 2.89% | 1.56% | 3.56% | 10.22% | 10.67% | 10.56% | 14.22% |
| IMF | 1.89% | 6.89% | 8.89% | 21.33% | 12.78% | 12.22% | 10.33% | 12.22% |
| All | 48.33% | 73.00% | 86.11% | 92.33% | 94.33% | 95.78% | 97.22% | 97.89% |
| Eigenvalue | RMS | STD | Peak | RMSEE | WFE | Kurtosis | Skewness | CRF | IMF |
|---|---|---|---|---|---|---|---|---|---|
| RMS | 79.67% | 79.00% | 80.33% | 82.78% | 83.89% | 85.11% | 86.33% | 86.11% | |
| STD | 79.67% | 79.00% | 80.33% | 82.78% | 83.89% | 84.67% | 86.33% | 86.00% | |
| Peak | 79.22% | 79.44% | 80.00% | 82.89% | 83.89% | 84.56% | 85.67% | 85.11% | |
| RMSEE | 79.67% | 81.33% | 79.78% | 82.89% | 83.78% | 85.33% | 86.00% | 86.22% | |
| WFE | 81.78% | 82.33% | 83.11% | 83.22% | 84.00% | 84.33% | 85.44% | 86.00% | |
| Kurtosis | 82.44% | 84.11% | 82.89% | 83.00% | 84.00% | 83.89% | 85.00% | 85.56% | |
| Skewness | 82.22% | 82.56% | 83.22% | 83.44% | 84.44% | 84.44% | 85.44% | 85.00% | |
| CRF | 81.33% | 80.44% | 81.11% | 81.44% | 82.33% | 84.89% | 85.33% | 85.00% | |
| IMF | 82.33% | 83.67% | 82.11% | 82.44% | 83.00% | 83.89% | 84.78% | 86.22% |
| Sliding Window Size | Optimal Feature Combination | Accuracy | |
|---|---|---|---|
| All | Optimal Combination | ||
| 120 | {Kurtosis,RMS,STD,Peak,RMSEE,WFE,Skewness,CRF} | 48.33% | 50.44% |
| 240 | {RMS,STD,Peak,RMSEE,WFE,Kurtosis,Skewness,CRF,IMF} | 73.00% | 73.00% |
| 360 | {RMS,STD,Peak,RMSEE,WFE,Kurtosis,Skewness,CRF} | 86.11% | 86.33% |
| 480 | {WFE,RMS,STD,Peak,RMSEE,Kurtosis,Skewness,CRF,IMF} | 92.33% | 93.00% |
| 600 | {RMS, STD,Peak,RMSEE,WFE,Kurtosis,Skewness,CRF,IMF} | 94.33% | 94.33% |
| 720 | {IMF,RMS,STD,Peak,RMSEE,WFE,Kurtosis,Skewness} | 95.78% | 96.44% |
| 840 | {Skewness,RMS,STD,Peak,RMSEE,WFE,Kurtosis,CRF,IMF} | 97.22% | 97.67% |
| 960 | {RMS,STD,Peak,RMSEE,WFE,Kurtosis,Skewness,CRF,IMF} | 97.89% | 97.89% |
| Parameter | Range Interval/Value |
|---|---|
| Number of hidden layers | 1 |
| Number of hidden layer units | [10, 100] |
| Learning rate | [0.0001, 0.1] |
| Momentum parameter | [0.001, 0.999] |
| RMSprop parameter | [0.001, 0.999] |
| Number of Particles | Learning Rate | Momentum Parameter | RMSprop Parameter | Number of Hidden Layer Neurons | Loss Value | Accuracy |
|---|---|---|---|---|---|---|
| 10 | 0.021404 | 0.999 | 0.999 | 100 | 0.372830 | 89.22% |
| 20 | 0.007614 | 0.609325 | 0.658986 | 58 | 0.479214 | 89.44% |
| 30 | 0.006649 | 0.573852 | 0.966601 | 81 | 0.464076 | 89.89% |
| 40 | 0.008156 | 0.467269 | 0.989776 | 77 | 0.467528 | 89.22% |
| 50 | 0.014367 | 0.998993 | 0.999 | 90 | 0.347928 | 90.11% |
| 60 | 0.010740 | 0.999 | 0.999 | 81 | 0.349434 | 89.67% |
| Eigenvalue | Sliding Window Size | |||||||
|---|---|---|---|---|---|---|---|---|
| 120 | 240 | 360 | 480 | 600 | 720 | 840 | 960 | |
| RMS | 40.00% | 58.89% | 78.33% | 87.11% | 89.22% | 88.78% | 91.56% | 92.00% |
| STD | 41.22% | 64.22% | 78.00% | 86.44% | 89.22% | 88.56% | 91.78% | 92.11% |
| Peak | 42.67% | 58.11% | 68.00% | 76.33% | 77.44% | 81.11% | 82.22% | 81.78% |
| RMSEE | 33.00% | 47.67% | 59.44% | 62.44% | 70.89% | 70.89% | 72.44% | 75.33% |
| WFE | 7.33% | 10.67% | 20.56% | 30.33% | 32.33% | 42.56% | 47.44% | 49.89% |
| Kurtosis | 5.89% | 11.44% | 24.33% | 25.67% | 21.00% | 23.11% | 41.44% | 47.00% |
| Skewness | 3.22% | 11.44% | 19.78% | 20.44% | 23.56% | 24.11% | 23.56% | 30.22% |
| CRF | 1.11% | 4.89% | 7.89% | 20.11% | 21.78% | 11.44% | 12.56% | 15.67% |
| IMF | 4.11% | 10.33% | 20.00% | 23.89% | 14.78% | 14.22% | 34.78% | 32.56% |
| All | 54.67% | 78.44% | 90.11% | 93.11% | 96.22% | 97.22% | 97.89% | 98.67% |
| PSO-ANN Model | Fault Type | |||||
|---|---|---|---|---|---|---|
| Normal State | Inner Race Fault | Rolling Element Fault | Outer Race Orthogonal@3:00 Fault | Outer Race Centered@6:00 Fault | Outer Race Opposite@12:00 Fault | |
| STD | 0 | 0.2979 | 0.0053 | 0.1500 | 0.2961 | 0.2507 |
| Peak | 0 | 0.267 | 0.0608 | 0.1630 | 0.2214 | 0.2878 |
| RMSEE | 0 | 0.2763 | 0.0846 | 0.1170 | 0.2759 | 0.2462 |
| Skewness | 0.0926 | 0.0674 | 0.1257 | 0.2928 | 0.227 | 0.1945 |
| Parameter Name | PSO-ANN Trained by a Single Feature | |||
|---|---|---|---|---|
| STD | Peak | RMSEE | Skewness | |
| PRE | 0.2941 | 0.2623 | 0.2672 | 0.1789 |
| CRD | 0.2934 | 0.2616 | 0.2665 | 0.1785 |
| MUN | 7.3255 | 8.8422 | 8.9058 | 11.2462 |
| MCRD | 2.1493 | 2.3132 | 2.3734 | 2.0073 |
| NMCRD | 0.243 | 0.2616 | 0.2684 | 0.227 |
| Fusion Times of DS | Fault Type | |||||
|---|---|---|---|---|---|---|
| Normal State | Inner Race Fault | Rolling Element Fault | Outer Race Orthogonal@3:00 Fault | Outer Race Centered@6:00 Fault | Outer Race Opposite@12:00 Fault | |
| 0 | 0.021 | 0.2317 | 0.0684 | 0.1769 | 0.2555 | 0.2465 |
| 1 | 0.002 | 0.2484 | 0.0217 | 0.1448 | 0.302 | 0.2811 |
| 2 | 0.0001 | 0.249 | 0.0065 | 0.1109 | 0.3338 | 0.2997 |
| 3 | 0 | 0.2435 | 0.0019 | 0.0828 | 0.36 | 0.3118 |
| Method | Sliding Window Size | |||||||
|---|---|---|---|---|---|---|---|---|
| 120 | 240 | 360 | 480 | 600 | 720 | 840 | 960 | |
| Basic DS | 67.89% | 82.00% | 92.44% | 95.89% | 97.44% | 97.89% | 98.89% | 98.89% |
| Literature [30] | 67.56% | 82.56% | 92.44% | 96.22% | 97.44% | 97.89% | 98.89% | 98.78% |
| Literature [31] | 68.44% | 81.78% | 92.33% | 96.22% | 97.44% | 98.00% | 98.78% | 98.89% |
| Literature [32] | 68.22% | 81.67% | 92.33% | 96.22% | 97.33% | 98.00% | 98.78% | 98.89% |
| We Proposed | 68.33% | 82.67% | 92.44% | 96.44% | 97.44% | 98.22% | 99.00% | 99.00% |
| Model | Sliding Window Size | |||||||
|---|---|---|---|---|---|---|---|---|
| 120 | 240 | 360 | 480 | 600 | 720 | 840 | 960 | |
| KNN | 57.78% | 74.45% | 84.33% | 90.11% | 93.11% | 94.67% | 95.44% | 96.44% |
| Decision tree | 57.22% | 75.44% | 86.89% | 91.44% | 94.00% | 95.67% | 97.11% | 98.22% |
| Random forest | 61.89% | 78.00% | 89.33% | 94.00% | 96.44% | 97.33% | 97.78% | 98.44% |
| Naive Bayes | 62.11% | 76.33% | 83.67% | 90.56% | 93.78% | 95.00% | 97.44% | 98.11% |
| ANN | 50.44% | 73.00% | 86.33% | 93.00% | 94.33% | 96.44% | 97.67% | 97.89% |
| SVM | 63.67% | 78.89% | 88.00% | 92.67% | 95.11% | 96.78% | 97.78% | 98.00% |
| LSTM | 57.89% | 72.89% | 80.11% | 84.22% | 88.33% | 91.56% | 93.00% | 96.11% |
| PSO-ANN | 54.67% | 78.44% | 90.11% | 93.11% | 96.22% | 97.22% | 97.89% | 98.67% |
| PSO-ANN-DS | 68.33% | 82.67% | 92.44% | 96.44% | 97.44% | 98.22% | 99.00% | 99.00% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, M.; Liu, Z. Research on Mechanical Fault Prediction Method Based on Multifeature Fusion of Vibration Sensing Data. Sensors 2020, 20, 6. https://doi.org/10.3390/s20010006
Huang M, Liu Z. Research on Mechanical Fault Prediction Method Based on Multifeature Fusion of Vibration Sensing Data. Sensors. 2020; 20(1):6. https://doi.org/10.3390/s20010006
Chicago/Turabian StyleHuang, Min, and Zhen Liu. 2020. "Research on Mechanical Fault Prediction Method Based on Multifeature Fusion of Vibration Sensing Data" Sensors 20, no. 1: 6. https://doi.org/10.3390/s20010006
APA StyleHuang, M., & Liu, Z. (2020). Research on Mechanical Fault Prediction Method Based on Multifeature Fusion of Vibration Sensing Data. Sensors, 20(1), 6. https://doi.org/10.3390/s20010006





