An Evidential Framework for Localization of Sensors in Indoor Environments
Abstract
1. Introduction
1.1. Enabling Technologies
1.2. Measurement Techniques
2. An Evidential Framework for Indoor localization
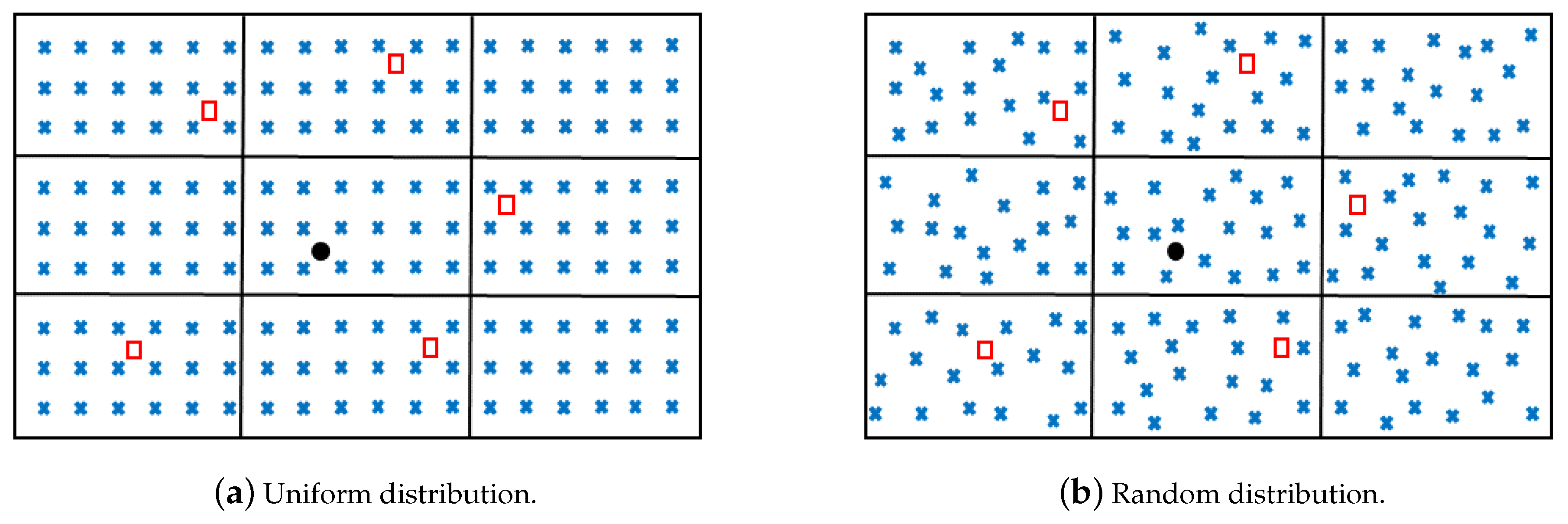
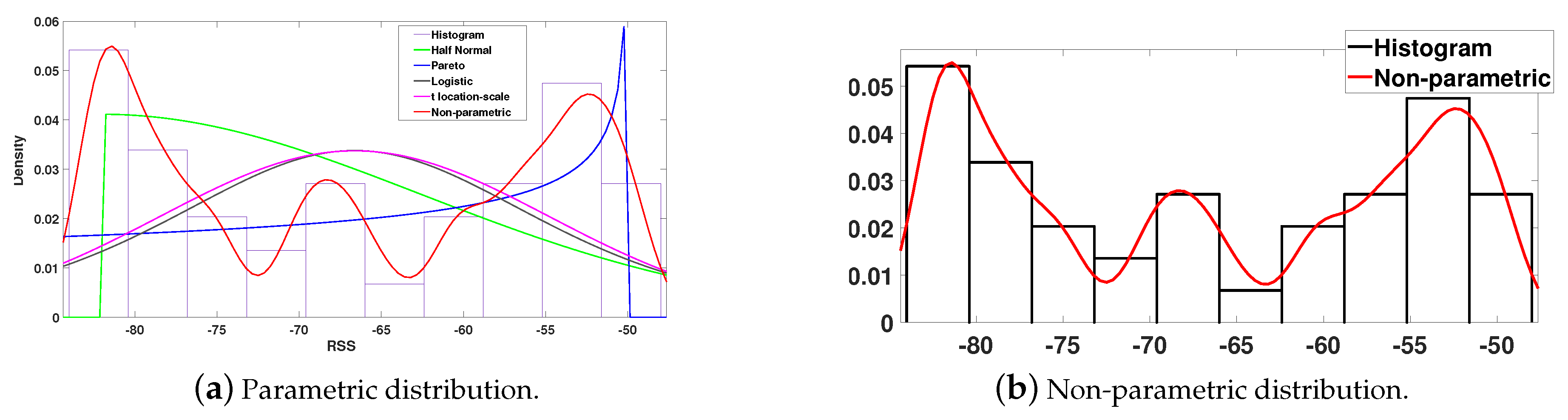
2.1. Statistical Representation of Data
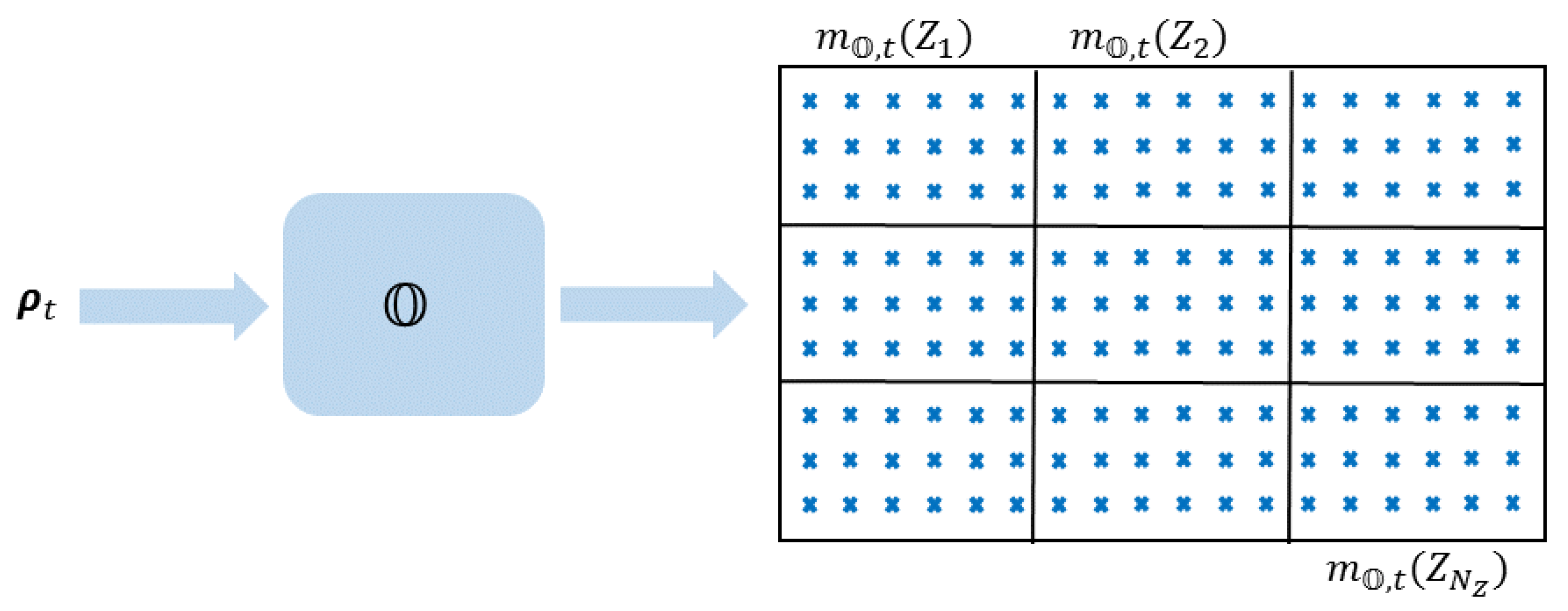
2.2. Mass Assignment
2.3. Discounting Operation
2.3.1. Classical Discounting
2.3.2. Contextual Discounting
2.4. Fusion of Evidence
2.4.1. Dempster’s Rule
2.4.2. Conjunctive Rule
2.4.3. Disjunctive Rule
2.5. Confidence Based Zone Estimation
3. Experimental Results
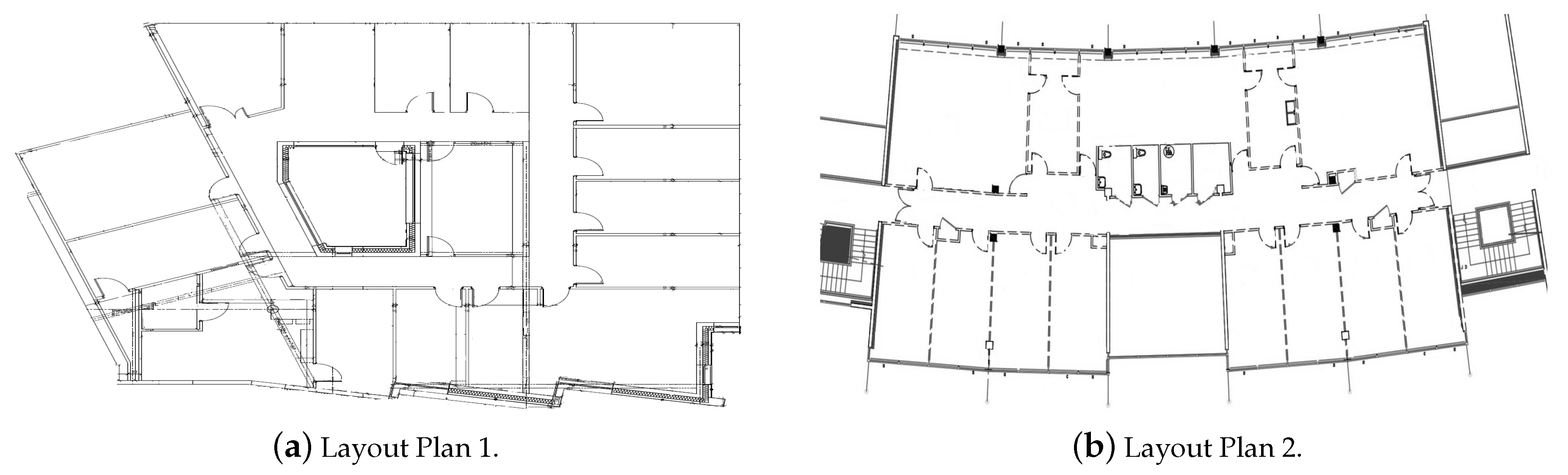
3.1. Experimental Setups
3.1.1. Influence of Discounting and Combination
3.1.2. Influence of Modeling and Reference Positions
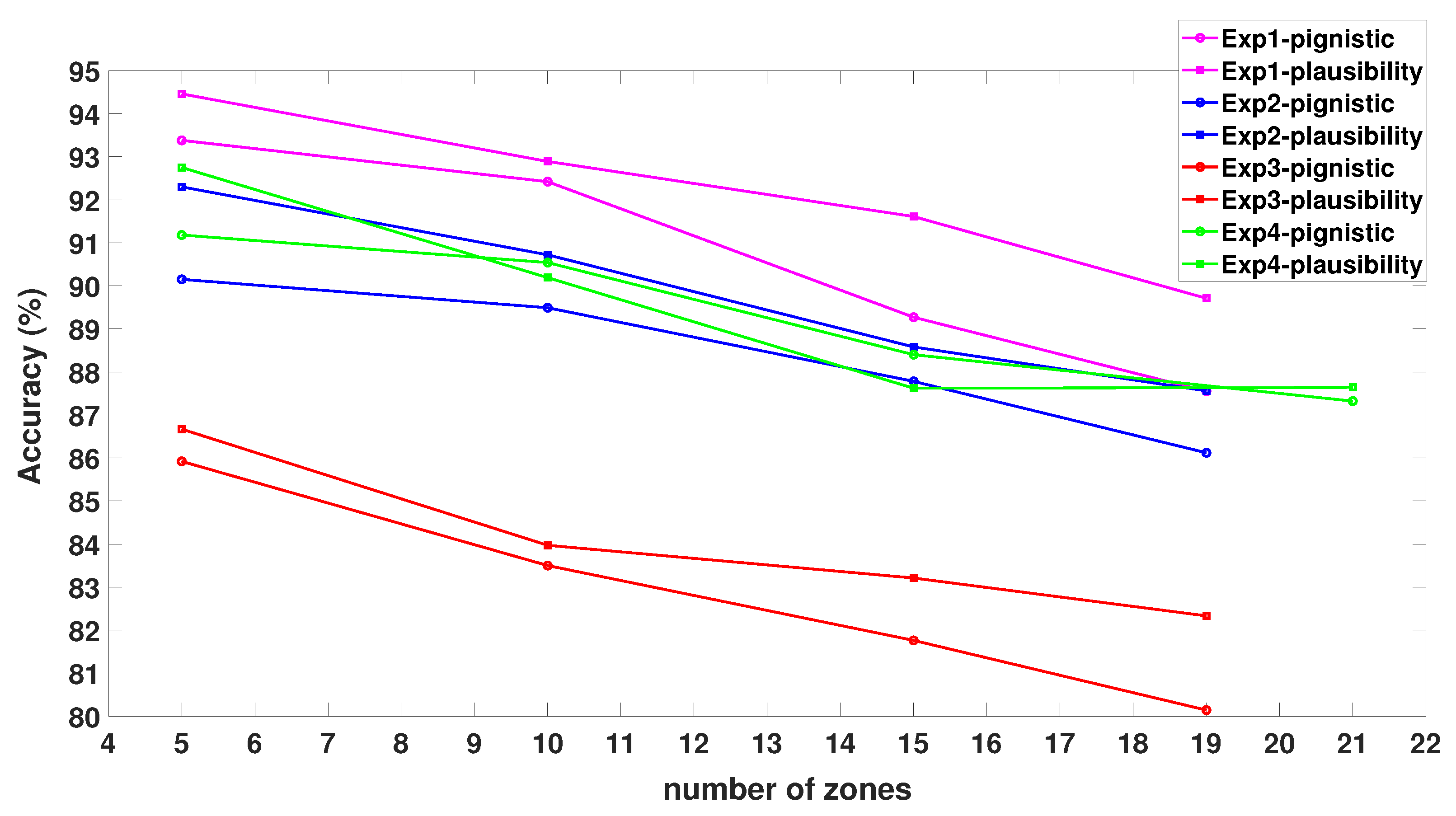
3.1.3. Influence of the Number of Zones and Decision-Making Criteria
3.2. Comparison with Other Techniques
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xiong, H.; Tang, J.; Xu, H.; Zhang, W.; Du, Z. A Robust Single GPS Navigation and Positioning Algorithm Based on Strong Tracking Filtering. IEEE Sens. J. 2018, 18, 290–298. [Google Scholar] [CrossRef]
- Oshin, T.; Poslad, S.; Ma, A. Improving the Energy-Efficiency of GPS Based Location Sensing Smartphone Applications. In Proceedings of the IEEE International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom), Liverpool, UK, 25–27 June 2012; pp. 1698–1705. [Google Scholar]
- Kim, B.H.; Roh, D.K.; Lee, J.M.; Lee, M.H.; Son, K.; Lee, M.; Choi, J.; Han, S. Localization of a mobile robot using images of a moving target. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seoul, Korea, 21–26 May 2001; pp. 253–258. [Google Scholar]
- Ravi, N.; Shankar, P.; Frankel, A.; Elgammal, A.; Iftode, L. Indoor localization using camera phones. In Proceedings of the IEEE Workshop on Mobile Computing Systems and Applications (WMCSA), Orcas Island, WA, USA, 1 August 2005; pp. 1–7. [Google Scholar]
- Hauschildt, D.; Kirchhof, N. Advances in thermal infrared localization: Challenges and solutions. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN), Zurich, Switzerland, 15–17 September 2010; pp. 1–8. [Google Scholar]
- Moreno, L.; Armingol, J.M.; Garrido, S.; De La Escalera, A.; Salichs, M.A. A genetic algorithm for mobile robot localization using ultrasonic sensors. J. Intell. Robotic Syst. 2002, 34, 135–154. [Google Scholar] [CrossRef]
- Shi, G.; Ming, Y. Survey of indoor positioning systems based on ultra-wideband (UWB) technology. In Wireless Communications, Networking and Applications; Springer: New Delhi, India, 2016; pp. 1269–1278. [Google Scholar]
- Zuo, J.; Liu, S.; Xia, H.; Qiao, Y. Multi-Phase Fingerprint Map Based on Interpolation for Indoor Localization Using iBeacons. IEEE Sens. J. 2018, 18, 3351–3359. [Google Scholar] [CrossRef]
- Zou, H.; Jin, M.; Jiang, H.; Xie, L.; Spanos, C.J. WinIPS: WiFi-Based Non-Intrusive Indoor Positioning System With Online Radio Map Construction and Adaptation. IEEE Trans. Wirel. Commun. 2017, 16, 8118–8130. [Google Scholar] [CrossRef]
- Rong, P.; Sichitiu, M.L. Angle of arrival localization for wireless sensor networks. In Proceedings of the IEEE Communications Society on Sensor and Ad Hoc Communications and Networks (SECON), Reston, VA, USA, 25–28 September 2006; pp. 374–382. [Google Scholar]
- Okello, N.; Fletcher, F.; Musicki, D.; Ristic, B. Comparison of recursive algorithms for emitter localisation using TDOA measurements from a pair of UAVs. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1723–1732. [Google Scholar] [CrossRef]
- Zhao, Y.; Fan, X.; Xu, C.Z.; Li, X. Er-crlb: An extended recursive cramér–rao lower bound fundamental analysis method for indoor localization systems. IEEE Trans. Veh. Technol. 2016, 66, 1605–1618. [Google Scholar] [CrossRef]
- Alshamaa, D.; Mourad-Chehade, F.; Honeine, P. Zoning based localization in indoor sensor networks using belief functions theory. In Proceedings of the 2016 IEEE 17th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Edinburgh, UK, 3–6 July 2016; pp. 1–5. [Google Scholar]
- Alshamaa, D.; Mourad-Chehade, F.; Honeine, P. Tracking of Mobile Sensors Using Belief Functions in Indoor Wireless Networks. IEEE Sens. J. 2017, 18, 310–319. [Google Scholar] [CrossRef]
- Alshamaa, D.; Mourad-Chehade, F.; Honeine, P. Localization of sensors in indoor wireless networks: An observation model using WiFi RSS. In Proceedings of the 2018 9th IFIP International Conference on New Technologies, Mobility and Security (NTMS), Paris, France, 26–28 February 2018; pp. 1–5. [Google Scholar]
- Patwari, N.; Ash, J.N.; Kyperountas, S.; Hero, A.O.; Moses, R.L.; Correal, N.S. Locating the nodes: cooperative localization in wireless sensor networks. IEEE Signal Process. Mag. 2005, 22, 54–69. [Google Scholar] [CrossRef]
- Achroufene, A.; Amirat, Y.; Chibani, A. RSS-Based Indoor Localization Using Belief Function Theory. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1163–1180. [Google Scholar] [CrossRef]
- Elkin, C.; Kumarasiri, R.; Rawat, D.B.; Devabhaktuni, V. Localization in wireless sensor networks: A Dempster–Shafer evidence theoretical approach. Ad Hoc Netw. 2017, 54, 30–41. [Google Scholar] [CrossRef]
- Lv, X.; Mourad-Chehade, F.; Snoussi, H. Decentralized localization using radio-fingerprints and accelerometer in WSNs. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 242–257. [Google Scholar] [CrossRef]
- Alshamaa, D.; Mourad-Chehade, F.; Honeine, P. A hierarchical classification method using belief functions. Signal Process. 2018, 148, 68–77. [Google Scholar] [CrossRef]
- Yiu, S.; Dashti, M.; Claussen, H.; Perez-Cruz, F. Wireless RSSI fingerprinting localization. Signal Process. 2017, 131, 235–244. [Google Scholar] [CrossRef]
- Alshamaa, D.; Chkeir, A.; Mourad-Chehade, F. Localization of Elderly People using WiFi: A Comparative Study on Parametric versus Kernel based Approaches. In Proceedings of the 2019 3rd International Conference on Bio-engineering for Smart Technologies (BioSMART), Paris, France, 24–26 April 2019; pp. 1–4. [Google Scholar]
- Alshamaa, D.; Mourad-Chehade, F.; Honeine, P. Decentralized Sensor Localization by Decision Fusion of RSSI and Mobility in Indoor Environments. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Rome, Italy, 3–7 September 2018; pp. 2300–2304. [Google Scholar]
- Elgammal, A.; Duraiswami, R.; Harwood, D.; Davis, L.S. Background and foreground modeling using nonparametric kernel density estimation for visual surveillance. Proc. IEEE 2002, 90, 1151–1163. [Google Scholar] [CrossRef]
- Alshamaa, D.; Mourad-Chehade, F.; Honeine, P. A weighted kernel based hierarchical classification method for zoning of sensors in indoor wireless networks. In Proceedings of the 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Kalamata, Greece, 25–28 June 2018; pp. 1–5. [Google Scholar]
- Alshamaa, D.; Mourad-Chehade, F.; Honeine, P. Decentralized kernel based localization in wireless sensor networks using belief functions. IEEE Sens. J. 2019, 19, 4149–4159. [Google Scholar] [CrossRef]
- Pichon, F.; Denœux, T. The unnormalized Dempster’s rule of combination: A new justification from the Least Commitment Principle and some extensions. J. Automated Reasoning 2010, 45, 61–87. [Google Scholar] [CrossRef]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976; Volume 42. [Google Scholar]
- Klein, J.; Destercke, S.; Colot, O. Idempotent conjunctive and disjunctive combination of belief functions by distance minimization. Int. J. Approximate Reasoning 2018, 92, 32–48. [Google Scholar] [CrossRef]
- Mercier, D.; Lefèvre, É.; Delmotte, F. Belief functions contextual discounting and canonical decompositions. Int. J. Approximate Reasoning 2012, 53, 146–158. [Google Scholar] [CrossRef][Green Version]
- Kurdej, M.; Cherfaoui, V. Conservative, proportional and optimistic contextual discounting in the belief functions theory. In Proceedings of the International Conference on Information Fusion (FUSION), Istanbul, Turkey, 9–12 July 2013; pp. 2012–2018. [Google Scholar]
- Smets, P. Analyzing the combination of conflicting belief functions. Inf. Fusion 2007, 8, 387–412. [Google Scholar] [CrossRef]
- Dempster, A.P. Upper and lower probabilities induced by a multivalued mapping. Ann. Math. Statist. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Giang, P.H. Decision with Dempster–Shafer belief functions: Decision under ignorance and sequential consistency. Int. J. Approximate Reasoning 2012, 53, 38–53. [Google Scholar] [CrossRef]
- Jaffray, J.Y. Linear utility theory for belief functions. Operations Res. Lett. 1989, 8, 107–112. [Google Scholar] [CrossRef]
- Yager, R.R. Decision making under Dempster-Shafer uncertainties. Int. J. General Syst. 1992, 20, 233–245. [Google Scholar] [CrossRef]
- Smets, P.; Kennes, R. The transferable belief model. Artificial Intell. 1994, 66, 191–234. [Google Scholar] [CrossRef]
- Smets, P. Decision Making in a Context where Uncertainty is Represented by Belief Functions. Belief Functions Bus. Decisions 2002, 88, 17–61. [Google Scholar]
- Smets, P. Belief functions: the disjunctive rule of combination and the generalized Bayesian theorem. Int. J. Approximate Reasoning 1993, 9, 1–35. [Google Scholar] [CrossRef]
- Smets, P. Quantifying beliefs by belief functions: an axiomatic justification. In International Joint Conference on Artificial Intelligence; Morgan Kaufmann Publishers Inc.: Chambery, France, 1993; Volume 1, pp. 598–603. [Google Scholar]
- Cuzzolin, F. On the relative belief transform. Int. J. Approximate Reasoning 2012, 53, 786–804. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Z. Belief Function Based Decision Fusion for Decentralized Target Classification in Wireless Sensor Networks. Sensors 2015, 15, 20524–20540. [Google Scholar] [CrossRef]
- Shang, Y.; Rumi, W.; Zhang, Y.; Fromherz, M. Localization from connectivity in sensor networks. IEEE Trans. Parallel Distributed Syst. 2004, 15, 961–974. [Google Scholar] [CrossRef]
| Parameter | Notation | Value | |
|---|---|---|---|
| Layout 1 | Layout 2 | ||
| Number of zones | 19 | 21 | |
| Number of APs | 23 | 38 | |
| Number of measurements per zone | 30 | 30 | |
| Accuracy (%) | Discounting | |||||||
|---|---|---|---|---|---|---|---|---|
| Classical | Contextual | |||||||
| Combination rule | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| Dempster’s | ||||||||
| Conjunctive | ||||||||
| Disjunctive | ||||||||
| Accuracy (%) | Type of Modeling | |||||||
|---|---|---|---|---|---|---|---|---|
| Parametric | KDE | |||||||
| Positions | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| Uniform | ||||||||
| Random | ||||||||
| Technique | Number of Experiment | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Connectivity | 84.17 | 84.05 | 84.42 | 82.56 |
| KNN | 81.88 | 78.24 | 74.19 | 82.31 |
| NN | 84.72 | 84.51 | 81.73 | 84.98 |
| SVM | 85.55 | 83.48 | 82.82 | 84.76 |
| Proposed | 89.71 | 87.65 | 82.33 | 87.64 |
| Technique | Number of Detected APs | |||
|---|---|---|---|---|
| 5 | 10 | 15 | 23 | |
| Connectivity | 65.56 | 69.44 | 76.67 | 84.17 |
| KNN | 70.22 | 74.78 | 77.17 | 81.88 |
| NN | 77.78 | 80.00 | 81.39 | 84.72 |
| SVM | 78.61 | 80.83 | 82.78 | 85.55 |
| Proposed | 82.22 | 83.33 | 85.27 | 89.71 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshamaa, D.; Mourad-Chehade, F.; Honeine, P.; Chkeir, A. An Evidential Framework for Localization of Sensors in Indoor Environments. Sensors 2020, 20, 318. https://doi.org/10.3390/s20010318
Alshamaa D, Mourad-Chehade F, Honeine P, Chkeir A. An Evidential Framework for Localization of Sensors in Indoor Environments. Sensors. 2020; 20(1):318. https://doi.org/10.3390/s20010318
Chicago/Turabian StyleAlshamaa, Daniel, Farah Mourad-Chehade, Paul Honeine, and Aly Chkeir. 2020. "An Evidential Framework for Localization of Sensors in Indoor Environments" Sensors 20, no. 1: 318. https://doi.org/10.3390/s20010318
APA StyleAlshamaa, D., Mourad-Chehade, F., Honeine, P., & Chkeir, A. (2020). An Evidential Framework for Localization of Sensors in Indoor Environments. Sensors, 20(1), 318. https://doi.org/10.3390/s20010318








