Development of an On-Board Measurement System for Railway Vehicle Wheel Flange Wear
Abstract
1. Introduction
1.1. Wheel Wear Prediction Models
1.2. Wheel Flange Wear Measurement Techniques
1.3. Conclusions
2. Materials and Methods
- (1)
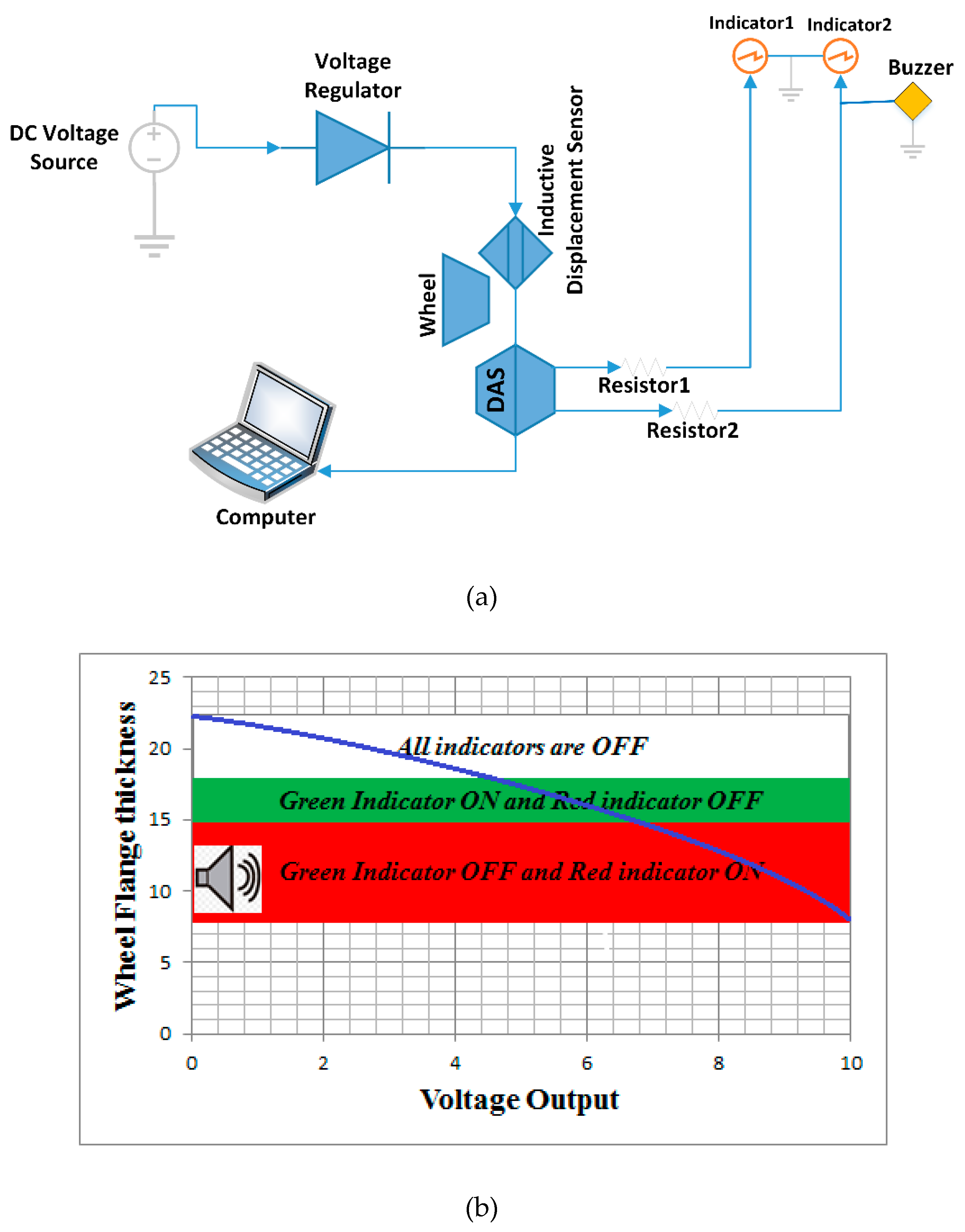
- The wheel flange thickness status data is recorded based using data acquisition system (see Figure 1a). In this mode, the active inductive displacement sensor in proximity to the wheel flange detects the reduction of the wheel flange thickness. The data from the sensor are processed and recorded on a computer. The processing of read data, the settings, and the recordings are done in the LabVIEW software. The data can be displayed in graphical format and/or tabular format. In addition, the data can be analyzed by railway engineers by using their preferred appropriate software.
- (2)
- The measurement output data obtained through the DAQ and LabVIEW codes are visualized in the train cab dashboard by two light emitting diodes based indicators (indicator 1 and indicator 2 as shown in Figure 1) to indicate the status of the wheel flange (see Figure 1). The first indicator notifies the half thickness reduction of a wheel flange (18.5 mm). It uses green color through its light emitting diodes (LEDs). The second indicator displays the minimum dimensions of the wheel flange thickness (15 mm) and the red color from the LEDs is used for this case (e.g., see Figure 1b).
- (3)
- Emergency short time data storage is done in case of the malfunction of the data acquisition system or the computer corruption. The USB cable connects the Arduino board to a computer and transfer data directly to a computer and retains all records. The Arduino code is used to monitor the working operation and the “PLX-DAQ” application software links Arduino code instructions with excel sheet by its macro. Therefore, both mode 2 and mode 3 share common interoperability software and the hardware printed circuit board.
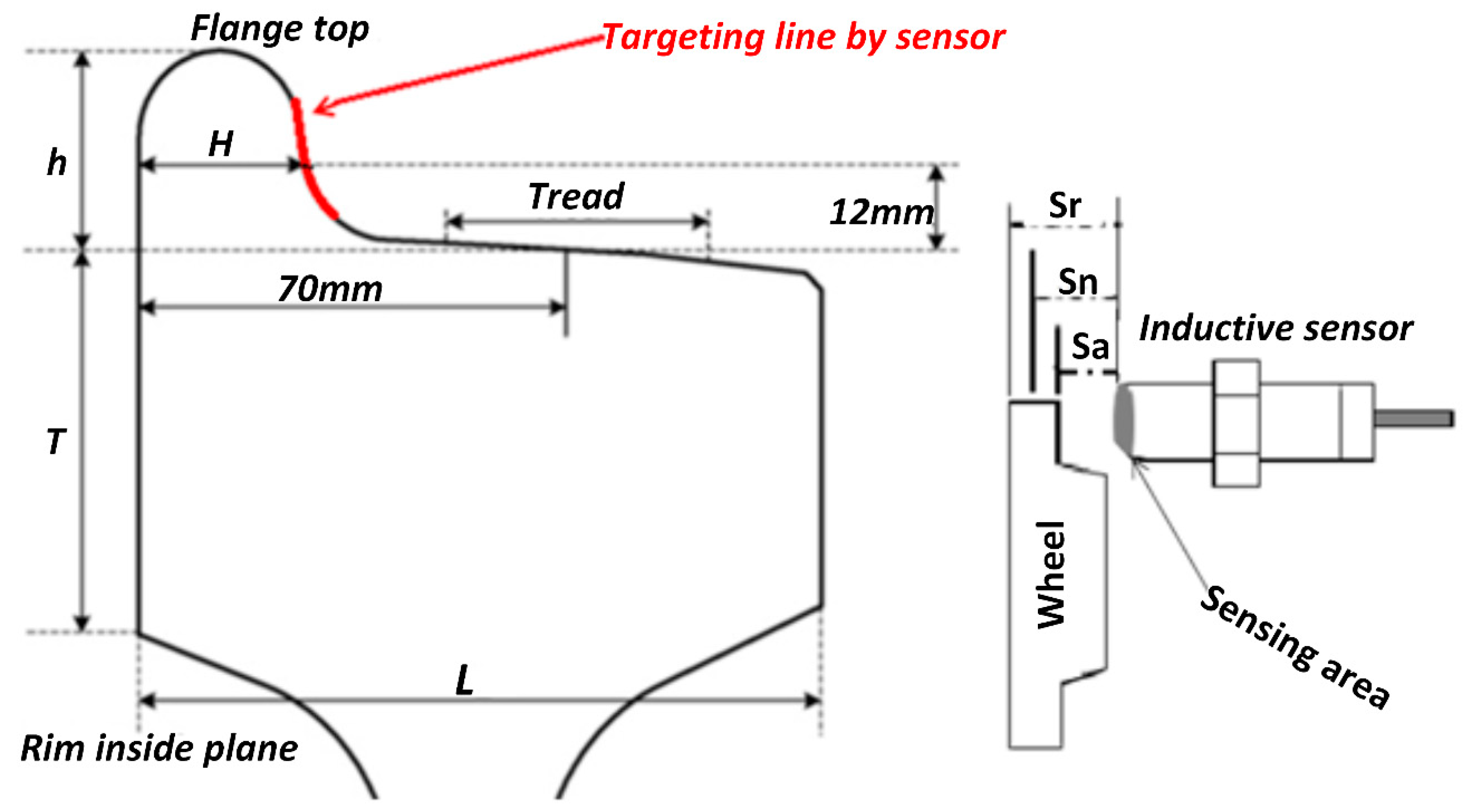
2.1. The Inductive Sensor-Based Measurement Method, Mechanics and Design
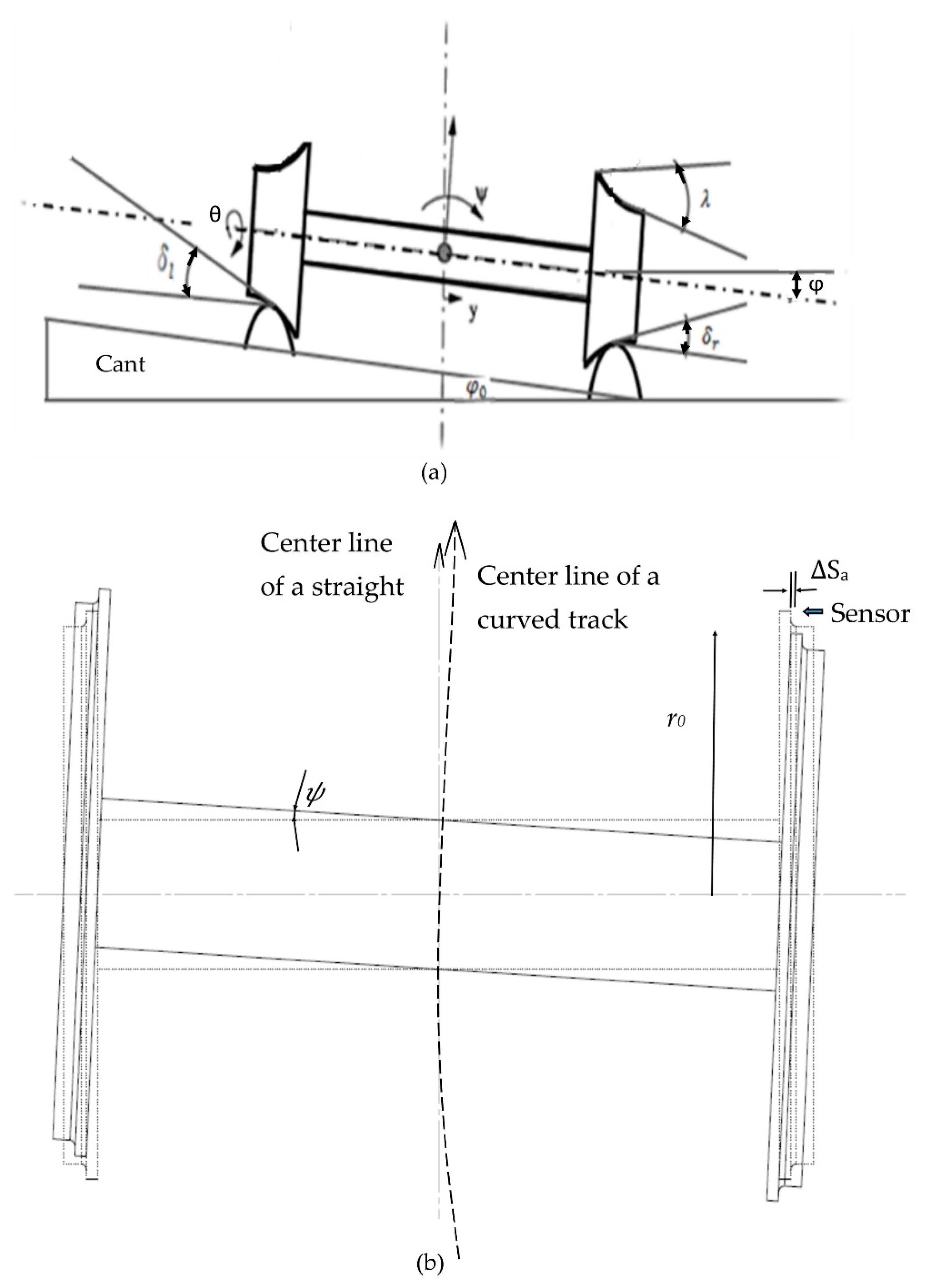
2.1.1. Quantifying the Effect of the Wheelset Dynamics at Curves
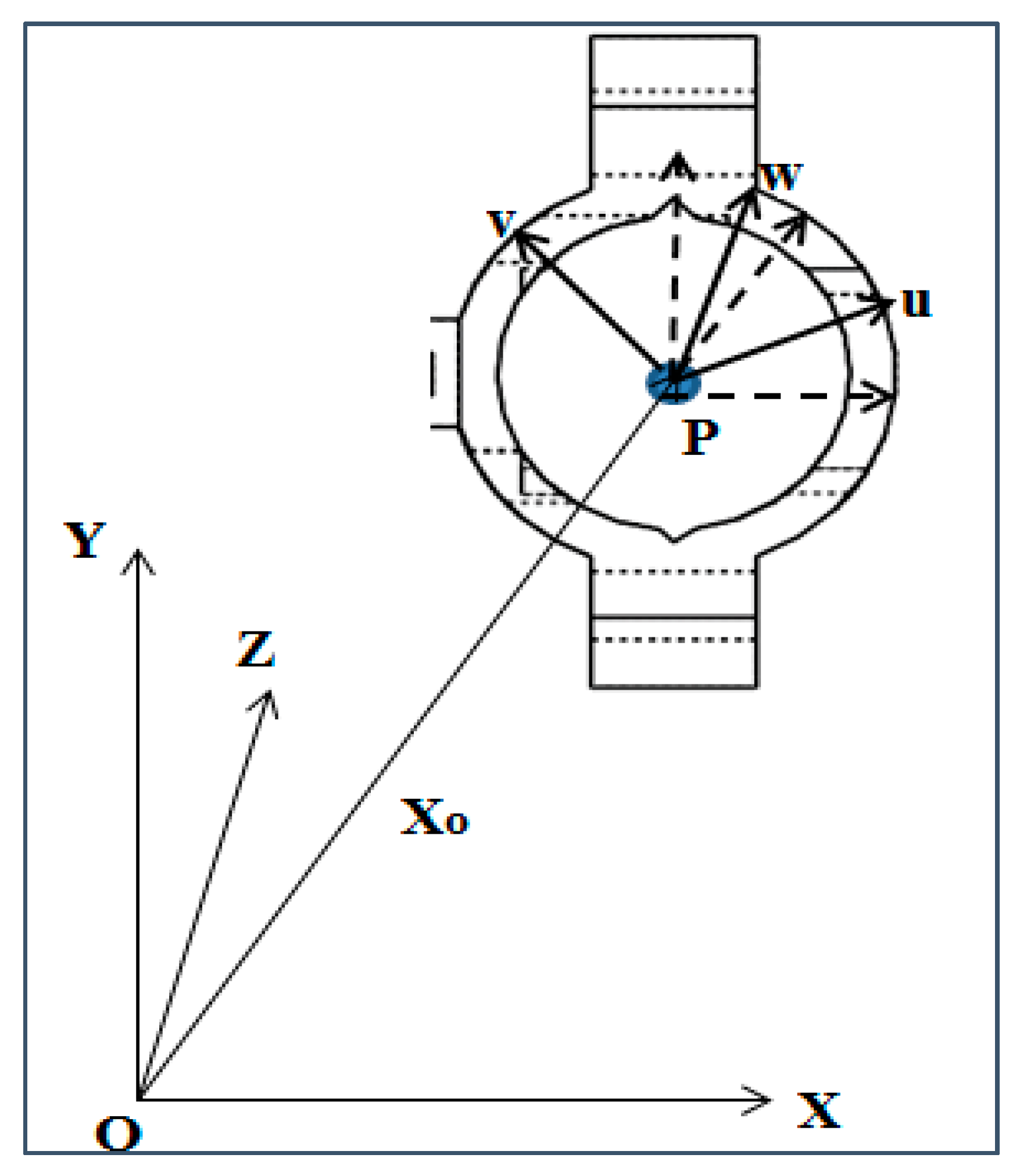
2.1.2. Kinematic Constraints of the Sensor Holding Fixture
2.1.3. CAD Model of the Designed Sensor Holding Fixture
2.2. Laboratory Experiments
3. Results and Discussion
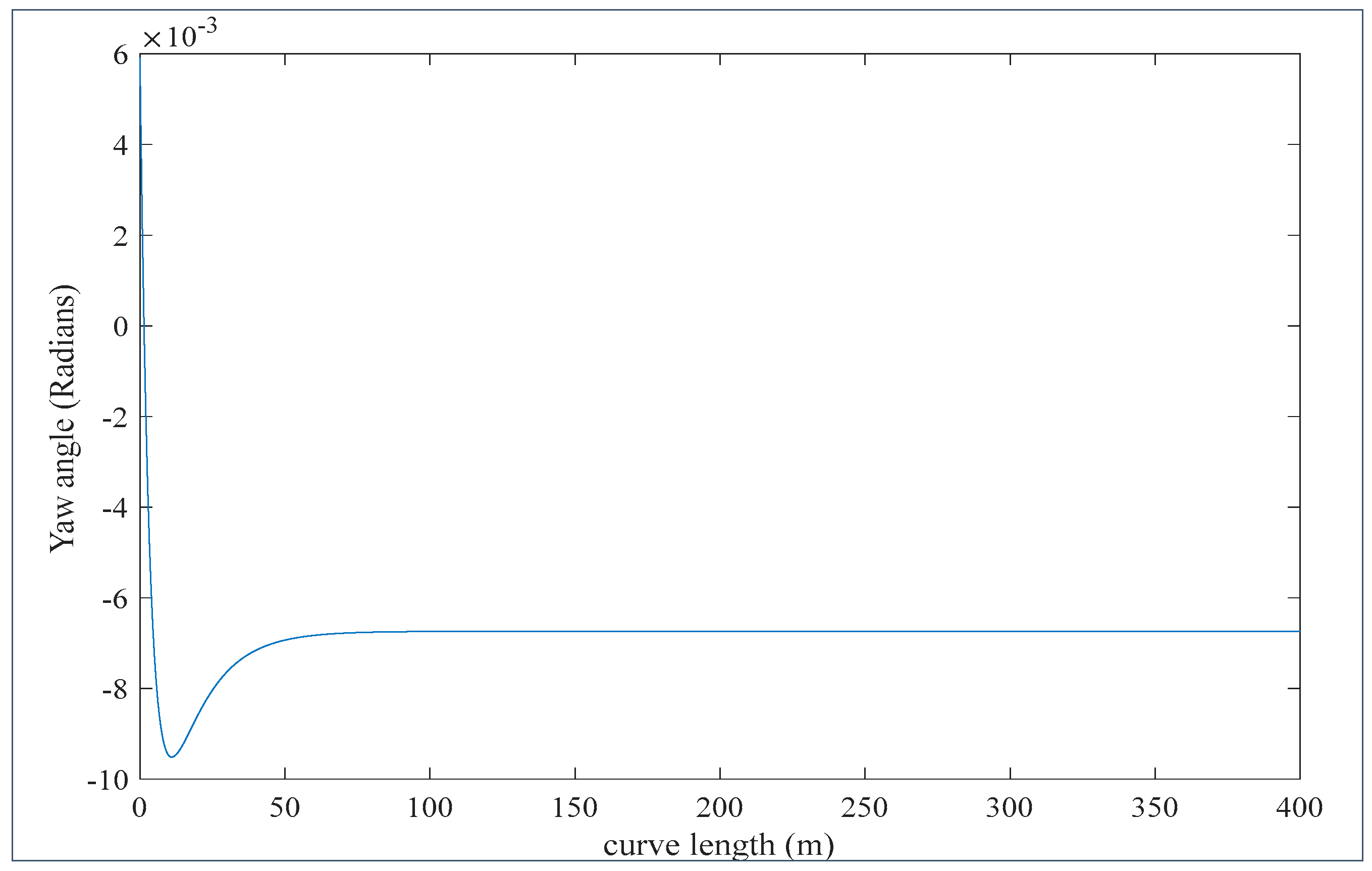
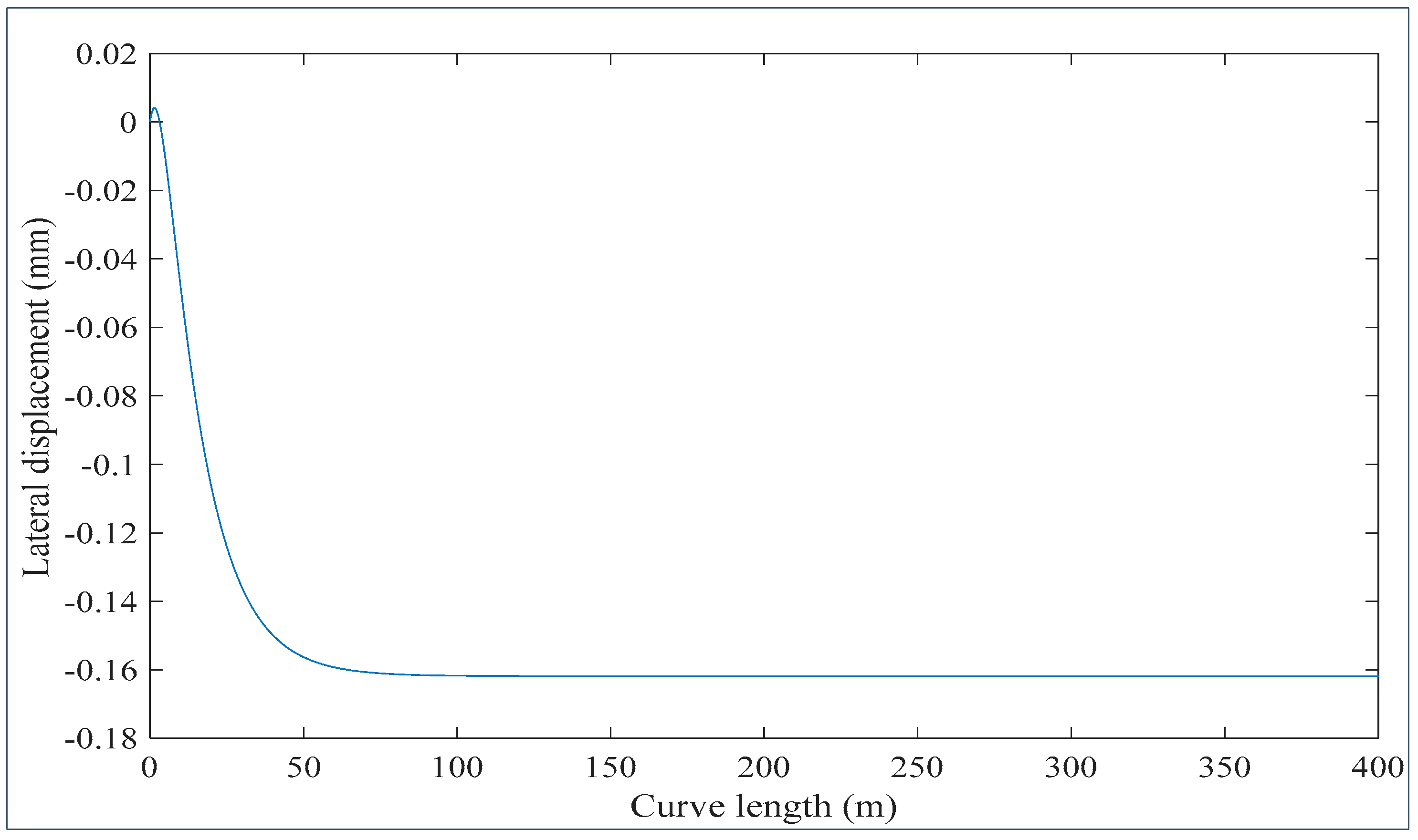
3.1. Wheelset Dynamics Results
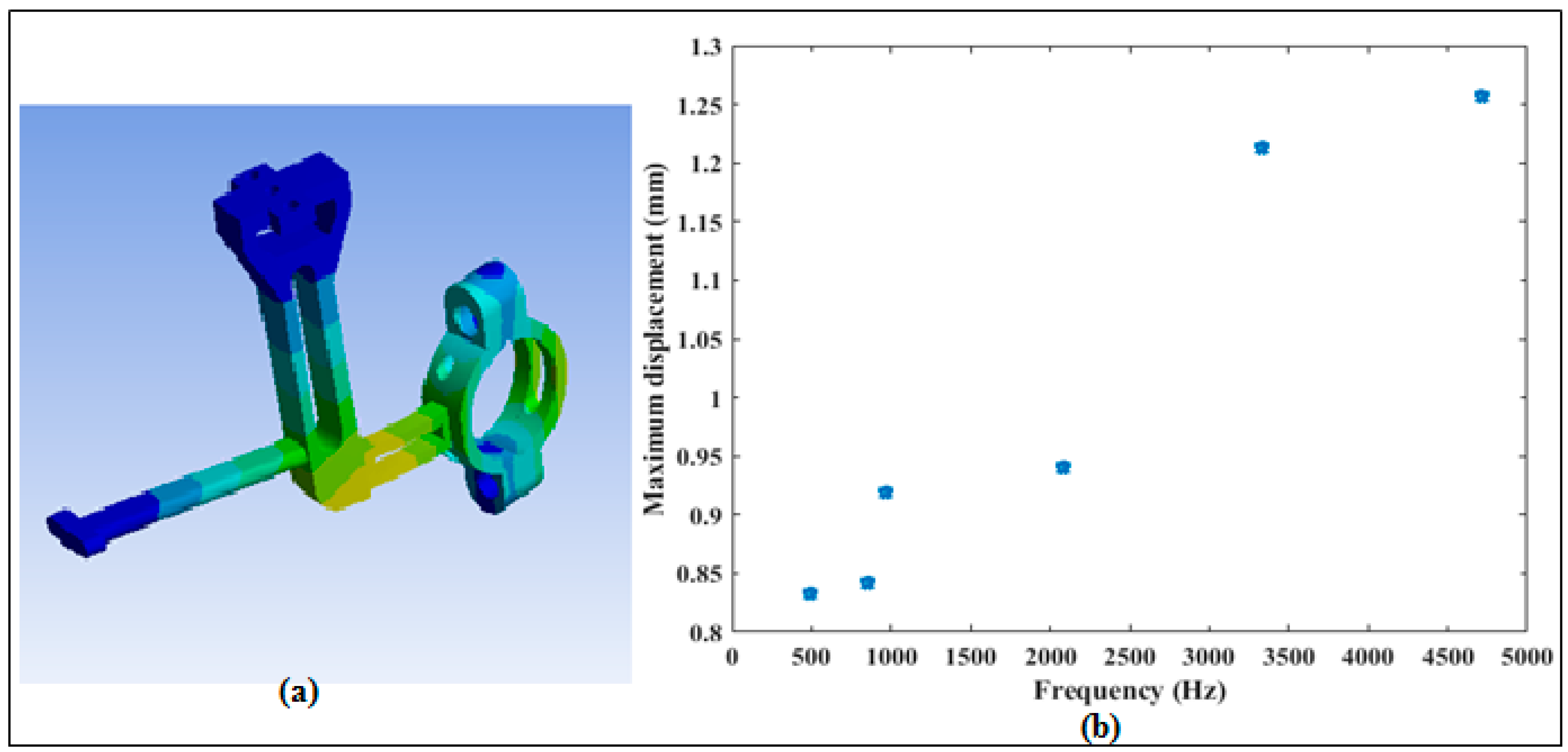
3.2. Fixture Vibration Analysis Using Finite Elements
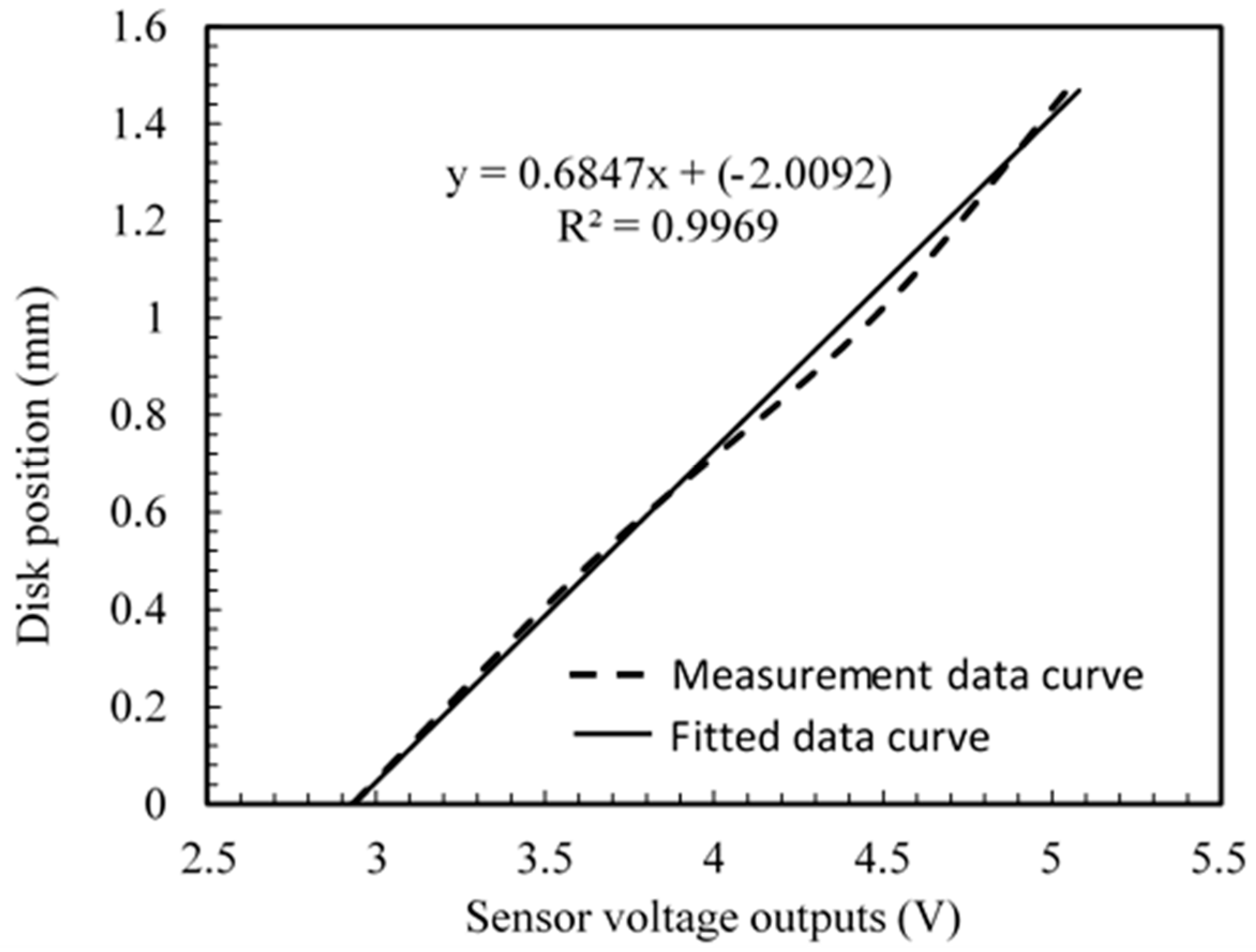
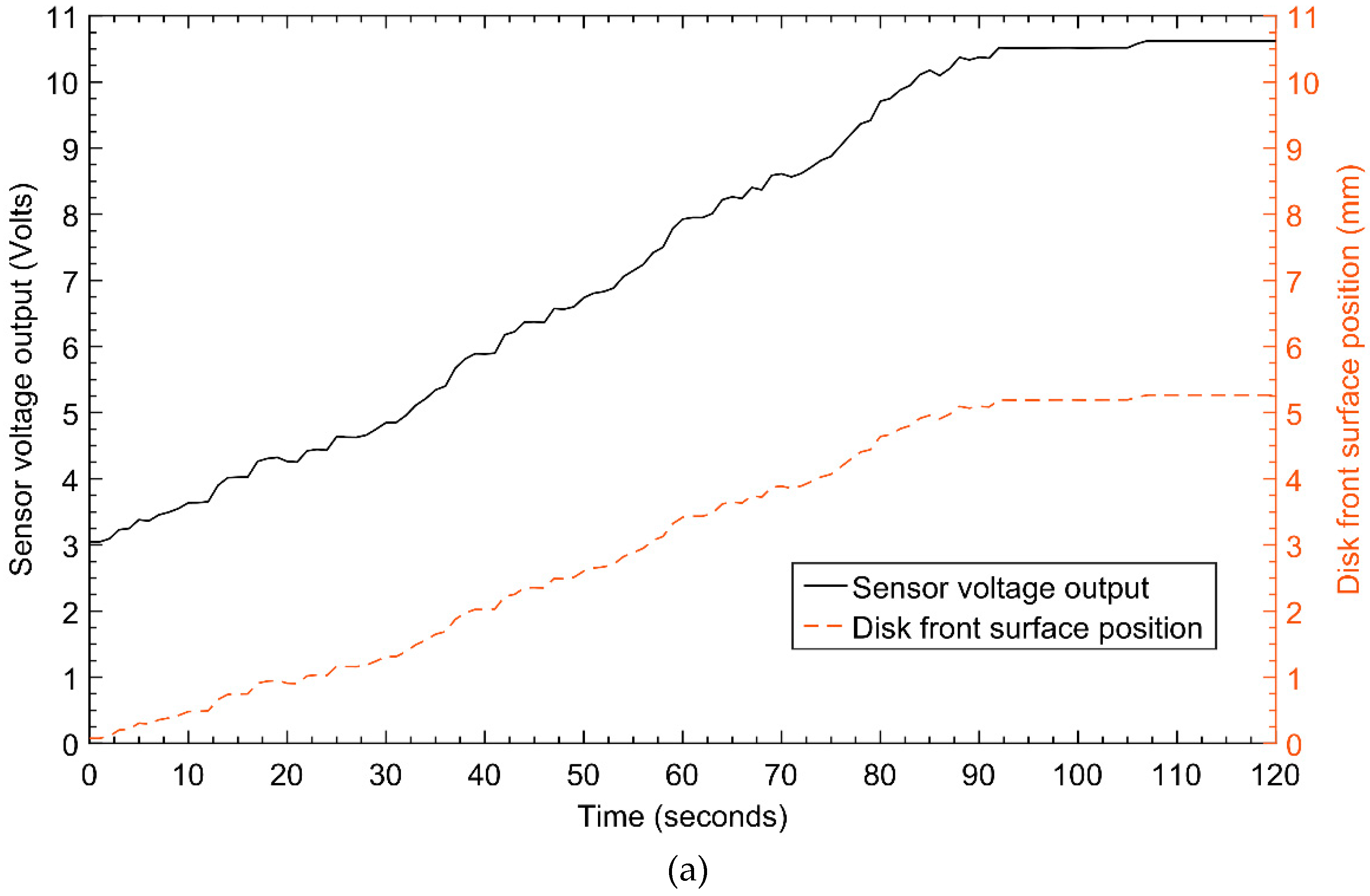
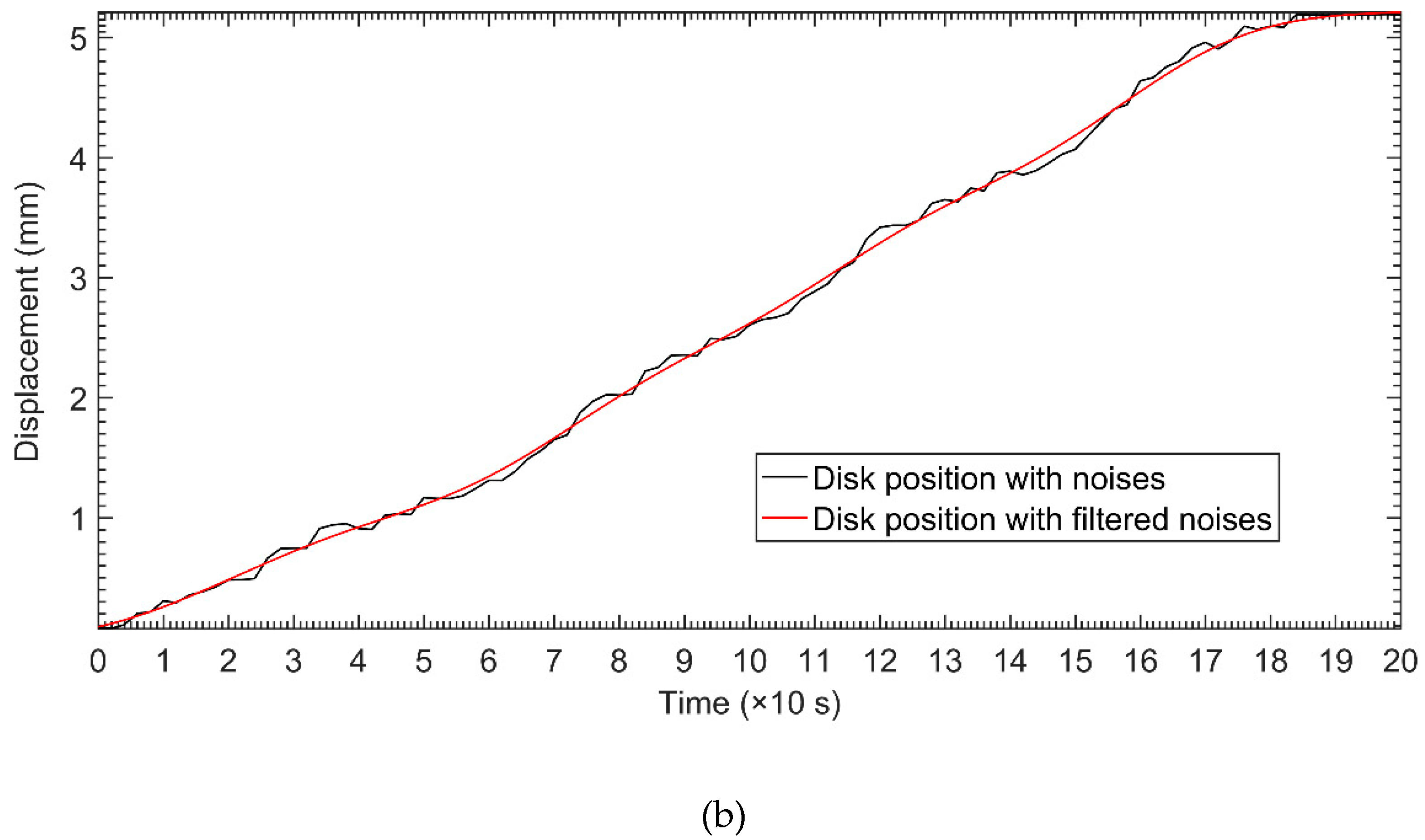
3.3. Laboratory Experimental Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, J.; Wang, P.; Wang, L.; Chen, R. Effects of profile wear on wheel–rail contact conditions and dynamic interaction of vehicle and turnout. Adv. Mech. Eng. 2016, 8. [Google Scholar] [CrossRef]
- Zobory, I. Prediction of wheel/rail profile wear. Veh. Syst. Dyn. 1997, 28, 221–259. [Google Scholar] [CrossRef]
- Pradhan, S.; Samantaray, A.K.; Bhattacharyya, R. Multi-step wear evolution simulation method for the prediction of rail wheel wear and vehicle dynamic performance. Simulation 2019, 95, 441–459. [Google Scholar] [CrossRef]
- Yuejian, C.; Zongyi, X.; Jianwei, L.; Yong, Q. The analysis of wheel-rail vibration signal based on frequency slice wavelet transform. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 1312–1316. [Google Scholar]
- Kim, M.-S.; Hur, H.-M. Braking/traction control systems of a scaled railway vehicle for the active steering testbed. In Proceedings of the WSEAS International Conference Mathematics and Computers in Science and Engineering, Stevens Point, WI, USA, 23–25 March 2009. [Google Scholar]
- Messouci, M. Steady state motion of rail vehicle with controlled creep forces on curved track. ARPN J. Eng. Appl. Sci. 2009, 4, 10–18. [Google Scholar]
- Lewis, R.; Dwyer-Joyce, R.S.; Olofsson, U.; Pombo, J.; Ambrosio, J.; Pereira, M.; Ariaudo, C.; Kuka, N. Mapping railway wheel material wear mechanisms and transitions. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2010, 224, 125–137. [Google Scholar] [CrossRef]
- Zhu, W.T.; Guo, L.C.; Shi, L.B.; Cai, Z.B.; Li, Q.L.; Liu, Q.Y.; Wang, W.J. Wear and damage transitions of two kinds of wheel materials in the rolling-sliding contact. Wear 2018, 398–399, 79–89. [Google Scholar] [CrossRef]
- Iwnicki, S. Simulation of wheel–rail contact forces. Fatigue Fract. Eng. Mater. Struct. 2003, 26, 887–900. [Google Scholar] [CrossRef]
- Na, W. The Measurement of a Wheel-Flange Wear Based on Digital Image Processing Technology. In Proceedings of the National Conference of Higher Vocational and Technical Education on Computer Information, Rizhao, China, 4 September 2010; pp. 227–229. [Google Scholar]
- Barke, D.; Chiu, W.K. Structural health monitoring in the railway industry: A review. Struct. Health Monit. 2005, 4, 81–93. [Google Scholar] [CrossRef]
- Chongyi, C.; Chengguo, W.; Ying, J. Study on numerical method to predict wheel/rail profile evolution due to wear. Wear 2010, 269, 167–173. [Google Scholar] [CrossRef]
- Li, X.; Jin, X.; Wen, Z.; Cui, D.; Zhang, W. A new integrated model to predict wheel profile evolution due to wear. Wear 2011, 271, 227–237. [Google Scholar] [CrossRef]
- Innocenti, A.; Marini, L.; Meli, E.; Pallini, G.; Rindi, A. Development of a wear model for the analysis of complex railway networks. Wear 2014, 309, 174–191. [Google Scholar]
- Feldmeier, C.; Li, H.; Yamazaki, Y.; Kato, T.; Fujimoto, T.; Kondo, O.; Sugiyama, H. Prediction of the wheel profile wear using railroad vehicle dynamics simulation: Comparison of simulation and test results. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2018, 232, 224–236. [Google Scholar] [CrossRef]
- Muhamedsalih, Y.; Stow, J.; Bevan, A. Use of railway wheel wear and damage prediction tools to improve maintenance efficiency through the use of economic tyre turning. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2019, 233, 103–117. [Google Scholar] [CrossRef]
- Tao, G.; Ren, D.; Wang, L.; Wen, Z.; Jin, X. Online prediction model for wheel wear considering track flexibility. Multibody Syst. Dyn. 2018, 44, 313–334. [Google Scholar] [CrossRef]
- Aceituno, J.F.; Wang, P.; Wang, L.; Shabana, A.A. Influence of rail flexibility in a wheel/rail wear prediction model. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2017, 231, 57–74. [Google Scholar] [CrossRef]
- Frohling, R.D.; Scheffel, H.; Ebersohn, W. The vertical dynamic response of a rail vehicle caused by track stiffness variations along the track. Veh. Syst. Dyn. 1996, 25, 175–187. [Google Scholar] [CrossRef]
- Nkundineza, C.; Turner, J.A. The influence of spatial variation of railroad track stiffness on the fatigue life. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 824–831. [Google Scholar] [CrossRef]
- Grossoni, I.; Andrade, A.R.; Bezin, Y.; Neves, S. The role of track stiffness and its spatial variability on long-term track quality deterioration. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2019, 233, 16–32. [Google Scholar] [CrossRef]
- Kassa, E.; Nielsen, J.C.O. Stochastic analysis of dynamic interaction between train and railway turnout. Veh. Syst. Dyn. 2008, 46, 429–449. [Google Scholar] [CrossRef]
- Alemi, A.; Corman, F.; Lodewijks, G. Condition monitoring approaches for the detection of railway wheel defects. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2017, 231, 961–981. [Google Scholar] [CrossRef]
- Bernal, E.; Spiryagin, M.; Cole, C. Onboard Condition Monitoring Sensors, Systems and Techniques for Freight Railway Vehicles: A Review. IEEE Sens. J. 2019, 19, 4–24. [Google Scholar] [CrossRef]
- Gong, Z.; Sun, J.; Zhang, G. Dynamic measurement for the diameter of a train wheel based on structured-light vision. Sensors 2016, 16, 564. [Google Scholar] [CrossRef] [PubMed]
- Soleimani, H.; Moavenian, M. Tribological Aspects of Wheel--Rail Contact: A Review of Wear Mechanisms and Effective Factors on Rolling Contact Fatigue. Urban Rail Transit 2017, 3, 227–237. [Google Scholar] [CrossRef]
- Mian, Z.F. Portable Electronic Wheel Wear Gauge. U.S. Patent 4,904,939, 27 February 1990. [Google Scholar]
- Cheng, X.; Chen, Y.; Xing, Z.; Li, Y.; Qin, Y. A novel online detection system for wheelset size in railway transportation. J. Sens. 2016, 2016, 9507213. [Google Scholar] [CrossRef]
- Zhan, D.; Yu, L.; Xiao, J.; Chen, T. Multi-camera and structured-light vision system (MSVS) for dynamic high-accuracy 3D measurements of railway tunnels. Sensors 2015, 15, 8664–8684. [Google Scholar] [CrossRef]
- Zhang, Z.-F.; Gao, Z.; Liu, Y.-Y.; Jiang, F.-C.; Yang, Y.-L.; Ren, Y.-F.; Yang, H.-J.; Yang, K.; Zhang, X.-D. Computer vision based method and system for online measurement of geometric parameters of train wheel sets. Sensors 2012, 12, 334–346. [Google Scholar] [CrossRef]
- Dwyer-Joyce, R.S.; Yao, C.; Lewis, R.; Brunskill, H. An ultrasonic sensor for monitoring wheel flange/rail gauge corner contact. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2013, 227, 188–195. [Google Scholar] [CrossRef]
- Gong, Z.; Sun, J.; Zhang, G. Dynamic structured-light measurement for wheel diameter based on the cycloid constraint. Appl. Opt. 2016, 55, 198–207. [Google Scholar] [CrossRef]
- Zhang, Z.; Su, Z.; Su, Y.; Gao, Z. Denoising of sensor signals for the flange thickness measurement based on wavelet analysis. Opt. J. Light Electron Opt. 2011, 122, 681–686. [Google Scholar] [CrossRef]
- Korotkikh, V.; Korotkikh, G. On Basic Principles of Intelligent Systems Design. In Proceedings of the 2006 Sixth International Conference on Hybrid Intelligent Systems (HIS’06), Rio de Janeiro, Rio de Janeiro, Brazil, 13–15 December 2006; p. 8. [Google Scholar]
- Shahdib, F.; Bhuiyan, M.W.U.; Hasan, M.K.; Mahmud, H. Obstacle detection and object size measurement for autonomous mobile robot using sensor. Int. J. Comput. Appl. 2013, 66, 28–33. [Google Scholar]
- Garg, V. Dynamics of Railway Vehicle Systems; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Asplund, M.; Gustafsson, P.; Nordmark, T.; Rantatalo, M.; Palo, M.; Famurewa, S.M.; Wandt, K. Reliability and measurement accuracy of a condition monitoring system in an extreme climate: A case study of automatic laser scanning of wheel profiles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2014, 228, 695–704. [Google Scholar] [CrossRef]
- Park, K.C. An improved stiffly stable method for direct integration of nonlinear structural dynamic equations. J. Appl. Mech. 1975, 42, 464–470. [Google Scholar] [CrossRef]
- Bringas, J.E. Handbook of Comparative World Steel Standards; ASTM International: West Conshohocken, PA, USA, 2004. [Google Scholar]
- Soukup, J.; Skočilas, J.; Skočilasová, B.; Dižo, J. Vertical vibration of two axle railway vehicle. Procedia Eng. 2017, 177, 25–32. [Google Scholar] [CrossRef]
- Chen, S.-C.; Le, D.-K.; Nguyen, V.-S. Inductive displacement sensors with a notch filter for an active magnetic bearing system. Sensors 2014, 14, 12640–12657. [Google Scholar] [CrossRef] [PubMed]
- Moreton, G.M. The Design and Development of a Planar Coil Sensor for Angular Displacements. Ph.D. Thesis, Cardiff University, Wales, UK, 25 July 2018. [Google Scholar]
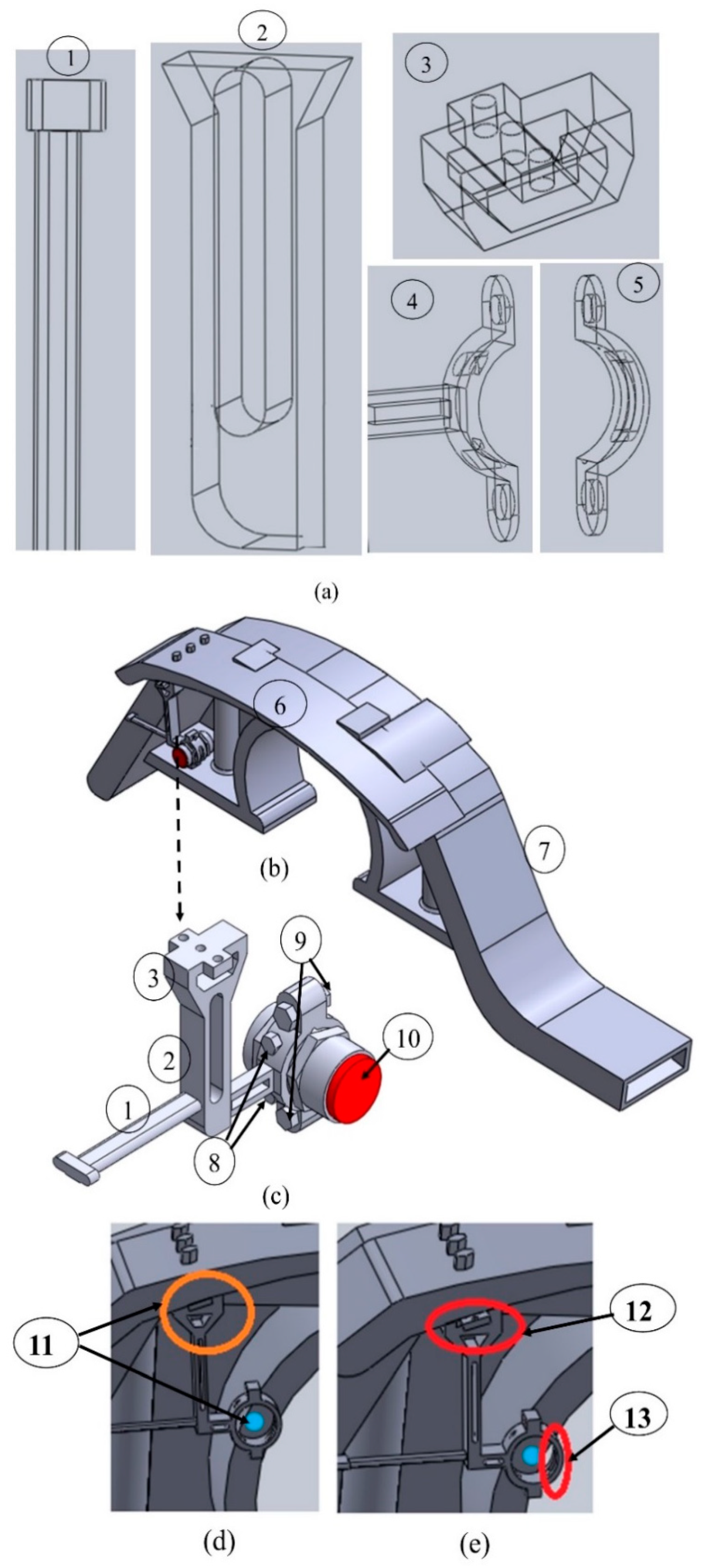

| S/N | Symbol | Value | Meaning |
|---|---|---|---|
| 1 | The track gauge | ||
| 2 | The half of track gauge or half of the distance between contact pints on two rails | ||
| 3 | The radius of curvature | ||
| 4 | Mass of the wheelset axle | ||
| 5 | Acceleration due to gravity | ||
| 6 | Iz | Roll moment of inertia of the wheelset | |
| 7 | Yaw moment of inertia of the wheelset | ||
| 8 | Spin moment of inertia of the wheelset | ||
| 9 | Nominal radius of the wheel | ||
| 10 | Axle speed | ||
| 11 | Lateral creep force coefficient | ||
| 12 | Lateral/spin creep force coefficient | ||
| 13 | Spin creep force coefficient | ||
| 14 | spin creep force coefficient | ||
| 15 | N | Longitudinal creep force coefficient | |
| 16 | Lateral stiffness | ||
| 17 | Lateral damping | ||
| 18 | kψ | Yaw stiffness | |
| 19 | cψ | Yaw damping | |
| 20 | Initial tapper angle | ||
| 21 | λ | Wheel conicity angle |
| Micrometer Measurements (mm) | Sensor output Voltage (Volts) | |||
|---|---|---|---|---|
| Same for All Records | 1st Records | 2nd Records | 3rd Records | 4th Records |
| 0.5 | 2.08 | 2.08 | 2.04 | 2.08 |
| 1 | 3.26 | 3.32 | 3.23 | 3.22 |
| 1.5 | 5.28 | 5.3 | 5.29 | 5.29 |
| 2 | 7.29 | 7.37 | 7.24 | 7.2 |
| 2.5 | 9.21 | 9.18 | 9.26 | 9.2 |
| 3 | 11.75 | 10.75 | 10.79 | 10.75 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turabimana, P.; Nkundineza, C. Development of an On-Board Measurement System for Railway Vehicle Wheel Flange Wear. Sensors 2020, 20, 303. https://doi.org/10.3390/s20010303
Turabimana P, Nkundineza C. Development of an On-Board Measurement System for Railway Vehicle Wheel Flange Wear. Sensors. 2020; 20(1):303. https://doi.org/10.3390/s20010303
Chicago/Turabian StyleTurabimana, Pacifique, and Celestin Nkundineza. 2020. "Development of an On-Board Measurement System for Railway Vehicle Wheel Flange Wear" Sensors 20, no. 1: 303. https://doi.org/10.3390/s20010303
APA StyleTurabimana, P., & Nkundineza, C. (2020). Development of an On-Board Measurement System for Railway Vehicle Wheel Flange Wear. Sensors, 20(1), 303. https://doi.org/10.3390/s20010303






