Beam Damage Detection Under a Moving Load Using Random Decrement Technique and Savitzky–Golay Filter
Abstract
1. Introduction
2. Basic Theories and Methodology
2.1. Theory of RDT for a Single-Channel Signal
2.2. Theory of RDT for Multi-Channel Signals
2.3. Theory of SGF for a Signal
3. The Numerical Model of a Simply Supported Beam Subjected to Moving Sprung Mass
4. Results and Discussion
4.1. Acceleration Signals, RDSs and SG-RDSs
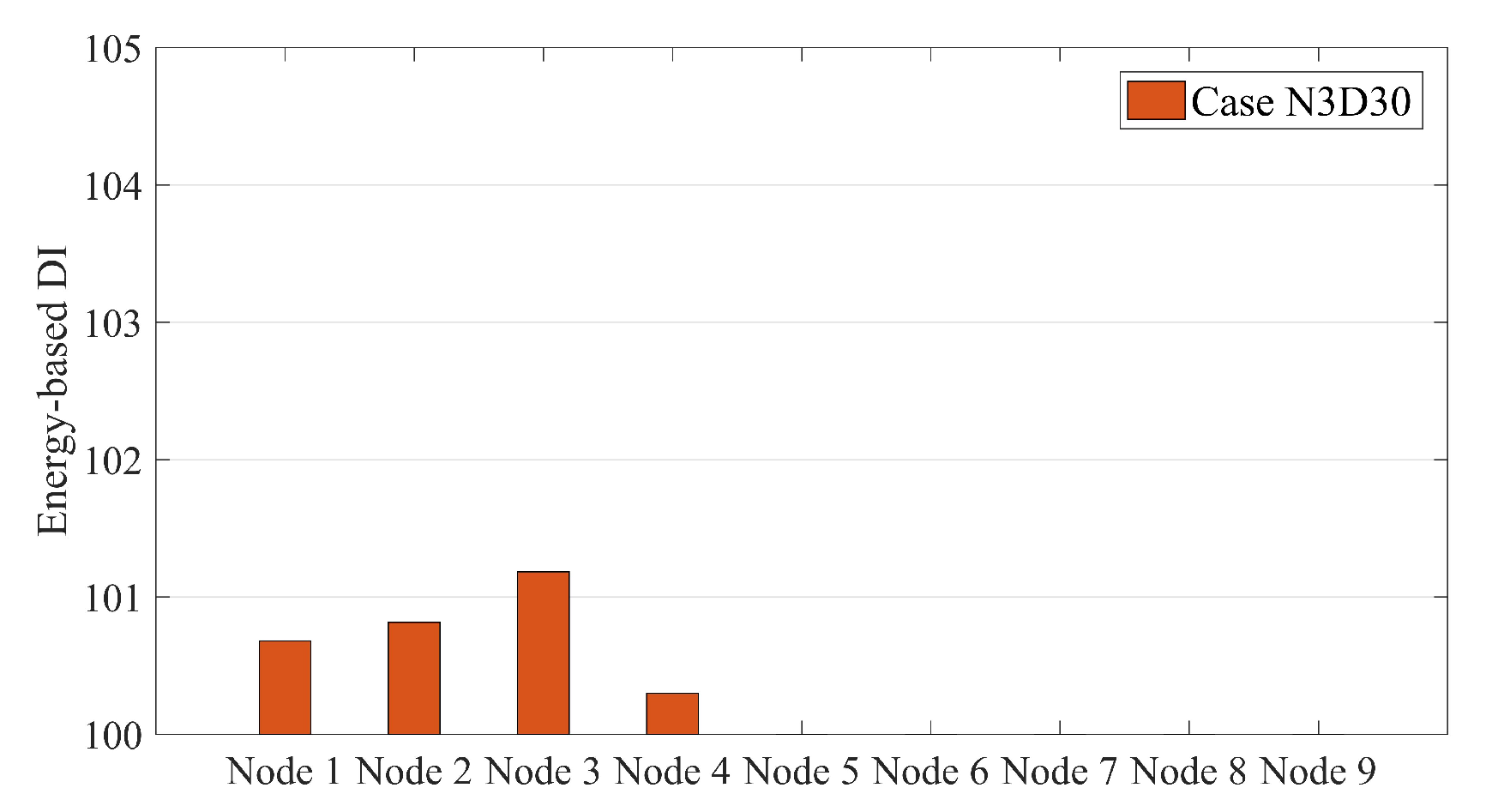
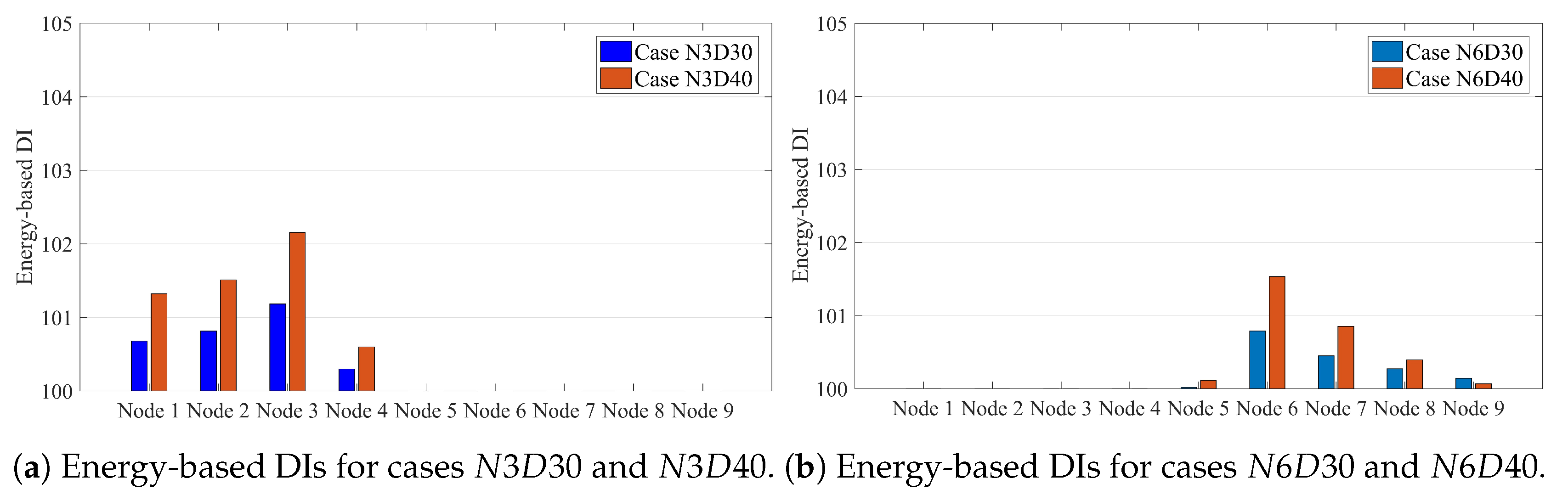
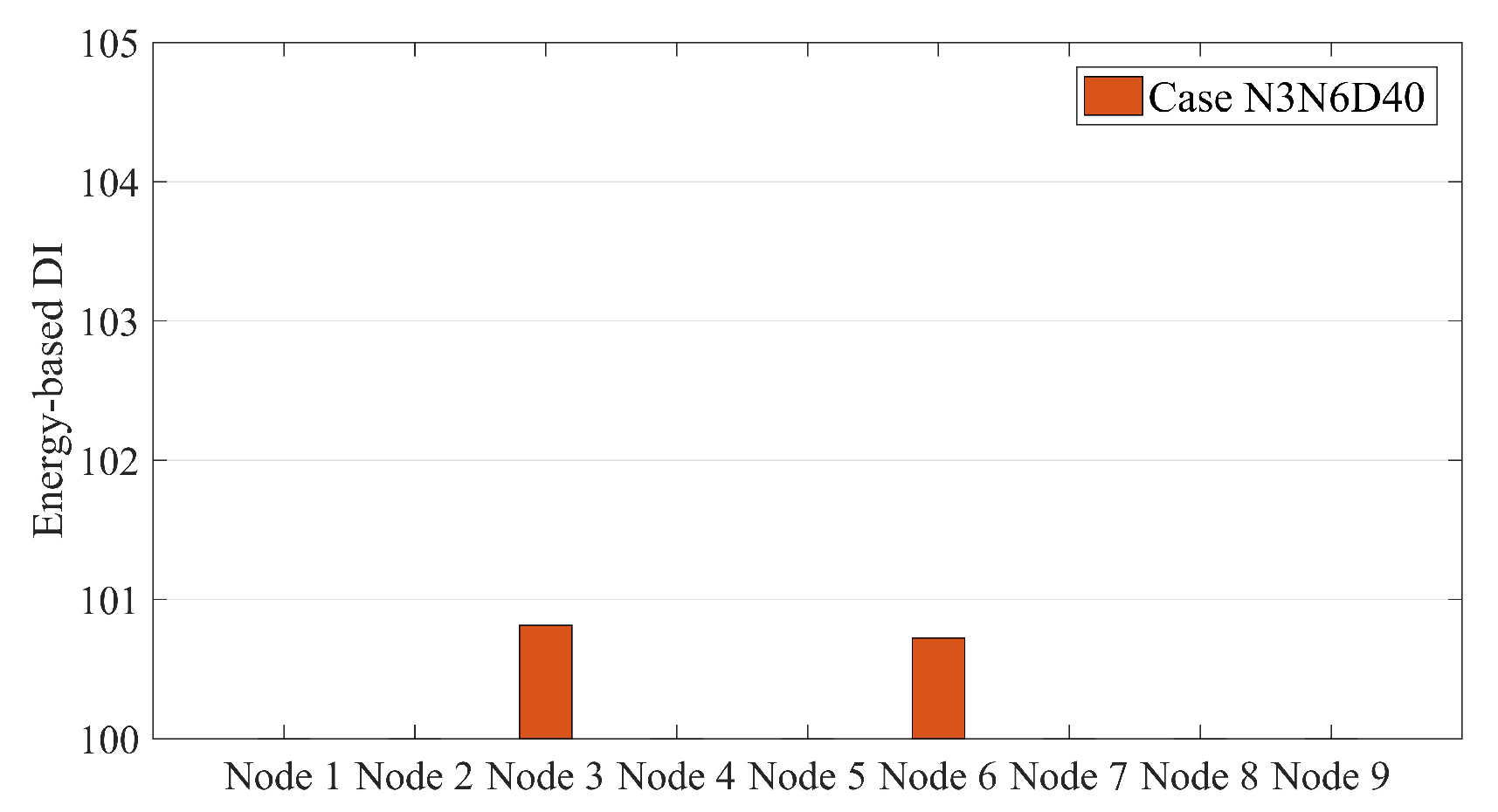
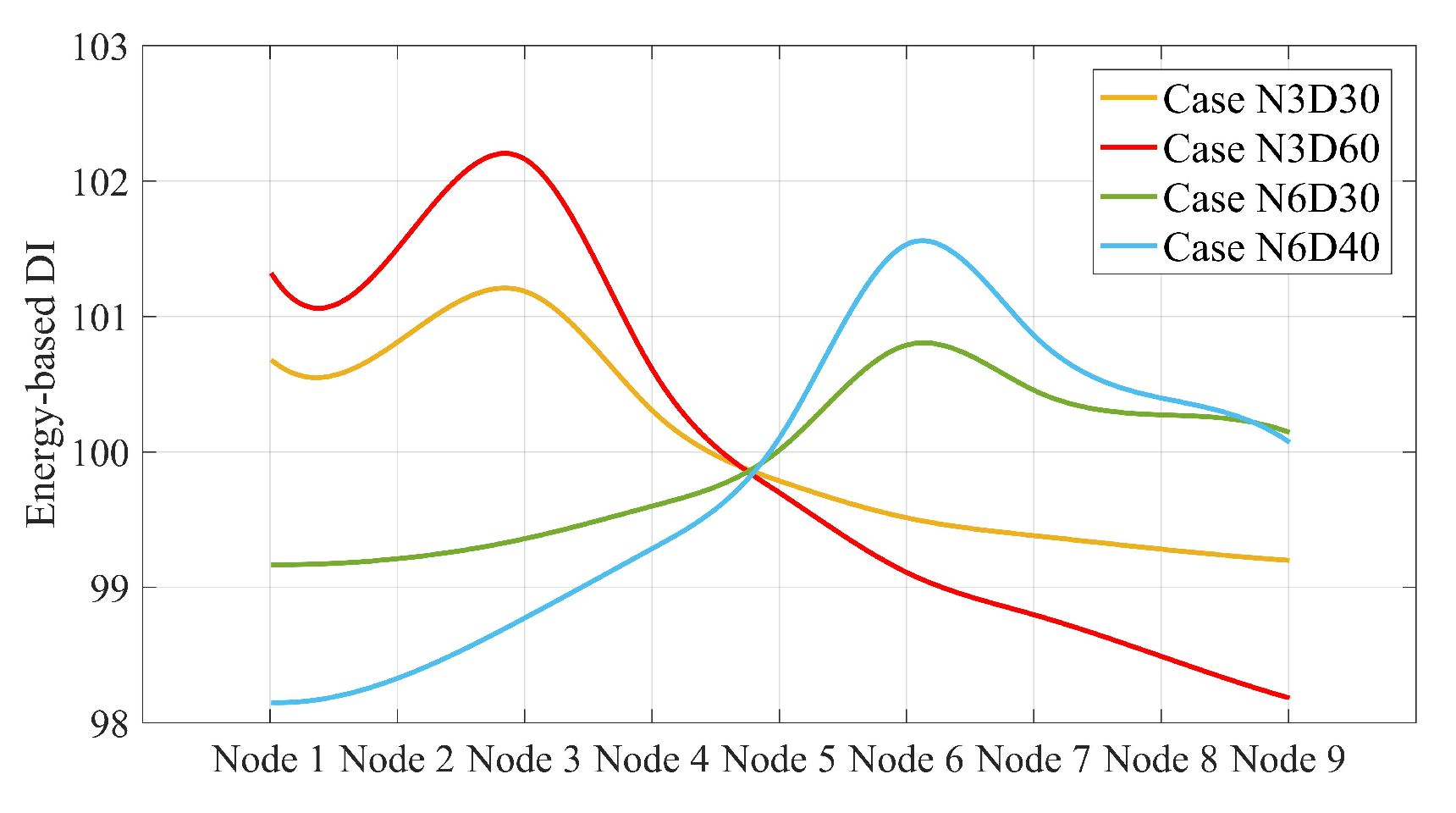
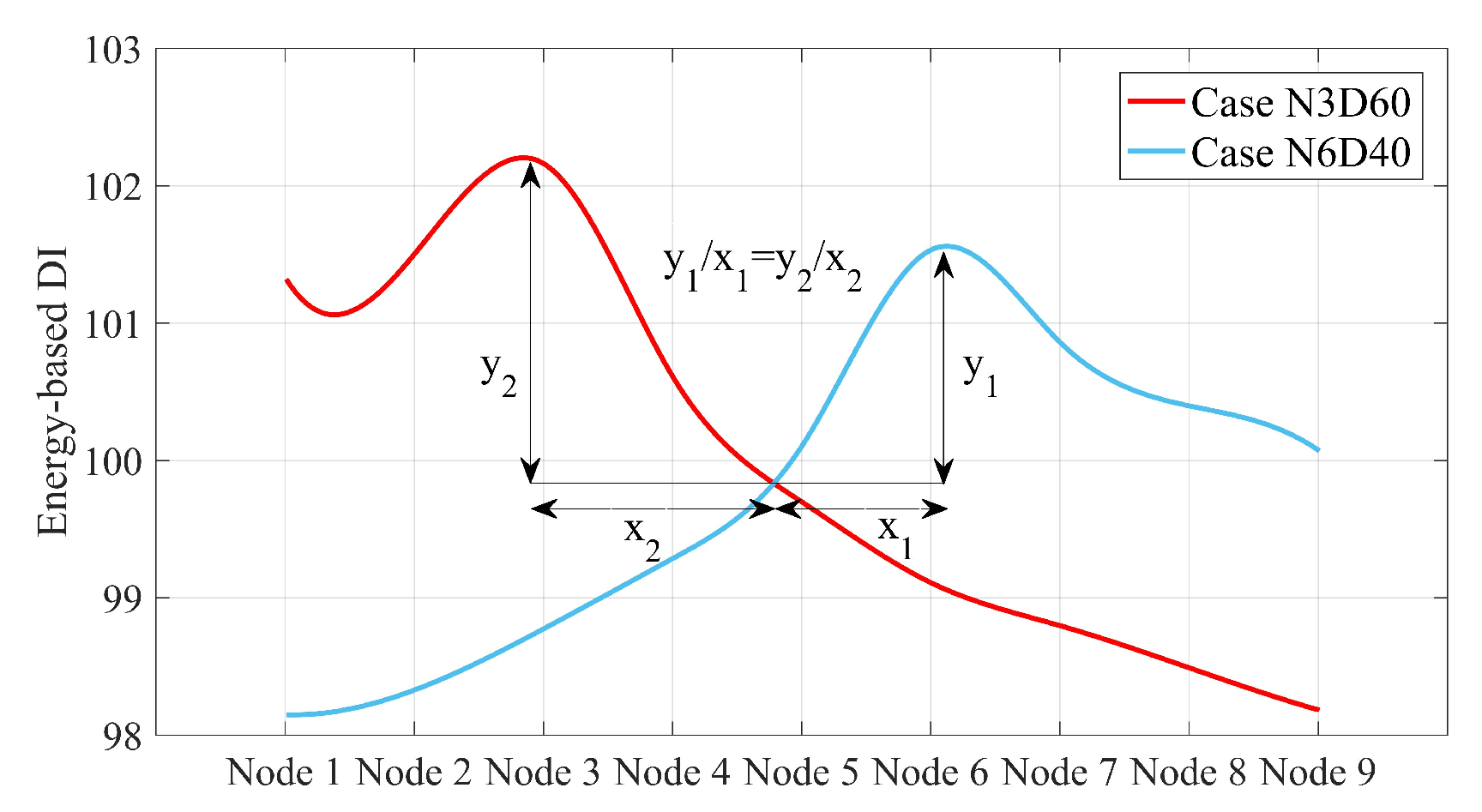
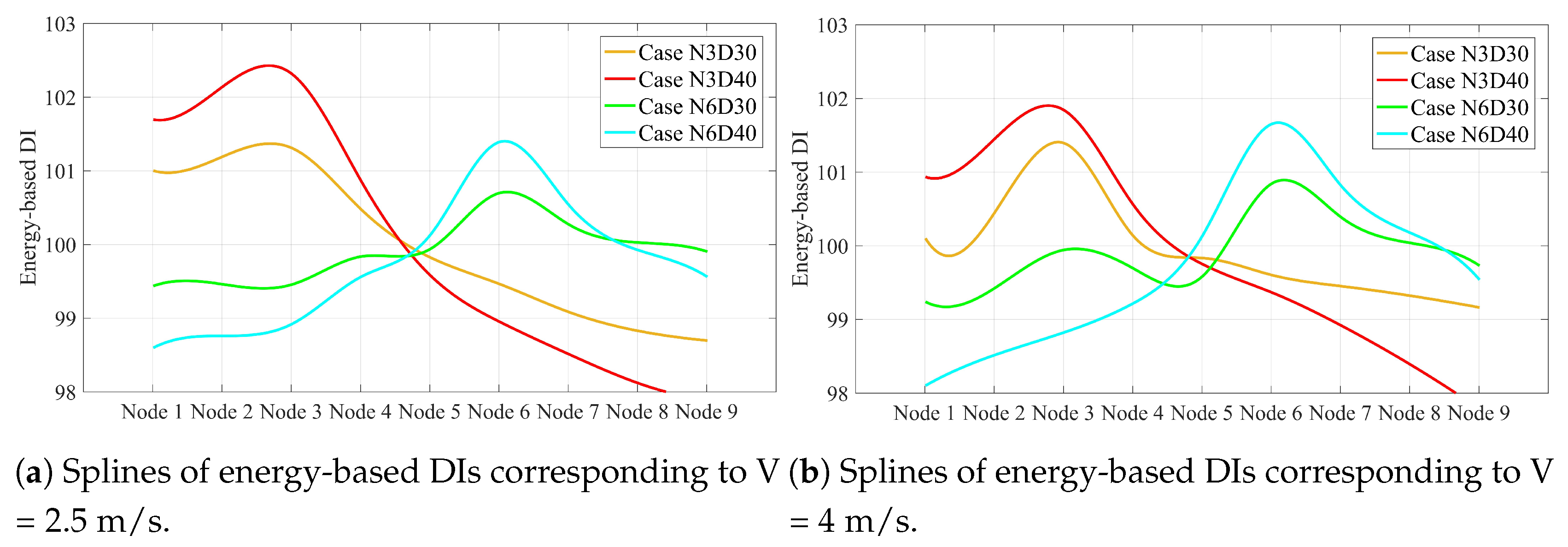
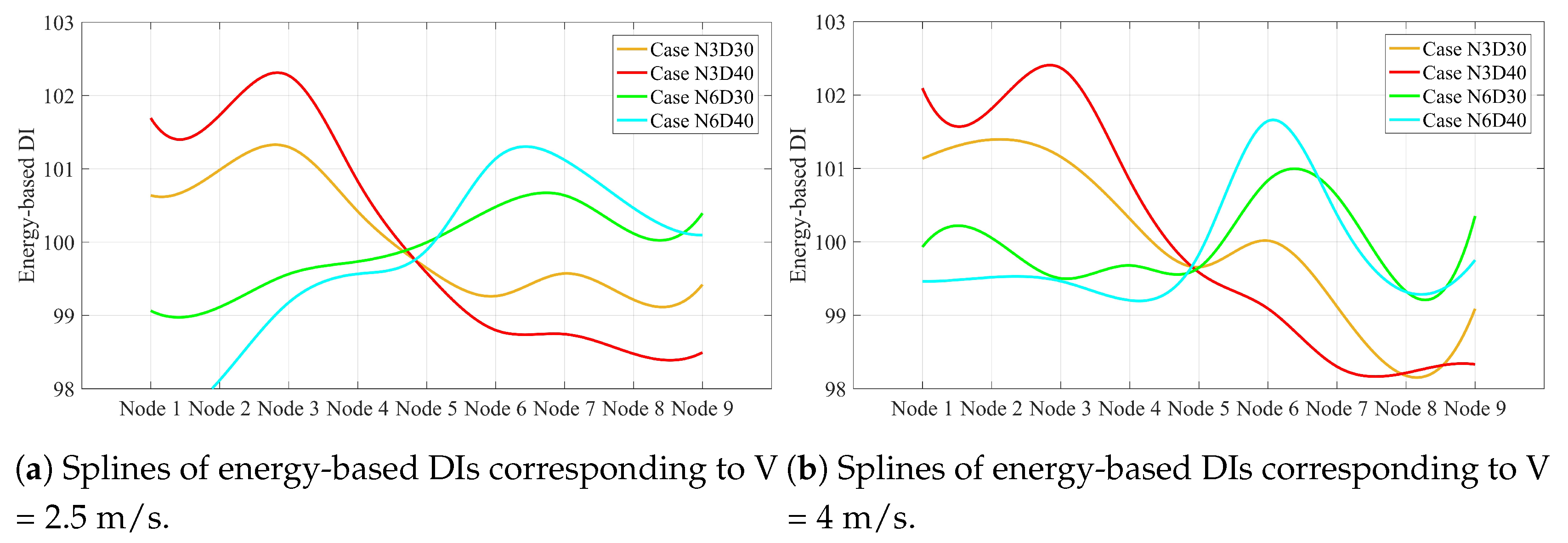
4.2. Energy-Based DI
4.3. Damage Localization of the Simply Supported Beam
4.4. Damage Quantification of the Simply Supported Beam for Single Damage Scenarios
4.5. Noise Consideration
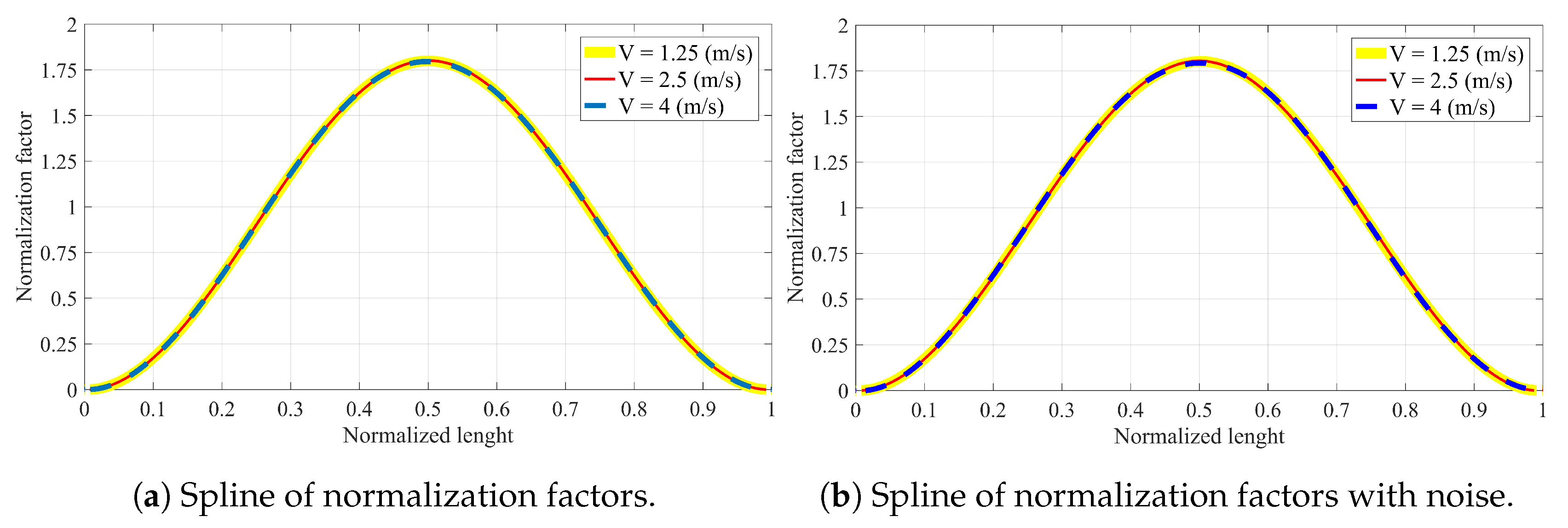
4.6. Normalization Factor
- The spline of normalization factor (SNF) is insensitive to noise (Figure 15a,b are almost the same).
- The SNF is not changed with the increase of velocity from to 4 m/s. Therefore, such insensitivity helps to find the SNF for a certain velocity and then apply it to other velocities. For instance, the SNF for a velocity of m/s can be used to find the damage at velocity or 4 m/s. This advantage helps to overcome the velocity determination problem and enables the proposed method to accurately work for any velocity between to 4 m/s in the process of damage localization and quantification.
- The SNF follows a Gaussian distribution. The SNF helps to calculate the normalization factors in the locations where no sensor is available. Hence, with SNF, there is no need to install sensors at the same distance before and after the damage.
5. Conclusions
- Due to the application of RDT and SGF, the method is not essentially sensitive to noise.
- The method is able to localize and quantify the damage in both noisy and noise-free environments.
- Introducing a general form of baseline by SNF, the proposed method is formulated as a baseline-free method.
- Unlike the conventional methods, the proposed method does not require any sensor at the same distance before and after the damage.
- The proposed method can address multi-damage scenarios in noise-free data.
- The method is flexible in choosing the speed since the SNF is not changed by velocity variations.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BHM | Bridge health monitoring |
| BSS | Blind source separation |
| DI | Damage index |
| MAF | Moving average filter |
| RDS | Random decrement signature |
| RDT | Random decrement technique |
| SGF | Savitzky–Golay filter |
| SHM | Structural health monitoring |
| SG-RDS | Trend line of RDS |
| SOBI | Second-order blind identification |
References
- Kordestani, H.; Xiang, Y.Q.; Ye, X.W. Output-only damage detection of steel beam using moving average filter. Shock Vib. 2018. [Google Scholar] [CrossRef]
- Kordestani, H.; Xiang, Y.Q.; Ye, X.W.; Jia, Y.K. Application of the random decrement technique in damage detection under moving load. Appl. Sci. 2018, 8, 753. [Google Scholar] [CrossRef]
- Pakrashi, V.; O’Connor, A.; Basu, B. A bridge-vehicle interaction based experimental investigation of damage evolution. Struct. Heal. Monit. 2010, 9, 285–296. [Google Scholar] [CrossRef]
- Hester, D.; Gonzalez, A. A wavelet-based damage detection algorithm based on bridge acceleration response to a vehicle. Mech. Syst. Signal. Process. 2012, 28, 145–166. [Google Scholar] [CrossRef]
- Balafas, K.; Kiremidjian, A.S. Development and validation of a novel earthquake damage estimation scheme based on the continuous wavelet transform of input and output acceleration measurements. Earthq. Eng. Struct. Dyn. 2015, 44, 501–522. [Google Scholar] [CrossRef]
- Cantero, D.; Basu, B. Railway infrastructure damage detection using wavelet transformed acceleration response of traversing vehicle. Struct. Control. Health. Monit. 2015, 22, 62–70. [Google Scholar] [CrossRef]
- Hester, D.; González, A. Impact of road profile when detecting a localised damage from bridge acceleration response to a moving vehicle. In Key Engineering Materials; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2013; pp. 199–206. [Google Scholar] [CrossRef]
- Zhu, X.; Law, S.S. Structural health monitoring based on vehicle-bridge interaction: accomplishments and challenges. Adv. Struct. Eng. 2015, 18, 1999–2015. [Google Scholar] [CrossRef]
- Asayesh, M.; Khodabandeloo, B.; Siami, A. A random decrement technique for operational modal analysis in the presence of periodic excitations. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2009, 223, 1525–1534. [Google Scholar] [CrossRef]
- Rodrigues, J.; Brincker, R. Application of the random decrement technique in operational modal analysis. In Proceedings of the 1st International Operational Modal Analysis Conference, Copenhagen, Denmark, 26–27 April 2005; pp. 191–200. [Google Scholar]
- Lee, J.W.; Kim, J.D.; Yun, C.B.; Yi, J.H.; Shim, J.M. Health-monitoring method for bridges under ordinary traffic loadings. J. Sound Vib. 2002, 257, 247–264. [Google Scholar] [CrossRef][Green Version]
- He, X.H.; Hua, X.G.; Chen, Z.Q.; Huang, F.L. EMD-based random decrement technique for modal parameter identification of an existing railway bridge. Eng. Struct. 2011, 33, 1348–1356. [Google Scholar] [CrossRef]
- Wu, W.H.; Chen, C.C.; Liau, J.A. A multiple random decrement method for modal parameter identification of stay cables based on ambient vibration signals. Adv. Struct. Eng. 2012, 15, 969–982. [Google Scholar] [CrossRef]
- Buff, H.; Friedmann, A.; Koch, M.; Bartel, T.; Kauba, M. Design of a random decrement method based structural health monitoring system. Shock Vib. 2012, 19, 787–794. [Google Scholar] [CrossRef][Green Version]
- Poncelet, F.; Kerschen, G.; Golinval, J.C.; Verhelst, D. Output-only modal analysis using blind source separation techniques. Mech. Syst. Signal. Process. 2007, 21, 2335–2358. [Google Scholar] [CrossRef]
- Kerschen, G.; Poncelet, F.; Golinval, J.C. Physical interpretation of independent component analysis in structural dynamics. Mech. Syst. Signal. Process. 2007, 21, 1561–1575. [Google Scholar] [CrossRef]
- Zhou, W.; Chelidze, D. Blind source separation based vibration mode identification. Mech. Syst. Signal. Process. 2007, 21, 3072–3087. [Google Scholar] [CrossRef]
- Huang, C.; Nagarajaiah, S. Experimental study on bridge structural health monitoring using blind source separation method: Arch bridge. Struct. Monit. Maint. 2014, 1, 69–87. [Google Scholar] [CrossRef]
- Loh, C.H.; Hung, T.; Chen, S.; Hsu, W. Damage detection in bridge structure using vibration data under random travelling vehicle loads. J. Phys. Con. Ser. 2015, 628, 012044. [Google Scholar] [CrossRef]
- OBrien, E.J.; Malekjafarian, A.; González, A. Application of empirical mode decomposition to drive-by bridge damage detection. Eur. J. Mech. 2017, 61, 151–163. [Google Scholar] [CrossRef]
- Nie, Z.; Ngo, T.; Ma, H. Reconstructed phase space-based damage detection using a single sensor for beam-Like structure subjected to a moving mass. Shock Vib. 2017. [Google Scholar] [CrossRef]
- Meredith, J.; González, A.; Hester, D. Empirical Mode Decomposition of the Acceleration Response of a Prismatic Beam Subject to a Moving Load to Identify Multiple Damage Locations. Shock Vib. 2012, 19, 845–856. [Google Scholar] [CrossRef]
- Gonzalez, A.; Hester, D. An investigation into the acceleration response of a damaged beam-type structure to a moving force. J. Sound Vib. 2013, 332, 3201–3217. [Google Scholar] [CrossRef]
- Ostertagova, E.; Ostertag, O. Methodology and application of savitzky-golay moving average polynomial smoother. Global. J. Pure. Applied. Math. 2016, 12, 3201–3210. [Google Scholar]
- Guinon, J.; Ortega, E.; Garcia-Anton, J.; Perez-Herranz, V. Moving average and savitzki-golay smoothing filters using mathcad. In Proceedings of the ICEE 2007, Coimbra, Portugal, 3–7 September 2007. [Google Scholar]
- Quaranta, G.; Carboni, B.; Lacarbonara, W. Damage detection by modal curvatures: Numerical issues. J. Vib. Control 2016, 22, 1913–1927. [Google Scholar] [CrossRef]
- Mosti, F.; Quaranta, G.; Lacarbonara, W.; Belhaq, M. Numerical and experimental assessment of the modal curvature method for damage detection in plate structures. In Structural Nonlinear Dynamics and Diagnosis; Springer: Cham, Swithzerland, 2015. [Google Scholar]
- Mario, d.O.; Nelcileno, A.; Rodolfo, d.S.; Tony, d.S.; Jayantha, E. Use of Savitzky–Golay Filter for Performances Improvement of SHM Systems Based on Neural Networks and Distributed PZT Sensors. Sensors 2018, 18, 152. [Google Scholar] [CrossRef]
- Cole, H.J. On-The-Line Analysis of Random Vibrations. 1968. Available online: https://ntrs.nasa.gov/search.jsp?R=19680043272 (accessed on 27 December 2019). [CrossRef]
- Vandiver, J.K.; Dunwoody, A.B.; Campbell, R.B.; Cook, M.F. A mathematical basis for the random decrement vibration signature analysis technique. J. Mech. Des. 1982, 104, 307–313. [Google Scholar] [CrossRef]
- Sim, S.H.; Carbonell-Márquez, J.F.; Spencer, B., Jr.; Jo, H. Decentralized random decrement technique for efficient data aggregation and system identification in wireless smart sensor networks. Probabilistic Eng. Mech. 2011, 26, 81–91. [Google Scholar] [CrossRef]
- Ibrahim, S.R. Random decrement technique for modal identification of structures. J. Spacecr. Rockets 1977, 14, 696–700. [Google Scholar] [CrossRef]
- Ibraham, S. Efficient Random Decrement Computation for Identification of Ambient Responses. 2001. Available online: https://scholar.google.com/scholar?hl=en&as_sdt=0 (accessed on 31 December 2019).
- Jeary, A.P. The description and measurement of nonlinear damping in structures. J. Wind Eng. Ind. Aerodyn. 1996, 59, 103–114. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Analyt. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Schafer, R. What Is a Savitzky-Golay Filter? (A Lecture Note). IEEE Signal Process. Mag. 2011, 28, 111–117. [Google Scholar] [CrossRef]
- He, W.Y.; Ren, W.X.; Zhu, S. Baseline-free damage localization method for statically determinate beam structures using dual-type response induced by quasi-static moving load. J. Sound Vib. 2017, 400, 58–70. [Google Scholar] [CrossRef]
- Zhang, W.; Li, J.; Hao, H.; Ma, H. Damage detection in bridge structures under moving loads with phase trajectory change of multi-type vibration measurements. Mech. Syst. Signal. Process. 2017, 87, 410–425. [Google Scholar] [CrossRef]
- Ouyang, H. Moving-load dynamic problems: A tutorial (with a brief overview). Mech. Syst. Signal Process. 2011, 25, 2039–2060. [Google Scholar] [CrossRef]
- Yang, Y.B.; Cheng, M.C.; Chang, K.C. Frequency variation in vehicle–bridge interaction systems. Int. J. Struct. Stab. Dyn. 2013, 13, 1350019. [Google Scholar] [CrossRef]
- Cantero, D.; OBrien, E.J. The non-stationarity of apparent bridge natural frequencies during vehicle crossing events. FME Trans. 2013, 41, 279–284. [Google Scholar]
- Cantero, D.; Rønnquist, A. Numerical Evaluation of Modal Properties Change of Railway Bridges during Train Passage. Procedia Eng. 2017, 199, 2931–2936. [Google Scholar] [CrossRef]
- Malekjafarian, A.; Brien, E.J. Identification of bridge mode shapes using short time frequency domain decomposition of the responses measured in a passing vehicle. Eng. Struct. 2014, 81, 386–397. [Google Scholar] [CrossRef]
- OBrien, E.J.; McGetrick, P.J.; Gonzalez, A. A drive-by inspection system via vehicle moving force identification. Smart. Struct. Syst. 2014, 13, 821–848. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P. Vibration-based damage identification methods: A review and comparative study. Struct. Heal. Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Qiao, P.; Cao, M. Waveform fractal dimension for mode shape-based damage identification of beam-type structures. Int. J. Solids Struct. 2008, 45, 5946–5961. [Google Scholar] [CrossRef]
- Yan, A.M.; De Boe, P.; Golinval, J.C. Structural damage diagnosis by Kalman model based on stochastic subspace identification. Struct. Heal. Monit. 2004, 3, 103–119. [Google Scholar] [CrossRef]
- Yan, A.M.; De Boe, P.; Golinval, J.C. Structural Integral Monitoring by Vibration Measurements. 2003. Available online: https://orbi.uliege.be/handle/2268/29928 (accessed on 31 December 2019).

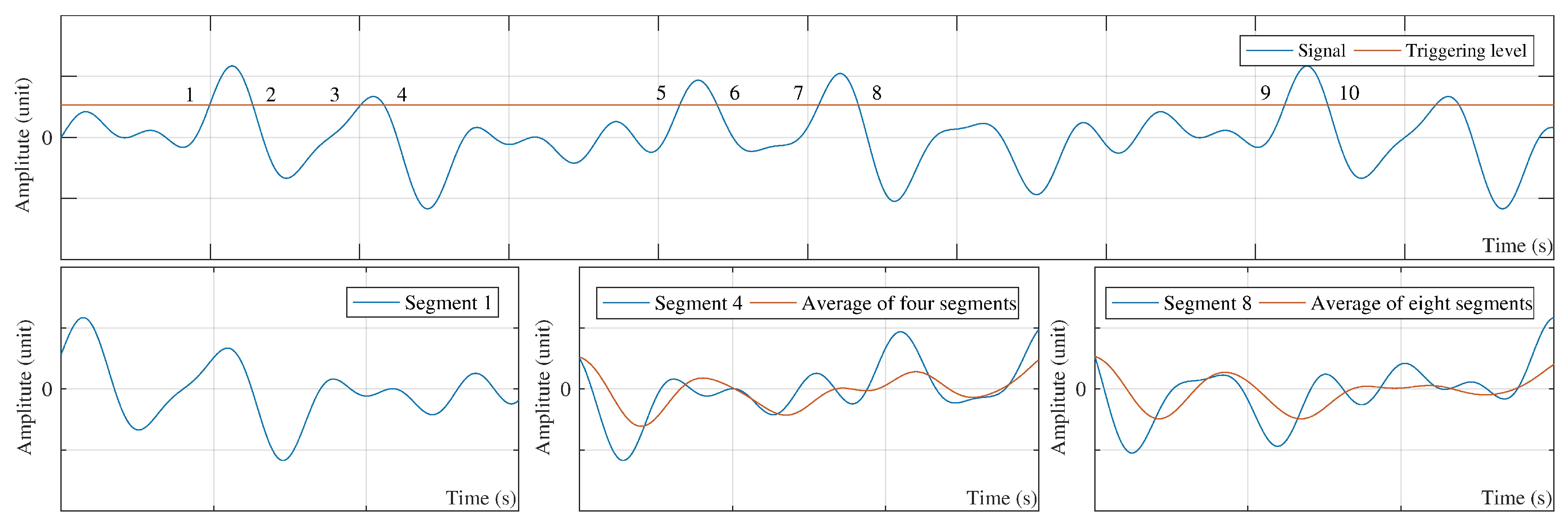
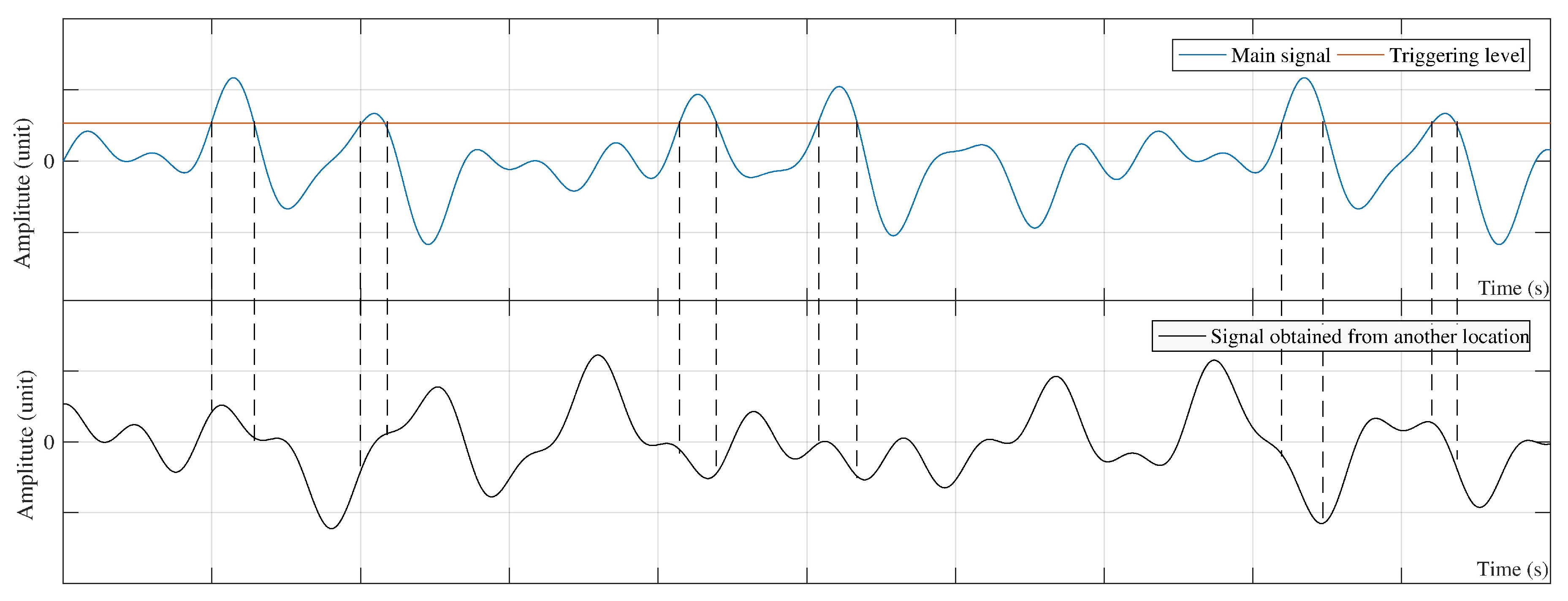


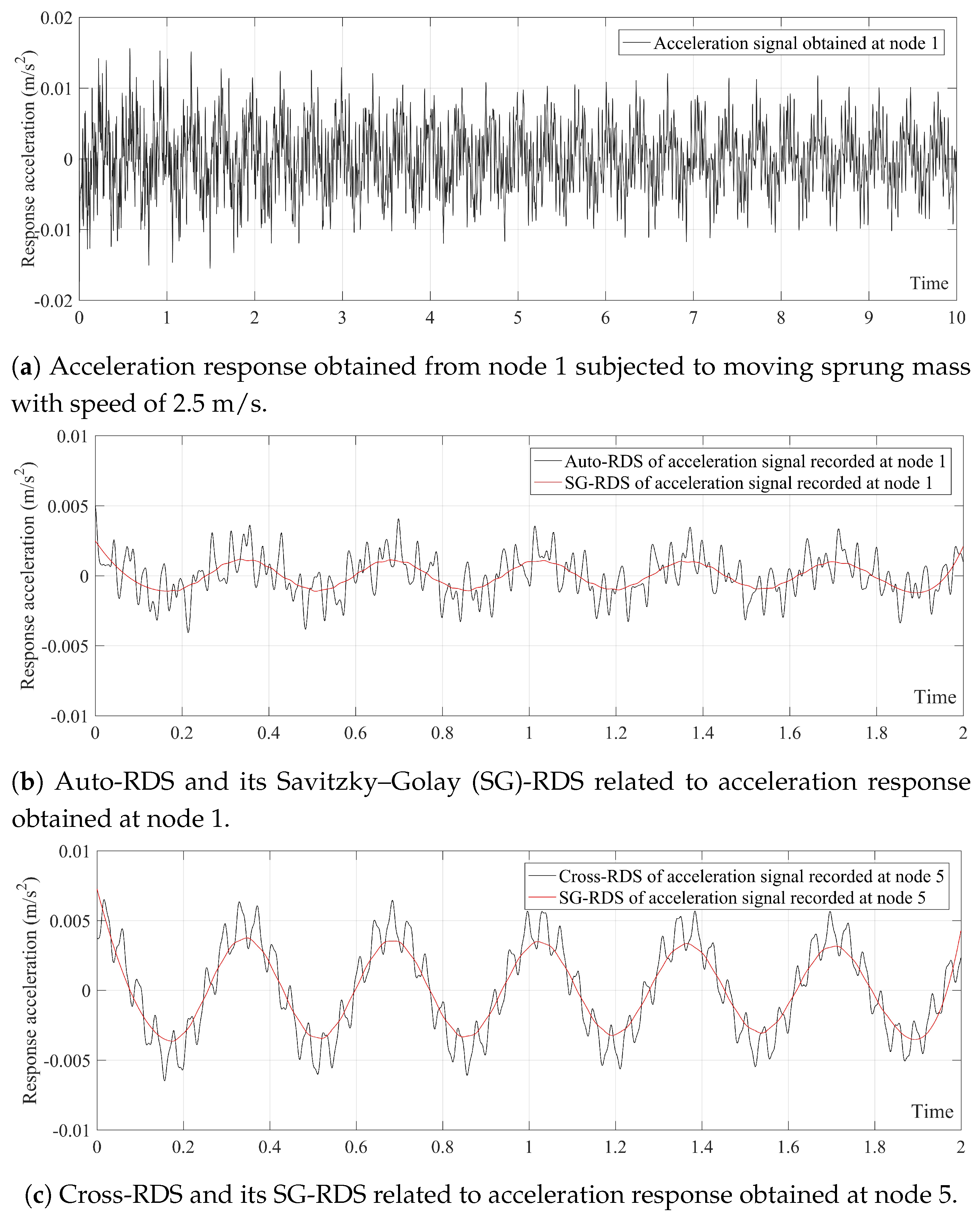
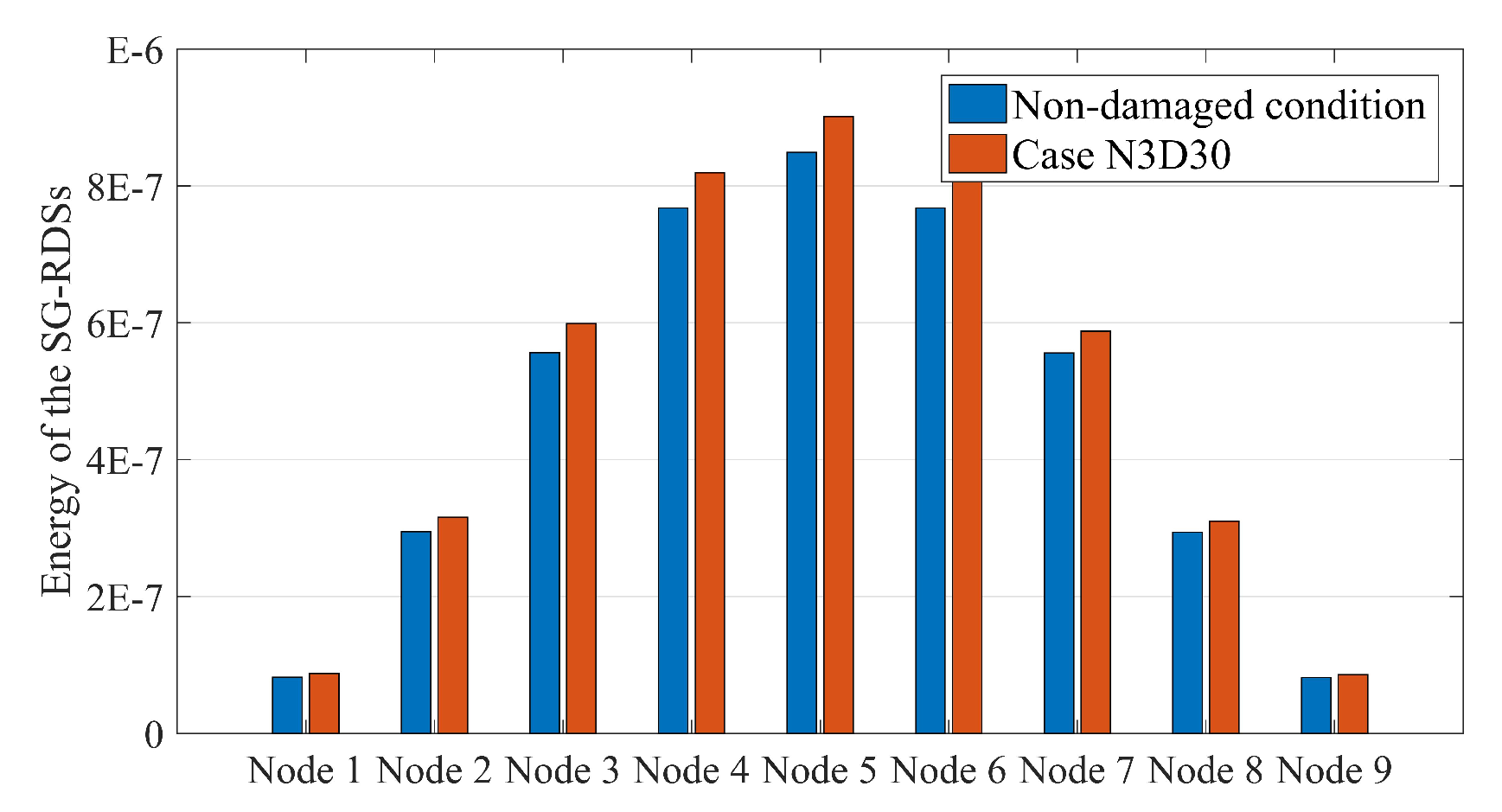
| Case NO | Description | Relation |
|---|---|---|
| 1 | Level-crossing | |
| 2 | Positive points | |
| 3 | Zero crossing with a positive or negative slope | |
| 4 | Local extremum |
| Properties | Unit | Symbol | Value |
|---|---|---|---|
| Length | m | L | 25 |
| Mass per unit | kg/m | 18,360 | |
| Stiffness | Nm | 4.865 × |
| Properties | Unit | Symbol | Value |
|---|---|---|---|
| Body mass | kg | 16,500 | |
| Axle mass | kg | 700 | |
| Suspension stiffness | Nm | 8 × | |
| Suspension damping | Nm | 2 × | |
| Tire stiffness | Nm | 3.5 × | |
| Velocity | m/s | V |
| Scenario | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Crack depth to the beam height ratio | |||||
| Location | At node 3 | At node 3 | At node 6 | At node 6 | At node 3 and 6 |
| Name |
| Scenario | Velocity (m/s) | Slope | Scenario | Velocity (m/s) | Slope |
|---|---|---|---|---|---|
| 4 | 4 | ||||
| 4 | 4 | ||||
| Average | Average |
| Speed | Node 1 | Node 2 | Node 3 | Node 4 | Node 5 | Node 6 | Node 7 | Node 8 | Node 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1.25 | |||||||||
| 2.5 | |||||||||
| 4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kordestani, H.; Zhang, C.; Shadabfar, M. Beam Damage Detection Under a Moving Load Using Random Decrement Technique and Savitzky–Golay Filter. Sensors 2020, 20, 243. https://doi.org/10.3390/s20010243
Kordestani H, Zhang C, Shadabfar M. Beam Damage Detection Under a Moving Load Using Random Decrement Technique and Savitzky–Golay Filter. Sensors. 2020; 20(1):243. https://doi.org/10.3390/s20010243
Chicago/Turabian StyleKordestani, Hadi, Chunwei Zhang, and Mahdi Shadabfar. 2020. "Beam Damage Detection Under a Moving Load Using Random Decrement Technique and Savitzky–Golay Filter" Sensors 20, no. 1: 243. https://doi.org/10.3390/s20010243
APA StyleKordestani, H., Zhang, C., & Shadabfar, M. (2020). Beam Damage Detection Under a Moving Load Using Random Decrement Technique and Savitzky–Golay Filter. Sensors, 20(1), 243. https://doi.org/10.3390/s20010243







