Numerical Study on Ultrasonic Guided Waves for the Inspection of Polygonal Drill Pipes
Abstract
:1. Introduction
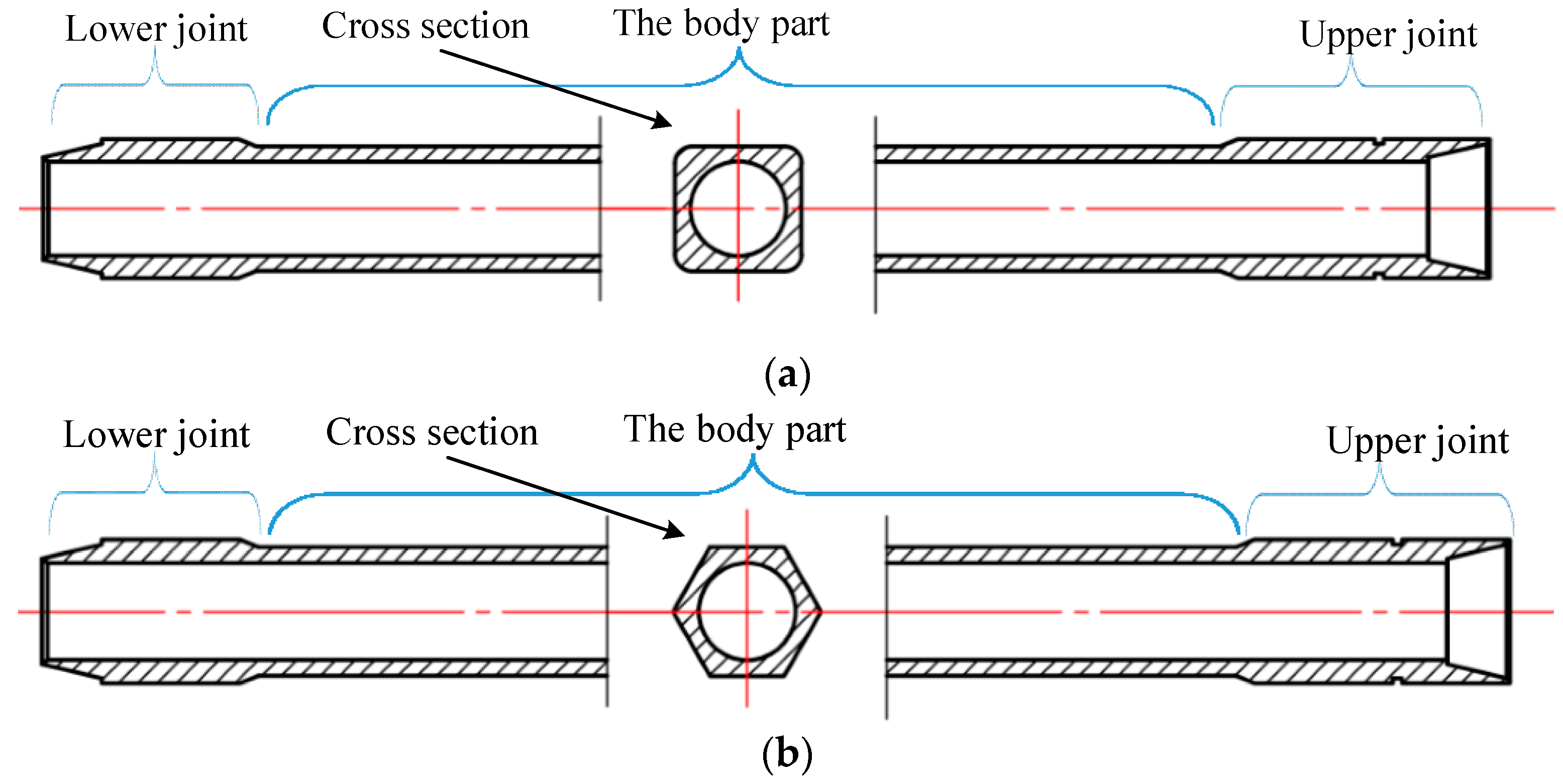
2. Characteristics of Guided Waves Propagating in Polygonal Drill Pipes
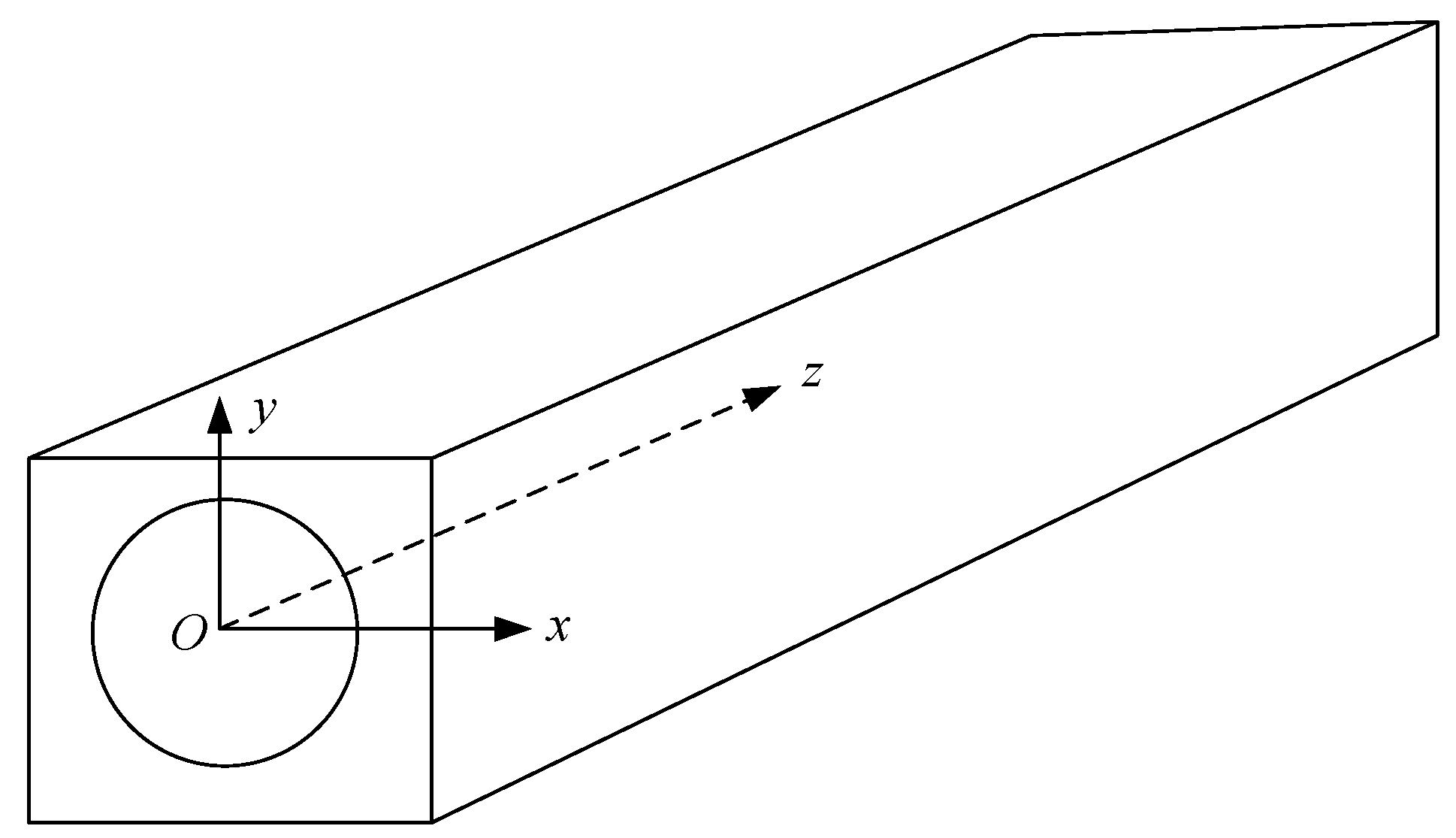
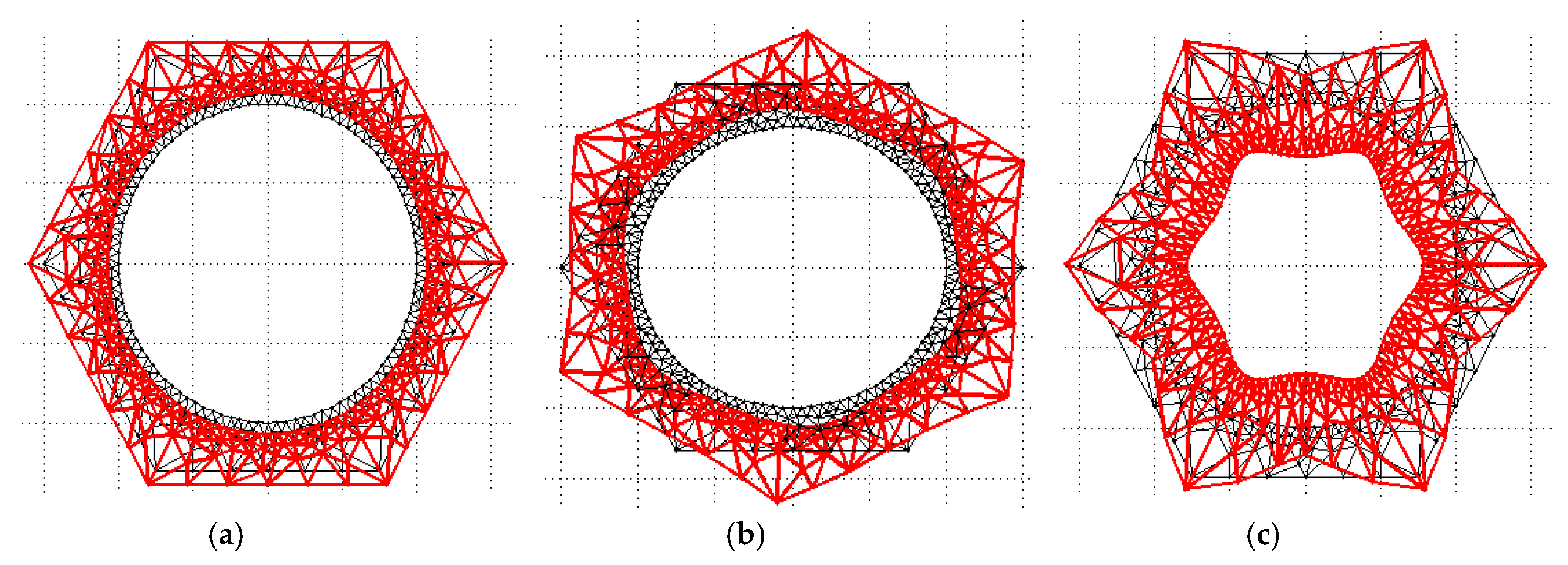
2.1. SAFE Formulations
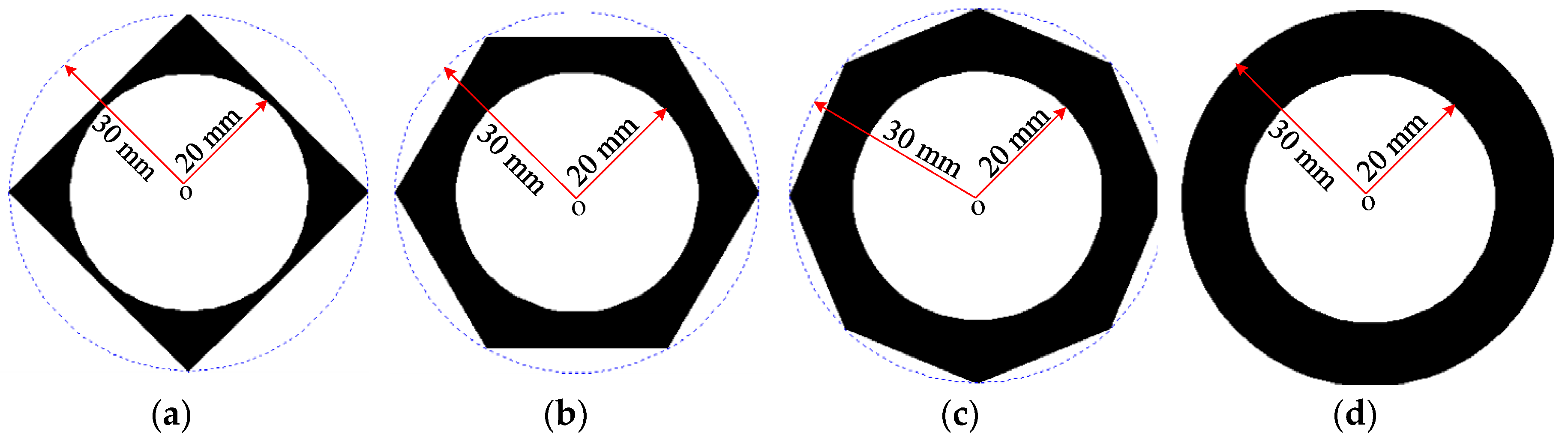
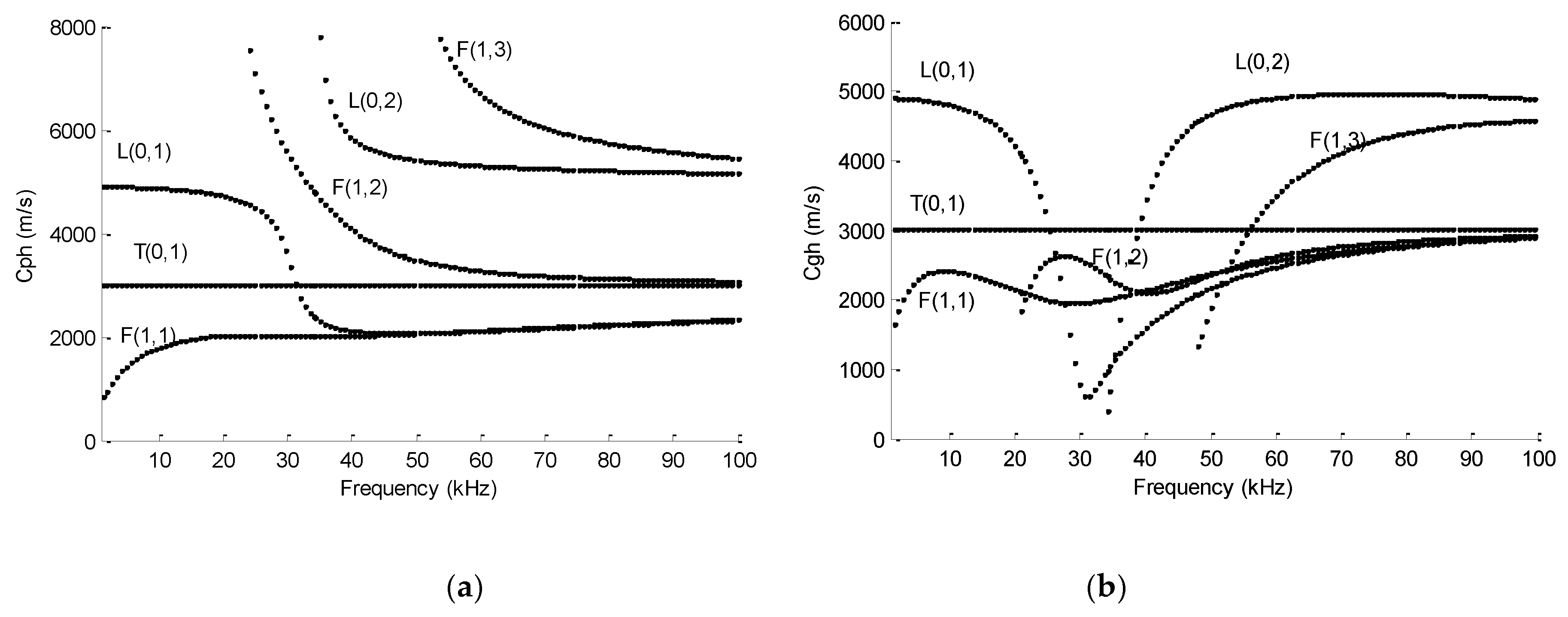
2.2. Phase and Group Velocity Dispersion Curves in Polygonal Drill Pipes
3. Numerical Setups
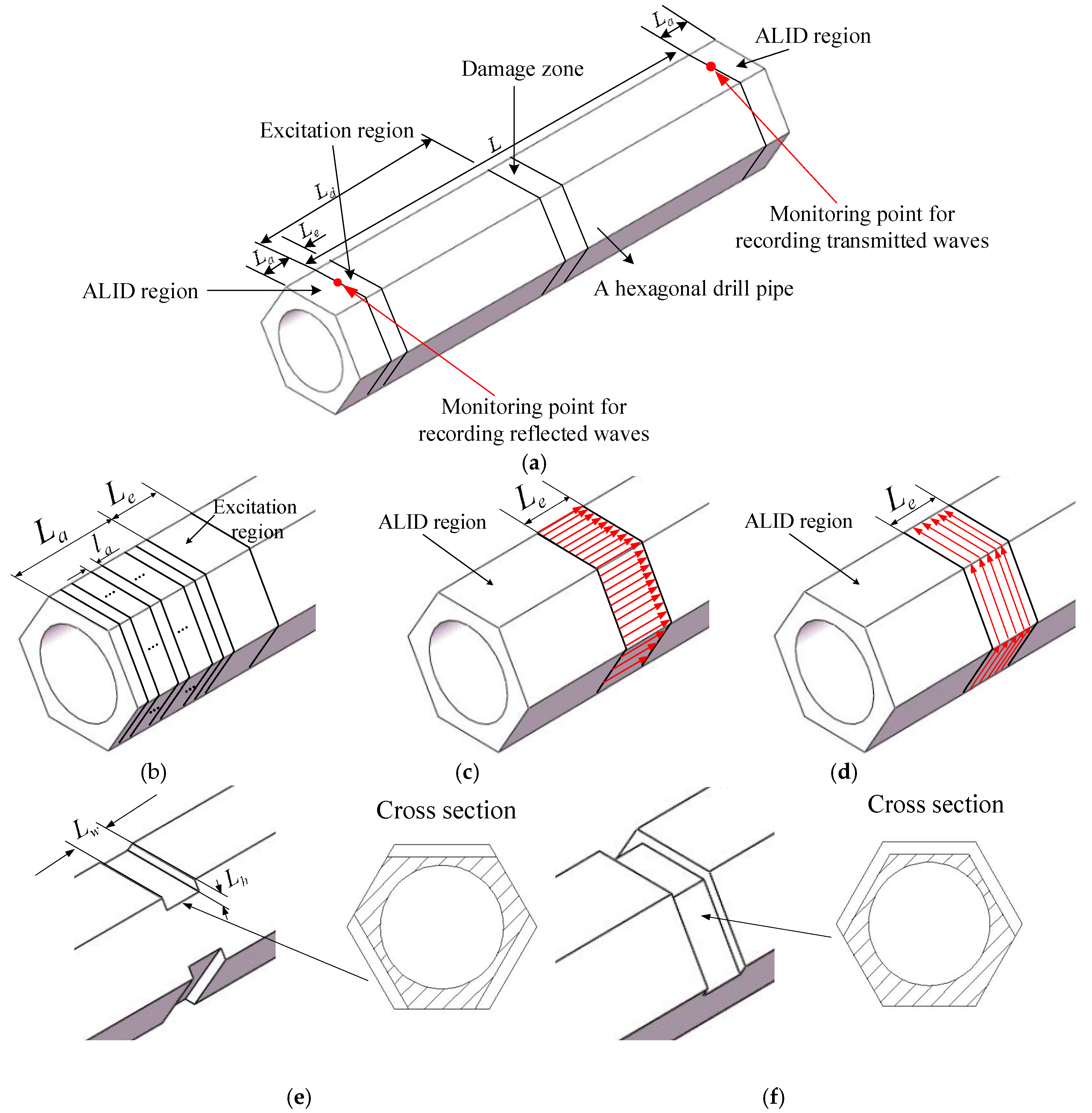
3.1. The ALID Technique
3.2. FE Model
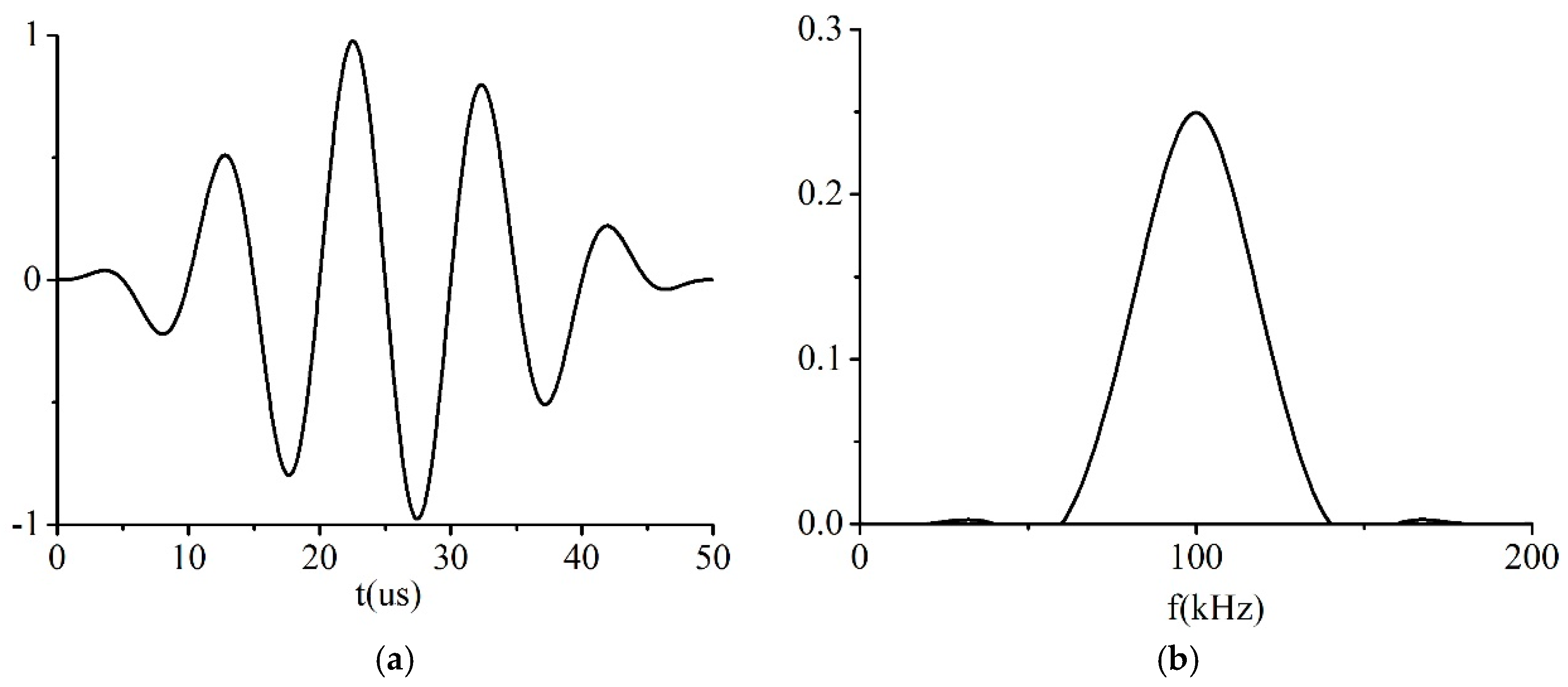
3.3. Excitation Signal
3.4. Element Size and Time Step
4. Results and Discussions
4.1. Influential Factors on the Ultrasonic Guided Waves Propagating in Polygonal Drill Pipes
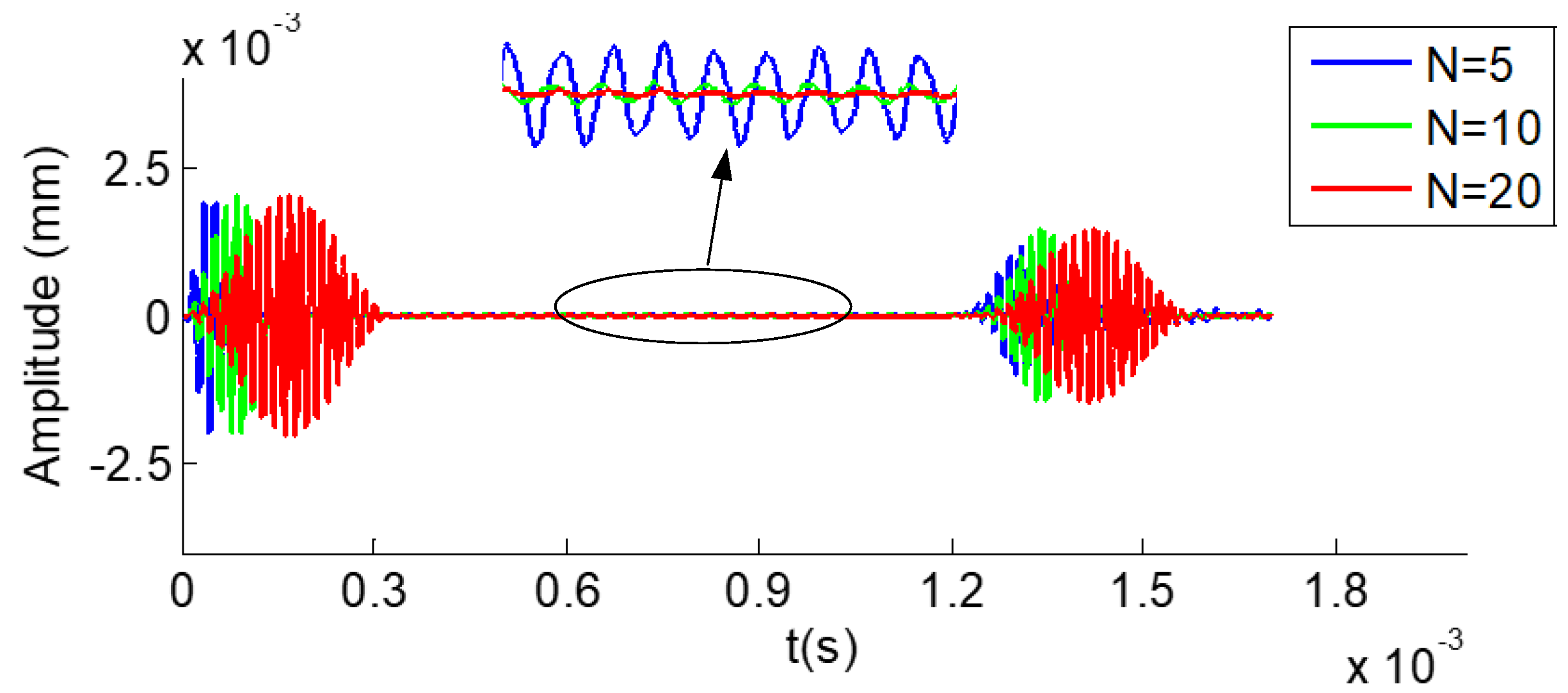
4.1.1. The Influence of the Number of Excitation Burst Cycles on Received Temporal Waveforms
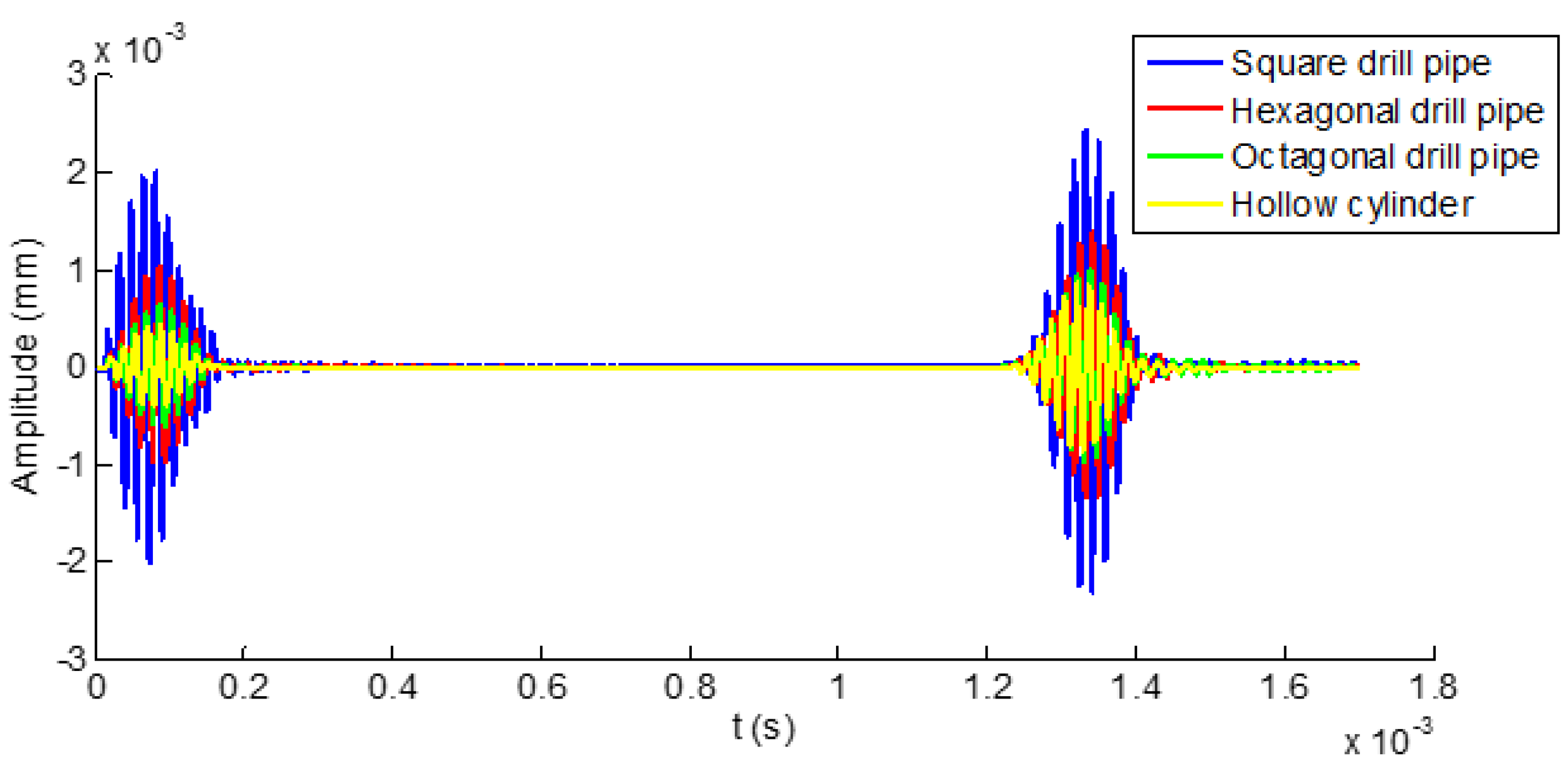
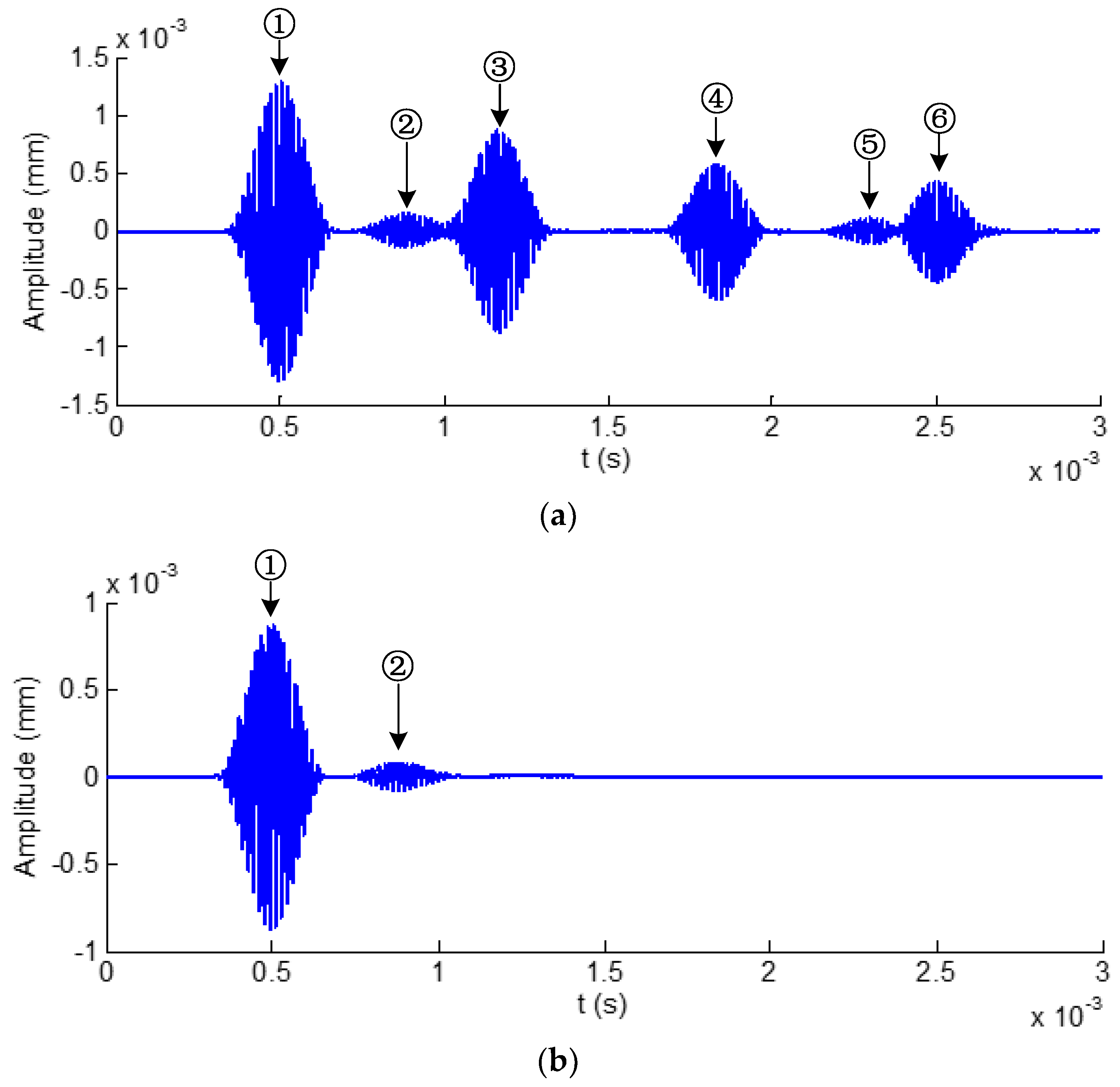
4.1.2. The Influence of the Outer Surfaces of Increasing Edges on Temporal Signals
4.1.3. Temporal Waveforms Received from Normal Hexagonal Drill Pipes with and without ALID Regions
4.2. Ultrasonic Guided Waves Interacting with Damages in Polygonal Drill Pipes
4.2.1. L(0,1) Mode at the Center Frequency of 15 kHz
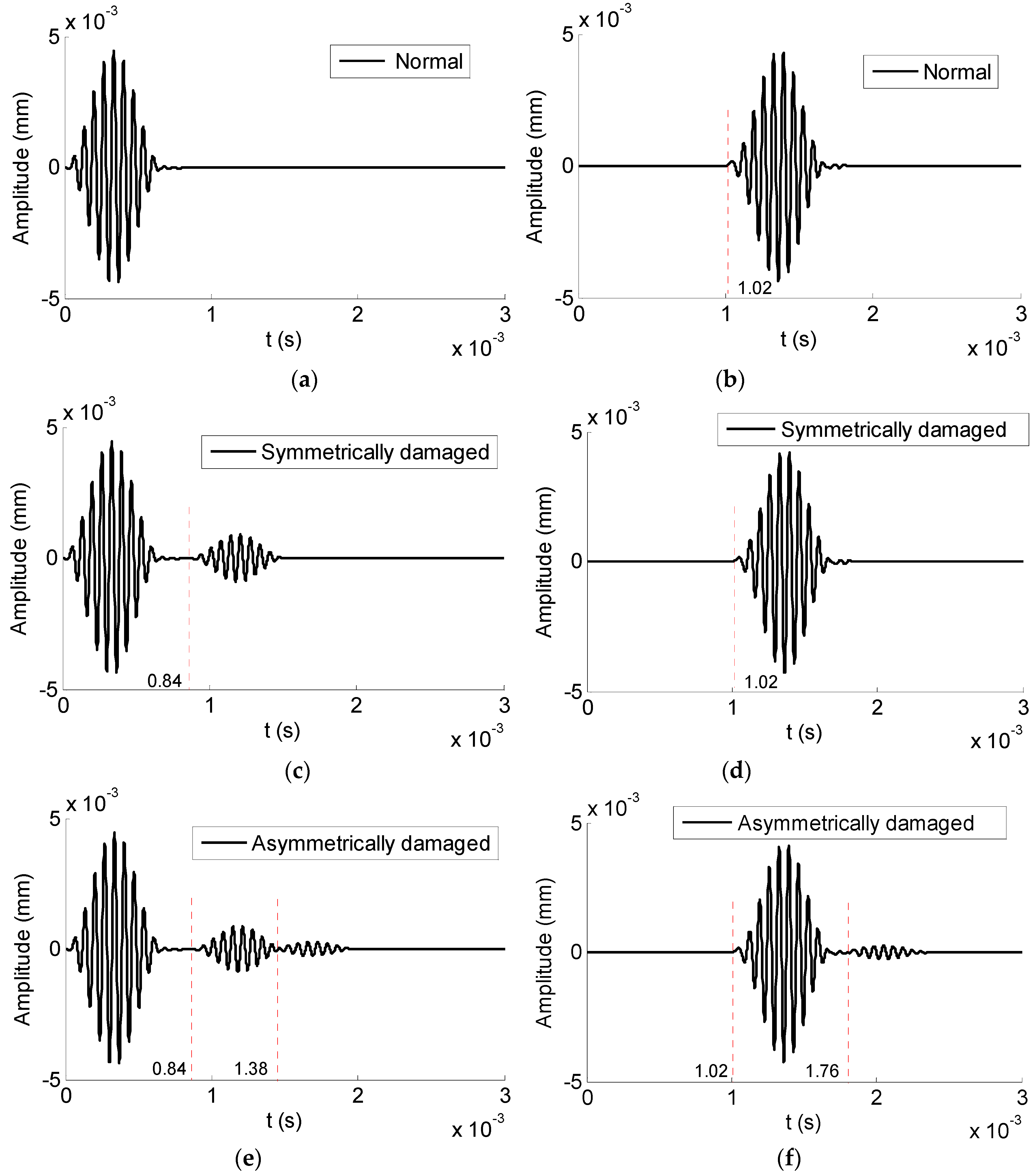
4.2.2. Exciting Longitudinal Modes at the Center Frequency of 60 kHz
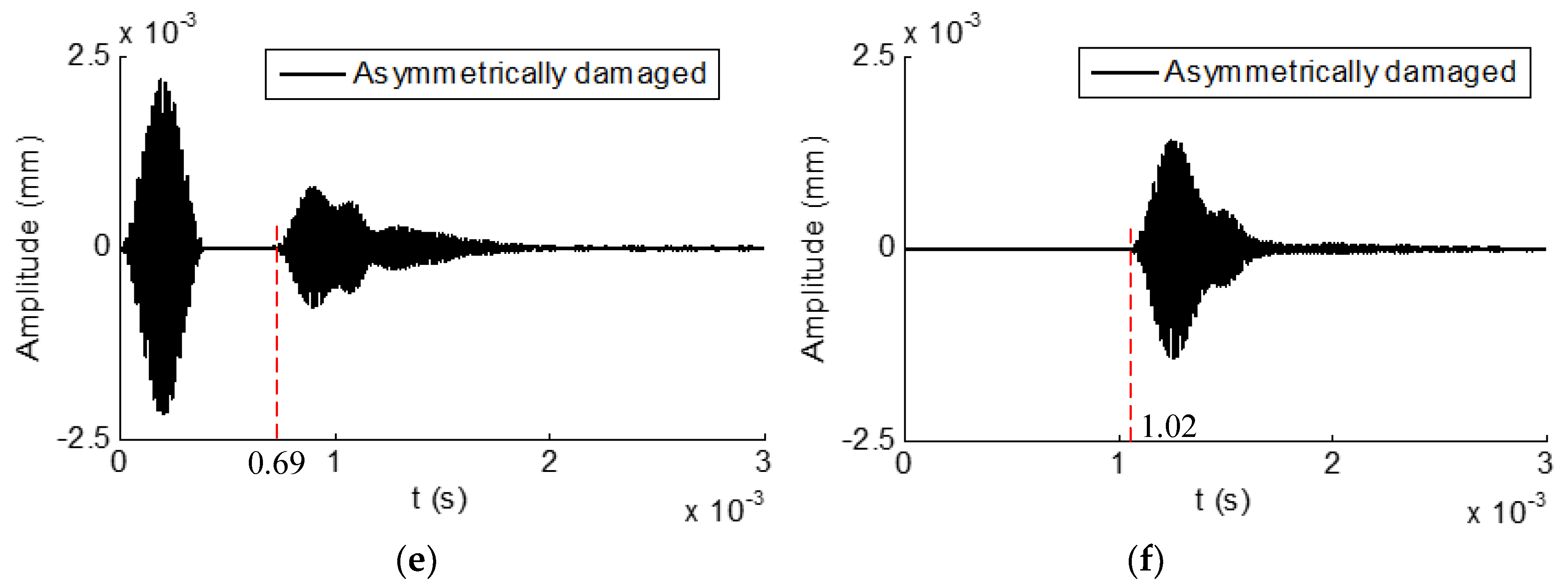
4.2.3. Exciting Torsional Mode at the Center Frequency of 50 kHz
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ushakov, V.M.; Davydova, V.I.; Mikhalev, V.V.; Davydov, D.M. Detection of cracks under threads of studs of power equipment and drill pipes during ultrasonic testing. Russ. J. Nondestruct. Test. 2009, 45, 627–630. [Google Scholar] [CrossRef]
- Tu, J.; Kang, Y.; Wu, J.; Sun, Y. A calibration method based on the reconstruction for automatic ultrasonic flaw detection of the upset region of the drill pipe. Int. J. Appl. Electromagn. Mech. 2014, 45, 131–135. [Google Scholar] [CrossRef]
- Chen, Z.; Co, Y. The detection of corrosion in the inner surface of drill pipes by Ultrasonic phased array technology. Nondestruct. Test. 2014, 36, 60–63. Available online: http://www.cnki.com.cn/Article/CJFDTotal-WSJC201408019.htm (accessed on 6 May 2019). (In Chinese).
- Fakih, M.A.; Mustapha, S.; Tarraf, J.; Ayoub, G.; Hamade, R. Detection and assessment of flaws in friction stir welded joints using ultrasonic guided waves: experimental and finite element analysis. Mech. Syst. Sig. Process. 2018, 101, 516–534. [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, Z. Quantitative characterization of disbonds in multilayered bonded composites using laser ultrasonic guided waves. NDT E Int. 2018, 97, 42–50. [Google Scholar] [CrossRef]
- Lais, H.; Lowe, P.S.; Gan, T.-H.; Wrobel, L.C.; Kanfoud, J. Characterization of the Use of Low Frequency Ultrasonic Guided Waves to Detect Fouling Deposition in Pipelines. Sensors 2018, 18, 2122. [Google Scholar] [CrossRef]
- Yan, S.; Zhang, B.; Song, G.; Lin, J. PZT-Based Ultrasonic Guided Wave Frequency Dispersion Characteristics of Tubular Structures for Different Interfacial Boundaries. Sensors 2018, 18, 4111. [Google Scholar] [CrossRef]
- Wan, X.; Tse, P.W.T.; Xu, G.H.; Tao, T.F.; Zhang, Q. Analytical and numerical studies of approximate phase velocity matching based nonlinear S0 mode Lamb waves for the detection of evenly distributed microstructural changes. Smart Mater. Struct. 2016, 25, 45023. [Google Scholar] [CrossRef]
- De Luca, A.; Caputo, F.; Khodaei, Z.S.; Aliabadi, M. Damage characterization of composite plates under low velocity impact using ultrasonic guided waves. Compos. Part B: Eng. 2018, 138, 168–180. [Google Scholar] [CrossRef]
- Zou, F.; Rao, J.; Aliabadi, M. Highly accurate online characterisation of cracks in plate-like structures. NDT E Int. 2018, 94, 1–12. [Google Scholar] [CrossRef]
- Wan, X.; Tse, P.W.; Zhang, X.; Xu, G.; Zhang, Q.; Fan, H.; Mao, Q.; Dong, M.; Wang, C.; Ma, H. Numerical study on static component generation from the primary Lamb waves propagating in a plate with nonlinearity. Smart Mater. Struct. 2018, 27, 045006. [Google Scholar] [CrossRef] [Green Version]
- Wan, X.; Zhang, Q.; Xu, G.; Tse, P.W.T. Numerical Simulation of Nonlinear Lamb Waves Used in a Thin Plate for Detecting Buried Micro-Cracks. Sensors 2014, 14, 8528–8546. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heinlein, S.; Cawley, P.; Vogt, T.; Burch, S. Blind trial validation of a guided wave structural health monitoring system for pipework. Mater. Eval. 2018, 76, 1118–1126. [Google Scholar]
- Heinlein, S.; Cawley, P.; Vogt, T. Reflection of torsional T(0,1) guided waves from defects in pipe bends. NDT E Int. 2018, 93, 57–63. [Google Scholar] [CrossRef] [Green Version]
- Tse, P.W.T.; Liu, X.C.; Liu, Z.H.; Wu, B.; He, C.F.; Wang, X.J. An innovative design for using flexible printed coils for magnetostrictive-based longitudinal guided wave sensors in steel strand inspection. Smart Mater. Struct. 2011, 20, 55001. [Google Scholar] [CrossRef]
- Wang, X.; Tse, P.W.T.; Mechefske, C.K.; Hua, M. Experimental investigation of reflection in guided wave-based inspection for the characterization of pipeline defects. NDT E Int. 2010, 43, 365–374. [Google Scholar] [CrossRef]
- Loveday, P.W.; Long, C.S.; Ramatlo, D.A. Mode repulsion of ultrasonic guided waves in rails. Ultrasonics 2018, 84, 341–349. [Google Scholar] [CrossRef]
- Bartoli, I.; Marzani, A.; Di Scalea, F.L.; Viola, E. Modeling wave propagation in damped waveguides of arbitrary cross-section. J. Sound 2006, 295, 685–707. [Google Scholar] [CrossRef]
- Mazzotti, M.; Marzani, A.; Bartoli, I.; Viola, E. Guided waves dispersion analysis for prestressed viscoelastic waveguides by means of the SAFE method. Int. J. Solids Struct. 2012, 49, 2359–2372. [Google Scholar] [CrossRef] [Green Version]
- Hayashi, T.; Tamayama, C.; Murase, M. Wave structure analysis of guided waves in a bar with an arbitrary cross-section. Ultrasonics 2006, 44, 17–24. [Google Scholar] [CrossRef]
- Hayashi, T.; Song, W.J.; Rose, J.L. Guided wave dispersion curves for a bar with an arbitrary cross-section, a rod and rail example. Ultrasonics 2004, 41, 175–183. [Google Scholar] [CrossRef]
- Bocchini, P.; Marzani, A.; Viola, E. Graphical user interface for guided acoustic waves. J. Comput. Civil Eng. 2010, 25, 202–210. [Google Scholar] [CrossRef]
- Drozdz, M.B. Efficient Finite Element Modelling of Ultrasound Waves in Elastic Media. Ph.D. Thesis, Imperial College London, London, UK, 2008. [Google Scholar]
- Wan, X.; Xu, G.; Zhang, Q.; Tse, P.W.T.; Tan, H. A quantitative method for evaluating numerical simulation accuracy of time-transient Lamb wave propagation with its applications to selecting appropriate element size and time step. Ultrasonics 2016, 64, 25–42. [Google Scholar] [CrossRef] [PubMed]
- Moser, F.; Jacobs, L.J.; Qu, J. Modeling elastic wave propagation in waveguides with the finite element method. NDT E Int. 1999, 32, 225–234. [Google Scholar] [CrossRef]
- Tang, S.; Tse, P.; Wang, X. The revelation of propagating ultrasonic guided waves through simulation when they encountered defects in a pipe. In Proceedings of the ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, San Diego, CA, USA, 30 August–2 September 2009. [Google Scholar]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, X.; Zhang, X.; Fan, H.; Tse, P.W.; Dong, M.; Ma, H. Numerical Study on Ultrasonic Guided Waves for the Inspection of Polygonal Drill Pipes. Sensors 2019, 19, 2128. https://doi.org/10.3390/s19092128
Wan X, Zhang X, Fan H, Tse PW, Dong M, Ma H. Numerical Study on Ultrasonic Guided Waves for the Inspection of Polygonal Drill Pipes. Sensors. 2019; 19(9):2128. https://doi.org/10.3390/s19092128
Chicago/Turabian StyleWan, Xiang, Xuhui Zhang, Hongwei Fan, Peter W. Tse, Ming Dong, and Hongwei Ma. 2019. "Numerical Study on Ultrasonic Guided Waves for the Inspection of Polygonal Drill Pipes" Sensors 19, no. 9: 2128. https://doi.org/10.3390/s19092128
APA StyleWan, X., Zhang, X., Fan, H., Tse, P. W., Dong, M., & Ma, H. (2019). Numerical Study on Ultrasonic Guided Waves for the Inspection of Polygonal Drill Pipes. Sensors, 19(9), 2128. https://doi.org/10.3390/s19092128






