An Efficient Hybrid RSS-AoA Localization for 3D Wireless Sensor Networks
Abstract
1. Introduction
- (i)
- We introduce a 3D hybrid localization that combines the RSS and the AoA measurements, where the channel parameters, i.e., the transmit power and the path loss exponent (PLE) are unknown.
- (ii)
- We propose a fast and accurate localization scheme where an unbiased solution is developed based on the hybrid measurements. In particular, we transform the original maximum likelihood estimator (MLE), which is non-convex and difficult to solve, into an alternative form after some suitable approximations, then apply a certain numerical optimization.
- (iii)
- We derive the Cramer–Rao lower bound (CRLB) and geometric dilution of precision (GDoP) analysis for the proposed weighted least squares (WLS).
- (iv)
- In the simulation results, we compare our work with other existing localization approaches under some likely practical conditions in terms of root mean squared error and bias.
2. System Description and Related Works
2.1. Notations
2.2. Problem Formulation
2.3. Strategy for Parameter Estimation
- Step 1: Set up initial guessing intervals for both and , and pick and .
- Step 2: Solve (3) using to obtain an estimate for .
- Step 3: Use to obtain the linear solutions for by the following.where . If either or does not lie in the predefined interval, i.e., or , then stop the iteration. Otherwise, go to the next step.
- Step 4: Use the update to solve (3) again and get a new update for , . Then, check the stopping criteria: stop if or , otherwise, , and go to Step 2.
2.4. Related Works
3. The Proposed Weighted Least Squares Approach
3.1. An Inspiring Example
3.2. Issues and Motivations
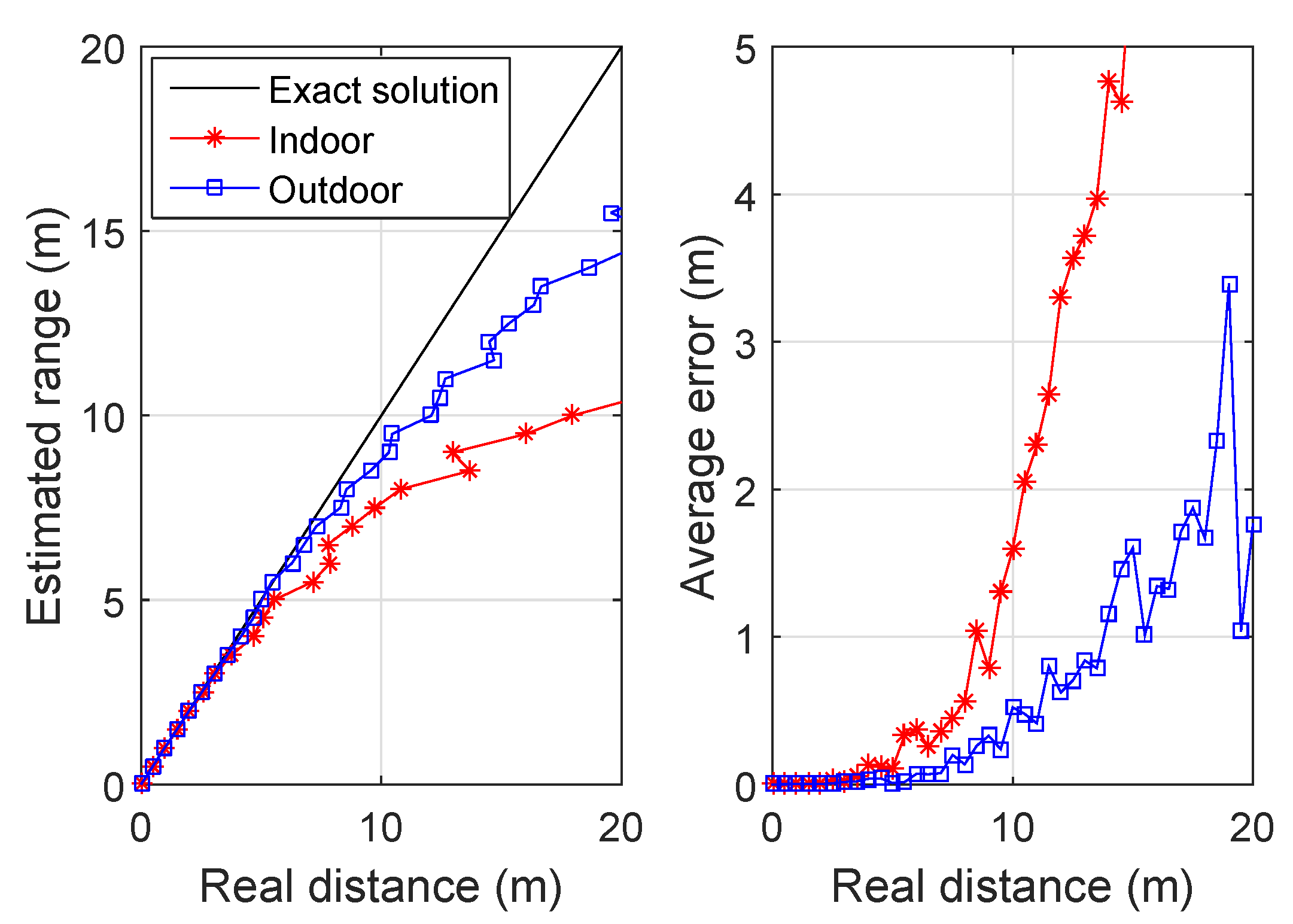
3.3. Quantized RSS-Based Ranging
3.4. Location Estimation
3.5. Linear Approximation and Channel Factor Refinement
3.6. Cramer–Rao Lower Bound for the Proposed Hybrid RSS-AoA Localization
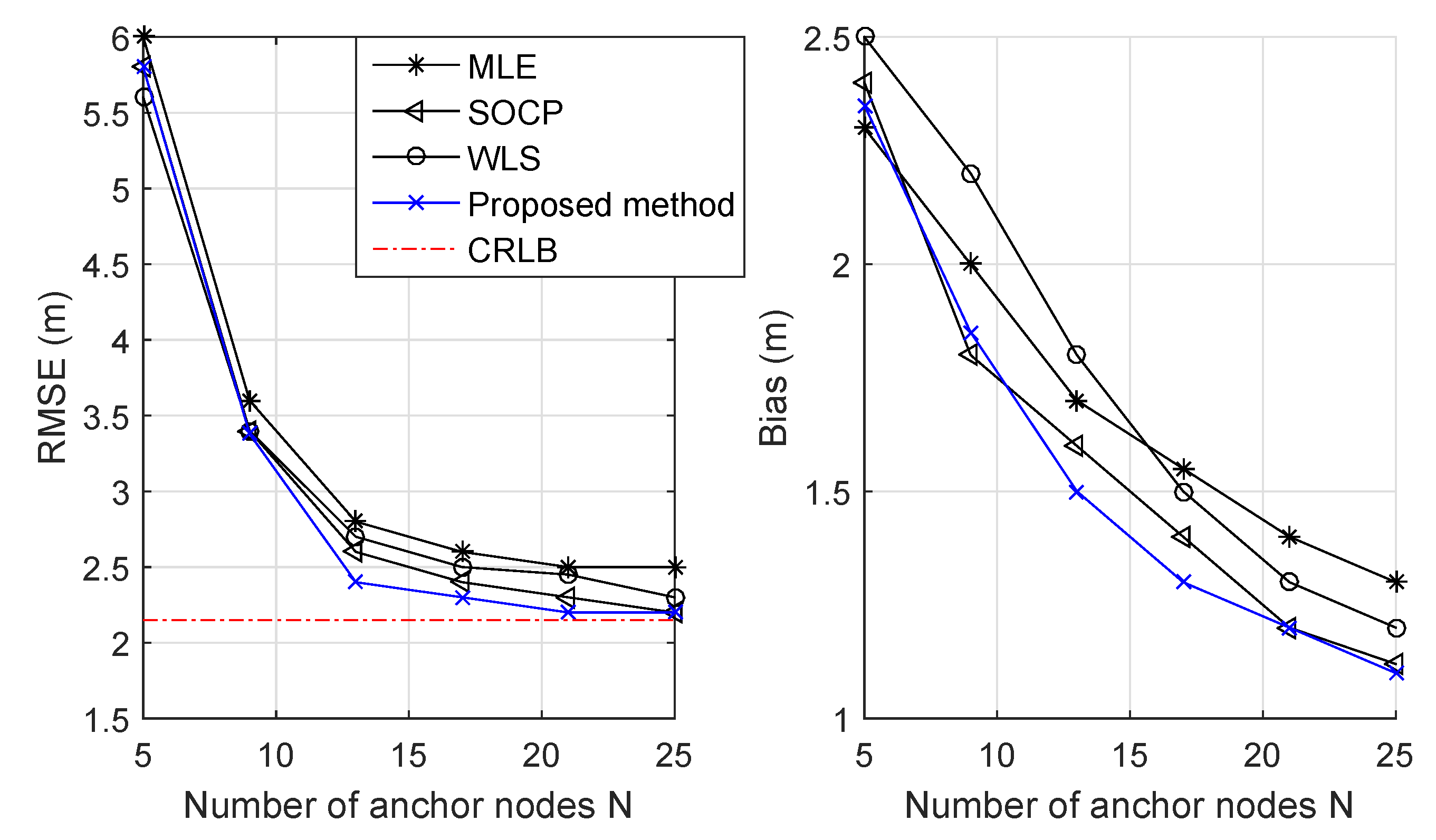
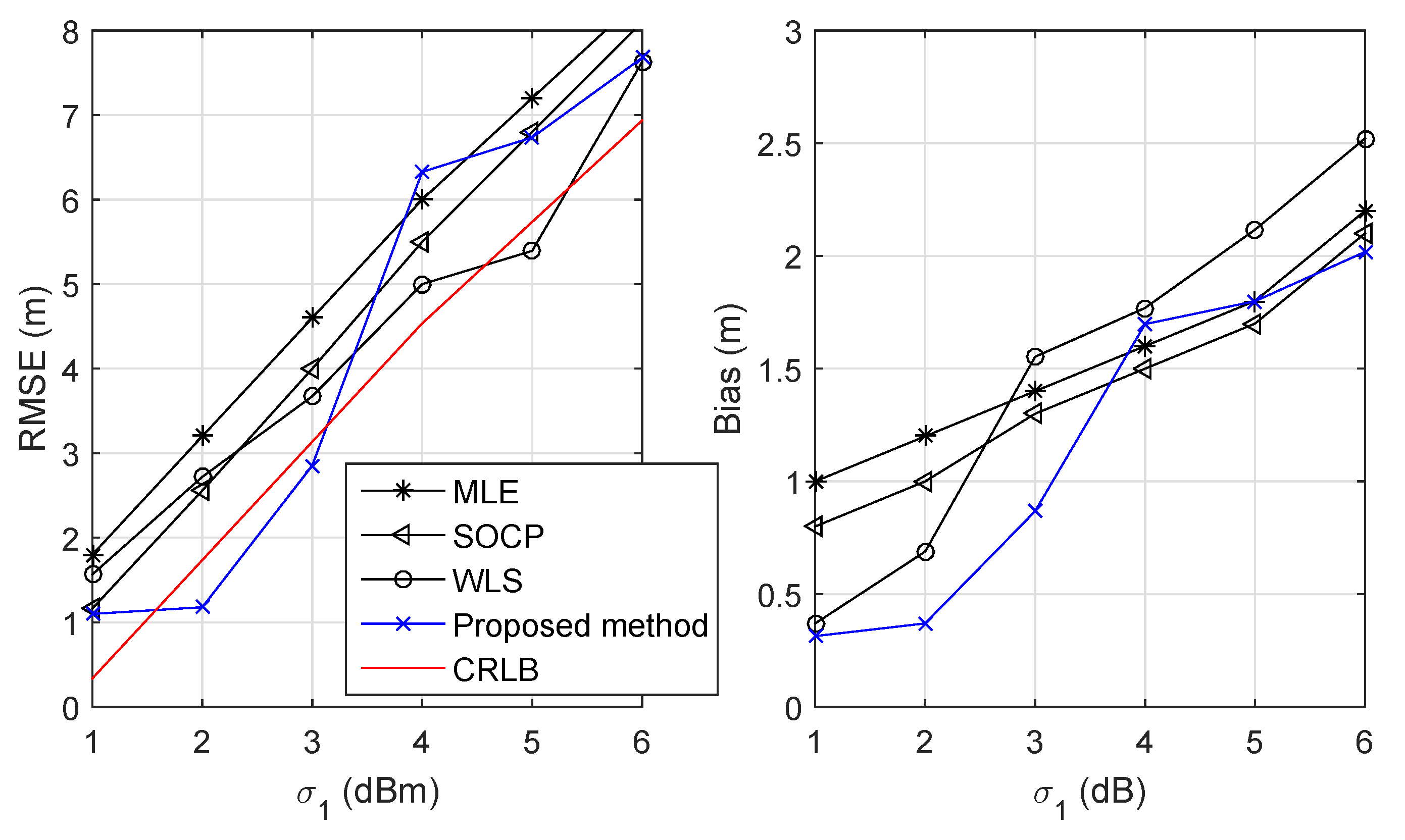
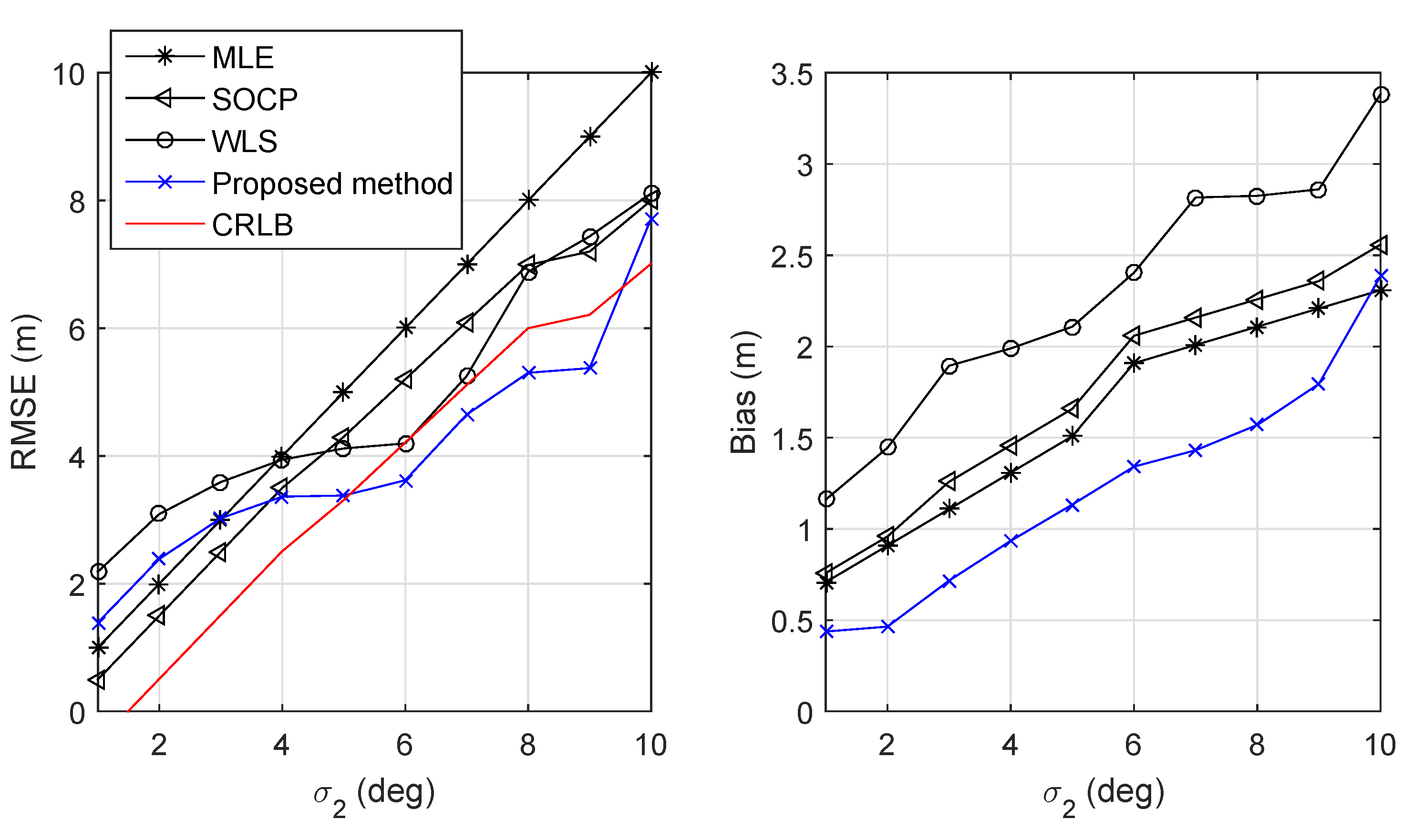
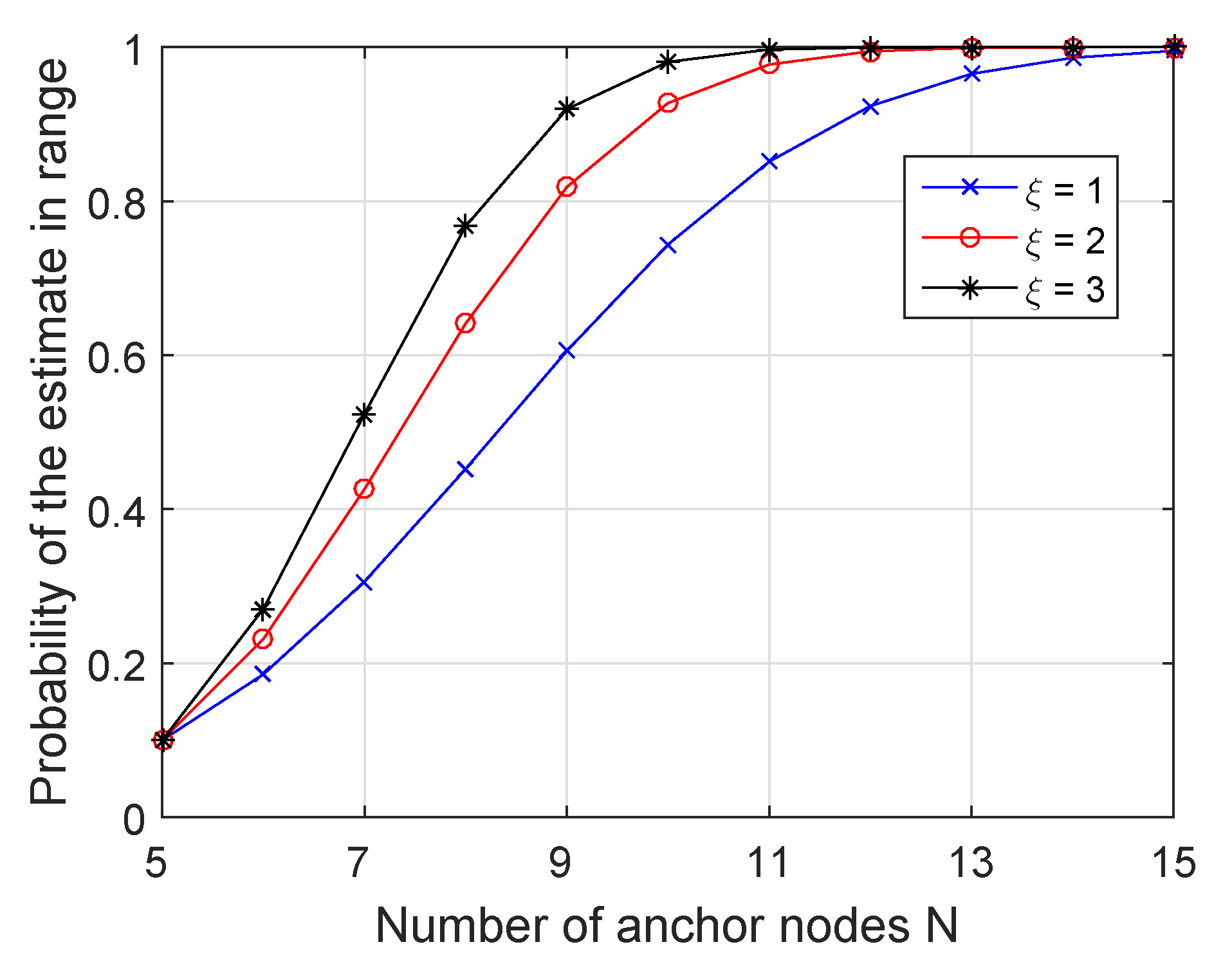
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| 3D | three-dimensional |
| AoA | angle-of-arrival |
| CRLB | Cramer–Rao lower bound |
| GDoP | geometric dilution of precision |
| IoT | Internet-of-things |
| LS | least squares |
| ML | maximum likelihood |
| MLE | maximum likelihood estimator |
| probability density function | |
| PLE | path loss exponent |
| SDP | semi-definite programming |
| SOCP | second-order convex programming |
| RMSE | root mean square error |
| ToA | time-of-arrival |
| TDoA | time-different-of-arrival |
| WLS | weighted least squares |
| WSN | wireless sensor network |
References
- Masazade, E.; Niu, R.; Varshney, P.K.; Keskinoz, M. Energy aware iterative source localization for wireless sensor networks. IEEE Trans. Signal Process. 2010, 58, 4824–4835. [Google Scholar] [CrossRef]
- Niu, R.; Vempaty, A.; Varshney, P.K. Received-signal-strength-based localization in wireless sensor networks. Proc. IEEE 2018, 106, 166–1182. [Google Scholar] [CrossRef]
- Dargie, W.; Poellabauer, C. Fundamentals of Wireless Sensor Networks: Theory and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2011; Chapter 2. [Google Scholar]
- International Electrotechnical Commission. Internet of Things: Wireless Sensor Networks. Available online: https://www.iec.ch/whitepaper/pdf/iecWP-internetofthings-LR-en.pdf (accessed on 6 May 2019).
- Atzori, L.; Iera, A.; Morabito, G. The internet of things: A survey. Comput. Netw. 2010, 54, 2787–2805. [Google Scholar] [CrossRef]
- Nguyen, T.L.N.; Shin, Y. A new approach for positioning based on AOA measurements. In Proceedings of the 2013 International Conference on Computing, Management and Telecommunications (ComManTel), Ho Chi Minh City, Vietnam, 21–24 January 2013; pp. 208–211. [Google Scholar]
- Gu¨venc, I.; Chong, C. A survey on TOA based wireless localization and NLOS mitigation techniques. IEEE Commun. Surv. Tutor. 2009, 11, 107–124. [Google Scholar] [CrossRef]
- Xu, J.; Ma, M.; Law, C.L. AOA cooperative position location. In Proceedings of the IEEE GLOBECOM 2008—2008 IEEE Global Telecommunications Conference, New Orleans, LO, USA, 30 November–4 December 2008; pp. 1–5. [Google Scholar]
- Wang, G.; Chen, H.; Li, Y.; Jin, M. On received-signal-strength based localization with unknown transmit power and path loss exponent. IEEE Wirel. Commun. Lett. 2012, 1, 536–539. [Google Scholar] [CrossRef]
- Dai, W.; Shen, Y.; Win, M.Z. Distributed power allocation for cooperative wireless network localization. IEEE J. Sel. Areas Commun. 2015, 33, 28–40. [Google Scholar] [CrossRef]
- Dogancay, K. 3D pseudolinear target motion analysis from angle measurements. IEEE Trans. Signal Process. 2015, 63, 1570–1580. [Google Scholar] [CrossRef]
- Badriasl, L.; Dogancay, K. Three-dimensional target motion analysis using azimuth/elevation angles. IEEE Aerosp. Electron. Syst. Mag. 2014, 50, 3178–3194. [Google Scholar] [CrossRef]
- Shao, H.J.; Zhang, X.P.; Wang, Z. Efficient closed-form algorithms for AOA based self-localization of sensor nodes using auxiliary variables. IEEE Trans. Signal Process. 2014, 62, 2580–2594. [Google Scholar] [CrossRef]
- Gazzah, L.; Najjar, L.; Besbes, H. Selective hybrid RSS/AOA weighting algorithm for NLOS intra cell localization. In Proceedings of the 2014 IEEE Wireless Communications and Networking Conference (WCNC), Istanbul, Turkey, 6–9 April 2014; pp. 2546–2551. [Google Scholar]
- Chan, Y.T.; Chan, F.; Read, W.; Jackson, B.R.; Lee, B.H. Hybrid localization of an emitter by combining angle-of-arrival and received signal strength measurements. In Proceedings of the 2014 IEEE 27th Canadian Conference on Electrical and Computer Engineering (CCECE), Toronto, ON, Canada, 4–7 May 2014; pp. 1–5. [Google Scholar]
- P, R.; Sichitiu, M.L. Angle of arrival localization for wireless sensor networks. In Proceedings of the 2006 3rd Annual IEEE Communications Society on Sensor and Ad Hoc Communications and Networks, Reston, VA, USA, 28 September 2006; pp. 374–382. [Google Scholar]
- Nasipuri, A.; Li, K. A directionality based location discovery scheme for wireless sensor networks. In Proceedings of the WSNA ’02 Proceedings of the 1st ACM International Workshop on Wireless Sensor Networks and Applications, Atlanta, GA, USA, 28 September 2002; pp. 105–111. [Google Scholar]
- Kim, E.; Yoo, S.; Kim, H.; Kim, H. Enhancing base station connectivity with directional information of movement. ICT Express 2016, 2, 122–125. [Google Scholar] [CrossRef]
- Yu, K. 3-D localization error analysis in wireless networks. IEEE Trans. Wirel. Commun. 2007, 6, 3473–3481. [Google Scholar]
- Wang, S.; Jackson, B.R.; Inkol, R. Hybrid RSS/AOA emitter location estimation based on least squares and maximum likelihood criteria. In Proceedings of the 2012 26th Biennial Symposium on Communications (QBSC), Kingston, ON, Canada, 28–29 May 2012; pp. 24–29. [Google Scholar]
- Tomic, S.; Beko, M.; Dinis, R.; Montezuma, P. A closed-form solution for RSS/AoA target localization by spherical coordinates conversion. IEEE Wirel. Commun. Lett. 2016, 5, 680–683. [Google Scholar] [CrossRef]
- Tomic, S.; Marikj, M.; Beko, M.; Dinis, R.; Orfao, N. Hybrid RSS-AoA technique for 3-D node localization in wireless sensor networks. In Proceedings of the 2015 International Wireless Communications and Mobile Computing Conference (IWCMC), Dubrovnik, Croatia, 24–28 August 2015; pp. 1277–1282. [Google Scholar]
- Tomic, S.; Beko, M.; Dinis, R. 3-D target localization in wireless sensor network using RSS and AoA measurement. IEEE Trans. Veh. Technol. 2017, 66, 3197–3210. [Google Scholar] [CrossRef]
- Multi-Level Solutions for Car Parking. Available online: https://www.nbmcw.com/product/car-parking/29700-multilevel-solutions-for-car-parking.html (accessed on 6 May 2019).
- Cheney, W.; Kincaid, D. Numerical Mathematics and Computing, 6th ed.; Brooks/Cole: Boston, MA, USA, 2008; Chapter 6. [Google Scholar]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming. Available online: http://cvxr.com/cvx (accessed on 6 May 2019).



| Method | Complexity |
|---|---|
| MLE [20] | |
| ine LS [19] | , where is the maximum number of steps in the bisection procedure |
| ine WLS [14] | , where K is the maximum number of steps in the bisection procedure [25] |
| ine SOCP [21] | , where is related to a search interval and the solution precision : is the minimum integer that satisfies . |
| ine Mixed SDP/SOCP [23] | At least |
| ine Proposed method | , where is the maximum number of iterations for solving (14). |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
L. N. Nguyen, T.; D. Vy, T.; Shin, Y. An Efficient Hybrid RSS-AoA Localization for 3D Wireless Sensor Networks. Sensors 2019, 19, 2121. https://doi.org/10.3390/s19092121
L. N. Nguyen T, D. Vy T, Shin Y. An Efficient Hybrid RSS-AoA Localization for 3D Wireless Sensor Networks. Sensors. 2019; 19(9):2121. https://doi.org/10.3390/s19092121
Chicago/Turabian StyleL. N. Nguyen, Thu, Tuan D. Vy, and Yoan Shin. 2019. "An Efficient Hybrid RSS-AoA Localization for 3D Wireless Sensor Networks" Sensors 19, no. 9: 2121. https://doi.org/10.3390/s19092121
APA StyleL. N. Nguyen, T., D. Vy, T., & Shin, Y. (2019). An Efficient Hybrid RSS-AoA Localization for 3D Wireless Sensor Networks. Sensors, 19(9), 2121. https://doi.org/10.3390/s19092121





