Modeling and Experimental Testing of an Unmanned Surface Vehicle with Rudderless Double Thrusters
Abstract
1. Introduction
- (1)
- The three-DOF dynamic model and propeller thrust model are established and combined for a USV with rudderless double thrusters. It guides the modeling of general USVs with rudderless double thrusters.
- (2)
- Since the direction of thrust generated by the propeller is always consistent with the heading of the USV, which makes the USV unstressed in the lateral direction, the three-DOF model simplifies the force analysis and model designing of the USV. It combines the propeller thrust model in which the unknown parameters are reduced from six to two to represent the thrust in more detail.
- (3)
- System identification is utilized to get the parameters of the three-DOF model and propeller thrust model.
- (4)
- Based on the established model, the path-following control of the USV is achieved through PD+LOS control algorithm. It links theory with practice, and provides guidance for the experimental tests.
2. THE FAS-01 USV
2.1. Propulsion System
2.2. Sensing, Communication and GNC System
3. Three-DOF Dynamic Model and Propeller Thrust Model
3.1. Three-DOF Dynamic Model
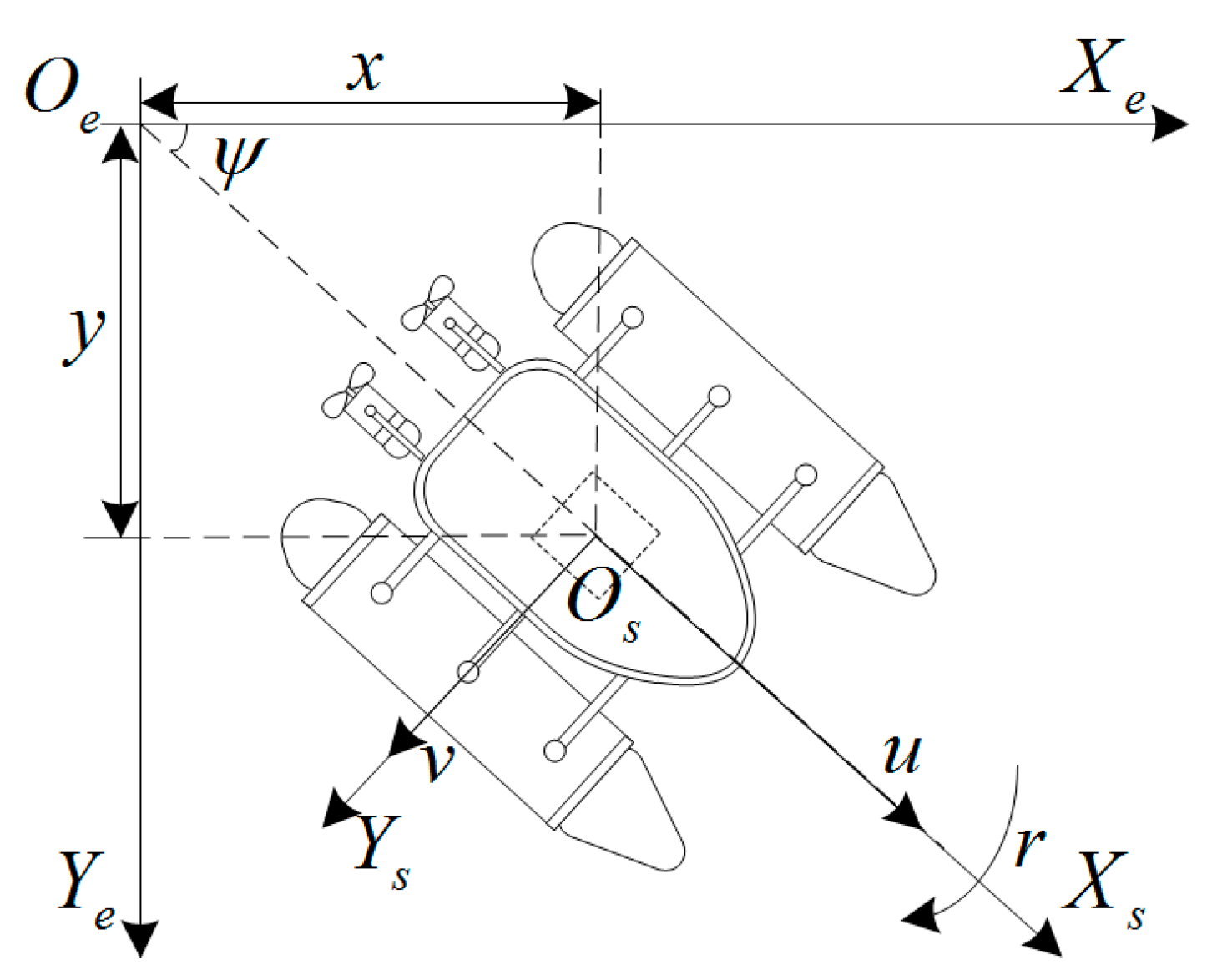
3.1.1. Kinematic
3.1.2. Kinetic
- (1)
- When the USV is slow (the maximum velocity of the USV is 1.5 m/s.), the effect of nonlinear drag term () can be ignored.
- (2)
- Because the effect of off-diagonal terms on the USV’s dynamics is smaller than the diagonal terms, the off-diagonal terms of and can be ignored.
- (3)
- Assuming the coincident center of added mass and gravity can be replaced by . A combination of approximate fore-aft symmetry and light draft suggests that the sway force arising from yaw rotation and the yaw moment induced by the acceleration in the sway direction are much smaller than the inertial and added mass terms. Therefore, in the Coriolis and centripetal matrix , .
- (4)
- Assuming the USV sails in a calm environment, the environmental disturbances can be neglected.
3.2. Propeller Thrust Model
4. System Identification and Experimental Validation
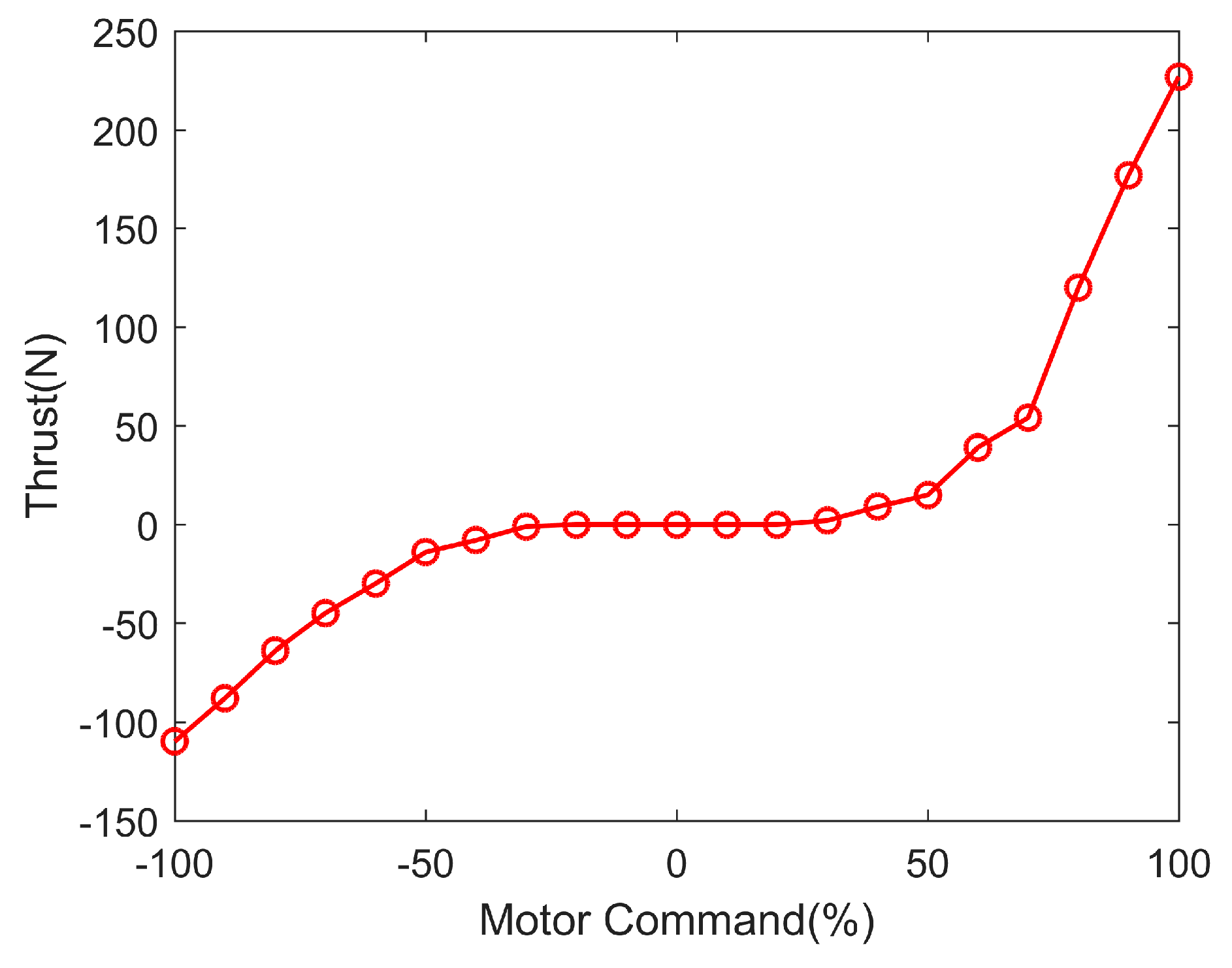
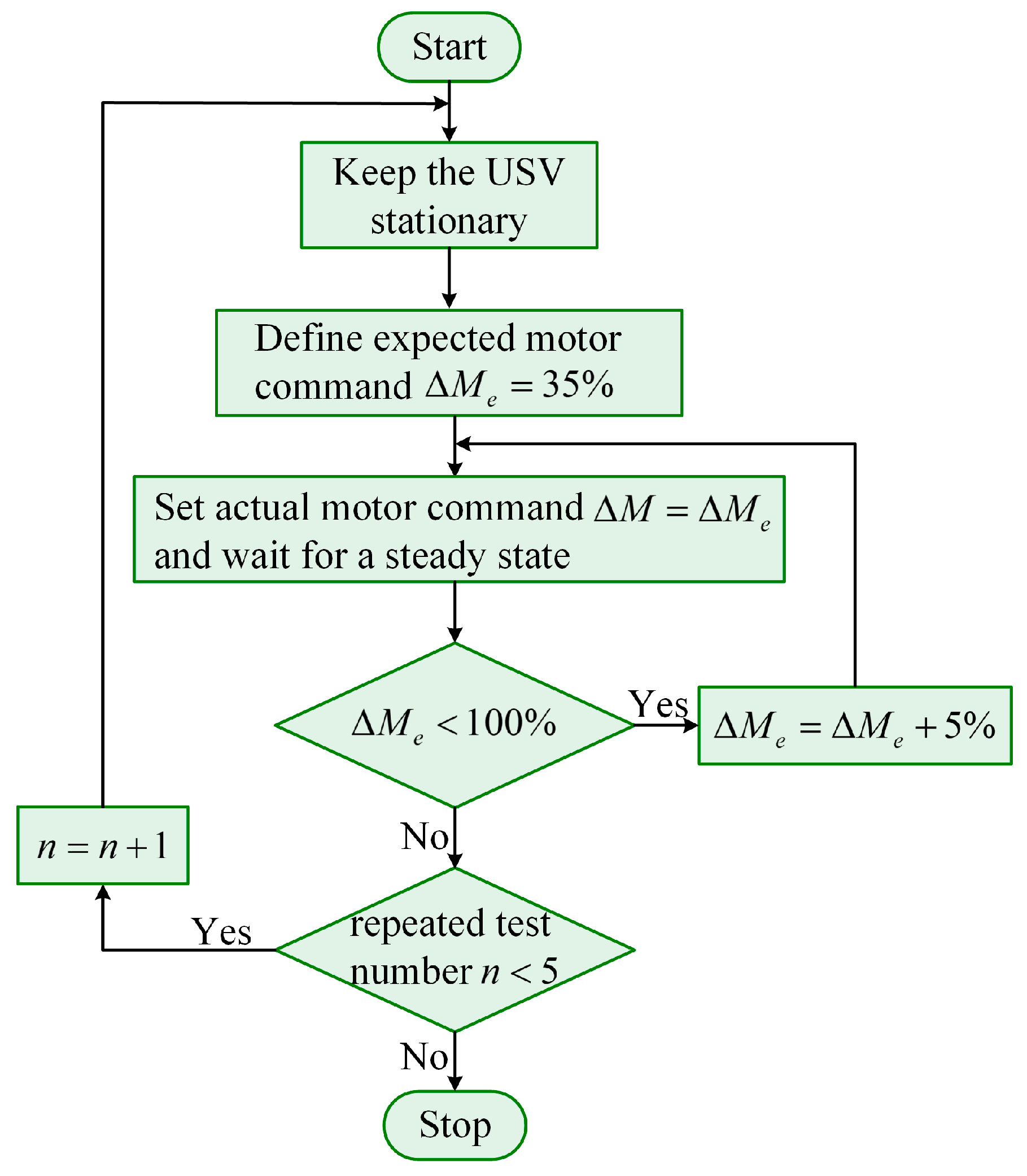
4.1. Thruster Performance Experiment
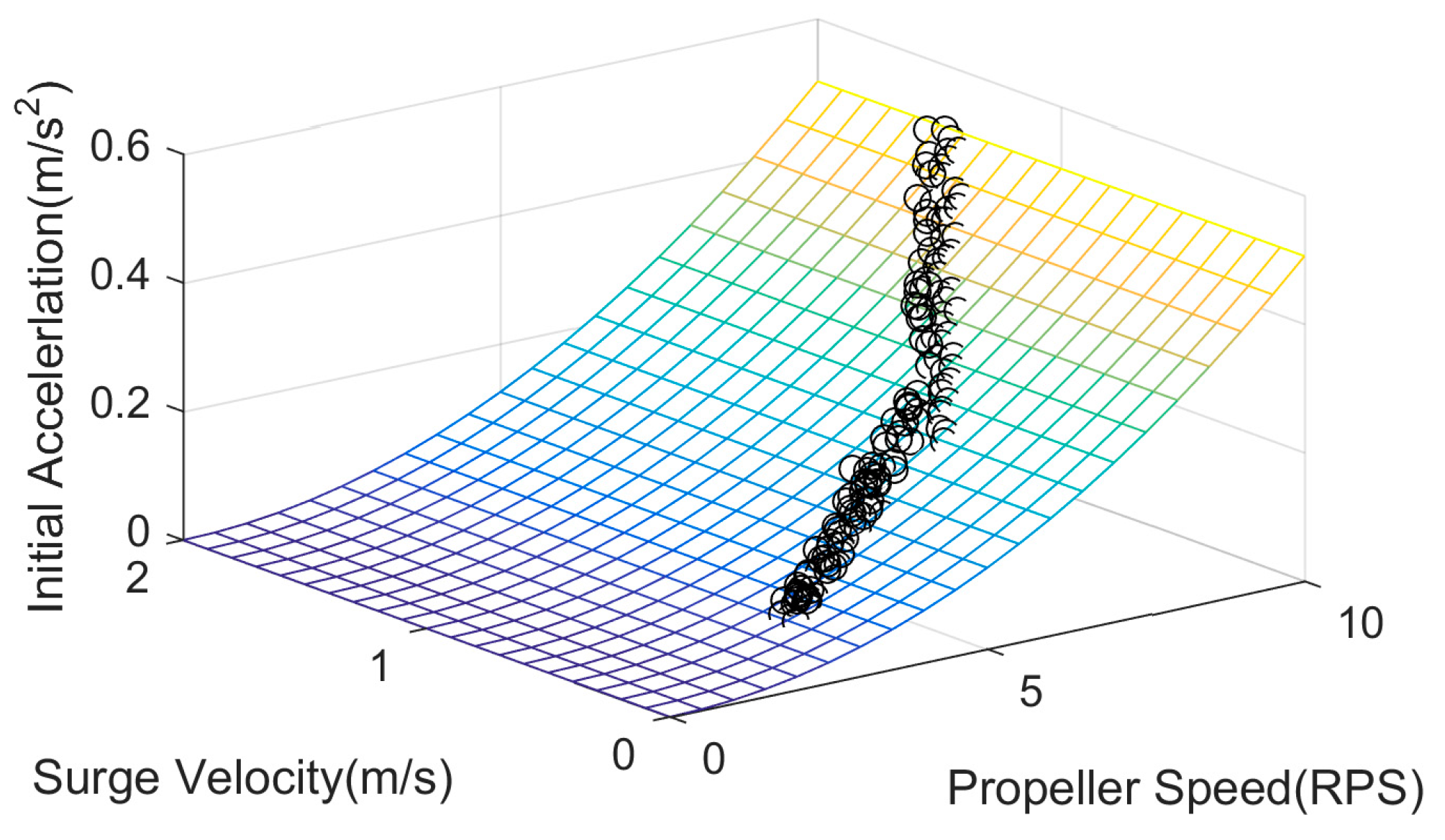
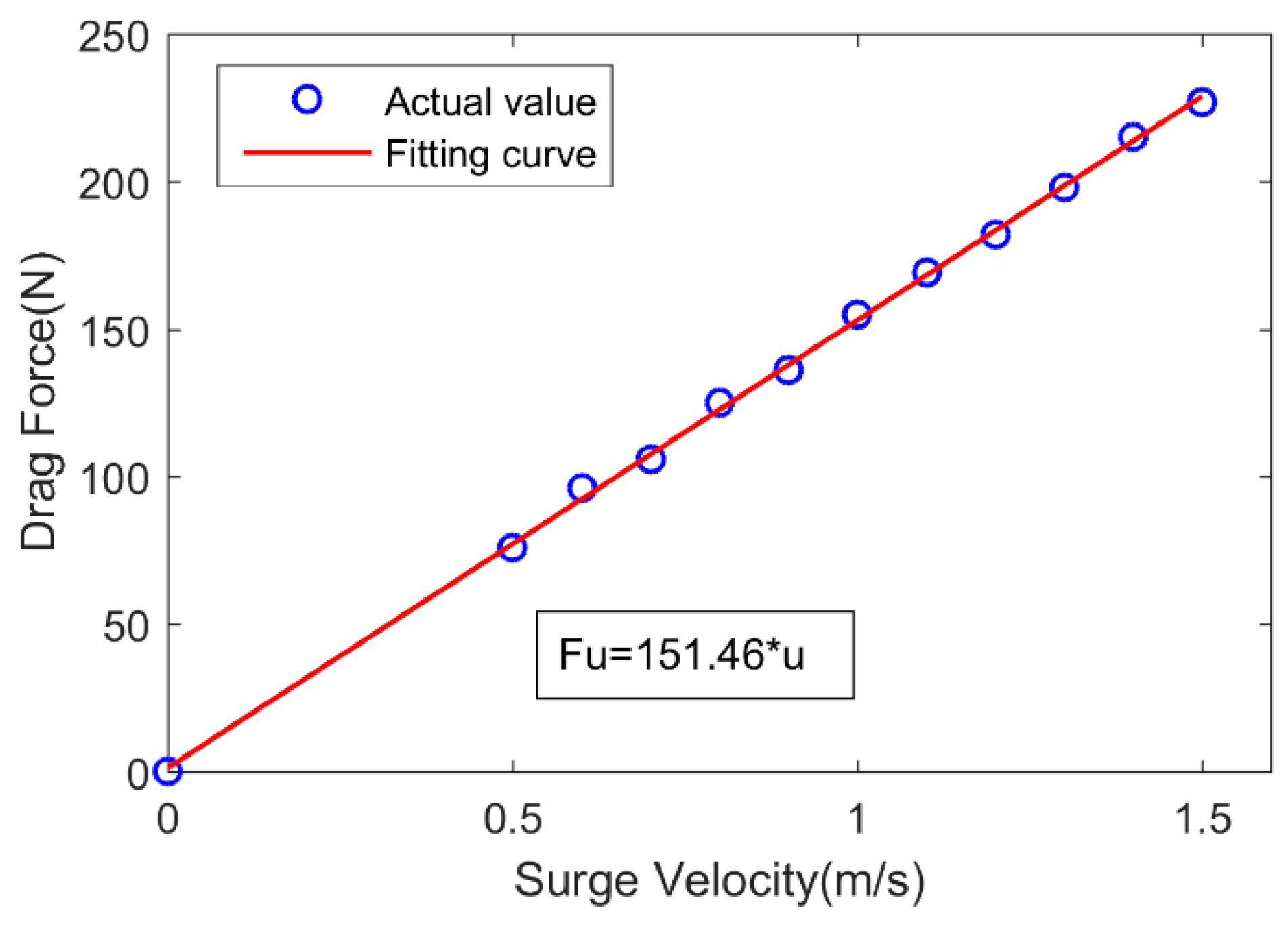
4.2. Propeller Thrust Model Identification
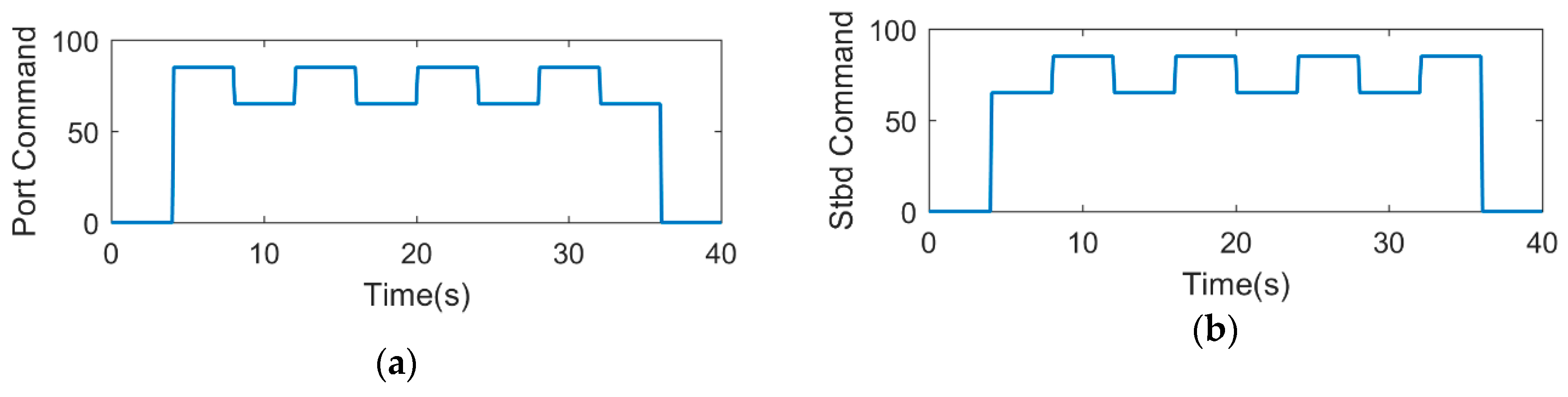
4.3. Three-DOF Model Identification
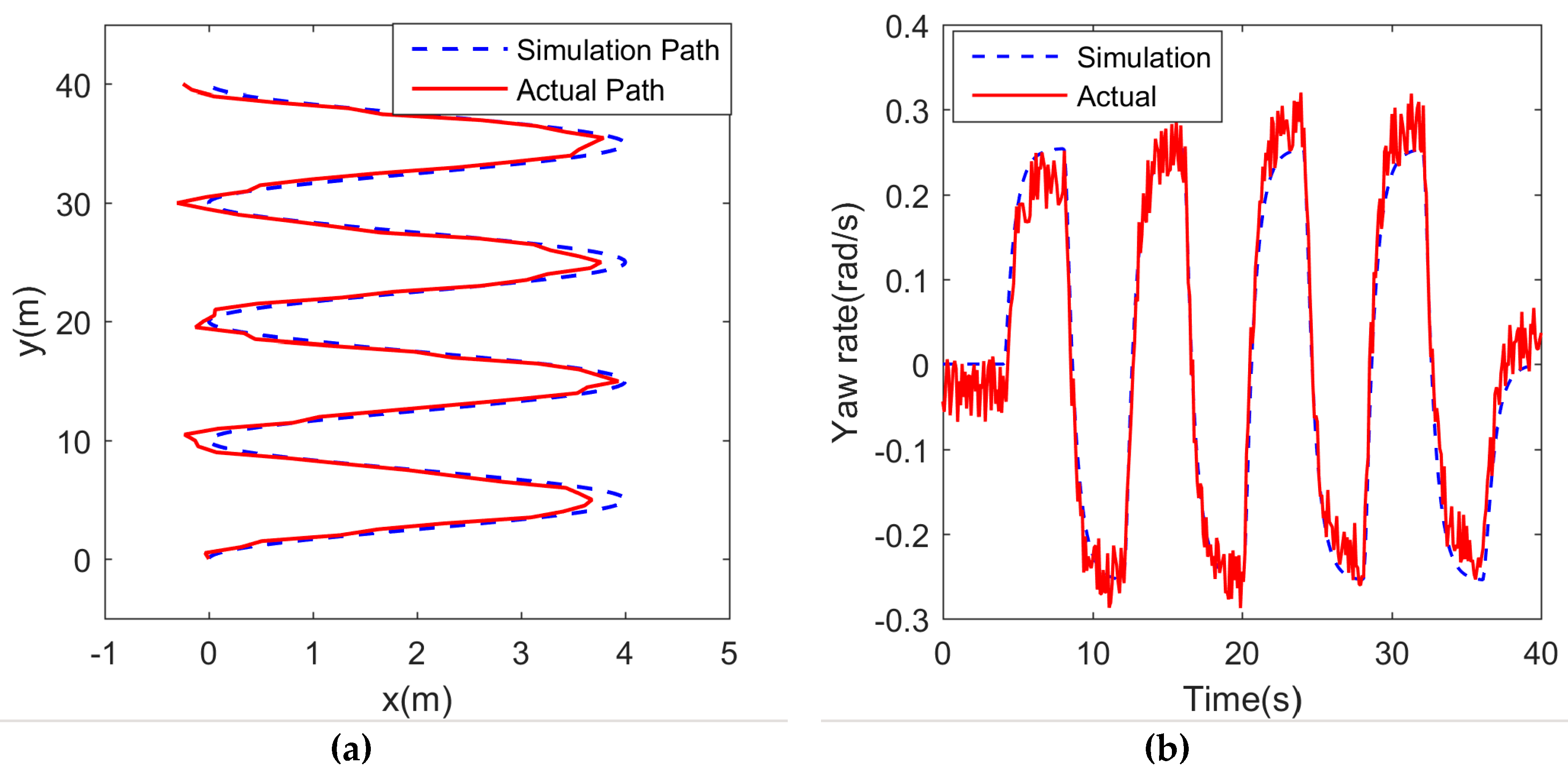
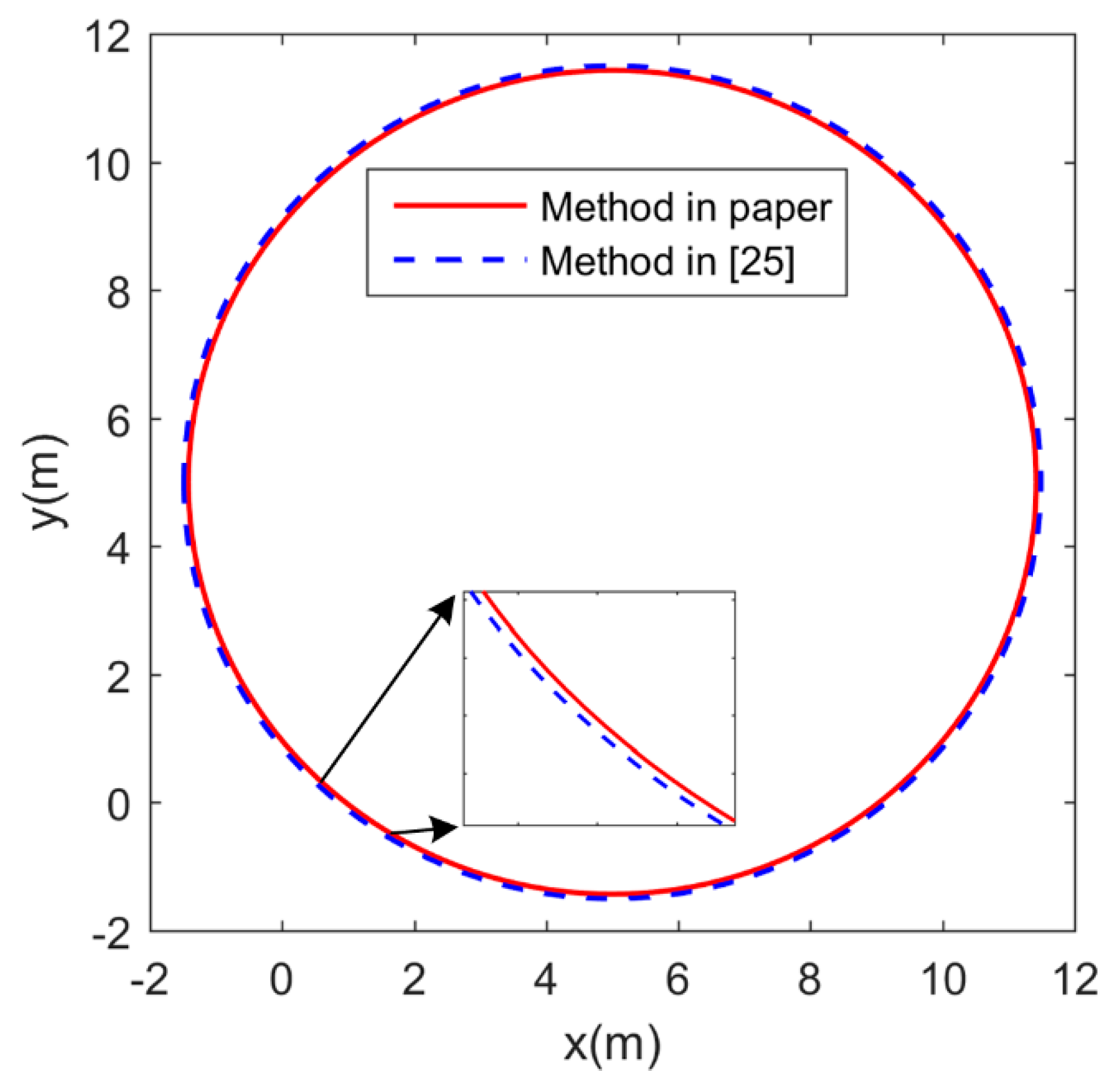
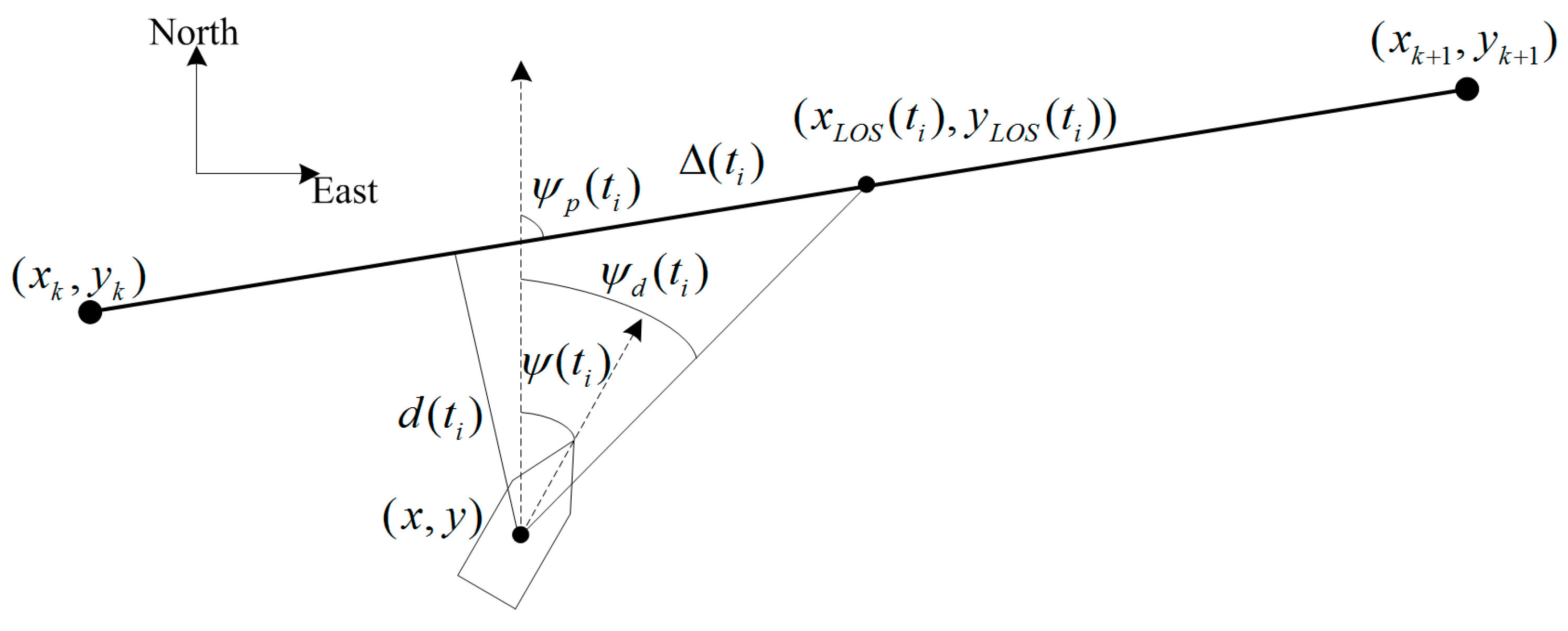
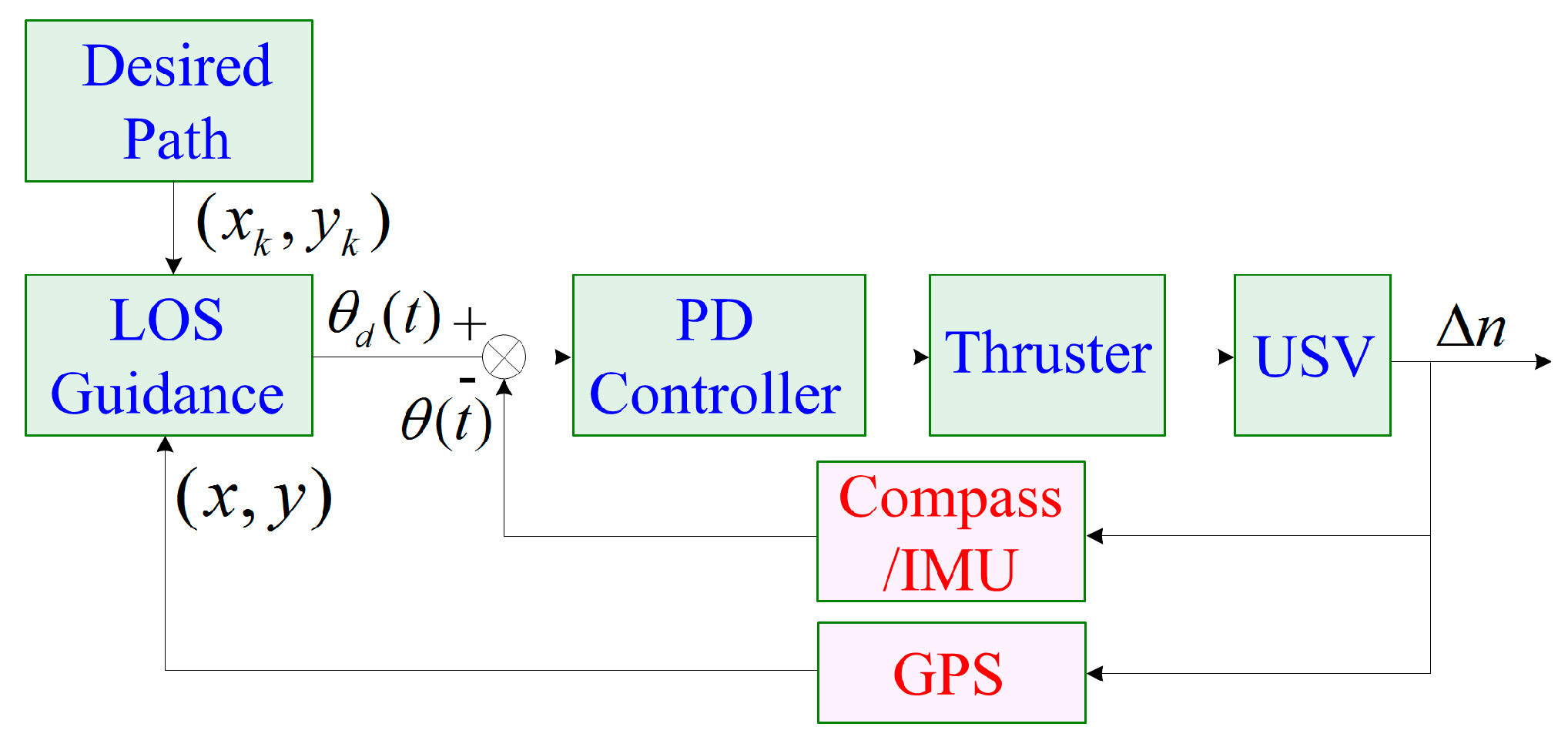
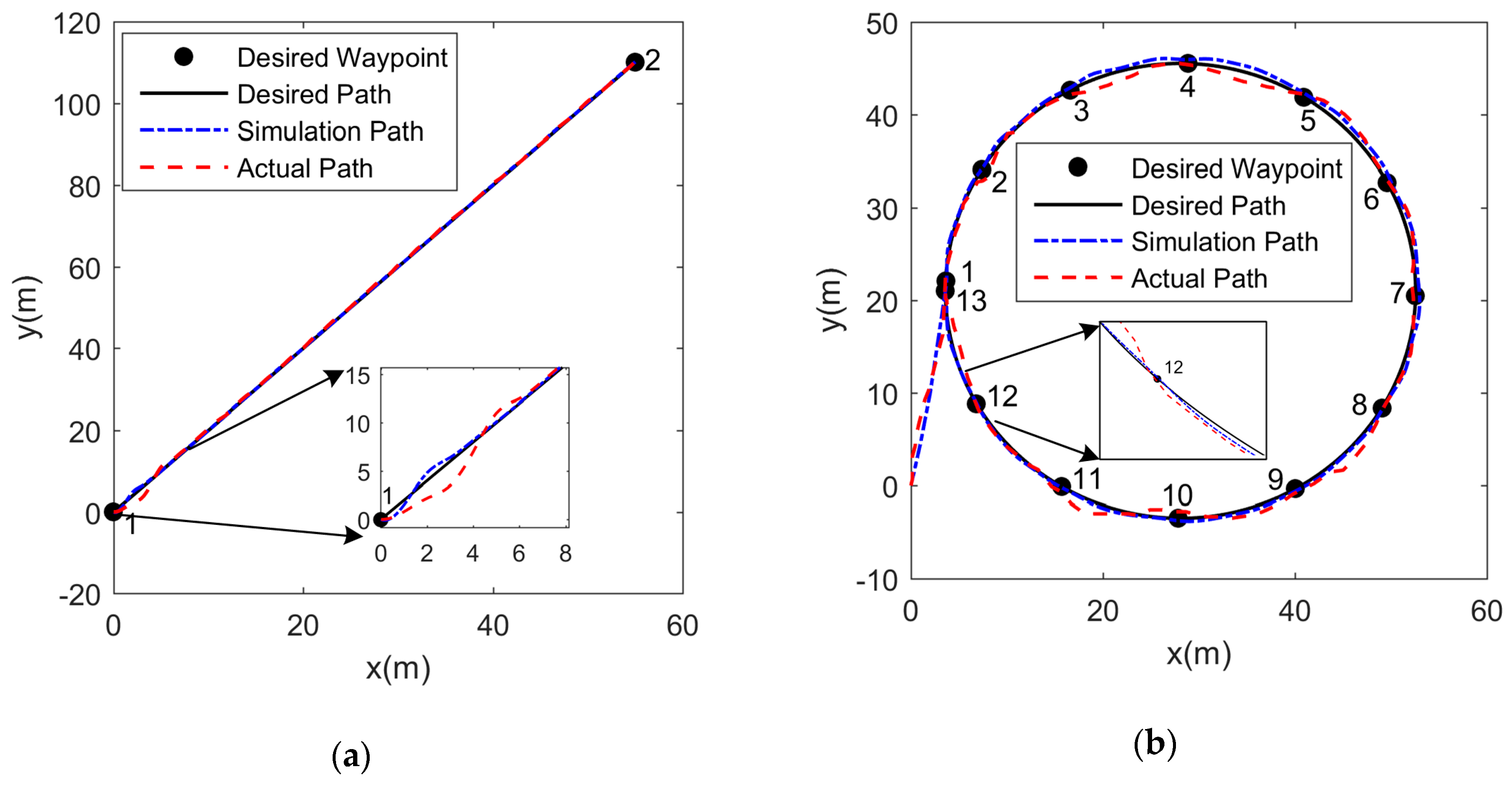
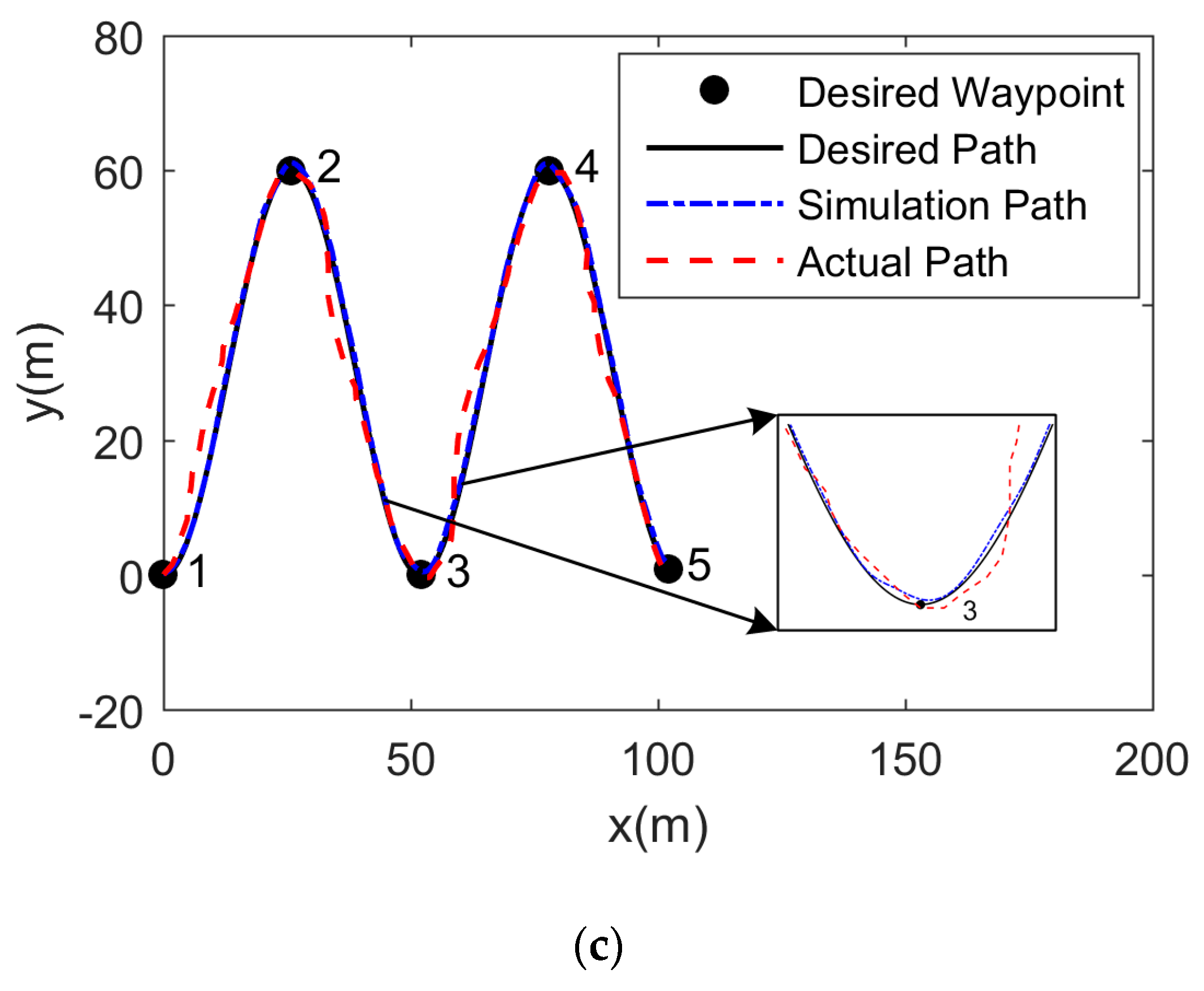
5. PD+LOS Control Algorithm
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Specht, C.; Świtalski, E.; Specht, M. Application of an Autonomous/Unmanned Survey Vessel (ASV/USV) in Bathymetric Measurements. Polish Marit. Res. 2017, 24, 36–44. [Google Scholar] [CrossRef]
- Jorge, V.A.; Granada, R.; Maidana, R.G.; Jurak, D.A.; Heck, G.; Negreiros, A.P.; dos Santos, R.H.; Gonçalves, L.M.G.; Amory, A.M. A survey on unmanned surface vehicles for disaster robotics: Main challenges and directions. Sensors 2019, 19, 702. [Google Scholar] [CrossRef]
- Yan, R.; Pang, S.; Sun, H.; Pang, Y. Development and missions of unmanned surface vehicle. J. Mar. Sci. Appl. 2010, 9, 451–457. [Google Scholar] [CrossRef]
- Manley, J.E. Unmanned Surface Vehicles, 15 Years of Development. In Proceedings of the OCEANS 2008, Quebec City, QC, Canada, 15–18 September 2008. [Google Scholar]
- Geng, X.; Wang, Y.; Wang, P.; Zhang, B. Motion Plan of Maritime Autonomous Surface Ships by Dynamic Programming for Collision Avoidance and Speed Optimization. Sensors 2019, 19, 434. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, X. Concise robust adaptive path-following control of underactuated ships using DSC and MLP. IEEE J. Ocean. Eng. 2014, 39, 685–694. [Google Scholar] [CrossRef]
- Sarda, E.I.; Qu, H.; Bertaska, I.R.; von Ellenrieder, K.D. Station-keeping control of an unmanned surface vehicle exposed to current and wind disturbances. Ocean Eng. 2016, 127, 305–324. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Y.; Yu, X.; Yuan, C. Unmanned surface vehicles: An overview of developments and challenges. Annu. Rev. Control 2016, 41, 71–93. [Google Scholar] [CrossRef]
- Jin, J.; Zhang, J.; Liu, D. Design and verification of heading and velocity coupled nonlinear controller for unmanned surface vehicle. Sensors 2018, 18, 3427. [Google Scholar] [CrossRef]
- Abkowitz, M.A. Lectures on Ship Hydrodynamics-Steering and Manoeuvrability; Hydro-Og Laboratorium: Lyngby, Denmark, 1964. [Google Scholar]
- Abkowitz, M.A. Measurement of Hydrodynamic Characteristics from Ship Maneuvering Trials by System Identification. SNAME Trans. 1980, 88, 283–318. [Google Scholar]
- Asmara, I.P.S.; Kobayashi, E.; Pitana, T. Simulation of Collision Avoidance in Lamong Bay Port by Considering the PAW of Target Ship using MMG Model and AIS Data. Mar. Eng. Front. 2014, 2, 31–38. [Google Scholar]
- Yasukawa, H.; Yoshimura, Y. Introduction of MMG standard method for ship maneuvering predictions. J. Mar. Sci. Technol. 2015, 20, 37–52. [Google Scholar] [CrossRef]
- Yang, L.; Tao, Y. CFD-Based calculation of Regular Transverse Wave Force in the Maneuvering Mathematical Modeling Group (MMG) Model. Appl. Mech. Mater. 2013, 380, 1716–1720. [Google Scholar] [CrossRef]
- Fossen, T.I.; Strand, J.P. Tutorial on nonlinear backstepping: Applications to ship control. Model. Identificat. Control 1999, 20, 83–134. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control, 1st ed.; John Wiley & Sons Ltd.: Chichester, West Sussex, UK, 2011; pp. 122–171. [Google Scholar]
- Larrazabal, J.M.; Peñas, M.S. Intelligent rudder control of an unmanned surface vessel. Expert Syst. Appl. 2016, 55, 106–117. [Google Scholar] [CrossRef]
- Švec, P.; Thakur, A.; Raboin, E.; Shah, B.C.; Gupta, S.K. Target following with motion prediction for unmanned surface vehicle operating in cluttered environments. Auton. Robot 2014, 383–405. [Google Scholar] [CrossRef]
- Sharma, S.K.; Naeem, W.; Sutton, R. An Autopilot Based on a Local Control Network Design for an Unmanned Surface Vehicle. J. Navig. 2012, 65, 281–301. [Google Scholar] [CrossRef]
- Sutton, R.; Sharma, S.; Xao, T. Adaptive navigation systems for an unmanned surface vehicle. J. Mar. Eng. Technol. 2014, 10, 3–20. [Google Scholar] [CrossRef]
- Naeem, W.; Sutton, R.; Chudley, J. Modelling and control of an unmanned surface vehicle for environmental monitoring. In Proceedings of the UKACC International Control Conference, Glasgow, Scotland, 30 August–1 September 2006. [Google Scholar]
- Savvaris, A.; Niu, H.; Oh, H.; Tsourdos, A. Development of collision avoidance algorithms for the c-enduro usv. In Proceedings of the 19th IFAC world congress (IFAC 2014), Cape Town, South Africa, 24–29 August 2014. [Google Scholar]
- Murphy, R.R.; Steimle, E.; Hall, M.; Lindemuth, M.; Trejo, D.; Hurlebaus, S.; Medina-Cetina, Z.; Slocum, D. Robot-Assisted Bridge Inspection. J. Intell. Robot. Syst. 2011, 64, 77–95. [Google Scholar] [CrossRef]
- Sutresman, O.; Syam, R.; Asmal, S. Controlling Unmanned Surface Vehicle Rocket using GPS Tracking Method. Int. J. Technol. 2017, 8, 709–718. [Google Scholar] [CrossRef]
- Mu, D.; Wang, G.; Fan, Y.; Sun, X.; Qiu, B. Modeling and Identification for Vector Propulsion of an Unmanned Surface Vehicle: Three Degrees of Freedom Model and Response Model. Sensors 2018, 18, 1889. [Google Scholar] [CrossRef]
- Subcommittee, S.H. Nomenclature for Treating the Motion of a Submerged Body through a Fluid. In Proceedings of the American Towing Tank Conference, New York, NY, USA, 11–14 September 1950. [Google Scholar]
- Sonnenburg, C.R. Modeling, Identification, and Control of an Unmanned Surface Vehicle. Ph.D. Dissertation, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2012. [Google Scholar]
- Fossen, T.I. Nonlinear modelling and control of underwater vehicles. Ph.D. Dissertation, Dept. of Marine Technology, Norwegian Institute of Technology, Trondheim, Norway, 1991. [Google Scholar]
- Zheng, J.; Meng, F.; Li, Y. Design and Experimental Testing of a Free-Running Ship Motion Control Platform. IEEE Access 2018, 6, 4690–4696. [Google Scholar] [CrossRef]
- Marquardt, J.G.; Alvarez, J.; von Ellenrieder, K.D. Characterization and System Identification of an Unmanned Amphibious Tracked Vehicle. IEEE J. Ocean. Eng. 2014, 39, 641–661. [Google Scholar] [CrossRef]
- Muske, K.R.; Ashrafiuon, H.; Haas, G.; Mccloskey, R. Identification of a Control Oriented Nonlinear Dynamic USV Model. In Proceedings of the American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 562–567. [Google Scholar]
- Fossen, T.I. Guidance and Control of Ocean Vehicles, 1st ed.; Wiley: New York, NY, USA, 1994; pp. 32–42. [Google Scholar]
- Mu, D.; Wang, G.; Fan, Y.; Sun, X.; Qiu, B. Adaptive LOS Path Following for a Podded Propulsion Unmanned Surface Vehicle with Uncertainty of Model and Actuator Saturation. Appl. Sci. 2017, 7, 1232. [Google Scholar] [CrossRef]
- Breivik, M.; Fossen, T.I. Path following of straight lines and circles for marine surface vessels. In Proceedings of the IFAC Conference on Computer Applications in Marine Systems - CAMS 2004, Ancona, Italy, 7–9 July 2004. [Google Scholar]
- Fossen, T.I.; Breivik, M.; Skjetne, R. Line-of-sight path following of underactuated marine craft. In Proceedings of the 6th IFAC Conference on Manoeuvring and Control of Marine Craft (MCMC 2003), Girona, Spain, 17–19 September 2003. [Google Scholar]
- Lekkas, A.M.; Fossen, T.I. A time-varying lookahead distance guidance law for path following. In Proceedings of the 9th IFAC Conference on Manoeuvring and Control of Marine Craft, Arenzano, Italy, 19–21 September 2012. [Google Scholar]
- Fossen, T.I.; Pettersen, K.Y.; Galeazzi, R. Line-of-sight path following for dubins paths with adaptive sideslip compensation of drift forces. IEEE Trans. Control Syst. Technol. 2015, 23, 820–827. [Google Scholar] [CrossRef]
- Lekkas, A.M.; Fossen, T.I. Integral LOS path following for curved paths based on a monotone cubic hermite spline parametrization. IEEE Trans. Control Syst. Technol. 2014, 22, 2287–2301. [Google Scholar] [CrossRef]
- Åström, K.J.; Hägglund, T. Revisiting the Ziegler-Nichols step response method for PID control. J. Process Control. 2004, 14, 635–650. [Google Scholar] [CrossRef]
- Pan, C.Z.; Lai, X.Z.; Yang, S.X.; Wu, M. An efficient neural network approach to tracking control of an autonomous surface vehicle with unknown dynamics. Expert Syst. Appl. 2013, 40, 1629–1635. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Length overall (LO) | 1.5 m |
| Waterline length (L) | 1.3 m |
| Draft (D) | 0.125 m |
| Beam overall (W) | 0.9 m |
| Diameter of the propeller | 0.27 m |
| Distance between two propellers (B) | 0.52 m |
| Mass | 50 kg |
| USV velocity (max) | 1.5 m/s |
| Motor Command (%) | −100 | −90 | −80 | −70 | −60 | −50 | −40 | −30 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Thrust (N) | −110 | −88 | −64 | −45 | −30 | −14 | −8 | −1 | 2 | 9 | 15 | 39 | 54 | 120 | 177 | 227 |
| Test | High Value (%) | Low Value (%) |
|---|---|---|
| 1 | 100 | 80 |
| 2 | 90 | 75 |
| 3 | 85 | 65 |
| 4 | 75 | 57 |
| 5 | 65 | 50 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Jiang, J.; Duan, F.; Liu, W.; Wang, X.; Bu, L.; Sun, Z.; Yang, G. Modeling and Experimental Testing of an Unmanned Surface Vehicle with Rudderless Double Thrusters. Sensors 2019, 19, 2051. https://doi.org/10.3390/s19092051
Li C, Jiang J, Duan F, Liu W, Wang X, Bu L, Sun Z, Yang G. Modeling and Experimental Testing of an Unmanned Surface Vehicle with Rudderless Double Thrusters. Sensors. 2019; 19(9):2051. https://doi.org/10.3390/s19092051
Chicago/Turabian StyleLi, Chunyue, Jiajia Jiang, Fajie Duan, Wei Liu, Xianquan Wang, Lingran Bu, Zhongbo Sun, and Guoliang Yang. 2019. "Modeling and Experimental Testing of an Unmanned Surface Vehicle with Rudderless Double Thrusters" Sensors 19, no. 9: 2051. https://doi.org/10.3390/s19092051
APA StyleLi, C., Jiang, J., Duan, F., Liu, W., Wang, X., Bu, L., Sun, Z., & Yang, G. (2019). Modeling and Experimental Testing of an Unmanned Surface Vehicle with Rudderless Double Thrusters. Sensors, 19(9), 2051. https://doi.org/10.3390/s19092051






