A Novel Energy Harvester for Powering Small UAVs: Performance Analysis, Model Validation and Flight Results
Abstract
:1. Introduction
2. Several Scenarios Proposed for Electric Power Consumption Model
2.1. MAV Platform Design
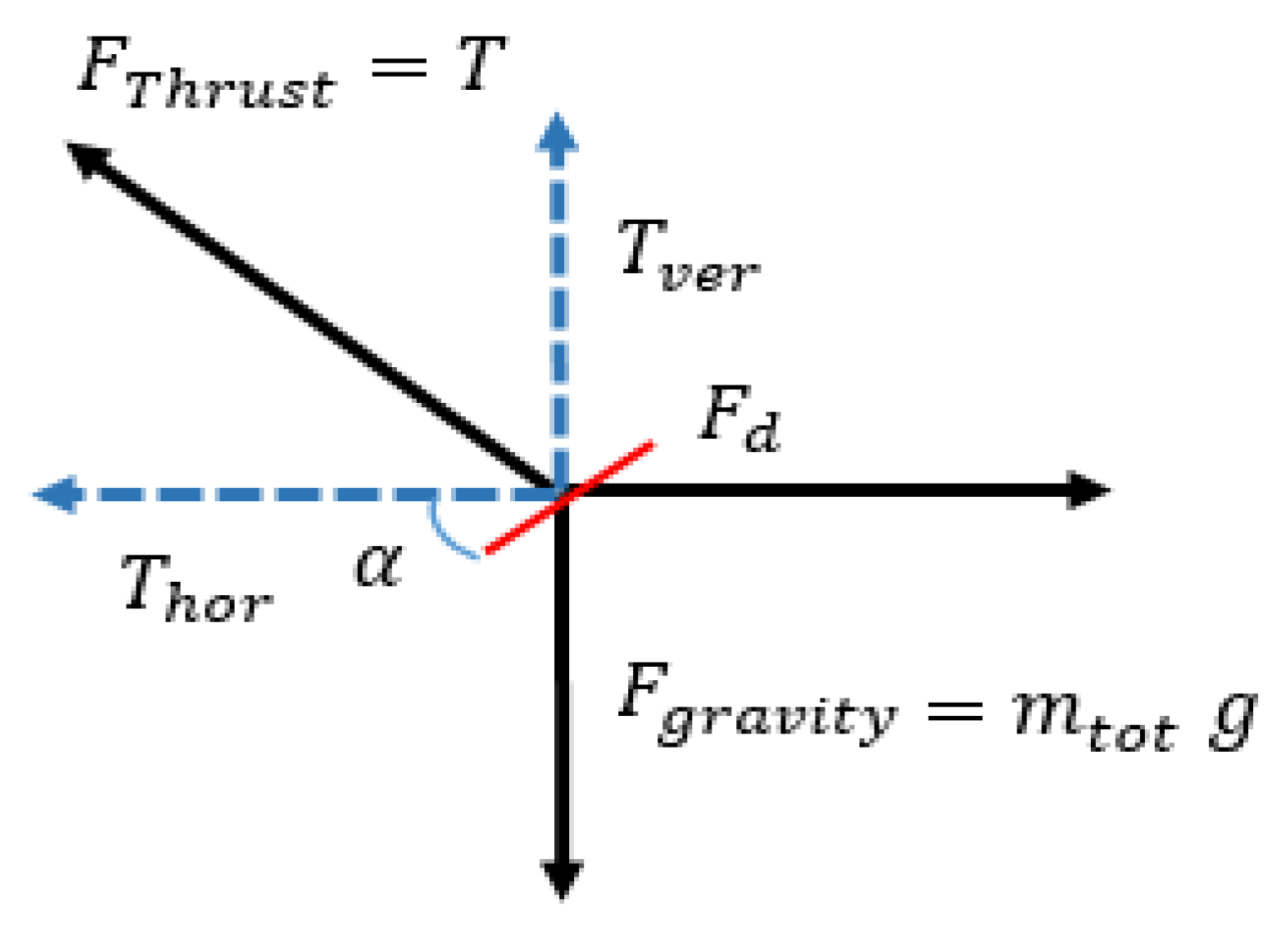
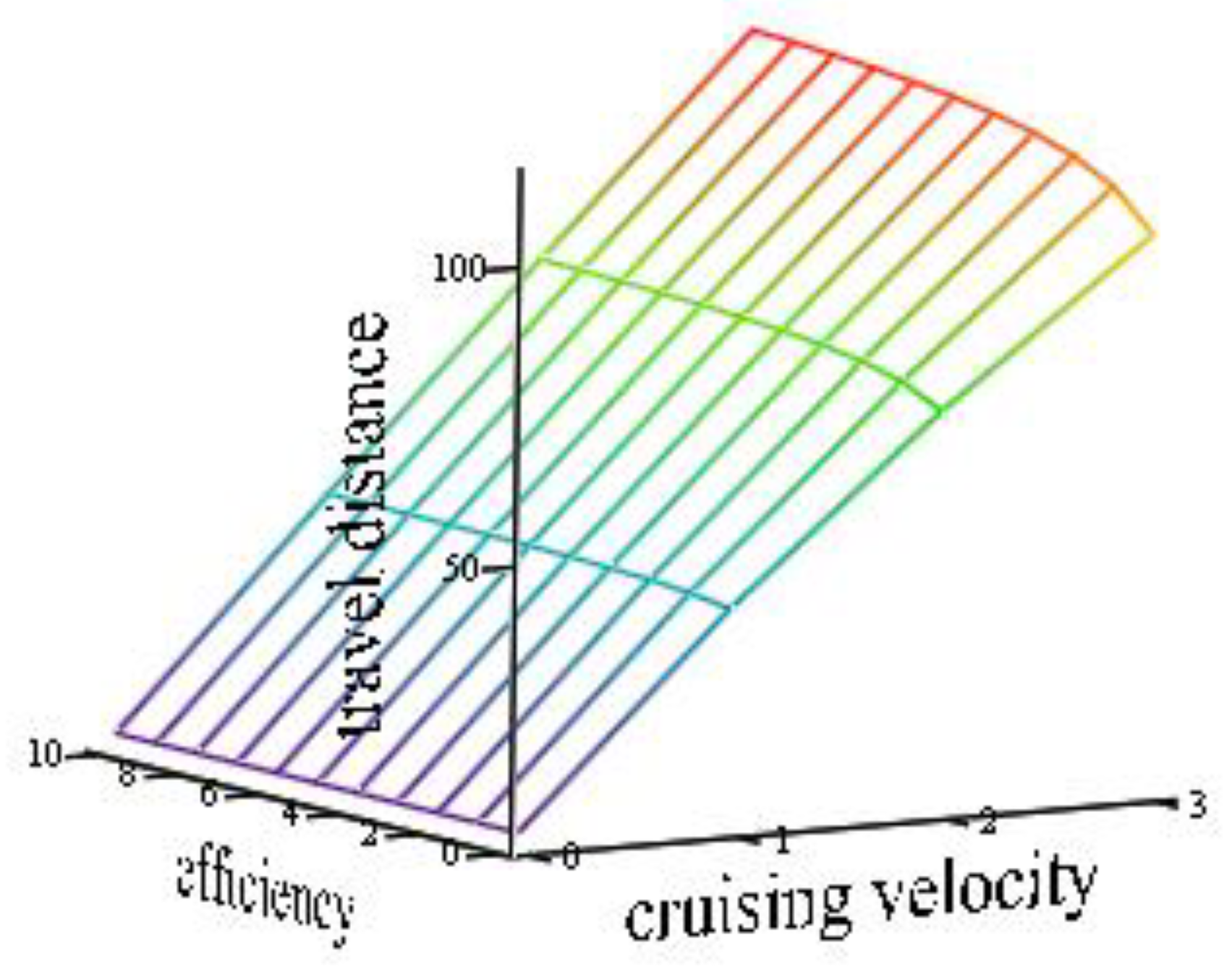
2.2. A Power Consumption Model for MAVs
- (1)
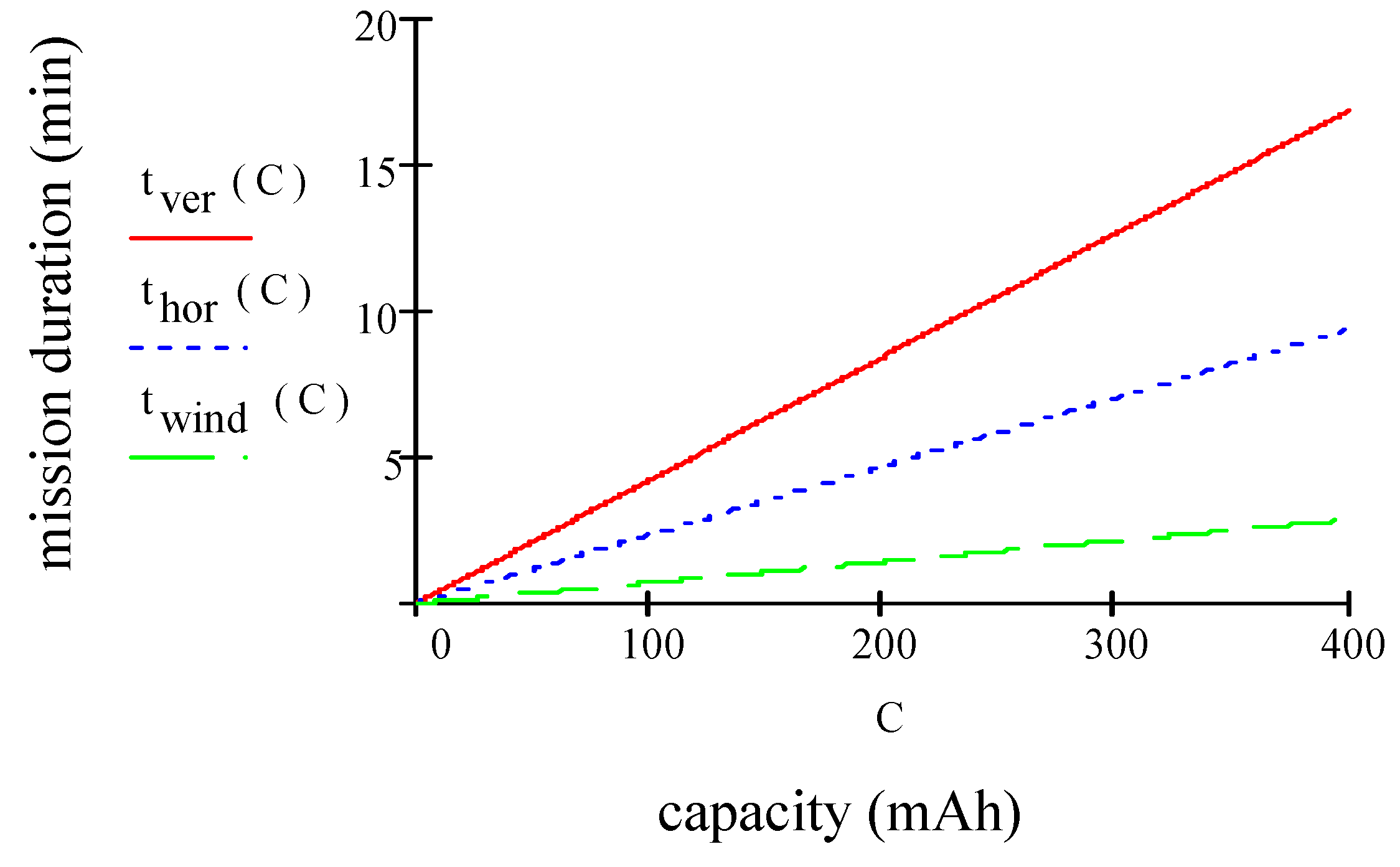
- Impact of Motion: The motions of a drone can be divided into hovering, vertical and horizontal moving. This paper investigates the power consumption of a drone in each motion type.
- (2)
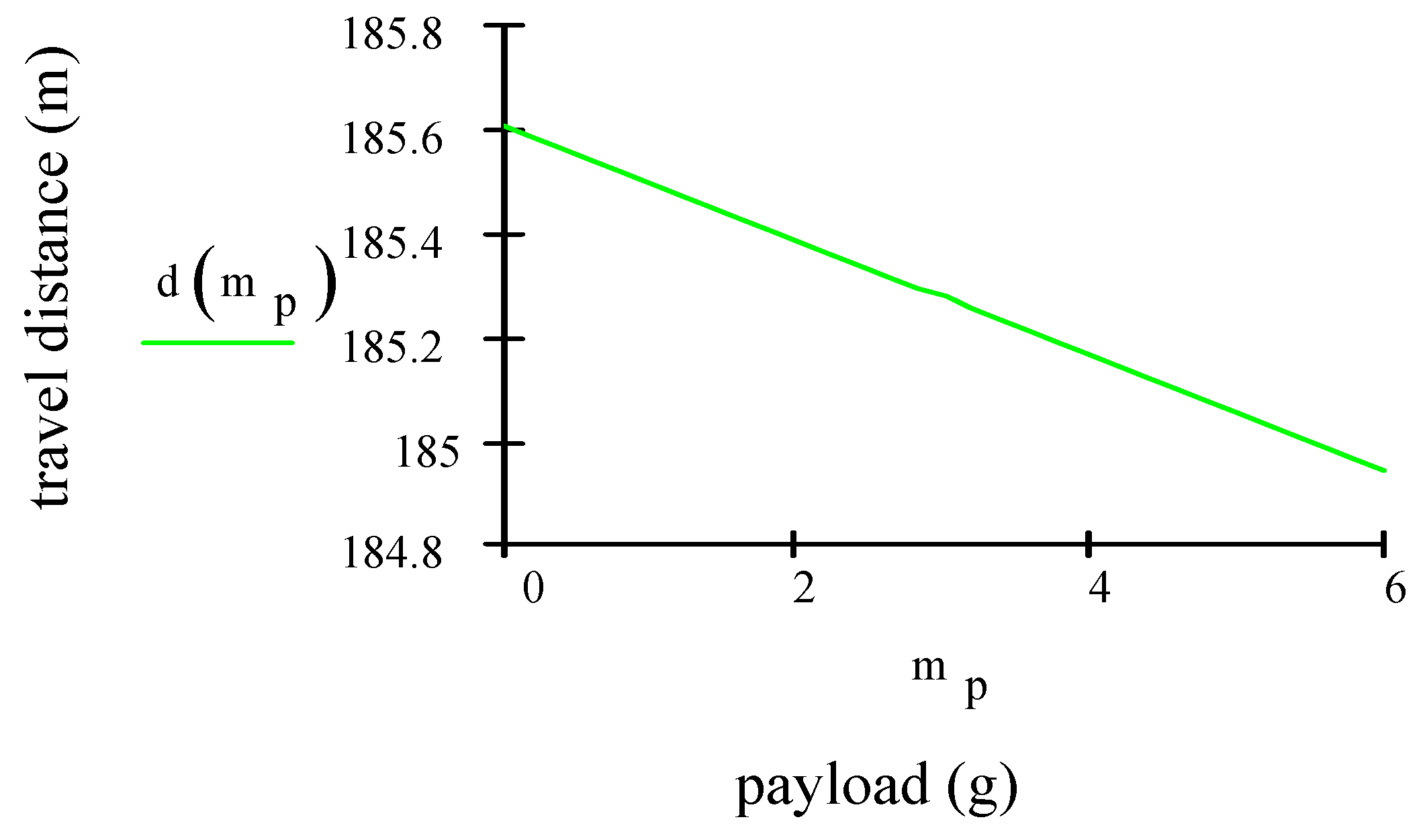
- Impact of Weight: We study how different weights of payloads limit their travel distance.
- (3)
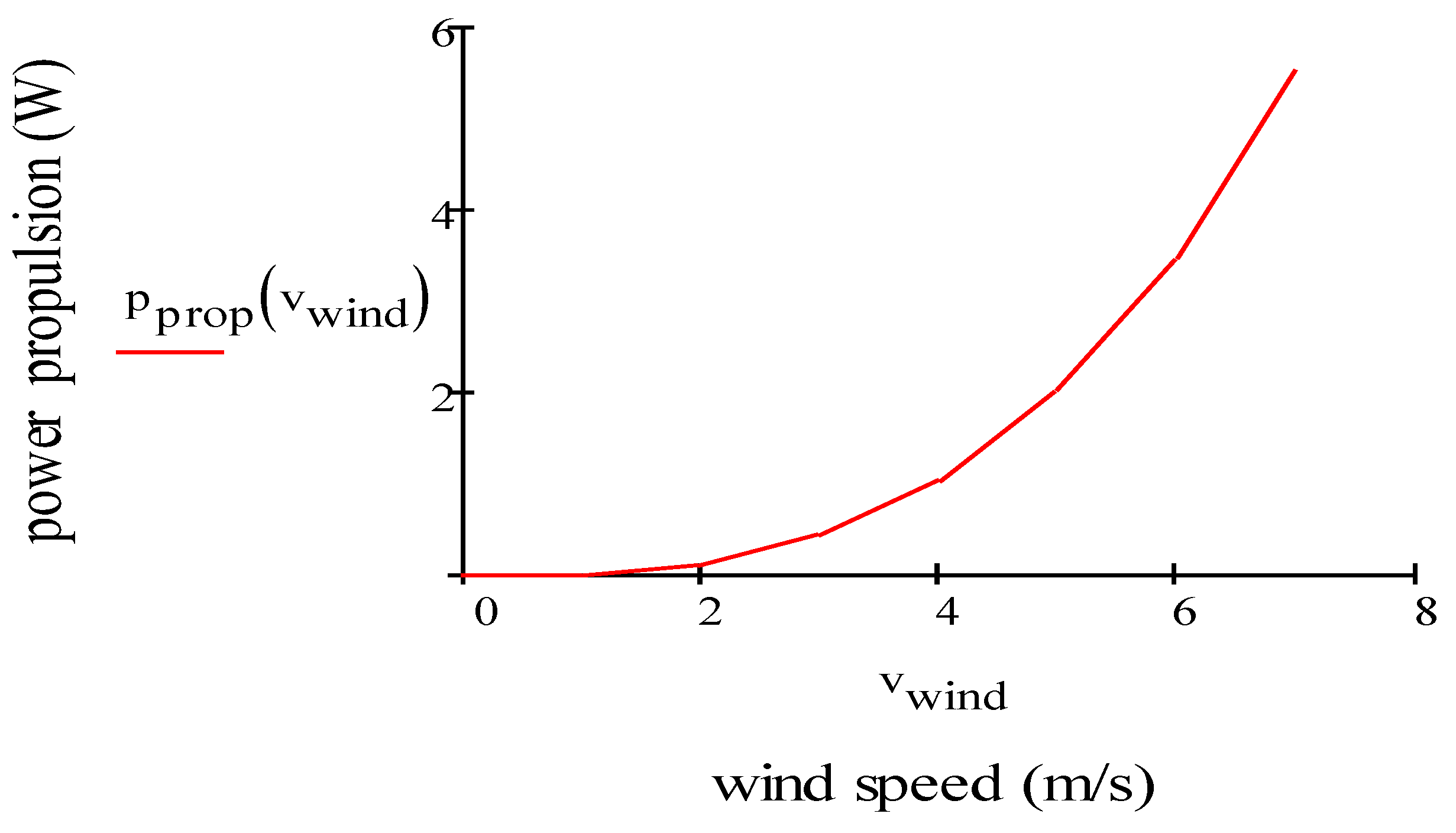
- Impact of Wind: The major environmental factor that affects the drone is wind. We study the power consumption of a drone in headwind conditions.
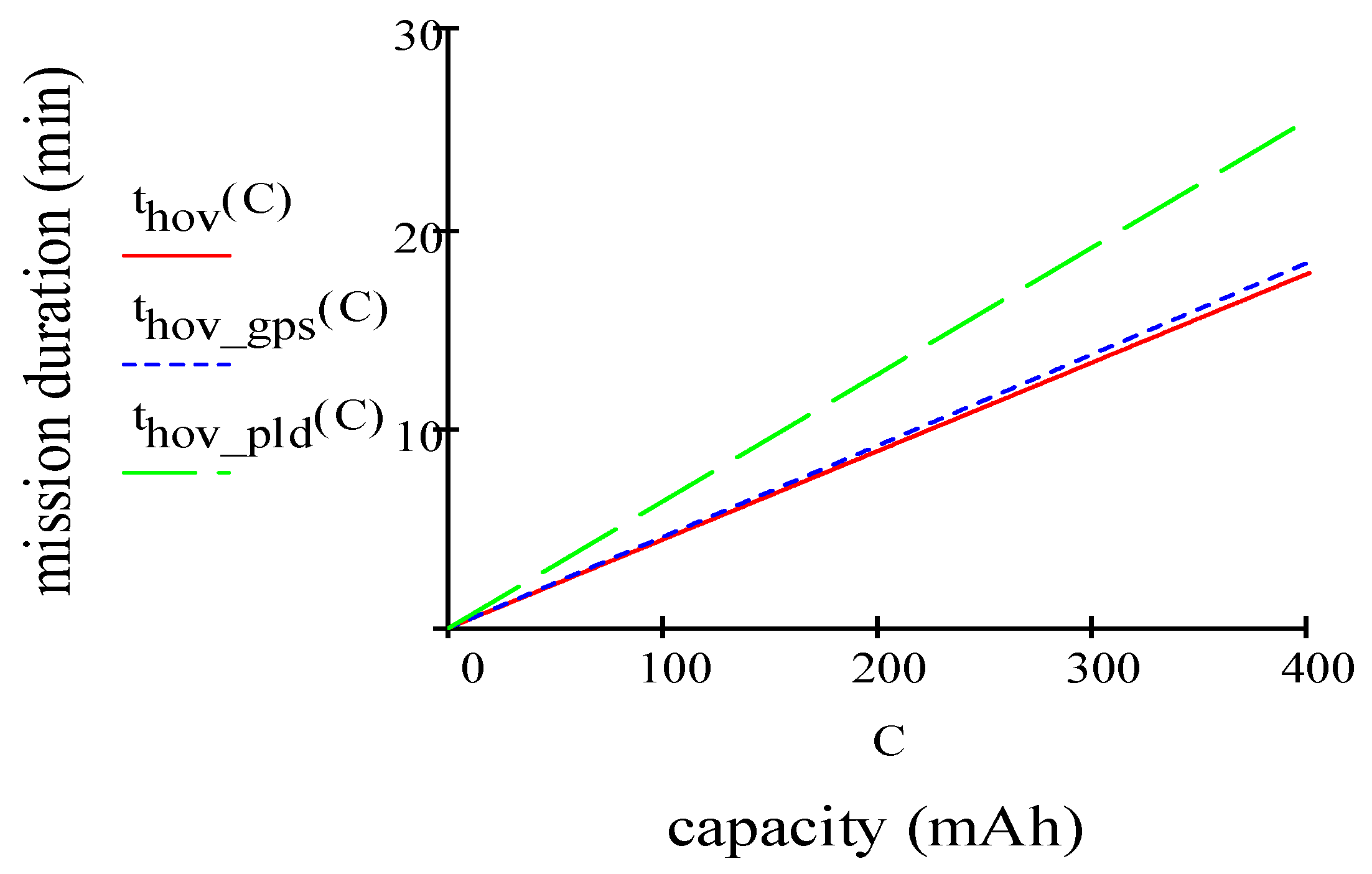
2.2.1. Impact of Motion: Hovering Condition
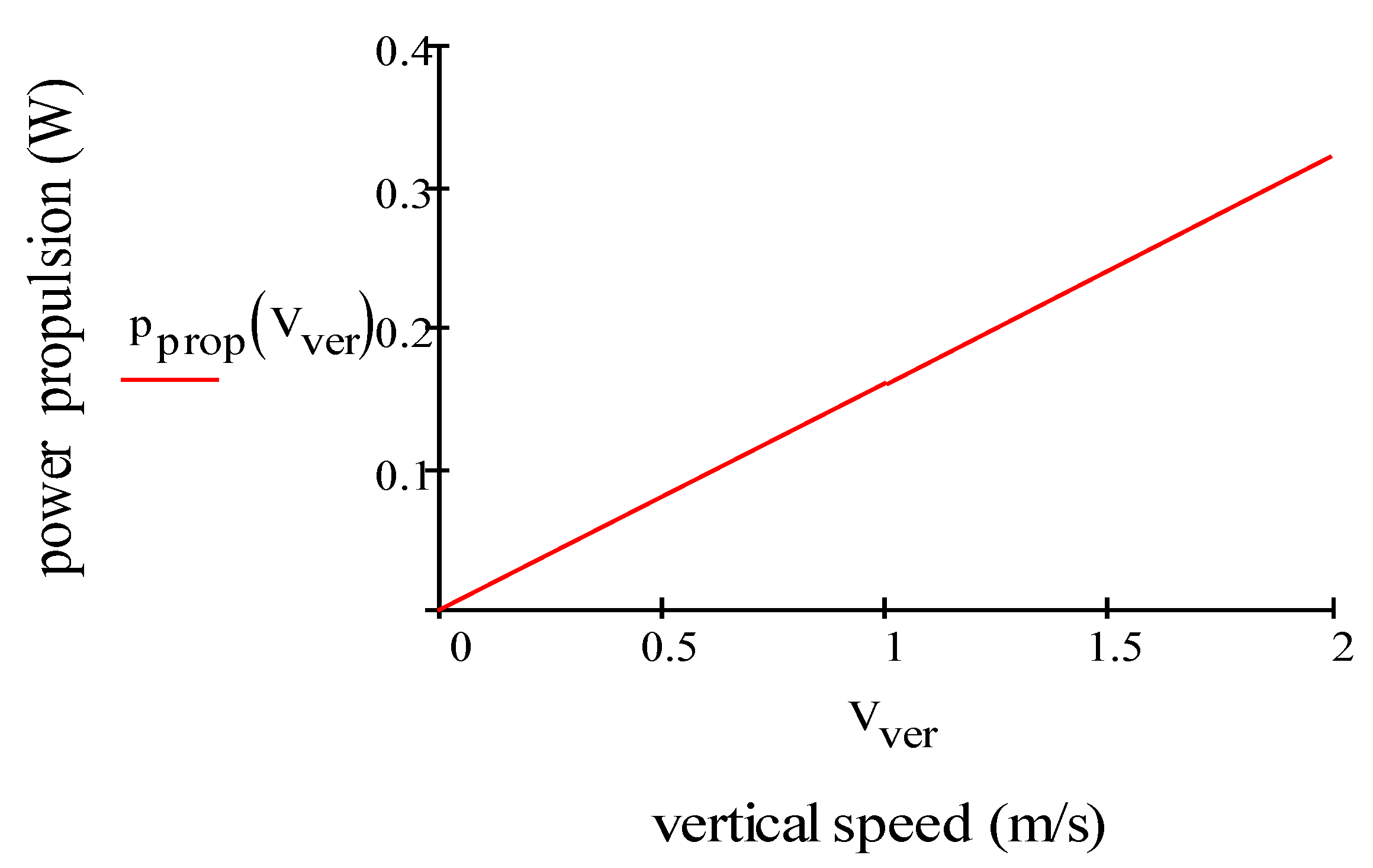
2.2.2. Impact of Motion: Vertical Condition
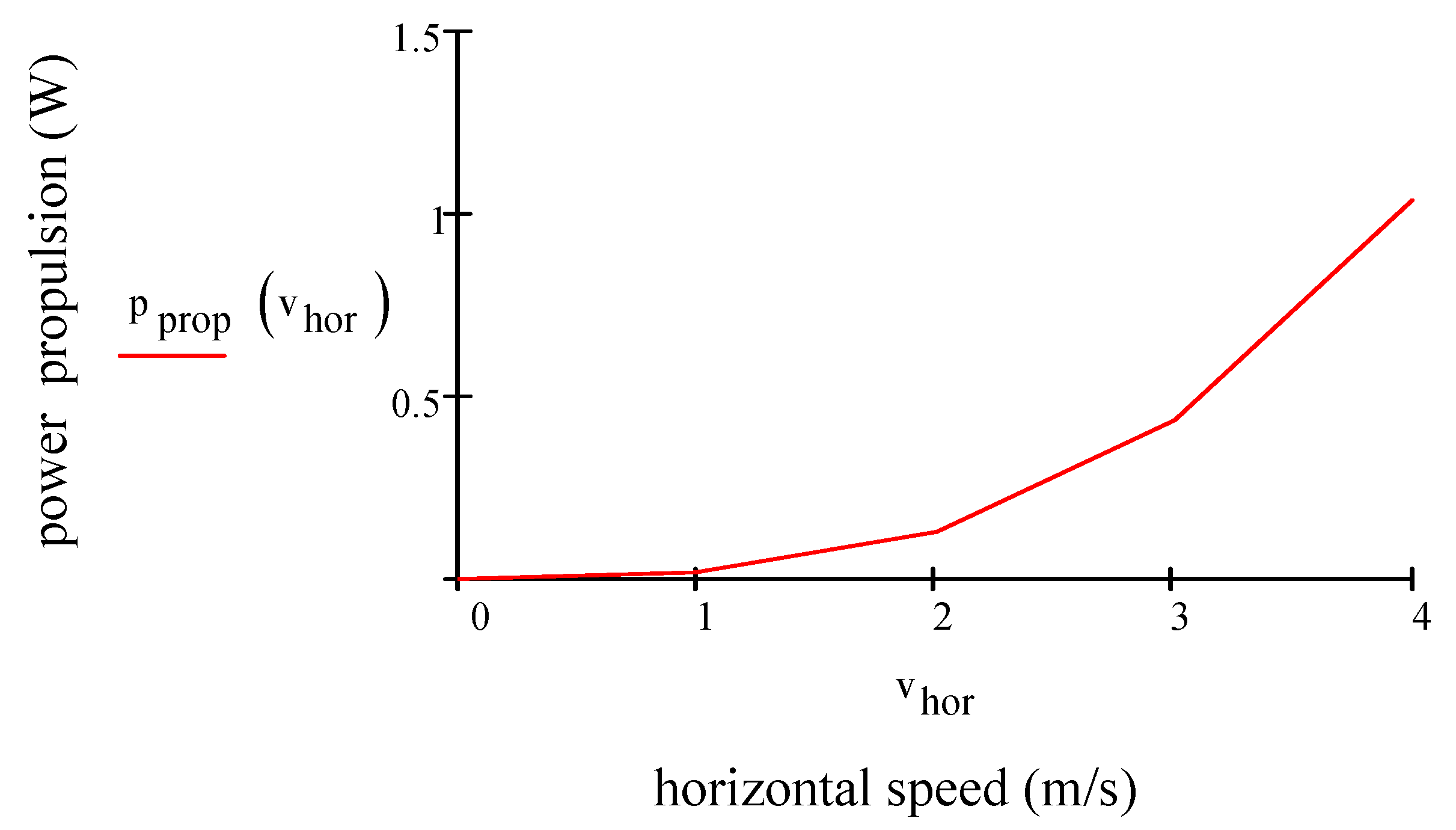
2.2.3. Impact of Motion: Horizontal Condition
2.2.4. Impact of Weights
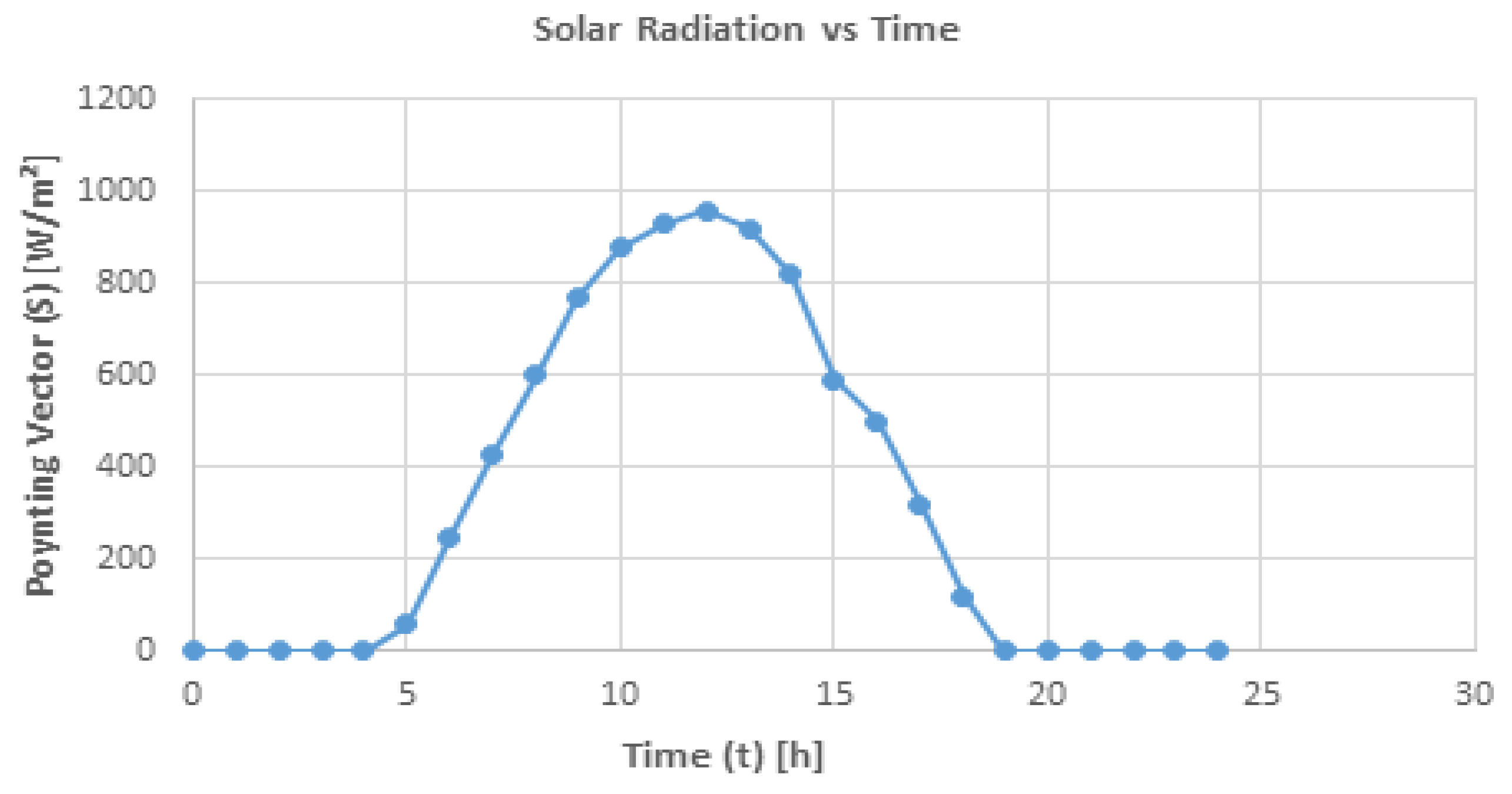
2.2.5. Impact of Wind
3. Economical Alternative to PV
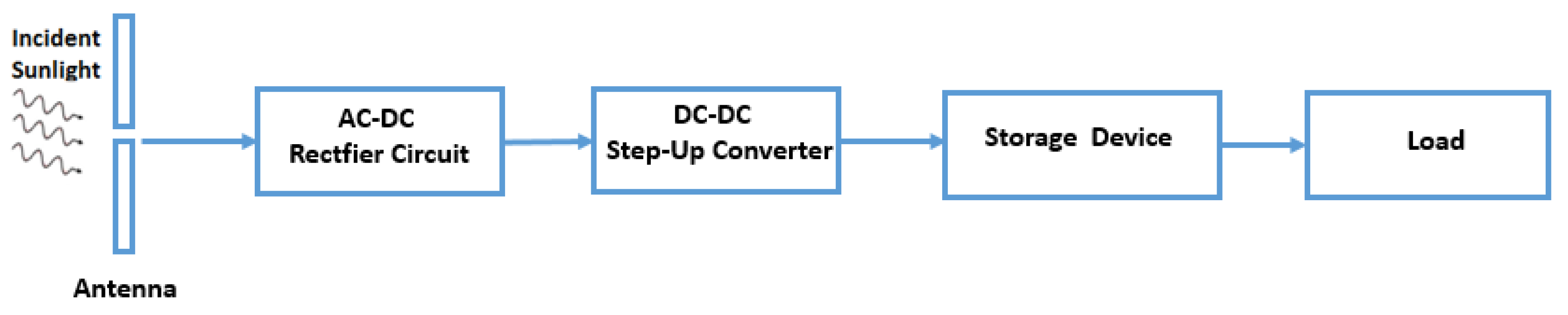
3.1. Novel Harvester to Power Small Aerial Vehicles
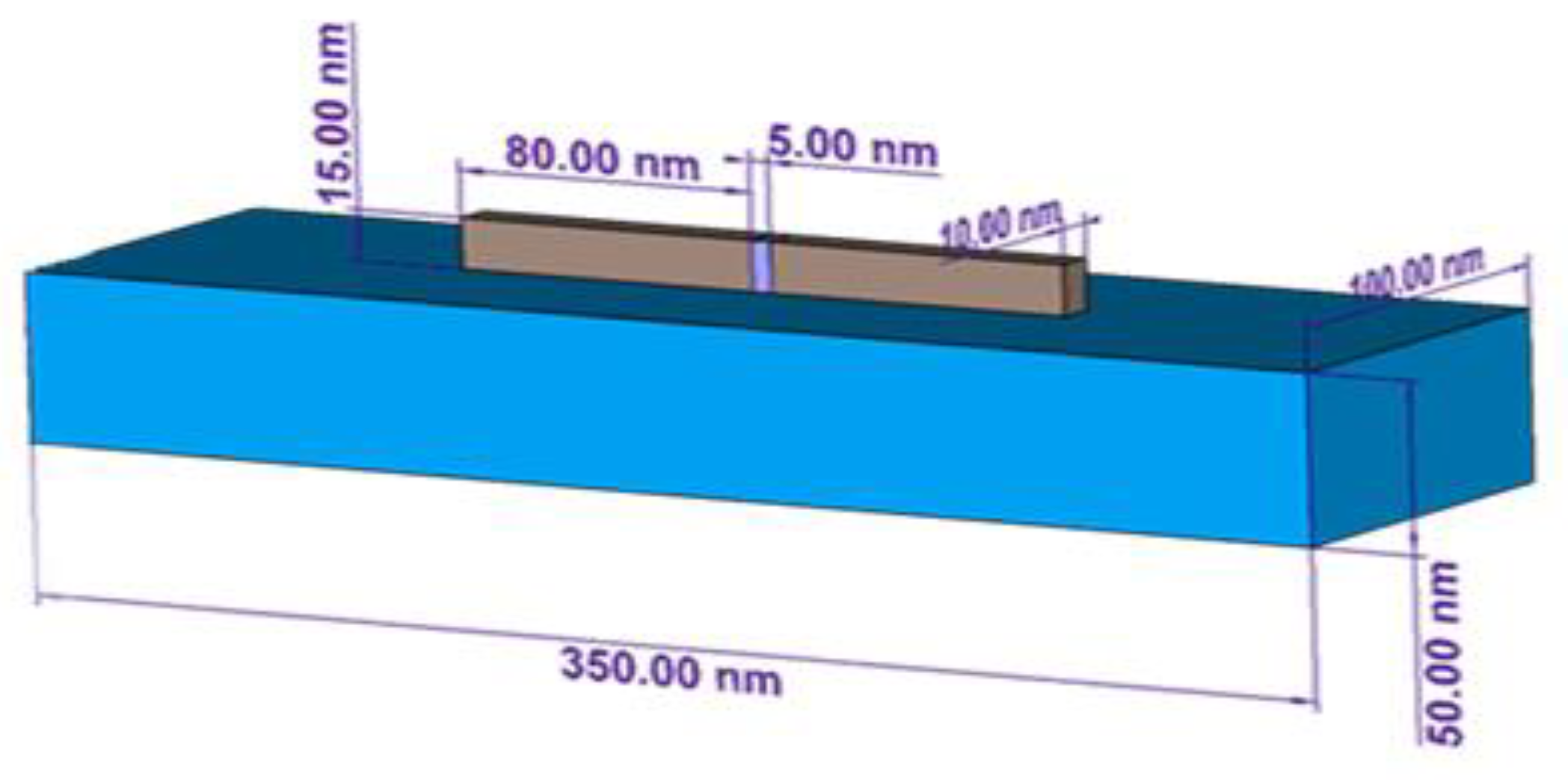
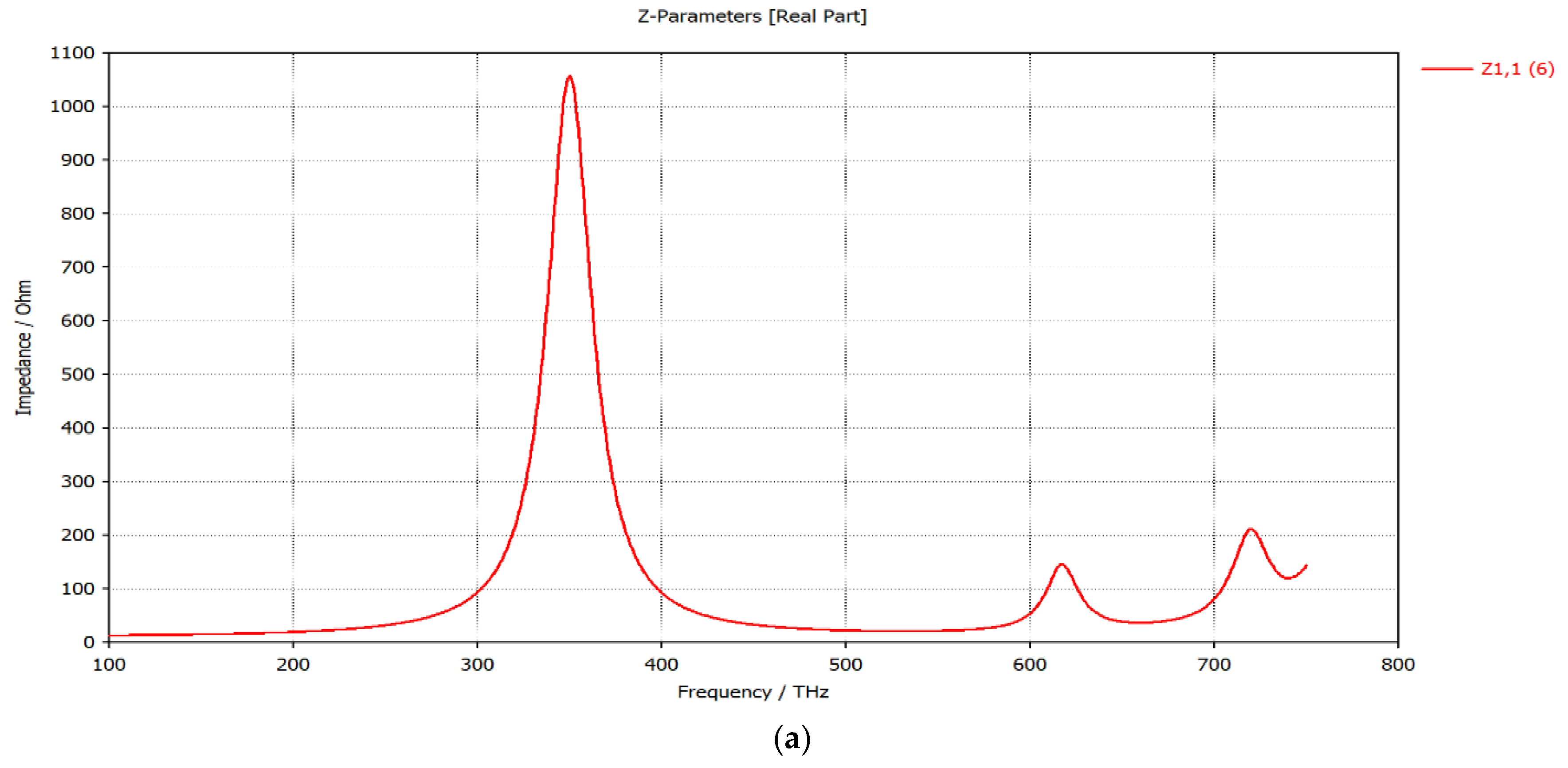
3.2. Internal Nano-Antenna Impedance Evaluation
3.3. Effective Area Evaluation
3.4. Electrical Parameters Evaluation
3.5. Design of a Rectenna Array
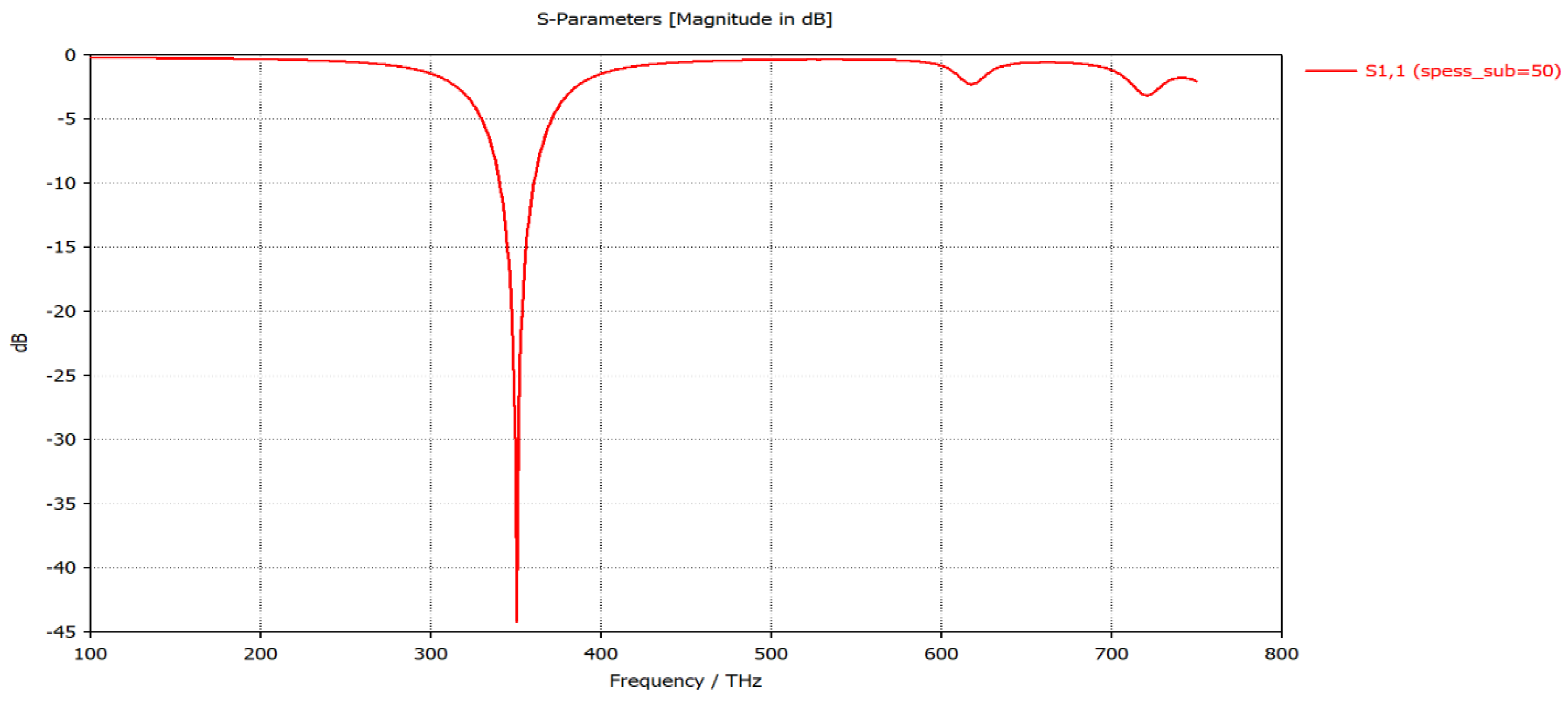
3.5.1. Impedance Matching
3.5.2. DC-DC Boost Power Converter
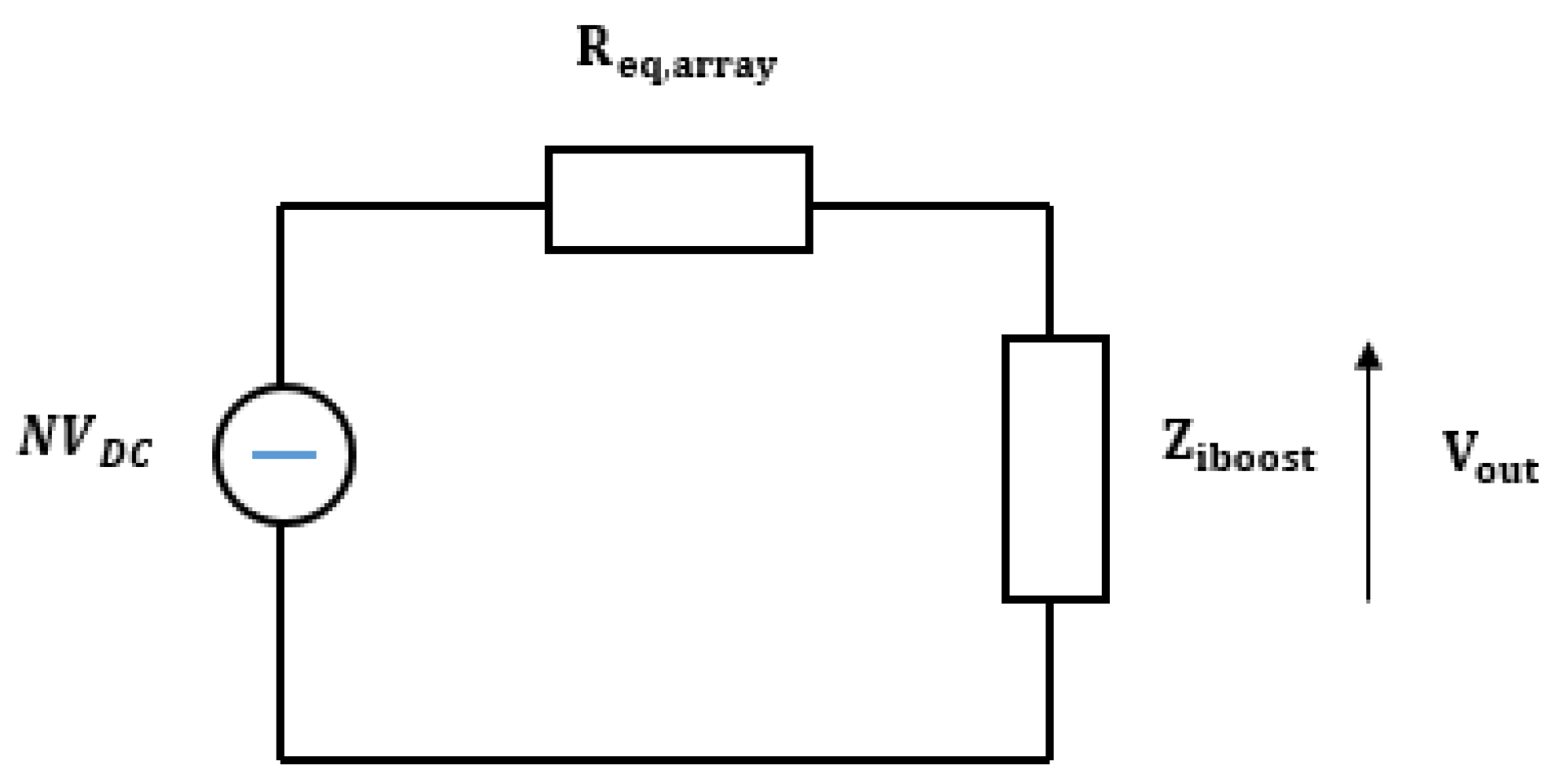
3.5.3. The Equivalent Circuit of an Array of Optical Rectennas
3.5.4. Load Power and Energy Evaluation
4. Energy Storage
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| UAVs | Unmanned Aerial Vehicles |
| MAVs | Micro Air Vehicles |
| MD | Mission Duration |
| EH | Energy Harvesting |
| SWIR | Shortwave Infrared |
| PV | Photovoltaic |
| TWR | Thrust to Weight Ratio |
| AC | Alternating Current |
| DC | Direct Current |
| MIM | Metal Insulator Metal diode |
| MIIM | Multi Insulator Metal diode |
References
- González-Jorge, H.; Martínez-Sánchez, J.; Bueno, M.; Arias, A.P. Unmanned Aerial Systems for Civil Applications: A Review. Drones 2017, 1, 2. [Google Scholar] [CrossRef]
- Citroni, R.; Passi, D.; Leggieri, A.; Di Paolo, F.; Di Carlo, A. The next generation: Miniaturized objects, self-powered using nanostructures to harvest ambient energy. In Proceedings of the 18th Italian National Conference on Photonic Technologies (Fotonica 2016), Rome, Italy, 6–8 June 2016; pp. 1–4. [Google Scholar]
- Citroni, R.; Leggieri, A.; Passi, D.; Di Paolo, F.; Di Carlo, A. Nano Energy Harvesting with Plasmonic Nano-Antennas: A review of MID-IR Rectenna and Application. Adv. Electromagn. 2017, 6, 1–13. [Google Scholar] [CrossRef]
- Petricca, L.; Ohlckers, P.; Grinde, C. Micro and Nano-Air Vehicles: State of the Art. Int. J. Aerosp. Eng. 2011, 2011, 214549. [Google Scholar] [CrossRef]
- Hoffmann, G.; Huang, H.; Waslander, S.; Tomlin, C. Quadrotor Helicopter Flight Dynamics and Control: Theory and Experiment. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit Hilton Head, Carolina, SC, USA, 20–23 August 2007; pp. 1–20. [Google Scholar]
- Lu, M.; Bagheri, M.; James, A.P.; Phung, T. Wireless Charging Techniques for UAVs: A Review, Reconceptualization, and Extension. IEEE Access 2018, 6, 29865–29884. [Google Scholar] [CrossRef]
- Oettershagen, P.; Melzer, A.; Mantel, T.; Rudin, K.; Lotz, R.; Siebenmann, D.; Leutenegger, S.; Alexis, K.; Siegwart, R. A solar-powered hand-launchable UAV for low-altitude multi-day continuous flight. IEEE Int. Conf. Robot. Autom. 2015, 2015, 3986–3993. [Google Scholar]
- Wilkins, G.; Fourie, D.; Meyer, J. Critical design parameters for a low altitude long endurance solar powered UAV. In Proceedings of the AFRICON 2009, Nairobi, Kenya, 23–25 September 2009; pp. 1–6. [Google Scholar]
- Rajendran, P.; Masral, M.H.; Kutty, H.A. Perpetual Solar-Powered Flight across Regions around the World for a Year-Long Operation. Aerospace 2017, 4, 20. [Google Scholar] [CrossRef]
- Papa, U.; Ponte, S. Preliminary Design of an Unmanned Aircraft System for Aircraft General Visual Inspection. Electronics 2018, 7, 435. [Google Scholar] [CrossRef]
- Moddel, G.; Grover, S. Rectenna Solar Cells, 1st ed.; Springer: Berlin, Germany, 2013. [Google Scholar]
- Mescia, L.; Massaro, A. New Trends in Energy Harvesting from Earth Long-Wave Infrared Emission. Adv. Mater. Sci. Eng. 2014, 2014, 252879. [Google Scholar] [CrossRef]
- Mescia, L.; Losito, O.; Prudenzano, F. Innovative Materials and Systems for Energy Harvesting Applications, 1st ed.; IGI Global: Hershey, PA, USA, 2015. [Google Scholar]
- Vandenbosch, G.A.E.; Ma, Z. Upper bounds for the solar energy harvesting efficiency of nano-antennas. Nano Energy 2012, 1, 494–502. [Google Scholar] [CrossRef]
- Chekini, A.; Sheikhaei, S.; Neshat, M. A Novel Plasmonic Nanoantenna Structure for Solar Energy Harvesting. In Proceedings of the 2016 Fourth International Conference on Millimeter-Wave and Terahertz Technologies (MMWaTT), Tehran, Iran, 20–22 December 2016; pp. 20–24. [Google Scholar]
- Di Garbo, C.; Livreri, P.; Vitale, G. Optimal matching between optical rectennas and harvester circuits. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–6. [Google Scholar]
- Kotter, D.K.; Novack, S.D.; Slafer, W.D.; Pinhero, P.J. Theory and Manufacturing Processes of Solar Nanoantenna Electromagnetic Collectors. J. Sol. Energy Eng. 2010, 132, 011014. [Google Scholar] [CrossRef]
- Tseng, C.M.; Chau, C.K.; Elbassioni, K.; Khonji, M. Autonomous Recharging and Flight Mission Planning for Battery-operated Autonomous Drones. arXiv, 2017; arXiv:1703.10049. [Google Scholar]
- Oettershagen, P.; Melzer, A.; Mantel, T.; Rudin, K.; Stastny, T.; Wawrzacz, B.; Hinzmann, T.; Alexis, K.; Siegwart, R. Perpetual flight with a small solar-powered UAV: Flight results, performance analysis and model validation. In Proceedings of the 2016 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2016; pp. 1–8. [Google Scholar]
- Valavanis, K.P.; Vachtsevanos, G.J. Handbook of Unmanned Aerial Vehicles, 1st ed.; Springer: Berlin, Germany, 2015. [Google Scholar]
- Filippone, A. Flight Performance of Fixed and Rotary Wing Aircraft, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Gopalakrishnan, E. Quadcopter Flight Mechanics Model and Control Algorithms. Master’s Thesis, Lulea University of Technology, Prague, Czech Republic, May 2017. [Google Scholar]
- Yacef, F.; Rizoug, N.; Bouhali, O.; Hamerlain, M. Optimization of Energy Consumption for Quadrotor UAV. In Proceedings of the International Micro Air Vehicle Conference and Flight Competition (IMAV), Toulouse, France, 18–21 September 2017; pp. 1–9. [Google Scholar]
- Johnson, W. Rotorcraft Aeromechanics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Traub, L.W. Range and Endurance Estimates for Battery-Powered Aircraft. J. Aircr. 2011, 48, 1–5. [Google Scholar] [CrossRef]
- Di Garbo, C.; Livreri, P.; Vitale, G. Solar Nanoantennas energy based characterization. In Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ), Madrid, Spain, 4–6 May 2016. [Google Scholar]
- Citroni, R.; Di Paolo, F.; Di Carlo, A. Replacing noble metals with alternative metals in MID-IR frequency: A theoretical approach. In Proceedings of the 3rd International Conference on Emerging Technologies: Micro to Nano, Rome, Italy, 23 July 2018; p. 020004. [Google Scholar]
- Alù, A.; Nader Engheta, N. Input Impedance, Nanocircuit Loading, and Radiation Tuning of Optical Nanoantennas. Phys. Rev. Lett. 2008, 101, 043901. [Google Scholar] [CrossRef]
- Xu, Y.; Tucker, E.; Boreman, G.; Raschke, M.B.; Lail, B.A. Optical nanoantenna input impedance. ACS Photonics 2016, 3, 881–885. [Google Scholar] [CrossRef]
- El-Toukhy, Y.M.; Hussein, M.; Hameed, M.F.O.; Heikal, A.M.; Abd-Elrazzak, M.M.; Obayya, S.S.A. Optimized tapered dipole nanoantenna as efficient energy harvester. Opt. Express 2016, 24, A1107–A1122. [Google Scholar] [CrossRef]
- Ma, Z.; Vandenbosch, G.A.E. Optimal solar energy harvesting efficiency of nano-rectenna systems. Sol. Energy 2013, 88, 163–174. [Google Scholar] [CrossRef]
- Ma, Z.; Vandenbosch, G.A. Input impedance of optical metallic nanodipole over 300 nm—1200 nm wavelength. In Proceedings of the IEEE 7th European Conference on Antennas and Propagation (EuCAP), Gothenburg, Sweden, 8–12 April 2013. [Google Scholar]
- Yana, S.; Tumendemberela, B.; Zhenga, X.; Vladimir Volskiya, V.; Vandenbosch, G.A.E.; Moshchalkova, V.V. Optimizing the bowtie nano-rectenna topology for solar energy harvesting applications. Sol. Energy 2017, 157, 259–262. [Google Scholar] [CrossRef]
- Grover, S.; Moddel, G. Metal Single-Insulator and Multi-Insulator Diodes for Rectenna Solar Cells, chapter 5. In Rectenna Solar Cells; Springer: Berlin, Germany, 2013; pp. 89–109. [Google Scholar]
- Kordetoodeshki, E.; Hassanzadeh, A. An ultra-low power, low voltage DC-DC converter circuit for energy harvesting applications. AEU Int. J. Electron. Commun. 2019, 98, 8–18. [Google Scholar] [CrossRef]
- Cheraghi Shirazi, N.; Jannesari, A.; Torkzadeh, P. Self-start-up fully integrated DC-DC step-up converter using body biasing technique for energy harvesting applications. AEU Int. J. Electron. Commun. 2018, 95, 24–35. [Google Scholar] [CrossRef]
- Ashraf, M.; Masoumi, N. High efficiency boost converter with variable output voltage using a self-reference comparator. AEU Int. J. Electron. Commun. 2014, 68, 1058–1064. [Google Scholar] [CrossRef]
- LTC3108 Datasheet. Available online: https://www.analog.com/en/products/ltc3108.html (accessed on 11 February 2019).
- Zhang, S.; Wang, L.; Xu, C.; Li, D.; Chen, L.; Yang, D. Fabrication of Ni-NiO-Cu Metal-Insulator- Metal Tunnel Diodes via Anodic Aluminum Oxide Templates. ECS Solid State Lett. 2013, 2, Q1–Q4. [Google Scholar] [CrossRef]
- Kim, J.; Yang, S.Y.; Song, K.D.; Jones, S.; Elliott, J.R.; Choi, S.H. Microwave power transmission using a flexible rectenna for microwave-powered aerial vehicles. Smart Mater. Struct. 2006, 15, 1243–1248. [Google Scholar] [CrossRef]
- Komatsu, S.; Katsunaga, K.; Ozawa, R.; Komurasaki, K.; Arakawa, Y. Power Transmission to a Micro Aerial Vehicle. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007; pp. 1–6. [Google Scholar]
- De, D.; Kumar Sahu, P. A Novel Approach towards the Designing of an Antenna for Aircraft Collision Avoidance System. AEU Int. J. Electron. Commun. 2017, 71, 53–71. [Google Scholar] [CrossRef]
- Lin, M.C.; Gong, M.; Lu, B.; Wu, Y.; Wang, D.Y.; Guan, M.; Angell, M.; Chen, C.; Yang, J.; Hwang, B.J.; et al. An ultrafast rechargeable aluminum-ion battery. Nature 2015, 520, 324–328. [Google Scholar] [CrossRef]
- Jayaprakash, N.; Das, S.K.; Archer, L.A. The rechargeable aluminum-ion battery. Chem. Commun. 2011, 47, 12610–12612. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, Y.; Zhang, F.; Sing Lee, C. A Novel Aluminum–Graphite Dual-Ion Battery. Adv. Energy Mater. 2016, 6, 1502588. [Google Scholar] [CrossRef]
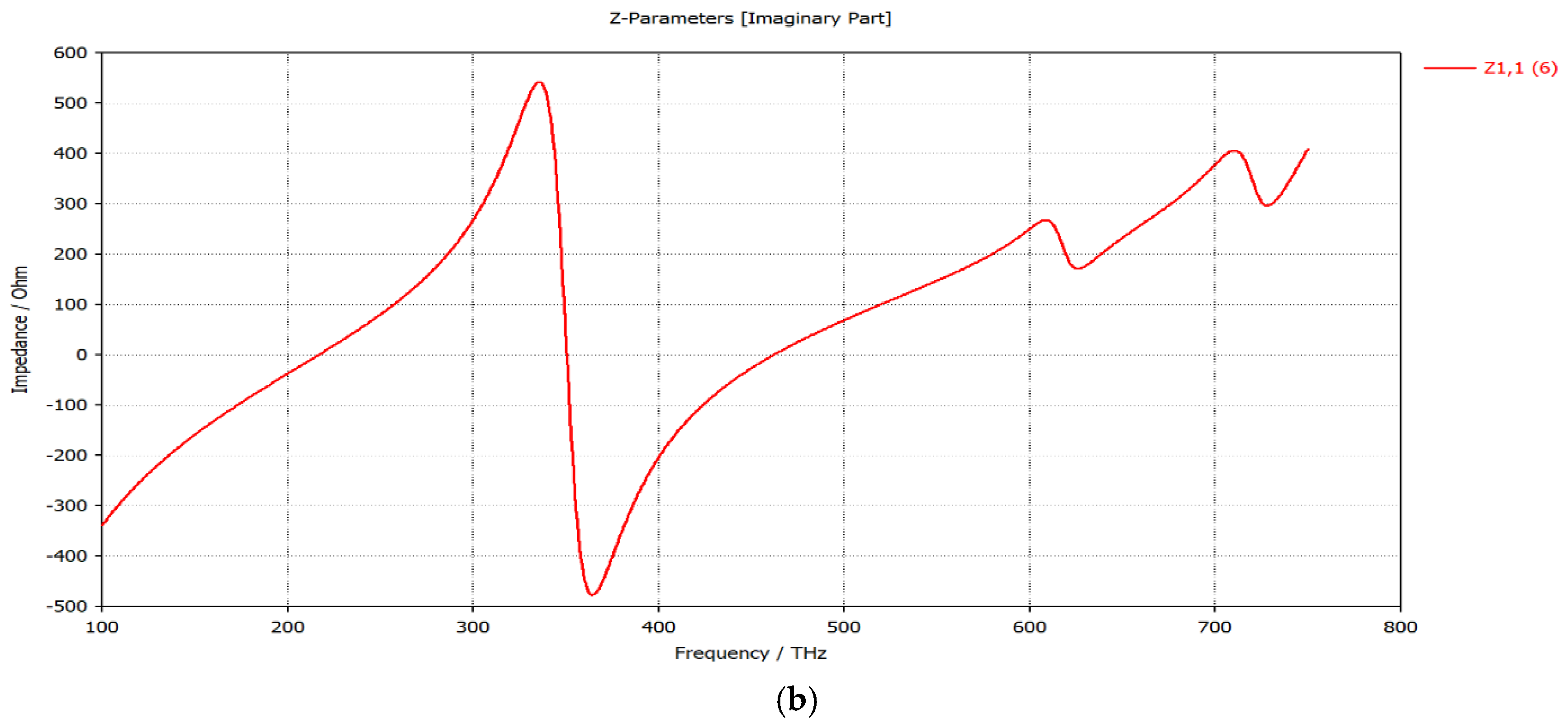
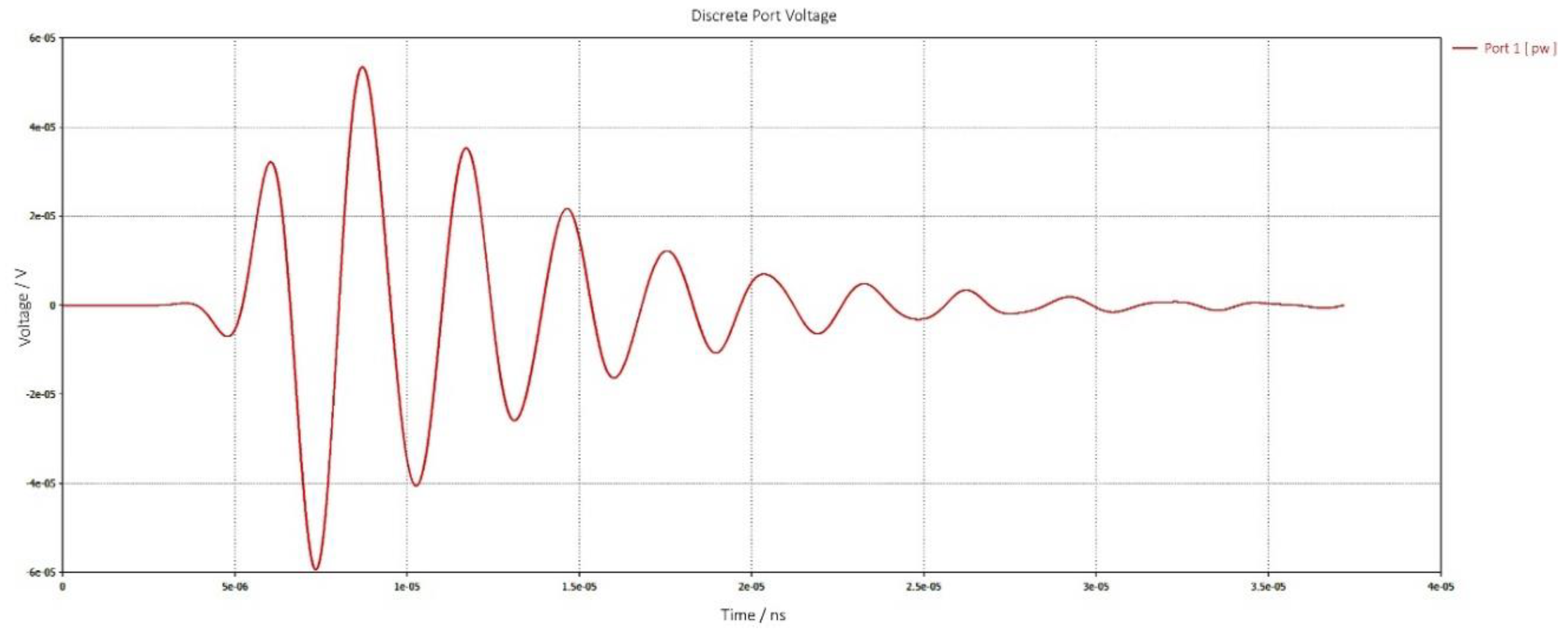
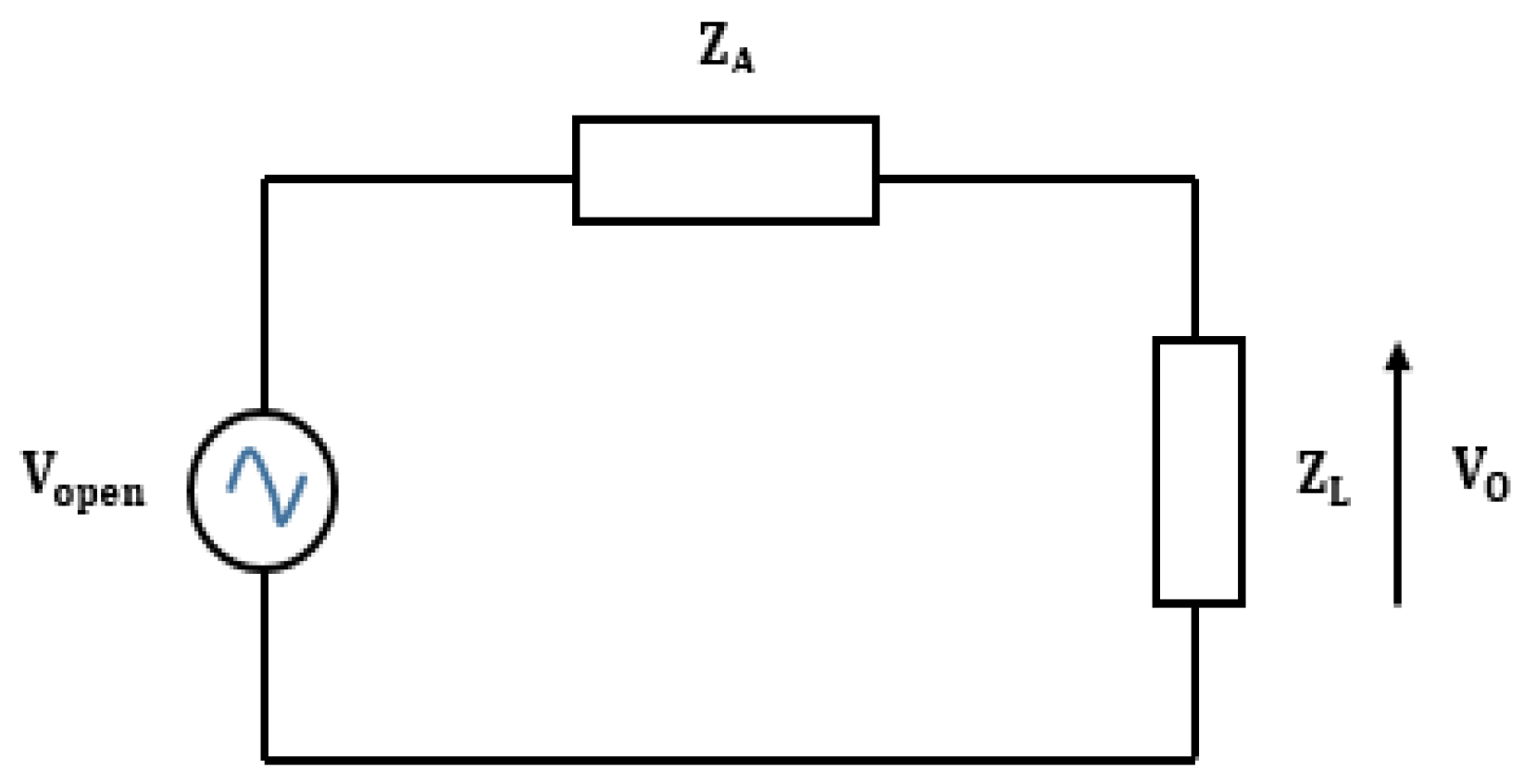
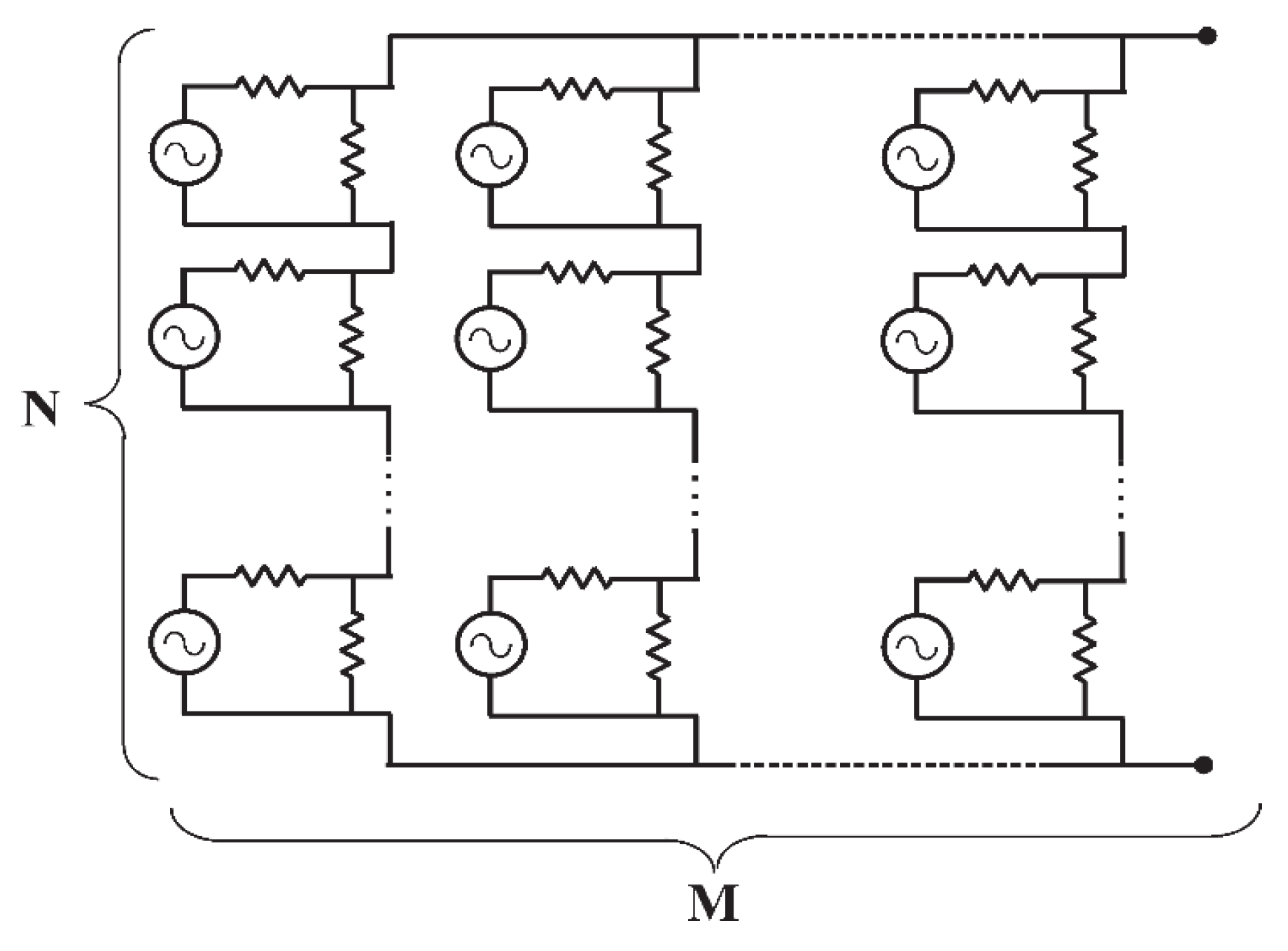
| Parameter | Value | Description |
|---|---|---|
| mprop | 24.4 (g) | Propulsion mass |
| mpayl | 6.3 (g) | Payload mass |
| mav | 23 (g) | Avionics mass (including all cabling) |
| mairframe | 10 (g) | Airframe mass |
| marray | 2 (g) | Dipole rectenna array mass |
| Wtot | 80 (g) | Total Weight MAV |
| L [nm] | Actual Poynting Vector <S’> [W/m2] | Power P [nW] |
|---|---|---|
| 80 | 70 | 15.6 |
| L [nm] | Ei [V/m] | Vopen [µV] | Vo [µV] |
|---|---|---|---|
| 80 | 230 | 50 | 25 |
| L [nm] | ZIboost [Ω] | VDC [µV] | Vo,array [mV] | N | M |
|---|---|---|---|---|---|
| 80 | 3 | 16 | 1000 | 62,800 | 22,066,058 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Citroni, R.; Di Paolo, F.; Livreri, P. A Novel Energy Harvester for Powering Small UAVs: Performance Analysis, Model Validation and Flight Results. Sensors 2019, 19, 1771. https://doi.org/10.3390/s19081771
Citroni R, Di Paolo F, Livreri P. A Novel Energy Harvester for Powering Small UAVs: Performance Analysis, Model Validation and Flight Results. Sensors. 2019; 19(8):1771. https://doi.org/10.3390/s19081771
Chicago/Turabian StyleCitroni, Rocco, Franco Di Paolo, and Patrizia Livreri. 2019. "A Novel Energy Harvester for Powering Small UAVs: Performance Analysis, Model Validation and Flight Results" Sensors 19, no. 8: 1771. https://doi.org/10.3390/s19081771
APA StyleCitroni, R., Di Paolo, F., & Livreri, P. (2019). A Novel Energy Harvester for Powering Small UAVs: Performance Analysis, Model Validation and Flight Results. Sensors, 19(8), 1771. https://doi.org/10.3390/s19081771







