Myocardium Detection by Deep SSAE Feature and Within-Class Neighborhood Preserved Support Vector Classifier and Regressor
Abstract
1. Introduction
1.1. Related Works
1.2. Motivation and Contribution
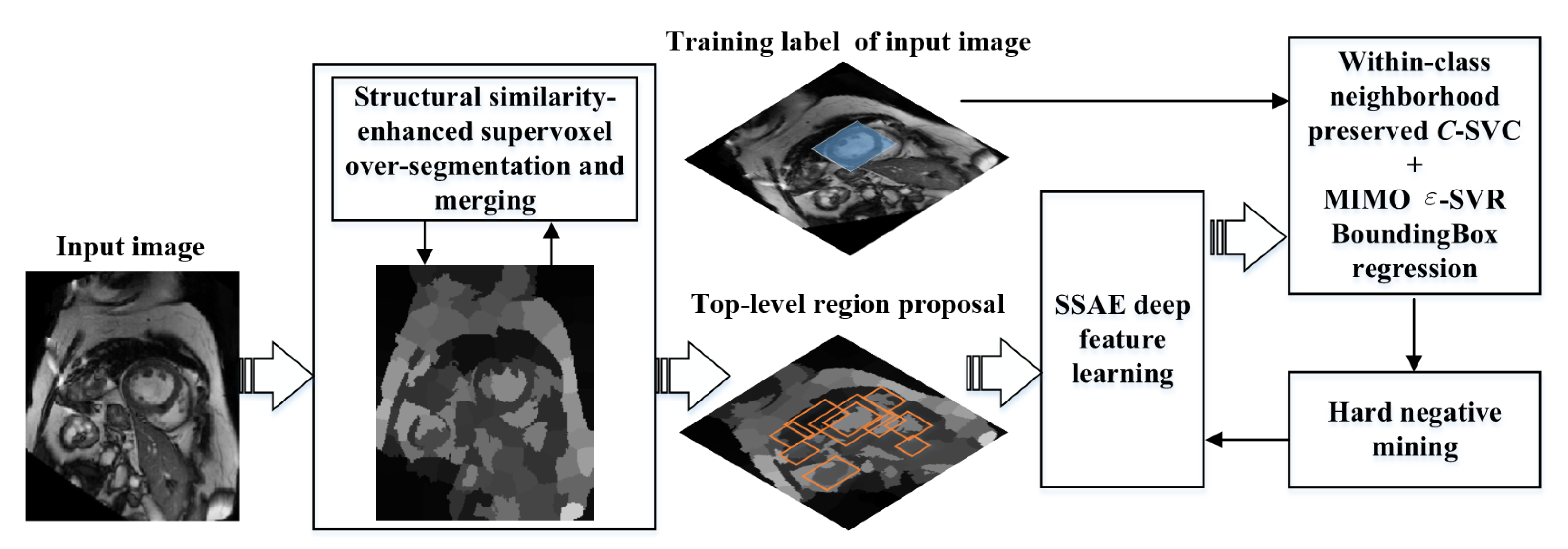
2. Proposed Method
2.1. Overview of Our Detection Model
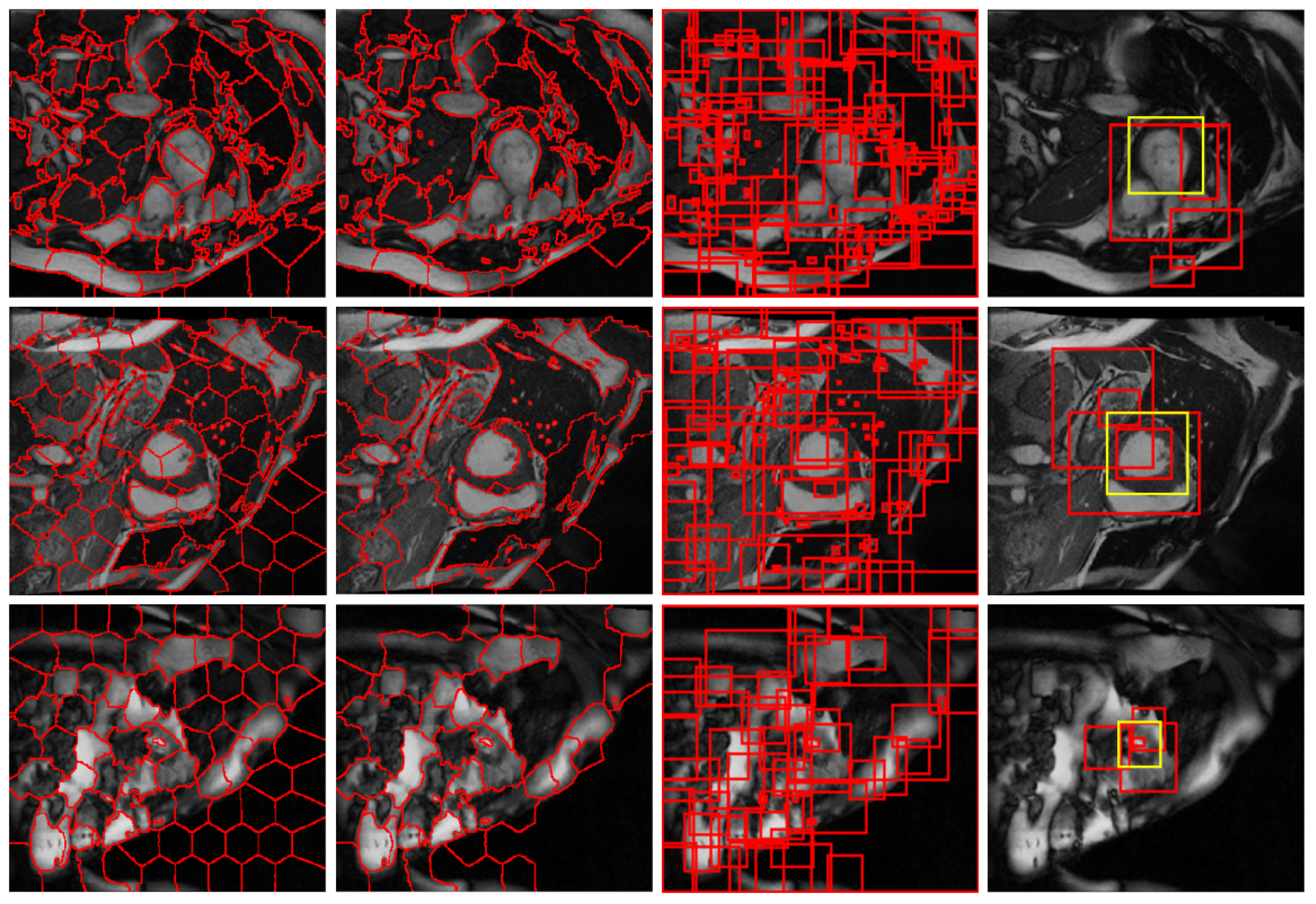
2.2. Candidate Region Proposal
2.2.1. Structural Similarity-Enhanced Supervoxel Over-Segmentation
2.2.2. Supervoxel Region Merging by Hierarchical Clustering
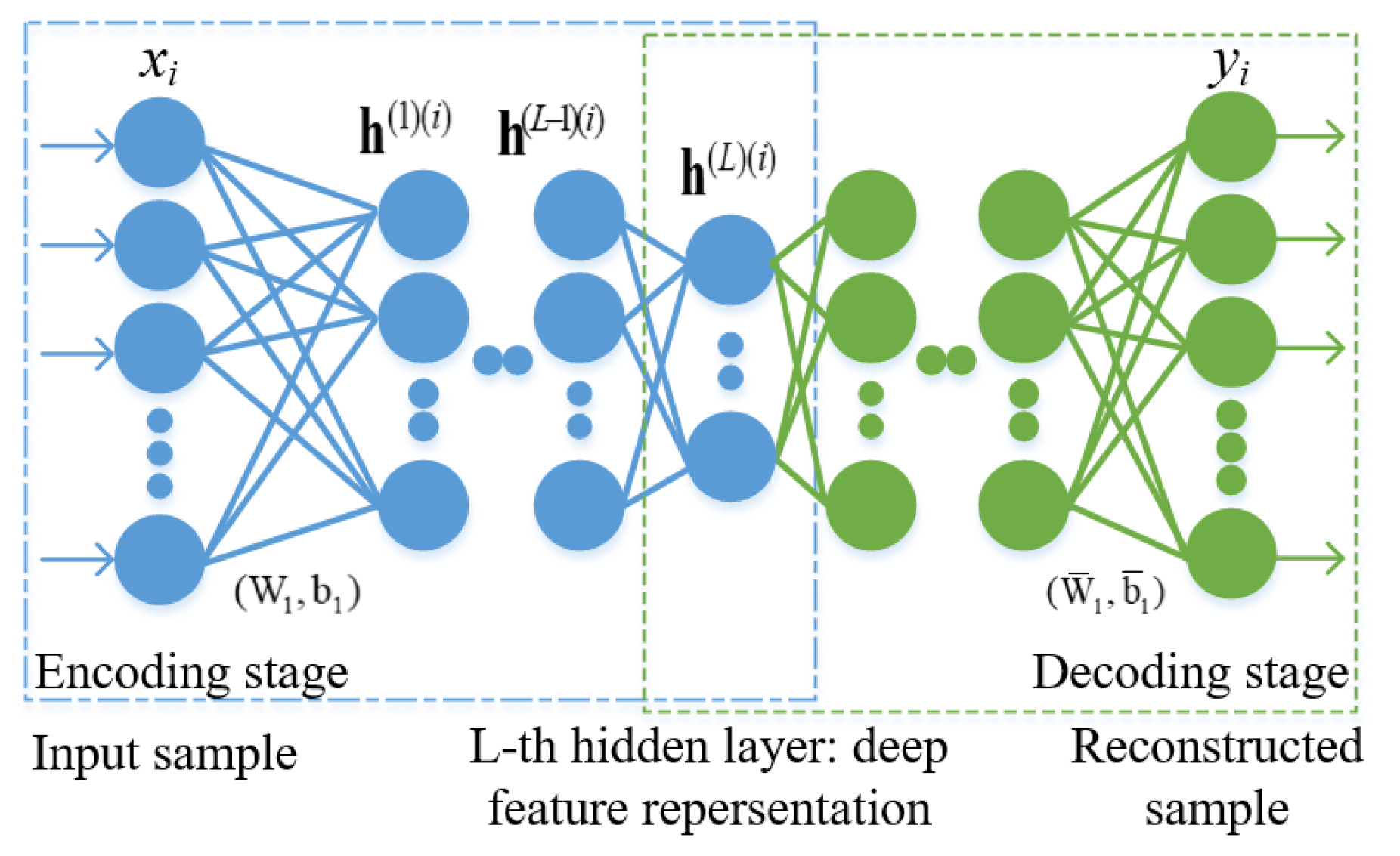
2.3. Deep SSAE Feature Learning
2.4. Within-Class Neighborhood Preserved C-SVC Classification
2.5. MIMO Within-Class Neighborhood Preserved -SVR Bounding Box Regression
2.6. Refinement
3. Datasets and Evaluation Metrics
3.1. Cardiac MRI Dataset and Preprocessing
3.2. Evaluation Metrics
4. Experimental Results and Discussion
4.1. Parameters Setting
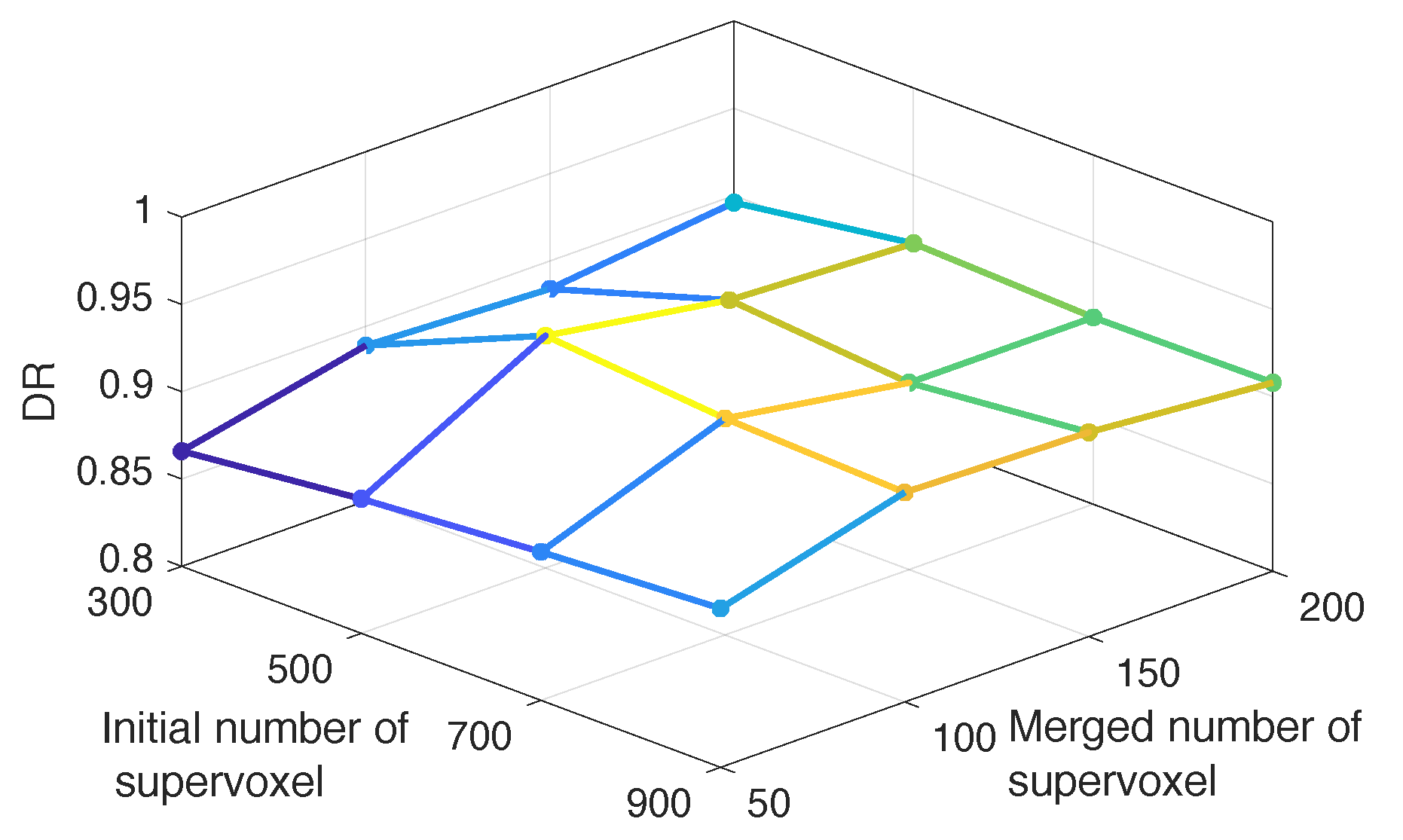
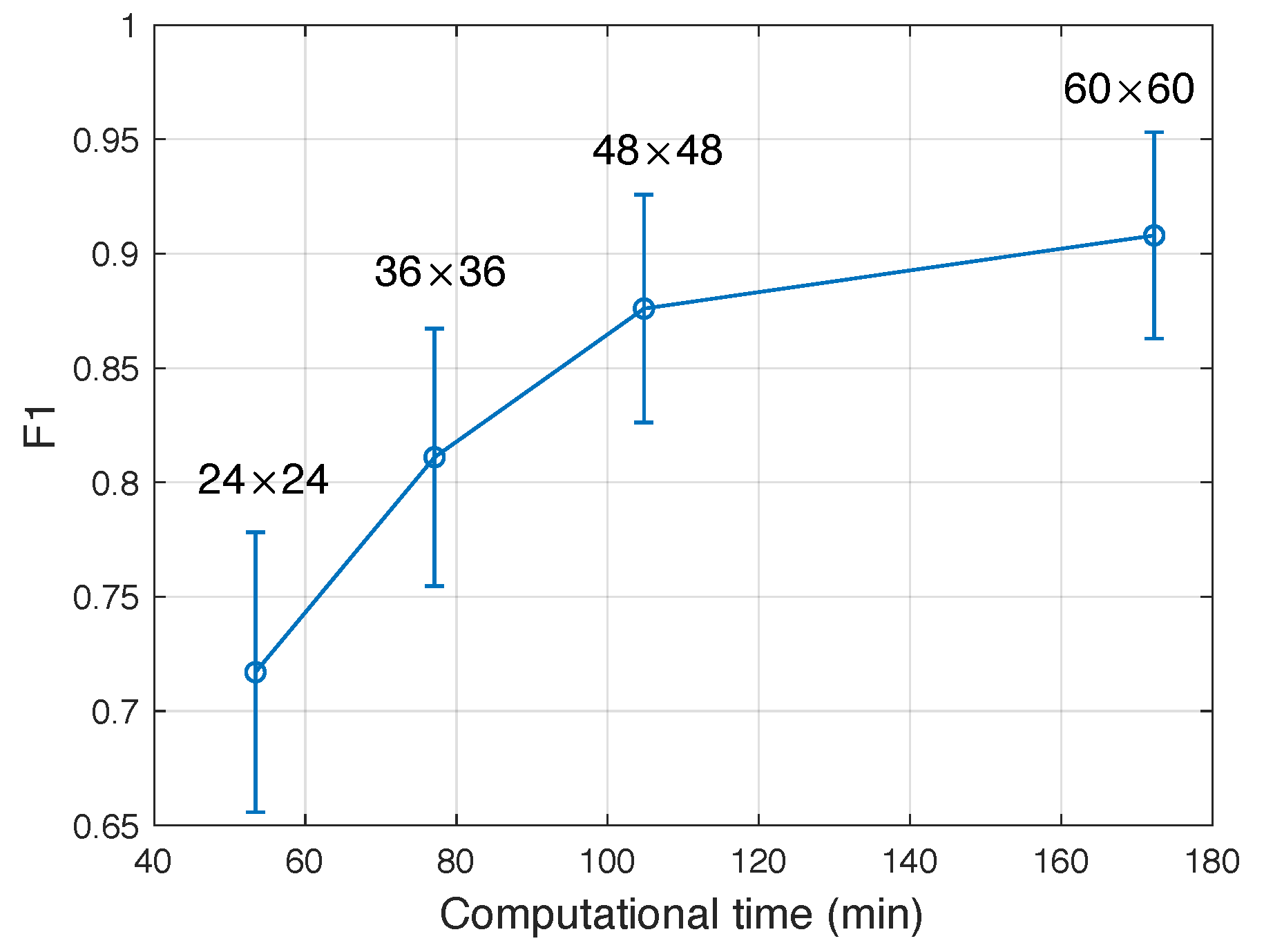
4.1.1. Number of Supervoxels and Training Image Set Building
4.1.2. Size of Proposed Region and SSAE Training
4.1.3. Parameters of Within-class Neighborhood Preserved C-SVC and -SVR
4.2. Validation of the Parts in Our Model
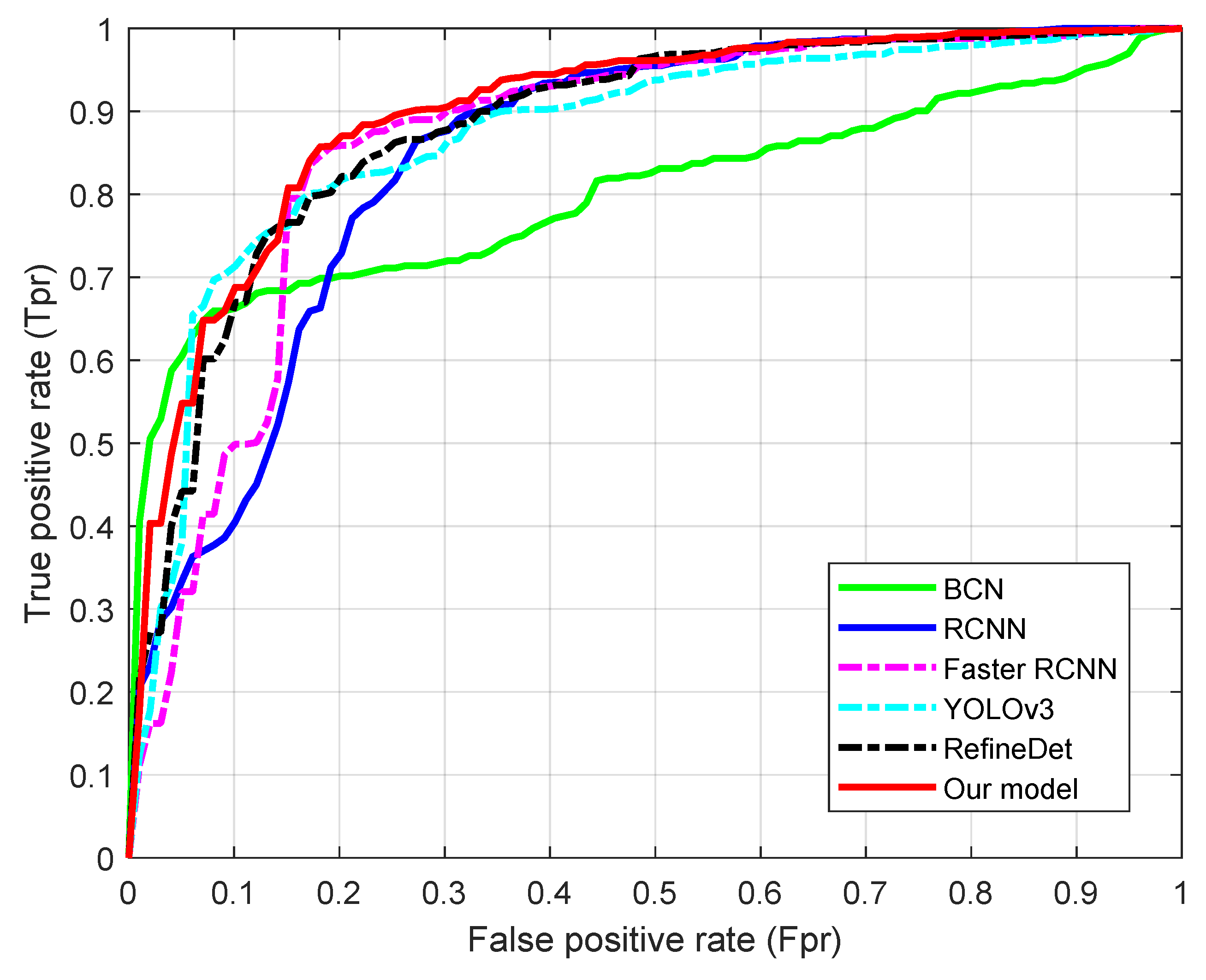
4.3. Comparison with Related Methods
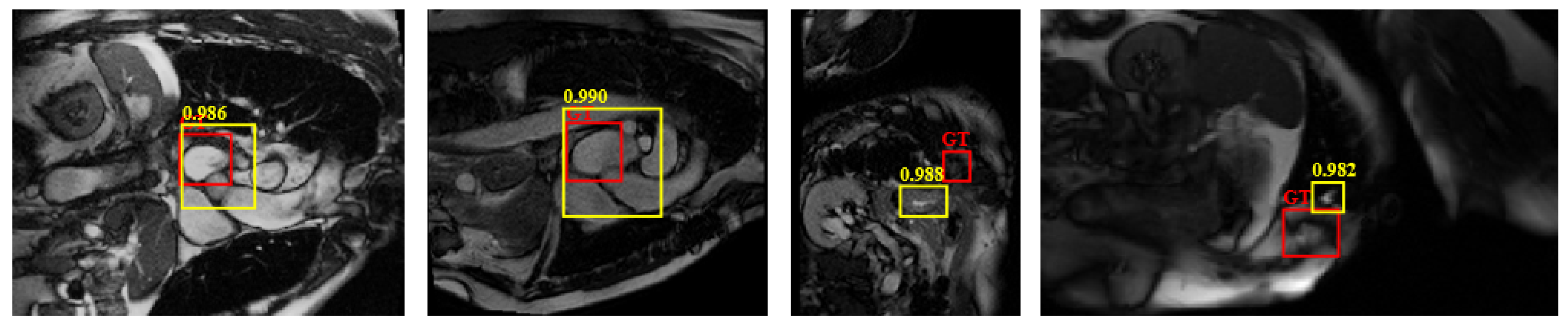
4.4. Discussion
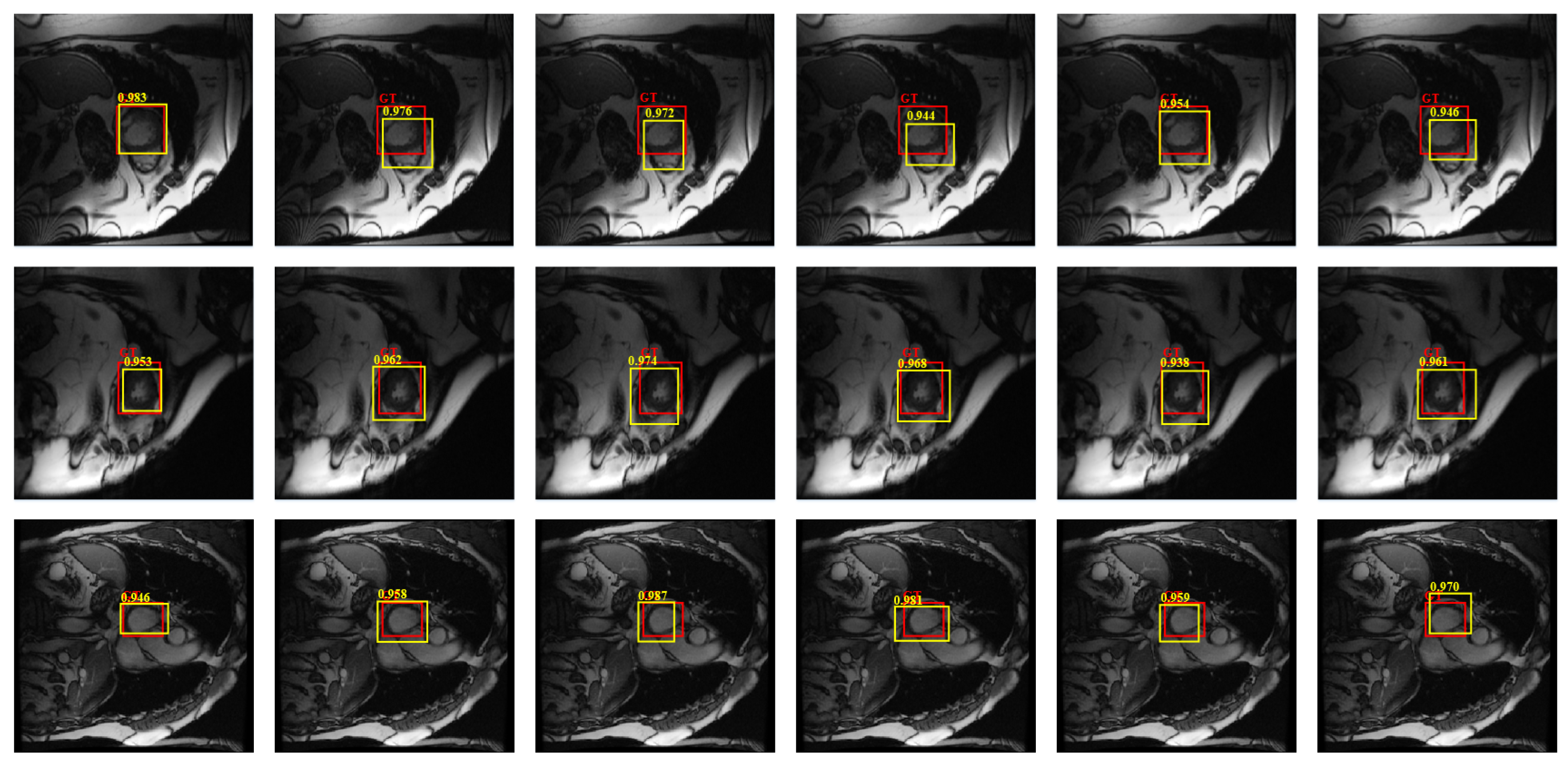
4.4.1. Detection Performance
4.4.2. Processing Speed
4.4.3. Limitations of the Work
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xue, W.; Brahm, G.; Pandey, S.; Leung, S.; Li, S. Full left ventricle quantification via deep multitask relationships learning. Med. Image Anal. 2018, 43, 54–65. [Google Scholar] [CrossRef]
- Khened, M.; Kollerathu, V.A.; Krishnamurthi, G. Fully convolutional multi-scale residual DenseNets for cardiac segmentation and automated cardiac diagnosis using ensemble of classifiers. Med. Image Anal. 2019, 51, 21–45. [Google Scholar] [CrossRef] [PubMed]
- Mo, Y.; Liu, F.; McIlwraith, D.; Yang, G.; Zhang, J.; He, T.; Guo, Y. The Deep Poincaré Map: A Novel Approach for Left Ventricle Segmentation. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2018; Frangi, A., Schnabel, J., Davatzikos, C., Alberola-López, C., Fichtinger, G., Eds.; Springer: Cham, Swetzerland, 2018. [Google Scholar] [CrossRef]
- Vigneault, D.M.; Xie, W.; Ho, C.Y.; Bluemke, D.A.; Noble, J.A. Ω-Net (Omega-Net): Fully automatic, multi-view cardiac MR detection, orientation, and segmentation with deep neural networks. Med. Image Anal. 2018, 48, 95–106. [Google Scholar] [CrossRef] [PubMed]
- Larroza, A.; Lopez-Lereu, M.P.; Monmeneu, J.V.; Bodi, V.; Moratal, D. Texture analysis for infarcted myocardium detection on delayed enhancement MRI. In Proceedings of the 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017), Melbourne, Australia, 18–21 April 2017; pp. 1066–1069. [Google Scholar]
- Viola, P.; Jones, M.J. Robust real-time face detection. Int. J. Comput. Vis. 2004, 57, 137–154. [Google Scholar] [CrossRef]
- Criminisi, A.; Shotton, J.; Bucciarelli, S. Decision forests with long-range spatial context for organ localization in CT volumes. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2009, London, UK, 20–24 September 2009; pp. 69–80. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems 28: Annual Conference on Neural Information Processing Systems 2015, Montreal, QC, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, Faster, Stronger. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 6517–6525. [Google Scholar]
- Fareed, M.M.S.; Chun, Q.; Ahmed, G.; Murtaza, A.; Asif, M.R.; Fareed, M.Z. Appearance-Based Salient Regions Detection Using Side-Specific Dictionaries. Sensors 2019, 19, 421. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; He, Y.; Sun, X.; Jia, X.; Zhang, B. Incorporating Negative Sample Training for Ship Detection Based on Deep Learning. Sensors 2019, 19, 684. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial pyramid pooling in deep convolutional networks for visual recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1904–1916. [Google Scholar] [CrossRef]
- Girshick, R. Fast R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, Boston, MA, USA, 7–12 June 2015; pp. 1440–1448. [Google Scholar]
- Dai, J.; Li, Y.; He, K.; Sun, J. R-FCN: Object detection via region-based fully convolutional networks. In Proceedings of the Advances in Neural Information Processing Systems 29: Annual Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 379–387. [Google Scholar]
- Cai, Z.; Fan, Q.; Feris, R.S.; Vasconcelos, N. A Unified Multi-scale Deep Convolutional Neural Network for Fast Object Detection. In Computer Vision—ECCV 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer: Cham, Switzerland, 2016; pp. 354–370. [Google Scholar]
- Cai, Z.; Vasconcelos, N. Cascade R-CNN: Delving Into High Quality Object Detection. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 6154–6162. [Google Scholar]
- Hu, H.; Gu, J.; Zhang, Z.; Dai, J.; Wei, Y. Relation Networks for Object Detection. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3588–3597. [Google Scholar]
- Cheng, K.; Chen, Y.; Fang, W. Improved Object Detection With Iterative Localization Refinement in Convolutional Neural Networks. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 2261–2275. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv, 2018; arXiv:1804.02767v1. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single shot multibox detector. In Computer Vision—ECCV 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Zhang, S.; Wen, L.; Bian, X.; Lei, Z.; Li, S.Z. Single-Shot Refinement Neural Network for Object Detection. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4203–4212. [Google Scholar] [CrossRef]
- Uijlings, J.R.; Van De Sande, K.E.; Gevers, T.; Smeulders, A.W. Selective search for object recognition. Int. J. Comput. Vis. 2013, 104, 154–171. [Google Scholar] [CrossRef]
- Yan, Z.; Zhan, Y.; Peng, Z.; Liao, S.; Shinagawa, Y.; Metaxas, D.N.; Zhou, X.S. Bodypart recognition using multi-stage deep learning. In Information Processing in Medical Imaging; Ourselin, S., Alexander, D., Westin, C.F., Cardoso, M., Eds.; Springer: Cham, Switzerland, 2015. [Google Scholar]
- De Vos, B.D.; Wolterink, J.M.; de Jong, P.A.; Viergever, M.A.; Išgum, I. 2D image classification for 3D anatomy localization: Employing deep convolutional neural networks. In Proceedings of the SPIE Medical Imaging, San Diego, CA, USA, 27 February–3 March 2016. [Google Scholar]
- Roth, H.R.; Lee, C.T.; Shin, H.C.; Seff, A.; Kim, L.; Yao, J.; Lu, L.; Summers, R.M. Anatomy-specific classification of medical images using deep convolutional nets. In Proceedings of the 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI), Brooklyn, NY, USA, 16–19 April 2015; pp. 101–104. [Google Scholar]
- Luo, G.; An, R.; Wang, K.; Dong, S.; Zhang, H. A deep learning network for right ventricle segmentation in short-axis MRI. In Proceedings of the 2016 Computing in Cardiology Conference (CinC), Vancouver, BC, Canada, 11–14 September 2016; pp. 485–488. [Google Scholar]
- Poudel, R.P.K.; Lamata, P.; Montana, G. Recurrent Fully Convolutional Neural Networks for Multi-slice MRI Cardiac Segmentation. In Reconstruction, Segmentation, and Analysis of Medical Images; Zuluaga, M.A., Bhatia, K., Kainz, B., Moghari, M.H., Pace, D.F., Eds.; Srpinger: Cham, Switzerland, 2016. [Google Scholar]
- Tan, L.K.; Liew, Y.M.; Lim, E.; McLaughlin, R.A. Convolutional neural network regression for short-axis left ventricle segmentation in cardiac cine MR sequences. Med. Image Anal. 2017, 39, 78–86. [Google Scholar] [CrossRef] [PubMed]
- Zitnick, C.L.; Dollár, P. Edge boxes: Locating object proposals from edges. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 391–405. [Google Scholar]
- Fulkerson, B.; Vedaldi, A.; Soatto, S. Class segmentation and object localization with superpixel neighborhoods. In Proceedings of the IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 27 September–4 October 2009; pp. 670–677. [Google Scholar]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Lau, R.W.H.; Liu, W.; Zhe, H.; Yang, Q. SuperCNN: A Superpixelwise Convolutional Neural Network for Salient Object Detection. Int. J. Comput. Vision 2015, 115, 330–344. [Google Scholar] [CrossRef]
- Stutz, D.; Hermans, A.; Leibe, B. Superpixels: An evaluation of the state-of-the-art. Comput. Vision Image Underst. 2018, 166, 1–27. [Google Scholar] [CrossRef]
- Kovesi, P. Phase Congruency Detects Corners and Edges. In Proceedings of the 7th International Conference on Digital Image Computing: Techniques and Applications, Sydney, Australia, 10–12 December 2003; pp. 309–318. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Zhuang, X.; Khan, H.; Haldar, S.; Nyktari, E.; Ye, X.; Slabaugh, G.G.; Wong, T.; Mohiaddin, R.; Keegan, J.; et al. A fully automatic deep learning method for atrial scarring segmentation from late gadolinium-enhanced MRI images. In Proceedings of the 14th IEEE International Symposium on Biomedical Imaging, Melbourne, Australia, 18–21 April 2017; pp. 844–848. [Google Scholar] [CrossRef]
- Yang, G.; Zhuang, X.; Khan, H.; Haldar, S.; Nyktari, E.; Ye, X.; Slabaugh, G.G.; Wong, T.; Mohiaddin, R.; Keegan, J.; et al. Segmenting Atrial Fibrosis from Late Gadolinium-Enhanced Cardiac MRI by Deep-Learned Features with Stacked Sparse Auto-Encoders. In Proceedings of the 21st Annual Conference on Medical Image Understanding and Analysis, Edinburgh, UK, 11–13 July 2017; pp. 195–206. [Google Scholar] [CrossRef]
- Yang, G.; Zhuang, X.; Khan, H.; Haldar, S.; Nyktari, E.; Li, L.; Ye, X.; Slabaugh, G.G.; Wong, T.; Mohiaddin, R.; et al. Multi-atlas propagation based left atrium segmentation coupled with super-voxel based pulmonary veins delineation in late gadolinium-enhanced cardiac MRI. In Proceedings of the SPIE 2017 Medical Imaging, Orlando, FL, USA, 11–16 February 2017. [Google Scholar] [CrossRef]
- Xu, J.; Xiang, L.; Liu, Q.; Gilmore, H.; Wu, J.; Tang, J.; Madabhushi, A. Stacked Sparse Autoencoder (SSAE) for Nuclei Detection on Breast Cancer Histopathology Images. IEEE Trans. Med. Imaging 2016, 35, 119–130. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.; Wang, X.; Niu, Y.; Tan, L.; Zhang, S. Segmenting Brain Tissues from Chinese Visible Human Dataset by Deep-Learned Features with Stacked Autoencoder. BioMed Res. Int. 2016, 2016, 5284586. [Google Scholar] [CrossRef]
- Tao, C.; Pan, H.; Li, Y.; Zou, Z. Unsupervised Spectral–Spatial Feature Learning With Stacked Sparse Autoencoder for Hyperspectral Imagery Classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2438–2442. [Google Scholar] [CrossRef]
- Yan, Y.; Tan, Z.; Su, N.; Zhao, C. Building Extraction Based on an Optimized Stacked Sparse Autoencoder of Structure and Training Samples Using LIDAR DSM and Optical Images. Sensors 2017, 17, 1957. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Parallel Distrib. Process. 1986, 323, 399–421. [Google Scholar] [CrossRef]
- Ju, Y.; Guo, J.; Liu, S. A Deep Learning Method Combined Sparse Autoencoder with SVM. In Proceedings of the 2015 International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery, Xi’an, China, 17–19 September 2015; pp. 257–260. [Google Scholar]
- Wang, X.; Niu, Y. Improved support vectors for classification through preserving neighborhood geometric structure constraint. Opt. Eng. 2011, 50, 087202. [Google Scholar]
- Wang, X.; Niu, Y. New one-versus-all v-SVM solving intra-inter class imbalance with extended manifold regularization and localized relative maximum margin. Neurocomputing 2013, 115, 106–121. [Google Scholar] [CrossRef]
- Fernández, M.S.; de Prado-Cumplido, M.; Arenas-García, J.; Pérez-Cruz, F. SVM multiregression for nonlinear channel estimation in multiple-input multiple-output systems. IEEE Trans. Signal Process. 2004, 52, 2298–2307. [Google Scholar] [CrossRef]
- Mao, W.; Xu, J.; Wang, C.; Dong, L. A fast and robust model selection algorithm for multi-input multi-output support vector machine. Neurocomputing 2014, 130, 10–19. [Google Scholar] [CrossRef]
- Wan, L.; Eigen, D.; Fergus, R. End-to-end integration of a convolution network, deformable parts model and non-maximum suppression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 851–859. [Google Scholar]
- Fonseca, C.G.; Backhaus, M.; Bluemke, D.A.; Britten, R.D.; Chung, J.D.; Cowan, B.R.; Dinov, I.D.; Finn, J.P.; Hunter, P.J.; Kadish, A.H. The Cardiac Atlas Project—An imaging database for computational modeling and statistical atlases of the heart. Bioinformatics 2011, 27, 2288–2295. [Google Scholar] [CrossRef]
- Tustison, N.J.; Avants, B.B.; Cook, P.A.; Zheng, Y.; Egan, A.; Yushkevich, P.A.; Gee, J.C. N4ITK: Improved N3 Bias Correction. IEEE Trans. Med. Imaging 2010, 29, 1310–1320. [Google Scholar] [CrossRef]

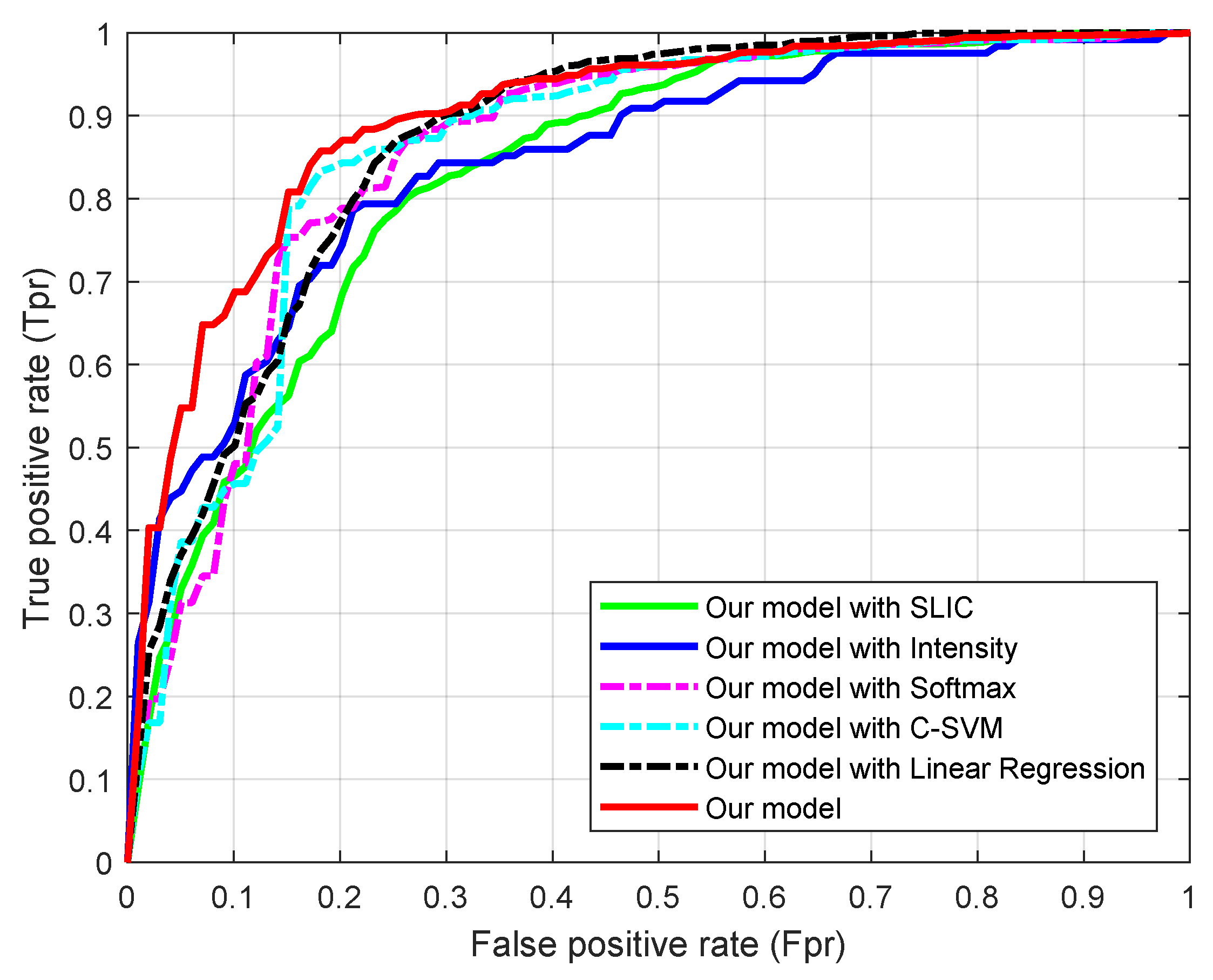
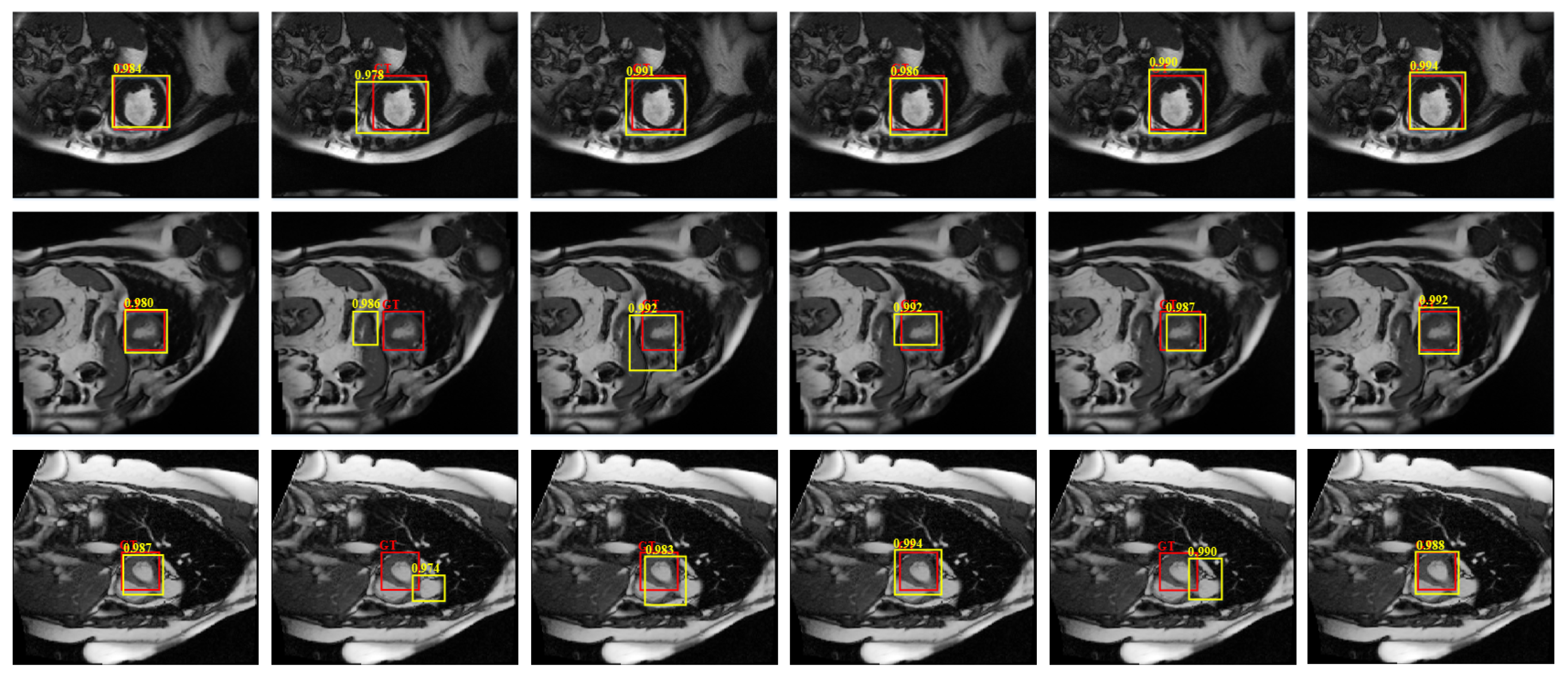
| Metric | Proposed Method with All Terms | Proposed Method with SLIC | Proposed Method with Intensity Feature | Proposed Method with Softmax | Proposed Method with C-SVM | Proposed Method with Linear Regression |
|---|---|---|---|---|---|---|
| 0.924 ± 0.034 | 0.852 ± 0.036 | 0.861 ± 0.038 | 0.878 ± 0.042 | 0.904 ± 0.035 | 0.898 ± 0.044 | |
| 0.936 ± 0.037 | 0.867 ± 0.048 | 0.884 ± 0.042 | 0.894 ± 0.040 | 0.915 ± 0.036 | 0.890 ± 0.038 | |
| 0.916 ± 0.028 | 0.838 ± 0.032 | 0.847 ± 0.037 | 0.866 ± 0.042 | 0.894 ± 0.039 | 0.885 ± 0.046 | |
| Area under ROC () | 0.891 ± 0.031 | 0.824 ± 0.026 | 0.838 ± 0.032 | 0.851 ± 0.024 | 0.857 ± 0.030 | 0.862 ± 0.033 |
| Metric | Proposed Method | BCD | RCNN | Faster RCNN | YOLOv3 | RefineDet |
|---|---|---|---|---|---|---|
| 0.924 ± 0.034 | 0.801 ± 0.092 | 0.870 ± 0.061 | 0.896 ± 0.058 | 0.878 ± 0.065 | 0.914 ± 0.046 | |
| 0.936 ± 0.037 | 0.805 ± 0.097 | 0.877 ± 0.062 | 0.908 ± 0.056 | 0.892 ± 0.062 | 0.918 ± 0.041 | |
| 0.916 ± 0.028 | 0.798 ± 0.103 | 0.863 ± 0.069 | 0.874 ± 0.062 | 0.862 ± 0.060 | 0.898 ± 0.045 | |
| Area under ROC () | 0.891 ± 0.031 | 0.798 ± 0.026 | 0.858 ± 0.037 | 0.872 ± 0.025 | 0.870 ± 0.032 | 0.875 ± 0.036 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, Y.; Qin, L.; Wang, X. Myocardium Detection by Deep SSAE Feature and Within-Class Neighborhood Preserved Support Vector Classifier and Regressor. Sensors 2019, 19, 1766. https://doi.org/10.3390/s19081766
Niu Y, Qin L, Wang X. Myocardium Detection by Deep SSAE Feature and Within-Class Neighborhood Preserved Support Vector Classifier and Regressor. Sensors. 2019; 19(8):1766. https://doi.org/10.3390/s19081766
Chicago/Turabian StyleNiu, Yanmin, Lan Qin, and Xuchu Wang. 2019. "Myocardium Detection by Deep SSAE Feature and Within-Class Neighborhood Preserved Support Vector Classifier and Regressor" Sensors 19, no. 8: 1766. https://doi.org/10.3390/s19081766
APA StyleNiu, Y., Qin, L., & Wang, X. (2019). Myocardium Detection by Deep SSAE Feature and Within-Class Neighborhood Preserved Support Vector Classifier and Regressor. Sensors, 19(8), 1766. https://doi.org/10.3390/s19081766




