A Novel Multi-Angle SAR Imaging System and Method Based on an Ultrahigh Speed Platform
Abstract
:1. Introduction
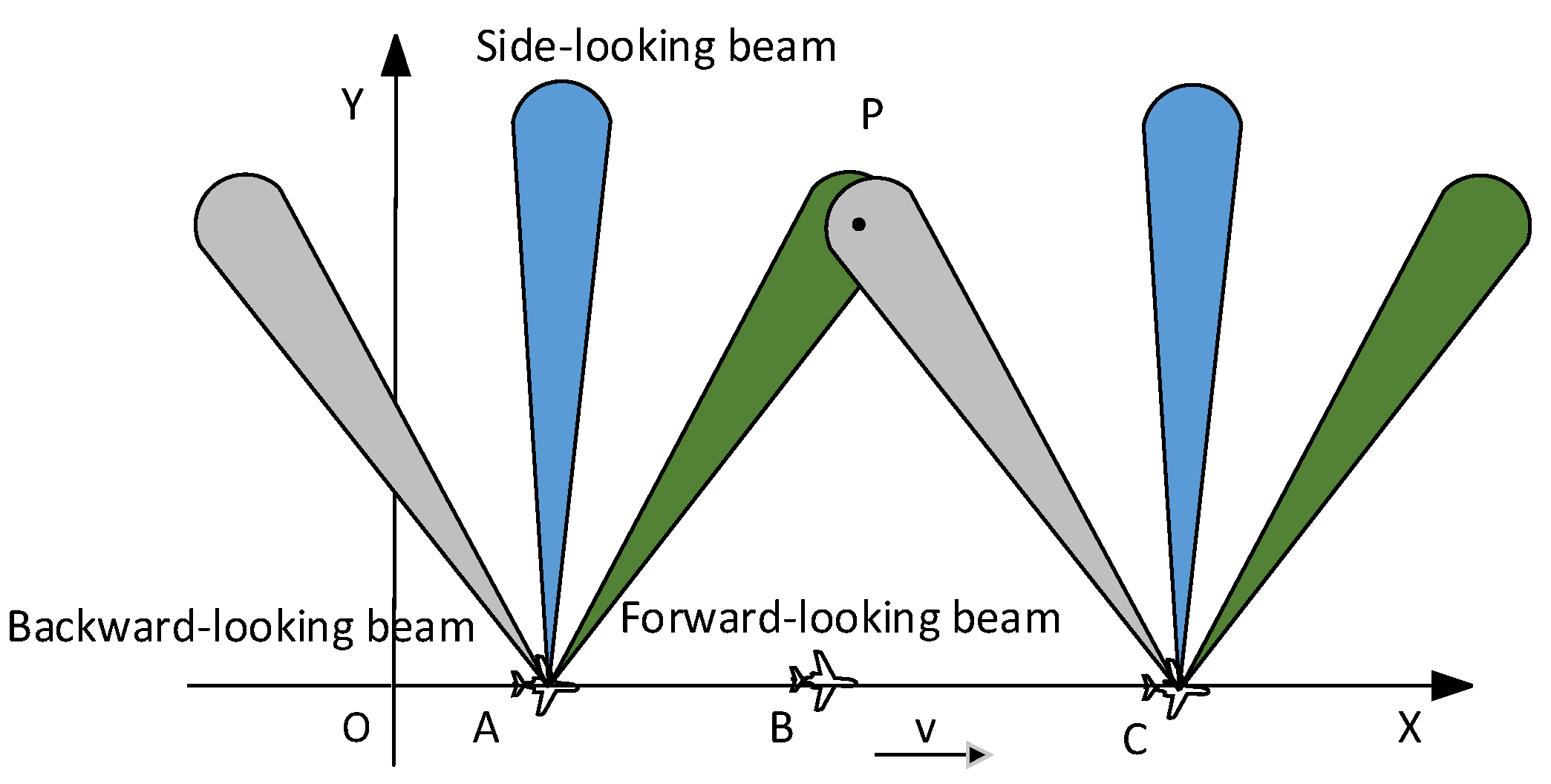
2. A Multi-angle SAR Imaging System and Signal Model on a High-Speed Platform
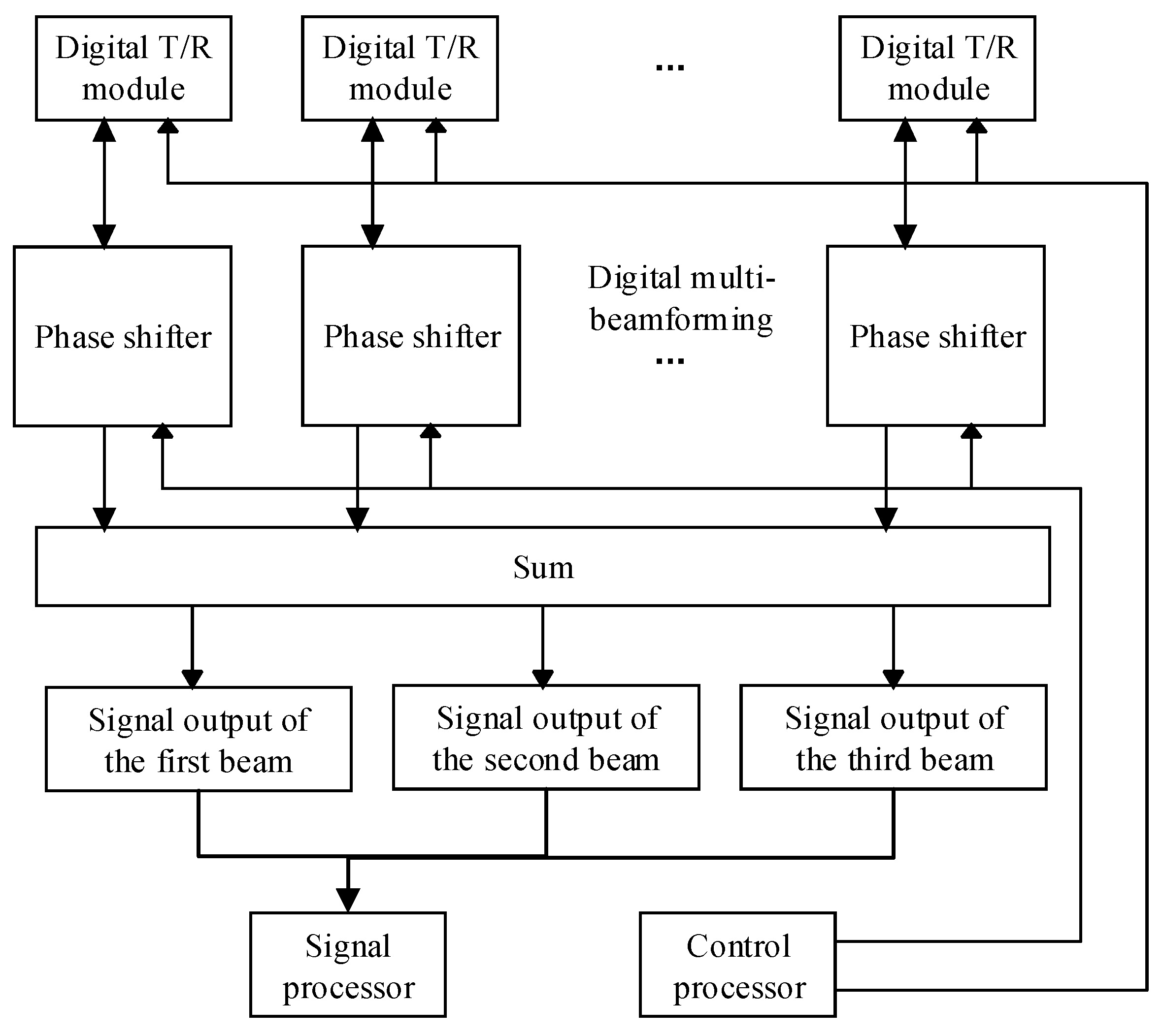
2.1. Digital Multi-Beamforming
2.2. Signal Model
3. Multi-Angle SAR Imaging Method Based on a Unified Coordinate
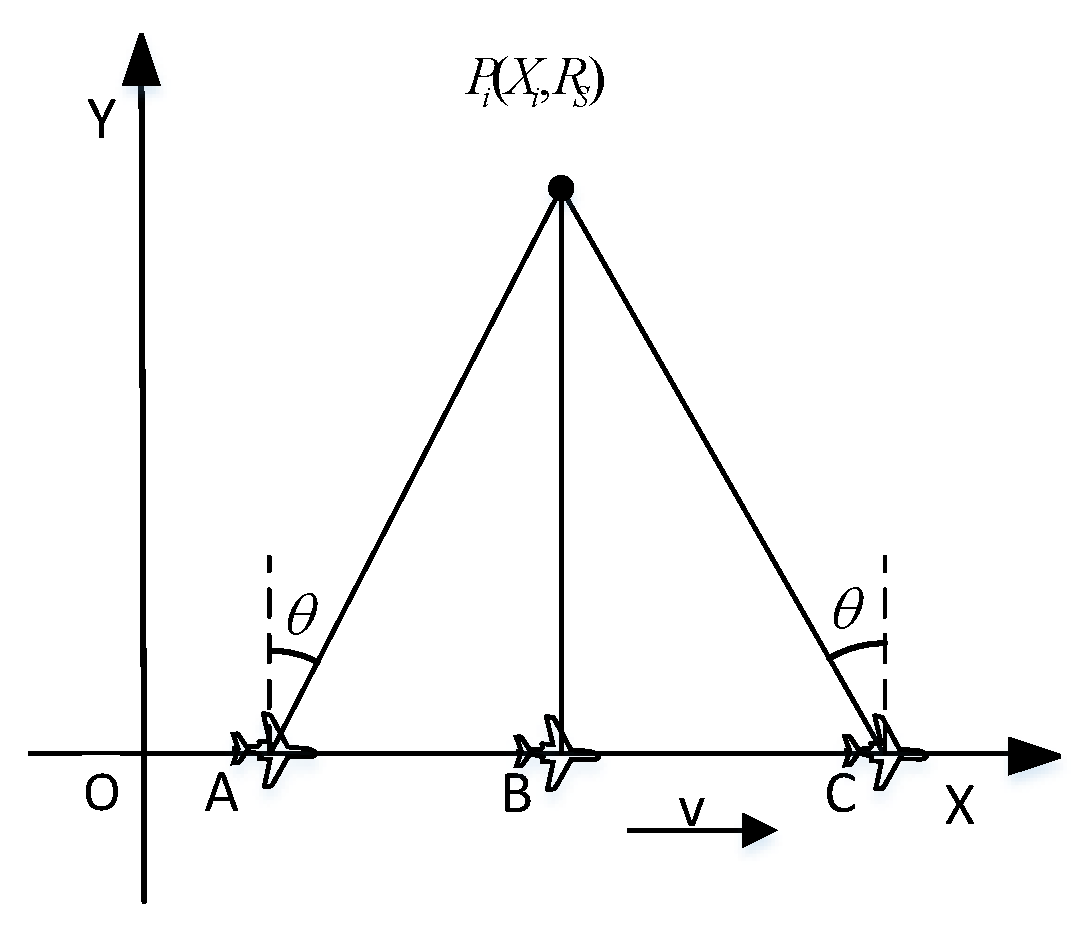
3.1. Problems of Multi-Angle SAR Registrations and Fusion
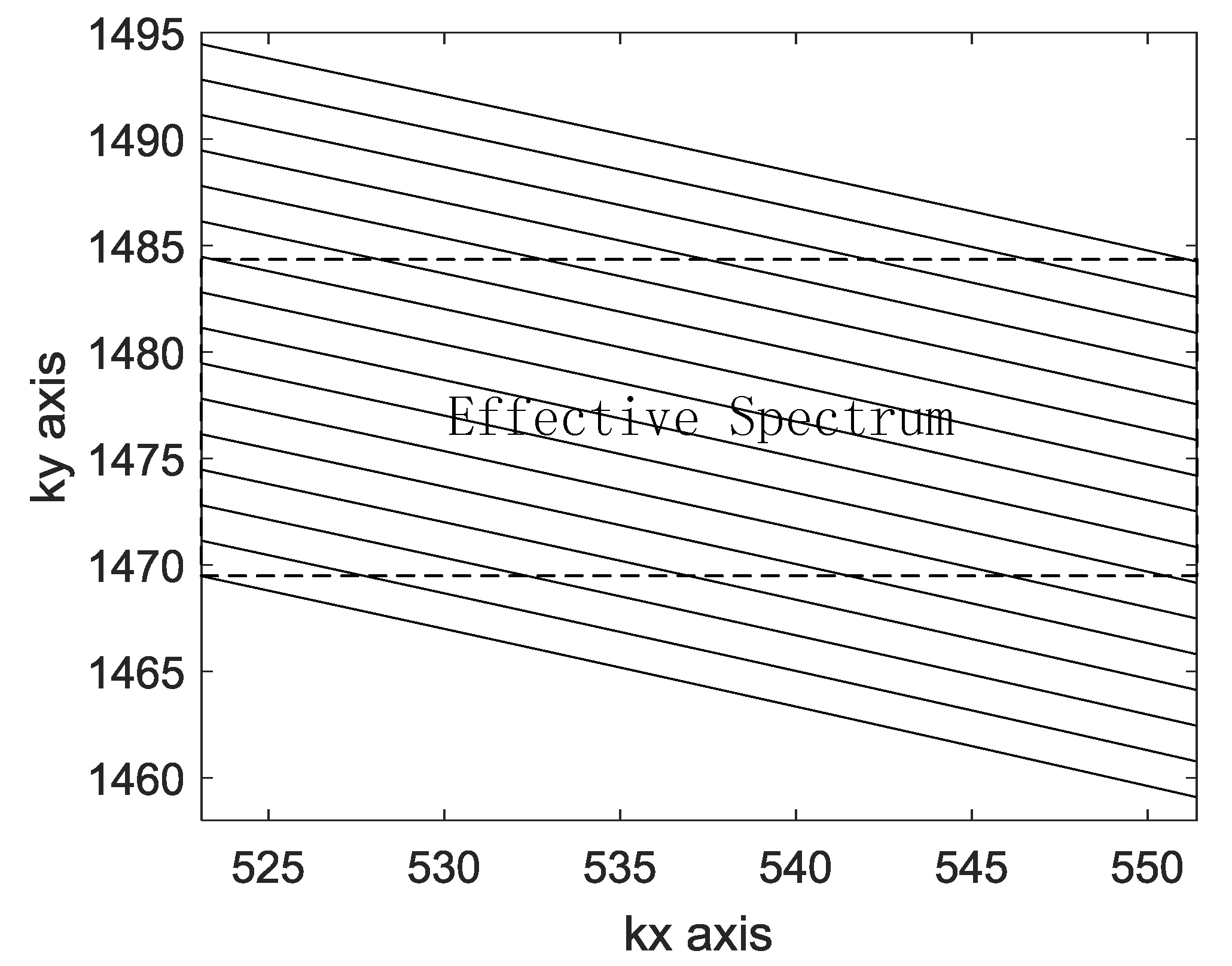
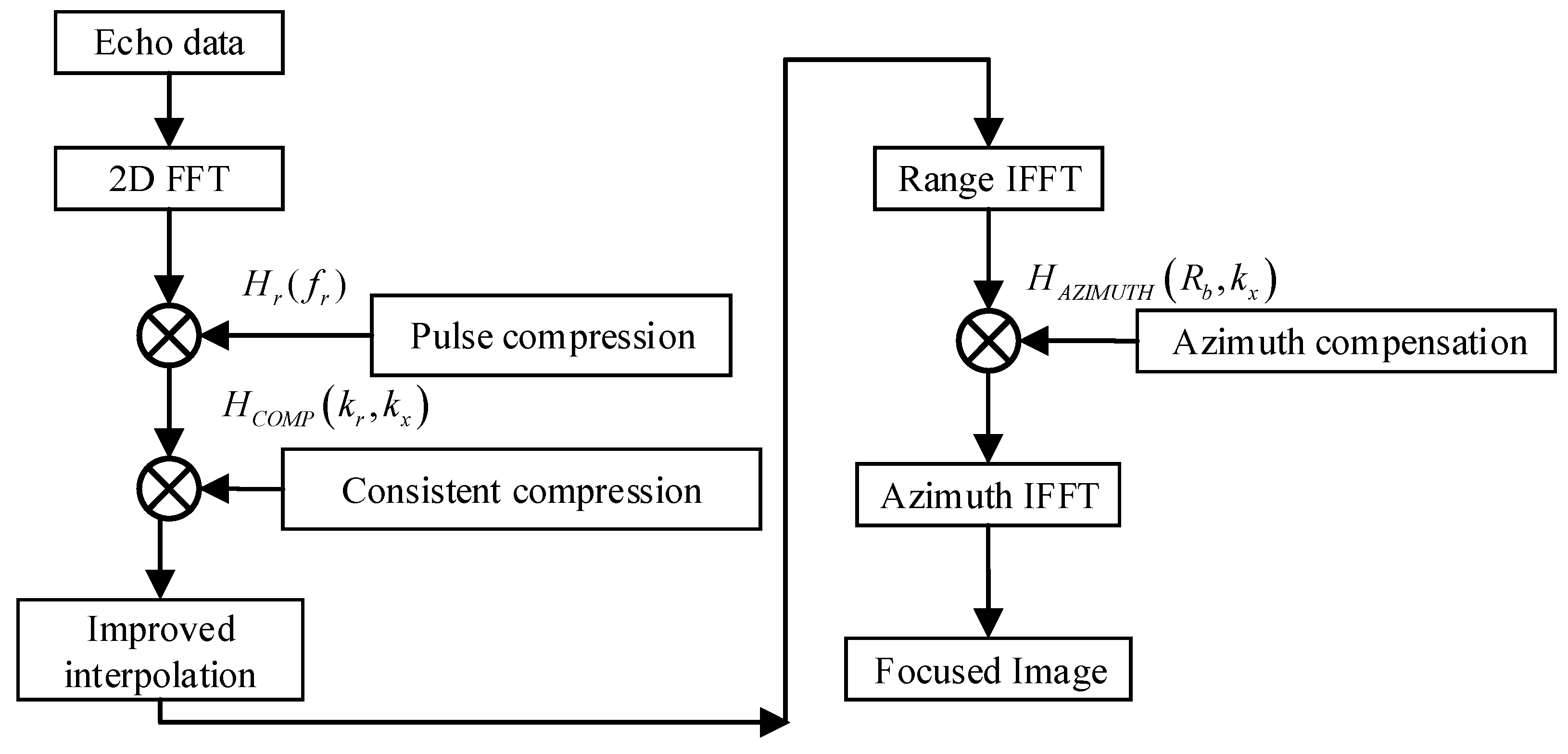
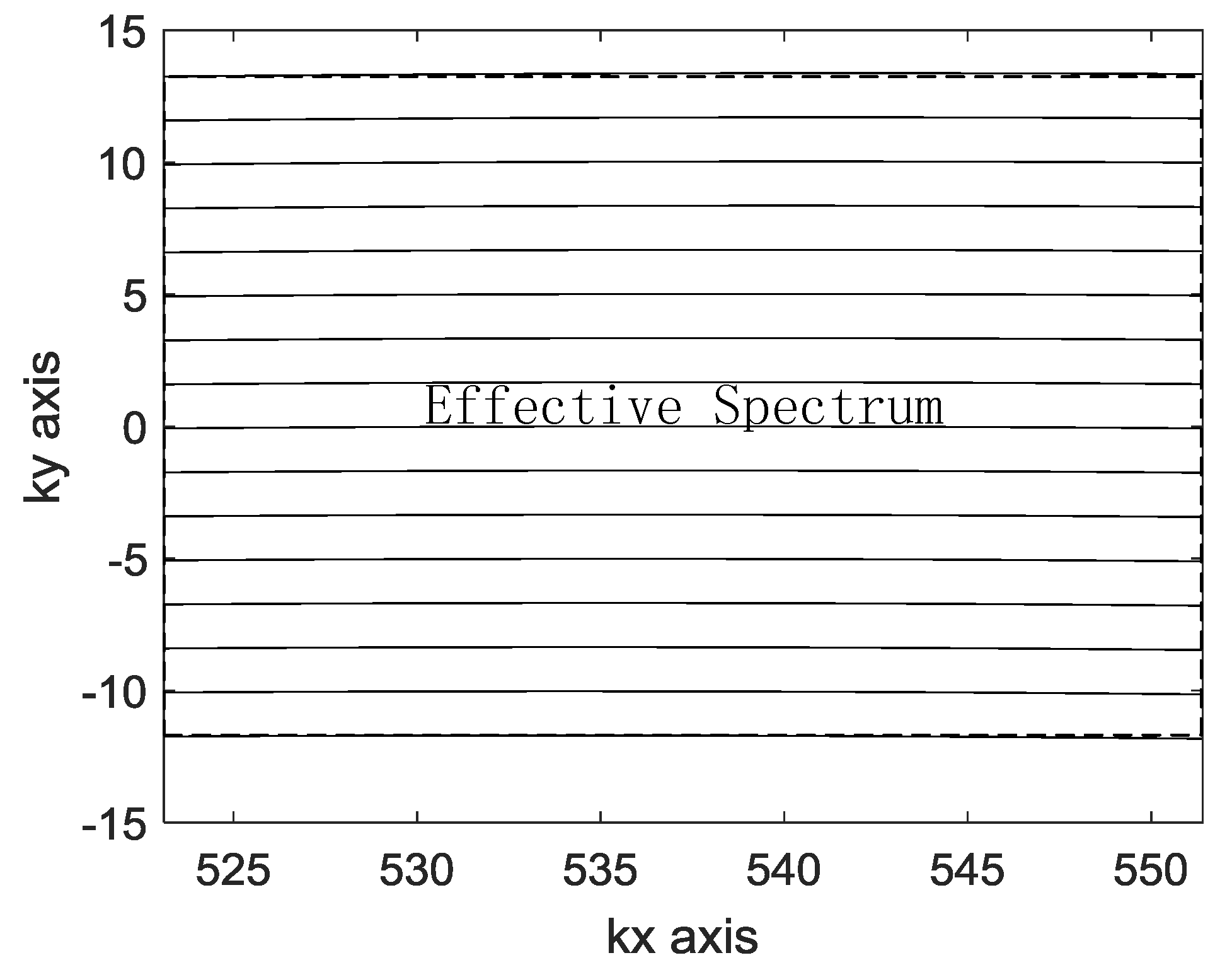
3.2. Improved RMA Algorithm
3.3. Application and Consideration
4. Experimental Simulation, Measured Data
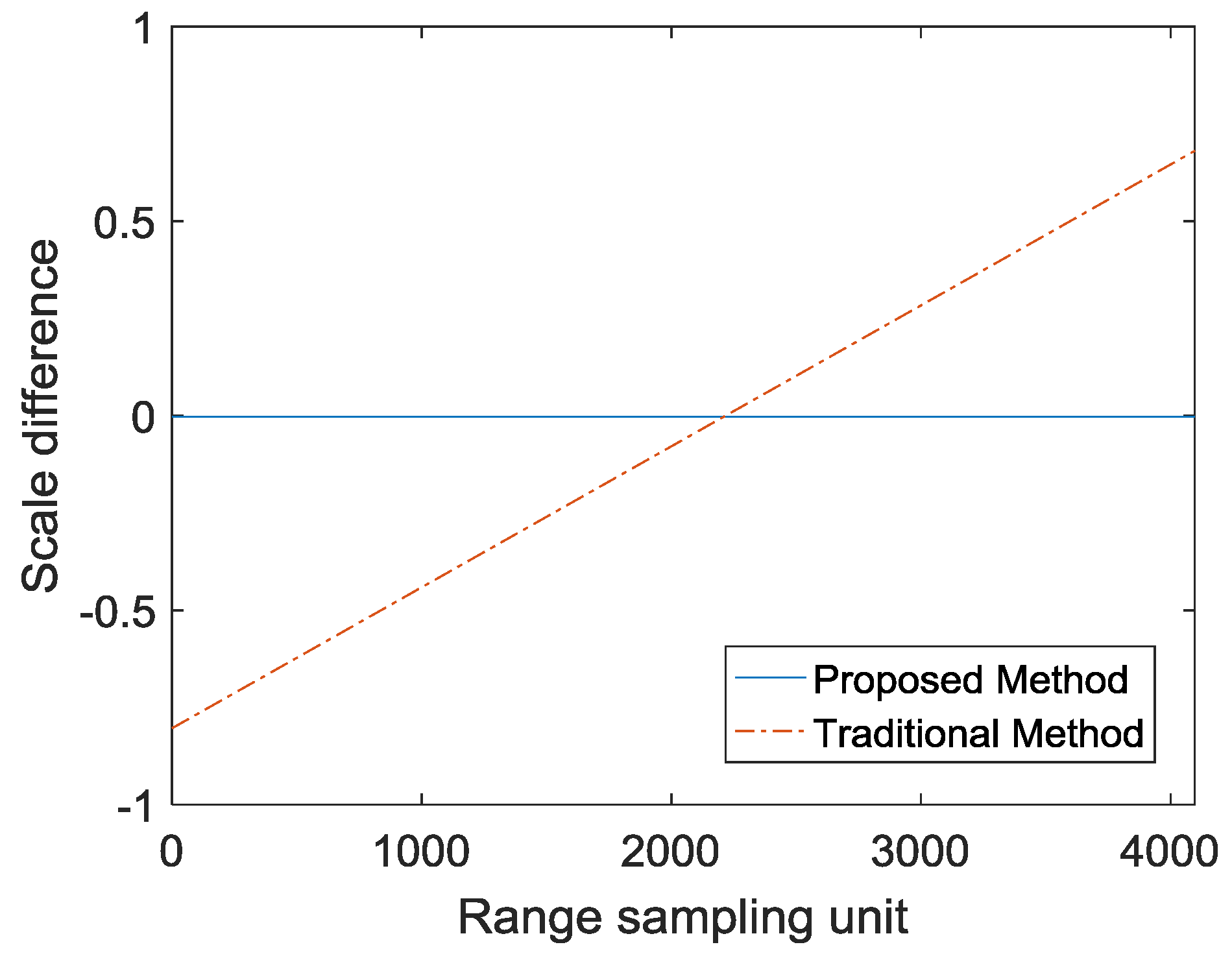
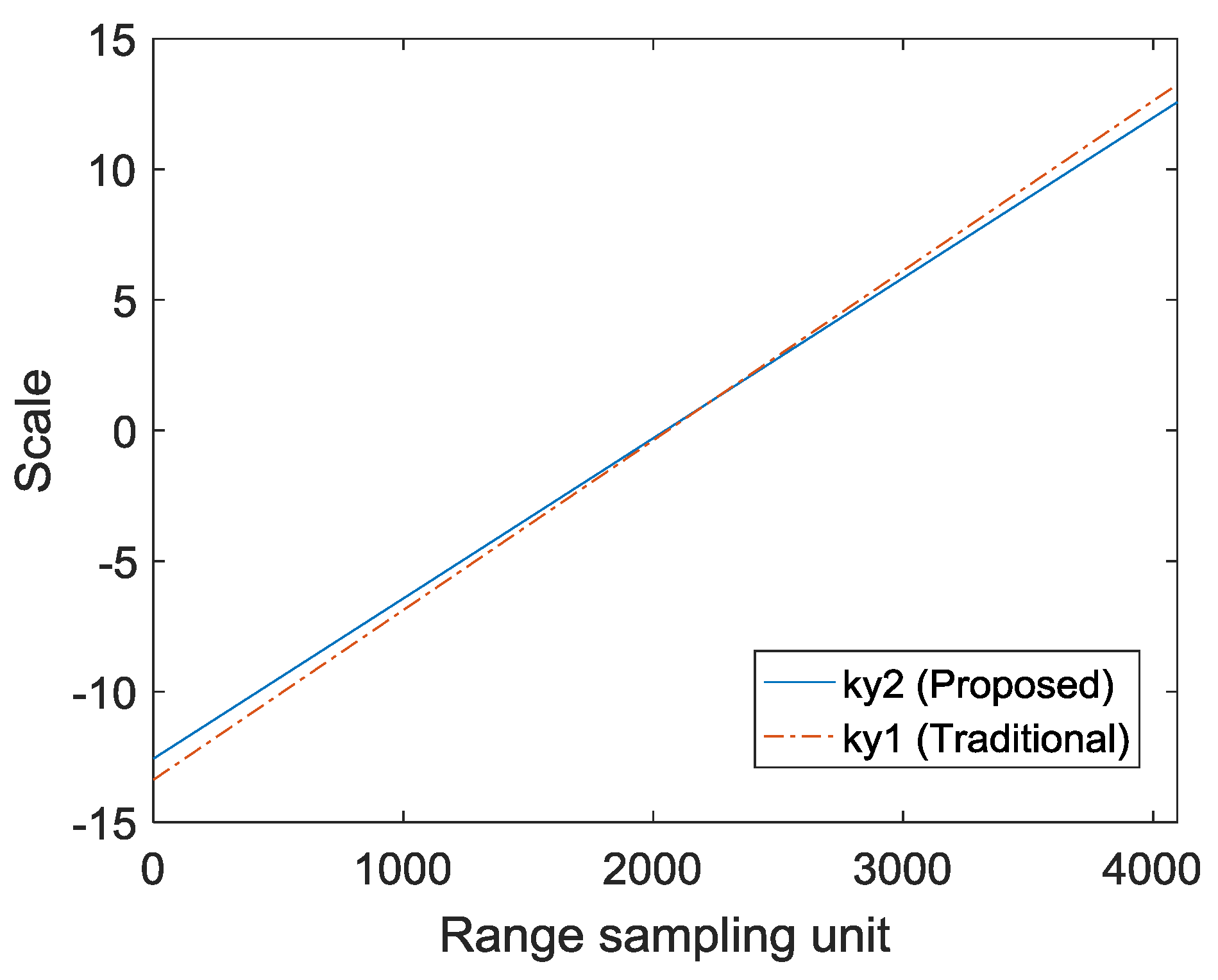
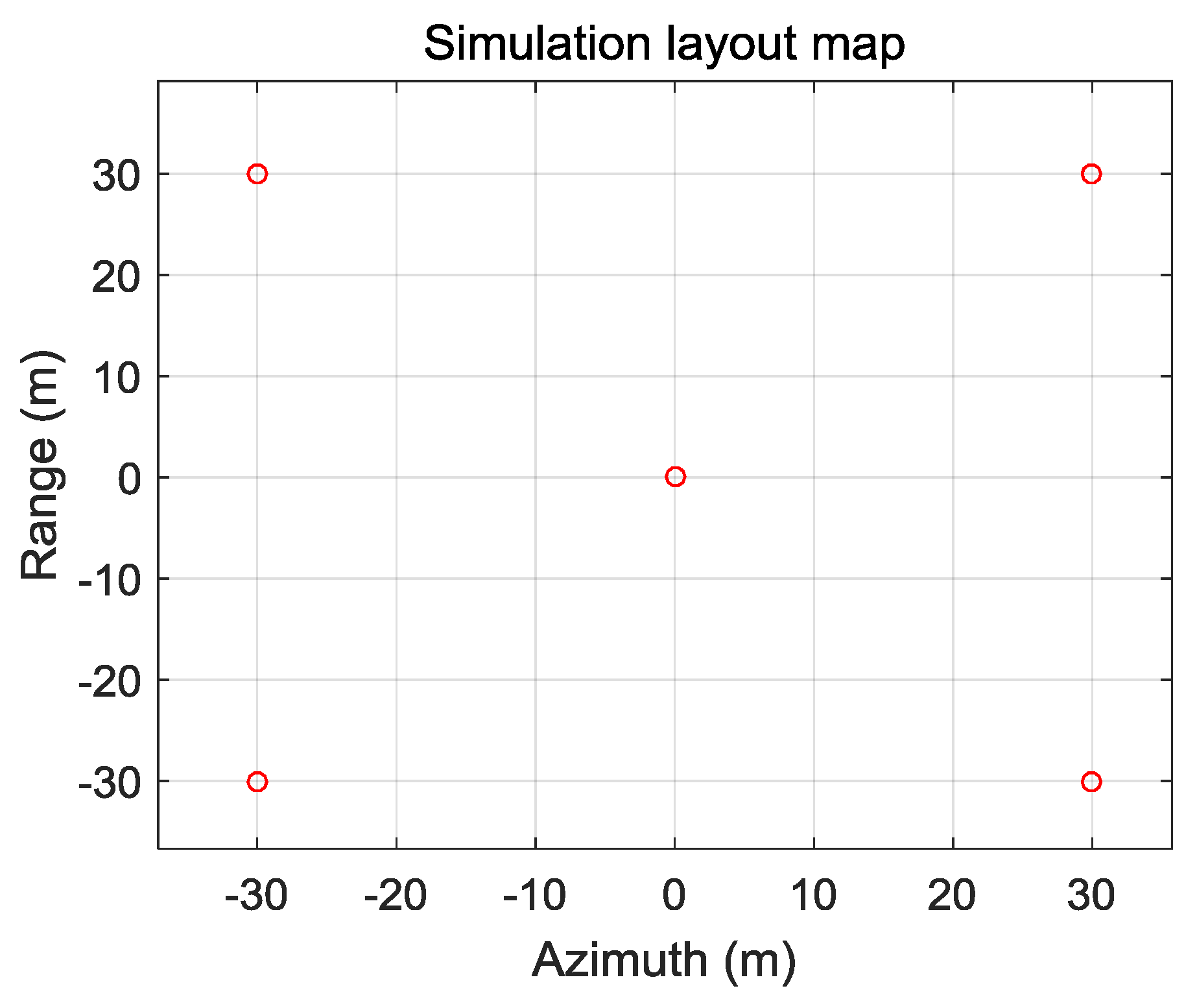
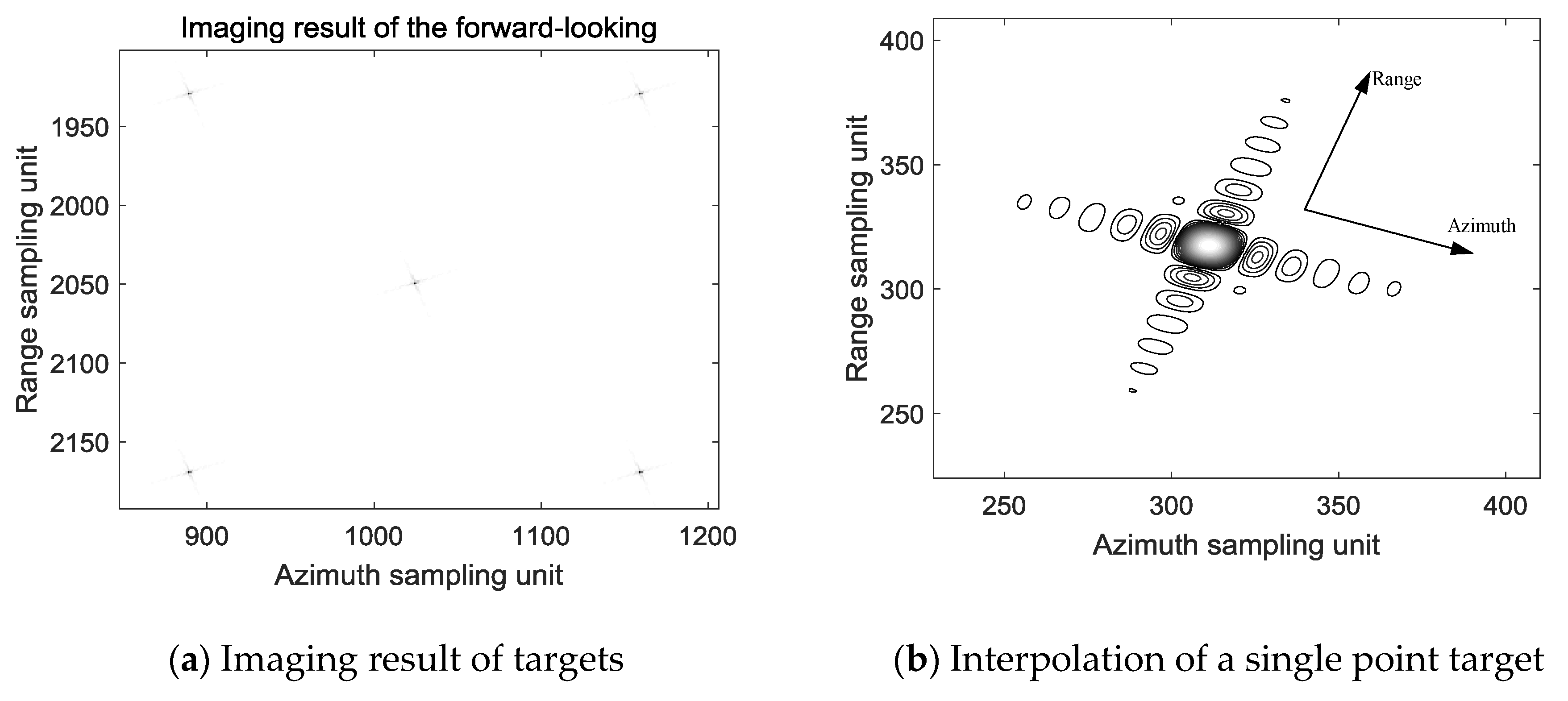
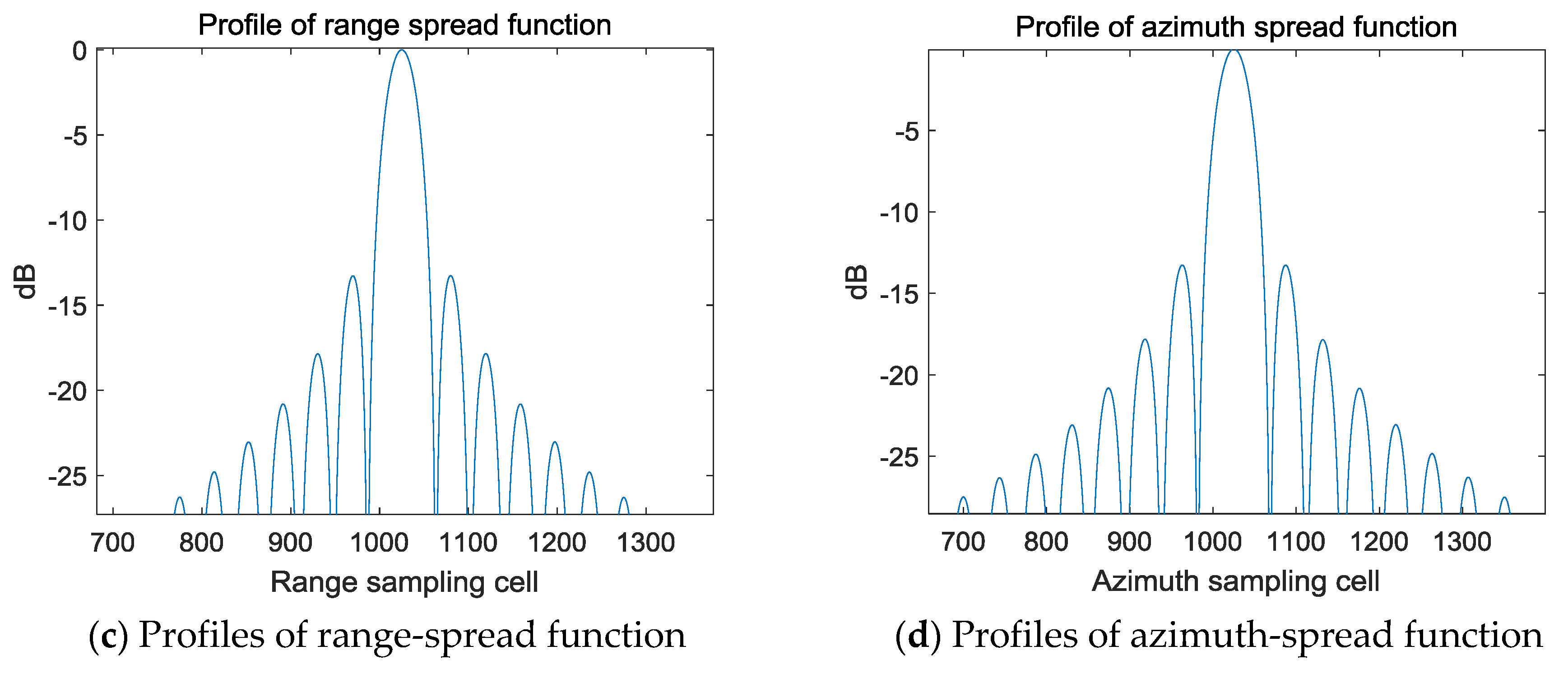
4.1. Experimental Simulation
4.2. Measured Data
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bao, Z.; Xing, M.; Wang, T. Radar Imaging Technology; Publishing House of Electronic Industy: Beijing, China, 2005. [Google Scholar]
- Sun, G.; Xing, M.; Xia, X.; Wu, Y.; Bao, Z. Beam Steering SAR Data Processing by a Generalized PFA. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4366–4377. [Google Scholar] [CrossRef]
- Tan, L.; Ma, Z.; Zhong, X. Preliminary result of high resolution multi-aspect SAR imaging experiment. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016; pp. 1–3. [Google Scholar]
- Sun, G.; Xing, M.; Xia, X.; Yang, J.; Wu, Y.; Bao, Z. A Unified Focusing Algorithm for Several Modes of SAR Based on FrFT. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3139–3155. [Google Scholar] [CrossRef]
- Yang, J.; Sun, G.; Chen, J.; Wu, Y.; Xing, M. A subaperture imaging scheme for wide azimuth beam airborne SAR based on modified RMA with motion compensation. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 608–611. [Google Scholar]
- Arii, M.; Nishimura, T.; Komatsu, T.; Yamada, H.; Kobayashi, T.; Kojima, S.; Umehara, T. Theoretical characterization of multi incidence angle and fully Polarimetric SAR data from rice paddies. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5670–5673. [Google Scholar]
- Vu, V.T.; Sjögren, T.K.; Pettersson, M.I. Fast factorized backprojection algorithm for UWB SAR image reconstruction. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 4237–4240. [Google Scholar]
- Wen, X.; Kuang, G.; Hu, J.; Zhang, J. Simultaneous multi-beam SAR mode using phased array radar. Sci. Sinica (Inf.) 2015, 45, 354–371. [Google Scholar] [CrossRef]
- Jiang, Y. Optical/SAR image registration based on cross-correlation with multi-scale and multi-direction Gabor characteristic matrixes. In Proceedings of the IET International Radar Conference 2013, Xi’an, China, 14–16 April 2013; pp. 1–4. [Google Scholar]
- Yu, H.; Liu, Y.; Li, L.; Yang, W.; Liao, M. Stable feature point extraction for accurate multi-temporal SAR image registration. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 181–184. [Google Scholar]
- Tao, Z.; Dongyang, A.; Cheng, H. Image registration of SAR and optical image based on feature points. In Proceedings of the IET International Radar Conference 2013, Xi’an, China, 14–16 April 2013; pp. 1–5. [Google Scholar]
- Shen, D.; Zhang, J.; Yang, J.; Feng, D.; Li, J. SAR and optical image registration based on edge features. In Proceedings of the 2017 4th International Conference on Systems and Informatics (ICSAI), Hangzhou, China, 11–13 November 2017; pp. 1272–1276. [Google Scholar]
- Zhu, S.; Ran, D. Multi-angle SAR image fusion algorithm based on visibility classification of non-layover region targets. In Proceedings of the 2017 International Conference on Security, Pattern Analysis, and Cybernetics (SPAC), Shenzhen, China, 15–17 December 2017; pp. 642–647. [Google Scholar]
- Zhang, Y.; Wu, T. An SAR image registration method based on pyramid model. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016; pp. 1–5. [Google Scholar]
- Cumming, I.G.; Neo, Y.L.; Wong, F.H. Interpretations of the omega-K algorithm and comparisons with other algorithms. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium. Proceedings, Toulouse, France, 21–25 July 2003; Volume 3, pp. 1455–1458. [Google Scholar]
- Wu, Y.; Song, H.; Shang, X.; Zheng, J. Improved RMA based on Nonuniform Fast Fourier Transforms (NUFFT’s). In Proceedings of the 2008 9th International Conference on Signal Processing, Beijing, China, 26–29 October 2008; pp. 2489–2492. [Google Scholar]
- Cumming, I.G.; Wong, F.H. Digital Signal Processing of Synthetic Aperture Radar Data; Artech House, Inc.: Norwood, UK, 2005. [Google Scholar]
- Xiong, T.; Xing, M.; Xia, X.; Bao, Z. New Applications of Omega-K Algorithm for SAR Data Processing Using Effective Wavelength at High Squint. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3156–3169. [Google Scholar] [CrossRef]
- Li, Z.; Xing, M.; Liang, Y.; Gao, Y.; Chen, J.; Huai, Y.; Zeng, L.; Sun, G.-C.; Bao, Z. A Frequency-Domain Imaging Algorithm for Highly Squinted SAR Mounted on Maneuvering Platforms With Nonlinear Trajectory. IEEE Trans. Geosci. Remote. Sens. 2016, 54, 4023–4038. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, L.; Guo, P.; Zhao, Y. An Omega-K Algorithm for Highly Squinted Missile-Borne SAR with Constant Acceleration. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1569–1573. [Google Scholar] [CrossRef]
- Li, Z.; Liang, Y.; Xing, M.; Huai, Y.; Gao, Y.; Zeng, L.; Bao, Z. An Improved range Model and Omega-K-Based Imaging Algorithm for High-Squint SAR with Curved Trajectory and Constant Acceleration. IEEE Geosci. Remote Sens. Lett. 2016, 13, 656–660. [Google Scholar] [CrossRef]
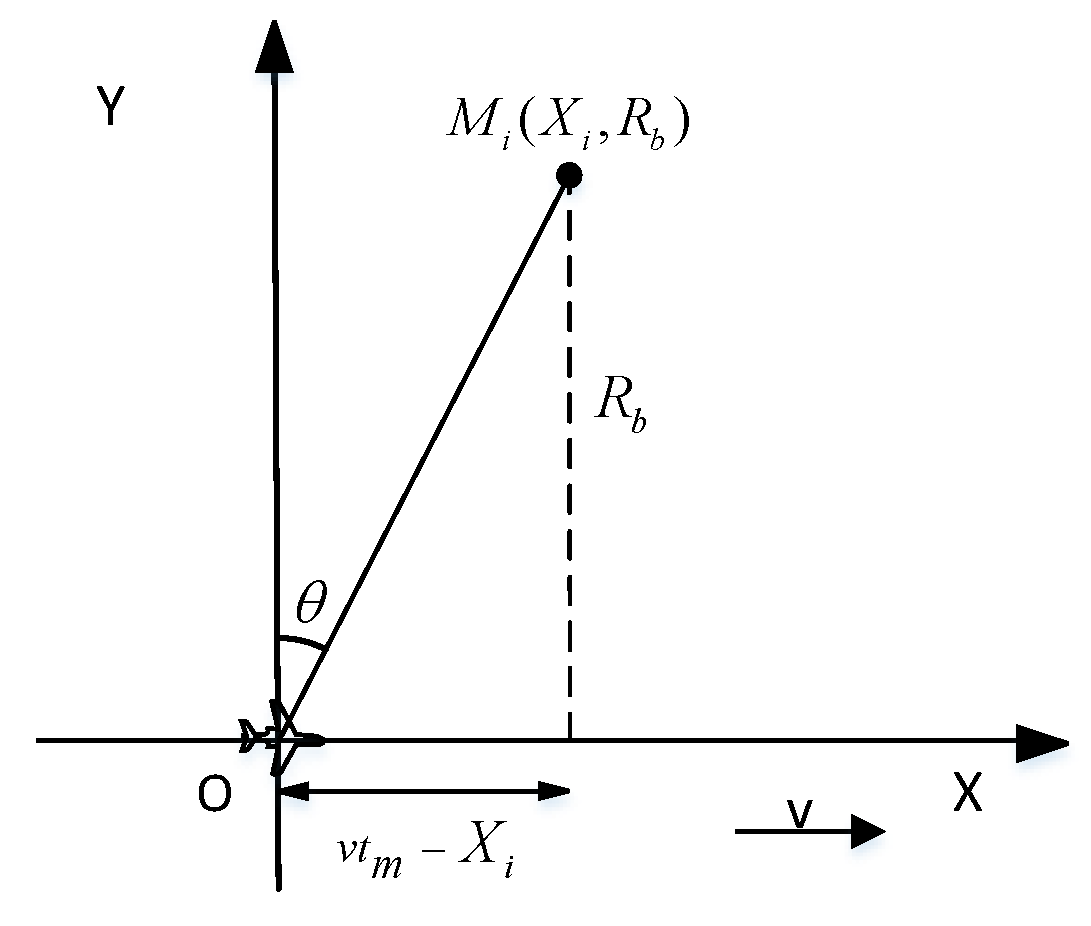
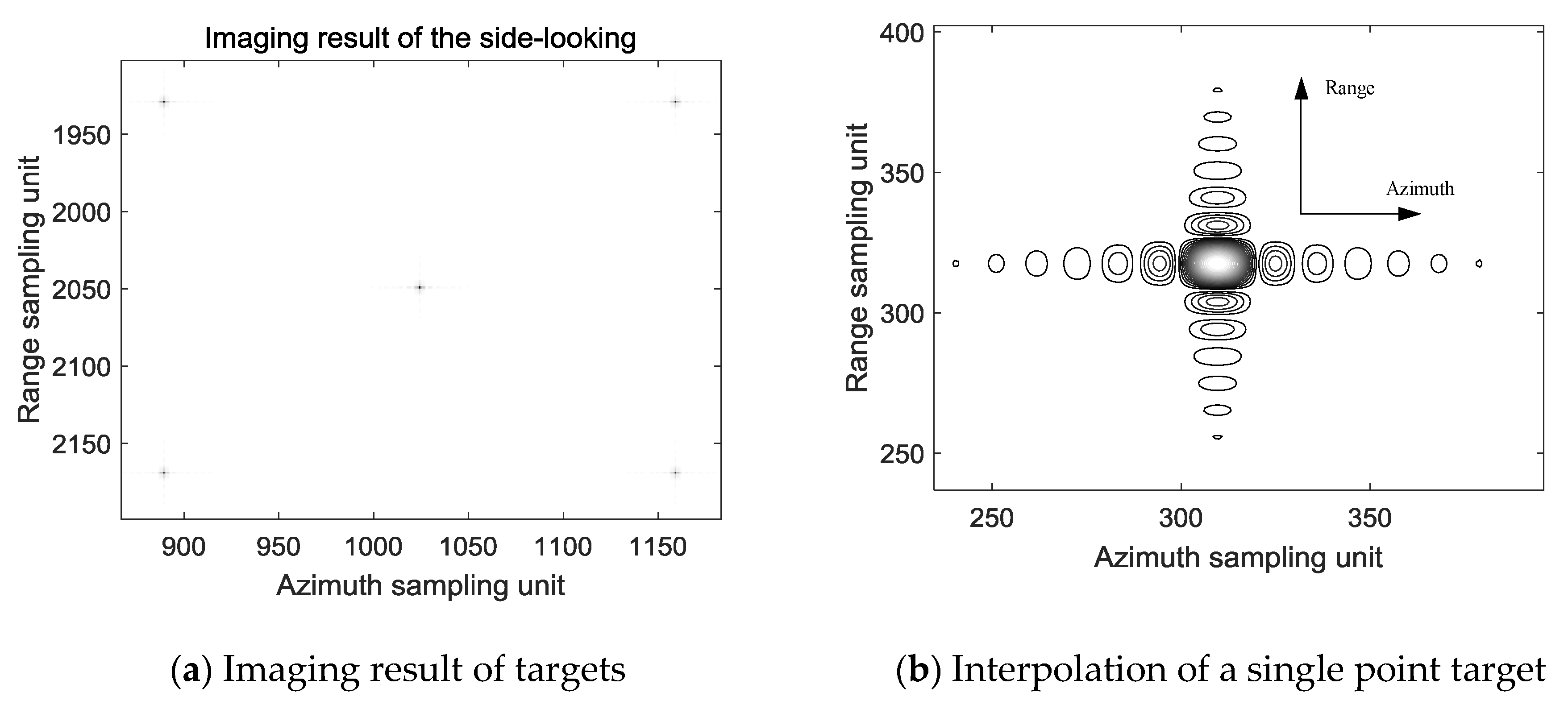
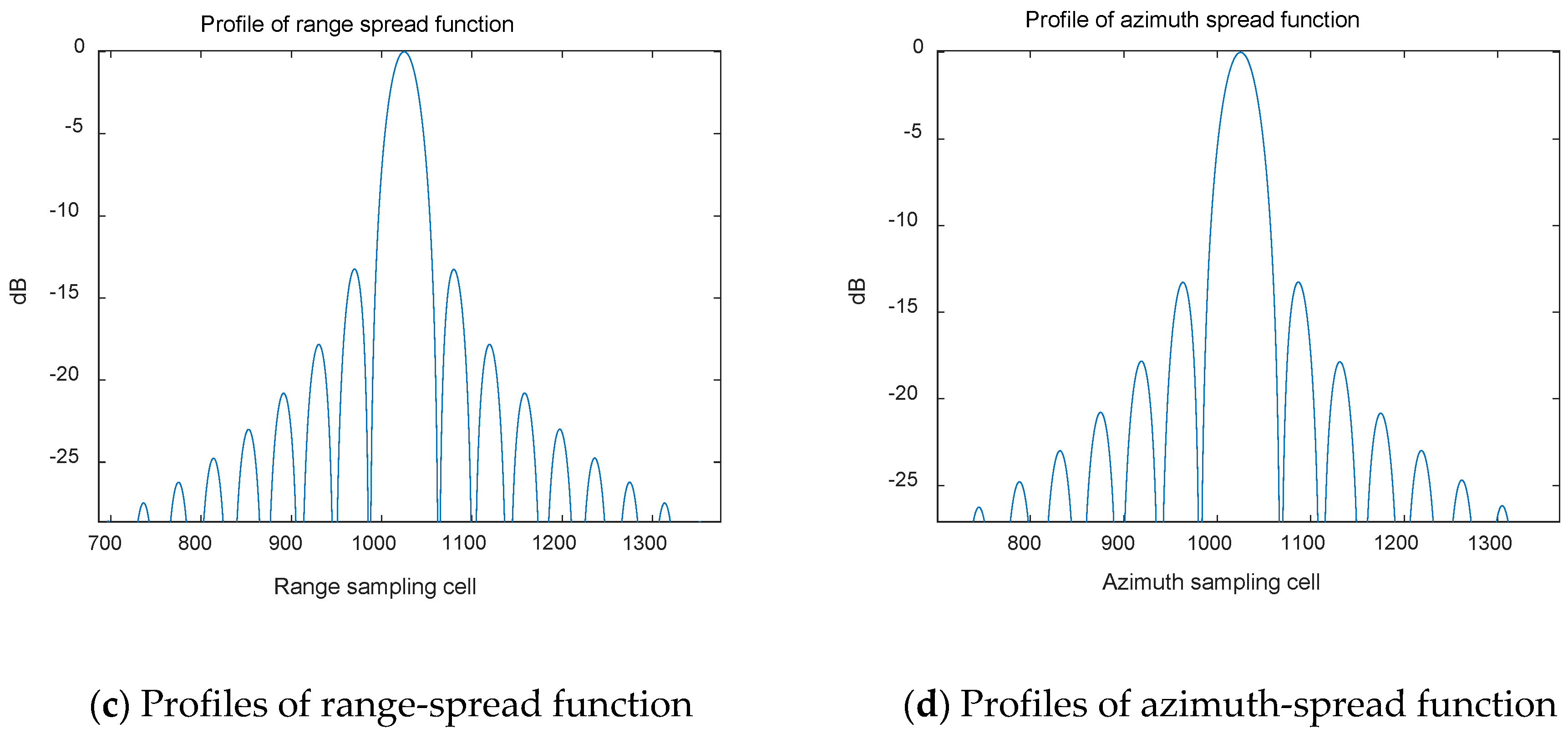
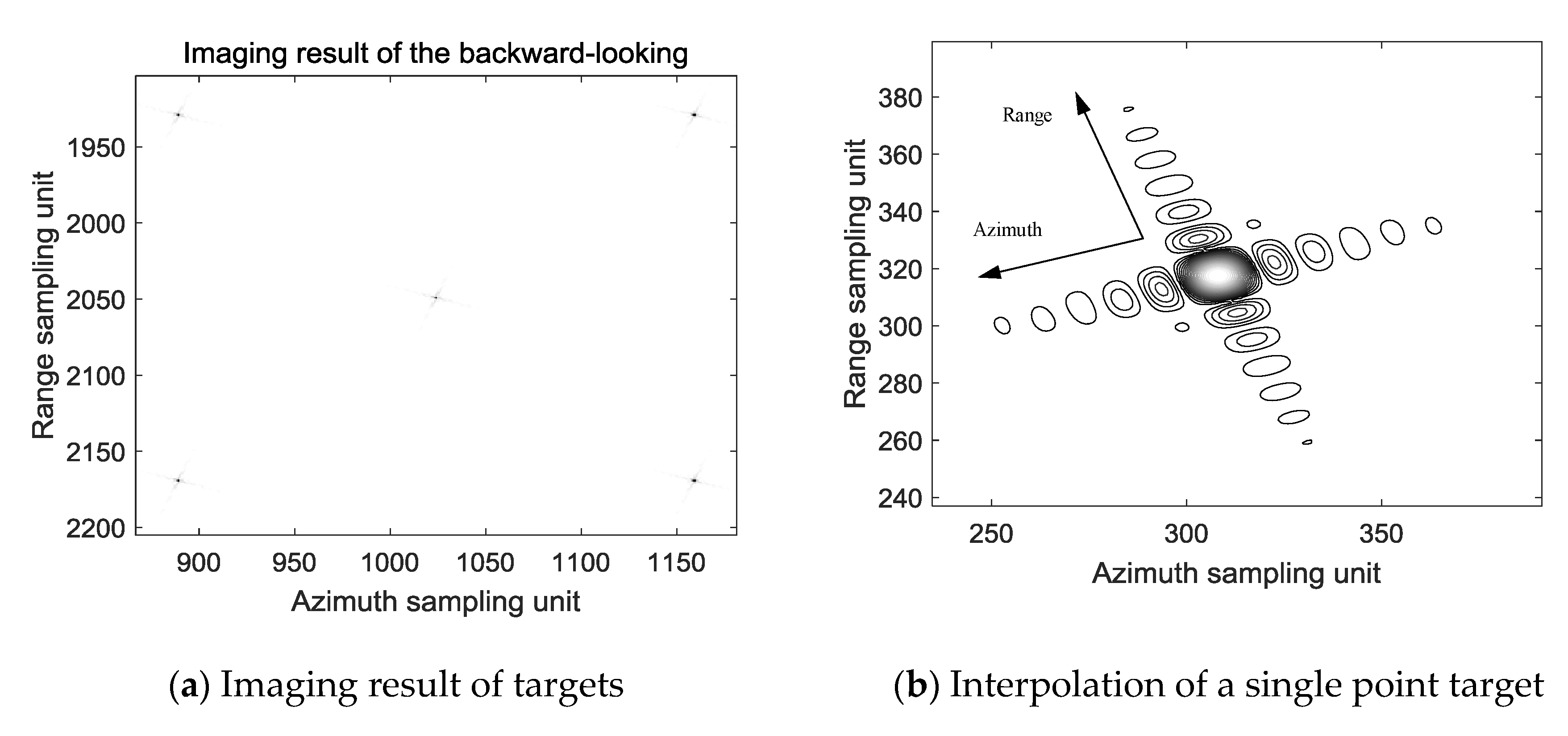
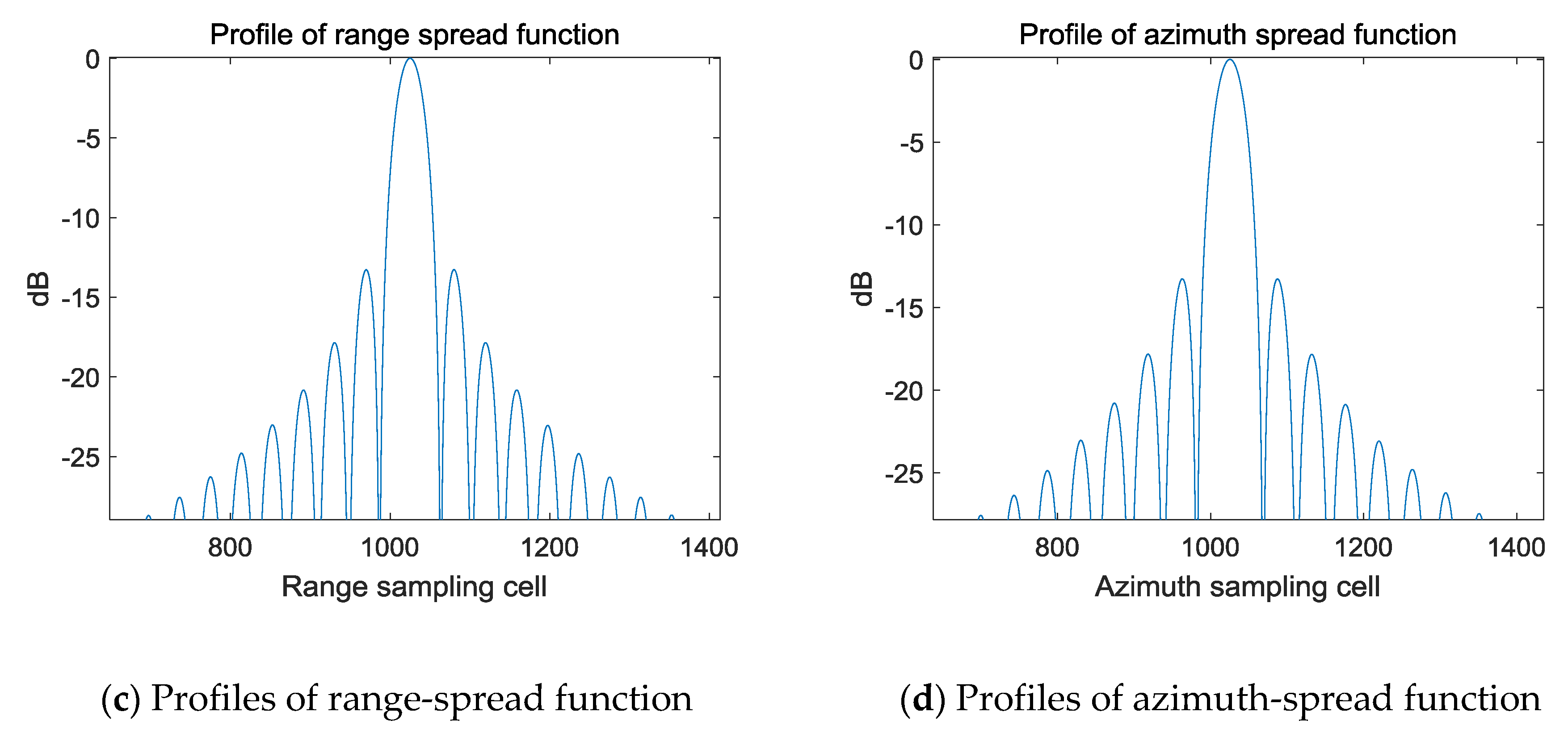
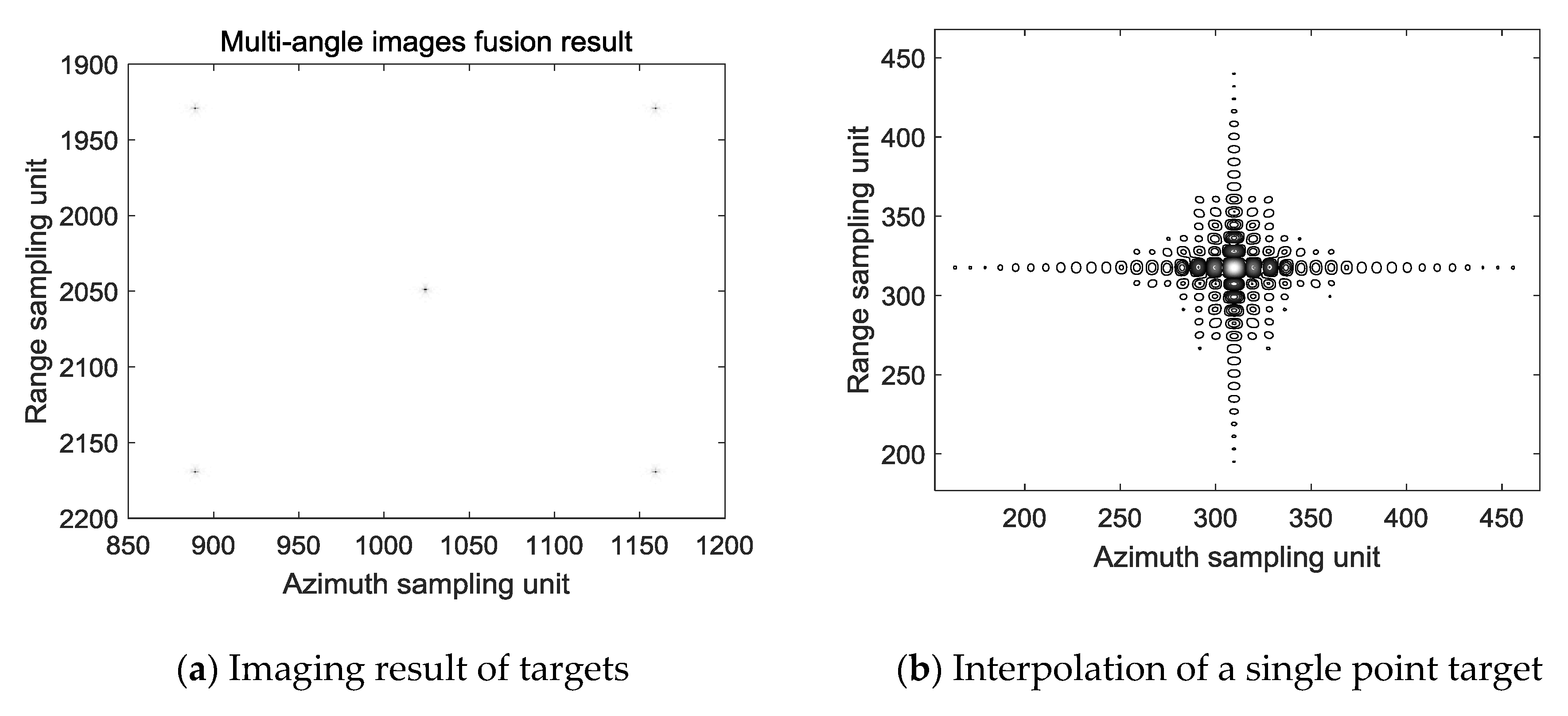
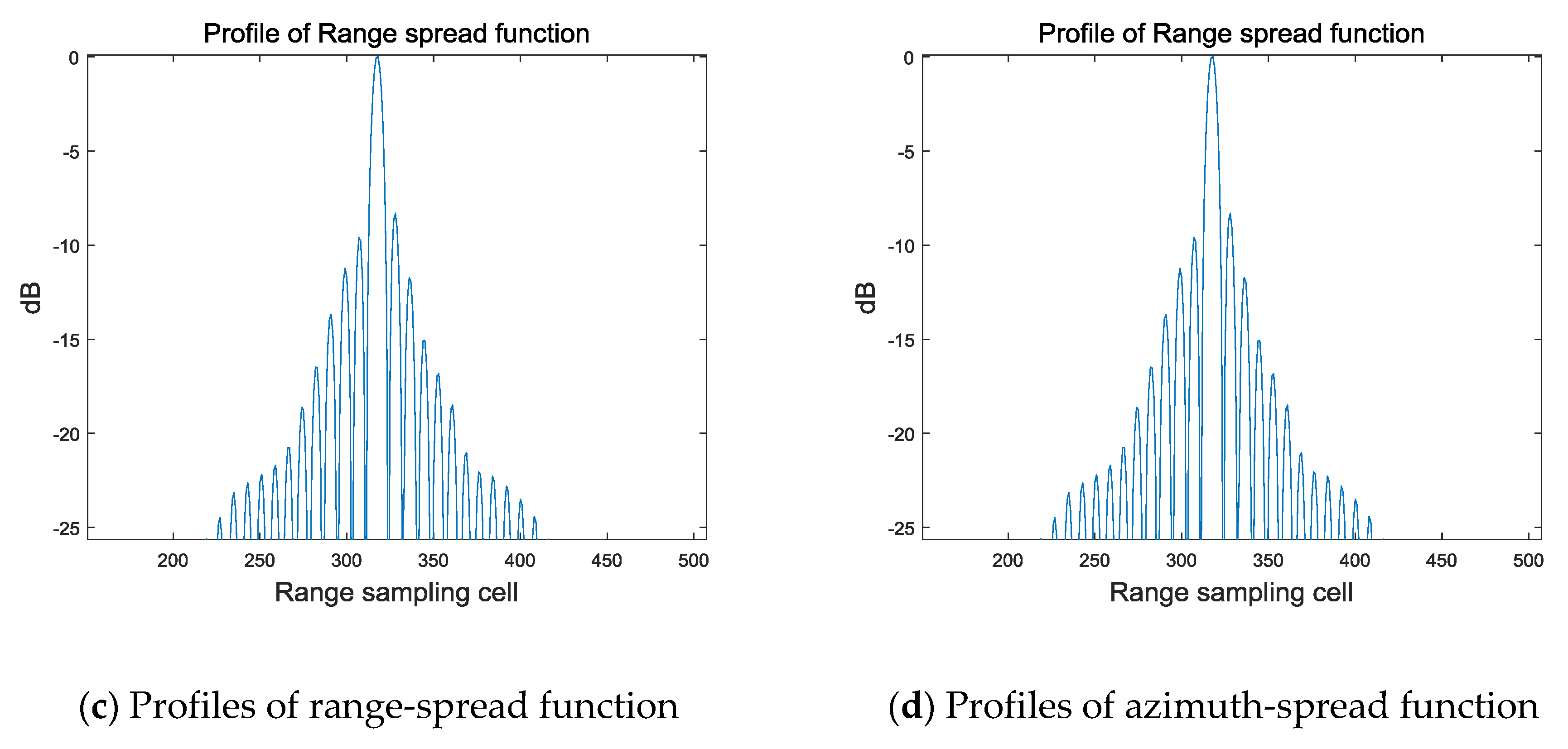

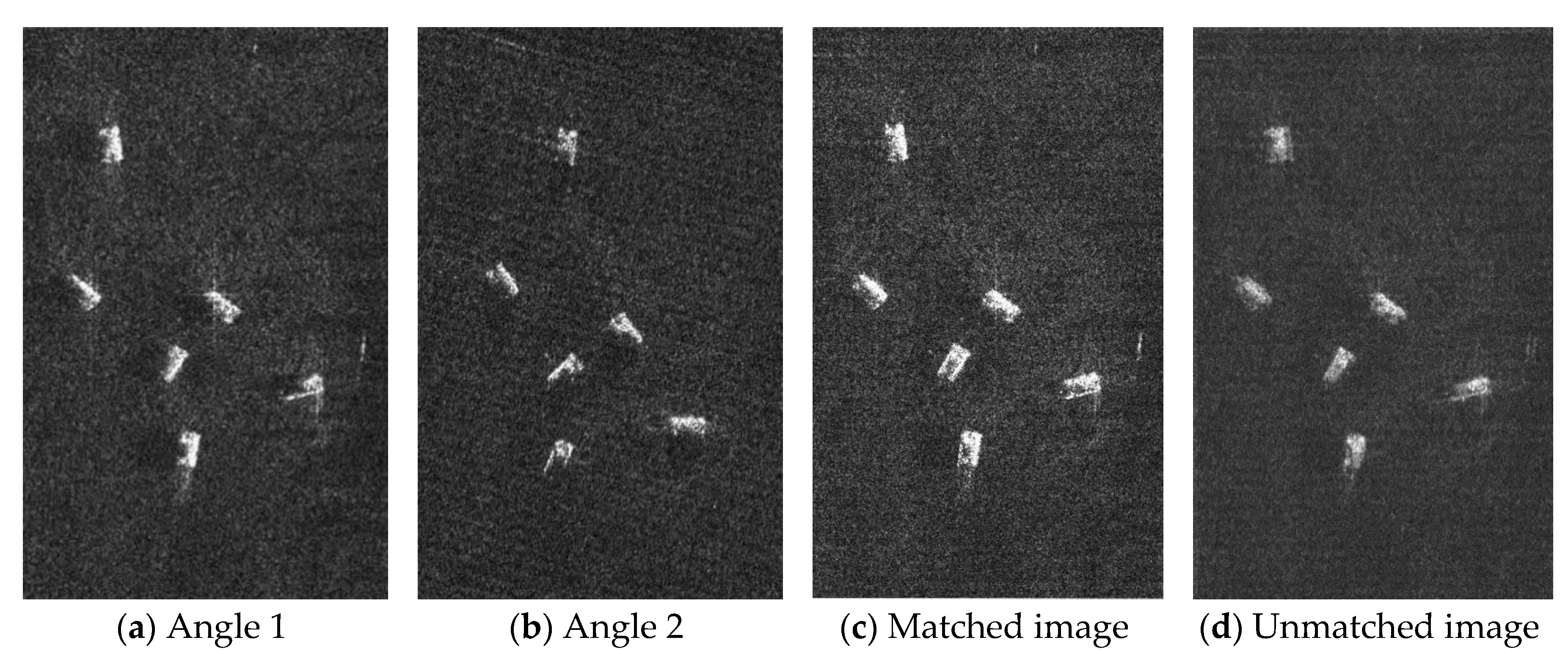
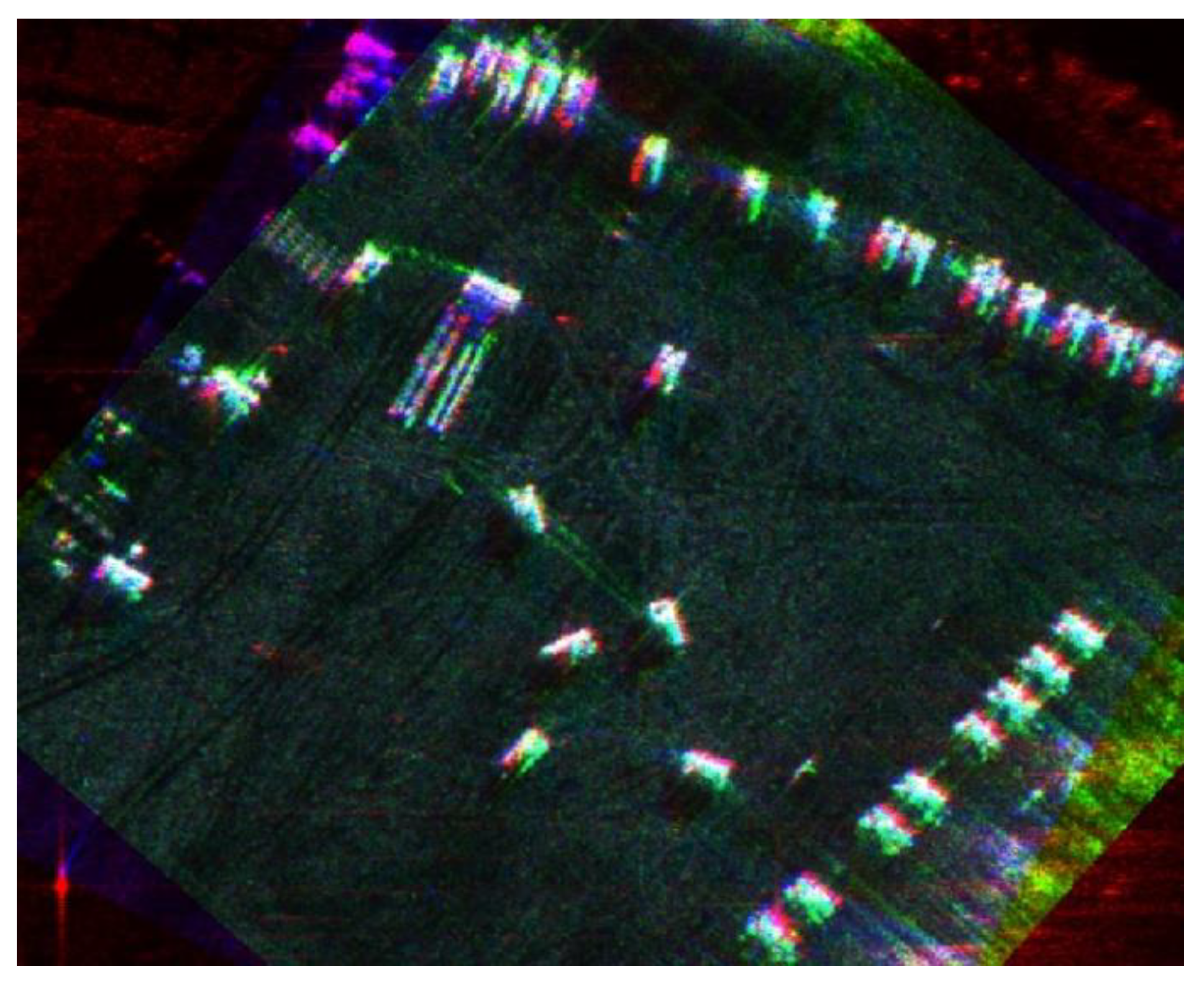

| Parameters | Value |
|---|---|
| Velocity | 102 m/s |
| Frequency band | 9.6 GHz |
| Bandwidth | 600 MHz |
| PRF | 312 Hz |
| Angle range | −30°–30° |
| Reference range | 34 km |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, W.; Tao, H.; Sun, G.; Wang, Y.; Bao, Z. A Novel Multi-Angle SAR Imaging System and Method Based on an Ultrahigh Speed Platform. Sensors 2019, 19, 1701. https://doi.org/10.3390/s19071701
Chang W, Tao H, Sun G, Wang Y, Bao Z. A Novel Multi-Angle SAR Imaging System and Method Based on an Ultrahigh Speed Platform. Sensors. 2019; 19(7):1701. https://doi.org/10.3390/s19071701
Chicago/Turabian StyleChang, Wensheng, Haihong Tao, Guangcai Sun, Yuqi Wang, and Zheng Bao. 2019. "A Novel Multi-Angle SAR Imaging System and Method Based on an Ultrahigh Speed Platform" Sensors 19, no. 7: 1701. https://doi.org/10.3390/s19071701
APA StyleChang, W., Tao, H., Sun, G., Wang, Y., & Bao, Z. (2019). A Novel Multi-Angle SAR Imaging System and Method Based on an Ultrahigh Speed Platform. Sensors, 19(7), 1701. https://doi.org/10.3390/s19071701






