Earthquake Magnitude Estimation Using a Total Noise Enhanced Optimization Model
Abstract
1. Introduction
2. Seismic Wave Measurement Using a Heterodyne Laser Interferometer
3. Earthquake Magnitude Estimation Using a TNEO Model
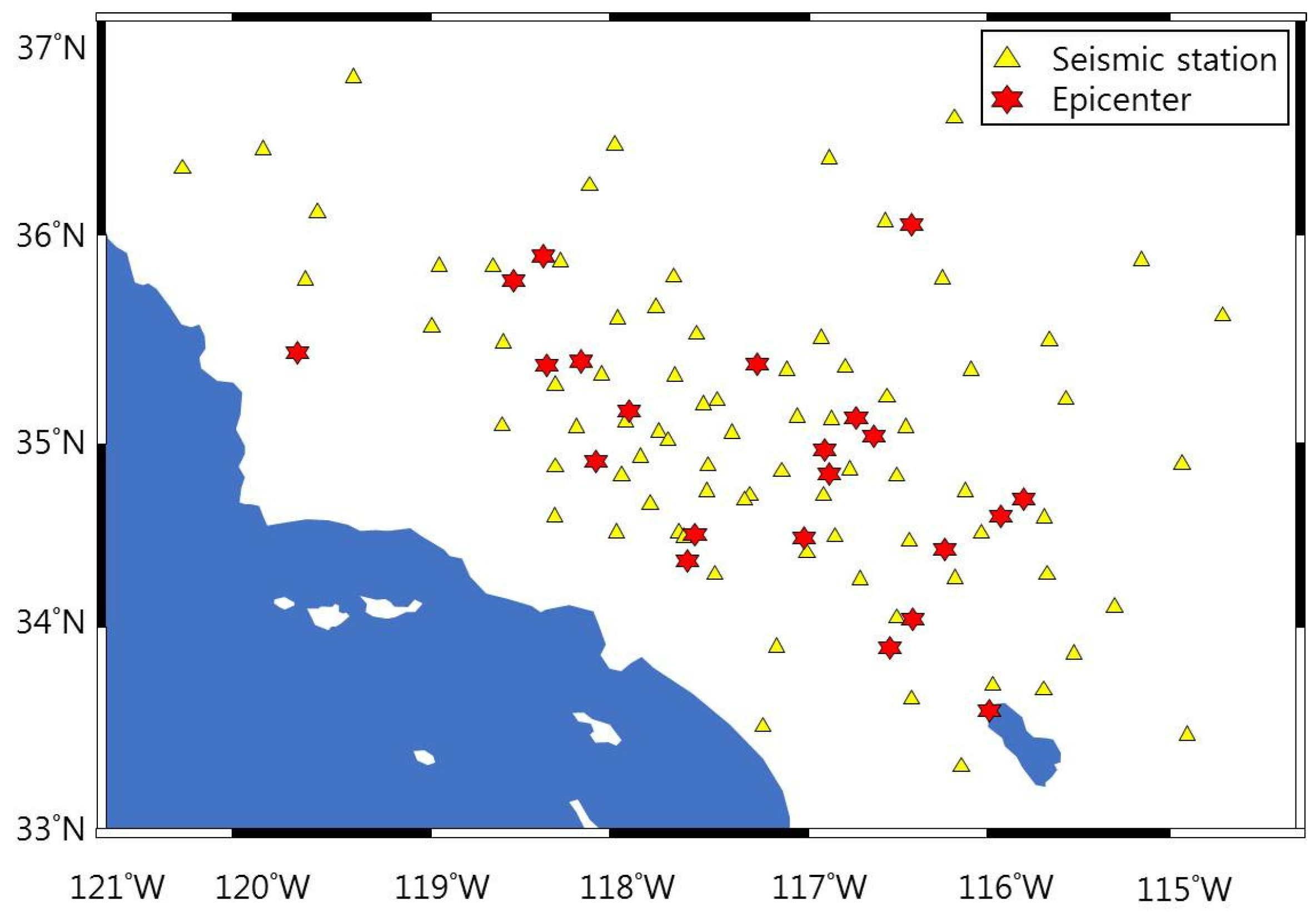
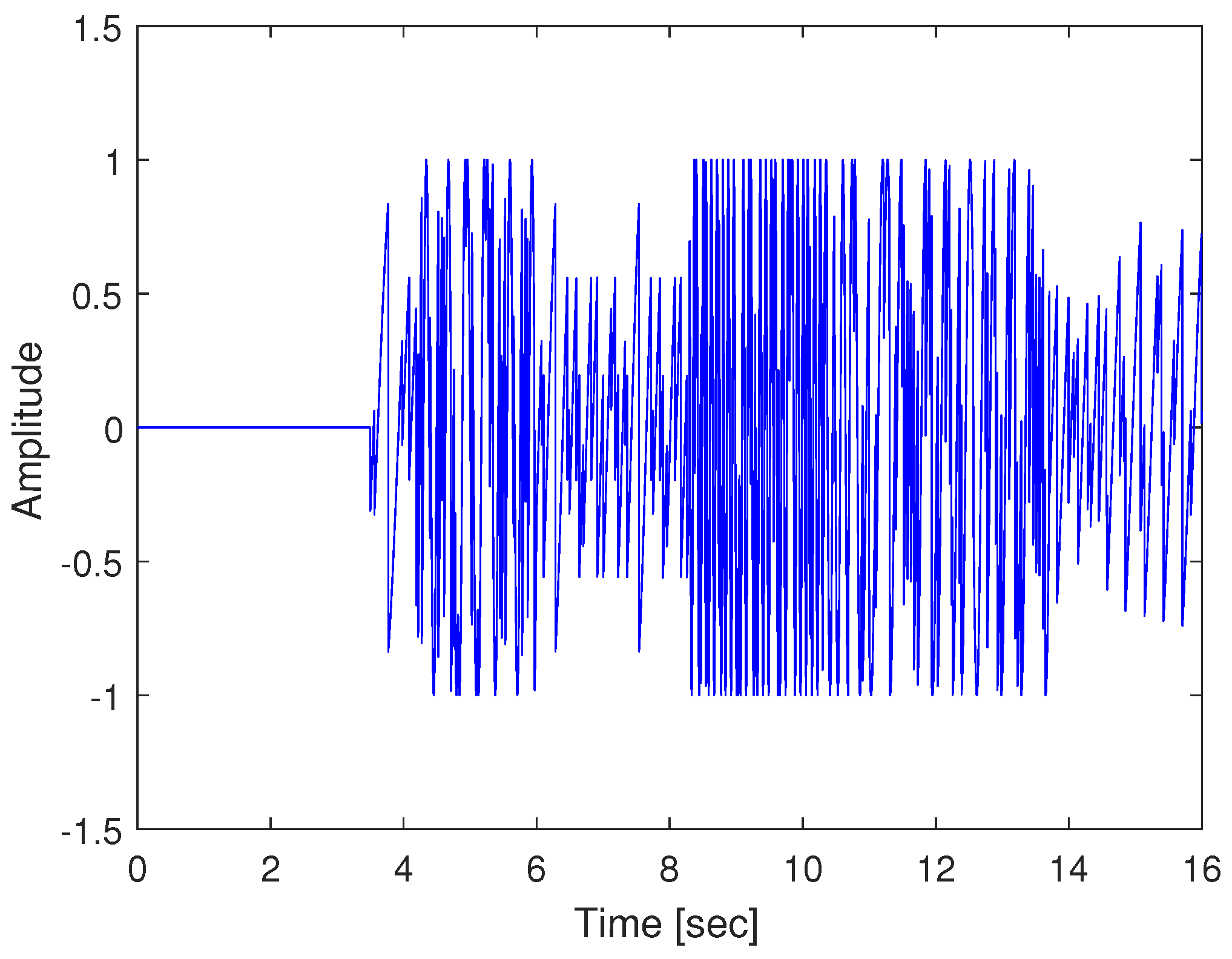
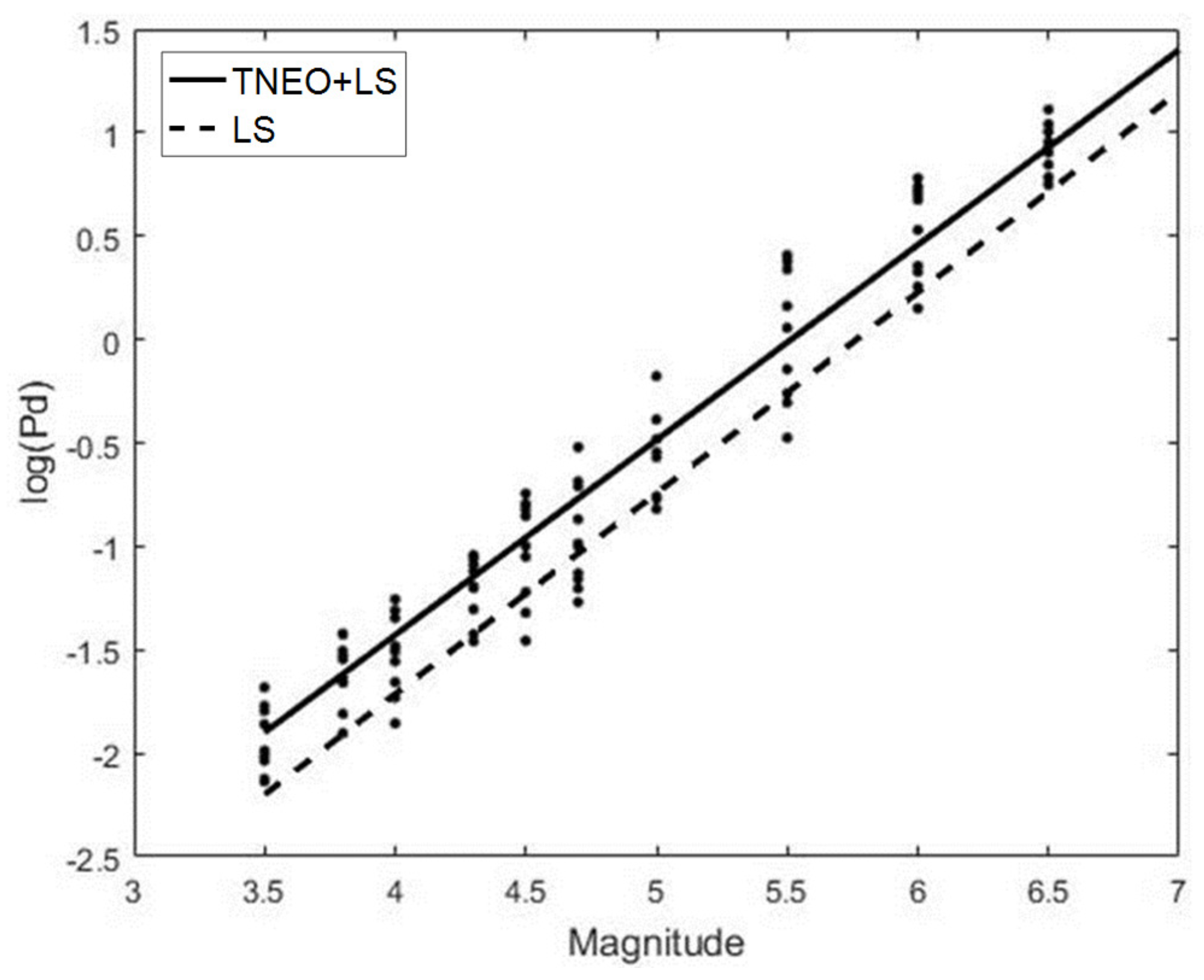
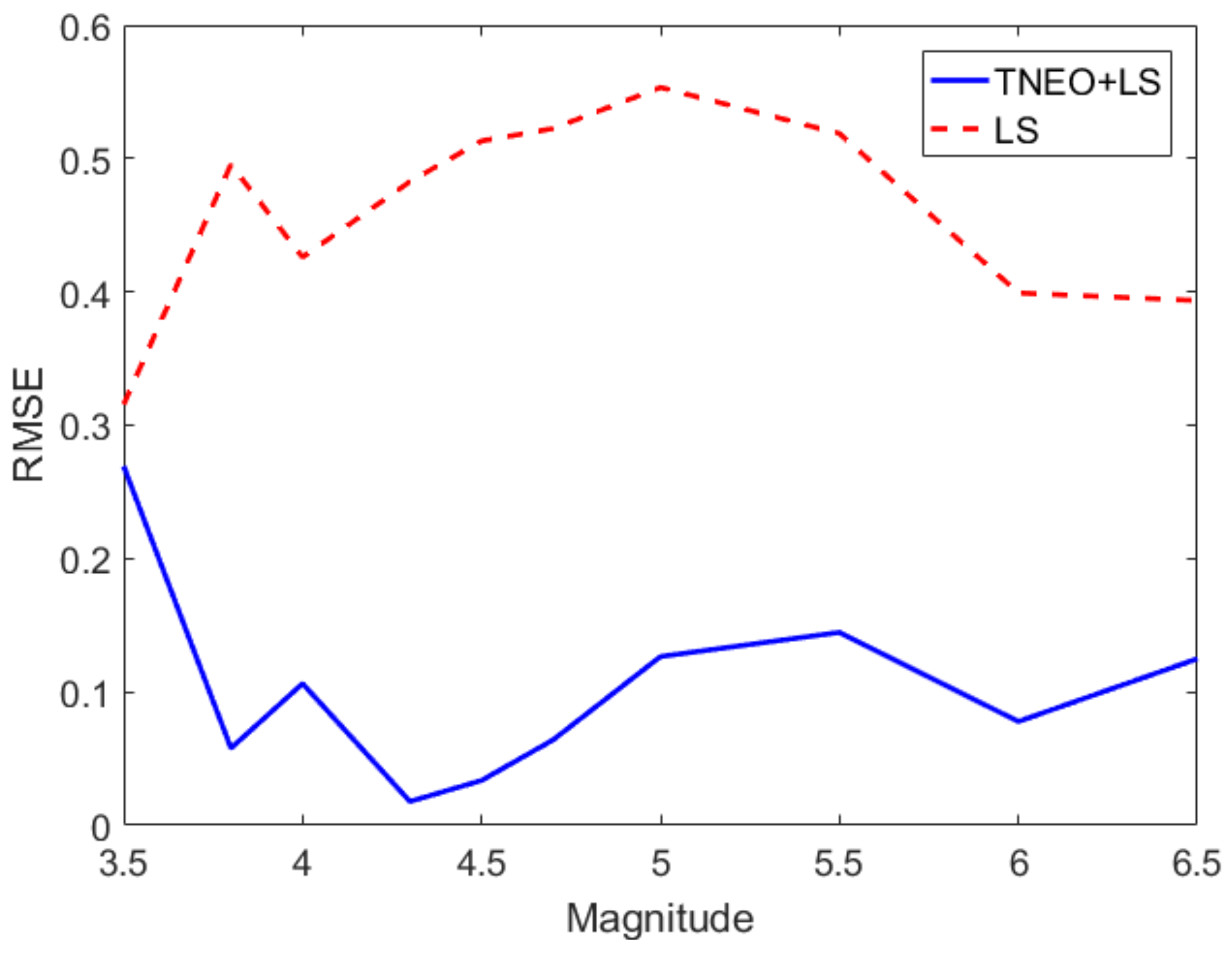
4. Simulation and Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kuyuk, H.; Allen, R. A global approach to provide magnitude estimates for earthquake early warning alerts. Geophys. Res. Lett. 2013, 40, 6329–6333. [Google Scholar] [CrossRef]
- Gitis, V.; Derendyaev, A.; Metrikov, P.; Shogin, A. Network geoinformation technology for seismic hazard research. Nat. Hazards 2012, 62, 1021–1036. [Google Scholar] [CrossRef]
- Zhan, Z.; Wei, S.; Ni, S.; Helmberger, D. Earthquake centroid locations using calibration from ambient seismic noise. Bull. Seismol. Soc. Am. 2011, 107, 1438–1445. [Google Scholar] [CrossRef]
- Kijko, A.; Singh, M. Statistical tools for maximum possible earthquake magnitude estimation. Acta Geophys. 2011, 59, 674–700. [Google Scholar] [CrossRef]
- Zhang, E.; Hao, Q.; Chen, B.; Yan, L.; Liu, Y. Laser heterodyne interferometer for simultaneous measuring displacement and angle based on the Faraday effect. Opt. Express 2014, 22, 25587. [Google Scholar] [CrossRef]
- Lee, K.; Pyo, Y.; You, K. Lagrange multiplier-based error compensation of heterodyne interferometer. Electron. Lett. 2016, 52, 1692–1694. [Google Scholar] [CrossRef]
- Lin, J.; Chen, K.; Chen, J. Measurement of small displacement based on surface plasmon resonance heterodyne interferometry. Opt. Lasers Eng. 2011, 49, 811–815. [Google Scholar] [CrossRef]
- Yang, H.; Lu, Y.; Hu, P.; Li, Z.; Zeng, T.; He, A.; Zhang, Z.; Tan, J. Measurement and control of the movable coil position of a joule balance with a system based on a laser heterodyne interferometer. Meas. Sci. Technol. 2014, 25, 064003. [Google Scholar] [CrossRef]
- Olyaee, S.; Yoon, T.; Hamedi, S. Jones matrix analysis of frequency mixing error in three-longitudinal-mode laser heterodyne interferometer. IET Optoelectron. 2009, 3, 215–224. [Google Scholar] [CrossRef]
- Hou, W.; Zhang, Y.; Hu, H. A simple technique for eliminating the nonlinearity of a heterodyne interferometry. Meas. Sci. Technol. 2009, 20, 105303. [Google Scholar] [CrossRef]
- Barmann, P. Development of a Heterodyne Laser Interferometer for Very Small High Frequency Displacements Detection; Lund Institute of Technology: Lund, Sweden, 1992; Available online: https://inis.iaea.org/search/search.aspx?orig_q=RN:24075615 (accessed on 25 March 2019).
- Olson, E.; Allen, R. The deterministic nature of earthquake rupture. Nature 2005, 438, 212–215. [Google Scholar] [CrossRef] [PubMed]
- Kircher, C.; Whitman, R.; Holmes, W. HAZUS earthquake loss estimation methods. Nat. Hazards Rev. 2006, 7, 45–59. [Google Scholar] [CrossRef]
- Wu, Y.; Zhao, L. Magnitude estimation using the first three seconds P-wave amplitude in earthquake early warning. Geophys. Res. Lett. 2006, 33, L16312. [Google Scholar] [CrossRef]
- Wurman, G.; Allen, R.; Lombard, P. Toward earthquake early warning in northern California. J. Geophys. Res. 2007, 112, B08311. [Google Scholar] [CrossRef]
- Joo, K.; Ellis, J.; Buice, E.; Spronck, J.; Schmidt, R. High resolution heterodyne interferometer without detectable periodic nonlinearity. Opt. Express 2010, 18, 1159–1165. [Google Scholar] [CrossRef] [PubMed]
- Olyaee, S.; Hamedi, S. A low-nonlinearity laser heterodyne interferometer with quadrupled resolution in the displacement measurement. Arab. J. Sci. Eng. 2011, 36, 279–286. [Google Scholar] [CrossRef]
- Yan, H.; Duan, H.; Li, L.; Liang, Y.; Luo, J.; Yeh, H. A dual-heterodyne laser interferometer for simultaneous measurement of linear and angular displacements. Rev. Sci. Instrum. 2015, 86, 123102. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.; Kwon, H.; You, K. Laser-interferometric broadband seismometer for epicenter location estimation. Sensors 2017, 17, 2423. [Google Scholar] [CrossRef]
- Nozato, H.; Kokuyama, W.; Ota, A. Improvement and validity of shock measurements using heterodyne laser interferometer. Measurement 2016, 77, 67–72. [Google Scholar] [CrossRef]
- Fu, H.; Hu, P.; Tan, J.; Fan, Z. Simple method for reducing the first-order optical nonlinearity in a heterodyne laser interferometer. Appl. Opt. 2015, 54, 6321–6326. [Google Scholar] [CrossRef] [PubMed]
- McRae, T.; Hsu, M.; Freund, C.; Shaddock, D.; Herrmann, J.; Gray, M. Linearization and minimization of cyclic error with heterodyne laser interferometry. Opt. Lett. 2012, 37, 2448–2450. [Google Scholar] [CrossRef] [PubMed]
- Beyreuther, M.; Wassermann, J. Continuous earthquake detection and classification using discrete hidden Markov models. Geophys. J. Int. 2008, 175, 1055–1066. [Google Scholar] [CrossRef]
- Yih-Min, W.; Kanamori, H.; Allen, R.; Hauksson, E. Determination of earthquake early warning parameters, τc and Pd, for southern California. Geophys. J. Int. 2007, 170, 711–717. [Google Scholar]
- Zollo, A.; Lancieri, M.; Nielsen, S. Earthquake magnitude estimation from peak amplitudes of very early seismic signals on strong motion records. Geophys. Res. Lett. 2006, 33, L23312. [Google Scholar] [CrossRef]
- Uyeda, S.; Nagao, T.; Kamogawa, M. Short-term earthquake prediction: Current status of seismoelectromagnetics. Tectonophysics 2009, 470, 205–213. [Google Scholar] [CrossRef]
- Zechar, J.; Jordan, T. Testing alarm-based earthquake predictions. Geophys. J. Int. 2008, 172, 715–724. [Google Scholar] [CrossRef]
- Weng, Y.; Qiao, X.; Guo, T.; Hu, M.; Feng, Z.; Wang, R.; Zhang, J. A robust and compact fiber Bragg grating vibration sensor for seismic measurement. IEEE Sens. J. 2011, 12, 800–804. [Google Scholar] [CrossRef]
- Kuyuk, H.; Allen, R. Optimal seismic network density for earthquake early warning: A case study from California. Seismol. Res. Lett. 2013, 84, 946–954. [Google Scholar] [CrossRef]
- Adeli, H.; Panakkat, A. A probabilistic neural network for earthquake magnitude prediction. Neural Netw. 2009, 22, 1018–1024. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; An, J.; Bu, X.; Sun, G. Constrained total least squares location algorithm using time difference of arrival measurements. IEEE Trans. Veh. Technol. 2010, 59, 1558–1562. [Google Scholar] [CrossRef]
- Lu, W.; Li, F. Seismic spectral decomposition using deconvolutive short-time Fourier transform spectrogram. Geophysics 2013, 78, 43–51. [Google Scholar] [CrossRef]
- O’Shea, P. A new technique for instantaneous frequency rate estimation. IEEE Signal Process. Lett. 2002, 9, 251–252. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, K.; Oh, J.; Lee, H.; You, K. Earthquake Magnitude Estimation Using a Total Noise Enhanced Optimization Model. Sensors 2019, 19, 1454. https://doi.org/10.3390/s19061454
Lee K, Oh J, Lee H, You K. Earthquake Magnitude Estimation Using a Total Noise Enhanced Optimization Model. Sensors. 2019; 19(6):1454. https://doi.org/10.3390/s19061454
Chicago/Turabian StyleLee, Kyunghyun, Jinhwan Oh, Hyukwoo Lee, and Kwanho You. 2019. "Earthquake Magnitude Estimation Using a Total Noise Enhanced Optimization Model" Sensors 19, no. 6: 1454. https://doi.org/10.3390/s19061454
APA StyleLee, K., Oh, J., Lee, H., & You, K. (2019). Earthquake Magnitude Estimation Using a Total Noise Enhanced Optimization Model. Sensors, 19(6), 1454. https://doi.org/10.3390/s19061454






