Absolute Radiometric Calibration of TESS-W and SQM Night Sky Brightness Sensors
Abstract
1. Introduction
2. Materials and Methods
2.1. Detector Modelling
2.2. Radiometric Calibration
2.3. Formalizing the Absolute (AB) Astronomical Magnitudes Units System
2.4. Experimental Calibration Setup
3. Results
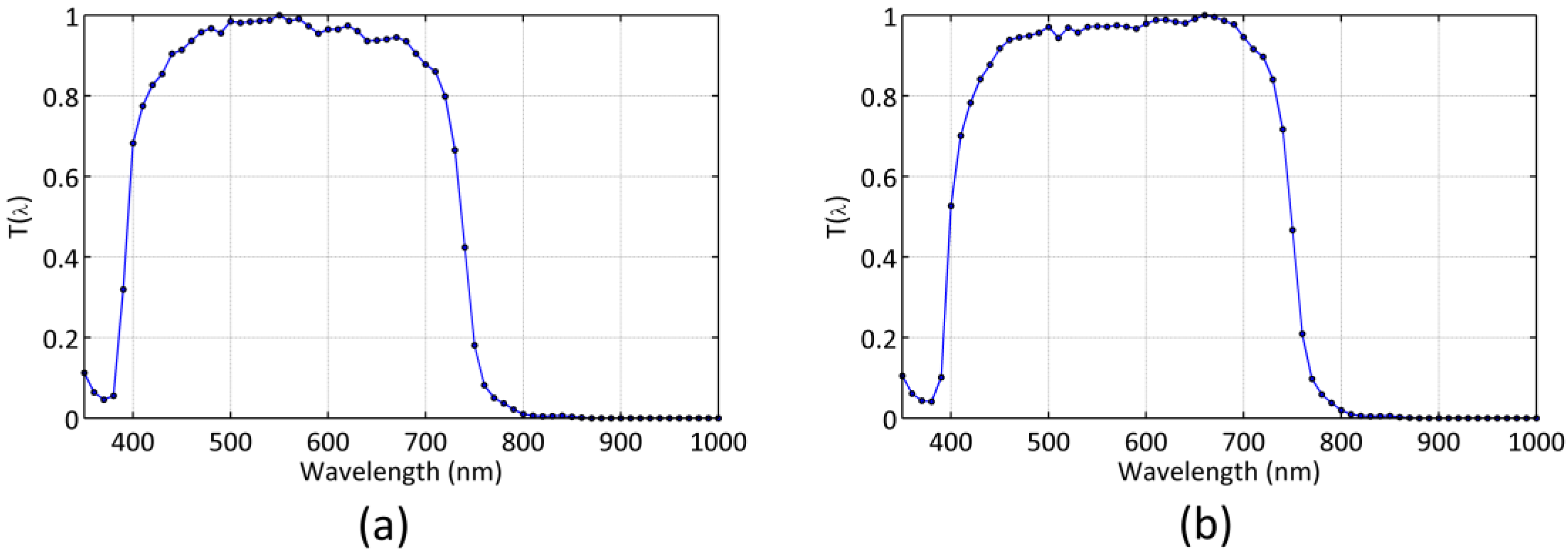
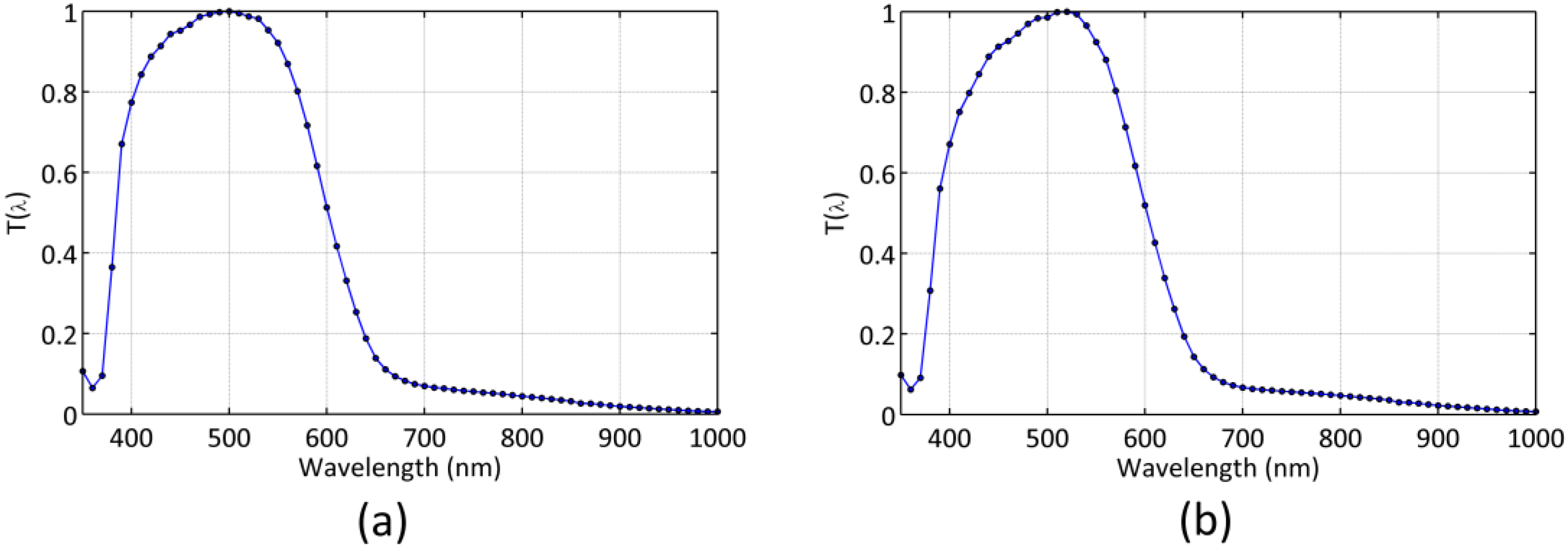
3.1. TESS-W Detectors
3.2. SQM Detectors
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Falchi, F.; Cinzano, P.; Duriscoe, D.; Kyba, C.C.M.; Elvidge, C.D.; Baugh, K.; Portnov, B.A.; Rybnikova, N.A.; Furgoni, R. The new world atlas of artificial night sky brightness. Sci. Adv. 2016, 2, e1600377. [Google Scholar] [CrossRef] [PubMed]
- Kyba, C.C.; Tong, K.P.; Bennie, J.; Birriel, I.; Birriel, J.J.; Cool, A.; Danielsen, A.; Davies, T.W.; Peter, N.; Edwards, W.; et al. Worldwide variations in artificial skyglow. Sci. Rep. 2015, 5, 8409. [Google Scholar] [CrossRef] [PubMed]
- Kocifaj, M. A review of the theoretical and numerical approaches to modeling skyglow: Iterative approach to RTE, MSOS, and two-stream approximation. J. Quant. Spectrosc. Radiat. Transf. 2016, 181, 2–10. [Google Scholar] [CrossRef]
- Walker, M.F. The California Site Survey. Publ. Astron. Soc. Pac. 1970, 82, 672–698. [Google Scholar] [CrossRef]
- Aubé, M.; Kocifaj, M. Using two light-pollution models to investigate artificial sky radiances at Canary Islands observatories. Mon. Not. R. Astron. Soc. 2012, 422, 819–830. [Google Scholar] [CrossRef]
- Gaston, K.J.; Duffy, J.P.; Gaston, S.; Bennie, J.; Davies, T.W. Human alteration of natural light cycles: Causes and ecological consequences. Oecologia 2014, 176, 917–931. [Google Scholar] [CrossRef] [PubMed]
- Hölker, F.; Wolter, C.; Perkin, E.K.; Tockner, K. Light pollution as a biodiversity threat. Trends Ecol. Evol. 2010, 25, 681–682. [Google Scholar] [CrossRef] [PubMed]
- Longcore, T.; Rich, C. Ecological light pollution. Front. Ecol. Environ. 2004, 2, 191–198. [Google Scholar] [CrossRef]
- Bará, S.; Nievas, M.; Sánchez de Miguel, A.; Zamorano, J. Zernike analysis of all-sky night brightness maps. Appl. Opt. 2014, 53, 2677–2686. [Google Scholar] [CrossRef] [PubMed]
- Bará, S.; Tilve, V.; Nievas, M.; Sánchez de Miguel, A.; Zamorano, J. Zernike power spectra of clear and cloudy light-polluted urban night skies. Appl. Opt. 2015, 54, 4120–4129. [Google Scholar] [CrossRef]
- Gallaway, T.; Olsen, R.N.; Mitchell, D.M. The economics of global light pollution. Ecol. Econ. 2010, 69, 658–665. [Google Scholar] [CrossRef]
- Kyba, C.C.M.; Hänel, A.; Hölker, F. Redefining efficiency for outdoor lighting. Energy Environ. Sci. 2014, 7, 1806–1809. [Google Scholar] [CrossRef]
- Marín, C.; Jafari, J. StarLight: A Common Heritage; StarLight Initiative La Palma Biosphere Reserve, Instituto De Astrofísica De Canarias, Government of The Canary Islands, Spanish Ministry of The Environment, UNESCO-MaB: Canary Islands, Spain, 2008.
- Elvidge, C.D.; Baugh, K.; Zhizhin, M.; Hsu, F.C.; Ghosh, T. VIIRS night-time lights. Int. J. Remote Sens. 2017, 38, 5860–5879. [Google Scholar] [CrossRef]
- Stefanov, W.L.; Evans, C.A.; Runco, S.K.; Wilkinson, M.J.; Higgins, M.D.; Willis, K. Astronaut Photography: Handheld Camera Imagery from Low Earth Orbit. In Handbook of Satellite Applications; Pelton, J.N., Madry, S., Camacho-Lara, S., Eds.; Springer International Publishing: Basel, Switzerland, 2017. [Google Scholar]
- Kyba, C.C.M.; Garz, S.; Kuechly, H.; Sánchez de Miguel, A.; Zamorano, J.; Fischer, J.; Hölker, F. High-Resolution Imagery of Earth at Night: New Sources, Opportunities and Challenges. Remote Sens. 2015, 7, 1–23. [Google Scholar] [CrossRef]
- Zheng, Q.; Weng, Q.; Huang, L.; Wang, K.; Deng, J.; Jiang, R.; Ye, Z.; Gan, M. A new source of multi-spectral high spatial resolution night-time light imagery—JL1-3B. Remote Sens. Environ. 2018, 215, 300–312. [Google Scholar] [CrossRef]
- Jiang, W.; He, G.; Long, T.; Guo, H.; Yin, R.; Leng, W.; Liu, H.; Wang, G. Potentiality of Using Luojia 1-01 Nighttime Light Imagery to Investigate Artificial Light Pollution. Sensors 2018, 18, 2900. [Google Scholar] [CrossRef] [PubMed]
- Hänel, A.; Posch, T.; Ribas, S.J.; Aubé, M.; Duriscoe, D.; Jechow, A.; Kollath, Z.; Lolkema, D.E.; Moore, C.; Schmidt, N.; et al. Measuring night sky brightness: Methods and challenges. J. Quant. Spectrosc. Radiat. Transf. 2018, 205, 278–290. [Google Scholar] [CrossRef]
- Kyba, C.C.M.; Wagner, J.M.; Kuechly, H.U.; Walker, C.E.; Elvidge, C.D.; Falchi, F.; Ruhtz, T.; Fischer, J.; Hölker, F. Citizen Science Provides Valuable Data for Monitoring GlobalNight Sky Luminance. Sci. Rep. 2013, 3, 1835. [Google Scholar] [CrossRef]
- Pravettoni, M.; Strepparava, D.; Cereghetti, N.; Klett, S.; Andretta, M.; Steiger, M. Indoor calibration of Sky Quality Meters: Linearity, spectral responsivity and uncertainty analysis. J. Quant. Spectrosc. Radiat. Transf. 2016, 181, 74–86. [Google Scholar] [CrossRef]
- Zamorano, J.; García, C.; González, R.; Tapia, C.; Sánchez de Miguel, A.; Pascual, S.; Gallego, J.; González, E.; Picazo, P.; Izquierdo, J.; et al. STARS4ALL Night Sky Brightness Photometer. Int. J. Sustain. Light. 2016, 35, 49–54. [Google Scholar] [CrossRef]
- Posch, T.; Binder, F.; Puschnig, J. Systematic measurements of the night sky brightness at 26 locations in Eastern Austria. J. Quant. Spectrosc. Radiat. Transf. 2018, 211, 144–165. [Google Scholar] [CrossRef]
- Pun, C.S.J.; So, C.W. Night-sky brightness monitoring in Hong Kong. Environ. Monit. Assess. 2012, 184, 2537–2557. [Google Scholar] [CrossRef] [PubMed]
- Zamorano, J.; de Miguel, A.S.; Nievas, M.; Tapia, C.; Ocaña, F.; Izquierdo, J.; Gallego, J.; Pascual, S.; Colomer, F.; Bará, S.; et al. Light Pollution Spanish REECL SQM Network. XXIX IAU FM 21: Mitigating Threats of Light Pollution & Radio Frequency Interference, Honolulu (Hawaii) 3-14/8/2015. Available online: https://www.noao.edu/education/files/Zamorano_IAU2015_REECL-SQM.pdf (accessed on 11 March 2019).
- TESS Plots. Available online: http://tess.stars4all.eu/plots/ (accessed on 15 January 2019).
- Bará, S. Anthropogenic disruption of the night sky darkness in urban and rural areas. R. Soc. Open Sci. 2016, 3, 160541. [Google Scholar] [CrossRef]
- TSL237 High-Sensitivity Light-to-Frequency Converter. Ams Datasheet [v1-01] 2018-Mar-27(Ams AG, Premstaetten, Austria). Available online: https://ams.com/light-sensors (accessed on 9 December 2018).
- Bessell, M.S. Standard Photometric Systems. Annu. Rev. Astron. Astrophys. 2005, 43, 293–336. [Google Scholar] [CrossRef]
- Oke, J.B.; Gunn, J.E. Secondary standard stars for absolute spectrophotometry. Astrophys. J. 1983, 266, 713–717. [Google Scholar] [CrossRef]
- Sánchez de Miguel, A.; Aubé, M.; Zamorano, J.; Kocifaj, M.; Roby, J.; Tapia, C. Sky Quality Meter measurements in a colour-changing world. Mon. Not. R. Astron. Soc. 2017, 467, 2966–2979. [Google Scholar] [CrossRef]
- Bará, S. Variations on a classical theme: On the formal relationship between magnitudes per square arcsecond and luminance. Int. J. Sustain. Light. 2017, 19, 104–111. [Google Scholar] [CrossRef]
| Constant | TESS-W Stars3 | TESS-W Stars222 | σ | Units |
|---|---|---|---|---|
| 1.22·10−6 | 1.16·10−6 | 0.06·10−6 | Wm−2sr−1Hz−1 | |
| 521.8 | 516.9 | 7.8 | Wm−2sr−1 | |
| 21.58 | 21.62 | 0.06 | magAB/arcsec2 |
| Constant | Serial#2370 | Serial#2747 | σ | Units |
|---|---|---|---|---|
| 1.51·10−6 | 1.49·10−6 | 0.08·10−6 | Wm−2sr−1Hz−1 | |
| 433.9 | 415.4 | 7.9 | Wm−2sr−1 | |
| 21.15 | 21.12 | 0.06 | magAB/arcsec2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bará, S.; Tapia, C.E.; Zamorano, J. Absolute Radiometric Calibration of TESS-W and SQM Night Sky Brightness Sensors. Sensors 2019, 19, 1336. https://doi.org/10.3390/s19061336
Bará S, Tapia CE, Zamorano J. Absolute Radiometric Calibration of TESS-W and SQM Night Sky Brightness Sensors. Sensors. 2019; 19(6):1336. https://doi.org/10.3390/s19061336
Chicago/Turabian StyleBará, Salvador, Carlos E. Tapia, and Jaime Zamorano. 2019. "Absolute Radiometric Calibration of TESS-W and SQM Night Sky Brightness Sensors" Sensors 19, no. 6: 1336. https://doi.org/10.3390/s19061336
APA StyleBará, S., Tapia, C. E., & Zamorano, J. (2019). Absolute Radiometric Calibration of TESS-W and SQM Night Sky Brightness Sensors. Sensors, 19(6), 1336. https://doi.org/10.3390/s19061336






